#tangent vector
Explore tagged Tumblr posts
Text
So at the moment, we're studying smooth manifolds in Riemannian Geometry before we actually get to do any Riemannian Geometry specifically. However, this means I've seen a lot of the stuff already because I'm reading Intro to Smooth Manifolds by Lee. At least that's what you'd think right? No it turns out my lecturer is using different notation for certain things and he's defining the tangent space via curves instead of derivations. Which ultimately means I have to remember two lots of constructions simultaneously and not accidentally use the stuff I've learnt in Lee in my Riemannian Geometry assignments/exam at the end
#it's not that bad#however I do prefer defining the tangent space as the space of derivations at p rather than using curves#cause I checked in the notes and the proof that it's a vector space takes nearly 3 pages#whereas you basically get it for free when using derivations#sure the advantage of the curves way is that they're more intuitive and geometric#but derivations are so nice to work with#maths posting#lipshits posts#project posting#kinda?#actually that gives me an idea for a poll
11 notes
·
View notes
Text
Hamiltonian mechanics is the feminine side of classical physics. Its masculine side is Lagrangian mechanics, formulated in terms of velocities (tangent vectors) rather than momenta (cotangent vectors). Lagrangian mechanics focusses on the difference of kinetic – potential energies; Hamiltonian mechanics focusses on their sum.
Richard Montgomery, reviewing a book by Stephanie Frank Singer and recalling lectures by Shing-Shen Chern
#Richard Montgomery#Stephanie Frank Singer#Shing-Shen Chern#Hamiltonian#Lagrangian#physics#science#feminine#masculine#vectors#momentum#cotangent#tangent#kinetic energy#potential energy#subtraction#addition#mathematics#maths#math#vector
61 notes
·
View notes
Text
You enjoyed flaunting it, Did you not~?
That adorable little brain of yours, all smug and quick, throwing around proofs and solving equations like it was nothing as if it made you special.
You were mid-sentence, some tangent about eigenvalues or some dirt like that, and I just tilted my head and whispered “Blank now.”
Just like that… it all started to slip
All the little cute symbols on the page stopped making sense first. You blinked, tried to reread them, but they just floated away, like leaves in the summer breeze~ Twisted into nonsense.
Next~ you forgot what the equation meant. What were you even trying to explain, little one~? You don't know. It's all just… Gone.
That gentle panic in your eyes as you realised what I took away, the power I hold over you~
Delicious. And now… look at you~ Mouth parted, Eyes foggy, trying so, so, so hard to hold onto something that isn't yours anymore.
You don’t get to be both clever and obedient. Hehe~ No… You get to kneel. You get to drool. You get to forget.
And next time, you feel like flaunting silly words like ‘vector’ or ‘matrix’ around like you are some kind of smart pet, you will feel that same sweet blankness drippingg into your mind~ Tugging you down.
deeep, deep down Into the lovely, helpless quiet where all your silly little thoughts belong…
With me~
100 notes
·
View notes
Text
Category theory has made us so accustomed to morphisms that it always feels wrong when a natural map isn't a morphism, at least not in the obvious category.
Like, take a manifold closed surface Σ. Write UTΣ for the "unit tangent bundle" of Σ, ie the space of unit vectors tangent to Σ. A loop γ in Σ gives a canonical loop (γ,γ') in UTΣ. Let's call that the lift of γ. So far so good.
It's natural to ask if this descends to homology. Let's take Z/2-homology to be simple. It actually doesn't, since any null-homotopic loop γ has γ' "do a full loop", so the homology class of the lift of a collection of null-homotopic loops depends on the parity of the number of loops.
But that's fixable. Let ζ be the homology class corresponding to a lift of a single null-homotopic loop. Then we do have a well-defined map φ: H_1(Σ) -> H_1(UTΣ) given by sending [γ] -> [(γ,γ')] - ζ. You can check that this is independent of representatives - you just play around with diagrams. The idea is that you're just measuring the "extra" spinning in γ', and ignoring the full turn that's necessary by yknow, being a circle.
This looks good! It's pretty natural, it sends 0 to 0, it feels very homomorphism like. But it's not! It satisfies φ(a+b) = φ(a) + φ(b) + (a•b)z, where �� is the intersection form. This is like, close enough to a homomorphism that you can work with it, but still! It goes against modern mathematical sentiments.
50 notes
·
View notes
Text
Design for autonomous maximus The great dome of iacon , vector sigma , and auntie vector sigma's avatar to the future
beneath the montain, vector sigma guided the transformers as their maternal god, and as society emerged around her resting place, the mountain came to life to protect it's mother computer by joining the autobots,
Remaining on the planet after vector Sigma's deactivation, it's said that autonomous maximus is still on cybertron to this day as its last autobot while his body became the basis for arks that Shepherd his fellow autobots off world



Deep bellow cybertron lay the allspark powered mother computer vector sigma, responsible for running the great machine that was cybertron, she sees the transformers as her children so she showered them with great love but infantilized them in her head as unable to do evil, so she did not act as their society corroded, secluded away in her chamber where she could gaze milions of years into the future, she guided cybertron's ecosystem into becoming a mechanical version of earth with robot animals and of course robot humans in the transformers, as she knew even back then that the unremarkable earth would play a great role in her children's history,

With her knowlege of the future she created messages put into the right places to allow her to comunicate wifh future generations she sees herself as a god but her nature is entirely mechanical, she doesn't even have a spark, and her ability to see the future is based on algorithms and what she already knows via the "sensory organs" of cybertron, so sometimes her messages spiral off into tangents and nonsense after having predicted the wrong response from her intended listener

In messages for earth, Vector Sigma uses an avatar called auntie as she sees earth as a sister to cybertron. Though its residents aren't fully on board with the idea, it's like that aunt or uncle you barely know that acts way too chumy with you in a way that's off-putting rather than charming,

Above her chamber stood the city of iacon, greatly respected, but over the years, it became the house of all corruption on cybertron as the functionist council excavated it's great dome to act as their captital. The building itself shackled as iacon grew into a massive metropolis, and all the spilled energon that naturally came from its massive population threatened to bring the building to life,
when the revolution tore down the government, the restrains were destroyed, and the building began reformating itself with a robot mode just as megatronus and liege maximo revealed their aliance with bruticus maximus. But before they could end the autobots with their opening assault autonomous maximus awakened, and in a split second decision, protected the autobots from harm with a single mighty punch

With the newly christened decepticons retreating, the autobots named themselves after the giant that saved them and over the course of the next milenia civil war between the autobots and decepticons raged until the two sides had captured so much terrain and became so diferent from each other they were separate nations, nations whose war plundered cybertron and the world off of it's resources until the planet was spent.
The autobots omit this part of the story, but it was the autobots who took the allspark and tossed it into space to keep it away from the hands of the decepticons, quickly regretting that action as the planet died around them, the part they do tell is that the surviving transformers hid away inside titans like autonomous maximus, overcome with the weight of sins on their back, they began to construct arks to search for the allspark, all based on autonomous maximus' design, each housing three great titans
While maximus himself opted to stay behind on cybertron. Loyal to it's mother above all even as her lifeless husk hung from the celling of her chamber, to give the arks power to lift off prima used the star saber to gather celestial power into the arks, dissipating her body entirely, while maximus fought off the decepticons wishing to attack the arks,
or at least thats what they tell you. Even a most basic analysis of the story would tell you the decepticons obviously also wanted to escape the planet, meaning the ancient autobots were willing to let their enemies die from their own atrocity. What could have happened to turn a culture like any other with its complexities and grey morality into heroes?
Guilt. With the fall of cybertron, the autobots became suicidal, and their leaders had to turn that self-destructive impulse into the service of others, ideas that permiated autobot ranks to this day, as new generations were born aboard the ships, that initial melancholy faded away as the new faces never stepped foot on cybertron,
but from the moment they came online, the autobots were taught to live for the well-being of others as their number one priority, till all are one, drilling that message into their heads is their society's one goal, as with anything their sucess rate varies (see barricade). While their search for the allspark became myth, then legend,
It was in that world that our autobots, natives of ark primax came from, and that leads us to today, with them telling the story to the earth's own population of transformers, most are skeptical of certain aspects of the tale, but the mistress of flame is enchanted by their story, dispite their claims otherwise, easily becoming part of her view of cybertronians as gods

#transformers#transformers fanart#cybertronian#robot#robots#character design#autobots#maccadams#maccadam#transformers from a to z#autonomous maximus#the last autobot#the autobot ark#transformers kingdom#iacon#iacon city#vector sigma#auntie#transformers marvel#auntie looking like shodan is very intentional#ominious hehehe
46 notes
·
View notes
Note
this might be silly but i was talking with my friend abt yulia and andrey arguing about philosophy/ideology (both designers but oh so vastly different ideologically) and it made me think about farkhad and if he truly would have been a utopian if he were alive….
thoughts?
okayyyy my fave ^_^ as far as my #thoughts go :
the Utopian faction depends on/of the Polyhedron¹. the only two that don't "fit the bill" are Mark Immortell (his deal = metanarrative existence, so it does fit the bill) and Vlad the Younger (his deal = doesn't show up okayyy but also = escape on the Upwards vector from pull into the Downward [his well]). The twins have built it, for the Kains it is a seashell for the pearl of the soul, it is a house, it is an attic, it is a womb, it is a nest, it is [...] it is the spear that is stretched between the grip of the past and the ribcage of the future, or vice versa, the present's the weapon. or whatever. for eva it is a miracle she so loves, a proof of the transcendance of the soul she will try to seek until (through) her death. alright? now, and this is only my belief, as iirc there's no explicit word on this, but as far as my #thoughts go:
Farkhad was killed before the Polyhedron was built. Farkhad was killed before the polyhedron was built; therefore, he cannot be of the faction that worships it as a soul as a cathedral as a shell as a child as a bird as a weapon. it is my intimate belief he was murdered before the polyhedron was built ; because (the twins thought) the polyhedron would not be built with him alive, could not be built with him alive, did not want to be built with him alive. in my mind, he was an active obstacle to its construction.
¹ this is not to say there couldn't be, or couldn't have been, an Utopian faction (or a Utopia at all) without a Polyhedron ; just that, as far as the narrative goes, the Polyhedron is the... glue that holds it together. it's the.... pardon the pun....... beating heart of the Utopian(s) (faction).
and even if, other option, he was killed after her construction : i believe in that case he would have been killed because he did not worship it as a bird as a cage as a weapon as a womb. his and the twins' "artistic different", in no small part, would have been about this; a culmination, of course, but this nonetheless.
in the first case, farkhad could not have been an utopian in life, for he was killed before the idol of utopian thought was built. in the second, farkhad would have not been an utopian either in life or death, for in my mind it is a disagreement over IN SOME PART the polyhedron that got him murdered.
in my mind it is important that he be un-aligned. narratively: he's un-aligned because he's dead. his potential alignment has been taken from him/from our eyes, about him because he was killed; the fact that he was murdered, then buried under a name that the twins have given him, means that they are in sole control of his narrative presence and existence (and that's personally what i looove to fuck around with : him existing as pockets of his own self-contained presence and existence, slipping away from the twins' grasp. in the canon where "the victors write history" [here, the twins writing his], the...... post-canon, meta-canon, peri-canon para-canon whatever it is you want to call it farkhad is like if history [written as a legend or a myth] was sentient. this was a long tangent)
he's un-aligned because he is a manifestation of something beyond man (person). he's un-aligned because he is a spear in the twins' flank.
what was i about? oh yeah
he's un-aligned because House of Atreus 🫵 marred by the eating of man and the killing that followed 🫵 you are porous with hatred, permeable with a curse that shall steep over the unattended hearth 🫵 you are a wooden box, your inhabitants termites biting their way through you, out of you 🫵 you are what will still stand once the curse has claimed all, for it cannot claim you: without hands, you cannot kill.
#SMILES VERY WIIIIIDE THANK YOU FOR ASKING#newtfvcker#farkhad pathologic#farkhad lore#allô (answers)
24 notes
·
View notes
Text

Wip of the witch from Kin no Tori. I’ll vector soon and fix the major tangent.
38 notes
·
View notes
Photo

Transformers: Mosaic #618 - "I Will Be A God!"
Originally posted on September 12th, 2011
Story - Wout Jut Art - Philip Knott Colours, Letters - Sam Palmer
deviantART | Seibertron | TFW2005 | BotTalk
wada sez: Wout Jut explained on deviantART: “The story is about the captured Megatron by the evil Optimus Prime. Optimus needed him to find the Key of Vector Sigma, so he can open a special gate. This gate brings you to other dimensions. It's also a little tribute to Stargate SG1.” On Seibertron, he went into more detail to explain why Megatron and Galvatron are separate individuals here: “I'm a big fan of Shattered Glass. Read the comic drawn by The Don and read Reunification. Loved that story. But I was sad about how simple Megatron died and how he became Galvatron. Like Gen1 has many universes, this universe is just a variant of the S.G universe. Things are just a little bit different. Since the IDW Galvatron I've hoped to see that the explanation was that they where brothers. Never happened. So I've took a little freedom and made them in the SG universe brothers. Still, It could happen that I maybe write a story where Galvatron is killed and later on that Megatron will be Galvatron. But maybe that's to much. A idea I've got this morning.” Many readers were confused by the inset panel of Optimus Prime pressing a button, as the control panel has an unfortunate tangent with Galvatron’s back, making it seem as if an unseen figure is pressing a button on Galvatron’s back. Philip Knott independently colored his own artwork, sharing it online as an alternate version; see below for that. Jut later re-released the strip with his own lettering, changing the dialogue slightly in the process; you can find that below as well, along with a huge swathe of behind-the-scenes material.


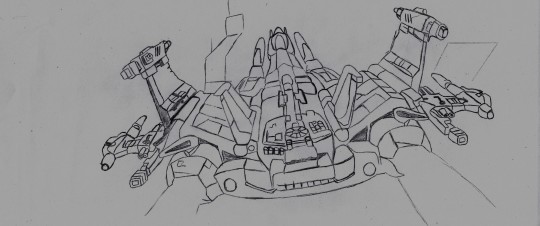







#Transformers#Transformers Mosaic#Maccadam#Shattered Glass#Shattered Glass Comics#Wout Jut#Philip Knott#Sam Palmer#Optimus Prime#Megatron#Galvatron
40 notes
·
View notes
Note
In principle a teleporter who conserves momentum could survive a long fall by teleporting to exactly the opposite side of the planet, then back again once they reached the peak of their arc. I think this is a very funny image in its own right.
It is! I laughed.
It does require certain assumptions about how the system of teleportation conceptualizes the arrangement of spacetime which make me anxious, though.
If your motion is contemplated as being on an absolute plane then the two 'downs' are opposite and cancel each other out. Which is easy to visualize, but it also puts you in grave danger of not having your speed and vector matched to that of the planet anymore in your new position and flying off on a 66k+mph tangent into the void of space. Or into the ground, depending. And that's just considering the rate of orbit around the sun, not the rotation of the galaxy etc.
I think that is too scary, and my teleportation system will coordinate relative to the gravity wells of planets whenever possible rather than trying to do advanced spaceship math every time I go anywhere. I would definitely die.
#ask#hoc est meum#Anonymous#all my hypothetical superpowers are glitched by my overthinking the physics impliations#i know just enough about so many topics to be elaborately dumb about them#svsss#indirectly#physics#teleportation
53 notes
·
View notes
Text
pulling up to this exam knowing that the tangent vector of the akuarch curve in r3 points to my dick. and nothing else
6 notes
·
View notes
Text
So I'm currently reading about tangent spaces and the differential of a smooth map and it's got me thinking, given a manifold M and a point p in M, is Tₚ a functor from the category of smooth manifolds and smooth maps to the category of vector space and linear maps? Or at least is there a functor related to this stuff?
Because smooth maps induce linear maps on tangent spaces and those maps respect the identity and the composition of smooth maps
#they were right. once you start learning category theory you start seeing it everywhere#maths posting#lipshits posts#new tag:#project posting#for my thoughts relating to my project and for more explanation-y posts I do that relate to my project#maths#mathblr#mathematics#math
13 notes
·
View notes
Text
the cotangent bundle (differential forms) is the feminine side of calculus-on-manifolds; the tangent bundle (vector-fields) is the masculine side.
Shing-Shen Chern, via Richard Montgomery
#Shing-Shen Chern#Richard Montgomery#Stephanie Frank Singer#differential forms#cotangent#bundles#vector bundle#tangent bundle#masculine#feminine#mathematics#differential geometry#physics#mechanics#maths#math#calculus#manifolds
35 notes
·
View notes
Text

…Man, the terminal does not like these messages, huh?
THE SIGNAL IS TANGENT TO NORMAL VECTORS.
Whuzzat mean?
I DON’T LIKE IT EITHER.
Pff. Okay, then, go ahead and scrap this one before we transmit. I’ve got the important bits here. Funny guys, those ones.
—————
…TRANSMITTING.
Alright! Sorry, had some confidentials to peruse— adding to the record, though, that we’ve identified a blinkspace anomaly at Annapurna Gate, roughly… eight minutes? Seriously?— yeah, eight minutes after the presumed kidnapping of AIP Abdullah. Now, I’m ringing the station manifest to see if anything was lost in that anomaly, but I’m gonna be surprised if she was there. Kaletka’s eight days out by nearlight.
TELL ME THAT MEANS NOTHING.
Don’t step on my line, you sly dog, I’ll step on yours. It CAN’T mean nothing.
Add it to the narrative, bud.
-BREAKFAST
…
[213.64H] AGO, NOAH ABDULLAH TRANSMITTED A DISTRESS-READY SIGNAL FROM IMPLANTED OMNI TRANSPONDER TO HESTIA-CLASS NHP “RENNES” FROM SOMEWHERE IN THE SUB-CAPITAL CITY OF NADUS, ESCHERI PROVINCE— KALETKA. FOUR MINUTES LATER A STAND-DOWN ORDER WAS GIVEN— SEVEN MINUTES FURTHER, AND A LOW-PRIORITY PING REACHED RENNES FROM LATENT SES MONITORING CHANNELS.
SOMETIME IMMEDIATELY FOLLOWING, RENNES’ SUBJECTIVITY WAS FORCIBLY DECLAWED. CONTACT WITH N. ABDULLAH LOST FROM THIS PERIOD TO [8.11H] AGO; N. ABDULLAH SIGHTED DISEMBARKING A SHUTTLE ONTO ANNAPURNA BLINK GATE, WHERE A BLINKSPACE ANOMALY WAS RECORDED EIGHT MINUTES AFTER LAST KNOWN CONTACT.
WE MUST LEARN MORE.
#lancer NHP#Los voladores#union administrative department#lancer ttrpg#pilot oc#oc rp#{gonna be in training for a while so leaving this sit for now}
6 notes
·
View notes
Text
Euler Class and Euler Characteristic
This is a follow-up to this post from November. Or more of a redo - I really didn't like how that turned out. Way too detail-focussed, and it didn't even get to the Euler characteristic.
So, this time, we'll take a different tack. As a reminder, here's the idea. Take a smooth closed m-manifold M. Often, if there's some property of M, we like to rephrase it as a property of the tangent bundle TM, and then see if it generalises to other vector bundles, like you can do for orientation. The aim here is to do that for the Euler characteristic.
Prerequisites: being comfortable enough with homology and cohomology, and e.g. sections of vector bundles. I think the most hard-core anything really gets is Poincare(-Lefschetz) duality, and the Kunneth theorem. In particular, I write the Kunneth pairing on cohomology H*(X)⊗H*(Y) -> H*(X×Y) as (a,b) -> a×b. Prewarning that this is fairly long.
Motivating Examples
Let's just take the easiest examples: S¹, S², and S³. Χ(S¹) = χ(S³) = 0, while χ(S²) = 2. What else is non-trivial in the S² case? The tangent bundle! In fact, it's a nice exercise to see that (by stereographic projection on fibres), TS² = S²×S² \ Δ, where Δ is the diagonal. Is there an easy way to see where the 2 comes from? Well, think about sections, i.e. vector fields. Both S¹ and S³ have non-zero sections - in particular, a generic section has 0 signed intersection number with the zero-section. The algtop student's favourite result, the hairy ball theorem, says that this isn't true for S². In fact, a generic section meets the zero section twice, or a generic vector field has two zeros, at the two "tufts of hair".
So we conjecture: the Euler characteristic is the number of signed intersections of a generic section with the zero section. In fact, it's a classical (?) theorem that a closed manifold M has a non-zero vector field iff χ(M) = 0. But we won't assume this.
Algebraifying and Generalising
The standard definition of the Euler characteristic as the alternating sum of ranks of (co)homology suggests that we want to codify this in terms of algebraic topology. So let's do that. Writing s : S² -> TS² for the generic section, and 0 for the zero section, [s⁻¹(0)] ∈ H₀(M;Z) is the signed number of self-intersections, up to some choice of generator. To help fix a generator, we need an orientation. Thus, we'll pass to a generic coefficient ring R, and assume M is R-oriented, with fundamental class [M]. To actually get a honest-to-god element of R, we actually define the Euler class e(M;R) ∈ Hᵐ(M;R) to be the Poincare dual of [s⁻¹(0)]. Then our conjecture is that the R-valued Euler characteristic χ(M;R) is the Kronecker pairing ⟨e(M;R), [M]⟩ of the Euler class. I'm gonna stop writing coefficients now.
But wait! This definition already didn't depend on our choice of vector bundle. If E -> M is any rank-m vector bundle, [s⁻¹(0)] ∈ H₀(M) is (almost) the number of signed intersections of s with the zero-section, and we can define e(E) ∈ Hᵐ(M) to be the Euler class of E. Then maybe we can ask what ⟨e(E), [M]⟩ is telling us. At the end, we'll also define it for arbitrary rank, but that's a little harder at this point.
The Thom Class, sort of
[s⁻¹(0)] is a bit of a pain algebraically. But actually so are vector bundles: since E deformation retracts onto M, we can't distinguish between vector bundles using homology. Instead, the standard trick is as follows. By choosing some metric, we can construct the disc bundle D(E), which is just the unit disc in each fibre. This is now compact, with boundary the sphere bundle S(E). And although the homology of D(E) only depends on M, the homology of the pair (D(E), S(E)) actually does depend on E! Exercise: if M = S¹ and E is the trivial bundle, show that D(E)/S(E) is homotopy equivalent to the wedge sum S¹ v S²; if E is the non-trivial bundle, then D(E)/S(E) is RP².
Ok, so let π : D(E) -> M be the projection, and let u' = π* e(E) ∈ Hᵐ(D(E)). Abuse notation and view M as a subspace of D(E) by the zero section, and let u ∈ Hᵐ(D(E),S(E)) be Poincare dual to [M]. Equivalently, since all sections are homotopic, u is Poincare dual to any section.
Then [s⁻¹(0)] = π_∗( [M ∩ s(M)]). Intersection is Poincare dual to the cup product, so
[M ∩ s(M)] = (u ⌣ u) ⌢ [D(E),S(E)] = u ⌢ [M,S(E)].
Alternatively, naturality of the cap product says that
[s⁻¹(0)] = e(E) ⌢ [M] = π_∗ ( u' ⌢ [M] ).
But since π_∗ is an isomorphism, as is capping with [M] or [M,S(E)], we get that u' is just the restriction of u. (If you're not super comfortable with relative classes, this is basically saying that u' is the "absolute" and u is the "rel boundary" version of the same thing.) This class u is called the Thom class of the vector bundle.
To summarise so far: if u is Poincare dual in D(E) to the zero section, and e(E) is Poincare dual in M to the preimage s⁻¹(0) of the zeros of a generic section, then the restriction u' ∈ Hᵐ(D(E)) is the same as the pullback π* e(E). Maybe this isn't super exciting, but u and u' seem easier to work with then e(E) does.
The Thom Isomorphism, sort of
This is very much not the usual construction of the Thom class, since it relies on Poincare(-Lefschetz) duality, so on the base space of the bundle being a closed manifold. In fact, the Thom class exists for any R-oriented vector bundle on an arbitrary CW complex (or even paracompact topological space!). There, it is usually defined as the unique class in Hᵐ(D(E),S(E)) such that, when restricting to each fibre, the it gives the R-orientation.
Let's show that such a class v exists. The previous post does it in detail, but the basic idea is that a CW structure of M induces one on D(E)/S(E), with one (i+m)-cell for each i-cell in M, and an extra 0-cell coming from the point S(E)/S(E). Then for any point in M, we can choose it to be a 0-cell, and if M is connected, the only 0-cell. So Hᵐ(D(E),S(E)) = R, and it is generated by something that generates the orientation over that point. But the point was arbitrary, so the generator restricts to the R-orientation on any fibre. We then choose v to be the generator.
The main point for us is that we have the following isomorphisms:
R = H⁰(M) -> Hᵐ(D(E),S(E)) -> Hₘ(D(E)) -> Hₘ(M).
This takes 1 to the Thom class v, then to the Poincare dual of v, then to some generator, which by following orientations is [M]. In particular, the Thom class v is exactly what we called u earlier! Thus u isn't just the Poincare dual of the zero section, it's also the unique class that restricts on fibres to give the orientation.
Diagonal Maps Are Often Useful
This next step might seem like it's coming out of nowhere, but it's a super useful trick that you almost certainly will see again. Let ∆ : M -> M×M be the diagonal map. Then TM is canonically isomorphic to the normal bundle NM by (x,v) -> ((x,x),(v,-v)). So we might as well think about e(NM) rather than e(M). For notational ease, I'll write E for some open tubular neighbourhood of Δ(M), thought of as the normal bundle. Then D(E) is just some smaller closed tubular neighbourhood, and Hᵐ(D(E),S(E)) = Hᵐ(M×M, M×M\∆) by excision. Restricting again to Hᵐ(M×M), write u'' for the image of the Thom class. Now e(M) = e(E) = ∆*(u''), so if we can understand u'', we should be ok.
The Slant Product, sort of
Instinctively, u'' is symmetric about the diagonal. Rigorously, this means that (1×α) ⌣ u'' = (α×1) ⌣ u'' for any cohomology class α ∈ H*(M). To prove this, basically observe that the two projections M×M -> M agree on the diagonal, so are homotopic on a small tubular neighbourhood, so induce the same map on cohomology. I'll leave the details as an exercise. So to compute u'', it might be useful to look at something that breaks the symmetry.
We have one map H*(M×M) -> H*(M), by ∆*. But this treats both components the same - can we find one that treats them differently? Sure! We can define μ: H*(M×M) -> H*(M) as follows. If φ ∈ Hʲ⁺ᵐ(M×M), then μ(φ) evaluates on simplices by eʲ -> φ(eʲ×[M]). For lower rank, μ(φ) = 0. This isn't a ring homomorphism, but it is linear. Two key facts to observe about this: for α ∈ Hʲ(M), β ∈ Hᵐ(M), and γ ∈ Hᵏ(M×M),
μ(α × β)= α ⟨β,[M]⟩ and μ((α × 1) ⌣ γ) = α ⌣ μ(γ).
The first condition captures the asymmetry in the definition; the second is an analogue of being a ring homomorphism.
Intuitively, μ sorta "divides by M on the right", so it seems like a good candidate for something that breaks symmetry. Also, since u'' is kinda just built from one copy of [M], maybe μ(u'')=1?
Field Coefficients
So let's compute! Fix a 0-simplex p. μ(u'') evaluates on it like u'' evaluates on p×[M], which by definition of u'' is how the Thom class u evaluates on the pushforward of p×[M] into Hₘ(M×M, M×M\∆) = Hₘ(D(E),S(E)). But under this pushforward, p×[M] is homologous to the fibre over p, and in a way that agrees with the orientation. Hence u evaluates to 1, since the fibre-restrictions of u generate the orientation. And since it evaluates to 1 on any 0-simplex, it's just 1 ∈ H⁰(M).
Quick recap of what's just happened: first, we moved from e(E) to the Thom class u. Now, we've moved to some symmetric u'' in Hᵐ(M×M), and defined a relatively well-behaved, asymmetric map μ that sends u'' -> 1. The aim will be to use μ to control what u'' can be, and hence what e(E) is.
We're going to assume that R is a field for a moment. This is just so that H*(M×M) = H*(M)⊗H*(M). In particular, for any basis {bᵢ} for H*(M), we can write u'' = Σ bᵢ×cᵢ, for some cᵢ.
Recall that (1×bᵢ) ⌣ u'' = (bᵢ×1) ⌣ u''. I didn't just mention that for no reason - let's apply μ to both sides. On the RHS, we get
μ((bᵢ×1) ⌣ u'') = bᵢ ⌣ μ(u'') = bᵢ.
This makes sense - μ is removing the [M] on the right, and since we know u'' is ~just one copy of [M]~ in some sense, the only thing left is the bᵢ on the left.
On the LHS, it's more complicated, since we're adding things to the right. Expanding, we get
Σ (-1)^{dim bⱼ} μ(bⱼ × (bᵢ ⌣ cⱼ)) = bᵢ.
By considering bases, we get that ⟨bᵢ ⌣ cⱼ, [M]⟩ = (-1)^{dim bⱼ} if i=j, and 0 or undefined otherwise.
Remember that e(M) = ∆*(u'') = ∆*(Σ bᵢ×cᵢ) = Σ bᵢ ⌣ cᵢ. So pairing with [M] gives exactly Σ (-1)^{dim bᵢ} = Σ (-1)ᵏ dim Hᵏ(M) = χ(M). Which is exactly what we wanted! The Euler characteristic is the pairing of the Euler class with the fundamental class.
This can seem almost magical, or in less kind words, unmotivated. But maybe here's another way to think of it. For any basis {bᵢ}, we can construct a dual basis b'ᵢ, such that ⟨bᵢ ⌣ b'ⱼ, [M]⟩ = δᵢⱼ is the Kronecker delta. In the notation above, b'ᵢ = (-1)^{dim bᵢ} cᵢ . Then u'' = Σ (-1)^{dim bᵢ} bᵢ × b'ᵢ. The fact that this sum gives u'' is kind of saying that u'' contains all of M, but is symmetric so also contains the dual. That's my intuition anyway. The fact that it really does just give the Euler characteristic is slightly magical, since it relies on the alternating sum showing up perfectly.
PID Coefficients
For a general PID, we fix this by just passing to the field of fractions. χ(M) is the same, and you can follow through our construction to check that e(M) and [M] are too. So once again, ⟨e(M), [M]⟩ = χ(M). For NON-PAID coefficients Kunneth fails, so it wouldn't surprise me if this failed to. But realistically who cares.
General Vector Bundles
Everything we did here was for rank-m bundles. But all of it basically works for arbitrary rank-k bundles, at least for m≥k. In this case, M ∩ s(M) has dimension m-k, so e(E) ∈ Hᵏ(M). Now it can't really be thought of as a number in any meaningful way, but it's still cool that we can think of it as a generalisation of the Euler characteristic!
For k>m, we just say e(E) = 0, since it ought to live in Hᵏ(M)=0. Slightly disappointing.
What Does e(E) Tell Us?
Here's the most often cited example, and our original motivation. If E admits a non-zero section, then e(E) = 0.
Proof: suppose s : M -> E\M is the section, and write i : E\M -> E for the inclusion. Then πis : M -> M is the identity map. π^*e(E) = u' by definition, so (πi)*e(E) = i* (u') = 0, since u' is the restriction of a relative class. So (πis)*e(E) = e(E) = 0.
You might think this is less helpful than the fact we started with, that a closed manifold M has a non-zero vector field iff χ(M;Z) = 0, since saying e(E) = 0 assumes we have a coefficient ring R such that E is R-oriented, whereas the theorem lets us use integral coefficients. However, nothing like that theorem is true for arbitrary vector bundles (or bundles on general CW complexes), when the Euler class is the best we have. So like all good generalisations, it does lose some information.
10 notes
·
View notes
Note
hi, I'm attracted to my crush Heizou like the earth is attracted to the sun— with a large force inversely proportional to the distance squared. He's the sin(90) 4 me. If we we're to be convertices, i wanna be the second convertex. to assure you that at the end of the line, i'll be there waiting for him. these formulas describe how much x²-1, if the value of x is 12. sin (π/2 – A) = cos A & cos (π/2 – A) = sin A
sin (π/2 + A) = cos A & cos (π/2 + A) = – sin Asin (3π/2 – A) = – cos A & cos (3π/2 – A) = – sin A sin (3π/2 + A) = – cos A & cos (3π/2 + A) = sin A sin (π – A) = sin A & cos (π – A) = – cos A sin (π + A) = – sin A & cos (π + A) = – cos A sin (2π – A) = – sin A & cos (2π – A) = cos A sin (2π + A) = sin A & cos (2π + A) = cos A. before seeing him, my heart is a nul set, but when a vector of magnitude from his eyes at a deviation of theta radians made a tangent to my heart, it differentiated. whenever I see him, it was like, I was electrocuted with an amount of 200-1700 volts of electricity. my love for him is like the derivative of e^x, it remains constant and never change. my baby, 1+tan2A = sec2A sec2A – 1 = tan2A (1/cos2A) -1 = tan2A. putting the value of cos A = ⅘.
(5/4)2 – 1 = tan2 A tan2A = 9/16 tan A = 3/4 (sin30° + cos30°) – (sin 60° + cos60°)
= ½ + √3/2 – √3/2 – ½ = 0 If cos A = 4/5, then tan A = Cos A = ⅘. my love for him is a quadratic equation with real roots, which only he can solve by making good binary relation with me. the cosine of my love for you extends to infinity. Baby, simplify 4x³+3x²+3x-1 where x=3. and he'll know what my heart says. He is an essential to me as an element to a set. the geometry of my life revolves around his acute personality. sin(2x) = 2sin(x) • cos(x) = [2tan x/(1+tan2 x)]cos(2x) = cos2(x)–sin2(x) = [(1-tan2 x)/(1+tan2 x)] cos(2x) = 2cos2(x)−1 = 1–2sin2(x)
tan(2x) = [2tan(x)]/ [1−tan2(x)] sec (2x) = sec2 x/(2-sec2 x) csc (2x) = (sec x. csc x)/2. my baby, when he solves this equation for "i" .

hiiii pookie how are you? i hope you're doing well!!!! kiss kiss/p
i'm not sure if this is a copypasta or not, but if it's not, that's extremely impressive and you're super smart hahahahahaha!!!
i'm doing as good as i can lol hopefully you slept well, i'm answering this after ur regular hours
15 notes
·
View notes
Note
What are your thoughts on education as a whole if you're pro school abolition? Doesn't that just make child abuse much easier to hide?
so something that i encounter a lot, is that school abolition necessitates family abolition, but a lot of people coming to school abolition do not know this and imagine, like, the way children are currently raised in society, just without schools. and i would agree that this would be terrible and make child abuse easier to both perform and to hide! but i think this is a function of the family unit--that the family unit, as it currently exists, is the single most effective structure to perpetuate child abuse, and that it is in and of itself psychologically damaging to children raised in it.
for a short and accessible primer on family abolition, i suggest taking a look at towards the abolition of the family. (note: i have a lot of foundational disagreements with lee shevek overall, and reccing this is a real "critical support" situation. it's the only clear, accessible introductory work i can find on family abolition, but all this means for me is that i desperately need to get my ass in gear and write my own one day, because i wince every time i link someone to a piece by lee "longform essays defending the practice of lynching people accused of rape" shevek. that's a tangent tho.)
anyway, you can also check out the entire NO! against adult supremacy series for a more all-encompassing and holistic set of writings dealing with school abolition and child abuse; there's abt 20 collections of essays so far, with each collection featuring a variety of authors writing on a wide variety of youth-liberation-related topics, and the majority of them deal with the two primary vectors of abuse children face in the modern world: the family and the school.
40 notes
·
View notes