#vector space linear algebra

[lipshits-continuous]

Let ℱ:={Fⁿ:n∈ℕ₀}/≅, where Fⁿ is the free group of rank n and F⁰:={e}, and let ∗:ℱ×ℱ->ℱ be the free product. Then (ℱ,∗) is a monoid. Moreover, (ℱ,∗) is isomorphic to (ℕ₀,+).

I have omitted the proof of the last claim because it isn't the main point of the proof and I currently only have half a proof for it. I will most likely post the proof once I have it though! (I'm doing it from scratch from a hint my lecturer gave about considering Hom(Fⁿ,ℝ))

[algebraic-dumbass]

this might be a dumb question but like. how do you learn math without a class/curriculum to follow. i have a pretty solid calculus understanding and I want to pursue more advanced math but like im not sure where to start. what even is like category theory it sounds so cool but so scary???. do you have any recommendations on specific fields to begin to look into/whether its best to learn via courses or textbooks or lectures/etc.? any advice would be super appreciated!! dope blog by the way

thanks for the compliment!

first of all it's not a dumb question. trust me i'm the algebraic-dumbass I know what I'm talking about. okay so uh. how does one learn math without a class? it's already hard to learn math WITH a class, so uhhh expect to need motivation. i would recommend making friends with people who know more math than you so you have like, a bit more motivation, and also because math gets much easier if you have people you can ask questions to. Also, learning math can be kind of isolating - most people have no clue what we do.

That said, how does one learn more advanced math?

Well i'm gonna give my opinion, but if anyone has more advice to give, feel free to reblog and share. I suppose the best way to learn math on your own would be through books. You can complement them with video lectures if you want, a lot of them are freely available on the internet. In all cases, it is very important you do exercises when learning: it helps, but it's also the fun part (math is not a spectator sport!). I will say that if you're like me, working on your own can be quite hard. But I will say this: it is a skill, and learning it as early as possible will help you tremendously (I'm still learning it and i'm struggling. if anyone has advice reblog and share it for me actually i need it please)

Unfortunately, for ""basic"" (I'm not saying this to say it's easy but because factually I'm going to talk about the first topics you learn in math after highschool) math topics, I can't really give that much informed book recommendations as I learned through classes. So if anyone has book recommandations, do reblog with them. Anyways. In my opinion the most important skill you need to go further right now is your ability to do proofs!

That's right, proofs! Reasoning and stuff. All the math after highschool is more-or-less based on explaining why something is true, and it's really awesome. For instance, you might know that you can't write the square root of 2 as a fraction of two integers (it's irrational). But do you know why? Would you be able to explain why? Yes you would, or at least, you will! For proof-writing, I have heard good things about The Book of Proof. I've also heard good things about "The Art of Problem Solving", though I think this one is maybe a bit more competition-math oriented. Once you have a grasp on proofs, you will be ready to tackle the first two big topics one learns in math: real analysis, and linear algebra.

Real analysis is about sequences of real numbers, functions on the real numbers and what you can do with them. You will learn about limits, continuity, derivatives, integrals, series, all sorts of stuff you have already seen in calculus, except this time it will be much more proof-oriented (if you want an example of an actual problem, here's one: let (p_n) and (q_n) be two sequences of nonzero integers such that p_n/q_n converges to an irrational number x. Show that |p_n| and |q_n| both diverge to infinity). For this I have heard good things about Terence Tao's Analysis I (pdf link).

Linear algebra is a part of abstract algebra. Abstract algebra is about looking at structures. For instance, you might notice similarities between different situations: if you have two real numbers, you can add them together and get a third real number. Same for functions. Same for vectors. Same for polynomials... and so on. Linear algebra is specifically the study of structures called vector spaces, and maps that preserve that structure (linear maps). Don't worry if you don't get what I mean right away - you'll get it once you learn all the words. Linear algebra shows up everywhere, it is very fundamental. Also, if you know how to multiply matrices, but you've never been told why the way we do it is a bit weird, the answer is in linear algebra. I have heard good things about Sheldon Axler's Linear Algebra Done RIght.

After these two, you can learn various topics. Group theory, point-set topology, measure theory, ring theory, more and more stuff opens up to you. As for category theory, it is (from my pov) a useful tool to unify a lot of things in math, and a convenient language to use in various contexts. That said, I think you need to know the "lots of things" and "various contexts" to appreciate it (in math at least - I can't speak for computer scientists, I just know they also do category theory, for other purposes). So I don't know if jumping into it straight away would be very fun. But once you know a bit more math, sure, go ahead. I have heard a lot of good things about Paolo Aluffi's Algebra: Chapter 0 (pdf link). It's an abstract algebra book (it does a lot: group theory, ring theory, field theory, and even homological algebra!), and it also introduces category theory extremely early, to ease the reader into using it. In fact the book has very little prerequisites - if I'm not mistaken, you could start reading it once you know how to do proofs. it even does linear algebra! But it does so with an extremely algebraic perspective, which might be a bit non-standard. Still, if you feel like it, you could read it.

To conclude I'd say I don't really belive there's a "correct" way to learn math. Sure, if you pursue pure math, at some point, you're going to need to be able to read books, and that point has come for me, but like I'm doing a master's, you can get through your bachelor's without really touching a book. I believe everyone works differently - some people love seminars, some don't. Some people love working with other people, some prefer to focus on math by themselves. Some like algebra, some like analysis. The only true opinion I have on doing math is that I fully believe the only reason you should do it is for fun.

Hope I was at least of some help <3

[canmom]

it's feedback loops and dynamical systems and entropy and linear algebra every time. whole damn universe made of stacking vector spaces on top of other vector spaces. spice with logarithms to taste

[tensorboi]

Why is the Pythagorean theorem true, really? (and a digression on p-adic vector spaces)

ok so if you've ever taken a math class in high school, you've probably seen the Pythagorean theorem at least a few times. It's a pretty useful formula, pretty much essential for calculating lengths of any kind. You may have even seen a proof of it, something to do with moving around triangles or something idk. If that's as far as you've gotten then you are probably unbothered by it.

Then, if you take a math class in university, you'll probably see the notion of an abstract vector space: it's a place where you can move things and scale them. We essentially use these spaces as models for the physical space we live in. A pretty important thing you can't do yet, though, is rotate things or say how long they are! We need to put more structure on our vector spaces to do that, called a norm.

Here's the problem, though: there are a *lot* of different choices of norm you can put on your vector space! You could use one which makes Pythagoras' theorem true; but you could also use one which makes a³ + b³ = c³ instead, or a whole host of other things! So all of a sudden, the legitimacy of the most well-known theorem is called into question: is it really true, or did we just choose for it to be true?

And if you were expecting me to say "then you learn the answer in grad school" or something, I am so sorry: almost nobody brings it up! So personally, I felt like I was going insane until very recently.

(Technical details: the few that do bring it up might say that the Pythagorean norm is induced from another thing called an inner product, so it's special in that way. But also, that doesn't really get us anywhere: you can get a norm where a⁴ + b⁴ = c⁴ if you are allowed to take products of 4 vectors instead!)

How is this resolved, then? It turns out the different norms are not created equal, and the Pythagorean norm has a very special property the others lack: it looks the same in every direction, and lengths don't change when you rotate them. (A mathematician would say that it is isotropic.) Now, all of a sudden, things start to make sense! We *could* choose any norm we like to model our own universe, but why are we going to choose one which has preferred directions? In the real world, there isn't anything special about up or down or left or right. So the Pythagorean norm isn't some cosmic law of the universe, nor is it some random decision we made at the beginning of time; it's just the most natural choice.

But! That's not even the best part! If you've gone even further in your mathematical education, you'll know about something called p-adic numbers. All of our vector spaces so far have been over the field of real numbers, but the p-adic numbers can make vector fields just as well. So... are the Pythagorean norms also isotropic in p-adic spaces? Perhaps surprisingly, the answer is no! It turns out that the isotropic norms in p-adic linear algebra are the ∞-norms, where you take the maximum coordinate (rather than summing squares)! So the Pythagorean theorem looks very different in p-adic spaces; instead of a² + b² = c², it looks more like a^∞ + b^∞ = c^∞.

If you're burning to know more details on this, like I am right now as I'm learning it, this link and pregunton's linked questions go into more details about this correspondence: https://math.stackexchange.com/questions/4935985/nature-of-the-euclidean-norm

The interesting thing is that these questions don't have well-known answers, so there is probably even more detail that we have yet to explore!

tl;dr: the pythagorean theorem is kind of a fact of the universe, but not really, but it kinda makes sense for it to be true anyway. also we change the squares to powers of infinity in p-adic numbers and nobody really knows why

[carmilla-the-dog]

What is the dual of the forgetful functor?

Ooooh my, this is going to be fun.

Ok, so first things first, what do we mean here by dual? Well, duality in category theory is a very loose concept, and one must examine the particular use case before deciding what dual means.

In this post, duality will be given by adjunction. And what is adjunction, you ask? Adjunction is when

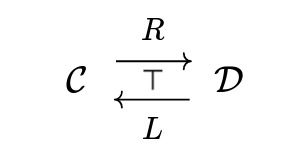
are related by

$$\mathcal{D}(x,Ry)\cong\mathcal{C}(Lx,y),$$

(the isomorphism being natural). And in this case we say that \(R\) is a right adjoint to \(L\) and \(L\) is a left adjoint to \(R\). By Yoneda bullshit, all right adjoints of a functor have to be isomorphic. (dually, the same is true for left adjoints).

THE SECOND THING is that forgetful functor is also a loosely defined concept (https://ncatlab.org/nlab/show/stuff%2C+structure%2C+property). But here I'll be talking about the family of functors of the form

$$U:\mathcal{E}\to\mathbf{Set},$$

in which \(\mathcal{E}\) is a concrete algebraic category like modules, vector spaces, groups or abelian groups. This functor takes an algebraic structure and send it to its underlying set.

Remark. More generally you can take the category of monoids, or the category of algebraic theory, over a category \(\mathcal{C}\) and you have a natural forgetful functor into \(\mathcal{C}\) itself.

OK. So if we want a left adjoint to \(U\), we require that, given a set \(x\) and a algebraic structure \(y\) (which has underlying set \(y\) because fuck you), we have

$$\mathbf{Set}(x,y)\cong\mathcal{E}(Lx,y).$$

That is, algebraic maps

$$\phi:Lx\to y,$$

are completely determined by the map in \(x\):

$$f:x\to y.$$

If you feel like this is familiar, you are not wrong! If you have any formal training in mathematics (and if you don't, I'm so sorry for using jargon and stuff… I can answer any questions after ^^( but I know for a fact that anon has formal training)) then you maybe recognize this from linear algebra.

Indeeeeeeeeed, given any vector spaces \(V\text{ and } W\), a linear map

$$T:V\to W$$

is completely determined by what it does to the basis of \(V\). Even more, if the set \(v\) is as basis for \(V\) (I am completely aware that my notation can cause psychic damage), then every function of sets

$$f:v\to W,$$

determine a linear transformation

$$T:V\to W.$$

AND EVEN FURTHER every linear transformation is obtained in this way. Abstracting again, the left functor \(L\) represents taking a set \(x\) and using it as a basis for a algebraic structure \(Lx\).

As algebraic structures with a basis are called free, the left adjoint of a forgetful functor is called the free functor. :)

If someone guess the name of the right adjoint of the forgetful functor, I'll give them a kiss

[questioning-my-identity-element]

as someone with a passing knowledge of knot theory & a dilettante interest in math I'm really interested in the behavior/rules of those graphs, could you talk a little more about them?

this is my first ask! and it's on my research!!! i still do research in this area. i am getting my phd in topological quantum computation. i saw someone else talk about categorical quantum in response to the post. as i understand, this is a related but distinct field from quantum algebra, despite both using monoidal categories as a central focus.

if you're familiar with knot theory, you may have heard of the jones polynomial. jones is famous for many things, but one of which is his major contributions to the use of skein theory (this graphical calculus) in quantum algebra, subfactor theory, and more.

For an reu, i made an animation of how these diagrams, mostly for monoidal categories, work:

https://people.math.osu.edu/penneys.2/Synoptic.mp4

to add onto the video, in quantum algebra, we deal a lot with tensor categories, where the morphisms between any two objects form a vector space. in particular, since these diagrams are representing morphisms, it makes sense to take linear combinations, which is what we saw in the post. moreover, any relationships you have between morphisms in a tensor category, can be captured in these diagrams...for example, in the fusion category Fib, the following rules apply (in fact, these rules uniquely describe Fib):

thus, any time, these show up in your diagrams, you can replace them with something else. in general, this is a lot easier to read than commutative diagrams.

[ceausescue]

i cant stop laughing at these answers to some poor kid in linear algebra

literally in the question they said they just got to inner products

[bubbloquacious]

So if your coordinates lie in an integral domain, the union of the solutions sets of two algebraic equations is itself the solution set of an algebraic equation, because xy = 0 if and only if x = 0 or y = 0. In this setting an algebraic set is a set that's the simultaneous solution set of a system of algebraic equations, which you can show pretty easily to be the same thing as the vanishing set of an ideal of polynomials. Algebraic sets are then closed under arbitrary intersections and finite unions, so they're the closed sets in a topology which we call the Zariski topology.

In other algebraic settings, though, this doesn't hold up! If you take two solutions sets of linear equations in some vector space, two lines through the origin for example, then their union is not generally the solution set of a linear equation, because we know that such sets are linear subspaces.

[lipshits-continuous]

Isn't it neat that every n-dimensional vector space over k is isomorphic to kⁿ? Like I didn't really appreciate that fact when I took linear algebra in first year but with hindsight that's the whole reason why linear algebra is so powerul

[azdoine]

You probably already know this, but for stoichiometry, instead of trying to solve Rv_1 = Pv_2, where R is the matrix of reactants and P the matrix of products, you can simply solve [R; -P] v = 0, which is cleaner, because you can just mechanically apply Gaussian elimination, instead of trying to guess and check. The visual intuition is simply that of finding some null-subspace within molecule-space (because within the null-space total atom/element count is constant)

:3 mhm, mhm; once someone pointed me at the linear algebra methods, I actually tried solving the problem sets I was given with Gaussian elimination, but I ended up going around in circles and giving myself headaches because I was shite at the recognized notation and I was using techniques I didn't really understand the implications of.

I ended up basically rebuilding similar ideas up out of geometric intuition wrt those vectors in moleculespace-

-using the matrix grids of numbers solely as writing shorthands and visual aids to extract linear equations, and cranking out elementary algebra on the linear equations.

my vague impression from independent research (i.e. stackexchange) is that all of this is totally babytier & direly insufficient for real srsbzns chemistry, b/c the ordering relationship between reactants and products in each equation is non-fundamental - that atomic species are conserved at this level (not accounting for nuclear reactions), but the recombinations of those species are determined by stochastic hops over gradients in the energy landscape, and can therefore somehow generate more pathologically complex balanced reactions than I'm prepared to understand with these techniques.

well, in the absence of a rationale to convince my chemistry department that I'm ready to sit in on higher-level lectures and get credits for it, that's why I'm self-studying more pure math in the mean time (i.e. watching 3blue1brown and very slowly working through the exercises in Linear Algebra Done Right, lol)

[scarubaru]

I feel linear algebra should be a course physical science majors take during their freshman year. And it should be...rigorous, if that terminology makes sense. Like less emphasis on 'here's how you manipulate matrices', more emphasis on 'this is what we mean when we say a collection of objects constitute a vector space. Here are the properties that follow.' The concepts are just so pervasive and important, even if they don't announce themselves as such in the hodgepodge of course work. You know those differential equations you keep seeing? those guys that look like Ly = 0? Yeah you're just messing with operators and the solutions, those functions, those are vectors. They constitute a vector space. And it would I think make a lot of things click early on.

[heirtocragflame]

Hii, fellow queer mathematician (CS and maths BSc 3rd year out of 4)! I don't know what to say really but I saw you liked getting non-anon asks so…

Currently wishing that my algebra module was less about linear algebra (the worst kind) and more about rings and other discrete maths things :( at least I'm enjoying my complex analysis module more than the real analysis one I took last semester.

So many queer math people! 🤩

I wouldn't say I specifically like getting non-anon asks, it's more that I like being able to check out the page of the person who's asking :3

I mean linear algebra is a necessary thing to motivate module theory (think vector spaces over a ring instead of a field). They're also good for group theory because we tend to want to be able to represent groups as matrices (although that also ends up involving a lot of module theory).

[spectrallysequenced]

Hi, I'm an undergrad CS and maths student. Usually I enjoy algebra more than analysis, and I greatly enjoyed learning about computability theory and a little earlier, group theory. Unfortunately, right now I'm taking a course (aka module) in real analysis and another in complex analysis. My algebra course is primarily about linear algebra, we learn about fields, rings, and all the linear algebra stuff like vector spaces and the like. I am surprisingly enjoying complex analysis, but I'm not the biggest fan of linear algebra, do you have any advice on how to stick through it until I get to some of the more fun generalised things, or is it gonna be like linear algebra from here on out?

It's hard to say without knowing more about why you dislike linear algebra at the moment. If your class is computation-based, I get it, it's boring. Hopefully you're learning proof-based linear algebra, but if you've already learned about groups, this might be a bit boring for you, since the start of linear algebra is pretty simple, and there's some "dirty work" to be done. If you've seen group theory, a lot of things might look familiar or even identical to you. I would try to see how many parallels you can draw for yourself between the theories. A lot of the underlying properties/theorems here can actually be stated much more generally (e.g. the isomorphism theorems). Edit: I accidentally posted this too early, here's the rest: Linear algebra does underlie a lot of mathematics (I'd say most of it, honestly), including a lot of analysis (Maybe not introductory complex analysis in particular, but multivariable analysis uses LOT of linear algebra and basic theory of inner product spaces). Additionally, a lot of arguments in algebra (and analysis!) reduce to (or use) linear algebra. A lot of arguments don't, but it seems to permeate the rest of your mathematical future. I can't say a lot more about how to motivate you in particular without knowing the course structure, and what exactly you aren't enjoying. I will say that with time and practice linear algebra will become pretty much second nature, and a very useful tool, and more advanced linear/multilinear algebra can actually be pretty fun if you've enjoyed algebra so far, but I will conclude by saying that more advanced algebra really really does not feel like linear algebra, even if some areas use it/generalisations of it quite a lot. Feel free to follow up with more info/dm me!

[enetarch-quantum-physics]

Topics to study for Quantum Physics

Calculus

Taylor Series

Sequences of Functions

Transcendental Equations

Differential Equations

Linear Algebra

Separation of Variables

Scalars

Vectors

Matrixes

Operators

Basis

Vector Operators

Inner Products

Identity Matrix

Unitary Matrix

Unitary Operators

Evolution Operator

Transformation

Rotational Matrix

Eigen Values

Coefficients

Linear Combinations

Matrix Elements

Delta Sequences

Vectors

Basics

Derivatives

Cartesian

Polar Coordinates

Cylindrical

Spherical

LaPlacian

Generalized Coordinate Systems

Waves

Components of Equations

Versions of the equation

Amplitudes

Time Dependent

Time Independent

Position Dependent

Complex Waves

Standing Waves

Nodes

AntiNodes

Traveling Waves

Plane Waves

Incident

Transmission

Reflection

Boundary Conditions

Probability

Probability

Probability Densities

Statistical Interpretation

Discrete Variables

Continuous Variables

Normalization

Probability Distribution

Conservation of Probability

Continuum Limit

Classical Mechanics

Position

Momentum

Center of Mass

Reduce Mass

Action Principle

Elastic and Inelastic Collisions

Physical State

Waves vs Particles

Probability Waves

Quantum Physics

Schroedinger Equation

Uncertainty Principle

Complex Conjugates

Continuity Equation

Quantization Rules

Heisenburg's Uncertianty Principle

Schroedinger Equation

TISE

Seperation from Time

Stationary States

Infinite Square Well

Harmonic Oscillator

Free Particle

Kronecker Delta Functions

Delta Function Potentials

Bound States

Finite Square Well

Scattering States

Incident Particles

Reflected Particles

Transmitted Particles

Motion

Quantum States

Group Velocity

Phase Velocity

Probabilities from Inner Products

Born Interpretation

Hilbert Space

Observables

Operators

Hermitian Operators

Determinate States

Degenerate States

Non-Degenerate States

n-Fold Degenerate States

Symetric States

State Function

State of the System

Eigen States

Eigen States of Position

Eigen States of Momentum

Eigen States of Zero Uncertainty

Eigen Energies

Eigen Energy Values

Eigen Energy States

Eigen Functions

Required properties

Eigen Energy States

Quantification

Negative Energy

Eigen Value Equations

Energy Gaps

Band Gaps

Atomic Spectra

Discrete Spectra

Continuous Spectra

Generalized Statistical Interpretation

Atomic Energy States

Sommerfels Model

The correspondence Principle

Wave Packet

Minimum Uncertainty

Energy Time Uncertainty

Bases of Hilbert Space

Fermi Dirac Notation

Changing Bases

Coordinate Systems

Cartesian

Cylindrical

Spherical - radii, azmithal, angle

Angular Equation

Radial Equation

Hydrogen Atom

Radial Wave Equation

Spectrum of Hydrogen

Angular Momentum

Total Angular Momentum

Orbital Angular Momentum

Angular Momentum Cones

Spin

Spin 1/2

Spin Orbital Interaction Energy

Electron in a Magnetic Field

ElectroMagnetic Interactions

Minimal Coupling

Orbital magnetic dipole moments

Two particle systems

Bosons

Fermions

Exchange Forces

Symmetry

Atoms

Helium

Periodic Table

Solids

Free Electron Gas

Band Structure

Transformations

Transformation in Space

Translation Operator

Translational Symmetry

Conservation Laws

Conservation of Probability

Parity

Parity In 1D

Parity In 2D

Parity In 3D

Even Parity

Odd Parity

Parity selection rules

Rotational Symmetry

Rotations about the z-axis

Rotations in 3D

Degeneracy

Selection rules for Scalars

Translations in time

Time Dependent Equations

Time Translation Invariance

Reflection Symmetry

Periodicity

Stern Gerlach experiment

Dynamic Variables

Kets, Bras and Operators

Multiplication

Measurements

Simultaneous measurements

Compatible Observable

Incompatible Observable

Transformation Matrix

Unitary Equivalent Observable

Position and Momentum Measurements

Wave Functions in Position and Momentum Space

Position space wave functions

momentum operator in position basis

Momentum Space wave functions

Wave Packets

Localized Wave Packets

Gaussian Wave Packets

Motion of Wave Packets

Potentials

Zero Potential

Potential Wells

Potentials in 1D

Potentials in 2D

Potentials in 3D

Linear Potential

Rectangular Potentials

Step Potentials

Central Potential

Bound States

UnBound States

Scattering States

Tunneling

Double Well

Square Barrier

Infinite Square Well Potential

Simple Harmonic Oscillator Potential

Binding Potentials

Non Binding Potentials

Forbidden domains

Forbidden regions

Quantum corral

Classically Allowed Regions

Classically Forbidden Regions

Regions

Landau Levels

Quantum Hall Effect

Molecular Binding

Quantum Numbers

Magnetic

Withal

Principle

Transformations

Gauge Transformations

Commutators

Commuting Operators

Non-Commuting Operators

Commutator Relations of Angular Momentum

Pauli Exclusion Principle

Orbitals

Multiplets

Excited States

Ground State

Spherical Bessel equations

Spherical Bessel Functions

Orthonormal

Orthogonal

Orthogonality

Polarized and UnPolarized Beams

Ladder Operators

Raising and Lowering Operators

Spherical harmonics

Isotropic Harmonic Oscillator

Coulomb Potential

Identical particles

Distinguishable particles

Expectation Values

Ehrenfests Theorem

Simple Harmonic Oscillator

Euler Lagrange Equations

Principle of Least Time

Principle of Least Action

Hamilton's Equation

Hamiltonian Equation

Classical Mechanics

Transition States

Selection Rules

Coherent State

Hydrogen Atom

Electron orbital velocity

principal quantum number

Spectroscopic Notation

=====

Common Equations

Energy (E) .. KE + V

Kinetic Energy (KE) .. KE = 1/2 m v^2

Potential Energy (V)

Momentum (p) is mass times velocity

Force equals mass times acceleration (f = m a)

Newtons' Law of Motion

Wave Length (λ) .. λ = h / p

Wave number (k) ..

k = 2 PI / λ

= p / h-bar

Frequency (f) .. f = 1 / period

Period (T) .. T = 1 / frequency

Density (λ) .. mass / volume

Reduced Mass (m) .. m = (m1 m2) / (m1 + m2)

Angular momentum (L)

Waves (w) ..

w = A sin (kx - wt + o)

w = A exp (i (kx - wt) ) + B exp (-i (kx - wt) )

Angular Frequency (w) ..

w = 2 PI f

= E / h-bar

Schroedinger's Equation

-p^2 [d/dx]^2 w (x, t) + V (x) w (x, t) = i h-bar [d/dt] w(x, t)

-p^2 [d/dx]^2 w (x) T (t) + V (x) w (x) T (t) = i h-bar [d/dt] w(x) T (t)

Time Dependent Schroedinger Equation

[ -p^2 [d/dx]^2 w (x) + V (x) w (x) ] / w (x) = i h-bar [d/dt] T (t) / T (t)

E w (x) = -p^2 [d/dx]^2 w (x) + V (x) w (x)

E i h-bar T (t) = [d/dt] T (t)

TISE - Time Independent

H w = E w

H w = -p^2 [d/dx]^2 w (x) + V (x) w (x)

H = -p^2 [d/dx]^2 + V (x)

-p^2 [d/dx]^2 w (x) + V (x) w (x) = E w (x)

Conversions

Energy / wave length ..

E = h f

E [n] = n h f

= (h-bar k[n])^2 / 2m

= (h-bar n PI)^2 / 2m

= sqr (p^2 c^2 + m^2 c^4)

Kinetic Energy (KE)

KE = 1/2 m v^2

= p^2 / 2m

Momentum (p)

p = h / λ

= sqr (2 m K)

= E / c

= h f / c

Angular momentum ..

p = n h / r, n = [1 .. oo] integers

Wave Length ..

λ = h / p

= h r / n (h / 2 PI)

= 2 PI r / n

= h / sqr (2 m K)

Constants

Planks constant (h)

Rydberg's constant (R)

Avogadro's number (Na)

Planks reduced constant (h-bar) .. h-bar = h / 2 PI

Speed of light (c)

electron mass (me)

proton mass (mp)

Boltzmann's constant (K)

Coulomb's constant

Bohr radius

Electron Volts to Jules

Meter Scale

Gravitational Constant is 6.7e-11 m^3 / kg s^2

History of Experiments

Light

Interference

Diffraction

Diffraction Gratings

Black body radiation

Planks formula

Compton Effect

Photo Electric Effect

Heisenberg's Microscope

Rutherford Planetary Model

Bohr Atom

de Broglie Waves

Double slit experiment

Light

Electrons

Casmir Effect

Pair Production

Superposition

Schroedinger's Cat

EPR Paradox

Examples

Tossing a ball into the air

Stability of the Atom

2 Beads on a wire

Plane Pendulum

Wave Like Behavior of Electrons

Constrained movement between two concentric impermeable spheres

Rigid Rod

Rigid Rotator

Spring Oscillator

Balls rolling down Hill

Balls Tossed in Air

Multiple Pullys and Weights

Particle in a Box

Particle in a Circle

Experiments

Particle in a Tube

Particle in a 2D Box

Particle in a 3D Box

Simple Harmonic Oscillator

Scattering Experiments

Diffraction Experiments

Stern Gerlach Experiment

Rayleigh Scattering

Ramsauer Effect

Davisson–Germer experiment

Theorems

Cauchy Schwarz inequality

Fourier Transformation

Inverse Fourier Transformation

Integration by Parts

Terminology

Levi Civita symbol

Laplace Runge Lenz vector

[md-learning]

A journey through Math: 001

A random curious journey to learn mathematical topics.

Simply, in this episode of I try to learn, I am curious to know about:

What is vector and vector space

How do they interact

And, what on earth is basis and why do we fuss about eigen- stuffs

Would I learn everything? No idea. By when I would learn this? No idea either.

Linear algebra, show me your beauty.

[questioning-my-identity-element]

Do you have any recommendations for learning about algebra beyond high school level? I'm in calculus right now and we just hit definite integrals, if that helps.

sure, ill give a handful of answers depending on your goals.

i would categorize "beyond high school algebra" into linear algebra (which is lower-div college level) and abstract algebra (which is upper-div college level). one could argue that linear algebra is a subfield of abstract algebra, but i am not going to.

linear algebra: lines, planes, hyperplanes, etc can all be fit into essentially the same framework of linear (or affine) equations. think of y=mx+b, except y, x, and b are vectors and m is a matrix. linear algebra is essentially just the study of problems like these and structures that are relevant to their study (e.g., vector spaces). this is inarguably the most important field of mathematics.

abstract algebra: this is a very broad subject which broadly studies structures and the way they interact with other structures. it is hard to get a good feel for abstract algebra without actually doing it, so here is a blog post from my website. you may not be familiar with the notation, but you can find hopefully everything important on the Wikipedia page for sets and functions.

my answer to the question is under the cut. i would encourage other mathblrs to add their opinions though

(A) you want to learn some (but not all) cool algebra without the painful detail

while abstract algebra can be touched with your background, there are certain topics which depend deeply on linear algebra. broadly, this is because linear algebra underlies almost all math. this splits my answer into two parts depending on if (A) you want to learn some (but not a lot of) cool algebra without the painful detail or (B) you want to deeply understand algebra.

try some general audience videos, like from numberphile. generally, videos by good presenters are amazing at teaching you the cool stuff. if you find this to be too little, pick up a lecture series on group theory for undergrads and try your best to follow along. if you can't keep up but still want to pursue it, go to (B).

(B) you want to deeply understand algebra

this is my recommended plan of action:

(1a) pick up some textbook on "discrete math and intro to proofs" (example) and work through a few problems in each section. abstract algebra in general has many prerequisites, and discrete math fills in the vast majority. the topics you should look out for are: proof techniques such as induction, functions and relations, and some basic combonatorics/counting.

(1b) pick up a textbook on "linear algebra and applications" (example) and do the same. i encourage taking a textbook directed at sciences for a few reasons: it's easier, applications can sometimes spark other interests, and most importantly applications give a deeper intuition for the meaning of the math. where possible, try to use your new proof skills to prove the things discussed!

(2) pick up a more serious book on abstract algebra and/or linear algebra and do as many exercises as possible (as in attempt every problem in every section). the standard reference for abstract algebra is dummit and foote but i prefer jacobson. for linear, i would just suggest linear algebra done right