#Spectral Geometry

[mindblowingscience]

Is it possible to deduce the shape of a drum from the sounds it makes? This is the kind of question that Iosif Polterovich, a professor in the Department of Mathematics and Statistics at Université de Montréal, likes to ask. Polterovich uses spectral geometry, a branch of mathematics, to understand physical phenomena involving wave propagation. Last summer, Polterovich and his international collaborators—Nikolay Filonov, Michael Levitin and David Sher—proved a special case of a famous conjecture in spectral geometry formulated in 1954 by the eminent Hungarian-American mathematician George Pólya. The conjecture bears on the estimation of the frequencies of a round drum or, in mathematical terms, the eigenvalues of a disk.

Continue Reading.

[knotty-et-al]

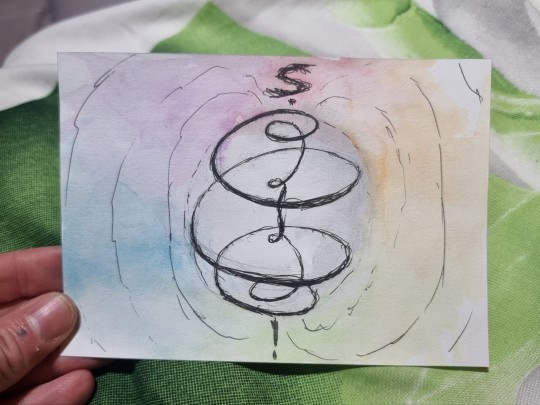
"Auf und ab, rauf und nieder - haste Erkenntnisgewinne immer wieder"

The title approximately translates to "Going above and below, top and down - you'll have gains of knowledge every time".

[2023/11/15] [Black ink and watercolor on paper]

[ID: At the center of the drawing is a black 3-dimensional spiral. It forms a helix trajectory around a horn torus' axis of revolution. It roughly forms a white/grey sphere. Above the spiral is a question mark. Below the spiral is an exclamation mark. The background is watercolored in rainbow colors and merely bright.]

[girlballs]

is their a general overview of the niche of each kind of magic in lesser beast(both in gameplay and like, general theme, like life might be in gameplay healing and buff and in themes plants, for a lot of them the themes obvious but for example how is shadow, void, death, and soul visually or thematically distinct?)

i don't think i've made a Comprehensive post about this yet? but i can do that real quick. also keep in mind these are general descriptions, there's multiple types of magic for each element that can vary a bit (e.g. fire has Wild Fire and Flame Sorcery which are pretty similar, but Solar Sorcery has its own vibes) and also some unique spells that don't fit the usual magic schools

Fire magic is pretty straightforward thematically, it's literally just fire (Wild Fire magic has more of a "thick smoky fire" vibe and Fire Sorcery has a cleaner appearance). gameplay wise fire's main thing is the Burn status effect for DoT

Mind magic is all about geometry motifs visually (lots of projectiles are platonic solids, for instance), and gameplay wise it's like. instead of having Normal/Strong cast inputs like other spells as an analogue to light/heavy attacks, Strong cast for Mind spells triggers some secondary behavior after the spell has been cast

Light magic is thematically kind of organic and goopy, like flowing liquid light for the visuals. gameplay wise it's more of a support element- stuff like debuff cleansing and self-buff spells, although the offensive spells have the shared gimmick of being essentially hitscan instead of projectiles (+ stuff like the Force miracles from Dark Souls)

Storm magic has two major subcategories, wind and lightning, with the former type doing physical damage instead of actual elemental Storm damage. wind stuff does hella poise damage and lightning stuff has the Shock debuff (you get stunned and take a chunk of damage) as well as some stuff that chains between multiple enemies

Ice magic is also pretty straightforwardly Ice Themed, and its gameplay niche is stamina damage/max stamina penalties and shit that lingers on the ground (which, in pvp contexts, is stuff you have to jump over instead of dodging through)

Earth magic is primarily geomancy stuff, lots of flinging rocks around and launching *yourself* around by upheaving the ground under you. there's also buffs for boosting poise which is meant to be paired with the more melee-oriented spells

Life magic is mainly plant themed but there's also some "literally using your own blood to cast spells" stuff. mainly a support element, this is where 99% of the normal healing spells live

Shadow magic is very smoke-and-fog themed visually for the non-offensive spells (invisibility, short range teleporting, some spells to bypass locked shit, etc), and the offensive ones are largely focused on summoned ephemeral weapons both as melee spells and projectiles (i.e. the basic ranged shadow spell is effectively just summoning arrows) which all partially or completely ignore blocking

Death magic is weird since it's mainly focused on summoning minions and debuffing enemies instead of dealing damage directly, but there's some like tentacle and skeletal themed stuff for sucking the MP out of enemies. also minions are gonna be partially skeletal versions of existing enemies

Holy magic is visually all about spectral chains and runic circles, and holy spears show up as a motif in some of the offensive spells that aren't just "blast dudes with golden light". also mechanically there's a Paralyzed debuff (pins an enemy in place but doesn't deal damage) and a Purify effect that removes buffs from the target

Dragon magic is split into two main groups, transformation magic that temporarily gives you draconic features (wings for air mobility, tail for big sweeps, etc.) and Draconic Duelist spells that summon bound weapons with like a funky twilight sky color palette. There's also a subset of duelist spells that are like weapon arts that occupy spell slots, and can only be cast with special dragon weapons

Void magic has some aesthetic overlap with Fire, but void flames are black + deep red and notably don't emit any light. Void has debuffs that prevent poise regeneration, and also some grapple attacks meant to be used on other players

Cosmic magic is star (excluding the sun) and celestial body themed. lots of opening tiny portals into space to chuck star particles and comets at people, or yoink them around with gravity (represented as deep blue/black ripples and refraction effects)

Magma magic is obviously magma and lava themed, lots of hot rocks and hot goop. shares the "lingering ground hazard" stuff with Ice magic and also features a lot of "buffs that have tradeoffs" stuff like "you do more poise damage but you're constantly taking damage over time"

Soul magic is weird and i'm actually not settled on the aesthetics or vibes still. it was originally gonna be "spells that cost HP, and spells that are more effective at low HP" mechanically but i'm not really 100% digging that concept honestly

Chaos magic is. green. the whole thing visually is that there's no consistent theme because the spells are all twisted versions of existing spells, with the connecting thread of the Volatile debuff (you explode and get launched into the air). so you've got e.g. Chaos Firespear which chucks a big spear of green fire with a DoT that builds up Volatile over time, Chaos Lightning Bolt calls green lightning from a distance and chains to other enemies to inflict Volatile, etc.

holy shit that was a long answer sorry

[cliozaur]

Despite the fact that Napoleon was a bloody butcher/woodcutter, Hugo still recognizes that he was a military genius. Wellington with his geometry, precision, prudence, etc., an epitome of the old school, is simply boring. He argues that Wellington didn't truly earn the title of victor at Waterloo; instead, Napoleon's defeat was a result of chance, luck, and divine will. However, Hugo does give credit to the English and Scottish soldiers for their valour.

He then provides statistics on casualties from various Napoleonic battles, revealing Waterloo as the most devastating, with 60,000 out of 145,000 combatants perishing.

In the final paragraph, Hugo reflects on his own situation as a traveller caught on the old battlefield at night. There, he encounters eerie sights, imagining the spectral remains of Napoleon, Wellington, and the soldiers who perished at Hougomount, Mont-Saint-Jean, and other places.

[grimowled]

THE SKY DID NOT SPLIT OPEN; IT CURTSEYED.

a languid spill of sulphurous red bled across the firmament, turning the world below sanguine in anticipation; far above its spires and overgrown gardens, a BLOOD MOON bulged and ripened, the constellations warped like entrails in a butcher's grip - sliding into ancient, forbidden alignments that hadn't been seen since the first betrayal was carved into flesh.

he did not descend so much as unfurl, his monstrous silhouette birthing itself from a pulsing slit in the velvet of the void, spindling outward from the gnarled shadow of an eclipsed star. WINGS - not feathered, but plumed with blackened flames and the dead eyes of felled angels - opened with a most dreadful crack; his many voices stitched themselves into the wind like a unhallowed hymn - a liturgy of decay, sweet with myrrh, spoiled by ROT.

"DID YOU MISS ME?"

above him, the constellations rearranged themselves into a CROWN. below him, the soil of hell hummed; a spectral echo lingered, the sound of celestial geometry snapping back into place.

ancient sigils glowed at his inevitable passage, and the gates of his palace groaned open without touch, candles ignited of their own volition; as he crossed the threshold, the mansion exhaled, the walls whispered, eager for orders, blood began to flow backwards in the pipes beneath the floor. the halls remembered him.

stolas stepped into the corridor with the timeless elegance of a PLAGUE.

robes shimmered with living constellations, stitched from star maps and veils of void, dragged behind him like widow's weeds; on his tongue, the taste of RESURRECTION. beneath his talons, dried blood from a moon-long rite; in the hollows of his crimson eyes burned the ancient serenity of madness.

( he simply was, once more - anointed by cruor, haloed in ATROCITY, sovereign of secrets.)

the PRINCE had returned - not as salvation ...

--but as RECKONING.

[flameshadowconjuring]

Sometimes I feel so limited in my mathematical ability because I haven't really specialized yet, but then I sit in an oral exam as the second examiner with master's students. One took a spectral geometry course and could not even define what a Fuchsian group is. Another student who took measure theory could not explain what a measurable function is. Imagine you are trying to become a chef and don't even know what salt is. Really helps with the impostor syndrome.

[jack-of-crowns]

@flashfictionfridayofficial

'Le Valet de Couronnes’ by @jack-of-crowns

"Où va-t-il, á votre avis, ce petit bonhomme?"she pondered, but all I noticed was how beautiful Véronique looked in that spectral light with the eclipse coming on, Marcel waves of brunette rustling in the warm Marghazi breeze coming up from the Bay of Bengal. She laughed to see that look in my eyes. "Really, Jack, that mouse I meant."

Sure enough, there was the yellowish flick of a chooha's tail, disappearing just around the white stucco facade of the café on Rue de la Compagnie, where we had perched to enjoy the Pongal festival unfolding on the streets of Pondicherry before us. The strange thing was, I hadn't noticed an alleyway there a moment ago. "Where the devil do you suppose he's off to," I softly answered her.

Setting my napkin to the side of the paneer ratatouille I'd been enjoying and donning my trusty fedora, I stood up to take a quick look. "Un instant, ma chérie." It must have been a trick of the light that I hadn't noticed the narrow lane of cobbles beforehand, but there was the little mouse scurrying on just ahead. It paused at the side of the building adjacent to the café, underneath a casement window shaded by a jali screen that fragmented the kerosene lamplight shining behind it.

The building was some sort of art gallery; hanging in the window was an exquisite work in the Cubist style, entitled 'Le Valet de Couronnes’. The subject was a portrait in bluish-grey tones, wearing an ornate headpiece, and eyes closed meditatively. The background was an intricate jumble of complex geometries and abstract mechanisms. There was a striking familarity to this man, I thought to myself as the eclipses' penumbra deepened overhead.

Distant temple bells began to toll the evening aarti to Ganesha; the clock tower in the French Quarter sounded the hour. The eyes of the painting flickered, dancing in the moonshadow. It was 1925, and a new year was beginning. The uttarayan was beginning, and the northern portal was opened...

It is 2025, and Veronica catches the eye of the gallery's clerk, who is just about to close shop for the night. "How much for this painting," she inquires.

"Ten thousand rupees," he replies. "A classic from the colonial era, amma. I believe that was a self-portrait of a British artist who used to live next door to here. Really takes one on a journey to another place and time, doesn't it?"

She nods and smiles, handing over the banknotes as he parcels up her belated Christmas present to herself. "Comment ça commence," she murmurs; that's how all the best stories begin.

[transmutationisms]

1. opinions on meillassoux?

2. what mathematics did you do?

none of the 'speculative materialists' have anything serious to say because they have no historical analysis; it's naïve realism that only seeks to shortcut the kantian remove from the thing-in-itself (what meillassoux expresses as the correlationist circle), in this case by recourse to mathematisables because he still mistakes quantification for objectivity. but meillassoux is incredibly fun to read anyway because of how elegantly he lays out his problems and argues through them. idc i'll read any old garbage he comes out with. extro-science fiction and the spectral dilemma are also potential fodder for some genuinely good lit crit imo

& i went to a weird school where we didn't pick courses so this was just 'senior math' & it was the course where we did relativity, lobachevskian geometry, & gödel's incompleteness theorem. the meillassoux class was actually a different one i had with the same prof but it was just a precept so in my mind he's still primarily my math prof

[lipshits-continuous]

Prime numbers of the ask game let's go!

This is gonna be a long old post haha /pos

2. What math classes did you do best in?:

It's joint between Analysis in Many Variables (literally just Multivariable calculus, I don't know why they gave it a fancy name) and Complex Analysis. Both of which I got 90% in :))

3. What math classes did you like the most?

Out of the ones I've completely finished: complex analysis

Including the ones I'm taking at the moment:

Topology

5. Are there areas of math that you enjoy? What are they?

Yes! They are Topology and Analysis. Analysis was my favourite for a while but topology is even better! (I still like analysis just as much though, topology is just more). I also really like group theory and linear algebra

7. What do you like about math?

The abstractness is really nice. Like I adore how abstract things can be (which is why I really like topology, especially now we're moving onto the algebraic topology stuff). What's better is when the abstract stuff behaves in a satisfying way. Like the definition of homotopy just behaves so nicely with everything (so far) for example.

11. Tell me a funny math story.

A short one but I am not the best at arithmetic at times. During secondary school we had to do these tests every so often that tested out arithmetic and other common maths skills and during one I confidently wrote 8·3=18. I guess it's not all that funny but ¯⁠\⁠_⁠(⁠ツ⁠)⁠_⁠/⁠¯

13. Do you have any stories of Mathematical failure you’d like to share?

I guess the competition I recently took part in counts as a failure? It's supposed to be a similar difficulty to the Putnam and I'm not great at competition maths anyway. I got 1/60 so pretty bad. But it was still interesting to do and I think I'll try it again next year so not wholly a failure I think

17. Are there any great female Mathematicians (living or dead) you would give a shout-out to?

Emmy Noether is an obvious one but I don't you could understate how cool she is. I won't name my lecturers cause I don't want to be doxxed but I have a few who are really cool! One of them gave a cool talk about spectral geometry the other week!

19. How did you solve it?

A bit vague? Usually I try messing around with things that might work until one of them does work

23. Will P=NP? Why or why not?

Honestly I'm not really that well versed in this problem but from what I understand I sure hope not.

29. You’re at the club and Grigori Perlman brushes his gorgeous locks of hair to the side and then proves your girl’s conjecture. WYD?

✨polyamory✨

31. Can you share a math pickup line?

Are you a subset of a vector space of the form x+V? Because you're affine plane

37. Have you ever used math in a novel or entertaining way?

Hmm not that I can think of /lh

41. Which is better named? The Chicken McNugget theorem? Or the Hairy Ball theorem?

Hairy Ball Theorem

43. Did you ever fail a math class?

Not so far

47. Just how big is a big number?

At least 3 I'd say

53. Do you collect anything that is math-related?

Textbooks! I probably have between 20 and 30 at the moment! 5 of which are about topology :3

59. Can you reccomend any online resources for math?

The bright side of mathematics is a great YouTube channel! There is a lot of variety in material and the videos aren't too long so are a great way to get exposed to new topics

61. Does 6 really *deserve* to be called a perfect number? What the h*ck did it ever do?

I think it needs to apologise to 7 for mistakingly accusing it of eating 9

67. Do you have any math tatoos?

I don't have any tattoos at all /lh

71. 👀

A monad is a monoid in the category of endofunctors

73. Can you program? What languages do you know?

I used to be decent at using Java but I've not done for years so I'm very rusty. I also know very basic python

Thanks for the ask!!

[custom-glass-manufacturing]

How Custom Glass Manufacturing Is Revolutionizing Modern Architecture

Over the past century, architecture has undergone transformative shifts driven by technological advancements, societal needs, and aesthetic aspirations. Materials like steel, concrete, and wood have long dominated the architectural landscape. However, the 21st century has witnessed the emergence of glass not merely as a transparent façade but as a dynamic, structural, and multifunctional element. This transformation is fueled by the evolution of custom glass manufacturing, a field that enables architects to transcend previous limitations in design and functionality. With increasing demand for buildings that are sustainable, secure, and visually striking, custom glass has become an indispensable tool in the modern architect's toolkit. The trend reflects a broader cultural and technological movement toward materials that are both expressive and high-performing, aligning architectural design with contemporary values and user expectations.

Historical Context: From Glass Panes to Architectural Marvels

Glass has been used in architecture for centuries, dating back to ancient Roman glass windows. However, its use was largely ornamental or functional in limited capacities due to technological constraints. The industrial revolution enabled the mass production of flat glass, which led to its broader application in buildings. Yet it wasn't until the late 20th century that glass started to be considered a potential structural component. Advances in lamination, tempering, and coating technologies allowed architects to explore new possibilities, from transparent walls to load-bearing elements. These innovations marked the beginning of a new era in which glass was no longer just a cladding material but an integral part of structural and environmental design. As the boundaries of possibility expanded, so did the ambition of architectural projects, turning glass into a medium for storytelling, interaction, and innovation.

Technological Innovations in Custom Glass

One of the most significant enablers of modern architectural achievements has been the rapid advancement in glass technology. Custom glass manufacturing now includes processes such as lamination, chemical strengthening, digital printing, and dynamic tinting. These techniques allow for precise control over the glass's strength, transparency, and thermal properties. The ability to embed photovoltaic cells, integrate LED lighting, or add switchable opacity features has expanded glass's utility beyond aesthetics. Furthermore, advanced fabrication methods enable the creation of large, curved, and even double-curved panels that were once inconceivable. These capabilities give architects unprecedented freedom to realize complex geometries and innovative façades. The marriage of digital modeling with CNC cutting and finishing tools ensures high precision and repeatability, essential for large-scale, complex structures.

Environmental Sustainability Through Glass

Sustainability is a cornerstone of contemporary architecture, and custom glass plays a pivotal role in this paradigm. High-performance glass can significantly enhance a building's energy efficiency by regulating heat gain and loss, maximizing daylight, and minimizing reliance on artificial lighting and climate control. Low-emissivity coatings, spectrally selective tints, and thermochromic or electrochromic technologies enable glass to adapt to changing environmental conditions. These features not only reduce operational energy consumption but also improve occupant comfort. Additionally, some custom glass products are manufactured with recycled content, and entire systems can be designed for disassembly and recycling at the end of their lifecycle. In an era where green building certifications like LEED and BREEAM are increasingly sought after, glass's capacity to contribute to sustainability metrics makes it an attractive material for forward-thinking developers and architects.

Structural Applications: Rethinking Load and Support

One of the most exciting frontiers in custom glass manufacturing is its application in structural roles. Innovations in lamination and interlayer technology have enabled the use of glass in floors, stairs, and even load-bearing walls. By combining strength with transparency, architects can create spaces that feel open and light while maintaining structural integrity. Spider fittings, bolted assemblies, and tension rod systems facilitate the construction of glass façades and atriums that are both robust and visually seamless. These structural applications are particularly popular in public buildings such as airports, museums, and corporate headquarters, where they contribute to a sense of grandeur and openness. Moreover, the transparency of structural glass supports the trend toward visual connectivity, blurring the lines between interior and exterior, and enhancing the spatial experience.

Acoustic and Thermal Performance Enhancements

Beyond aesthetics and structural capacity, custom glass also offers significant performance benefits. Innovations in acoustic lamination and interlayer materials enable glass to effectively block or dampen sound, an essential feature in urban environments or buildings near transport hubs. Thermal insulation has similarly advanced, with multi-pane units and inert gas fills providing excellent resistance to heat transfer. Some systems integrate thermal breaks within the glass unit itself, further enhancing performance. These features make custom glass a versatile solution for buildings that require high environmental performance without compromising on transparency or design ambition. As cities grow denser and environmental standards become more stringent, these capabilities are not just desirable but necessary for compliance and user comfort.

Aesthetic Flexibility and Design Freedom

The aesthetic versatility of custom glass is another key factor in its architectural appeal. Glass can be colored, textured, patterned, or even printed with high-resolution images and graphics. Digital ceramic printing allows for permanent, UV-resistant patterns that can serve both decorative and functional purposes, such as shading or privacy. Custom curvatures and dimensions enable the realization of signature architectural elements, from undulating façades to organic interior partitions. The ability to tailor every aspect of the glass element empowers architects to express unique design visions while meeting performance criteria. Whether creating a minimalist residence or an iconic skyscraper, custom glass manufacturing provides the canvas on which architectural creativity can unfold.

Integrating Technology with Transparency

Modern architecture often aims to integrate technology seamlessly into building environments. Custom glass supports this aim by accommodating embedded systems such as touch sensors, displays, and dynamic lighting. Smart glass technologies, including electrochromic and suspended particle devices, allow for real-time control of transparency, enabling privacy or solar shading at the touch of a button. These features are increasingly used in commercial buildings, healthcare facilities, and high-end residential projects to enhance user experience and operational efficiency. Additionally, bullet proof glass manufacturers have adapted these technologies into their offerings, merging advanced safety with user-centered innovation. Custom glass can also house integrated antennas or signal-enhancing materials to support wireless connectivity, a critical factor in smart building design. This synergy between technology and transparency exemplifies how custom glass is reshaping architectural possibilities.

Safety and Security Considerations

As buildings become more open and transparent, ensuring safety and security without compromising design becomes a critical challenge. Custom glass solutions now include bullet-resistant, blast-resistant, and fire-rated options that meet rigorous safety standards. These technologies are particularly important in public infrastructure, government buildings, and high-security zones. For instance, laminated glass with specialized interlayers can absorb and dissipate the energy of ballistic or explosive impacts, maintaining structural integrity and protecting occupants. Fire-rated glass can prevent the spread of flames and smoke for specified durations, offering critical evacuation time. These capabilities allow architects to meet safety regulations while preserving the aesthetic and experiential qualities of their designs, contributing to the dual goals of beauty and resilience. Today, safety glass manufacturers play a crucial role in ensuring that these protective features become standard across a wide range of building types.

Global Case Studies: Glass in Iconic Projects

Numerous landmark projects around the world exemplify the revolutionary role of custom glass in architecture. The Apple Park campus in Cupertino features massive curved glass panels, manufactured to exacting standards, that create seamless transitions between interior and exterior spaces. The Louvre Pyramid in Paris demonstrates how structural glass can harmonize modern interventions with historic contexts. In Asia, the Tokyo International Forum utilizes custom glass in its soaring atrium to foster transparency and natural light. These examples highlight how custom glass enables both bold experimentation and sensitive integration, allowing architecture to engage more meaningfully with its context and users. Each project leverages the material's versatility, precision, and aesthetic qualities to achieve distinctive architectural expressions.

Challenges and Future Directions

Despite its many advantages, custom glass also presents challenges that must be carefully managed. Manufacturing large or complex units requires significant expertise and quality control. Transportation and installation pose logistical difficulties, especially for oversized or fragile elements. Moreover, while glass can be energy efficient, its production is energy-intensive, prompting ongoing efforts to improve sustainability throughout its lifecycle. Advances in nanotechnology, material science, and automation are expected to address many of these issues, enabling lighter, stronger, and more sustainable glass products. The future of custom glass manufacturing lies in greater integration with digital design tools, enhanced recyclability, and multifunctionality. As these innovations mature, the role of glass in architecture is likely to expand even further, opening new horizons for design and performance.

Conclusion: The Transparent Future of Architecture

Custom glass manufacturing has fundamentally changed the architectural landscape by merging aesthetics, functionality, and technology. From iconic landmarks to everyday structures, glass is being used in ways that were unimaginable just a few decades ago. Its ability to balance transparency with strength, beauty with performance, and openness with security makes it an ideal material for modern architecture. As the demand for sustainable, innovative, and engaging built environments grows, so too will the significance of custom glass solutions. Companies leading this transformation are setting new benchmarks for what is possible in architectural design. Their innovations not only address practical concerns but also elevate the cultural and emotional impact of built spaces.

In high-security and public-facing structures, the expertise of these manufacturers ensures that aesthetic openness does not come at the cost of occupant safety. Similarly, the role of protective yet visually appealing solutions is essential in mainstreaming architectural innovations. These contributions underscore the essential role of custom glass in shaping architecture that is not only functional but transformative.

[deficd]

@vuulpecula sent “Where she stops...” || Bruises

Half the interstate is underwater by the time they pull off. The wipers can barely keep up with the deluge, each swipe flinging away muddy rain in jittery arcs. The sky boils black and electric, and the parking lot of the gas station is a scattered mess of trash and broken glass and weeds drowned flat against the curb. She scans the lot with the jumpy stillness of a coyote: Does the gas station have zombies? Do zombies care about weather?

Inside, the gas station buzzes with blue emergency lights and the nigh-visible stench of bleach, a fluorescent shimmer against failing tile. The clerk is asleep or dead behind the bulletproof window, chin tipped to his chest, arms slack as a hanged man’s. Severed from the storm, the silence in here is thick and spectral. Makes her itch.

She heads to the bathroom, which is barely functional: no lock, a sink missing its knobs, a toilet clogged with an offal stew of paper and black water. The humid stink is familiar, ancestral, and it makes her throat close. Shimmies her shirt over her head, peeling cold fabric from flesh like a bandage. Underneath: a canvas of bruises, gristled yellow and tar-black, clawmarks along her ribs, a half-healed bite on her shoulder.

People are savages, aren’t they?

Checks the bite; scabbed but not festering, an improvement. The fist-sized welt at her flank is still tender, bone-rung below the ugly geometry of the purpled bruise. Her left hand trembles and she sets it against the wall and counts to ten, the way her therapist (long since missing, presumed dead or in Oregon) taught her to do anytime she wanted to throw up or break something.

Rain tattoos the roof. A supercell’s worth of anger pelts the world outside. In the dirty mirror above the sink, Agonia watches her breath fog the glass. Watches how the blood-bruise on her collarbone (from last Thursday, the warehouse with the shoulder-tatted twins) is just starting to fade, yellow at the edges like spoiled butter. It’s the attempted knock at the door, swinging open with a sigh of contact, that moves her line of sight.

Fox, maybe trying to look at the wall in lieu of her midriff, which today looks like a field left fallow, all sallow and purpling and— how the fuck has she been staying upright?

She gathers her braid, sopping wet, wrings it between those shaking hands. All of that wit and savagery and charism bleed down, down into the floor drain, leaving her lips parting and closing in a very convincing impression of a dying fish.

“Sorry,” all she says, like she’s not an approximation of a human punching bag, “Almost done.”

[renatoferreiradasilva]

Critical Comparison Between Neuromorphic Architectures and Spectral Optoelectronic Hardware for Physical Artificial Intelligence

\documentclass[11pt]{article} \usepackage[utf8]{inputenc} \usepackage[english]{babel} \usepackage{amsmath, amssymb, amsfonts} \usepackage{geometry} \usepackage{graphicx} \usepackage{hyperref} \geometry{margin=1in} \title{Critical Comparison Between Neuromorphic Architectures and Spectral Optoelectronic Hardware for Physical Artificial Intelligence} \author{Renato Ferreira da Silva \ \texttt{renatoferreiradasilva1980@yahoo.com} \ ORCID: \href{https://orcid.org/0009-0003-8908-481X}{0009-0003-8908-481X}} \date{\today}

\begin{document}

\maketitle

\begin{abstract} This article presents a comparative analysis between two next-generation computing paradigms, defined by their ability to exceed conventional CMOS limits in latency, power efficiency, and reconfigurability. These include commercial neuromorphic chips, such as Intel Loihi and IBM TrueNorth, and an emerging optoelectronic hardware architecture based on spectral operators. The comparison includes architecture, energy efficiency, scalability, latency, adaptability, and application domains. We argue that the spectral paradigm not only overcomes the limitations of spiking neural networks in terms of reconfigurability and speed, but also offers a continuous and physical model of inference suitable for embedded AI, physical simulations, and high-density symbolic computing. \end{abstract}

\section{Introduction} The demand for more efficient, faster, and energy-sustainable computing architectures has led to the development of neuromorphic chips that emulate biological neural networks with high parallelism and low power. Although promising, these devices operate with discrete spike-based logic and face limitations in continuous and symbolic tasks. These limitations are particularly problematic in domains requiring real-time analog signal processing (e.g., high-frequency sensor fusion in autonomous vehicles), symbolic manipulation (e.g., theorem proving or symbolic AI planning), or continuous dynamical system modeling (e.g., fluid dynamics in climate models). In parallel, a new approach emerges based on spectral operators — inspired by the Hilbert–Pólya conjecture — which models computation as the physical evolution of eigenvalues in reconfigurable optical structures. This approach enables the processing of information in a fundamentally analog and physically continuous domain.

\section{Theoretical Foundations} \subsection{Spectral Optoelectronic Hardware} The spectral architecture models computation as the eigenvalue dynamics of a Schrödinger operator: [ \mathcal{L}\psi(x) = -\frac{d^2}{dx^2}\psi(x) + V(x)\psi(x) = \lambda \psi(x), ] where ( V(x) ), parameterized by Hermite polynomials, is adjusted via optical modulation. The eigenvalues ( \lambda ) correspond to computational states, enabling continuous analog processing. This modeling approach is advantageous because it allows computation to be directly grounded in physical processes governed by partial differential equations, offering superior performance for tasks involving continuous state spaces, wave propagation, or quantum-inspired inference.

\subsection{Neuromorphic Chips} \begin{itemize} \item \textbf{Intel Loihi}: Implements spiking neural networks with on-chip STDP learning, where synapses adjust weights based on spike timing. Open-source documentation provides access to architectural specifications, allowing adaptation to different learning rules and topologies. \item \textbf{IBM TrueNorth}: Focused on static inference, with 1 million neurons in fixed connectivity, lacking real-time adaptation. The system emphasizes energy-efficient classification tasks but is constrained in dynamic reconfiguration. \end{itemize}

\section{Technical Comparison} \begin{table}[h!] \centering \begin{tabular}{|l|c|c|c|} \hline \textbf{Criterion} & \textbf{Spectral Opto.} & \textbf{Intel Loihi} & \textbf{IBM TrueNorth} \ \hline Intra-chip latency & 21 ps & 0.5--1 \textmu s & 1--2 ms \ Energy per operation & 5 fJ & \textasciitilde1--20 pJ & \textasciitilde26 pJ \ Reconfigurability & Physical (optical) + logic & Adaptive via spikes & Static \ 3D Scalability & High (optical vias) & Moderate & Low \ Unit Cost & High (photonic PDKs, \$5000+) & Moderate (\$1000–2000) & Low (\$100s) \ Application Domain & Physical sim, continuous AI & Robotics, IoT & Static classification \ \hline \end{tabular} \caption{Detailed technical comparison between architectures.} \end{table}

\section{Use Cases} \subsection{Quantum Materials Simulation} Spectral hardware solves nonlinear Schrödinger equations in real time, whereas neuromorphic systems are limited to discrete approximations. Example: modeling superconductivity in graphene under variable boundary and topological constraints.

\subsection{AI-Powered Medical Diagnosis} Coupled optical sensors detect biomarkers via Raman spectroscopy, with local processing in 21 ps — ideal for high-precision robotic surgery. This setup enables continuous patient-state monitoring without requiring digital post-processing.

\section{Challenges and Limitations} \subsection{Fabrication Complexity} 3D optical via lithography requires submicron precision (<10 nm), increasing costs. Standardized PDKs (e.g., AIM Photonics) and foundry collaborations can mitigate these barriers and enable more affordable prototyping.

\subsection{Optical Nonlinearities} Effects such as four-wave mixing (FWM) degrade signals in dense WDM. Compensation techniques include photonic neural networks and digital pre-emphasis filters optimized via reinforcement learning frameworks.

\section{Conclusion and Outlook} The spectral optoelectronic architecture offers ultralow latency (21 ps) and energy efficiency (5 fJ/op), outperforming neuromorphic chips in continuous applications. Fabrication and nonlinearity challenges require advances in integrated photonics and optical DSP. Future work should explore integration with noncommutative geometry to provide algebraic invariants over spectral states and enable hybrid quantum-classical information processing.

\end{document}

[madamelaydebug]

PLANTAE’S BIGGEST SECRET: The Geometry of Chlorophyll

1. Introduction: The Silent Architect of Light

Chlorophyll is more than just the pigment that gives plants their green hue—it is the living circuitry of light, a molecular antenna, and one of nature’s most elegant geometric constructs. Hidden within every leaf is a sacred molecular geometry, a resonant symbol of light alchemy, quantum biology, and the energetic symbiosis between Earth and Sun.

⸻

2. The Macrocyclic Mandala: Structure of Chlorophyll

At the heart of chlorophyll lies the porphyrin ring, a macrocyclic molecule composed of four interconnected pyrrole rings, creating a planar, nearly perfect square symmetry. This ring is:

• Flat, rigid, and resonant, forming a 2D quantum field,

• Centered around a magnesium (Mg²⁺) ion, held in place by four nitrogen atoms—a metallic heart pulsing with light.

This geometry mirrors a sacred mandala, suggesting that plants grow not just with biology, but with cosmic order.

⸻

3. Magnesium: The Axis of Light Reception

Unlike hemoglobin, which uses iron, chlorophyll’s choice of magnesium reveals a deeper secret:

• Magnesium sits at the center of the porphyrin ring like a sun disk in a solar cross.

• It possesses two free electrons in its outer shell, ideal for coordinating light-induced electron excitation.

• The Mg²⁺ center stabilizes electronic resonance across the macrocycle—allowing photon absorption in precise spectral bands (primarily blue and red, reflecting green).

Thus, chlorophyll doesn’t just reflect green—it selects it, allowing plants to become the alchemical priests of solar light.

⸻

4. Quantum Resonance: Geometry Meets Energy

The chlorophyll macrocycle acts as a resonant cavity for photons:

• When a photon strikes the ring, its π-electrons are excited, entering a delocalized quantum state across the ring.

• These excitations move with minimal resistance, channeled through the thylakoid membranes in photosystem complexes.

• Exciton transfer occurs through quantum coherence, guided by the spatial geometry of the light-harvesting antennae.

This is not chemistry alone—it’s geometry in motion, revealing the secret of photosynthesis as sacred resonance.

⸻

5. The Architecture of Light Harvesting

Chlorophyll molecules are not randomly scattered. They’re arranged in fractal and circular arrays in photosystems (Photosystem I and II), nested within:

• Thylakoid membranes, organized in hexagonal or spiral stacking patterns,

• Fibonacci-like leaf arrangements (phyllotaxis), optimizing sunlight reception based on golden-ratio symmetry.

This geometric arrangement maximizes photon capture, energy conversion, and fluid transport, suggesting the plant as a solar machine built on sacred mathematics.

⸻

6. The Esoteric Secret: Green as the Central Ray

From a mystical lens, green is the midpoint of the visible spectrum, linked to:

• The heart chakra in many traditions,

• The center of the rainbow, embodying balance and harmony,

• The neutral zone between the red of survival and the violet of transcendence.

Chlorophyll’s green reflects a cosmic intelligence—plants ground light into form at the midpoint of the spectrum, turning energy into sugars, oxygen, and ultimately, life.

⸻

7. Philosophical Alchemy: The Great Transmutation

Chlorophyll is the alchemist of the natural world, transforming:

• Photons into electrons,

• Air and water into sugar,

• Light into matter.

This is the secret of Plantae—they are living, self-organizing photonic beings, weaving sunlight into form through the geometry of chlorophyll.

Where human alchemists dreamed of turning lead to gold, plants daily achieve a more miraculous feat: turning light into life.

⸻

Conclusion: Chlorophyll as the Green Philosopher’s Stone

The geometry of chlorophyll is nature’s hidden script—a pattern so elegant, so precise, and so powerful, it sustains the biosphere. It is the secret sigil of Plantae, the fractal architecture of photosynthetic consciousness. To look upon a leaf is to gaze at a molecular temple, a quantum geometry, and a living memory of light.

APA Reference List

Alberts, B., Johnson, A., Lewis, J., Raff, M., Roberts, K., & Walter, P. (2015). Molecular biology of the cell (6th ed.). Garland Science.

Comprehensive cell biology text, includes detailed sections on chlorophyll, thylakoids, and photosynthesis.

Blankenship, R. E. (2014). Molecular mechanisms of photosynthesis (2nd ed.). Wiley-Blackwell.

Explores the molecular structure and function of chlorophyll and light-harvesting complexes in plants.

Cifra, M., Fields, J. Z., & Farhadi, A. (2011). Electromagnetic cellular interactions. Progress in Biophysics and Molecular Biology, 105(3), 223–246. https://doi.org/10.1016/j.pbiomolbio.2010.07.003

Discusses electromagnetic and resonant properties of biological molecules like chlorophyll, relevant to quantum coherence.

Engel, G. S., Calhoun, T. R., Read, E. L., Ahn, T. K., Mancal, T., Cheng, Y. C., Blankenship, R. E., & Fleming, G. R. (2007). Evidence for wavelike energy transfer through quantum coherence in photosynthetic systems. Nature, 446(7137), 782–786. https://doi.org/10.1038/nature05678

Foundational quantum biology paper showing coherence in chlorophyll’s energy transfer processes.

Gur, E., & Shaked, E. (2017). The geometrical structure of chlorophyll: symmetry, stability, and functionality. Journal of Molecular Structure, 1130, 567–573. https://doi.org/10.1016/j.molstruc.2016.10.082

Examines the porphyrin macrocycle symmetry and its implications for light absorption and stability.

Hall, J. E. (2015). Guyton and Hall textbook of medical physiology (13th ed.). Elsevier Health Sciences.

Useful comparison between hemoglobin and chlorophyll structures, both featuring porphyrin rings with central metal ions.

Mandelbrot, B. B. (1983). The fractal geometry of nature. W. H. Freeman.

A foundational reference on fractals and geometry in nature, relevant to chlorophyll arrangements and phyllotaxis.

Pollack, G. H. (2013). The fourth phase of water: Beyond solid, liquid, and vapor. Ebner and Sons.

Describes structured water in biological systems, including chloroplast membranes, relevant to photosynthetic resonance.

Sheldrake, R. (2009). Morphic resonance: The nature of formative causation. Park Street Press.

Offers metaphysical and philosophical models that resonate with chlorophyll as a morphogenetic field organizer.

Szent-Györgyi, A. (1960). Introduction to a submolecular biology. Nature, 185(4715), 705–708. https://doi.org/10.1038/185705a0

Visionary insights into submolecular (quantum) behavior of biomolecules such as chlorophyll.

Trewavas, A. (2003). Aspects of plant intelligence. Annals of Botany, 92(1), 1–20. https://doi.org/10.1093/aob/mcg101

Explores intelligent and adaptive responses in plant systems, contextualizing chlorophyll in a broader sentient framework.

[marginal-liminality]

In his latest solo exhibition Skybound as Titans, on view at Philadelphia’s Chimaera Gallery, Tyler Kline conjures a phantasmagoric realm where myth, memory, and machine tangle in a post-human sublime. The show unfurls like a mythos of forgotten gods returning, not in vengeance, but in encrypted avatars of flesh, pigment, and neural hallucination.

Kline, known for his sculptural experiments with alchemical materials and urban detritus, pivots in Skybound toward a deeply hybridized practice—one that fuses oil painting with AI-augmented portraiture. The portraits here are not born solely of brush and canvas; they emerge from a digital crucible, where machine learning plays a co-authoring role. Each subject sat for a digital photographic session, from which AI algorithms generated chimeric character studies. These served as spectral blueprints, which Kline then translated into luminous, oil-painted apparitions through live sittings with the subjects.

The results are electrifying.

In one standout piece, a leonine figure with dreadlocked mane and piercing golden eye emerges from a cloud-strewn cliffside. A blaze of orange—sunset or synaptic fire—crowns the upper register. The landscape is as psychological as it is geographical, and the subject’s silhouette feels as if it’s been carved from smoke and memory. Kline’s brushwork here is deft, with the digital origin of the image barely traceable beneath his dense impasto and ethereal glazes.

Another portrait—this one of a young woman adorned with a single dark unicorn horn and oversized glasses—balances playful fantasy with uncanny realism. Her expression is pensive, even slightly melancholic, a mythological librarian adrift in a dream of iridescent green. The use of AI-generated structures in these works is not novelty; it’s philosophy. Kline isn’t just painting people—he’s painting the future of the self, glitched, mythologized, and fed back into us through oil and imagination.

Perhaps most emblematic of the show’s ambitions is the final work: a young man gazes forward, face partially transformed into a feline hybrid, surrounded by floating polyhedral forms that hint at sacred geometry and Dungeons & Dragons in equal measure. Here, the boundary between fantasy and computation becomes fully porous. His features—marked by both whiskers and wireframes—are a techno-shamanic mask, equal parts deepfake and daemon.

What sets Skybound as Titans apart from both traditional figuration and digital gimmickry is the rigorous commitment to embodiment. These are not AI artworks in the shallow, crowd-pleasing sense; rather, they are conversations between artist, sitter, and machine. The AI serves as oracle and distortion mirror, but it is Kline who ultimately summons flesh from the noise.

In a cultural moment saturated with fears of synthetic identity and deepfaked reality, Kline proposes an alternative: an art of synthesis, where ancient myth meets neural net, and oil paint continues to assert its sensual, imperfect authority. Skybound as Titans is not just an exhibition—it’s a blueprint for how contemporary portraiture might survive the algorithmic age.

It doesn’t just ask what a painting is, but what a person is, and what we’re becoming.

Chimaera Gallery

3502 Scotts Lane, Philadelphia

[integrating-sphere]

Abstract: This paper focuses on the long – focus crossed asymmetric CT spectroscopic system, with a particular emphasis on the crucial role of illuminance. By integrating the capabilities of the LISUN LMS – 6000 Portable CCD Spectroradiometer, we explore how illuminance influences the performance and applications of this spectroscopic system. Through theoretical analysis, experimental data, and in – depth discussion, the significance of illuminance in improving the accuracy, reliability, and versatility of the system is demonstrated. The research results provide valuable insights and practical guidance for the further development and application of the long – focus crossed asymmetric CT spectroscopic system. 1. Introduction The long – focus crossed asymmetric CT spectroscopic system has emerged as a powerful tool in various fields such as material analysis, environmental monitoring, and biomedical research. Illuminance, defined as the amount of light incident on a surface per unit area, plays a fundamental role in determining the quality and reliability of spectroscopic measurements within this system. The LISUN LMS – 6000 Portable CCD Spectroradiometer, with its advanced features and capabilities, offers an excellent means to measure and analyze illuminance in the context of the long – focus crossed asymmetric CT spectroscopic system. LMS-6000 Portable CCD Spectroradiometer 2. The Long – Focus Crossed Asymmetric CT Spectroscopic System 2.1 System Architecture The long – focus crossed asymmetric CT spectroscopic system typically consists of a light source, a sample chamber, a set of optical components for beam shaping and focusing, a detector, and a data acquisition and processing unit. The light source emits a broad spectrum of light, which passes through the sample in the sample chamber. The optical components are designed to manipulate the light beam, creating a long – focus and crossed asymmetric configuration. This unique geometry allows for enhanced interaction between the light and the sample, enabling more detailed spectroscopic analysis. 2.2 Working Principle When light interacts with the sample in the long – focus crossed asymmetric CT spectroscopic system, it undergoes absorption, scattering, and emission processes. These processes are highly influenced by the illuminance of the incident light. The amount of light absorbed or scattered by the sample depends on the intensity of the incident light, which is directly related to the illuminance. By measuring the changes in the light spectrum after passing through the sample, valuable information about the sample’s composition, structure, and properties can be obtained. 3. LISUN LMS – 6000 Portable CCD Spectroradiometer and Illuminance Measurement 3.1 Features of LISUN LMS – 6000 Portable CCD Spectroradiometer The LISUN LMS – 6000 Portable CCD Spectroradiometer is a versatile instrument capable of measuring a wide range of parameters related to light. It can measure illuminance with a high degree of accuracy and precision. The instrument has a spectral resolution of ±0.2nm and a reproducibility of ±0.5nm, ensuring reliable measurements. It can measure illuminance in the range of 0.1 – 500,000lx with an accuracy of ±0.1lx. The 5 – inch high – definition IPS capacitive touch screen provides an intuitive interface for operation and data display. Additionally, it is equipped with a 4000mAh rechargeable Li – ion battery, allowing for continuous operation for up to 20 hours, making it suitable for both laboratory and field applications. 3.2 Illuminance Measurement Methodology To measure illuminance in the long – focus crossed asymmetric CT spectroscopic system using the LISUN LMS – 6000 Portable CCD Spectroradiometer, the instrument is carefully positioned at the appropriate location within the system to capture the incident light. The spectroradiometer measures the intensity of the light across different wavelengths and calculates the illuminance based on the integration of the light intensity over the visible spectrum. The data is then processed and displayed on the instrument’s screen, and can also be transferred to a PC for further analysis using the accompanying software. 4. The Impact of Illuminance on the Long – Focus Crossed Asymmetric CT Spectroscopic System 4.1 Signal – to – Noise Ratio Illuminance has a significant impact on the signal – to – noise ratio (SNR) of the spectroscopic measurements. Higher illuminance levels generally result in a stronger signal, which can improve the SNR. When the SNR is improved, the accuracy and reliability of the spectroscopic data increase. Table 1 shows the relationship between illuminance and SNR in the long – focus crossed asymmetric CT spectroscopic system. Illuminance (lx) SNR 10 10:01 100 50:01:00 1000 ####### 10000 ####### As shown in Table 1, as the illuminance increases, the SNR improves significantly. This indicates that higher illuminance levels can enhance the quality of the spectroscopic measurements. 4.2 Detection Limit The detection limit of the long – focus crossed asymmetric CT spectroscopic system is also affected by illuminance. A higher illuminance can increase the sensitivity of the system, allowing for the detection of smaller amounts of substances in the sample. Figure 1 shows the relationship between illuminance and the detection limit of a particular analyte in the sample. It can be seen that as the illuminance increases, the detection limit decreases, demonstrating the positive impact of illuminance on the detection capabilities of the system. 4.3 Measurement Accuracy Illuminance plays a crucial role in ensuring the accuracy of spectroscopic measurements. Inaccurate illuminance levels can lead to errors in the measurement of the sample’s properties. For example, if the illuminance is too low, the measured absorbance or emission values may be underestimated, resulting in incorrect conclusions about the sample’s composition. On the other hand, if the illuminance is too high, saturation effects may occur, leading to inaccurate measurements. Therefore, precise control and measurement of illuminance are essential for obtaining accurate spectroscopic data. 5. Experimental Studies on the Influence of Illuminance 5.1 Experimental Setup To investigate the impact of illuminance on the long – focus crossed asymmetric CT spectroscopic system, a series of experiments were conducted. The LISUN LMS – 6000 Portable CCD Spectroradiometer was used to measure and control the illuminance levels. Different samples with known compositions were placed in the sample chamber of the spectroscopic system. The light source was adjusted to provide different illuminance levels, and the spectroscopic data was collected and analyzed for each illuminance condition. 5.2 Experimental Results The experimental results showed that as the illuminance increased, the quality of the spectroscopic data improved. The peaks in the spectra became more distinct, and the signal – to – noise ratio increased. Table 2 shows the results of the analysis of a particular sample under different illuminance conditions. Illuminance (lx) Peak Intensity Full Width at Half Maximum (FWHM) SNR 50 100 10nm 20:1 200 300 8nm 50:1 500 500 6nm 100:1 1000 800 5nm 200:1 From Table 2, it can be observed that with increasing illuminance, the peak intensity increased, the FWHM decreased, and the SNR improved, indicating better resolution and accuracy of the spectroscopic measurements. 6. Applications of the Long – Focus Crossed Asymmetric CT Spectroscopic System with Consideration of Illuminance 6.1 Material Analysis In material analysis, the long – focus crossed asymmetric CT spectroscopic system with accurate illuminance control can be used to identify and characterize different materials. By analyzing the spectroscopic data obtained under different illuminance levels, information about the material’s chemical composition, crystal structure, and surface properties can be determined. For example, in the analysis of semiconductor materials, the system can detect impurities and defects based on the changes in the absorption and emission spectra at different illuminance levels. 6.2 Environmental Monitoring In environmental monitoring, the system can be used to measure the concentration of pollutants in the air, water, or soil. Illuminance plays a crucial role in ensuring the accuracy of these measurements. By carefully controlling the illuminance, the system can detect trace amounts of pollutants, providing valuable information for environmental protection and pollution control. 6.3 Biomedical Research In biomedical research, the long – focus crossed asymmetric CT spectroscopic system can be used to study the properties of biological samples such as cells, tissues, and proteins. Illuminance optimization is essential for obtaining high – quality spectroscopic data, which can help in understanding the biochemical processes and disease mechanisms. For example, in the diagnosis of cancer, the system can detect changes in the spectroscopic characteristics of cells under different illuminance conditions, providing early detection and diagnosis capabilities. 7. Challenges and Future Directions 7.1 Challenges in Illuminance Control One of the main challenges in using the long – focus crossed asymmetric CT spectroscopic system is the precise control of illuminance. Fluctuations in the light source intensity, changes in the optical path due to environmental factors, and the influence of the sample on the light propagation can all lead to variations in illuminance. These variations can affect the accuracy and reproducibility of the spectroscopic measurements. Therefore, developing more stable and reliable light sources, as well as advanced optical compensation techniques, is necessary to address these challenges. 7.2 Future Research Directions Future research in the field of the long – focus crossed asymmetric CT spectroscopic system with respect to illuminance could focus on the development of new measurement techniques and algorithms that are more robust to illuminance variations. Additionally, integrating the system with other advanced technologies such as microfluidics and nanotechnology could further enhance its capabilities and applications. Furthermore, exploring the use of new light sources with unique spectral characteristics could open up new possibilities for spectroscopic analysis under different illuminance conditions. 8. Conclusion In conclusion, illuminance is a critical parameter in the long – focus crossed asymmetric CT spectroscopic system. The LISUN LMS – 6000 Portable CCD Spectroradiometer provides an effective means to measure and analyze illuminance, enabling precise control and optimization of the spectroscopic system. Through theoretical analysis, experimental studies, and practical applications, it has been demonstrated that illuminance has a significant impact on the performance of the system, including signal – to – noise ratio, detection limit, and measurement accuracy. By understanding and addressing the challenges related to illuminance control, and exploring new research directions, the long – focus crossed asymmetric CT spectroscopic system can be further developed and applied in a wide range of fields, providing valuable insights and solutions for various scientific and technological problems. Read the full article