#compounded polyhedra

[knotty-et-al]

Polyhedra on dotted isometric paper

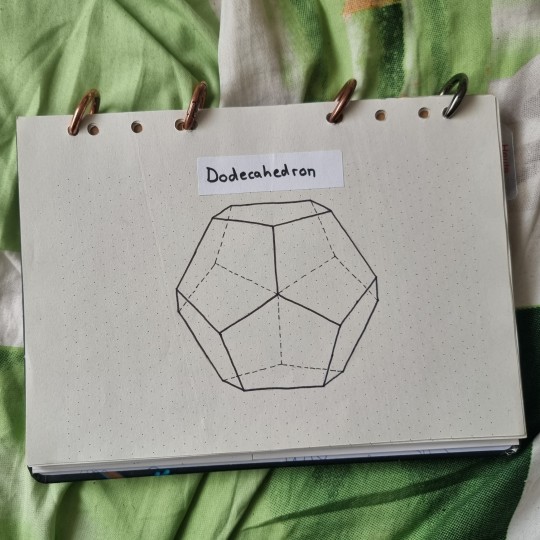
Drawing polyhedra on dotted isometric paper is so calming. One does not need to use a ruler or a compass. Instead one can just count dots to determine the length, and play around with the angles.

[notreallyherehahaha]

The Compound of the Cuboctahedron and Its Dual, the Rhombic Dodecahedron

Created with Stella 4d, which you can try for free here.

[dailypolyhedra]

Daily Polyhedra Archive

(An ongoing list of polyhedra that have already been covered by this blog, mostly for my own convenience. This is a work-in-progress.)

Platonic solids

Cube

Dodecahedron

Icosahedron

Octahedron

Tetrahedron

Kepler-Poinsot polyhedra

Great dodecahedron

Great icosahedron

Great stellated dodecahedron

Small stellated dodecahedron

Archimedean solids

Cuboctahedron

Great rhombicuboctahedron

Icosidodecahedron

Rhombicosidodecahedron

Small rhombicuboctahedron

Snub cube

Snub dodecahedron

Truncated cube

Truncated dodecahedron

Truncated icosahedron

Truncated icosidodecahedron

Truncated octahedron

Truncated tetrahedron

Catalan solids

Deltoidal hexecontahedron

Deltoidal icositetrahedron

Disdyakis dodecahedron

Disdyakis triacontahedron

Pentagonal hexecontahedron

Pentagonal icositetrahedron

Pentakis dodecahedron

Rhombic dodecahedron

Rhombic triacontahedron

Tetrakis hexahedron

Triakis icosahedron

Triakis octahedron

Triakis tetrahedron

Prismatic polyhedra

Triangular prism

Pentagonal prism

Schönhardt polyhedron

Decagrammic antiprism

Square antiprism

Pyramidal polyhedra

Square pyramid

Hexagonal pyramid

Johnson solids

Square pyramid (J1)

Triangular bipyramid (J12)

Gyroelongated pentagonal rotunda (J25)

Square orthobicupola (J28)

Pentagonal orthobicupola (J30)

Elongated pentagonal gyrobicupola (J39)

Gyroelongated pentagonal cupolarotunda (J47)

Gyroelongated pentagonal birotunda (J48)

Triaugmented hexagonal prism (J57)

Augmented tridiminished icosahedron (J64)

Biaugmented truncated cube (J67)

Gyrate rhombicosidodecahedron (J72)

Snub disphenoid (J84)

Sphenomegacorona (J88)

Hebesphenomegacorona (J89)

Disphenocingulum (J90)

Bilunabirotunda (J91)

Triangular hebesphenorotunda (J92)

Near-miss Johnson solids

Edge-contracted icosahedron

Tetrated dodecahedron

Truncated triakis tetrahedron

Pentahexagonal pyritoheptacontatetrahedron

Rectified truncated icosahedron

Chamfered cube

Chamfered dodecahedron

Hemipolyhedra

Small dodecahemicosahedron

Tetrahemihexacron

Small icosihemidodecahedron

Zonohedra

Rhombic enneacontahedron

Bilinski dodecahedron

Truncated rhombicosidodecahedron

Rhombic icosahedron

Star polyhedra

Small snub icosidodecahedron

Rhombicosahedron

Great snub icosidodecahedron

Inverted snub dodecadodecahedron

Excavated dodecahedron

Great rhombic triacontahedron

Great triakis icosahedron

Great dirhombicosidodecahedron

Cubitruncated cuboctahedron

Quasitruncated great stellated dodecahedron

Uncategorised polyhedra

Chamfered icosahedron

Triamond stretched octahedron

Diminished rhombic dodecahedron

Császár polyhedron

Szilassi polyhedron

Biscribed orthotruncated propello octahedron

Rectified triangular prism

Escher's solid

Polyhedral compounds

Compound of five cubohemioctahedra

Compound of twenty octahedra

Compound of four cubes

Compound of two icosahedra

Compound of two great retrosnub icosidodecahedra

Compound of eight octahedra

Rhomboctahedron (compound of four triangular prisms)

Compound of five tetrahedra

[sozeugs]

two truncated tetrahedra

IN COMPOUND WITH A CUBE

Inspiration:

[nicovincenti]

Max Brückner’s Collection of Polyhedral Models (1900) Max Brückner (1860–1934) was a German geometer, known for his collection of stellated and uniform polyhedra, which he documented in his 1900 book Vielecke und Vielflache: Theorie und Geschichte (Polygons and Polyhedra: Theory and History). Included in the influential study was a compound of three octahedra, made famous by M. C. Escher's 1948 print Stars, which depicts the shape floating through space in the form of a cage with two chameleons inside it.

[sjweminem]

hi this might be the weirdest ask uve ever gotten but

https://newtonpermetersquare(.)tumblr(.)com/post/671754854936543232/weve-been-fooled

i like this meme but dont know enough math to properly ID it, and youre literally the only person on tumblr i can think to ask about math things...is there a special name for each of the the 3d functions? i think that polyhedron is a 5 cube compound????

answering wicked late cuz there's a massive pileup in my inbox (16 dead, 38 wounded) but oh this is FAR from my weirdest ask..

ok first of all let me just say i would suck a dick to get this on a shirt. but to answer your question (possibly) those first 2 graphs look a lot like the riemann zeta function. the third, with which i'm less familiar, looks like a twin dodecahedron? it's just another one of infinitely many polyhedra (if the name seems wild just know that the simple cube and pyramid, AKA a tetrahedron, are in that family- it basically just means "many sides" and the prefix states how many. my favorite is the octahedron!!!!). however idk if this graph is being used for any mathematical purpose beyond representing the shape three-dimensionally. that last graph is too small to figure out but my first instinct is to categorize it as a representation of a logarithmic spiral in 3D (once again if that label is unfamiliar, a much more well-known logarithmic function is the fibonacci sequence AKA the golden ratio). hopefully i'm wrong and it's something better cuz i fucking HATED logarithms in college

[polyhedronguy]

This shape is a compound of six cubes. It has the same overall symmetry as a cube (or octahedron), but the component cubes appear to be at crazy orientations to each other. It was not at all easy to make.

With compound polyhedra like this one, I always enjoy choosing one colour after another and mentally tracing the single cube within the overall shape.

It is quite difficult to find a good and accurate mathematical description of this shape, though pictures of it are common enough. Note that some well-known online mathematical resources do not seem to give the right construction. Here is my own attempt:

It is possible to inscribe an octahedron O within a cube C as follows. We will assume C has edge length 1. Select two opposite edges e1 and e2 of C. The midpoints of these will be two vertices of O. Now consider the two faces of C (f1 and f2) whose corners meet the ends of e1 and e2. The remaining four vertices of O are then found on the (other) diagonals of f1 and f2, a distance of (sqrt2 - 1)/2 from each end. With basic geometry you can convince yourself that O is indeed a regular octahedron, also with edge length 1. Now, use all the symmetries of O to make images of C. You will find that the complete set of these images (including C itself) forms the compound shape.

[materialsscienceandengineering]

Gold glue really does bond nanocages 'contradicting' logic

It has long been known that gold can be used to do things that philosophers have never even dreamed of. The Institute of Nuclear Physics of the Polish Academy of Sciences in Cracow has confirmed the existence of 'gold glue': bonds involving gold atoms, capable of permanently bonding protein rings. Skilfully used by an international team of scientists, the bonds have made it possible to construct molecular nanocages with a structure so far unparalleled in nature or even in mathematics.

The world of science has been interested in molecular cages for years. Not without reason. Chemical molecules, including those that would under normal conditions enter into chemical reactions, can be enclosed within their empty interiors. The particles of the enclosed compound, separated by the walls of the cage from the environment, have nothing to bond with. These cages can therefore be used, for example, to transport drugs safely into a cancer cell, only releasing the drug when they are inside it.

Molecular cages are polyhedra made up of smaller 'bricks', usually protein molecules. The bricks can't be of any shape. For example, if we wanted to build a molecular polyhedron using only objects with the outline of an equilateral triangle, geometry would limit us to only three solid figures: a tetrahedron, an octahedron or an icosahedron. So far, there have been no other structural possibilities.

Read more.

[kaishirase]

This model was designed by Alex Doskey using Great Stella. It was then exported to VRML format, which was used to build the physical model in a ZCorp stereolithograph machine. The model is only about 6 inches across, and has all regular non-intersecting faces.

Models by Adam Stolicki

Models by Adam Stolicki

Model by Adam Stolicki Model by Adam Stolicki Models by Adam Stolicki

Model by Adam Stolicki Model by Adam Stolicki Models by Adam Stolicki

Models by Giacomo Artoni

Hollow spherical model Stellation of Small Icosihemidodecahedron Stellation of Snub Cube Stellation of Great Dodecahemidodecahedron

Hollow spherical model

designed using this tutorial Compound of 6 Dodecahedra Stellation of Small Stellated

Truncated Dodecahedron Compound of 5 Octahedra

Models by Richard Stratton

Stellation of Great Ditrigonal Dodecicosidodecahedron Stellation of Small Icosihemidodecahedron Stellation of Snub Cube Stellation of Great Dodecahemidodecahedron

Stellation of Great Ditrigonal

Dodecicosidodecahedron Stellation of Small

Icosihemidodecahedron Stellation of Snub Cube Stellation of Great

Dodecahemidodecahedron

Models by Marc Picquendar

Stellation of Rhombic Triacontahedron Stellation of Rhombic Triacontahedron Small Snub Icosicosidodecahedron

Stellation of Rhombic Triacontahedron Final Stellation of Rhombic

Triacontahedron Small Snub

Icosicosidodecahedron

Compound of 5 Cubes Stellation of Truncated Octahedron Pentagonal Hexecontahedron Pentagonal Icositetrahedron

Compound of 5 Cubes Stellation of Truncated

Octahedron Pentagonal

Hexecontahedron Pentagonal

Icositetrahedron

Models by Robert Rech

Stellation of Great Ditrigonal Dodecicosidodecahedron Stellation of Small Icosihemidodecahedron

Stellation of Strombic Icositetrahedron Stellation of Triakisoctahedron

Models by Linda Zurich

Stellation of Cubitruncated Cuboctahedron Another stellation Stellation of Icosahedron Another stellation

Stellation of Cubitruncated

Cuboctahedron Another stellation Stellation of Icosahedron Another stellation

Models by Karlos Alonso Mediavilla

Compound of 5 Tetrahedra Compound of 3 Cubes Faceted Cube Compound of Dodecahedron and Great Dodecahedron

Compound of 5 Tetrahedra Compound of 3 Cubes Faceted Cube Compound of Dodecahedron

and Great Dodecahedron

Models by Steve Waterman

Waterman polyhedra

The first ten Waterman polyhedra in each of the three types available in Great Stella.

Models by Michael Barltrop

Compound of 15 Cuboids Compound of 4 Cubes Stellation of the Small Dodecahemicosahedron

Compound of 15 Cuboids Compound of 4 Cubes Stellation of the Small Dodecahemicosahedron

Monoacral stellation of Compound of 15 Cuboids Stellation of Small Dodecahemicosahedron Stellation of Great Dodecahemicosahedron

Monoacral stellation of

Compound of 15 Cuboids Stellation of Small Dodecahemicosahedron Stellation of Great Dodecahemicosahedron

A stellation Stellation of Small Stellated Truncated Dodecahedron

Stellation of the first Faceted

Rhombicosidodecahedron found in

Stella's Library Stellation of Small Stellated

Truncated Dodecahedron

Models by Keith Davison

See also: What people have to say about Stella.

[joyfuldelusionchaosvaliant]

Science and Chemistry Classes

Hyper-CEST NMR technique reveals missing structure of a novel container molecule

by Forschungsverbund Berlin e.V. (FVB)

Using the Hyper-CEST NMR technique, the team led by Leif Schröder from the Leibniz-Forschungsinstitut für Molekulare Pharmakologie (FMP) and the Deutsches Krebsforschungszentrum (DKFZ) has managed to reveal two previously little researched variants of a type of transport container from the class of metal–organic polyhedra (MOPs). The researchers want to use this knowledge to develop a novel type of contrast agent in MR (magnetic resonance) imaging.

The concept of a modular construction system proves useful in many applications for assembling complex structures for specific functions from individual, repeated sub-units. In chemistry, the principle can be used to construct a self-assembling network from smaller molecular units that acts as a transport container of a defined size. For example, several metal ions can be linked with organic molecules. These MOPs (metal–organic polyhedra) are used, for instance, to capture greenhouse gases or to pave the way for more effective chemotherapeutic agents by loading them with certain drugs, which they then release in the tumor. Several aspects of the behavior of these structures have not yet been adequately explored. This is partly because there are not always appropriate techniques available to observe the loading and unloading of these MOPs at the molecular level—often, no differences can be measured between the empty and loaded variants for either the container or its contents.

In cooperation with a team from the University of Oulu in Finland, Leif Schröder's research group has now investigated MOPs that spontaneously assemble in solution from iron ions and an organic compound to form tetrahedra. In the process, the organic struts can be attached differently to the iron "nodes." Essentially, this influences the properties of MOPs, such as their capacity to kill tumor cells. In the case of the MOP under study, however, it was previously thought that only one of the three theoretically predicted variants existed. The other two variants were considered too unstable because no analytical methods were able to detect them. Using a new method of magnetic resonance (hyper-CEST NMR), Schröder's team member Jabadurai Jayapaul has now succeeded in demonstrating that these previously unknown variants do exist.

The colleagues from Finland were able to confirm the signals of these "hidden" MOPs using theoretical calculations. Although they only occur in very small proportions, the measurements showed that altering the attachment of struts causes dramatic changes in the loading and unloading of containers. Certain sub-types of containers can be selected to speed up the process. The researchers are now using this knowledge to develop a novel type of contrast agent in MR imaging in which the loading of the container influences the MRI signal. But observations also show that there is greater potential for new insights for further optimizing drug carriers. In other words, the first impression gained of these structures may not always be the right one. A substantial part of their nature may remain hidden until we are able to detect them using far more sensitive methods.

[knotty-et-al]

Compound of 3 rhombic dodecahedra

In motion:

[Rhombus module by Nick Robinson]

[notreallyherehahaha]

A Cube, Held Prisoner by a Stella Octangula

I made this three-part compound using Stella 4d (available here) to repeatedly tetstell a truncated octahedron.

[dailypolyhedra]

Polyhedron of the Day #89: Compound of twenty octahedra

The compound of twenty octahedra is a uniform polyhedral compound. It has 160 faces, 240 edges, and 60 vertices. It is a special case of the compound of 20 octahedra with rotational freedom. It shares its edge arrangement with several other polyhedra. Its vertex figure is a stellated octagon. Its dual is a compound of twenty cubes.

Compound of twenty octahedra image created using Robert Webb's Stella software, found at http://www.software3d.com/Stella.php.

[nicovincenti]

Max Brückner’s Collection of Polyhedral Models (1900)

Max Brückner (1860–1934) was a German geometer, known for his collection of stellated and uniform polyhedra, which he documented in his 1900 book Vielecke und Vielflache: Theorie und Geschichte (Polygons and Polyhedra: Theory and History). Included in the influential study was a compound of three octahedra, made famous by M. C. Escher's 1948 print Stars, which depicts the shape floating through space in the form of a cage with two chameleons inside it.

[bobacupcake]

Some suggestions for your consideration: An alternate to a middle mouse button. Plenty of people don't have one; I certainly don't; I use a laptop w/ a trackpad. Also maybe add new, additional types of chunk shapes? (Specifically, I think a rhombic dodecahedron or medial rhombic triacontahedron would look really super rad, but there's a bunch of stellated, & compound polyhedra in general that would be really satisfying as chunks) I don't know how much effort that would be to model those, though.

ah thank you!! i will keep those in mind [nods in agreement as if i know what those shapes are and definitely not currently googling them] there are a few different chunk models in the Game Files that i never got around to including. complex shapes such as: cube. but i will look into it for the next update!! . 

[kitwallace]

Miller indices to polyhedra

Using OpenSCAD CSG operations

A while back (well 6 years ago) , I got interested in computing gem cuts in OpenSCAD.  My approach then used the CSG operations to put facets on a sphere as in this post on diamond cuts. The specification of a gem facet uses spherical coordinates : azimuth,  polar angle and radial distance. These correspond to the settings on a faceting machine with which muliple facets around the z axis can be cut at even increments by stepping the azimuth for a fixed polar angle. 

This led to an interest in crystal forms and the use of Miller indices to define the form.  Individual faces are defined by the normal to the face and its distance from the origin. eg  110,1. My approach here to was to use CSG operations as in this post.  Crystal descriptions use a base indice and symmetry rules which depend on the crystal system, eg  {100} , 1 , cubic  to generate the set of simple face indices - here the 6 faces -  001,010,100,001,010,100  where 1  mean -1 [usually written as 1 with bar over] This worked well and allowed me to create some of the irregular polyhedral in the cubic system as well as crystal forms with descriptions taken from the Dexter programme by Mark Holtkamp .  

Computing vertices and faces

The CSG approach allows the solids to be constructed and printed, but I wanted to be able to produce other forms of the solids, such as the open-face form or a net of the solid.  These transformations require vertex and face data which is not available from the constructed OpenSCAD objects. The aim then was to transform a crystal’s description into vertex/face data computationally.  The full procedure involves a  number of steps:

1.  Expand the crystal description using the defined symmetry rules into a set of simple Miller indices.  This was addressed in the previous work using CSG to create the solids.  So far I have handled only cubic systems.

2   Face normals to vertices The algorithm for this is outlined by Eric Dowty , the developer of the impressive Shape software. Every combination of three faces is intersected,  ignoring those with parallel faces.  Any such vertex which is outside any of the faces, based on perpendicular distance to the face is ignored. Finally we remove duplicate vertices. 

3  Vertices to hull Initial OpenSCAD code for an incremental construction of the hull was provided by Alexander Pruss on Thingiverse which yields triangular faces.  

4  Merge coplanar triangular faces  This stitches together adjacent coplanar triangles to form a polygonal face.

5  Generate forms from the vertex/face descriptions.  Here I am able to use my existing OpenSCAD code to generate solid, wireframe and open-face forms as well as nets, and can also use the conway operations to further transform the resultant polyhedra.

Tolerance is needed on most numeric tests, such as coplanarity, vertex identity and sidedness.

By comparison, the conversion from the representation as vertices and faces to Miller indices is trivial, so the easy way to check that the procedure is working is to round-trip a known solid from polyhedron to Miller and then back to a polyhedron or vice-versa. The only restriction is that only convex solids can be so transformed.

Examples

The Gyroid  (pentagonal icositetrahedron)

The regular version is one of the catalan solids. The pentagonal face is irregular.  In crystallography, the shape has a Miller index of {3 2 1}  and gyroid symmetry, resulting in irregular pentagonal faces.

Openface form

Nets 

Irregular solids 

An advantage of the Miller representation of a solid is that the position of each face can be changed by altering its distance from the origin.  This corresponds to different growth rates on different faces of a crystal, but by Steno’s law,the    law of constancy of interfacial angles, leaves the mineral shape unchanged.  So a random pertubation of the face distances gives rise to a randomly varied solid. Here is a rhombic dodecahedron {110} 

with perturbated faces:

which are now a mixture of 4-,5 and 6-sided faces.

Text on Faces

With a vertice/face description, we can also place text on a face.  Here is a unfair die - made by adjusting the two xy-faces - there are better uses of labeling :)

The solid can also be oriented so it is placed on its largest face for printing.

Compound solids

Another feature of the Miller representation is that we can create compounds of solids by concatenating the lists of Miller indices for each component. So a combination of a cube and a tetrahedron is simple to construct and to vary by  changing the face distances.

One benefit is that a form can be cut in any plane by adding a single indice - for example to cut a crytstal form in half vertically for ease of printing we can add [[0,0,-1],0 ].

Quasi crystal

Physical crystals are a lattice of the same molecule so Miller indices of physical crystals are restricted to integer values.  However computationally we are not so restricted. Many of the regular solids can be created from Miller indices as the work of  Zefiro and Ardigo shows. For example, the regular dodecahedron can be represented as {1 phi 0 } where phi is the golden ratio:

Crystals

The forms of real mineral crystals can be repesented as compounds of a number of simpler forms.  This is one of the forms of Boracite from the Smorf database

and its net:

and this version of Zircon from AuntDaisy on Thinigiverse 

Last word

It’s been a while to get to this stage in the quest to generate crystal forms from Miller representations using only user-space computations in OpenSCAD.  Some code is available on GitHub .  There is still work to do, particulaly to handle crystal systems with non-orthogonal axes. 

I have been inspired and helped by many in the Thingiverse (now sadly only useful as an archive it seems ) and OpenSCAD communities, for which grateful thanks.