#pair of linear equations in two variables
Explore tagged Tumblr posts
Text
Pair of Linear Equations in Two Variables
10th Standard Mathematics (CBSE)
A pair of linear equations in two variables consists of two equations, each representing a straight line in a two-dimensional plane. Typically expressed in the form ax + by = c, these equations can be solved using various methods, such as substitution, elimination, or graphical representation. The solution to the system is the point of intersection of the two lines, which can yield one unique solution, no solution (parallel lines), or infinitely many solutions (coincident lines).
0 notes
Text
Class 10 maths chapter 3 pair of linear equations in two variables most expected competency focused practice questions: https://www.youtube.com/playlist?list=PLR9VlrPIVynqlOxwLZXWTHIaoo7TZi-ye
Class 10 maths chapter 3 pair of linear equations in two variables most expected competency focused questions cbse
#cbse class 10 maths#chapter 3#pair of linear equations in two variables#competency focused practice questions
1 note
·
View note
Text
a Basic Linear Regression Model
What is linear regression?
Linear regression analysis is used to predict the value of a variable based on the value of another variable. The variable you want to predict is called the dependent variable. The variable you are using to predict the other variable's value is called the independent variable.
This form of analysis estimates the coefficients of the linear equation, involving one or more independent variables that best predict the value of the dependent variable. Linear regression fits a straight line or surface that minimizes the discrepancies between predicted and actual output values. There are simple linear regression calculators that use a “least squares” method to discover the best-fit line for a set of paired data. You then estimate the value of X (dependent variable)
n statistics, simple linear regression (SLR) is a linear regression model with a single explanatory variable.[1][2][3][4][5] That is, it concerns two-dimensional sample points with one independent variable and one dependent variable (conventionally, the x and y coordinates in a Cartesian coordinate system) and finds a linear function (a non-vertical straight line) that, as accurately as possible, predicts the dependent variable values as a function of the independent variable. The adjective simple refers to the fact that the outcome variable is related to a single predictor.
It is common to make the additional stipulation that the ordinary least squares (OLS) method should be used: the accuracy of each predicted value is measured by its squared residual (vertical distance between the point of the data set and the fitted line), and the goal is to make the sum of these squared deviations as small as possible. In this case, the slope of the fitted line is equal to the correlation between y and x corrected by the ratio of standard deviations of these variables. The intercept of the fitted line is such that the line passes through the center of mass (x, y) of the data points.
Formulation and computation
[edit]
This relationship between the true (but unobserved) underlying parameters α and β and the data points is called a linear regression model.
Here we have introduced
x¯ and y¯ as the average of the xi and yi, respectively
Δxi and Δyi as the deviations in xi and yi with respect to their respective means.
Expanded formulas
[edit]
Interpretation
[edit]
Relationship with the sample covariance matrix
[edit]
where
rxy is the sample correlation coefficient between x and y
sx and sy are the uncorrected sample standard deviations of x and y
sx2 and sx,y are the sample variance and sample covariance, respectively
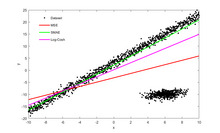
Interpretation about the slope
[edit]
Interpretation about the intercept
Interpretation about the correlation
[edit]
Numerical properties
[edit]
The regression line goes through the center of mass point, (x¯,y¯), if the model includes an intercept term (i.e., not forced through the origin).
The sum of the residuals is zero if the model includes an intercept term:∑i=1nε^i=0.
The residuals and x values are uncorrelated (whether or not there is an intercept term in the model), meaning:∑i=1nxiε^i=0
The relationship between ρxy (the correlation coefficient for the population) and the population variances of y (σy2) and the error term of ϵ (σϵ2) is:[10]: 401 σϵ2=(1−ρxy2)σy2For extreme values of ρxy this is self evident. Since when ρxy=0 then σϵ2=σy2. And when ρxy=1 then σϵ2=0.
Statistical properties
[edit]
Description of the statistical properties of estimators from the simple linear regression estimates requires the use of a statistical model. The following is based on assuming the validity of a model under which the estimates are optimal. It is also possible to evaluate the properties under other assumptions, such as inhomogeneity, but this is discussed elsewhere.[clarification needed]
Unbiasedness
[edit]
Variance of the mean response
[edit]
where m is the number of data points.
Variance of the predicted response
[edit]
Further information: Prediction interval
Confidence intervals
[edit]
The standard method of constructing confidence intervals for linear regression coefficients relies on the normality assumption, which is justified if either:
the errors in the regression are normally distributed (the so-called classic regression assumption), or
the number of observations n is sufficiently large, in which case the estimator is approximately normally distributed.
The latter case is justified by the central limit theorem.
Normality assumption
[edit]
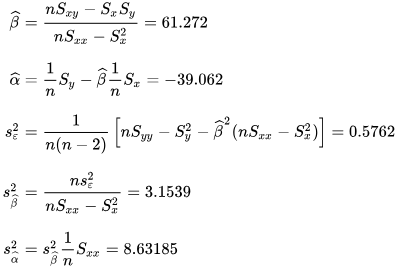
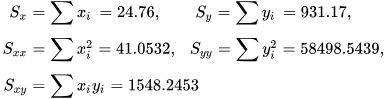
Asymptotic assumption
[edit]
The alternative second assumption states that when the number of points in the dataset is "large enough", the law of large numbers and the central limit theorem become applicable, and then the distribution of the estimators is approximately normal. Under this assumption all formulas derived in the previous section remain valid, with the only exception that the quantile t*n−2 of Student's t distribution is replaced with the quantile q* of the standard normal distribution. Occasionally the fraction 1/n−2 is replaced with 1/n. When n is large such a change does not alter the results appreciably.
Numerical example
[edit]
See also: Ordinary least squares § Example, and Linear least squares § Example
Alternatives
[edit]Calculating the parameters of a linear model by minimizing the squared error.
In SLR, there is an underlying assumption that only the dependent variable contains measurement error; if the explanatory variable is also measured with error, then simple regression is not appropriate for estimating the underlying relationship because it will be biased due to regression dilution.
Other estimation methods that can be used in place of ordinary least squares include least absolute deviations (minimizing the sum of absolute values of residuals) and the Theil–Sen estimator (which chooses a line whose slope is the median of the slopes determined by pairs of sample points).
Deming regression (total least squares) also finds a line that fits a set of two-dimensional sample points, but (unlike ordinary least squares, least absolute deviations, and median slope regression) it is not really an instance of simple linear regression, because it does not separate the coordinates into one dependent and one independent variable and could potentially return a vertical line as its fit. can lead to a model that attempts to fit the outliers more than the data.
Line fitting
[edit]
This section is an excerpt from Line fitting.[edit]
Line fitting is the process of constructing a straight line that has the best fit to a series of data points.
Several methods exist, considering:
Vertical distance: Simple linear regression
Resistance to outliers: Robust simple linear regression
Perpendicular distance: Orthogonal regression (this is not scale-invariant i.e. changing the measurement units leads to a different line.)
Weighted geometric distance: Deming regression
Scale invariant approach: Major axis regression This allows for measurement error in both variables, and gives an equivalent equation if the measurement units are altered.
Simple linear regression without the intercept term (single regressor)
[edit]
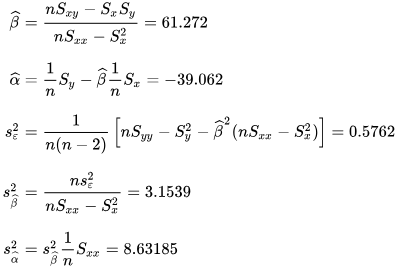
2 notes
·
View notes
Text
ch 3 maths class 10 ncert solutions
Class 10 Maths Chapter 3, Pair of Linear Equations in Two Variables," features the most important questions strictly aligned with CBSE board exam standards. All the questions are either directly from the NCERT textbook or have been asked in previous board exams. Emphasis is placed on concepts that are frequently tested, ensuring students focus on what is essential for the exams. This study material is perfect for quickly revising key topics and gaining a thorough understanding of the concepts that matter most for success in the CBSE board exams.
0 notes
Text
Benefits of Learning: Digital Classes for 9th & 10th Math and Science

We all know that 9th and 10th class math and science could be difficult. It is generally the first important year of examinations for students, which can be difficult. Parents frequently believe that taking their children to extra classes would help them perform better. While this may be true, it might be difficult for students.
That’s the reason why online courses come in useful. They work similarly to smart classrooms, allowing students to view and engage with the material they are studying. Instead of simply remembering information, people may observe how things function. Learning becomes as simple as installing an app!

Now, students in 9th and 10th grade do not have worries about their classes. Using digital class apps allows them to follow along with their math and science classes. It helps them understand every detail and increases their problem-solving abilities.
Students can also access lessons from other educational platforms when taking classes digitally. Therefore, you are free to explore different syllabi while you are studying the current one. These days, learning is more about truly understanding things than taking exams.
Also, look at the most recent 9th and 10th class syllabuses, which may be helpful!
Class 9 Math's: Unit-wise
Unit 1-Real numbers
Unit 2-Polynomials and Factorization
Unit 3-The Elements of Geometry
Unit 4-Lines and Angles
Unit 5-Co-Ordinate Geometry
Unit 6-Linear Equations in Two Variables
Unit 7-Triangles
Unit 8-Quadrilaterals
Unit 9-Statistics
Unit 10-Surface Areas and Volumes
Unit 11-Areas
Unit 12-Circles
Unit 13-Geometrical Constructions
Unit 14-Probability
Unit 15-Proofs in Mathematics
Class 9 Physics Syllabus: Chapter-wise
Chapter 1-Matter Around Us
Chapter 2-Motion
Chapter 3-Laws of Motion
Chapter 4-Refraction of Light at Plane Surfaces
Chapter 5-Gravitation
Chapter 6-Is Matter Pure?
Chapter 7-Atoms and Molecules
Chapter 8-Floating Bodies
Chapter 9-What is inside the Atom?
Chapter 10-Work and Energy
Chapter 11-Heat
Chapter 12-Sound
Class 9 Biology Syllabus: Chapter-wise
Chapter 1-Cell its structure and functions
Chapter 2-Plant tissues
Chapter 3-Animal tissues
Chapter 4-Plasma membrane
Chapter 5-Diversity in Living Organism
Chapter 6-Sense Organs – I
Chapter 7-Sense Organs – II
Chapter 8-Animal behavior
Chapter 9-Challenges in Improving Agricultural Products
Chapter 10-Adaptations in Different Ecosystems
Chapter 11-Soil pollution
Chapter 12-Bio geochemical cycles
The Telangana State Board (TS) students who are looking for the Class 9 Physics, Biology Syllabus can find it in the syllabus mentioned above. moreover, review the AP Class 9th syllabus also.
Class 10 Math and Science Syllabus:
The Telangana State Board Class 10 math's syllabus is given below; class tenth With the use of this TS 10th Class Math's Textbooks Syllabus, students may prepare for their final exams and have an effective understanding of the subject matter, therefore achieving the highest marks possible.
10th Class Math's: Unit Wise
Unit 1-Real numbers
Unit 2-Sets
Unit 3-Polynomials
Unit 4-Pair of Linear Equations in Two Variables
Unit 5-Quadratic Equations
Unit 6-Progressions
Unit 7-Coordinate Geometry
Unit 8-Similar Triangles
Unit 9-Tangents and Secants to a Circle
Unit 10-Mensuration
Unit 11-Trigonometry
Unit 12-Applications of Trigonometry
Unit 13-Probability
Unit 14-Statistics
Class 10 Physics Syllabus: Chapter Wise
Chapter 1-Reflection of Light by Different Surfaces
Chapter 2-Chemical Reactions and Equations
Chapter 3-Acids, Bases and Salts
Chapter 4-Refraction of Light at Curved Surfaces
Chapter 5-Human Eye and Colorful World
Chapter 6-Structure of Atom
Chapter 7-Classification of Elements – Periodic Table
Chapter 8-Chemical Bonding
Chapter 9-Electric Current
Chapter 10-Electromagnetism
Chapter 11-Principles of Metallurgy
Chapter 12-Carbon and Compounds
10th Class Biology Syllabus: Chapter-Wise
Chapter 1-Nutrition
Chapter 2-Respiration
Chapter 3-Transportation
Chapter 4-Excretion
Chapter 5-Coordination
Chapter 6-Reproduction
Chapter 7-Coordination in Life Processes
Chapter 8-Heredity
Chapter 9-Our Environment
Chapter 10-Natural Resources
The TS Board Class 10 Math's & Science topic syllabus is available above, complete with chapter-by-chapter details. Students can go through the most recent math and science syllabus to be aware of all the key subjects they need to study for exams.
Additionally, visit the below pages. We hope you found these pages useful:
Telangana Board Syllabus Related Links
Telangana Board Class 6 Syllabus
Telangana Board Class 7 Syllabus
Telangana Board Class 8 Syllabus
Telangana Board Class 9 Syllabus
#elearning#digital class#digital classes online#digital classroom#digital content#digital learning#digital teacher#smart class#online learning
1 note
·
View note
Video
youtube
Class 10 Pair of Linear Equation in two variable example solution | Ch 3...
0 notes
Link
Equation Reducible To Linear Equation Ex 3.5 |Pair Of Linear Equations In Two Variables CBSE 10 Math
#cbse 10th maths online classes#equation reducible to pair of linear equations in two variablespair of linear equations in two variableslinear equations in two variables cl
2 notes
·
View notes
Text
Today I learned how fun it is to draw a hyperbolic paraboloid.

Pictured above is one example of it, the graph of the function f : IR² → IR defined by the equation f(x,y) := xy, with some points of the input plane marked and height of the graph indicated in four points. It is drawn only for a square around the origin (that makes it easy to draw), but if you imagine extending it on the edges to make a rounder shape, you might be able to see the (probably) most famous rendition of the hyperbolic paraboloid shape, the Pringles chip:
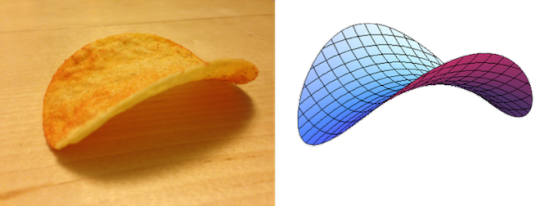
So why is the hyperbolic paraboloid so fun to draw? Well, a defining property (and according to Wikipedia, one of the oldest definitions) of the shape is that it may be generated by a moving line that is parallel to a fixed plane and crosses two fixed skew lines.
Skew lines are lines that don't cross but are also not parallel.
In the above example, this property is easily explained like this: if you fix either x or y into place (treat it like a constant) in the equation z = xy, you get the points z of the cross-section of the graph of f and the plane corresponding to the equation y = c or x = c, depending on which variable you fixed to the constant c. This is now a linear equation, which represents a straight line.
So, whenever you have two points that you know are in the graph, which also lie in the same plane parallel to either the xz-plane or the yz-plane, we now know that the straight line that contains both of them is also completely contained in the graph. This provides us with a fairly simple way to draw (part of) this beautiful shape:
Draw a square around the origin in the xy-plane and for it's corners find the corresponding z values in the graph. In this case, I chose a square with sidelength 2, but the actual values don't matter that much.
Having found four points (above and below the corners of the square), connect them with straight lines parallel to the sides of the square. These are in the graph.
Choose two of those lines which are opposite each other, segment them evenly with the same segment lengths, and connect corresponding points with straight lines.
Technically, in the last step you have to draw infinitely many lines to get the real shape. But then again, technically to get the actual real shape, in the first step you would have to draw an infinitely large square (or connect both of the pairs of opposite lines with infinitely long straight lines, that works too). But the great thing is, your brain will automatically fill in the rest of the shape for you if you have enough segments.
More generally, the definition given above means you can really take any two skew lines, find the plane they are both parallel to, and then connect them with straight lines that lie in planes that cross that plane with a 90 degree angle. I think it's really cool how you can draw such a complicated looking shape with so few and easy instructions, and only using straight lines. In fact, if I understood the Wikipedia arcticle correctly, this property is probably one of the reasons Pringles are even made in this shape, because it makes manufacturing fairly simple.
40 notes
·
View notes
Link

We are International Exponential Education Pvt. Ltd. (IXPOE), a coaching institute founded by IITians in 2013. IXPOE was conceptualized by IIT alumni to provide quality education for competitive exams to select students and deliver best results year after year. Our teachers are experienced and experts in training students for various competitive examinations. The focus in our classes is to equip the students to handle the curriculum of the Indian Board (CBSE/ICSE/PUC) and International Board (IGCSE/IB/HL/SL/AS Level/A Level) and up skill them to handle competitive exams like JEE Mains, CET, JEE Advanced, COMEDK, BITSAT etc. We have emerged as the preferred Institute in a short span of time. IXPOE ensures high quality of education in all the courses offered. We have our branches at located in Thubarahalli,Whitefield. We have created three more channels namely, "THE IXPERTS DESK" (all the educational related teaching content will be taught in English), "THE IXPERTS ROOM" (all the educational related contents will be completely taught only in Hindi language) and another "Ixperts Opinion" (One stop channel for experts opinions and advice on any important topics). Request you to kindly follow and subscribe them too for more daily updates on those channels as well. Please find the links below for both the channels. THE IXPERTS DESK: https://www.youtube.com/watch?v=iXtGAvGrXOw, . Subscribe to all our channels for more such videos and hit the bell icon if not yet done, such that you do not miss any of our new videos . Please do let us know if you want us to make any videos on particular topic(s), such that we can publish those videos at the earliest.
#IXPOE#CBSE ICSE PUC IGCSE IB A Level PHYSICS CHEMISTRY#MATH#BIOLOGY#Methods in Pair of Linear Equations in two variables by Mr. Sant Kumar (in Hindi) - Part 2 | IXPOE
0 notes
Text
Gordon Freeman’s thesis is titled Observation of Einstein-Podolsky-Rosen Entanglement on Supraquantum Structures by Induction Through Nonlinear Transuranic Crystal of Extremely Long Wavelength (ELW) Pulse from Mode-Locked Source Array in this essay i will pick it apart piece by piece to better understand what the fuck it means
Einsten-Podolsky-Rosen Entanglement This bit is one of the staples of Quantum Mechanics, called the EPR paradox/entanglement. We should already know that entanglement, as a basic part of quantum physics, is when two separate particles rely on each other on their positions. It's the idea that if you measure/observe one particle, you could accurately predict the other particle because the two are ~entangled~ The EPR paradox is a a thought experiment, like a lot of quantum physics is.
The thought experiment involves a pair of particles prepared in an entangled state (note that this terminology was invented only later). Einstein, Podolsky, and Rosen pointed out that, in this state, if the position of the first particle were measured, the result of measuring the position of the second particle could be predicted. If, instead, the momentum of the first particle were measured, then the result of measuring the momentum of the second particle could be predicted. They argued that no action taken on the first particle could instantaneously affect the other, since this would involve information being transmitted faster than light, which is forbidden by the theory of relativity. They invoked a principle, later known as the "EPR criterion of reality", positing that, "If, without in any way disturbing a system, we can predict with certainty (i.e., with probability equal to unity) the value of a physical quantity, then there exists an element of reality corresponding to that quantity". From this, they inferred that the second particle must have a definite value of position and of momentum prior to either being measured. This contradicted the view associated with Niels Bohr and Werner Heisenberg, according to which a quantum particle does not have a definite value of a property like momentum until the measurement takes place.
Supraquantum Structures I can't find any definitions nor anything in scientific papers that tell me what this is without me having to go down a rabbithole of terminology. So instead I'm going to look at the terminology itself to see what it means. Supra is a prefix meaning "above" or "beyond". The definition of quantum is "a discrete quantity of energy proportional in magnitude to the frequency of the radiation it represents." That's a little obtuse for a definition so let's just go witth this instead. "Quantum mechanics is a fundamental theory in physics that describes the physical properties of nature at small scales, of the order of atoms and subatomic particles." If we take "quantum" to mean "atoms/subatomic particles" then Supraquatum would just mean something bigger than a particle, right? A supraquantum structure could be a single cell organism.
Now, lets put the first bit together, EPR Entanglement on supraquantum structures. These are observations on the entanglement of objects bigger than particles, which is hard to prove in it of itself, so the next bit must be important to the entire puzzle Induction through Nonlinear Transuranic Crystal of Extremely Long Wavelength Induction is a way of charging objects. In the induction process, a charged object is brought near but not touched to a neutral conducting object. The presence of a charged object near a neutral conductor will force (or induce) electrons within the conductor to move.Nonlinear dynamics is the branch of physics that studies systems governed by equations more complex than the linear, aX+b form. Nonlinear systems, such as the weather or neurons, often appear chaotic, unpredictable or counter-intuitive, and yet their behavior is not random. Transuranic just means any element with a higher atomic number than uranium (92) So i seemed to have glanced over the "pulse" bit in the thesis title because of the acronym throwing me off. so the ELW pulse from a mode-locked source array is the electric pulses coming from the test chamber's laser "source array", and its Mode-Locked.
Mode-locking is a technique in optics by which a laser can be made to produce pulses of light of extremely short duration
I can't find any definition of souce array so im going to assume that's what the laser machine is. This bit was easy, but to go on about it; the electric pulses/lasers theyre using to induct the crystal is on the long part of the wavelength scale, which doesnt make much sense considering that it looks like electricity. It makes more sense once you consider what the scientists say before you enter the test chamber "I'm afraid we'll be deviating a bit from standard analysis procedures today, Gordon" "This is the purest sample we've seen yet, and potentially the most unstable" Now, the actual machine is called the Anti-Mass Spectrometer, and it only really exists in half-life. but if i pick apart the name i can figure out what it really does. A spectrometer is a scientific instrument used to separate and measure spectral components of a physical phenomenon. Spectrometer is a broad term often used to describe instruments that measure a continuous variable of a phenomenon where the spectral components are somehow mixed. Anti-mass is just another term for Negative Mass, something that also only really exists in theoretical physics, or at least is only referred to in a theoretical sense.
In theoretical physics, negative mass is a type of exotic matter whose mass is of opposite sign to the mass of normal matter, e.g. −1 kg. Such matter would violate one or more energy conditions and show some strange properties, stemming from the ambiguity as to whether attraction should refer to force or the oppositely oriented acceleration for negative mass. It is used in certain speculative hypotheses, such as on the construction of traversable wormholes and the Alcubierre drive. Currently, the closest known real representative of such exotic matter is a region of negative pressure density produced by the Casimir effect.
So this spectrometer would analyze negative mass. This is already getting into science fiction but you can also call theoretical physics "science fiction" itself, just with more math.
To go on, we must assume that the anti-mass spectrometer should be mode-locking an ELW to induct a transuranic crystal, but in reality it's not an ELW at all. Long wavelengths are invisible, most wavelengths are. an extremely long wavelength would probably? be longer than radio waves, and this is going into the electromagnetic spectrum
"Extremely Long Wavelength" isn't even a real term, so we'll have to turn it into one. "Extremely Low Frequency" is the closest real term in name
Extremely low frequency (ELF) is the ITU designation for electromagnetic radiation (radio waves) with frequencies from 3 to 30 Hz, and corresponding wavelengths of 100,000 to 10,000 kilometers, respectively. In atmospheric science, an alternative definition is usually given, from 3 Hz to 3 kHz. In the related magnetosphere science, the lower frequency electromagnetic oscillations (pulsations occurring below ~3 Hz) are considered to lie in the ULF range, which is thus also defined differently from the ITU radio bands.
ELF's also have multiple definitions depending on who you ask.
ELF is a subradio frequency. Some medical peer reviewed journal articles refer to ELF in the context of "extremely low frequency (ELF) magnetic fields (MF)" with frequencies of 50 Hz and 50–80 Hz. United States Government agencies, such as NASA, describe ELF as non-ionizing radiation with frequencies between 0 and 300 Hz. The World Health Organization (WHO) have used ELF to refer to the concept of "extremely low frequency (ELF) electric and magnetic fields (EMF)" The WHO also stated that at frequencies between 0 and 300 Hz, "the wavelengths in air are very long (6000 km at 50 Hz and 5000 km at 60 Hz), and, in practical situations, the electric and magnetic fields act independently of one another and are measured separately."
A real life example of the usage of these electromagnetic frequencies is the US government using ELFs to communicate with deeply submerged submarines. If this is the type of wavelength Gordon plans on using to induct a transuranic crystal, then he wouldn't need to have a spectrometer do it, nor any mode-locked source array. So it couldn't be ELFs, right? let's forget this tangent and move on IF it is an electromagnetic wave he's using to induct a transuranic crystal, then it would more likely be above the visible light spectrum. The thing is, the electricity in the scene with the anti-mass spectrometer lands within the visible light spectrum. It's green, and green has a wavelength of 500–565 nm (frequency of 530–600 THz). thats 500 nanometers, not a long wavelength at all.
I'm sure whatever writer at valve decided to write out this thesis title didn't research these terms as much as i have just now, either that or they purposefully made it sound obtuse enough to fit into science fiction without it needing to make sense. But the fun of science fiction is that it's based on real science IMO. so lets forget that it says ELW and go the other direction. Extremely Short Wavelength.
Inducting anything with ionizing radiation of a gamma ray would definitely get you results, under any spectrometer. now, i want to go back to the tangent of the transuranic crystal. It's completely possible that there is no such thing and it was made up for the game with the in-game lore that it's from Xen or whatever, but i want to look into the possibility of using elements that exist.
The game implies that they found the crystal but it doesn't outright say it, which covers their ass on the fact that transuranic elements are synthetically made. Neptunium and Plutonium are made through decay chains in Uranium and can also be found in atmospheric tests after a nuclear explosion. So Neptunium and Plutonium can technically be "found".
So let's go through all the transuranic elements and see if any of them can become crystals! Since they all are unstable i'm also gonna list their half-lives for fun. For reference, STP means standard temperature and pressure
Neptunium (93) - solid at stp, appears silvery and metallic. the most stable isotopes are Np-237 with a half-life of 2.14 million years; Np-236 with a half-life of 154,000 years; and Np-235 with a half-life of 396 days. it's also pyrophoric so not a contender. Plutonium (94) - solid at stp, appears silvery white but oxidizes into grey. it can turn into a pyrophoric powder. Pu-239 has a half-life of 24,100 years and Pu-241's half-life is 14.4 years. Amercium (95) - solid at stp, also a silvery white look, oxidizes. it's used in smoke detectors! half life of 432.2 years Curium (96) - solid stp, its a hard, dense silvery metal that glows purple in the dark. oxidizes very easily, half life ~162 days Berkelium (97) - solid stp. described as a soft silvery-white metal with a half-life of 330 days, but the previous elements would decay into elements with a lower atomic number, where as Berkelium decays into Californium Californium (98) - This one crystalizes under normal pressure, slowly tarnishes under air. silvery appearance. can be used to start up nuclear reactors. Has 20 known isotopes and all their half-lives vary, but its about 2.6 years. Einstienium (99) Silvery and glows blue in the dark, has a paramagnetic field and it's most common isotope has a half-life of 20.47 days Fermium (100) - the last of the elements that can be created by bombarding lighter elements with neutrons. Longest lived half-life is 100 days, not much is known about it. Mendelevium (101) - can only be produced in particle accelerators, half life between 51 days and 1.17 hours Nobelium (102) - also only avalible through particle accelerators, half life between 58 minutes and 3.1 minutes. the shorter half-lifed isotope is easier to create and therefore used more often for research Lawrencium (103) - from here on out theres less and less information for each transuranic element, including this one. half-life of 11 hours. Rutherfordium (104) - half life of 1.3 hours Dubnium (105) - half life of 28 hours Seaborgium (106) - half life of 14 minutes Bohrium (107) - half life unconfirmed but its between 61 seconds and 690 seconds
I'm gonna go ahead and stop right there since they tend to follow a pattern. The lower the half-life, the less research there is on the element, and it only gets shorter and shorter. So it seems like Californium is the only possible element that could've been used in the experiment because it forms a crystallized structure under normal pressure, as well has having usage in modern nuclear science to start up nuclear reactors, as well as having pretty stable/long-lasting isotopes. the most stable isotope has a half-life of 898 years but the most commonly used isotope is 2.6 years. now, it should be noted that the lower the half-life the more radioactive an element is. all of the transuranic elements decay radioactively and Californium is no exception. Californium's radioactivity has a tendency to disrupt the formation of red blood cells by bio-accumulating in skeletal tissue.
Here's some more information on it's physical properties:
Californium is a silvery white actinide metal with a melting point of 900 ± 30 °C (1,650 ± 50 °F) and an estimated boiling point of 1,745 K (1,470 °C; 2,680 °F). The pure metal is malleable and is easily cut with a razor blade. Californium metal starts to vaporize above 300 °C (570 °F) when exposed to a vacuum. Below 51 K (−222 °C; −368 °F) californium metal is either ferromagnetic or ferrimagnetic (it acts like a magnet), between 48 and 66 K it is antiferromagnetic (an intermediate state), and above 160 K (−113 °C; −172 °F) it is paramagnetic (external magnetic fields can make it magnetic).
The element has two crystalline forms under 1 standard atmosphere of pressure: a double-hexagonal close-packed form dubbed alpha (α) and a face-centered cubic form designated beta (β).
This is a Californium-252 crystal, the one I predict would’ve been used in the test. It has a 2.6 year half-life.

That’s all the research i’ve got for you.
TL;DR I predict that they’re using Gamma rays through the anti-mass spectrometer to induct Californium into making teleportation real with quantum entanglement.
#gordon freeman#half-life#half life#HLVRAI#gordon#freeman#dr freeman#doctor freeman#txt#quantum entanglement#quantum physics#quantum mechanics#inorganic chemistry#electromagnetic spectrum
489 notes
·
View notes
Link
Explore 100% online expert created video lectures, pdf notes and assignments for Pairs of Linear Equations in Two Variables Class 10 Maths.
https://www.ashishkumarletslearn.com
#pairs of linear equations in two variables#class 10 maths#homeschooling#homeschool#education#maths#ashish kumar let's learn#ncert solutions
0 notes
Text
what is quantum mechanics ?
Topic: what is quantum mechanics ? what are quantum mechanics?

Quantum physics (QP):
Quantum Physics is the branch of Physics that deals with study of matter at small scale.
Introduction to Quantum mechanics-
A fundamental Theory in physics that describes the physical properties of matter at small scales is called Quantum mechanics .
This is the only theory that gave foundation of all quantum physics together with Quantum Field Theory, Quantum chemistry , and Quantum information science and technology.
Why Quantum physics is So Weird?
Quantum Physics is totally different from Classical Physics because in classical Physics everything is present in Particle form but in Quantum Physics everything in the universe has wave nature as well as particle nature.This is the reason why we say Quantum Physics is so weird.The Foundation of quantum mechanics were established by :
Max Planck
Niels Bohr
Werner Heisenberg
Louis de Broglie
Albert Einstein
Erwin Schrödinger
Satyendra Nath Bose
And many others Scientists contributed in foundation of Quantum Mechanics .Because of these Scientists Quantum Mechanics Became widely accepted theory during the first half of the 20th Century.
Most Famous Equation: Schrödinger's Equation
The Schrödinger equation is a linear partial differential equation that describes the wave function of a quantum-mechanical system. This is an important result in quantum mechanics, and its discovery was an important milestone in the development of quantum mechanics. The equation is named after Irwin Schrödinger, who gave the equation in 1925, and published it in 1926, which resulted in his Nobel Prize in Physics in 1933.The concept of a wave function is a fundamental signal of quantum mechanics; The wave function defines the state of the system at each spatial position and time.The solutions of Schrödinger's equation describe not only molecular, atomic and sub-atomic systems, but also macroscopic systems, possibly the entire universe. With the help of Schrödinger equation not only we can study quantum mechanical systems and make predictions but also we can study like Other aggregates of quantum mechanics include matrix mechanics, introduced by Werner Heisenberg, and the main integral formulation, developed by Richard Feynman. Paul Dirac incorporated matrix mechanics and the Schrödinger equation into one formulation.
Heisenberg's Uncertainty Principle:
In quantum mechanics, Heisenberg's uncertainty principle is any kind of mathematical inequalities that provide a fundamental limit to the extent to which values for physical pairs of certain particles, such as position, x, and momentum, p, can occur. Predicted from initial conditions. Such variable pairings are known as complementary variables or canonically conjugated variables, and, depending on the interpretation, the uncertainty principle is limited to the extent that such conjugate properties retain their approximate meaning, Because the mathematical framework of quantum physics does not support the notion of simultaneous well. Defined conjugate properties expressed by a single value. First introduced in 1927 by the German physicist Werner Heisenberg, the principle of uncertainty states that the more precisely the position of a particle, the more precisely its motion can be predicted from the initial conditions. And vice versa. Since uncertainty theory is such a fundamental result in quantum mechanics, specific experiments in quantum mechanics regularly observe its aspects. However, some experiments may deliberately explore a particular form of uncertainty theory as part of their main research program. For example, superconducting or quantum optics systems involve tests of number-phase uncertainty relationships. Applications that rely on the principle of uncertainty for their operation include techniques with extremely low noise such as those required in
gravitational wave
interferometers.
Quantum Field Theory:
A theoretical framework that combines classical field theory, special relativity and quantum mechanics in theoretical physics is called Quantum Field Theory.
(Note: Quantum Field Theory Doesn't combines General relativity).Quantum field theory is used in particle physics to construct physical models of sub-atomic particles and in condensed matter physics to construct models of quipiparticles.Quantum field theory treats particles as quanta of their underlying fields, which are more fundamental than particles. The interactions between the particles are described by the interaction terms in the Lagrangian involving their respective regions. Each interaction can be visualized by Feynman diagrams according to disturbance theory in quantum mechanics.
Photoelectric Effect:
The emission of electrons when electromagnetic radiation(light rays) hits a material is called photoelectric effect. The Electrons Which are emitted in this manner are called Photoelectrons. We study this phenomenon mainly in electronic physics and in fields of chemistry such as quantum chemistry and electrochemistry.According to classical electromagnetic theory, photoelectric effect can be attributed to the transfer of energy from light to electron. From this point of view, a change in the intensity of light induces a change in the kinetic energy of electrons emitted from the metal. According to this theory, sufficiently dim light is expected to show a time interval between the initial brightness of its light and the subsequent emission of an electron.But experimental results were not associated with either of the two predictions made by classical theory. Instead, experiments have shown that electrons are disliked only by scattering of light when it reaches or exceeds the threshold frequency. Because a low-frequency beam at high intensity cannot produce the energy required to produce photoelectrons such that if the energy of light were constant like a wave, Einstein proposed that a beam of light propagating from space Not a waveform, but rather a collection of discrete wave packets (photons).
Revolutionary Principles of Quantum Mechanics:
-Wave Particle Duality
-Quantized properties
Wave Particle Duality:
Wave-particle duality is the concept in quantum mechanics that each particle or quantum unit can be described as a particle or a waveform. It expresses the inability of classical concepts "particles" or "waves" to fully describe the behaviour of quantum-scale objects.Current scientific theories assume that all particles exhibit a wave nature and vice versa. This is proven with the help of the work done by many Scientists like Max Planck, Albert Einstein, Louis de Broglie, Arthur Compton, Niels Bohr, and many others.This phenomenon has been verified not only for elementary particles, but also for compound particles such as atoms and even molecules. For macroscopic particles, wave properties cannot usually be detected, due to their extremely short wavelengths.
Quantized properties:
Some properties, such as position, speed, and color, can sometimes occur only in a specific, set amount, much like a dial that "clicks" from number to number. This challenged a fundamental notion of classical mechanics, stating that such properties must exist on a smooth, continuous spectrum. To describe the idea that some properties 'clicked' like a dial with specific settings, scientists coined the term 'quantized'.
About post :
So far we have studied many terms like quantum field theory , dual nature of particles and many more and also we have learnt how quantum physics became the revolutionary theory in 20th century and also many scientists like max planck , albert einstein and co. contributed to this theory .You can read about. I hope you guys have learnt many things from Article: what is quantum mechanics ? what are quantum mechanics? or quantum mechanical model and enjoyed as well. So thats it for today , If you want to read more then you can read other articles given below.
Originally posted on : https://astroquantumphysics.com/
Click to read more
11 notes
·
View notes
Link
1 note
·
View note
Text
CBSE Class 10 Maths Chapter 3 - Pair of Linear Equations in Two Variables Objective Questions
Chapter 3- Pair of Linear Equations in Two Variables from CBSE Class 10 Maths textbook explains all about the pair of linear equations in two variables. Two linear equations in two variables also called the pair of linear equations in two variables can be represented graphically and algebraically. Algebraically, students can use the Substitution method, Elimination method or Cross-multiplication method to solve the pair of linear equations in two variables. In this article, find the CBSE Class 10 Maths Chapter 3-Pair of Linear Equations in Two Variables objective questions to provide practice solving MCQs for students.
Click Here:- https://myncertguide2020.blogspot.com/2021/05/cbse-class-10-maths-chapter-3-pair-of.html
1 note
·
View note
Link
#BalajiPublicationsMathematicsClass10#BalajiMathsBook#BalajiClass10MathsSolutionsChapter3#BalajiPublicationsSolutionsPdf#UPBoardSolutions
19 notes
·
View notes
Text
KC Sinha Maths Solutions Class 10 Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3
Free PDF download of KC Sinha Maths Solutions Class 10 Chapter 3 Pair of Linear Equations in Two Variables Ex 3.3 solved by Expert Teachers as per NCERT (CBSE) Book guidelines.
2 notes
·
View notes