#quintic equation

[kuiperoid]

The History of the Cubic Equation, the Original Celebrity Feud

[also posted here]

[paper that I wrote for a class in undergrad that mostly served as an exercise in using LaTex]

Abstract

This document will describe the history and methods behind how the cubic equation was solved, specifically focusing on the work of specific sixteenth century Italian mathematicians. It will also touch upon the quartic and quintic equations.

1 The Life and Times of Tartaglia

Niccolo Fontana, known as “Tartaglia,” meaning “the stammerer,” was a Venetian mathematician during the early sixteenth century. His many accomplishments included engineering, working as a bookkeeper, and creating the first Italian translations of the works of Archimedes and Euclid, but he is most famous for his involvement in the 1535 Bologna University Mathematics Competition. Some years before, University of Bologna's Chair of Arithmetic and Geometry, Sciopione dal Ferro, solved one case of the cubic equation, a polynomial equation in which the highest variable exponent is three, a case only involving positive numbers. Though it is believed that dal Ferro solved this form around 1515, he kept it a secret until just before his death in 1526, at which point he shared this solution with his student and far inferior mathematician, Antonio Fior. Rumors began to spread that the cubic had been solved, eventually reaching Tartaglia. Tartaglia managed to find his own partial solution to the cubic in this time, leading the overconfident Fior to challenge him to a public math competition. According to the rules, each gave the other thirty problems to solve over the course of forty to fifty days. All of Fior's problems were set to the form x^3 + mx = n which dal Ferro had found, believing that Tartaglia would not be able to figure it out. However, Tartaglia had not only managed to solve all of the problems Fior had presented him with within the course of two hours, but he found a general method for solving all forms of the cubics before the contest was over. This ensured Tartaglia's victory [1].

Figure 1: A graph resulting from a cubic function

2 Enter Cardano

News of Tartaglia's win spread across Italy, eventually reaching Milan-based mathematician and general eccentric character Gerolamo Cardano. Though brilliant in mathematics and medicine, Cardano's illegitimate birth and generally abrasive personality had limited his opportunities, leading to a somewhat inconsistent professional life. Cardano managed to bring himself to prominence in the world of math with the publication of The Practice of Arithmetic and Simple Mensuration, the first of one hundred and thirty-one books he would write in his lifetime [2]. Cardano approached Tartaglia in 1539 with hopes of adding his solutions to the cubic to his next book, Practica Arithmeticae. Tartaglia was reluctant to share his method, having previously coded his method in a cryptic poem so that no one would figure it out, but did so after Cardano made an oath to not publish his ideas. Using this knowledge, Cardano spent the next six years working on the cubic and quartic equations, sometimes with the help of his assistant Lodovico Ferrari [1].

Ferrari was born in Bologna, Italy in 1522, a particularly politically tumultuous time for Northern Italy. Ferrari's father was killed in the army, meaning he had to move in with his uncle, Vincent. It so happened that Vincent's son Luke had run away to Milan for work and ended up briefly as a servant to Cardano. Luke ended up tiring of the work and going back home without telling Cardano. Cardano contacted Vincent to send his servant back, but Vincent thought that his fourteen-year-old nephew might make a better candidate. Upon Ferrari's arrival to Cardano's in November of 1936, Cardano learned that the teenager was literate and made him a secretary rather than a servant. He began to teach him mathematics, at which Ferrari proved to be so talented that he was able to teach by the age of eighteen and, by the age of twenty, he began working as a public lecturer in geometry. During this time, he and Cardano also worked on Tartaglia's cubic solutions in an attempt to solve the quartic as well. Between Tartaglia's findings and the work of another mathematician, Zuanne da Coi, Ferrari eventually found a solution for the quartic equation, polynomials for which the highest variable exponent is four. He wanted his work published, but it would be impossible to do so without revealing the work Tartaglia had produced, which Cardano had previously vowed to keep a secret. The two did further research and decided that because technically dal Ferro had solved a form of the cubic before Tartaglia, they could publish the findings about the cubic and the quartic without it being considered breaking Cardano’s oath. He featured these works in his book Ars Magna in 1545 [3].

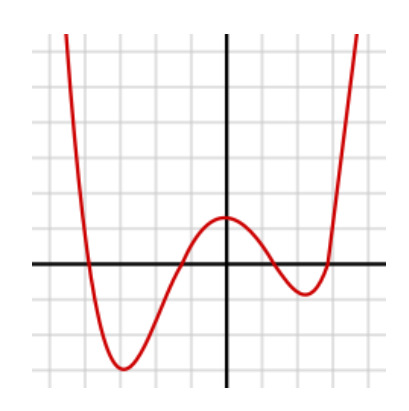
Figure 2: A graph resulting from a quartic function

3 Ferrari Reigns Victorious

Needless to say, Tartaglia did not take well to the news of his findings being published, especially by someone who had previously promised not to. The alleged loophole counted for naught, as the portion about the cubic was very much Tartaglia's work. Ferrari responded to Tartaglia's anger by writing him an insulting letter in which he also challenged him to a public debate. Tartaglia saw no point in debating the relatively-unknown Ferrari, but did respond in an attempt to bring Cardano in. Tartaglia and Ferrari exchanged publicly read insulting letters for about a year. The rivalry was brought to its conclusion in 1548. Tartaglia was offered a job as a lecturer in Brescia and needed to participate in a public math competition with Ferrari to prove that he was worthy of the spot. Though less experienced in the ways of public debate than Tartaglia, Ferrari proved himself far more understanding of the concepts at hand, not only his own quartic equation, but the cubic as well. Tartaglia left that night in shame, leaving Ferrari as the winner [4].

4 The Failed Quintic

Though all proven mathematically brilliant, neither Ferrari, Cardano, nor Tartaglia ever even attempted to breach the quintic equation. It is thought that the first mathematician to attempt to actually solve for a specific quintic equation was French mathematician Joseph-Louis Lagrange in the eighteenth century. He tirelessly studied the previously developed methods for the quadratic, cubic, and quartic equations for clues. He focused on how rational numbers changed under permutations, but could not find an expression for powers above four. His successor came in the form of Italian mathematician Paolo Ruffini. Ruffini's work focused on the properties of permutations with the goal of proving that the quintic was not solvable. Though Ruffini did develop proofs, his work was considered vague for its focus on patterns instead of computation and was not well-accepted by mathematicians at the time. In the nineteenth century, Norwegian mathematician Niels Henrik Abel carried on with Ruffini’s work, publishing the completed versions of the proofs, and confirming that quintic functions cannot be solved with a single equation. This work is known to this day as Abel's Impossibility Theorem,or the Abel-Ruffini Theorem [5].

References

[1] Mastin, Luke. 16th Century Mathematicians. The Story of Mathematics, 2010.

http : //www.storyof mathematics.com/16thtartaglia.html

[2] JJ O’Connor and EF Robertson. Quadratic, Cubic, and Quartic Equations University of St. Andrews, February 1996.

http : //www−groups.dcs.st−and.ac.uk/history/HistT opics/Quadraticetcequations.html

[3] JJ OConnor and EF Robertson. Giralamo Cardano. School of Mathematics and Statistics at the University of Saint Andrews, June 1998

http : //www−history.mcs.st−andrews.ac.uk/Biographies/Cardan.html

[4] JJ OConnor and EF Robertson. Lodovico Ferrari. School of Mathematics and Statistics at the University of Saint Andrews, September 2005.

http : //www−groups.dcs.st−and.ac.uk/history/Biographies/F errari.html

[5] Fiona Brunk. Galois' Predecessors. School of Mathematics and Statistics at the University of Saint Andrews, January 2005.

http : //www−history.mcs.st−and.ac.uk/P rojects/Brunk/Chapters/Ch1.html

[sabakos]

You can find the numerical values of the roots of quintic equations, but you can't "solve" them, where the word "solve" means [group theory nonsense] or in simplified terms, that you can't express a general solution to a quintic equation in terms of rational powers ("radicals") like e.g. the quadratic equation.

[yourbestamericangirlmp3]

students keep emailing me begging for a better grade, including one who wants to write an essay for 2 points in a precalc class, and i'm so tempted to say that they can get an A if they find me a formula to solve a quintic equation

[amarantine-amirite]

We’ve all seen this before, but this one has been a backstory: the equation written on the pages the simplest example of a quintic whose solutions can’t be expressed as a combination of radicals. Basically, the simple equation can’t be solved unless you plot the curve on a graph. Of course, most 11th graders wouldn’t know this. Apparently, neither did the teacher.

This kid knew, but she couldn’t quite put into words why the equation couldn’t be solved. She didn’t want write “this has no solution” because she couldn’t formulate the argument to back it up, so she did this.

Was this the right call? Only time will tell...

[professionalchaoticdumbass]

maron⁵

ime a fucking quintic equation!!

[falseandrealultravival]

Background of Group Theory - Galois' Misfortune: Mathematics Note- 12 (Essay:last episode)

Galois

Galois is a French mathematician. Known as the originator of "group theory", he received after Abel of Norway proved that "there is no formula for the solution of quintic equations",he proved the theorem of impossibility that "there is no formula for the solution of algebraic equations of degree 5 or higher" in group theory.

Gauss guaranteed that there would always be a solution by means of the "Fundamental Theorem of Algebra", but Abel and Galois showed the impossibility and insecurity that the procedure for finding the solution cannot be known unless you try it.

"Galois lives a cursed life." A kind of madness called the French Revolution casts a dark shadow over Galois' life of only 21 years. He himself threw himself into the revolution, discovering the great theorems of insecurity and impossibility in the midst of intrigue and bargaining. However, the French mathematics community at that time was cold to Galois.

His papers have been lost or ignored many times. The paper was lost by Cauchy (seemingly on purpose), and Fourier died while in custody because of him. He wanted to enter the École Polytechnic (French's best science and engineering university), but he got angry when the examiner asked him too trivial questions and threw his quilts at him. It seems that he was treated as a kind of dangerous person.

Meanwhile, Galois falls into the trap of having a duel over a certain woman. On the eve of the duel, he scribbles a letter to his friend describing his idea of group theory and its application, the theorem of insecurity and impossibility. He blurted out, "No time, no time!" And he loses. On his deathbed, Galois tells his younger brother, "Don't cry! It takes all the courage to die at the age of twenty-one." He entrusted, "I want you to show this paper to the Germans, Gauss or Jacobi."

Gauss would have never doubted that "there is nothing left to do" when it comes to algebraic equations. But there was something he had overlooked, which Galois and his colleagues discovered. It can be said that the chaos of the French Revolution gave birth to group theory.

Group theory is not usually called “Théorie de Galois”. Names are only in French. It is the cowardice of the French to bully Galois so much and then to use Galois' name shrewdly.

(2023.04.22)

Rei Morishita

[bacanthony]

EXTREME quintic equation! (very tiring)

[g-g-gh00st]

POV I’m trying to match up a Quintic (visually a quadratic) to a quadratic as a piece-wise function but my STUPID $100 CALCULATOR keeps telling me that my 5 different equations that took 5 whole minutes to type in is FALSE‼️ YOURE FALSE!!!!!!

[calebmatthew1]

Make use of the online root calculator to calculate the nth root

An Allcalculator.net's  root calculator aids in finding the roots of a given polynomial. You can quickly get the roots of any polynomial with the online roots calculator. Tools for using roots calculators speed up calculations and quickly display the roots or value of a variable.

What are the instructions for the root calculator?

Enter the number of the root in the root calculator you wish to calculate from in the "Number" field.

Enter the degree (default is 2) in the "Degree" field.

Change the calculation's precision by choosing the required number from the "Decimal" drop-down menu (the default is 20 decimal places).

In most circumstances, you do not need to click "Result" since the root calculator automatically discovers roots as you type letters or alter setting values.

Click "Reset" to return the calculator to its default settings.

How to find the root calculator?

Linear polynomials are those that have a degree of 1.

A quadratic polynomial has a degree of two.

A cubic polynomial has a degree of three.

A quartic polynomial has a degree of four.

A quintic polynomial has a degree of five.

An nth-degree polynomial is a polynomial with a degree (n) larger than 5.

Any degree of a polynomial reduces it to zero and identifies the roots of a given polynomial.

From the term "quad," which means square, comes the word "quadratic." In other terms, an "equation of degree 2" is a quadratic equation.

An equation of the form ax2 + bx + c = 0, where a is not equal to 0, is called a quadratic equation. a, b, and c are the coefficients of the quadratic equation. The discriminant formula to solve the quadratic equation is given:

X = -b ± √b2 – 4ac / 2a

What are the properties of square roots?

Some of the important properties of a square root calculator are as follows:

If two integers are multiplied in an equation using square roots, the entire equation may be written as a single sentence. 

                        √a x √b = √ (a x b) 

When two integers are split into their square roots in an equation, you can combine their square roots into a single one. 

                        √a / √b = √ (a / b)

You can divide the numbers into the root if a single number is the derivative of two different integers. 

                          √ (a x a) = a 

                          √9 = √ (3 x 3) = 3

If you want to express the square root exponentially, use the formula 1/2 

                          a = a1/2.    

The radicands (numbers inside the square root) can add or subtract two or more integers.

For instance, since 9 and 4 have identical radicals within, they may be added to or subtracted from. 

The square root of an equation becomes square if it is moved from the left to the right side or vice versa. 

                   √9 = 4 becomes

                   9 = 42

The square becomes a square root in the same way when it is shifted to the opposite side.  

                                         42= 9

                                          4= 92

If a square root referenced number is not a perfect derivative of any other number, it does not yield a clear result when multiplied. The solution will always be decimal or irrational.

For example, 

√26 = 5.09999.

The number's root will be illogical if it has zeros at the end. 

           √4000 = 63.24555.

An odd integer will always have an odd square root. 

For example, √9 = 3 and √121 = 11.

[imperiumallaboveall]

Watch "Why you can't solve quintic equations (Galois theory approach) #SoME2" on YouTube

Proof

Second and gain for adds up new faces happy.

[sortai]

fuckimg

hate quintic equations

[rugessnome]

Revenge of the Fifth

[sabakos]

🔥matiyasevich's theorem/hilbert's tenth problem

Maybe something like matiyasevich's theorem was what Hilbert himself had in mind when he proposed the tenth problem, but I find "some of these are unsolvable" to be an entirely unsatisfying and incomplete theory of the solvability of diophantine equations!

For second degree diophantine equations in two variables (i.e. conic sections), we know how to determine the solvability of any given diophantine equation. I would like to see something similar like "For diophantine equations in m or fewer variables, of most nth degree..." which determines the upper bound on which diophantine equations can be solved. Similar to how we know that the quintic equation can't be solved in general in terms of radicals, but we know that the quartic can. Without that, I don't think we have a general theory of solvability yet.

[dat-physics-boi]

Guess which are real physics / math things, and which are not.

Put your answer in the notes or reblog with your lists. Make 3 lists: “definitely physics/math” “definitely not physics/math” and “no fucking idea” Here the list of stuff:

Euler’s theorem, the monster group, the infinite square well, nuclear pasta, injections, degenerate states, degeneracy pressure, degenerate matter, strange matter, odd matter, the triple point, the exclusion principle, big O notation, bottom quarks, normalization, denormalization, renormalization, stereographic projection, orthographic projection, cartographic projection, complete differential equation, exact differential equation, partial differential equation, the baby monster group, the eldritch group, the quintic formula, Taylor series, Fourier series, Gauß series, Fermi problems, the Basel problem, the Yorkshire method, Schrödinger’s cat, Langdon’s ant, Gauß’s sparrow, Occam’s razor, Archimede’s screw, Euler’s disk, honeycomb, dimensional analysis, the stress tensor, the fear vector, the Kardeshev scale, the Minkowski metric, the Boltzman ruler, the Lebesgue measure, bosons, fermions, luxions, gluons, antiphotons, pions, countability, measureability, analyseability, and last but not least a margin of error.

[backslashdelta]

becky my beloved

props of nothing, what are the most top 5 math equations that are v satisfying and ✨just make sense✨ and what are the ones that are technically correct but don't pass the vibe check?

Myle my beloved!

This is a difficult question because I actually find that the ones that might "seem" incorrect are the most satisfying? Like, it's just so cool that something can look so complicated or weird (or so stupidly simply) and yet still be correct. I love that.

So instead, I'm going to kind of combine the two parts of your question, and give you five math things that I find really satisfying, but may not necessarily pass your vibe check.

c^2 = a^2 + b^2

We're starting out easy. The Pythagorean theorem. You have a right triangle and this is just always true regardless of the size and I just. Love it. So so neat.

x = [-b +/- sqrt(b^2 - 4*a*c)] / 2*a

The quadratic formula! This one is admittedly a bit more complicated, but really not that bad, and it's been drilled into my head since high school. I will never forget this formula and for that reason alone I feel like it needs to be included in this list. How cool is it that you can just always pop your a b and c into this formula and get all of the solutions to your quadratic equation? I think that's just so cool. Fun fact: there are also cubic and quartic formulas (they get very complicated), but it's been mathematically proven that you cannot have a formula for finding the solution of quintic polynomials or polynomials of any higher degree.

d (e^x) / dx = e^x

The derivative of e^x is itself. I just think that's so cool! Derivatives! If you were to continually take the derivative of any polynomial you would eventually get 0 but that never happens with e^x, you just e^x, forever, regardless of how many times you take it's derivative. What a fun property.

(A ⇒ B) ⇔ (¬B ⇒ ¬A)

The equivalence of contrapositives feels like cheating but it's not really an equation, but it's logic and it's an equivalence so I'm including it anyway. The way to read this in plain English is: "if 'if A then B' is true, then 'if not B then not A' is true, and vice versa". That probably didn't help. Let me give you an example instead.

Suppose A is the statement "The weather is warm," and B is the statement "I am wearing shorts." Then A ⇒ B says "If the weather is warm, then I am wearing shorts."

For the other side of the equivalence, using the statements we've chosen, ¬A is "The weather is not warm," and ¬B is "I am not wearing shorts." So ¬B ⇒ ¬A says "If I am not wearing shorts then the weather is not warm."

Now let's see if these statements are equivalent. If it's true that warm weather means I'm wearing shorts, then if I'm not wearing shorts it can't possibly be warm. And conversely, if me wearing something other than shorts means it's not warm, then if it is warm I must not not be wearing shorts, i.e. I am wearing shorts.

Maybe that didn't help either. Oops. I tried. Anyway, logic is cool as hell and I love it.

e^(pi*i) + 1 = 0

This is the equation that blows every math student's mind at some point because it's just. ridiculous. e, pi, and i are all ridiculous numbers. e and pi are both irrational and i isn't even a real number, and yet. And yet. You raise e to the power of pi*i and you add 1 and you get 0. It's just. Flabbergasting. It absolutely should not work but it does and it's so absolutely fantastic. She's beautiful I love her.

[associahedron]

There is a quintic formula!

One of the most common pieces of math misinformation that gets spread around is “there’s no general solution to quintic equations”. It’s famously true that not every quintic can be solved using only the operations of arithmetic and taking n-th roots. But that doesn’t mean there’s not a general formula at all! In fact, there are multiple formulas approaching the problem from different perspectives. 

One approach adds in one thing that’s kind of like n-th roots, the “Bring radical” (see Wikipedia). Another, pioneered by Klein, directly exploits the connection between quintics and the symmetries of an icosahedron (the same connection that guarantees there’s not a traditional formula “in radicals”, because of the complexity of the icosahedron) and uses “hypergeometric functions”. A third approach uses “elliptic functions” which come up in more contexts than the more-artificial Bring radical. A fourth, by Ramanujan, uses continued fractions to solve things. 

Some of this was made into a poster about “Solving the Quintic” made to advertise Mathematica that is sold at https://store.wolfram.com/view/misc/#quintic-poster and is connected to code at https://library.wolfram.com/infocenter/TechNotes/158/