#statisticalmechanics

[fadia2000]

What is Thermodynamics? A Complete Guide to Energy, Heat, Work, and Entropy

Thermodynamics is the science of energy interactions, explaining how heat, work, temperature, and entropy govern physical and chemical processes. This guide explores the key laws of thermodynamics, the origin of entropy, and the connection between macroscopic properties and microscopic behavior. Whether you're a student, researcher, or engineer, this is your go-to resource for understanding energy transformation and its limits.

Get it now from here

Get it now from here

Get it now from here

[alishaaishu2000]

Theoretical chemistry

Theoretical chemistry is a branch of chemistry that uses mathematical models and computational techniques to understand, predict, and explain chemical phenomena. By applying quantum mechanics, molecular dynamics, and statistical mechanics, theoretical chemists explore the electronic structure, reactivity, and properties of molecules, materials, and complex biological systems. This field provides insights that aid in the design of new compounds and materials, simulating chemical reactions and understanding molecular behavior in various states of matter. It bridges the gap between experimental chemistry and pure physics, offering a powerful framework for predicting chemical behavior at atomic and molecular scales.

International Chemistry Scientist Awards

Website: chemistryscientists.or

Contact us: contact@chemistryscientist.org

Nominate  now: https://chemistryscientists.org/award-nomination/?ecategory=Awards&rcategory=Awardee

  #sciencefather#researchawards#Professor,#Lecturer,#Scientist,#Scholar,#Researcher#TheoreticalChemistry #QuantumChemistry #MolecularModeling #ComputationalChemistry #QuantumMechanics #MolecularDynamics #ChemicalPhysics #ElectronicStructure #ChemInSilico #StatisticalMechanics #MolecularSimulation #ChemicalReactivity #QuantumComputations #MaterialsScience #PredictiveChemistry #AtomisticSimulations #ComputationalScience #QuantumSystems #ChemicalTheory

[eddieantonio84-blog]

When my friend @cherifsabri says that I’m “ intelligent” and then this is what he does for a living 🤷🏻‍♂️(see photo) 📚 #eddieantónio #emorgado84 #intelligent #student #arab #tunisian #friend #bestfriend #physicist #aixmarseilleuniversité #mechanical #statistics #marseille #france #bookworm #book #bigbangtheory #instalike #statisticalmechanics #instagreat #instagood #instadaily #followme #follow (at Aix-Marseille Université)

[jobrxiv]

Postdoc positions in Statistical Mechanics and Soft Matter at Tel Aviv University Tel Aviv University Application Deadline: 2022-07-31 Yair Shokef's group at Tel Aviv University is hiring postdoctoral fellows. Current research in the group covers multiple topics in non-equilibrium statistical mechanics, with close collaborations with leading experimental groups, in topics ranging from topological mechanics to active matter. Candidates should be highly motivated, with experience and interest in theoretical or computational research, and should hold a Ph.D. degree in physics, chemistry, engineering, or applied math. Please send cover letter, CV, research statement, and names of at least three academic references. Informal inquiries are welcome. See the full job description on jobRxiv: https://jobrxiv.org/job/tel-aviv-university-27778-postdoc-positions-in-statistical-mechanics-and-soft-matter-at-tel-aviv-university/?feed_id=19200 #ScienceJobs #hiring #research #StatisticalMechanics, #SoftMatter, #MechanicalMetamaterials, #ActiveMatter

[before-5am-europe]

“A hundred times every day I remind myself that my inner and outer life are based on the labors of other men, living and dead, and that I must exert myself in order to give in the same measure as I have received and am still receiving.” - Albert Einstein Follow: @before5ameurope ⏰⏰ #selfportrait #alberteinstein #theoreticalphysics #developer #relativity #physics #philosophy #science #advancedstudies #doctoralstudent #doctoral #blackandwhitephotography #quantummechanics #massenergyequivalence #equation #e=mc2 #nobelprize #photoelectriceffect #quantumtheory #patent #swiss #charlesuniversity #statisticalmechanics #molecules #nuclear #nuclearfusion ⏰⏰ #germany🇩🇪 #zurich (at Planet Earth) https://www.instagram.com/p/B-5NGc1A9sq/?igshid=c84evboxv9yb

[themoleculeclub]

Josiah Willard Gibbs * 11 February 1839 in New Haven, Connecticut was a n American engineer and scientist. He coined the term statistical mechanics and his Gibbs free energy formula G=H-TS is very famous. #gibbsfreeenergy #gibbs #statisticalmechanics #physics #chemistry#energy #scientist #physik #chemie #wissenschaft #freieenergie #enthalpie #enthalpy #entropy #entropie #forscher #yale #researcher #mechanics #fizyka #physique #fisica #thermodynamics photo: Daguerreotype of Josiah Willard Gibbs as a student. Dated c. 1840? although he appears older here than an 1855 photo. Datebetween circa 1840 and circa 1860 Source #Yale University Historical New Haven Digital Collection https://ift.tt/37ff8jL

[haykh]

Paradox of dissipative statistical mechanics [or] where the hell is the second bob

In this post I would like to introduce a rather interesting topic especially for those who're concerned about how nature works but are not majoring in theoretical physics. I do not hold any degree in physics yet, so this post is going to be just a glance of a pretty much amateur, fresh undergrad, who is currently working on several very narrow theoretical physics problems. Hence, of course, I want to obtain an adequate feedback and harsh criticism, as I believe there are many people who know these topics better than I do. The main purpose of this outline is to provoke a discussion between those who care.

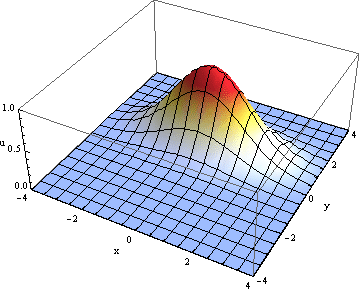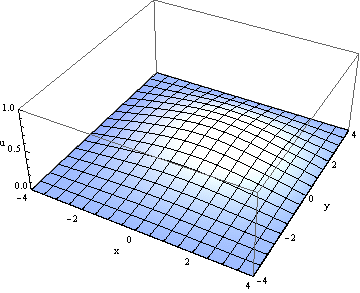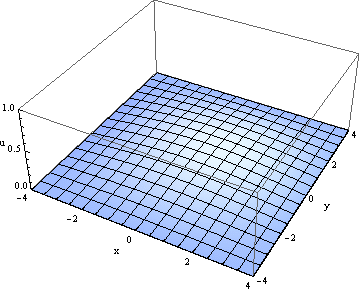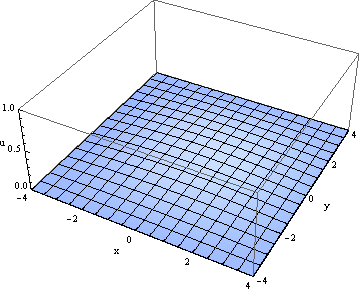
For those not majoring in physics, there may appear several unknown words in the title, so let’s first review all of them before moving forward to the problem itself.

What is “statistical mechanics”? As you probably know from school, mechanics is a science (sometimes rashly considered as a part of physics) about the movement and evolution of elementary and complex objects and systems under the impact of some abstract forces. Statistical mechanics, however, is a science about the determination of statistical characteristics of complex (multi-particle) systems. When you have a system with, say, billions of particles, there is no need to know about the coordinate and velocity of every single particle, because you still cannot determine them experimentally. Instead, it would be more useful to know what portion of particles in that system have particular energy, or how many of them are in a given part of the box etc. So these are the statistical characteristics of the system. Those who are familiar to physics may call to mind the energy distribution function and number density.

The second unknown concept is “dissipative”. When you give an initial impulse to a piece of wood on the table, it would stop soon after being pushed, losing its initial energy. Without going deep into the reasons of stop, we will call this stopping process the dissipation. The same phenomena can be observed by simply putting a glass of hot water on the kitchen table. After a while it will lose heat getting colder and colder until it finally gets the room temperature. This process of energy spill is called the dissipation process, when the energy from smaller parts of our system are being permeated into the whole macroscopic system.

So coming back to our topic, what is the characteristic feature of dissipative processes? One can notice, that, i.e., if you have a process where the dissipation is quite weak like colliding billiard balls, you can invert all the velocities of the balls, and they will come to their initial positions. Well, of course, if you neglect the tension with the table, these balls will never stop, but that’s not the point. However, the main thing is, that processes described by the laws of classical mechanics are time-invertible (the inversion of time is the same as the inversion of velocities)! That comes from the time-invariance of Newton’s law.

On the other hand, one can consider a balloon with some gas bursting in a large room. No matter how long you wait, the gas will never come back to gather into the balloon. In physics this phenomena is called the second law of thermodynamics, or the law of the entropy increasing. Entropy in physics is effectively the measure of randomness and chaotic state of the system. The higher the entropy, the more chaotic the system is. And the second law of thermodynamics says, that in general physical systems the entropy can only increase, so the measure of chaos of the system can only get higher and higher by the time. Boltzmann was the first to derive this law in XIX century, and there is even further derivation from more general and precise ideas by Bogolyubov in 1946.

But hey, if the classical mechanics in its origin is time-invariant, and the statistical mechanics is just a generalization of classical mechanics for the systems of many particles, then why something being a derivative of something time-invariant is NOT time-invariant? Well, this a quite complicated paradox that has not been answered carefully during so many years. The thing is, that any sort of derivation of the 2nd law of thermodynamics contain in its very origins statistical, hence nondeterministic origins, which in further evolution of the theory leads to non-time-invariant laws like entropy increasing law.

Of course, advanced ones might say that in any case there are quantum nondeterministic effects that anyway play some role on time evolution of the system. Thus, these effects can lead to non-time-invariant processes, and from the glance of quantum mechanics, there is no paradox at all. However, first, statistical nature of these processes is appeared to be characteristic even without quantum consideration, as the basic statistical mechanics is simply a derivative of classical mechanics. And moreover, in statistical systems, like air in our rooms, quantum effects are extremely weak and neglectable, as the temperature is quite high enough and the density of air molecules is pretty low.

The question we'd like to review now is, how to deal with this paradox, and what are the possible solutions for it. Well, of course there are just numerous possible answers and speculations about this question. But I’d like to introduce, in my opinion, the most refined and understandable one. So the question is, why the entropy can only increase, and why the gas leaked out of balloon will never get back to its original form of the balloon? The one possible answer is, it will eventually get back, we just can't wait that much. You see, there is a mathematical theorem relating to dynamical systems defined by ordinary differential equations called Poincaré reccurence theorem. It states that certain systems will, after a sufficiently long but finite time, return to a state very close to the initial state. And the Poincaré recurrence time is the length of time elapsed until the recurrence. Of course, this time may vary greatly depending on the exact initial parameters and degrees of freedom of our system, but the keyword in this theorem is the word “finite”. So for the system of balloon in the room Poincaré time may appear to be larger than the age of the Universe, but it will still be finite theoretically.

Another more visual explanation of the paradox was demonstrated by one of my professors in Lebedev Physical Institute. Those who remember physics demonstrations at school can memorize an interesting experiment with a device called a coupled pendulum: two bobs with a spring connecting them hanged on rods, that are free two oscillate around one of their ends.

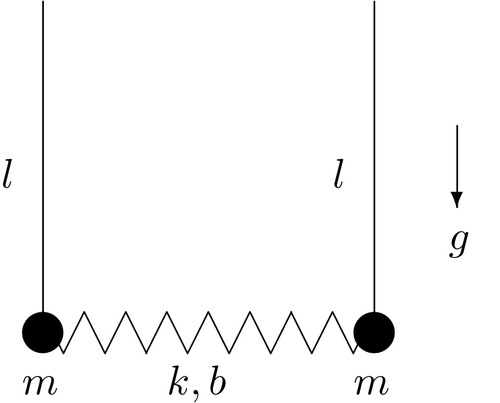
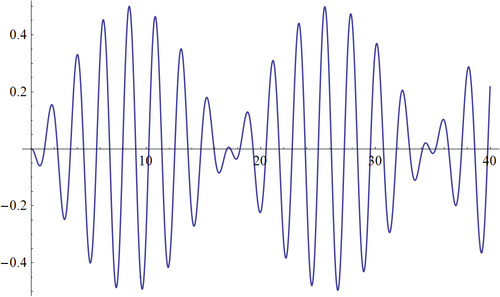
If you push one of these bobs, you will see an interesting kind of motion. During some time, one of these bobs will oscillate intensively, and the other one will nearly rest. After that, the one resting will start to oscillate, and the other one will nearly stop, reversing this process back and forth. So talking physically, we’ll say that these bobs are oscillating with opposite phases. Graphically this fact can be represented by this plot of the position of two bobs during time. As you can see, when one of these bobs is nearly at rest, the amplitude of the other one is in its highest value.

I made an animation of this pendulum system in Wolfram Mathematica (link to .nb file). The spring is represented by a dashed line between two black bobs.

But how is this connected with the problem of dissipative statistical mechanics and Poincaré recurrence time? Well, the one thing you need to do in order to understand it, is to put a light bulb on one of these bobs and turn off the environment light in the room. What will happen is that you’ll see the motion of just one of these bobs, and for a person who’s not aware of the second bob, the motion of the light one will appear very strange and will definitely look something that is very like to dissipation. But then hey, after it stops, it starts oscillating again! This weird motion is incredibly hard to explain without any idea about the second bob.

So returning to the questions of Poincaré recurrence, what if there is some another non-observable degree of freedom (like the second bob in the coupled pendulum), that will make our system to dissipate and then get back to its normal motion repeatedly. And what if that second bob in our case is so heavy, that we can’t even observe its motion. Well, nobody knows this certainly, but this idea and its visual interpretation seemed to me interesting, and definitely worth sharing with others. 

[socraticastudios]

View this post on Instagram

A post shared by Socratica (@socraticastudios)

Memory Spring! Some special alloys of brass can be made to have a shape memory triggered by temperature. These springs quickly change their length from 1 cm to 2.5cm when heated above 90 C (done here with hot water) and just as quickly shrink back to original size when cooled (immersed in cold water). Useful in many applications, especially things like automatic fire sprinkler valves. This amazing property is probably due to a solid state phase transition similar to that of Nitinol wire called a martensitic transformation. ➡️ Repost from @physicsfun. Follow the link in their profile for information on where to buy this and many other physics toys. . . . . . #STEM #memorywire #physics #physicstoy #phasetransition #martensitic #memoryalloy #nitinol #alloy #thermodynamics #statisticalmechanics #thermostat #science #scienceisawesome 

[jobrxiv]

Ph.D. positions in Statistical Mechanics and Soft Matter at Tel Aviv University Tel Aviv University Application Deadline: 2022-07-31 Yair Shokef's group at Tel Aviv University is hiring Ph.D. students for multiple research projects in mechanical metamaterials and active matter. Candidates should be highly motivated, with experience and interest in theoretical or computational research, and should hold an M.Sc. degree or equivalent in physics, engineering, or applied math. The fully-funded 4-year Ph.D. program at Tel Aviv University focuses mainly on research, with a small number of advanced courses that are given in English. Ph.D. studies are conditional on acceptance to the university, and can begin any time during the year. Please send personal statement of interest, CV, transcripts of grades, and names of at least two academic references. Informal inquiries are welcome. See the full job description on jobRxiv: https://jobrxiv.org/job/tel-aviv-university-27778-ph-d-positions-in-statistical-mechanics-and-soft-matter-at-tel-aviv-university/?feed_id=19195 #ScienceJobs #hiring #research #StatisticalMechanics, #SoftMatter, #MechanicalMetamaterials, #ActiveMatter