#Logarithm Examples and Answers

[askagamedev]

What are common keywords any game design resume should include?

It depends on the kind of designer position you're aiming for. We want to see key words for common tasks that those kind of designers have done. Here are some examples:

Common

Experience, craft, create, live, season, update, content, schedule, create, design, team, player, UX.

Level Design

Layout, place, trigger, volume, spawn, point, reward, treasure, quest, lighting, light, dark, texture, object, obstacle, blocking, whitebox, direct, draw, through, inviting, space, place, multiplayer, competitive, cooperative, co-op, deathmatch, capture the flag, ctf, domination, asymmetric, symmetric.

Quest Design

Text, reward, spawn, balance, level, pace, pacing, word, budget, localization, loc, narrative, item, itemization, dialogue, branch, spawn, difficulty, player, multiplayer, encounter, placement, place, trigger, chain, pre req, pre-requisite, condition, scripting, faction, seasonal, event.

Cinematic Design

Narrative, camera, character, blocking, screen, position, ease-in, ease-out, pan, cut, smash, storyboard, frame, framing, beat, cue, pacing, feel, shot, zoom, sfx, vfx, mark, contextual, conditional, quick time, event, timing.

System Design

Balance, numbers, formula, spreadsheet, excel, curve, quadratic, linear, logarithmic, growth, plot, level, power, over, under, even, normal, distribution, player, total, analysis, scale, scaling, script, scripting, math.

If you're at all familiar with the regular kind of duties and tasks that any of these kind of designers do on a regular basis, you'll immediately start to see how these words fit into describing what we do day in and day out. These are going to be the kind of words we see used to describe the sort of experience we expect to see on a resume/CV from someone who has done this kind of work before. We won't expect all of them in every resume, but we expect a good many of these words on the resume/CV of a reasonable candidate.

[Join us on Discord] and/or [Support us on Patreon]

Got a burning question you want answered?

Short questions: Ask a Game Dev on Twitter

Short questions: Ask a Game Dev on BlueSky

Long questions: Ask a Game Dev on Tumblr

Frequent Questions: The FAQ

[imagineanime2022]

A True Friend

Caspian Keyes X GN!Reader

Word Count: 776

Requested: Anon @kalebell46

Request: On god please I need more Caspian Keyes fan fiction. This internet is so dry, there's like none out there. Could be of a him x reader while he's finding himself, the first real friend in his life that isn't there by the choice of someone else. And he'd be so paranoid about it too. Gooooodddddd please. AND I would love for a caspian fic please there are none

Caspian had been alone for so long, since he was young he had always been the outsider, the black sheep, the target and he thought that was how it was going to be for the rest of his school life. That is until he met (Y/N). Now (Y/N) for all intents and purposes probably wasn’t the best example for Caspian, they got into trouble, paid around and never listened to anyone who assumed that they knew better than them. Except when they were with Caspian, who they had only met because they needed tutoring.

(Y/N) wasn’t stupid though most people treated them that way, in fact they had a basic grasp on most things that were taught in class, they just didn’t seem to get it down on paper very well. Caspian was asked to tutor them and the rest followed with time, tutoring sessions turned into skateboard races and trips to the comic book store. Caspian learned quickly that his new companion was not stupid as he had heard a lot of the others in their year saying so he did make sure that some of their time was dedicated to bringing up his grades, in the end it didn’t matter though.

The world crumbled around Caspian as he found out about the real reason behind his birth, with his father gone and his mother keeping more of a watchful eye on him then usual, the only place he thought he might even be a little bit safe was with (Y/N) but then the thought crossed his mind… What if you had something to do with Logarithm's little experiment. That was why he stood outside your door hand hovering to knock, he jumped when you opened it smiling at him “what are you doing?” They asked “thought you were going to knock but you seemed like you were thinking about something.” They stepped to the side giving him space to come in but he didn’t move. “What?” “Are you really my friend?” He asked. “Really your friend?” They asked “of course I am.” “Really because I just found out a lot about myself that doesn’t make sense.” He answered. “Okay talk me through it.” They prompted stepping out and closing the door behind them. “I found something on my computer, they’ve been watching me.” Caspian answered. “They’ve been watching you?” They asked frowning, you were either genuinely confused or very good at acting. “Logarithms!” He answered more frustrated at having to explain himself at all. “Logarithms? Caspian you're going to have to start from the beginning if you want me to understand, remember I’m the slow friend.” They reminded him as he looked at you, that seemed to calm him down as he spoke again. “Don’t call yourself slow.” He grumbled, they shrugged as they looked at him waiting for him to continue. He took a second to calm down and then explained everything that had happened over the past few days.

It was easy to prove that you weren’t a part of it when you looked back at Stephen Holstroms life and realised that he didn’t have a best friend or a friend of any kind at Caspian’s age. (Y/N) was the only person that Caspian could trust but that didn’t mean that he wanted to drag them into everything that was happening, he still didn’t understand how they ended up in the car with him and Cary going to meet Maddie. “I’ll find a way to get you back home after all of this.” He promised. “Home?” They asked. “Why would I go home, you need someone right? Someone to trust?” “Yeah but-” “And we’ve proven that I can be trusted?” They asked. “Yes but-” “Then I stay.” they leaned back in their chair as Caspian glanced at her through the rear view mirror. “Why?” He asked. “Because I'm your friend, this is how friends work… Real ones anyway.” You shrugged. “Real friends?” Caspian asked. “Alright, how about this, I promise to be the one person that you can trust, a true friend, pillar to lean on and person to talk to, if you promise to stop thinking that you don’t deserve it. You didn’t ask to be made this way and no matter how you were born you are no less human than anyone else I know.” You said. “Alright, fine, as long as you don’t keep calling yourself the slow friend.” He answered. “Alright deal.” And that was the first time that he felt like he could trust someone, accept someone, turn away and they would still be there, a true friend he liked that security.

Request Here!!

[ophizz]

Ramblings of a Lunatic - 3rd Quarter reflection🌝 🌸

⚠️W A R N I N G⚠️

Firstly sir, before you subject yourself to reading this reflection of my learning journey, I would like you to know that you may need to take some of the information with a grain of salt. I am an over dramatic person sir, and I may have over dramatised my experiences. I apologise in advance for whatever I am about to write. I was not built for pisay, nor did I actually ever want to go through this harsh academic plan (or however you call it. training??). Thank you for being our teacher sir, thank you for your patience, I hope mag skip ka through a lot of parts, FYI boring siya sir

a. How would you describe your Math 3 second quarter learning journey?

It could be easily described with 3 simple words. I Give Up. I have given up sir, I'm not smart, I'm not hardworking, I'm not good, so it was only natural for my course in life to give up. No matter how many times the topic was discussed, no matter how many times I tried and redo all the problems, my brain can't handle it. My brain is unable to physically store it within its cells. “Memory Full, only 0.2 megabytes left” type of situation if you get me sir, like when my phone can't open WuWa because it takes up too much space. That's me in math, my brain can't run the math application  because the memory is full, and math takes up too much space. Adding onto that, I'm not prepared for the LT, nor have I passed the graphing activity you gave us sir. Further proving my point of giving up entirely on Math 3. It's not you sir i promise, it's a me problem that I'm too lazy to fix. 

b. Which topic did you find most enjoyable? What made it enjoyable for you? Provide clear

The topic I found most enjoyable was the easy ones. I felt like I was going on the right track but apparently it's like a roller coaster. At first it was fine and dandy, but as time went on, you could slowly feel the dread as it builds up inside. Then boom you're going up, down, left, right, and side to side, while your brain tries to grasp onto something to stabilise itself but whoopsies, apparently the handlebars broke. When you get off the ride, you tell yourself at least you enjoyed the beginning. The easy, calming, joyful part of the ride. To me, that part of the Ride was us learning the basics, the exponential to logarithmic and vice versa, as well as the properties of logarithm. To me, those were the best times of the helling ride. 

c. What concepts did you find easy to learn? What do you think made them easy for you?

The topics are the same as the previous question. I think they were easy for me because it only involved common sense, minimal memorisation, and simple arithmetic. Honestly sir, that's all my brain could handle. My brain overheats when it has too many things to do, so when we went to the solving parts of the later topics... thats when my processor got weaker. So basically I found the topics, exponential to logarithmic (vice versa) and properties of logarithm easy topics.

🌸♥*♡∞:｡.｡ P h o t o s ｡.｡:∞♡*♥🌸

Sir! I didn't say that my answers are correct sir🥺..... sorry sa photo dump po hehehe

d. What concepts did you find most interesting/inspiring? Why do you think so?

For me, the most interesting one was the compounded interest. I now know how to manage finances because of that topic as well as sir Mike's crash course on investing! In all honestly, it's because its the one with the closest correlation to real life use, unlike logarithms, or graphing. That's why I see it as the most interesting/inspiring. Especially when you want to invest in a Condo, or house for example, and you now know how to actually compute for the price and know how to compare to know where you save the most money in the long run. It prepares us for the future! :D

e. What concepts have you mastered most? Why do you think so?

I will mention again and again, exponential to logarithmic and vice versa. It is because it is the easiest, just simple arithmetic and you're done. I admit that my arithmetic may not be the best, but I think I can do the arithmetic for that specific topic sir.

˖ ᡣ𐭩 ⊹ ࣪ P H O T O S ౨ৎ ° ₊

f. What concepts have you mastered the least? Why do you think so?

Sir I have not mastered graphing. I am so sorry sir, but I did not understand your discussion sir... But I have an excuse! I was undergoing through the trials of satan. Pushed to my limits as a girl forced to face the consequences of not having a parasite growing inside my uterus. The burning pain of cramps and a migraine. Sir I'm so sorry I truly don't understand anything and I know there is no use for an excuse. That the excuse does not veil my stupidity for not listening and understanding the topic. Im sorry sir.

˖ ᡣ𐭩 ⊹ ࣪ P H O T O S ౨ৎ ° ₊

sir I actually have no photos to show you... I haven't even done the activity in google classroom. Im sorry sir... genuinely sir...

g. What quick notes do you have for:

i. your teacher;

Sir, Im sorry for not reading your messages properly and thoroughly...Sir especially when you asked about the competition sir... Sir I'm scared to apologise to you in person sir, but Im sorry for wasting your time po... Im sorry for all the things I have done that might have offended you sir, or annoyed you sir... Ill try my best to be a better person sir... Sir if I did anything mean or anything of that same nature sir, I promise it wasn't intentional sir... Im sorry sir....

ii. your classmates; and

I just now noticed that the water was boiling. Thankfully I got out immediately.

iii. yourself?

Maybe, I should give up. Sometimes it's okay to start all over again. Push your limits, but not too far. You could always work on yourself but you're just lazy. Thats all you are. Lazy. You will never amount to anything, humble yourself. No matter how hard you try, your work will never be appreciated. You will never shine in your family of stars. Know your place in life.

⚠️sir this is a joke⚠️

Maybe I should actually review for my subjects... maybe I don't try because Im scared that if I try nothing will improve. Im scared that if I try I would still amount to nothing.

I wish he was real and I could steal his black card. I could manage his finances with compound interest, trust! Sylus save me from Lucifer's infected urethra!

Sir, thank you for managing to read it all the way here if ever you did sir. Im sorry you had to read all of that. Sir, I hope you don't mind the fact that I am slowly going crazy over the length of this post. I hope you have a good day after looking at this submission sir... truly my sincerest apologies.

⋅˚₊‧ ୨Thank you for reading!୧ ‧₊˚ ⋅

ଘ(੭ˊᵕˋ)੭ ੈ♡‧₊˚

[erbiumspectrum]

Hi! Do you have any tips for studying chemistry? For some reason I cant seem to get all the formulas in my brain.

Hey!

My unhelpful but still favorite advice for shoving formulas into one's brain is to understand them 😅 A purely memorization-based approach is very bad for chemistry.

If the problem seems to be particularly understanding/ remembering formulas:

Ask yourself if this particular formula is just words turned into numbers and mathematical symbols. I think it may not work for everyone, but for example I found it easier to remember the literal definition of pH that is "the negative decimal logarithm of hydrogen ion concentration" rather than "pH = -log [H+]" bc otherwise I'd keep forgetting about the minus sign.

Check if you find deriving a formula from another formula easier than just memorizing it. Again, my personal example is I hate memorizing things so much I never really bothered to remember the equation that describes Ostwald's law of dilution - bc I knew I could easily, quickly, and painlessly derive it from the equilibrium constant for concentration + degree of dissociation (and I've done it so many times now it stuck in my brain anyway).

When all else fails, I turn to mnemotechnics. To this day I remember that Clapeyron's equation goes pV = nRT because many years ago someone on the internet shared a funny sentence whose words start with these 5 letters. The sillier the better.

If the issue is with chemistry in general:

Take it chapter by chapter. Chemistry, like most STEM subjects, is just blocks of knowledge upon blocks of knowledge. For example, if you want to learn electrolysis, you need to understand redox reactions first. Try to identify where the struggle begins and work from there.

Once you've picked a topic you want to work on, follow the reasoning in your textbook. If you get stuck, that might be a sign you're simply missing a piece of information from a previous chapter. If an example comes up, try to solve it along with the tips in the textbook.

If anything remains unclear, it's usually not the best idea to just leave it and move on. If the textbook becomes unhelpful, turn to the internet or maybe a friend. Otherwise, the next chapter may just turn out to be needlessly confusing.

Practice problems practice problems practice problems!! And not just the numerical ones. The theory-based ones where they ask you about reactions, orbitals, the properties of the elements etc. are important too.

Choose understanding over memorizing whenever possible.

Try to look at the big picture: the way certain concepts are intertwined, how one law may be a logical consequence of another law you learnt before, why some concepts are taught together, why you had to learn something else first to get to what you're studying now. Again, as an example, I think it's particularly fun to see towards the end of ochem, somewhere around the biomolecules: you need to integrate your knowledge of aromatic compounds, ketones and aldehydes, alcohols, carboxylic acids... Stack new information upon what you already know.

Study methods I'm a big fan of: spaced repetition, solving past papers (anything I can get my hands on tbh), flashcards for the things I absolutely have to memorize, exchanging questions and answers with a friend, watching related videos.

If by any chance you end up taking pchem, I have a post for that specifically.

I hope you can find something helpful here :) Good luck!

[mathblog-ocasen]

F. What concepts have you mastered the least?

To that I answer, graphing of logarithms. Without a doubt, graphing logarithms is the topic I mastered the least because of how hard it is for me to understand. On a personal note, it’s because I’m not particularly good at graphing, it’s definitely one of my prominent weaknesses in mathematics.  And in this example (which is also part of exercise 4.6 from the texbook), the longer I look at my answer, the more I'm starting to think this answer is wrong, whoops.

[chroniclesofschool]

f. What concepts have you mastered the least? Why do you think so? Provide clear images of your solutions to sample problems or exercises on the topic.

Compound interest and the more advanced parts of logarithms are forever my opponents. Oh. my. goodness.

LIKE as soon as I solve one aspect of a problem that combines everything I'm weak at, my brain stops working and doesn't know how to tackle it afterwards. For example:

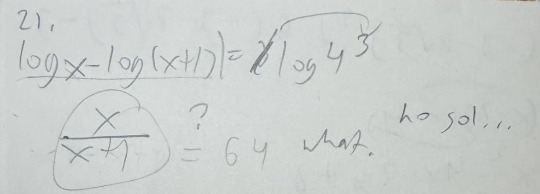
As written, I only found out there was no solution once the answers were finally discussed whilst I kept mulling over what to do the whole time. I haven't quite figured where to keep proceeding from and where to stop when it comes to solving any of our topics if I'm being honest...

Here is another example po in which I had to get help from a friend of mine:

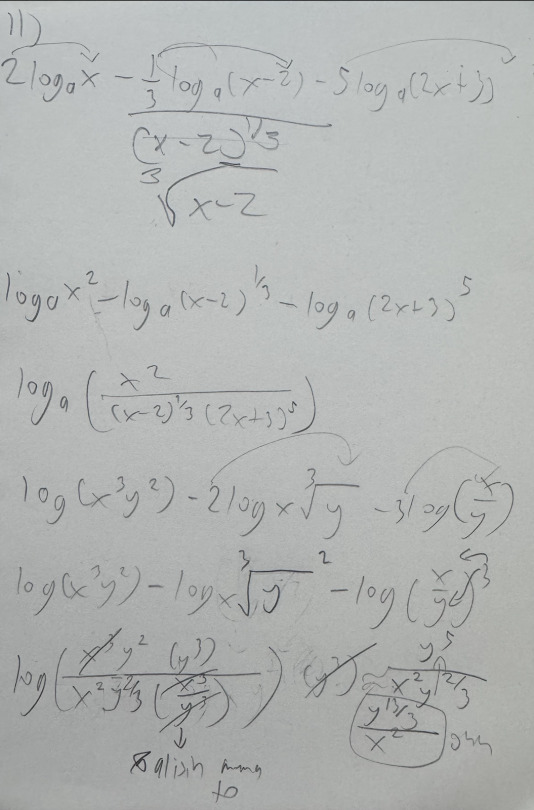
GUILTY CONFESSION ALERT: Sir Joseph I labyu I'm so sorry but this was what I was doing during the later discussion of compound interest because I genuinely couldn't comprehend what was happening anymore... 🥹🙏

[ponderlyunbiasednews]

Is math invented or discovered?

Fact Box

Some of the most famous mathematicians include “Father of Geometry” Euclid, Pythagoras, Archimedes, Thales of Miletus, and Aristotle. 

The Pythagorean Theorem, logarithms, calculus, and the Law of Gravity take the cake as the most recognizable and impactful mathematical equations. 

In a Research Now Group, Inc. survey reviewed by 1,000 US students, almost 46% of students enjoyed math compared to the 24% who didn’t. 

The 2022 Hechinger Report revealed the highest performing countries in regards to mathematics: Singapore, Macao (China), Chinese Taipei, Hong Kong, and Japan.

Mark (Discovered)

When considering all fact-based evidence, we can only conclude that mathematics is indeed a discovered concept. Math is reflected in the natural order, demonstrated by the Fibonacci Sequence and the Golden Ratio method. These patterns exist independently of human observation and have been observed consistently across cultures, showing they are intrinsic properties inherent in the natural world. 

Similarly, all equations result from a concentric loop of indisputable facts. Math is simply the language of showing what already exists and is observable in nature. Math expresses the way the world works, not the other way around in which humans invented math, and now the world happens to work that way. Science equations like those found in chemistry operate by the same principle. The periodic table describes a material reality that already preceded its existence.

If humanity suddenly ceased existing, mathematical truths would still prevail, just as the words “first” and “last” would exist, even if the terms had never been established. Math preceded humanity and gave us a clearer understanding of universal law. Plato theorized that math existed long before man, even attributing it to God. The Bible also reflects this same concept, positing that nothing in creation originates from man. Math is a concept—which can only come from a mind—and it was made discoverable.

The theory of discovery is further supported by famed mathematicians Isaac Newton and Gottfried Liebnitz. Both men arrived at the same discoveries, independently of one another, long before such concepts existed. It actually incited some conflict between them, but this further reinforces the idea that math is governed by one undeniable law of truth. As with science, our understanding of mathematics grew through research and exploration, making it a discovery as it's far too complex and irrefutable to have been invented.  

Andrew (Invented)

While the relationships between numbers, shapes, angles, etc., are essentially laws of nature, the ways in which we describe, manipulate, and use these relationships are completely man-made and invented. A clear example of a mathematical invention is “PEMDAS,” an acronym for remembering the order of operations: Parenthesis, Exponents, Multiplication, Addition, Subtraction. This is an agreed-upon and standardized method that is totally arbitrary and a complete human fabrication. This organization of relationships and accepted method for organizing numbers is what mathematics is at its core.

It is possible to “discover” that if you have two eggs and find two more, you have four eggs. But this isn’t math. The invention of math allows humans to add, subtract, multiply, and much more with any number of abstract hypothetical eggs and understand the quantity. In other words, the invention of math is an abstraction of real-world phenomena. Likewise, this principle of abstraction allows us to ensure that our knowledge is absolute. We can measure the angles of a triangle and find that, added together, they equal one hundred eighty degrees. Still, our abstract knowledge of this concept allows us to demonstrate that a triangle of any size or shape will always have the same principle.

The most difficult math questions require a great deal of human ingenuity to solve. The answers are not found or discovered but arrived at through a process that is both creative and scientific. Mathematicians must invent new and clever ways to approach problems in order to solve them. If they used the same old discovery methods, many of these problems would go unsolved.

[thursdayisbetterthanfriday]

Some of the most intelligent people I know are continually asking questions which, in many circumstances, would get them labelled as idiots by some. The point is, they're not afraid to admit their ignorance AND they're also not afraid to use that as a springboard to find out more. It's an excellent attitude which allows them, and those they work and interact with, to be more accepting of their own limitations and can allow those with knowledge to share and help them to better things.

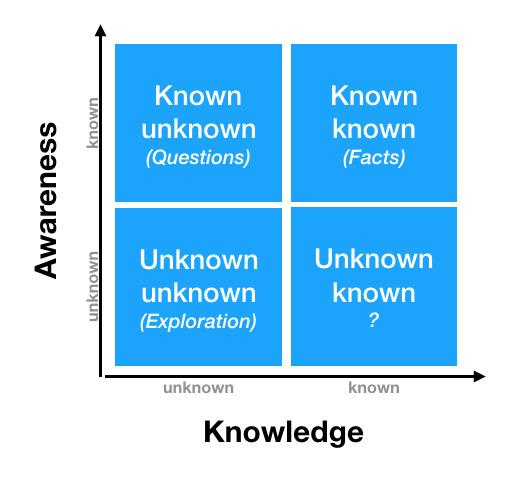
You'll sometimes see the above Awareness/Knowledge matrix cited when people talking about knowledge. I like to use it as a demonstrational tool for people.

If you don't ask questions, then your known unknowns remain unknown. It doesn't end there however, as the Unknown unknowns you would likely have uncovered by asking the question remain unknown. In other words, your ignorance compounds like bank interest. But take the opposite. Asking questions can not only help you turn Known unknowns into Known knowns, it can also uncover new Unknown unknowns which you hadn't considered, and might be crucial to what you're interested in, or doing.

In fact, if you assume each question uncovers a uniform number of Unknown unknowns each time, and you seek answers to all questions (a highly unrealistic example, but go with it for now) you can see even only 2 unknown pieces of information per question can quickly balloon to if you try to get answers to them all. If it's 4 then, well, just note that the y axis here is logarithmic. This is a feeling familiar to anyone who has done a Wikipedia binge or has encountered a human child. This is likely overwhelming, but note that this is more of an illustration of how much information can compound over time.

Asking questions also allows others, who know Unknown knows relative to you, to do the same. It's really a win-win situation if done right, creating a kind of compound interest of knowledge that builds over time. But unlike bank interest, the rate isn't fixed. One question can uncover multiple Unknown unknowns which become Known unknowns, leading to quadratic, or higher, rates of knowledge depending on how much time you have to find answers.

Not only that, by helping others do the same you can get increasing compounding knowledge as you both turbocharge each other's knowledge.

Luckily information usually isn't just individual, non-linked, snippets. It often, contextually, ties into itself, giving a network effect which can allow you to assimilate new information and fit it into frameworks of understanding that you already possess. If you're new to a subject, such as a small child or a first-timer amateur, you'll need to acquire knowledge to make your own internal information base but, again, this will compound its usefulness over time. As you gain more knowledge, it allows you to create your own internal knowledge structures which make it SO much easier to understand the world, and means you get to better know which questions to ask.

Anyway - It can be difficult to ask questions at first, and create new habits, but it's often worth the effort. By inspiring others to do the same you can significantly increase your collective knowledge base. Or if you want, which is also a completely legitimate choice, you can choose not to know. Knowledge gathering is a time consuming task after all. Just don't judge people for wanting more.

Just remember: There's no such thing as a stupid question, if it leads to you gaining understanding more about the world.

There's a whole demographic of people who are profoundly incurious and just assume everyone else is too, so when they see something unfamiliar they immediately rush to declare that not only have they never heard of it, none of you did either. You're just pretending. You had to look it up, don't lie. You didn't know this

And like, so what if someone had to look something up. That's how you learn new things. People usually say this about knowledge that's pretty damn basic, but I can't get over how they're not only scornful at the idea of people trying to learn something new, they casually assume everyone else is, too

[whats-in-a-sentence]

If you were to join together two such containers, doubling the total volume and number of air molecules, you might guess that you'd double the entropy. Detailed calculations confirm¹ this conclusion and show that, all else being equal (unchanging temperature, density, and so on), the entropies of familiar physical systems are proportional to their volumes.

1. For the mathematically inclined reader, recall from note 6 of Chapter 6 that entropy is defined as the logarithm of the number of rearrangements (or states), and that's important to get the right answer in this example. When you join two Tupperware containers together, the various states of the air molecules can be described by giving the state of the air molecules in the first container, and then by giving the state of those in the second. Thus, the number of arrangements for the joined containers is the square of the number of arrangements of either separately. After taking the logarithm, this tells us that the entropy has doubled.

"The Fabric of the Cosmos" - Brian Greene

[jonathankatwhatever]

I’m not sure what I’m doing. I have 2 or maybe 3 notes I’ve held back. I’ve had 3 reasons occur to me. One is that I felt I was working on something but I wasn’t sure what it was. Another is that I could see that it’s large, like really large. And the most recent is a bout of maybe I should just quit. As usual, it is motivated by concern that I’m an idiot about you. My typical response is that believing in you is literally integral to advancing this work, and that more belief - you should see the weird connections I’m drawing at this moment, a series of reflections in which what I imagine about you in Storyline becomes dramatically more real. That’s a fourth reason: I couldn’t get into Storyline. Like not at all. And I wasn’t sure if that was a good or a bad Thing because I’ve been feeling more and more left-sided, more shifted in more dimensions over the dividing 1-0Segment.

How does that work? Over the dividing segment, which is orthogonal, which is - witches - where insertion occurs, where penetration occurs, which explains a lot about Storyline and about how lines are drawn.

I had a name for that kind of thought which grabs you but which makes no sense when you step back. It’s when you’re the actor versus observer: as actor, you hear or see or otherwise experience and that can be in thought form, which is often in my experience a combination of all those modes of perception composited so I sometimes hear words exactly as I type them, while at other times I’m ‘hearing’ something that must also be images because they can’t be described in linear form. They can create a picture but this other is a picture because it conveys the depth of a grid box to a grid square.

That is the importance of the base conception front&back, another notation I’ve had trouble accepting. I use it plenty because it is so basic: front&back forms a grid box because there are now 3 pairs, with 2 of those connecting the f&b. To visualize, imagine two squares like pieces of paper on top of each other, then imagine the space between the square pieces of paper is also square pieces of paper, and then you see that you’ve introduced 2 new pairs.

It may sound silly but this is why the root2 appears in quantum calculations; the projection into a gs means the potential within the grid box projects. So that root2 embodies the potential across the box, nicely idealized. That’s actually pretty cool when I think about it. I keep under-estimating what I’m doing because I do it so much now. Used to take months of effort to wring some truth out of ideas like logarithms. I couldn’t accept it was actually counting 1+1 in a specific manner, which was the first idea that came to me many years ago. How could I? I knew the answer but not why it was the answer.

This may actually be getting good enough to post.

I said to myself I’m ready when I can explain this clearly. Here’s one: I was working out Regularization of bT, with the fundamental concept that each 1-0Segment of the bT represents one of these pairs of dimensions in a grid box. I got stuck at the next point, which appears to be that each gs forms as D6 drops to D4, meaning a pair is ‘lost’ through Regularization. That visualizes as 4 distorted bT, and the next step is each side becomes 1 to the other side’s 2. I can now see how this works with 5: one side of 3 becomes 2, and that Regularizes.

How then does this work? Regularization works because we see what makes it through, meaning this gsProcess constructs and also acts as a sieve to remove what doesn’t make it through. I’ve never been able to state that so clearly. It’s important to grasp how the Sticks work.

This is a perfect example of my life experiences. I first met the Sticks in Storyline which developed when I was reading science fiction in my early teens. I met with them. They would communicate to me what was unique about each instance we were investigating so we could understand the contamination process, the gsProcess which generates from within in the negative where the negative reactions, defensive reactions, predator and prey reactions, negative implications of offensive reactions, etc. are deemed positive, meaning they emerge into the ++ quadrant though they are not responsive to higher dimensions.

I sort of hate to say this but it’s a lot like lefties, which I also worked on, because handedness is a flow effect where the flow is across the intangible, which then manifests into the tangible. You can see how other-handedness generates: it can be local, like eddies, or it can be having characteristics which work well enough with and against the flow. That idea has a lot of applications. Amazing what happens when you see intangible relationships.

I’m starting to see the abc and a bunch of others as clear implications of gsProcess. What does it mean that there’s a finite number of triples which are coprime and where C>rad(abc)^n+Epsilon?

I’m very tired. I’ll post this now and the other parts tomorrow if I make more progress.

[homeimprovementway]

How to Use Calculator for Log: Master the Logarithm Functions

To use a calculator for log, simply press the "Log" button and enter the number. Logarithms help solve complex mathematical problems by finding the exponent for a given number. Logarithms are a fundamental mathematical concept with numerous applications in fields such as science, engineering, and finance. Using a calculator to compute logarithms can simplify complex calculations and help in problem-solving. By understanding how to use the log function on a calculator, individuals can efficiently determine the power to which a base must be raised to produce a specific number. This can aid in various scenarios, such as analyzing exponential growth or decay, calculating the time required for an investment to double, and solving equations involving exponential functions. Mastering the use of log on a calculator can enhance mathematical proficiency and streamline problem-solving processes in diverse academic and professional settings.

Using A Calculator

When it comes to solving logarithms, using a calculator can be a real time-saver. With the convenience of modern graphing calculators, you can easily calculate logarithms of any base, simplify complex equations, and perform calculations with small numbers. In this blog post, we will explore different ways to use a calculator for logarithms. Whether you are a student or a professional, this guide will help you make the most of your calculator's 'Log' button, enter logarithms on a graphing calculator, use other log bases, handle small numbers, and even divide natural logs with ease. Using The 'log' Button The 'Log' button on your calculator is specifically designed to calculate logarithms. To use it, simply enter the number you want to calculate the logarithm for and press the 'Log' button. The result displayed on your calculator is the exponent of the base number you entered. It's that simple! This feature is especially useful when you want to quickly find the logarithm of a number without manually performing complex calculations. Entering Logarithms On A Graphing Calculator If you're using a graphing calculator, entering logarithms is a little different. Most graphing calculators have a dedicated 'Log' button, usually located near the trigonometry functions. To calculate a logarithm on a graphing calculator, enter the base of the logarithm, followed by the value you want to find the logarithm of. For example, to calculate the logarithm base 10 of 100, you would enter "log(100,10)" into the calculator. The result will be displayed on the screen, giving you the logarithm of the specified number with the specified base. Using Other Log Bases Calculators usually default to base 10 logarithms. However, you may come across equations that require logarithms with different bases. Fortunately, most calculators allow you to enter logarithms with any base you desire. Simply use the log function followed by the base number in parentheses. For example, to calculate a logarithm base 2 of 8, enter "log(8,2)" into your calculator. The resulting value will be the logarithm of 8 with base 2. Using Logarithms With Small Numbers Working with small numbers can be tricky, but calculators make it much easier. To calculate the logarithm of a small number, simply enter the number as it appears in scientific notation. For example, if you want to find the logarithm of 0.001, you would enter "log(1 x 10^-3)" into your calculator. The calculator will then display the logarithm of the small number, giving you the solution you need. Dividing Natural Logs With A Calculator Dividing natural logs can be cumbersome, but with a calculator, it's a breeze. To divide natural logs, use the division operation ("/") and enter the two natural logs you want to divide. For example, to divide the natural log of 10 by the natural log of 2, you would enter "ln(10) / ln(2)" into your calculator. The result will be displayed on the screen, providing you with the answer to your division problem.

Tips And Tricks

When dealing with logarithms, there are various tips and tricks that can streamline the process and make calculations faster and more efficient. In this section, we will uncover some useful hacks that can help you quickly calculate logarithms without the need for a calculator. Quickly Calculate Logarithms Without A Calculator Calculating logarithms without a calculator can be simplified by utilizing a few strategic techniques. One method involves using the concept of inverses. Since logarithms are inverses of exponentials, you can utilize this relationship to simplify certain calculations. For example, if you need to find the logarithm of a number to a specific base, you can transform it into an exponential form and simplify the calculation. Another handy trick for quickly computing logarithms is to remember the common logarithm values. Having key logarithm values such as log 2, log 3, and log 5 memorized can aid in swiftly approximating logarithms of other numbers. Additionally, familiarizing yourself with the properties of logarithms, such as the product and quotient rules, can expedite the computation process and minimize the need for a calculator. https://www.youtube.com/watch?v=kqVpPSzkTYA

Calculating Logarithms On Different Calculator Brands

Calculating logarithms using different calculator brands can be a versatile skill. Below, we explore how logarithms can be calculated on various popular calculator brands. Using Logarithms On A Casio Calculator Calculating logarithms on a Casio calculator is straightforward. Follow these steps: - Press the "Log" button on your Casio calculator. - Enter the number you want to find the logarithm of. - Press the "=" button to display the result. Using Logarithms On An Iphone Calculator Utilizing logarithms on an iPhone calculator is convenient. Here's how you can do it: - Open the Calculator app on your iPhone. - Turn your iPhone to landscape mode to reveal the scientific calculator. - Tap the "Log" button followed by entering the number to calculate the logarithm. By following these simple steps, you can efficiently compute logarithms on your Casio calculator or iPhone calculator.

Frequently Asked Questions On How To Use Calculator For Log

How Do You Do Log On A Calculator? To calculate a logarithm on a calculator, press the "Log" button and enter the number you want to find the logarithm of. How Do You Do Log On A Normal Calculator? To find the logarithm on a normal calculator, press the "Log" button followed by the number. What Is The Easiest Way To Calculate Logs? The easiest way to calculate logs is using a calculator. Press the "Log" button, enter the number, and the result is the logarithm. How Do You Calculate Log10? To calculate log10, use a scientific calculator by pressing the "log" button and entering the number. The result displayed is the logarithm with base 10.

Conclusion

Using a calculator for logarithms can simplify complex calculations and save time. By following the steps outlined in this blog post, anyone can harness the power of logarithms in their mathematical endeavors with ease. So, go ahead, grab your calculator, and dive into the world of logarithms with confidence. Read the full article

[lunarsilkscreen]

Exponent in Programming

Binary is read right to left when we're talking programming.

Starting at 1

[64][32][16][8][4][2][1]

Notice something interesting about it? Binary is base-two, and like every counting system, every digit is essentially an Exponent of the second digit. In this case: 2.

Look

[x⁶][x⁵][x⁴][x³][x²][x¹][x⁰]

Provided there's a one in one of those columns, you can get the total simply. And if you want to go up, or down a square, you can simply bit shift.

If, for example, you start at 1, and bit shift left (0-fill) you go from 1 to 2, and then further to 4, 8, 16 etc... all of them are exponents of 2

What's really neat about this, is you can do a fast exponent by selecting a different base equivalent of the number you'd like to raise to a power, and then shift that number into the requisite digit, and then turn into base ten, and voila; your answer.

It even works in base ten.

It can even easily identify logarithms by shifting right, without having to go through every single number. Provided that number is a digit of the base you're working with.

[thewestcoastmathtutor]

Perfect Square ? Yes or No? | The Westcoast Math Tutor

Perfect Square ? Yes or No? | The Westcoast Math Tutor https://www.youtube.com/watch?v=yhPIvlwvcSI How do we know if this trinomial is a perfect square. That's simple. We just have to ask three questions. 1. Is the first term a square? 2. Is the second term a square? 3. Is the middle term twice the product of 2x and 3 ? Since the answers to these questions are all yes, 9x^2+24x+16 is a perfect square. 🔔 Join The Westcoast Math Tutor to watch more content on High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ✅ Stay Connected To Me. 👉 Facebook: https://ift.tt/504pYH1 ✅ For Business Inquiries: thewestcoastmathtutor@gmail.com ============================= ✅ Recommended Playlists: 👉 Decimal to Fraction https://www.youtube.com/watch?v=3J8Dnl0wLQE&list=PLPSu23Z8U7JG3C22WEiDhDf2bBXZ2yQJK 👉 Improper Fraction to Mixed Number https://www.youtube.com/watch?v=VvL7fXAYtHg&list=PLPSu23Z8U7JG0ErjzsUGv6KfDThOE7SxO 👉 Linear Equation https://www.youtube.com/watch?v=UUeuIQ6bUxU&list=PLPSu23Z8U7JGhun3PPquRpkjrMdNFAggz&pp=iAQB ✅ Other Videos You Might Be Interested In Watching: 👉 Evaluating Logarithms https://www.youtube.com/watch?v=ve9BMVUC6fE 👉 Exponential to Logarithmic Form & Logarithmic to Exponential Form https://www.youtube.com/watch?v=KbEULbAjvtI 👉 Logarithms Easy ! 2 Explanations https://www.youtube.com/watch?v=77msni1vacc 👉Boundedness Theorem, 2 Examples https://www.youtube.com/watch?v=NWPFmBmu380 ================================ ✅ About The Westcoast Math Tutor: Hello Friends! I’m The Westcoast Math Tutor, and with this channel, I will provide tutorial videos to better your understanding of different high school math topics. Once in a while, I will also make other interesting math videos outside of high school math topics. If you have any questions, please ask me in the comments. This channel is what I’ve been doing for you. If you want to do something for me, hit the bell button, like, and share. Thanks for watching, and happy learning, everyone! ✅For Appointment and Business inquiries, please use the contact information below: 📩 Email: thewestcoastmathtutor@gmail.com 🔔Subscribe for more High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ================================= #logarithmroots #inverseproperty #logarithmbasics #logarithmtutorial #mathexplained #logarithmproblems Disclaimer: I do not accept any liability for any loss or damage incurred by you acting or not acting as a result of watching any of my publications. You acknowledge that you use the information I provide at your own risk. Do your research. Copyright Notice: This video and my YouTube channel contain dialogue, music, and images that are the property of The Westcoast Math Tutor. You are authorized to share the video link and channel and embed this video in your website or others as long as a link back to my Youtube Channel is provided. © The Westcoast Math Tutor via The Westcoast Math Tutor https://www.youtube.com/channel/UCqP_EgHF0TGr65xMEcFPcjA October 20, 2023 at 05:17AM

[archibaldtuttle]

@fluffycloudhead answering here so the thread doesn't get derailed

honestly, I'm biased as hell, but I'm gonna say color grading. I understand that it's really tough to actually see it if you don't train your eye (trust me, my life is a nightmare now that I can't help seeing it), but it is THE step in filmmaking that is the most overlooked.

What most people don't know is that nowadays, all the footage coming out of cameras is log footage. "Log" is short for "logarithmic", because it does this to the visual data :

What this means is that, in order to lose as little information as possible, the camera makes the image flat and grey and awful. Here's an example of log footage :

This is what footage looks like right out of the camera - because it allows them to keep as much information as possible. If you have "burned whites" or "smothered black" (this is a literal translation of the French terms for this don't come for me I'm tired), then even if you make the image brighter/darker, you'll just have a patch of uniform grey, because there is no nuance within that black/white.

So all films and shows look like this ugly grey mess before they go through our hands - we have to basically recreate the lighting, atmosphere and contrast that the director of photography elaborated on set. We go through films shot by shot and make sure everything matches - some scenes were shot piece by piece, weeks or months apart, and we have to make them match.

I like to compare filmmaking to Frankenstein's monster. Writing a film is like making the anatomical drawings - where all the pieces will go, what kind of brains will you need, how tall will it be etc... Shooting the film is like gathering all the body parts in the graveyard! Sometimes you don't find what you thought you would, sometimes you have to make do with inferior limbs, sometimes you find a much better brain than you planned. Things happen on set that you can't predict. Editing is like sewing the monster together - you discard the parts you don't need in the end, you carefully stitch the disembodied limbs to one another, you make it as lifelike as possible.

Color Grading (and Sound design/mixing) is the lightning bolt. Without those things, the film would look like a rotting corpse. Grey, lifeless, boring.

And as a bonus, here's a quit edit I did on my phone 💜

hello I am ill and would like some movie related questions as a reminder I am a professional post-production technician so if you're curious about things like that don't hesitate

[mathsai]

How to Solve Log: A Step-by-Step Guide with Maths.ai

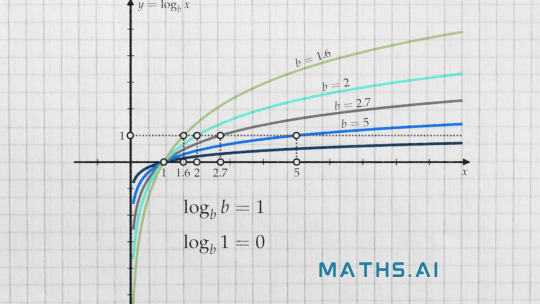
Welcome to Maths.ai, your reliable AI-based companion for solving challenging math problems! In this article, we'll dive into the world of logarithms, exploring their properties and presenting a comprehensive step-by-step guide to solve log equations. With the assistance of our Maths.ai, we'll walk you through the process and provide real-life examples to solidify your understanding.

Section 1: Understanding Logarithms

Before we jump into solving logarithmic equations, it's crucial to grasp the concept of logarithms. A logarithm is the inverse operation of exponentiation. In other words, it answers the question, "What exponent do I need to raise a particular base to, to obtain a given value?" The notation for a logarithm is as follows:

If \(b^x = y\), then \(\log_{b}(y) = x\).

Here, \(b\) is the base, \(x\) is the exponent, and \(y\) is the result of the exponentiation. Logarithms are particularly useful in solving problems involving exponential growth, decay, and complex calculations.

Section 2: Properties of Logarithms

Before we proceed with solving logarithmic equations, let's review some key properties of logarithms:

1. Product Rule: \(\log_b(xy) = \log_b(x) + \log_b(y)\)

2. Quotient Rule: \(\log_b\left(\frac{x}{y}\right) = \log_b(x) - \log_b(y)\)

3. Power Rule: \(\log_b(x^n) = n \cdot \log_b(x)\)

These properties allow us to manipulate logarithmic expressions and simplify complex equations into more manageable forms.

Section 3: Solving Basic Logarithmic Equations

Now, let's delve into solving basic logarithmic equations. Consider the equation:

\(\log_2(x) = 3\)

Step 1: Recognize the Base and Result

Identify the base of the logarithm, which is \(2\) in this case, and the result of the logarithmic expression, which is \(3\).

Step 2: Rewrite the Equation in Exponential Form

To solve for \(x\), rewrite the equation in exponential form:

\(2^3 = x\)

Step 3: Evaluate the Exponent

Compute the result of \(2^3\):

\(2^3 = 8\)

Step 4: Determine the Solution

The value of \(x\) that satisfies the equation \(\log_2(x) = 3\) is \(8\).

Section 4: Solving Logarithmic Equations with Variables

Now, let's tackle a more complex logarithmic equation involving variables:

\(\log_3(x+2) - \log_3(x) = 2\)

Step 1: Combine Logarithms

Apply the quotient rule to combine the two logarithms:

\(\log_3\left(\frac{x+2}{x}\right) = 2\)

Step 2: Express Equation in Exponential Form

Rewrite the equation in exponential form:

\(3^2 = \frac{x+2}{x}\)

Step 3: Solve for \(x\)

To solve for \(x\), isolate \(x\) on one side of the equation:

\(9x = x + 2\)

Step 4: Simplify and Solve

Combine like terms and isolate \(x\) on one side:

\(9x - x = 2\)

\(8x = 2\)

\(x = \frac{2}{8} = \frac{1}{4}\)

Step 5: Verify Solution

Check if the solution \(x = \frac{1}{4}\) is valid by ensuring that \(x\) is positive in the original equation:

\(\log_3\left(\frac{\frac{1}{4}+2}{\frac{1}{4}}\right) - \log_3\left(\frac{1}{4}\right) = \log_3\left(\frac{\frac{9}{4}}{\frac{1}{4}}\right) - \log_3\left(\frac{1}{4}\right) = \log_3(9) - \log_3(1) = 2 - 0 = 2\)

The solution \(x = \frac{1}{4}\) satisfies the original equation.

Section 5: Solving Logarithmic Equations with Advanced Techniques

In more advanced problems, logarithmic equations may require additional techniques for simplification. Let's consider an example:

\(\log_2(x^2 - 9) - \log_2(x+3) = 1\)

Step 1: Combine Logarithms

Apply the quotient rule to combine the two logarithms:

\(\log_2\left(\frac{x^2 - 9}{x+3}\right) = 1\)

Step 2: Express Equation in Exponential Form

Rewrite the equation in exponential form:

\(2^1 = \frac{x^2 - 9}{x+3}\)

Step 3: Solve for \(x\)

To solve for \(x\), isolate the expression on one side of the equation:

\(2(x+3) = x^2 - 9\)

Step 4: Expand and Simplify

Expand the left side of the equation:

\(2x + 6 = x^2 - 9\)

Step 5: Move All Terms to One Side

Move all terms to one side of the equation to obtain a quadratic equation:

\(x^2 - 2x - 15 = 0\)

Step 6: Factor and Solve

Factor the quadratic equation:

\((x-5)(x+3) = 0\)

Set each factor to zero and solve for \(x\):

\(x-5 = 0 \Rightarrow x = 5\)

\(x+3 = 0 \Rightarrow x = -3\)

Step 7: Verify Solutions

Check if the solutions \(x = 5\) and \(x = -3\) are valid by ensuring that the expressions inside the logarithms are positive:

For \(x = 5\):

\(\log_2(5^2 - 9) - \log_2(5+3) = \log_2(16) - \log_2(8) = 4 - 3 = 1\) For \(x = -3\):

\(\log_2((-3)^2 - 9) - \log_2((-3)+3) = \log_2(0) - \log_2(0)\)

Since the expression inside the first logarithm is non-positive, the solution \(x = -3\) is invalid.

Congratulations! You have now mastered the art of solving logarithmic equations, thanks to the step-by-step guidance of Maths.ai . Remember the fundamental properties of logarithms and apply them to simplify and solve log equations. With practice, you'll become adept at handling logarithms and excel in your mathematical journey. Keep exploring the fascinating world of mathematics with the support of Maths.ai, your online maths tutor for all your maths-related support.

[allmathtricks]

In this video tutorial explained about logarithm applications with examples and solutions based the logarithmic formulas