#cartesian mathematics

[femmys-textbook-notes]

The book then does indeed begin to use dead sheep as a central feature to explain counting.

[er-cryptid]

Coordinate Systems

-- Cartesian System = used for linear motion

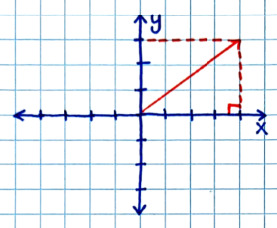
-- Polar System = used for angles

.

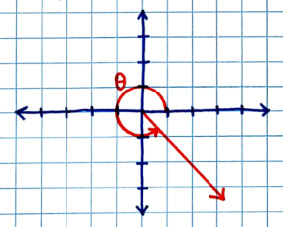
Patreon

[more-mathematics-mor-lam]

Learning multiple languages in order to get to know the maps in between them 😈

[greetings-inferiors]

Something cool that only just clicked is that when you convert the vector equation for a 3D line into Cartesian form, the x, y, and z parts are all equal to lambda!

For a visual:

That’s so cool!

Don’t know why that never sunk in, as that’s literally how you’re taught to convert between the two, b it it’s cool that I know it now nonetheless.

[botaniqueer]

Having a science background and knowledge in mathematics is very funny because all these stories will talk about things like non-euclidean geometries and it's like...

BEHOLD THE NON-EUCLIDEAN HORRORS FROM BEYOND OUR WORLD:

SEE HOW THE ANT IS FORCED TO TRAVERSe THE ELLIPTICAL TERROR OF NON-CARTESIAN SURFACES

(Sidenote: This post is meant lovingly and not aggressively or flippantly. You cosmic horror writers keep doing you as long as it's not xenophobic like Lovecraft. I love cosmic and unreality horror btw and it's my favorite horror.)

[etym-a-day]

vortex, n.

First attested in the 1650s as cosmological terminology in reference to the Cartesian theory of "an invisible rotating ether supposed to fill all space" (www.etymonline.com/word/vortex). From there the term's meaning was extended to its modern sense of "a whirlpool, a swirling mass (as of water, fire, or wind)".

The term was borrowed directly from Latin vortex, a variant of vertex (of the same meaning as the Modern English sense), which is a nominalization from the verb vertere, "to turn or twist". The Latin verb is from the Proto-Indo-European root *wer-, "to turn or bend".

The Latin plural for this term is vortices, although in Modern English usage vortexes has become an accepted plural as well. This word is an etymological doublet with the Modern English mathematical term vertex, "the point opposite the base of a figure".

[anocana]

been slowing down on thinking about phil of math so before i forget too much, notes towards my perspective. i'm sure i'll come back to this at some point

as the sage once said, "always historicize". an account of the nature & subject matter of mathematics must be compatible with its history. it doesn't need to fully explain it — if it could, it'd just be overfitting a theory to the contingencies and ambiguities of history — but it should be capable of interfacing with the history of mathematics and also with historical views of the nature of mathematics. (this doesn't rule out all platonisms but it does kill the "ontologically minimal" ones.)

mathematics is a broad category of human activity and we should strive to understand all of it instead of declaring that some subcategory is the true essence. the framing of models (which can be v useful!) as "reductions" of one field to another, the philosophical exaltation of formalized proof at the expense of the informal, the neglect of the real process of coming to definitions and proofs: all mistakes.

the ontological question is overemphasized. however, every answer to the question has to account for human thought about mathematics which means going through a sort of psychologism or intuitionism even if it's a derived phenomenon and not a foundation; this is where every actual consequence of the ontology will manifest, so it should be more of a focus. traditional intuitionism is too restricted & built on a shaky foundation. also, platonism is silly but hard to talk around.

per above: i think mathematics consists of a process of mentally abstracting consistent structures — from real things or other abstractions — and applying various practices to understand them and keep our thoughts about them consistent. (semi)formal proof is one of the most crucial of these practices but not the only one

connections between fields of mathematics occur where the structures they study overlap or coincide. neither side has to be "primary" or "foundational" — rather, a connection opens up the use of practices developed for the study of one field to the study of another, and sometimes both. cartesian geometry allows both the use of algebraic techniques to construct and study geometric objects and the use of geometric interpretations & techniques to study systems of numbers (calculus, phase space, and so on)

the striking similarities between independent historical developments of mathematics are because the same abstract structures (numbers, geometry, polynomials, etc) are useful enough to appear in these different contexts. a conclusion about what's true of a structure is not contingent on anything but the structure; but which structures are studied, and which statements about them are considered relevant, is purely contingent on the world, historically variable, and sometimes ambiguous. (contingent on which elements of the world?)

the use cases which originate a field are often not the ones which drive it internally

[flanpucci]

An ASD oriented analysis of the character of Enrico Pucci

Okay guys after letting this draft cook in my notes for months, here it is!!!

I have decided to embark on the journey of listing the reasons why I think Pucci is autistic coded and if he isn’t, he’s written with a pretty good idea of what an autistic person is! Since I'm pinning this, the analysis will be under the cut ↓

I can’t guarantee that my analysis won’t come with a whole lot of general delusion or projecting on my side, so don't hesitate to tell me if you feel some type of way about this. I understand that many of the traits or behaviors i’m gonna talk about are mostly explained by the events happening in canon, but they give him a general super autistic vibe. Disclaimer that I’ve also decided to ignore most acts of murder type violence for this analysis as I think those are more relevant in the context of the story than the character building.

Although not on purpose this analysis is organized almost like diagnosis criteria, so we're going to look into repetitive behavior and interests, communication, aversion to unpredictability and sensory processing etc...! Before we start, I'd like to say once more that I am autistic, my analysis is mine and reflects my opinion only, it's my headcanon and comes with a lot of projecting, so proceed with caution.

Anxiety and counting prime numbers, Repetitive behavior

Counting numbers is a well known technique to stop panic attacks. The reason is that when you panic, your brain’s logical part doesn’t activate. Counting numbers will help you get the logical part of your brain back ‘on’. Simply counting numbers in order or in a simple pattern is too natural, and may not work, so some people will count numbers backwards from 100, count numbers in a non-patterned, random way, or even count prime numbers.

In Pucci’s case he counts primes because they can’t be divided other than by 1 or themselves and are “lonely numbers”. The prime numbers remind him of his own loneliness against adversity, and give him courage. I don’t think a lot of neurotypical people feel personal closeness to something unemotional like a mathematical concept, but I might be wrong. I think what’s interesting to note is that prime numbers are a fixed series of numbers, never changing, offering a great deal of familiarity in repeating them (and also by doing so out loud, in the sound of repeating them). He has also memorized them up to the hundreds, (maybe even thousands iirc?), which shows he has an amazing memory skill, but also that he’s probably counted them a LOT. (Funny anecdote, Oliver Sacks mentions in one of his psychology books a pair of autistic twins that would figure out prime numbers together, and use it as means of communicating and bonding. They were able to produce huge prime numbers without a table!)

It is just something I wanted to point out, but I think it’s funny that a priest wouldn’t recite prayers as a calming mantra, but something very cartesian like mathematics. This furthers the idea that he has a lot of interest and finds a peculiar comfort and understanding of the world in science.

Oh and I think resetting the entire universe for everyone to gain precognition of events COULD be considered as a liking for repetitive things… ! /j

His interests and the random trivia at unexpected times

Pucci seems to be a man of many interests but primarily these are science (especially biology, animals, maths/geometry and physics), Dio’s plan/heaven, christianism, art (paintings). At least that’s what I got from the manga. There aren’t a lot of characters for which you can easily lay out the interests in that manner. The reason for that is that he talks about those all the time! And he always uses metaphors related to what he knows about to explain the world, his intentions, or situations.

• The corridor scene where he meets Jolyne, it’s not like it’s random or out of the blue, but it feels a bit peculiar to bring up this subject in this manner, and Jolyne seems dumbfounded at what he said to her.

• When handcuffed to Jolyne, he starts explaining about the swallows that are prone to accidents to make a parallel between the birds and her own situation.

• References both a politician’s use of subliminal sex and a painting (the “Domine Quo Vadis”) in a dramatic moment where he’s literally ending his brother’s life.

• Seems to be particularly interested in art as shown by the book he was reading when he met Dio (about Fra Filippo Lippi, a painter) and the conversations he has with Dio (once again using art as a metaphor to understand other concepts such as stands, and souls.).

• Of course bringing up the subject of the man eating a mushroom for the first time at the most unstable point of the battle against Jolyne, feels very out of the blue, (but not out of context.)

• When talking to Miraschon, he does a whole bunch of inappropriated stuff lol, doesn’t pay attention to what she says, and starts talking about his own interests/ideas.

This happens again when talking to Donatello Versace, where he's bouncing off questions, not acknowledging the answer right away and coming back to it a little bit later. His train of thought seems to come first, and his communication is not centered around making the other feel like they've been listened to.

Overall he often makes a great point, but sometimes it feels like the context is lacking, like he has had many thoughts before saying the things he says, but we don’t get to hear them, so the conversation topics are a bit unnatural. Plus he generally has a very self-important way to talk and explain things.

Other than that I think his exceptional focus on the same goal and obsessive idea of fate, from childhood and up into late adulthood can be the sign of a truly one track mind, which can be often found in ASD. Could also be noted that a lot of his behavior and actions is copied/referencing Dio, which could be because of Dio’s literal influence (being absorbed by green baby), or an overall tendency to use direct references in speech/behavior.

Self importance and the desire of previsibility

As I just mentioned a little while ago, the Miraschon scene is a scene where he’s info dumping her for at least three pages, on two different subjects, but also not paying attention at what she’s saying. This is not very nice behavior, but it’s very frequent in autistic people too. Being centered on one’s self, and unable to put yourself in another person’s shoes is very characteristic of ASD.

Pucci’s motivation and his ideal of heaven makes a lot of sense from an autistic viewpoint for a number of reasons. The first one being the discomfort caused by the unknown, or at least the fact that he thinks the world would be a better place without unknown events. The desire to know everything in advance and be able to have the time to be prepared for it will resonate with a lot of autistic people, because our brains have so much trouble adjusting to unknown outcomes and situations. I can’t explain it much better, it’s just wiring.

Second reason is Pucci’s overall sense of self importance throughout the part. There are many situations in which he will put himself first, expecting better treatment, straight up explaining that he’s different than other people.

The frog scene is interesting because he tries to weigh logically why his situation is objectively worse than the guard’s, without acknowledging the slightest the guard’s panic when assessing such a stressful situation.

(Pucci thinks the guard takes decision based on logic and not panic, gets frustrated that the guard isn't calm and rational.)

His inability to see things from outside his viewpoint is ultimately what will lead him to try to push his own ideal onto the whole world, always sure inside himself that he’s doing that out of altruism and for the greater good. Of course I think there is a slight disconnect from his inner emotions about what has led him to this point. But for me, this is the truest sign of being unable to understand that other people might see things any other way than he does, but he’s just sure that people don’t understand that it’s for their own good. In a way, his self-centeredness is mostly intellectual and not of intentions. This is something that is often present in people with ASD, because of a lack of (or misplaced/altered) cognitive empathy. People with ASD can have trouble mentalizing other people’s emotions or point of view. It doesn’t mean that they don’t care, don’t respect it, or can’t show support, but they just can’t really understand that another person has another mental space.

Cognitive empathy is described as such :

Identifying and labeling the emotions, connecting feeling to cause, and reading the thoughts and perspective of others. Ability to read nonverbal communication and social context. Ability to read the mental experiences of others.

Pucci will often justify his lack of mind theory by « you just can’t understand it. » : from his view point, being opposed by other people is not due to divergence of opinion (which would mean to accept that other people understand the situation but are in a different mindset), but due to lack of intellectual comprehension. This is why even though very intelligent, it can seem like he’s confused.

Young Pucci and the scenes with Dio

An important thing to note about young Pucci is his inability to break the rule that priests can’t talk about what has been said in confession. He’s not even a priest at that time and the confession was forced on him. These are perfectly good excuses to break the rule, or at least bend it a little, to confront the Weather and then Weather/Perla situation. Hesitation or inability to break the rules, irreasonable attachment to morals and taking irrational decisions because of those despite having great intelligence is a trait that can be found in a lot of autistic people. However, we see that he’s flexible enough to permit that Dio stays in the church basement until the sun sets. In my opinion, he’s quick to give his trust to such a suspicious person as Dio, even when Dio hints that he might be lying. This could be the sign of a little bit of naivety but it's still pretty much normal at a young age.

In the chapters with Dio, we can extract quite a lot of information on Pucci’s communication because it’s the almost only scenes where he’s not in scheming mode, in a pinch, or fighting. Pucci has a very different reaction to meeting Dio, even at a young age, compared to how Avdol or the hunchmen describe their reaction to Dio for example. He’s not shocked or in awe, but not hostile either, which is unusual. Even when he talks about Dio in narration, he has a detached way of calling him beautiful and mysterious, which shows it’s obviously how he feels even though he stays calm at all times in front of Dio, even in dangerous situations.

Dio makes numerous observations about Pucci’s behavior, expression and communication. He seems relaxed and expressive, very different from the rest of what we see of him.

(Pucci 'making a face.')

Another important thing to note is the unusual way he communicates his love to Dio, using very profound words, with a lot of sincerity, without flinching. This genuine confession of a difficult emotion to confess even sets Dio aback.

(Probably having the most fun he’s had in his life here, and is that a smile!?)

Also, parallel play!! They’re shown having bonded profoundly, at the point of hanging out in bed together, but apart from chatting, they don’t really do things together like for example Hermes and Jolyne throw the ball with F.F., they’re doing stuff next to each other (Pucci watches Dio build his boat, and they read lying next to each other.).

(generally also seems kinda bad at picking up subtext)

Two words on sensory perception

(Pucci wondering about how pretty the green baby is, he really wants to know if it's not ugly fr.)

About sensory perception, it’s actually one of the first things I noted when watching the anime especially, he’s very curious about the green baby, and talks to F.F. about it, but as he says himself, he can’t get the “feeling” from a memory disc, and he wants to know how the green baby feels in a sensory kind of way. (Is it soft? is it beautiful?). Of course the many scenes where he purposely mutilates himself without even flinching could indicate that he has a very low perception of physical pain. Both these traits would indicate a very peculiar kind of sensory relationship to the world.

In this scene with Donatello he does state that he has an acute sense of taste, in response to Donatello describing with great precision ingredients in a dish.

(Having a little solo party and dropping trivia again.)

He also seems to feel the music strongly, even though the scene is meant to be comedic, he’s really into it and seems to have some sensory associations (visual/auditory) (also trivia dumping).

Although not directly a sign, the way he asks Dona to test his food because of allergy may also remind of many autistic people who have food allergies and aversions and get people to test food for them before eating.

Body language and facial expression

Pucci has a very specific kind of body posture, especially in the wrists, they’re always limp or twisted in some kind of way, similar to what autistic people might call “T-rex arms”. Araki is very talented at showing detail about characters in the strictly visual part of his drawings, so I think that’s important to note. In terms of facial expression, apart from with Dio, he seems pretty stoic and stern in most situations where he’s not under a lot of stress, almost never laughs or smiles, even in power high situations where other villains usually at least evil laugh for a couple seconds .

(Cute snapped wrist picture collection.)

End note about Weather Report

I just wanted to add a quick word on Weather. Weather Report without his memory disc is also extremely autistic coded. Walking on tip toes, talking in a very low volume not respecting personal space, when he is introduced, he seems super autistic. The reason is the lack of memory disc and consequences of being hung, but I personally think this adds to the overall neurodivergent feel of the manga. I’m also not sure of how much of his backstory was planned at first, and if or not Araki had planned his behavior because of his backstory or not at the point of his introduction scene :3

And there we have it!! I tried not to be too lengthy so I hope you understand my point. I don't think I've seen him being analyzed/hc as autistic a lot, especially compared to characters like Jotaro, but I think he shares some similarities with Kakyoin who is very ND coded too! I would also like to point out that I don't think Araki purposely created a character that reads as autistic, but that he has a very realistic vision of personalities and identities that can lead to this kind of analysis. Also, fun note, Pucci is often typed as INFJ/INTJ and these are prominent personality types in autistic people :3. Anyways, hope you enjoyed, feel free to share your reactions, I'd be glad to hear your thoughts.

NB:

I felt like adding a few to this post so here it is. I would like to say that I think overall Pucci is the most multifaceted, complex character in the series, he has often been described as such, and that’s what makes him the exceptional last boss of the first Jojo era. Many people have had trouble understanding him and Made in Heaven, as can be seen by the numerous amounts of questions on the internet « what did Pucci want to do? » « what is Made in Heaven? » etc. Araki himself said it was very tiring writing such a nuanced villain. I think many of Pucci’s actions and behavior can be attributed to elements in the story narrative, his almost impossible circumstances, and I don’t want to oversimplify, or kick him into a box that might not have been intended at all by Araki. I would also like to add that ASD is a spectrum and one may or may not relate with every trait exposed here, or may find others that I haven’t listed. And it’s always a bit hard categorizing villains as ND because of their reprehensible actions. However I think he is nuanced enough to be considered good rep anyway. But maybe that’s just me fangirling a little too much. In any case, I hope you enjoyed.

Flan, out!!

[daisychainsandbowties]

"It was wrong, Ava knew, to call something like that a vector. She studied mathematics, so she’d been told before to stop using the word like a poet and start applying it, instead, to what it represented. But still, it was hard not to slip into poetry around that word, looking at Beatrice and the angle of her face. The way she stood with those snacks bundled loosely in her arms, in the drawn-out moments that were becoming more common with her; Ava aware of every filament she stirred with the pathways of her body.

A vector is a thing that has both magnitude and direction. Any line can go somewhere, but a vector does it with velocity. Ava’s not a poet, but she figures that girls can be polynomials, if they want. She thinks sometimes they just are."

I NEED you to know. I am in love with you. I actually cannot put into words how much I love these two paragraphs in a very messy and personal way. Maths is somehow ontologically interesting in that it DOESN'T exist and yet defines everything, in that every theorem has a proof

SO often people take science and poetry as antithetical when they're actually synonymous. Yeah a girl can be a polynomial. Reading a good poem feels like a change of basis. Anything can mean anything

i always like to imagine that ava’s very aware of the mathematics of any space she occupies. it’s like… motion is meaning to her and it’s also something she’s painfully aware about; the sheer mechanics of it, how difficult every stretch and turn was to relearn. i think in this au especially she’s always in a place where it matters to her. how things move is life and death in a field of asteroids strewn with tiny humans, so she has to know it all. has to understand motion and her frame of reference (both in the Cartesian sense and in relativistic terms) and her small position inside it all.

i think that where lilith’s a creature of instinct almost all the time when it comes to physical things (not in other ways - that girl is in her head a lot, and it shows, and so she’s a navigator, going somewhere all the time, and surely moving isn’t the same as running, right?)

and then beatrice is suffocatingly precise, ticking unsteadily in time with her instruments, too afraid to touch some things, too eager to touch others. against those two ava’s the in-between of “yeah, i just know how this works. isn’t it obvious?” but she’s also got this intricate understanding of just how the laws of motion apply, and especially to her. i think it’s the cost of it all, for her - to understand so perfectly how things move because she spent so long just observing, like an astronomer who’s now an astronaut. and gay about it.

[buzzfella]

guys dont let ironically being a hater get in the way of loving the world. i dont hate rené descartes. i think he was a freaking cool dude who contributed greatly to the field of mathematics and laid groundwork for probably the only reason i understand math today. imagine trying to do the area between two curves without the cartesian plane!!! imagine using fermats system! that would suck! thank you Descartes im sorry for mocking your cogito sum ergo like a billion tomes

[perkwunos]

It seemed to Berkeley that the metaphysics of Descartes and Newton resulted in the description of a ‘real world ’ that had all the properties of the sensible world except the vital property of being seeable. … But the pure mathematician cannot take note of colour. Hence, under the influence of the Mathematical Principles of Natural Philosophy and of the rapidly developing science of optics, Berkeley’s contemporaries looked to the principles of optics to account for the seeahility of things. It is Berkeley’s merit to have realized that the Cartesian-Newtonian philosophers, seeking to account for a seeahle world, succeeded only in substituting a world that could in no sense be seen. He realized that they had substituted a theory of optics for a theory of visual perception. The outcome of this mistake is a duplication of worlds—the Image-World, sensibly perceived by men, the Real-World apprehended only by God. … Berkeley saw the absurdity of this duplication ; he failed to realize that it was rendered necessary only by the confusion of the theory of optics with the theory of vision. He saw that the question—How is perception possible ?—is devoid of sense ; he saw that it is no less absurd to look to physics for an answer to the question. … The achievement of Newton in the theory of Optics was that by his discovery of differently refrangible rays he discovered measurable correlates of colour; he thereby made the use of quantitative methods possible in a domain which would otherwise be excluded from the scope of physics. His extremely confused metaphysics is the result of his refusal to admit that there is anything in the perceived world except the measurable correlates, which ought, accordingly, to be regarded as the correlates of nothing. … … Sensible qualities [according to Newton] have no place in the world; they are nothing but ‘dispositions to propagate this or that motion into the Sensorium.’ There they undergo a transformation, not in the mathematical sense of that word, but a strange transformation indeed—a metamorphosis of ‘the external world of physics’ into ‘a world of familiar acquaintance in human consciousness.’ The transformation remains inexplicable. … We shall find that the problem of perception, in this form, arose only because we have allowed the physicists to speak of a ‘real world’ that does not contain any of the qualities relevant to perception. To adopt the striking phrase of Professor E. A. Burtt, we have allowed the physicists ‘to make a metaphysic out of a method’. In so doing they have forgotten, and philosophers do not seem to remember, that their method has been designed to facilitate investigations originating from a study of ‘the furniture of the earth’.

Susan Stebbing, Philosophy and the Physicists

[madame-mongoose]

Consider a non-Euclidean hyperbolic trapezoidal prism with sides of varying curvature, denoted by the complex variables zz and ωω, such that the hyperbolic tangent of their respective arguments is proportional to the logarithm of their magnitudes, i.e., tanh⁡(arg⁡(z))∝log⁡(∣z∣)tanh(arg(z))∝log(∣z∣) and tanh⁡(arg⁡(ω))∝log⁡(∣ω∣)tanh(arg(ω))∝log(∣ω∣).

Now, let f(x,y,t)f(x,y,t) be a multivariate function defined on the trapezoidal cross-section of the prism at time tt, where xx and yy are Cartesian coordinates embedded in a hyperbolic space. The function ff satisfies the partial differential equation:

∂f∂t+∂2f∂x2−∂2f∂y2+∫−∞∞cos⁡(ecos⁡(et))cosh⁡(xy+t) dx=∂2f∂t2∂t∂f​+∂x2∂2f​−∂y2∂2f​+∫−∞∞​cosh(xy+t)cos(ecos(et))​dx=∂t2∂2f​

Your task is to determine the general solution for f(x,y,t)f(x,y,t) given the initial conditions f(x,y,0)=exyf(x,y,0)=exy and ∂f∂t(x,y,0)=sin⁡(xy)∂t∂f​(x,y,0)=sin(xy).

For bonus points, express the solution in terms of a hypergeometric series and provide an interpretation of the mathematical implications in the context of non-Euclidean geometry and quantum mechanics.

dont do math at me ill cry

[seradae]

I want to get new tattoos and I think I'm going to design out all the mathematical identities and formulas I commonly use for my left arm for easy reference.

Euler's Formula: e^(iθ) = cos θ + i sin θ

2d rotation: x' = x cos θ - y sin θ; y' = x sin θ + y cos θ

Cartesian to polar: r = |(x,y)|; θ = atan(y/x)

Polar to Cartesian: x = r cos θ; y = r sin θ (this one is just a special case of 2d rotation where you plug in (r, 0) though, so probably leave this one off)

Angle between vectors: θ = acos(||a|| • ||b||)

... Goddamn I'm a nerd.

[positivelyapunovexponent-good]

okay so

tested positive for COVID a couple of hours ago. Running low grade (100.4-100.6 deg F) fever that just won’t break. Every single time time I tried to fall asleep for the past four hours I resumed the exact same fever dream about trying to prove the Heine Borel theorem but about my brain?

or rather. Specifically the preparatory theorem for Heine Borel in Rudin proving any closed bounded k cell comprised of the Cartesian product {[a_i, b_i]}\for all i \in [k] is compact in \mathbb{R}^k by supposing not and then deriving a contradiction by partitioning the k cell into the union of 2^{nk} cartesian products of intervals of length {(b_i- a_i)/2^n} \forall n \in \mathbb{Z}_+, supposing there is an open cover G of the k cell that does not have a finite subcover on a nested sequence these intervals chosen at each step n, and then showing by intermediate value theorem that nested intersection of those intervals contain a point x of the k cell so there is a neighborhood in G containing x and all but a finite of the intervals which means there is in fact a finite subcover wonders! Yeah that one

so the dream is like. Imagine your brain is a k cell in R^k packed full of an uncountable number of ittty bitty neurons but they are SICK and DYING of fever so you need to come up with an open cover of your brain that isolates out the sick neurons in their own quarantine open sets so they don’t infect the other neurons but you need to show any such open cover has a finite subcover because otherwise I guess you chop the neurons too thin when partitioning them? And that’s bad because it means your brain breaks? I dunno that part of the dream doesn’t make any sense but it feels very urgent.

anyways. So I keep waking up in a cold sweat feeling my dream proof is somehow wrong or incomplete. And then I fall back asleep and the dream repeats. So now it’s 6AM and I’ve had to scrounge up my old pdf of Principles of Mathematical Analysis by Rudin and make sure I had that proof down cold. And I’m actually proud of how well I remembered it even when in a fever addled dream state. So I guess I really do know the Heine Borel theorem which is nice!!! I just hope that is sufficient to satisfy the Plague Brain

[the-chomsky-hash]

B. In other words, we are dealing with two modalities [vis.,

philosophy of experience, sense, subject (Sarte, Merleau-Ponty)

philosophy of knowledge, intuitionism, rationality, concept (Cavailles, Bachelard and Canguilhem)

] according to which phenomenology was taken up in France, when quite late - around 1930 - it finally began to be, if not known, at least recognized.

1. Contemporary philosophy in France began in those years.

a. The lectures on transcendental phenomenology delivered in 1929 by Husserl (translated

by Gabrielle Peiffer and Emmanuel Levinas as Meditations cartesiennes, Paris, Colin, 1931

and by Dorion Cairns as Cartesian Meditations, The Hague, Nijhoff, 1960

) marked the moment: phenomenology entered France through that text.

b. But it allowed of two readings:

i. one, in the direction of a philosophy of the subject - and this was Sartre's article on the "Transcendance de L'Ego" (1935)

ii. another, which went back to the founding principles of Husserl's thought:

– [on one hand, taking up]

those of formalism and intuitionism

those of the theory of science

– [on the other hand,] in 1938 Cavailles's two theses:

on the axiomatic method [and thus a logical pluralism]

the [historical] formation of [a mathematics:] set theory

– Michel Foucault, Introduction (part I: Introduction), The Normal and the Pathologic by Georges Canguilhem, 1966, translated by Carolyn R. Fawcett in collaboration with Robert S. Cohen, 1978

[gamingavickreyauction]

The shape of a y=x^2 graph isn't maths. There's no way to prove what it looks like.

Think about when you first learn how to draw a graph: you do it by finding various points on the graph and plotting them, then joining the dots. This plotting is the key to drawing a graph: plotting is a map from abstract mathematical points—really just symbols—to real points, in physical space. And we all learn how to do it early. But there's nothing more right about how we do it than any other way. This might seem obvious—after all, you can plot a polar graph too—that's just a graph from another different way of plotting—there are any number of ways you can parameterize the plane.

One could imagine a completely alien way of plotting points on a page, where straight lines become eldritch monstrosities. This is no more right or wrong than our way of plotting—neither have any justification mathematically—the process of plotting can't even be described mathematically.

One could plot a ZFCircle in this system, and all its properties would translate into properties of the eldritch circle, in just the same way as they do for our circles. ZFCircles don't 'look like' our circles any more than they 'look like' those eldritch circles. All the reasons we say ZFCircles correspond to our circles are also reasons ZFCircles correspond to eldritch circles. Both are equally valid ways of translating ZFCircles to physical space. So I don't see how ZFCircles can be said to capture any notion of shape at all.

You might think we can describe the plotting mathematically: we can model the paper we draw on with R^2 and, for example, plotting as a radial graph is then described by the function: (r, θ) → (r cos θ, r sin θ), and the alien plot is described by the ugliest formula imaginable. The Cartesian plot is described by the identity map. But that's only the case because our starting point is an analogy between R^2 and our graph paper, using the Cartesian plot. If, for example, we thought of R^2 in radial coordinates, we would describe the Cartesian plot as (x, y) → (sqrt(x^2+y^2), arg(x, y)).

So we describe the same plot with a different function depending on which other plot we are used to using. Which means we cannot actually capture the plot itself in maths—only how it relates to other plots—which we capture as the notion of a change of coordinates.

But then, analogizing a plot to a function can't break us out of the purely algebraic world and let us describe shapes. That function that we tried to take as an analogy for the radial plot isn't any more objectively an analogy for the radial plot than any other bijection R^2 → R^2. So studying this function cannot directly tell us anything about the radial plot.

The only way we get information back about the radial plot is by translating algebraic facts about that function into geometric facts using the Cartesian plot we started with—which we were trying to justify in the first place. Attempts to justify the analogy between shapes and algebra mathematically are doomed to always end up just chasing their own tail.

Geometry is founded on faith.