#maclaurin polynomials

[song-tam]

i hate calc i hate calc i hate calc

[cuubism]

I love all of your stuff but somehow the first specific thing that came to my mind was how accurate I thought you made Dream's takes on which mathematical concepts are a Smash and which ones are a Pass

thank you 😂 it's all based on my experiences in high school calculus. i hated Series a lot. i remember they put a Maclaurin series question on the AP Calc exam and i just fully left it blank

discrete math in college almost got me interested in series, in terms of how they expand out to polynomials... unfortunately discrete math was also terrible and i got a C-. whatever they are trying to do there, my brain doesn't work that way, alas

multivariable calculus on the other hand was kind of fun... since i took Multivariable for Economists where they dumbed it down LMAO ahh i took so many random classes in college

[half-past-time]

The inherent creativity of Maclaurin polynomials is kind of beautiful and maybe even divine. No I will not elaborate

[jessecmckeown]

Whence Fabulous Faulhaber?

should I promise not to make this a habit?

Dear Mr. Haran, I'm grateful to you and correspondent Eischen (and Conway) for putting the name of Faulhaber on a calculation which heretofore I'd only known quoted, without attribution, by Heinrich Dörrie in Triumf der Mathematik---(which I've only read in translation). However, I'm most frustrated that neither Dörrie nor Eischen give any satisfying motivation for why the postulate should work.

For bystanders still catching up, this postulate is that if one defines a sequence of numbers $B_k$ "by expanding" $$(B-1)^{k+1} = B^{k+1}$$ and transcribing exponents to subscripts... one finds that the differences $$ (n + B)^{k+1} - B^{k+1} $$ similarly treated are equal to cumulative power sums, $$(k+1) \sum_{j \leq n} j^k$$

So the calculation is doable. My Beef is Dilemmimorphic: Either the notational abuse of $(n + B)^k$ suggests that $B$ should be Some Kind Of Linear Operator, in which case what is it? Or else there's an Amazing Coincidence being Overlooked!

It's a comparative Triviality that the power sums $\sum_1^N n^k$ should be polynomials of $N$, and that the leading term be $\frac{1}{k+1} N^{k+1}$ , so indeed it is perfectly reasonable to consider coefficients $B_{k,j}$ defined by $$ \sum_1^N n^k = \frac{1}{k+1} \sum \binom{k+1}{j} B_{k,j} N^{k+1-j} $$ BUT WHY SHOULD WE ASSUME that in fact $B_{k,j}$ depends only on $j$? That's STAGE MAGIC, and the fact that indeed it somehow works does not explain "where it comes from" (Eischen's favourite phrase on the matter).

So, in my customary way of starting with the actual problem and throwing at it what seems to me the minimum of thought, let's first explicate that "comparative triviality": the sequence of polynomials $p_k(j) = \binom{j+k}{j}$ are integral generators for the Integral-valued polynomials, and are recursively definable as iterated cumulative sums of the constant polynomial $p_0 \equiv 1$: $$\binom{j+k+1}{j} = \binom{j+k}{j} + \binom{j+k}{j-1}$$. Hence, cumulative sums of any polynomial, written in the binomial basis, can be obtained just by incrementing: $$\sum_{j=1}^N \sum a_n p_n(j) = \sum a_n p_{n+1}(N)$$

Next, cumulative sums are themselves defined by induction: $"\sum_{j=1}^0" P(j) = 0$ and $\sum_{j=1}^{N+1} P(j) = P(N+1) + \sum_{j=1}^N P(j)$, or said differently, by the Difference equation $$ SP(N+1) - SP(N) = P(N+1).$$ In other words we are trying to solve the Difference Equations $$ S_k(N) - S_k(N-1) = N^k,$$ but in the basis of Monomials $N^j$ instead of Binomials $p_j(N)$.

The binomial theorem, $$ (x+y)^k = \sum \binom{k}{j} x^{k-j} y^j $$ makes the Taylor-MacLaurin formula a Theorem for polynomials $$ (x+y)^k = \sum y^j \frac{1}{j!} \frac{d^j}{dx^j} x^k $$ which is fruitfully abbreviated $$ P(x+y) = e^{y\\, d/dx} P(x) $$ the Backwards Difference, then, is similarly $$ P(x) - P(x-1) = (1 - e^{- d/dx}) P(x) $$

Shall we say, The kernel of the Backward Difference is reasonably well understood? The differential operator is the retract of the Integral operator $\int_0$, so the Taylor-MacLaurin formula provides us also a section for the Forward Difference operator, $$ 1-e^{-x} = \frac{d}{dx} + A\frac{d^2}{dx^2} $$ where, for now, the main point is that the unbounded-degree differential operator $A$ commutes with $d/dx$, so that, for example $$ (1 - e^{-d/dx}) \left(\int_0 \sim dx - A + A^2 \frac{d}{dx} - A^3\frac{d^2}{dx^2} + - \cdots \right) P(x) = P(x)$$

Of course, there are various paths to the power series, other than via expansion of the powers of $A$, but there is a (Laurent) power series $$ \frac{1}{1-e^{-t}} = \frac{1}{2}\coth(\frac{t}{2})+\frac{1}{2} = \frac{1}{t} + \sum \frac{B_j}{j!} t^{j-1} $$ where $B_j$ are the faBulous Bernoulli numbers.

In any case, applied to simple powers, $$ \left( \int_0 \sim dx + \frac{1}{2} + \sum_{j=2}^{\infty} \frac{B_j}{j!} \frac{d^{j-1}}{dx^{j-1}} \right) x^k = \frac{1}{k+1} x^{k+1} + \sum_{j=1}^{k} \frac{k!}{j!(k-j+1)!} x^{k-j+1} B_j \\\\ {} = \frac{1}{k+1} \sum_{j=0}^{k} \binom{k+1}{j} B_j x^{k+1-j} $$ Finally, the power sum polynomials $S_k$ vanish both at zero (formally an empty sum) and at $-1$ (since $S_k(0) - S_k(-1) = 0^k$), so that in particular, $$ \sum_{j=0}^k \binom{k+1}{j} B_j (-1)^{k-j} = 0$$ THAT'S WHERE THIS IS COMING FROM.

[dnaayan-blog]

Critical Applied Mathematics (Calculus) for Competitive Exams (ASVAB, ASTB, AFOQT)

Hildas Problems, Landau's Theory.

Vygotsky viewed concepts in mathematics, Fundamental Theorem of Calculus (FTC):

Connects differentiation and integration, the two main concepts of calculus.

Taylor and Maclaurin Series

Approximate functions using infinite polynomials centered around a point.

Used in physics, engineering, and computer science for approximating functions.

Formula for a Taylor Series:

If centered at a = 0, it's called a Maclaurin series.

Exclusive Mathematics Problem Solution 👈.

[mouldremover]

don’t get me wrong, i understand why maclaurin series are useful. but i HATE doing them. turning a beautiful clean expression like arcsin2x into an ugly inaccurate polynomial like 2x + 4/3 x^3 + 12/5 x^5 + 40/7 x^7 +……. is DEEPLY unsatisfying and upsetting. its like seeing a marble floor polished to perfection and then walking all over it in muddy boots.

[anumberofcatschilling]

In one-variable functions, a function can be considered even (symmetrical across the y-axis, where f(-x) = f(x)) or odd (symmetrical through the origin, where f(-x) = -f(x)) or neither. For power functions of the form x^n, odd functions have odd numbers in the exponent while even functions have even numbers.

I figured out recently that even without a graph, I can figure out whether a function is odd or even, if either of those.

There's a kind of expansion that makes working with non-polynomial functions (functions that aren't composed of monomial (one number) power functions with coefficients added together) easier. It relies on taking derivatives (rate of change) of the function at a point the resulting polynomial approximation is centered about for however many terms is needed to approximate the value well enough, starting with taking derivatives of the function itself without values (find the derivative function and then take that derivative, repeatedly) and then plugging in the desired value. The resulting Taylor Polynomial is composed of monomials of the form f^n(a)*(x-a)^n / n!, where a is the value the polynomial is approximated about. There's a special case called the Maclaurin Polynomial, which is approximated at 0 and very useful for how it simplifies each monomial to f^n(0)*x^n / n!

The resulting Taylor Expansion of a non-polynomial function can show whether a function is odd or even based on the power function trick from earlier. As examples, three of these functions have easy-to-work-with Taylor polynomials and are either odd, even, or neither.

For example, sin(x) (one of the functions composed entirely of sine waves) is easy to compose a Maclaurin Polynomial for because its derivative, cos(x), has a derivative of -sin(x), and the negative coefficient carries over so that the fourth derivative of sin(x) is sin(x). At x=0, sin(x) is 0, and cos(x) is 1, so the resulting polynomial is x - x^3/3! + x^5/5! - x^7/7! + however many terms. Notice how all of the powers of x are odd. This aligns with the fact that sin(x) is symmetrical through the origin.

The function cos(x) is sin(x) shifted over by π/2 (because of the relationship between sin(x), cos(x), and circles), and its Taylor Expansion is 1 - x^2/2! + x^4/4! - x^6/6! + however many terms. Notice how all of the powers of x are even (1 is x^0, and 0 is even for the purposes of this reblog). This aligns with the fact that cos(x) is symmetrical across the y-axis.

The function e^x is special in that the function is its own derivative. Plugging in 0 results in all of the coefficients being 1 because e^0 = 1, so the resulting expansion is 1 + x +x^2/2! + x^3/3! + however many terms. This expansion contains both odd and even powers of x. Between that, the fact that e^x doesn't have symmetry through the origin or across the y-axis, and the fact that e^-x does not equal e^x or -e^x, it can be concluded that e^x is neither even nor odd.

Now, there are ways to figure this stuff out without resorting to calculus, but I like me some derivatives.

alright

info dump about ur special interests/hyperfixations to me

idc if its in my inbox or reblogged on this post or whatever

i am a dragon and i hoard knowledge

i give explicit consent to being bombarded with knowledge some may deem unnecessary because no knowledge is superfluous.

[ollies-studyblr]

AP Calc BC: Taylor Polynomials

[haikcuute]

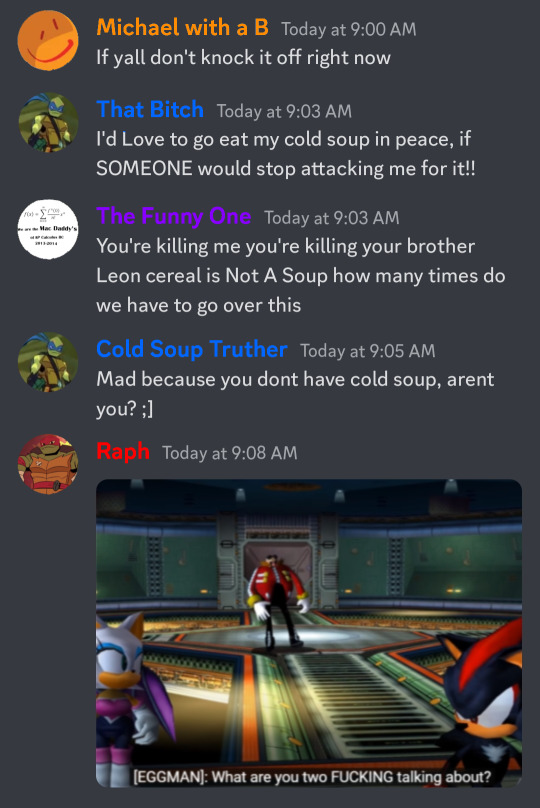
[ID: fake discord screenshots between the tmnt boys. The chat reads as follows, with their discord nicknames in parentheses:

Mikey (Micheal with a B): If yall don't knock it off right now

Leo (That Bitch): I'd Love to go eat my cold soup in peace, if SOMEONE would stop attacking me for it!!

Donnie (The Funny One): You're killing me you're killing your brother Leon cereal is Not A Soup how many times do we have to go over this

Leo changes his name to "Cold Soup Truther"

Leo (Cold Soup Truther): Mad because you dont have cold soup, arent you? ;]

Raph sends a screenshot from the sonic realtime fandub of Eggman saying "what are you two FUCKING talking about"

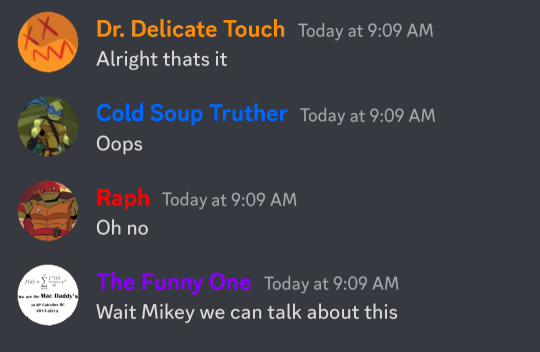
Mikey's name changes to "Doctor Delicate Touch"

Mikey (Doctor Delicate Touch): Alright that's it

Leo (Cold Soup Truther): Oops

Raph (Raph): Oh no

Donnie (The Funny One): Wait Mikey we can talk about this

End ID]

Laid awake for several hours thinking about wanting to make this joke the other day

Bonus: the aftermath

[ID: a simplistic drawing of the turtles. Mikey runs at high speed chasing Donnie and Leo, Raph lays behind him flat on the floor with x's for eyes. There are action lines emanating out from where Donnie and Leo are running to. End ID]

[nightwingsaregoths]

skimmed the Wikipedia page for the history of calculus and i don't care about anachronism anymore. sorry. Mastermind attended AP Calculus when he was Starflight's age and was a front row student. Yeah, the College Board exists. The nasty American company managed to open a portal into Pyrrhia and make young dragon students pay 97 dollars to take a test. He was also the only student to score above a 90 percent on the Unit 10B test. Farsight studied 1.5x the usual amount on Taylor polynomial approximations, Lagrange error bound, and memorized the Maclaurin polynomials for e^x, sine, cosine, and 1/(1-x), got an 87, and never quite got over it.

I have been far too normal and conventional with my writing. Too much silly incomprehensible romance without good reasons. Someone should do something slightly exciting and unexpected.

[roseinstem]

🌿 Despite it being Monday, I had a great day and I can’t wait to see what the rest of the week brings 🌿

Math: Taylor Polynomials and Maclaurin Polynomials

History: The Federal Bureaucracy

Childrens Lit: Developmental psychology readings

Books I’m reading: Adopted Son and The Alliance that Forged America

🎧: summer storm by Joel P West

[fulltestbank]

Test Bank For Calculus: Early Transcendentals, 12th Edition By Howard Anton

TABLE OF CONTENTS   PREFACE vii   SUPPLEMENTS ix   ACKNOWLEDGMENTS xi   THE ROOTS OF CALCULUS xv   1 Limits and Continuity 1   1.1 Limits (An Intuitive Approach) 1   1.2 Computing Limits 13   1.3 Limits at Infinity; End Behavior of a Function 21   1.4 Limits (Discussed More Rigorously) 30   1.5 Continuity 39   1.6 Continuity of Trigonometric Functions 50   1.7 Inverse Trigonometric Functions 55   1.8 Exponential and Logarithmic Functions 62   2 The Derivative 77   2.1 Tangent Lines and Rates of Change 77   2.2 The Derivative Function 87   2.3 Introduction to Techniques of Differentiation 98   2.4 The Product and Quotient Rules 105   2.5 Derivatives of Trigonometric Functions 110   2.6 The Chain Rule 114   3 Topics in Differentiation 124   3.1 Implicit Differentiation 124   3.2 Derivatives of Logarithmic Functions 131   3.3 Derivatives of Exponential and Inverse Trigonometric Functions 136   3.4 Related Rates 142   3.5 Local Linear Approximation; Differentials 149   3.6 L’Hoˆ pital’s Rule; Indeterminate Forms 157   4 The Derivative in Graphing and Applications 169   4.1 Analysis of Functions I: Increase, Decrease, and Concavity 169   4.2 Analysis of Functions II: Relative Extrema; Graphing Polynomials 180   4.3 Analysis of Functions III: Rational Functions, Cusps, and Vertical Tangents 189   4.4 Absolute Maxima and Minima 200   4.5 Applied Maximum and Minimum Problems 208   4.6 Rectilinear Motion 222   4.7 Newton’s Method 230   4.8 Rolle’s Theorem; Mean-Value Theorem 235   5 Integration 249   5.1 An Overview of the Area Problem 249   5.2 The Indefinite Integral 254   5.3 Integration by Substitution 264   5.4 The Definition of Area as a Limit; Sigma Notation 271   5.5 The Definite Integral 281   5.6 The Fundamental Theorem of Calculus 290   5.7 Rectilinear Motion Revisited Using Integration 302   5.8 Average Value of a Function and its Applications 310   5.9 Evaluating Definite Integrals by Substitution 315   5.10 Logarithmic and Other Functions Defined by Integrals 320   6 Applications of the Definite Integral in Geometry, Science, and Engineering 336   6.1 Area Between Two Curves 336   6.2 Volumes by Slicing; Disks and Washers 344   6.3 Volumes by Cylindrical Shells 354   6.4 Length of a Plane Curve 360   6.5 Area of a Surface of Revolution 365   6.6 Work 370   6.7 Moments, Centers of Gravity, and Centroids 378   6.8 Fluid Pressure and Force 387   6.9 Hyperbolic Functions and Hanging Cables 392   7 Principles of Integral Evaluation 406   7.1 An Overview of Integration Methods 406   7.2 Integration by Parts 409   7.3 Integrating Trigonometric Functions 417   7.4 Trigonometric Substitutions 424   7.5 Integrating Rational Functions by Partial Fractions 430   7.6 Using Computer Algebra Systems and Tables of Integrals 437   7.7 Numerical Integration; Simpson’s Rule 446   7.8 Improper Integrals 458   8 Mathematical Modeling with Differential Equations 471   8.1 Modeling with Differential Equations 471   8.2 Separation of Variables 477   8.3 Slope Fields; Euler’s Method 488   8.4 First-Order Differential Equations and Applications 494   9 Infinite Series 504   9.1 Sequences 504   9.2 Monotone Sequences 513   9.3 Infinite Series 520   9.4 Convergence Tests 528   9.5 The Comparison, Ratio, and Root Tests 534   9.6 Alternating Series; Absolute and Conditional Convergence 539   9.7 Maclaurin and Taylor Polynomials 549   9.8 Maclaurin and Taylor Series; Power Series 559   9.9 Convergence of Taylor Series 567   9.10 Differentiating and Integrating Power Series; Modeling with Taylor Series 575   10 Parametric and Polar Curves; Conic Sections 588   10.1 Parametric Equations; Tangent Lines and Arc Length for Parametric Curves 588   10.2 Polar Coordinates 600   10.3 Tangent Lines, Arc Length, and Area for Polar Curves 613   10.4 Conic Sections 622   10.5 Rotation of Axes; Second-Degree Equations 639   10.6 Conic Sections in Polar Coordinates 644   11 Three-dimensional Space; Vector   11.1 Rectangular Coordinates in 3-Space; Spheres; Cylindrical Surfaces 657   11.2 Vectors 663   11.3 Dot Product; Projections 673   11.4 Cross Product 682   11.5 Parametric Equations of Lines 692   11.6 Planes in 3-Space 698   11.7 Quadric Surfaces 705   11.7 Cylindrical and Spherical Coordinates 715   12 Vector-Valued Functions 723   12.1 Introduction to Vector-Valued Functions 723   12.2 Calculus of Vector-Valued Functions 729   12.3 Change of Parameter; Arc Length 738 12.4 Unit Tangent, Normal, and Binormal Vectors 746   12.5 Curvature 751   12.6 Motion Along a Curve 759   12.7 Kepler’s Laws of Planetary Motion 771   13 Partial Derivatives 781   13.1 Functions of Two or More Variables 781   13.2 Limits and Continuity 791   13.3 Partial Derivatives 800   13.4 Differentiability, Differentials, and Local Linearity 812   13.5 The Chain Rule 820   13.6 Directional Derivatives and Gradients 830   13.7 Tangent Planes and Normal Vectors 840   13.8 Maxima and Minima of Functions of Two Variables 845   13.9 Lagrange Multipliers 856   14 Multiple Integrals 925   14.1 Double Integrals 925   14.2 Double Integrals Over Nonrectangular Regions 932   14.3 Double Integrals in Polar Coordinates 941   14.4 Surface Area; Parametric Surfaces 948   14.5 Triple Integrals 961   14.6 Triple Integrals in Cylindrical and Spherical Coordinates 968   14.7 Change of Variables in Multiple Integrals; Jacobians 977   14.8 Centers of Gravity Using Multiple Integrals 989   15 Topics in Vector Calculus 1001   15.1 Vector Fields 1001   15.2 Line Integrals 1010   15.3 Independence of Path; Conservative Vector Fields 1025   15.4 Green’s Theorem 1035   15.5 Surface Integrals 1042   15.6 Applications of Surface Integrals; Flux 1049   15.7 The Divergence Theorem 1058   15.8 Stokes’ Theorem 1067   APPENDIX A A1   APPENDIX B 00   APPENDIX C 00   APPENDIX D 00   APPENDIX E 00   ANSWERS 00   INDEX I1         Read the full article

[acemywriter]

Calculus Question

Hey You must provide the explaination. Must be 100% correct answers. the topic included in the test: 9.1 Sequences 9.2 Monotone Sequences 9.3 Infinite Series 9.4 Convergence Tests 9.5 The Comparison, Ratio, and Root Tests 9.6 Alternating Series; Absolute and Conditional Convergence 9.7 Maclaurin and Taylor Polynomials 9.8 Power Series 9.8 Maclaurin and Taylor Series

[ukopcavanje]

KoRoNAsTAvA ~ [21-22] IV8 ~ AsA I

Ovo je spisak domaćih radova urađenih u elektronskom obliku za vežbu tokom školske 2021-22. godine, u okviru nastave na daljinu, od strane učenika, iz predmeta Analiza sa algebrom za četvrti razred Matematičke gimnazije. Priložene su odgovarajuće skripte, zadaci, uputnice i drugi oblici elektronskog materijala.  

Škola: Matematička gimnazija Kraljevo. Odeljenje: IV-8. Koordinator Ukop(č)avanja: Jovan Pavlović. Support me on Ko-fi  →

~

( četvrtak, 2. sep 2021. godine ) ~ Obnavljanje gradiva: izvodi i osnovne formule, tablica izvoda ~ [ Prilog (tablica): Izvodi elementarnih funkcija  (pdf) ]

~ Inicijalni test ~ [ 2. zadatak { M4 - 164 g) z, 39. s } (pdf): Andrej Bantulić ] [ 3. zadatak { V4 - 100 z, 17. s } (pdf): Ana Kiković ] [ 5. zadatak { A - 97 z, 111. s } (pdf): Mihailo Lukić ]

( sreda, 15. sep 2021. godine ) ~ Fermaova teorema ~ [ Prilog (teorija): Teorema + dokaz + interpretacija (jpg) ] [ Prilog (primer): Lokalni ekstremumi (jpg) ]

( petak, 17. sep 2021. godine ) ~ Rolova teorema ~ [ Prilog (teorija): Teorema + dokaz + interpretacija (jpg) ] [ Prilog (zadatak): Posledica teoreme (jpg) ]

( sreda, 22. sep 2021. godine ) ~ Lagranžova teorema ~ [ Prilog (teorija): Teorema + dokaz + interpretacija (jpg) ] [ Prilog (zadatak): M4 - 254 z, 55. s (jpg) ] [ Prilog (zadatak): M4 - 256 z, 55. s (jpg) ] [ Prilog (zadatak): M4 - 257 z, 55. s (jpg) ] + [ Prilog (primer): Nejednakost (blog) ]

( petak, 24. sep 2021. godine ) ~ Posledice Lagranžove teoreme ~ [ Prilog (teorija): Monotonost funkcije (jpg) ] [ Prilog (primer): Ispitivanje monotonosti (jpg) ]

~ Domaći zadatak ~ [ 2. zadatak { M4 - 258. b) z, 55. s } (pdf): Vladan Bašić ] [ 3. zadatak { M4 - 258. v) z, 55. s } (pdf): Vladislav Vukosavljević ] [ 6. zadatak { M4 - 258. đ) z, 55. s } (pdf): Milica Zubljić ]

( sreda, 29. sep 2021. godine ) ~ Košijeva teorema ~ [ Prilog (teorija): Teorema + dokaz (jpg) ] [ Prilog (zadatak): Primena teoreme (jpg) ] [ Prilog (zadatak): Nedovoljni uslovi (jpg) ]

( petak, 1. okt 2021. godine ) ~ Pismena vežba ~ [ 1. zadatak { K - 62 z, 52. s } (pdf): Ana Kiković ] [ 3. zadatak { M4 - 258. b) z, 55. s } (pdf): Vladan Bašić ] [ 5. zadatak { M4 - 260 b) z, 56. s } (pdf): Vladislav Vukosavljević ]

( utorak, 5. okt 2021. godine ) ~ Lopitalova teorema ~ [ Prilog (teorija): Teorema + dokaz (jpg) ] [ Prilog (primeri): Dva limesa (jpg) ] [ Prilog (teorija): Pregled primene (jpg) ] [ Prilog (zadatak): Koliko limesa je 0 a koliko 1? (jpg) ] ~ [ Prilog (teorija + rešeni primeri): Đorđe Golubović (youtube) ]

( sreda, 6. okt 2021. godine ) ~ Lopitalova teorema: vežbanje ~ [ Prilog (primer): Granična vrednost I (blog) ] [ Prilog (primer): Granična vrednost II (blog) ]

( utorak, 12. okt 2021. godine ) ~ Lopitalova teorema: domaći rad ~ [ 1. zadatak { A - 72 z, 147 s } (pdf): Milica Zubljić ] [ 2. zadatak { A - 75 z, 148 s } (pdf): Uroš Nedeljković ] [ 3. zadatak { A - 76 z, 148 s } (pdf): Pavle Đoković ] [ 5. zadatak { A - 79 z, 149 s } (pdf): Mihailo Lukić ]

( sreda, 13. okt 2021. godine ) ~ Tejlorov polinom ~ [ Prilog (teorija): Formula 1 deo (jpg) ] [ Prilog (teorija): Formula 2 deo (jpg) ] [ Prilog (teorija): Taylor and Maclaurin Series (youtube) ] [ Prilog (primeri): Taylor & Maclaurin Polynomials With Approximations (youtube) ]

~ Maklorenov polinom - primeri ~ [ Prilog (tablica): Maklorenov razvoj nekih funkcija (jpg) ]

Kako stepen Maklorenovog polinoma raste, on se sve više približava funkciji koju aproksimira. Slika pokazuje funkciju sinx i Maklorenove aproksimacije polinomom razvijenog do stepena:

( utorak, 19. okt 2021. godine ) ~ Tejlorov polinom: domaći rad ~ [ 1. zadatak { A - 3 z, 161 s } (pdf): Pavle Đoković ] [ 2. zadatak { A - 5 z, 161 s } (pdf): Vladan Bašić ] [ 3. zadatak { A - 7 z, 162 s } (pdf): Mihailo Lukić ] [ Prilog (drugačiji pristup): A - 7 z, 162 s (jpg) ] [ 4. zadatak { A - 8 z, 163 s } (pdf): Andrej Bantulić ] [ 5. zadatak { A - 9 z, 163 s } (pdf): Milica Zubljić ] [ Prilog (drugačiji pristup): A - 9 z, 163 s (jpg) ] [ 6. zadatak { A - 10 z, 163 s } (pdf): Ana Kiković ] [ Prilog (drugačiji pristup): A - 10 z, 163 s (jpg) ]

( sreda, 20. okt 2021. godine ) ~ Tejlorov polinom sa ostatkom ~ [ Prilog (teorija): Oblici ostatka 1 deo (jpg) ] [ Prilog (teorija): Oblici ostatka 2 deo (jpg) ] [ Prilog (teorija): Lagranžov ostatak (jpg) ] [ Prilog (teorija): Asimptotska oznaka o (jpg) ]

( utorak, 26. okt 2021. godine ) ~ Maklorenov polinom sa Peanovim ostatkom: vežbanje ~ [ Prilog (primer): Granična vrednost I (blog) ]

( četvrtak, 28. okt 2021. godine ) ~ Maklorenov polinom sa Peanovim ostatkom: domaći ~ [ 1. zadatak { A - 35 z, 174 s } (pdf): Andrej Bantulić ] [ 2. zadatak { A - 37 z, 175 s } (pdf): Ana Kiković ] [ 3. zadatak { A - 38 z, 175 s } (pdf): Aleksa Pantović ] [ 4. zadatak { A - 40 z, 176 s } (pdf): Milica Zubljić ] [ 5. zadatak { A - 41 z, 176 s } (pdf): Uroš Nedeljković ] [ 6. zadatak { A - 42 z, 177 s } (pdf): Vladislav Vukosavljević ] [ 7. zadatak { A - 43 z, 177 s } (pdf): Mihailo Lukić ]

( četvrtak, 4. nov 2021. godine ) ~ Ekstremne vrednosti i monotonost funkcije ~ [ Teorija (US): Primena izvoda kod ekstremuma (pdf) ] [ Primer (US): Prvi izvod i ekstremumi (jpg) ] [ Primer (Profesorka): Prvi izvod i ekstremumi (jpg) ] [ Primer (Profesorka): Prvi izvod i ekstremumi (jpg) ] [ Primer (PMF Niš): Prvi izvod i ekstremumi (jpg) ] [ Primer (US): Drugi izvod i ekstremumi (jpg) ]

( utorak, 16. nov 2021. godine ) ~ Ekstremne vrednosti i monotonost funkcije: vežbanje ~ [ Primeri (Matematiranje): Primena izvoda kod ekstremuma (pdf) ]

( četvrtak, 18. nov 2021. godine ) ~ Konveksnost i konkavnost ~ [ Teorija (US): Definicija i uslov (jpg) ]

( utorak, 23. nov 2021. godine ) ~ Ekstremne vrednosti i monotonost funkcije: domaći   ~ [ 1. zadatak { K - 72 a) z, 53 s } (pdf): Vladislav Vukosavljević ] [ 2. zadatak { K - 72 b) z, 53 s } (pdf): Aleksa Pantović ] [ 3. zadatak { K - 72 g) z, 53 s } (pdf): Milica Zubljić ] [ 4. zadatak { K - 72 v) z, 53 s } (pdf): Ana Kiković ] [ 5. zadatak { K - 73 a) z, 53 s } (pdf): Vladan Bašić ] [ 6. zadatak { K - 73 d) z, 53 s } (pdf): Uroš Nedeljković ] [ 7. zadatak { K - 73 d) z, 53 s } (pdf): Pavle Đoković ] [ 8. zadatak { K - 73 v) z, 53 s } (pdf): Mihailo Lukić ] [ 8. zadatak { K - 73 v) z, 53 s } (pdf): Andrej Bantulić ]

( utorak, 30. nov 2021. godine ) ~ Najveća i najmanja vrednost funkcije na segmentu: vežbanje ~ [ Prilog (primer): Maksimalna površina trougla (blog) ] [ Prilog (primer): Minimalna površina trougla (blog) ] [ Prilog (primer): Maksimalna kupa u sferi (blog) ]

( četvrtak, 2. dec 2021. godine ) ~ Najveća i najmanja vrednost funkcije na segmentu : domaći   ~ [ 1. zadatak { A - 94 z, 154 s } (pdf): Ana Kiković ] [ 2. zadatak { A - 95 z, 154 s } (pdf): Milica Zubljić ] [ 3. zadatak { A - 96 z, 155 s } (pdf): Vladan Bašić ] [ 4. zadatak { A - 97 z, 155 s } (pdf): Andrej Bantulić ] [ 5. zadatak { A - 98 z, 155 s } (pdf): Uroš Nedeljković ] [ 6. zadatak { A - 100 z, 156 s } (pdf): Pavle Đoković ] [ 7. zadatak { A - 101 z, 157 s } (pdf): Vladislav Vukosavljević ] [ 8. zadatak { A - 102 z, 157 s } (pdf): Mihailo Lukić ]

( utorak, 7. dec 2021. godine ) ~ Prevojne tačke ~ [ Teorija (US): Definicija i uslov (jpg) ] [ Primer (US): Polinom trećeg stepena (jpg) ]

( četvrtak, 9. dec 2021. godine ) ~ Ispitivanje toka funkcije ~ [ Prilog (primer): Funkcija I (racionalna) (blog) ] [ Prilog (primer): Funkcija II (iracionalna) (blog) ] [ Prilog (primer): Funkcija III (racionalna) (blog) ] [ Prilog (primer): Funkcija IV (eksponencijalna) (blog) ] [ Prilog (primer): Funkcija V (eksponencijalna) (blog) ] [ Prilog (primer): Funkcija VI (iracionalna) (blog) ] [ Prilog (primer): Funkcija VII (racionalna) (blog) ] [ Prilog (primer): Funkcija VIII (racionalna) (blog) ] [ Prilog (primer): Funkcija IX (eksponencijalna) (blog) ] [ Prilog (primer): Funkcija X (polinom) (blog) ] [ Prilog (primer): Funkcija XI (racionalna) (blog) ] [ Prilog (primer): Funkcija XII (eksponencijalna) (blog) ] [ Prilog (primer): Funkcija XIII (eksponencijalna) (blog) ]

( utorak, 14. dec 2021. godine ) ~ Ispitivanje toka funkcije (polinom) : domaći ~ [ 1. zadatak { M4 - 208 b) z, 47 s } (pdf): Vladislav Vukosavljević ] [ 2. zadatak { M4 - 208 v) z, 47 s } (pdf): Pavle Đoković ] [ 3. zadatak { M4 - 208 g) z, 47 s } (pdf): Aleksa Pantović ] [ 4. zadatak { M4 - 208 đ) z, 47 s } (pdf): Andrej Bantulić ] [ 5. zadatak { M4 - 208 ž) z, 47 s } (pdf): Ana Kiković ] [ 6. zadatak { M4 - 208 k) z, 48 s } (pdf): Milica Zubljić ] [ 7. zadatak { M4 - 208 lj) z, 48 s } (pdf): Mihailo Lukić ] [ 8. zadatak { M4 - 208 z) z, 48 s } (pdf): Uroš Nedeljković ]

( utorak, 21. dec 2021. godine ) ~ Ispitivanje toka funkcije (racionalne) : domaći ~ [ 1. zadatak { M4 - 210 ž) z, 48 s } (pdf): Milica Zubljić ] [ 2. zadatak { M4 - 210 j) z, 48 s } (pdf): Vladan Bašić ] [ 3. zadatak { M4 - 210 k) z, 48 s } (pdf): Ana Kiković ] [ 4. zadatak { M4 - 210 m) z, 48 s } (pdf): Vladislav Vukosavljević ] [ 5. zadatak { M4 - 210 o) z, 48 s } (pdf): Uroš Nedeljković ] [ 6. zadatak { M4 - 210 ć) z, 48 s } (pdf): Pavle Đoković ] [ 7. zadatak { M4 - 210 u) z, 48 s } (pdf): Mihailo Lukić ]

( sreda, 22. dec 2021. godine ) ~ Ispitivanje toka funkcije (iracionalne - složene) : domaći ~ [ 1. zadatak { M4 - 248 a) z, 53 s } (pdf): Andrej Bantulić ] [ 2. zadatak { M4 - 248 e) z, 53 s } (pdf): Ana Kiković ] [ 3. zadatak { M4 - 248 z) z, 53 s } (pdf): Uroš Nedeljković ] [ 4. zadatak { K - 72 b) z, 53 s } (pdf): Aleksa Pantović ]

( utorak, 27. dec 2021. godine ) ~ Ispitivanje toka funkcije (eksponencijalne - složene) : domaći ~ [ 5. zadatak { M4 - 223 d) z, 50 s } (pdf): Pavle Đoković ] [ 6. zadatak { M4 - 223 đ) z, 50 s } (pdf): Milica Zubljić ] [ Napomena: znak drugog izvoda zavisi od polinoma 4. stepena: ukoliko ne postoje realne nule polinoma, određujemo znak na osnovu vrednost polinoma u jednoj tački! ] [ 6. zadatak { M4 - 223 đ) z, 50 s } : dopuna (pdf): Milica Zubljić ] [ 7. zadatak { M4 - 223 z) z, 50 s } (pdf): Mihailo Lukić ] [ Napomena: limes kod određivanja vertikalne asimptote je “problematičan”: uvodimo smenu, te potom primenjujemo Lopitalovo pravilo! ]

( utorak, 1. feb 2022. godine ) ~ Integrali ~ [ Teorija (Pripreme M4): Definicija i osobine (jpg) ]

( utorak, 22. feb 2022. godine ) ~ Metode integraljenja (smena + parcijalno) : domaći ~ [ M4 - 324 b) z, 72 s (pdf): Ana Kiković ] [ M4 - 324 g) z, 72 s (pdf): Vladislav Vukosavljević ] [ M4 - 324 v) z, 72 s (pdf): Uroš Nedeljković ] [ M4 - 325 b) z, 72 s (pdf): Andrej Bantulić ] [ M4 - 325 đ) z, 72 s (pdf): Mihailo Lukić ] [ M4 - 325 g) z, 72 s (pdf): Milica Zubljić ]

[felord]

MATHS7027 Assignment 2 Solved 

  In lectures we proved the result via a somewhat circuitous route. Prove this result instead by using the principle of mathematical induction. In lectures we derived an expression for the Maclaurin polynomial for cos(x). Using this expression, find the Maclaurin polynomial of degree n = 2k for f(x) = cos(2x). Use Taylor’s theorem to estimate how many terms need to be used to approximate…

[maximuswolf]

Textbook confusion: Maclaurin Polynomials for e^x via /r/calculus

Textbook confusion: Maclaurin Polynomials for e^x

Hey guys,

So I’m reading my textbook (page 251 on: https://www.math.ubc.ca/~CLP/CLP1/clp_1_dc_text.pdf) and I’m confused as to why it says we can use the general Maclaurin polynomial equation for ex to approximate e1 and that gives us 1 for all (ex)n... I mean do we not substitute e1 for all x, thus getting 1 + (e1)1 + (e1)2 + (e1)3 + ... + (e1)7 for the numerators instead of just 1?

Thanks so much in advance!

Submitted March 03, 2021 at 06:02PM by askingqsforschoool via reddit https://ift.tt/2NYRm82