#math model

[art-of-mathematics]

Wobbly Sierpinski-fractal model/toy

Made with foil strips of equal length and book screws.

The larger triangle at the center is stable because the outer tinier triangles stabilize it. (The larger triangles have a side length of two foil strips. The smallest triangles ("the building blocks") have a side length of 1 foil strip. The largest triangle is this entire model with side length of 4 foil strips.)

The largest triangle (4foil strips) is stable, because the tiniest (1foil strip) triangles stabilize each other as well as the larger (2foil strips) triangle.

The sierpinski pattern has interesting properties regarding its "stability" I have to admit.

Normally I struggle to make equilateral triangles of side length "2 foil strips" stable enough without adding an inner triangle. This construction (using outer tiny triangles) is a good solution if you want a "larger triangle hole".

[sirchlorox]

fell off a fence, broke my phone and lost all of my ibispaint wips )-: Have a ranchers sketch until I'm able to make new things again.

(design inspired by @watcheraurora 's perfection/saint au)

[smorhe]

just a normal teenage girl doing normal teenage girl stuff

[catgirl-lucy]

Ultrafilters & Ultrapowers

Hey! Call me Lucy. I might make an introduction blog later, but I first wanted to make a blog-post about ultrapowers.

Ultrafilters are a concept from set theory, I'll try my best to explain what they are and why they're defined as they are.

First, a quick overview of what we will do: we will extend the real number line by adding new numbers through the use of an ultrapower, these new numbers are called "hyperreals". Roughly, this means that we will have infinite sequences [a₀,a₁,a₂,...] of real numbers representing hyperreal numbers, where similar sequences are regarded as equal. We will also show a surprising theorem: although there are seemingly more hyperreals than reals, hyperreals look the same as real numbers "from within".

If we have a sequence of reals like this: [0,1,1/2,1/3,1/4,...] (I'll call this sequence "ε"), the hyperreal that it represents can be viewed as the "limit" of the sequence. Since a large number of entries of this sequence is smaller than any positive real number r > 0, ε will be smaller than any positive real number r, but since also a large number of entries is larger than 0, ε will be larger than 0. ε is thus an infinitesimal hyperreal number. This is mostly just intuition though, so don't worry if you don't entirely get it.

Two hyperreal numbers x = [x₀,x₁,x₂,...] and y = [y₀,y₁,y₂,...] are equal if x_i = y_i for a large number of indices i. But what does "large" mean in this context?

Well, that's where the ultrafilter comes in. Ultrafilters split a family of sets into sets that are "large" and sets that are "small". In this case, we split sets of natural numbers (numbers 0, 1, 2, 3, etc) into large sets and small sets, so we have an ultrafilter on ℕ, the set of natural numbers. Ultrafilters are identified by the family of large sets: if some set A is in an ultrafilter U, then it is large, and if it's not, then it is small.

We do want our notion of "large sets" and "small sets" to make sense: for example, a hyperreal should always be equal to itself, so we want the whole set of natural numbers, {0, 1, 2, 3, 4, ...} (which is the set of indices for which a sequence is equal to itself), to be large.

Obviously, it would make sense that if a set A is large and B is larger than A, then B is also large. Thus, if A ∈ U is a member of an ultrafilter U ("∈" is the membership symbol), and if B ⊃ A contains everything A contains too ("⊃" is the superset symbol), then B ∈ U is a member of the ultrafilter as well.

We also want hyperreal equality to be transitive, thus if [x₀,x₁,x₂,...] = [y₀,y₁,y₂,...] and [y₀,y₁,y₂,...] = [z₀,z₁,z₂,...], then we want [x₀,x₁,x₂,...] = [z₀,z₁,z₂,...]. If A = {i ∈ ℕ | x_i = y_i} is the set of points at which x and y are equal and B = {i ∈ ℕ | y_i = z_i} is the set of points at which y and z are equal, then C = {i ∈ ℕ | x_i = z_i}, the set of points at which x and z are equal, includes the set A ∩ B = {i ∈ ℕ | x_i = y_i ∧ y_i = z_i}, the set of points at which x is equal to y and y is equal to z. It thus makes sense to have our ultrafilter be closed under intersections: if two sets A and B are large, then the set of points that are both in A and in B, called the "intersection" of A and B (denoted A ∩ B), is a large set as well (and thus also in the ultrafilter).

It would also make sense that, if two hyperreal numbers are nowhere equal, then they aren't equal. So the empty set, {} = ∅, is small.

The five axioms above describe a filter:

A filter F on κ is a family of subsets of κ.

A filter F on κ must contain the whole set κ.

A filter F on κ must be upwards closed, thus for every large set A ∈ F, and every larger set B ⊃ A, B ∈ F is large as well.

A filter F on κ must be downwards directed, thus for every large set A ∈ F and every large set B ∈ F, the intersection of A and B, A ∩ B ∈ F, is large as well.

A filter F on κ may not contain the empty set.

However, these are the axioms of a filter, and not of an ultrafilter. Ultrafilters have one additional axiom.

Suppose we have the hyperreal [0,1,0,1,0,1,...]: an alternating sequence of 0's and 1's. Is this equal to 0 = [0,0,0,0,...], or to 1 = [1,1,1,1,...], or is it its own thing? (Note: the 0 in 0 = [0,0,0,0,...] is a hyperreal and the 0's in 0 = [0,0,0,0,...] are real numbers, so they're different (kind of) numbers both called "0"). If it is its own thing, then is it smaller than 1? If it is smaller than 1, then it must be smaller on a large set of indices, meaning it's equal to 0 on a large set of indices, meaning it's equal to 0. If it's not smaller than 1, well, it can't be larger, so it'd only make sense if it's equal to 1, but no axiom about filters says it should! That's why we have this last axiom for ultrafilters, which makes them "decisive": for every set A, it is either large (thus, A ∈ U), or small, meaning that its complement, Ac = {i | i ∉ A}, the set of all points that aren't in A, is large.

And so we have our six axioms of an ultrafilter:

An ultrafilter U on κ is a family of subsets of κ, these subsets are called "large sets".

κ is large.

U is upwards closed.

U is downwards directed.

∅ is not large.

For every set A ⊂ κ, either A ∈ U or Ac ∈ U.

But we're still missing one thing. We can take our ultrafilter U to be the set of all sets of natural numbers that contain 6. ℕ is large, as it contains 6. It is upwards closed: if A contains 6 and B contains everything that A contains and more, then B also contains 6. U is downwards directed: if both A and B contain 6, then the set of all points that are in both A and B still contains 6. The empty set does not contain 6, and every set either does contain 6 or does not contain 6. With this ultrafilter, two hyperreals x and y are equal simply when x₆ and y₆ are equal, so we don't get cool infinitesimals and infinities, and that makes me sad :(

These kinds of boring ultrafilters are called principal ultrafilters. Formally, a principal filter on κ is a filter F on κ for which there is some set X ⊂ κ so that any set A ⊂ κ is large only if it contains everything in X. This filter is often denoted as ↑X. If you want a principal filter U to be an ultrafilter, X needs to be a singleton set, meaning it only contains a single point x. Proving this is left as an exercise for the reader.

Let U be a non-principal ultrafilter on ℕ. This post is getting a bit long, so I won't show why such an ultrafilter exists. Now, we can take the ultrapower of ℝ, the set of real numbers, by U. This ultrapower is often denoted as ℝ^ℕ/U. Members of this ultrapower are (equivalence classes of) functions from ℕ to ℝ, meaning that they send natural numbers/indices to real numbers (the sequence [x₀,x₁,x₂,...] maps the natural number i to the real number x_i). These functions/sequences/equivalence classes are called hyperreal numbers. Two hyperreal numbers, x and y, are equal if {i ∈ ℕ | x(i) = y(i)}, the set of points at which they are equal, is large (i.e. a member of U). We can also define hyperreal comparison and arithmetic operations: x < y if {i | x(i) < y(i)} is large, (x + y)(i) = x(i) + y(i) and (x · y)(i) = x(i) · y(i). Every real number r also has a corresponding hyperreal j(r), which is simply [r,r,r,r,...] (i.e. j(r)(i) = r for all i).

In general, if M is some structure, κ is some set and U is some ultrafilter on κ, then we can take the ultrapower M^κ/U, which is the set of equivalence classes of functions from κ to M, where any relation R in M (for example, "<" in ℝ) is interpreted in M^κ/U as "R(x₁,...,xₙ) if and only if {i ∈ κ | R(x₁(i),...,xₙ(i))} ∈ U is large" and any function f in M (for example, addition in ℝ) is interpreted in M^κ/U as "f(x₁,...,xₙ)(i) = f(x₁(i),...,xₙ(i)) for all i ∈ κ".

A quick note on equivalence classes: in M^κ/U, points aren't actually functions from κ to M, but rather sets of functions from κ to M that are all equal on a large set of values. Given a function f: κ → M, the equivalence classes that f is in is denoted [f]. In this way, if f and g are equal on a large set of values, then [f] and [g] are actually just equal.

The hyperreal [0,1,2,3,4,...], which sends every natural number i to the real number i, is often called ω.

This part of the blog will get a bit more technical, so be warned!

In the beginning of this blog-post, I mentioned that hyperreals look the same as real numbers. I'll make this statement more formal:

For any formula φ that can be built up in the following way:

φ ≡ "x = y" for expressions x and y (expressions are variables and "a + b" and "a · b" for other expressions a and b)

φ ≡ "x < y" for expressions x and y

φ ≡ "ψ ∧ ξ" (ψ and ξ are both true) for formulas ψ and ξ

φ ≡ "ψ ∨ ξ" (ψ or ξ is true (or both)) for formulas ψ and ξ

φ ≡ "¬ψ" (ψ is not true) for an formula ψ

φ ≡ "∃x ψ(x)" (there exists a value for x for which ψ is true) for a variable x and an formula ψ

φ ≡ "∀x ψ(x)" (for all values of x, ψ is true) for a variable x and an formula ψ

We have that ℝ ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ, where variables can have real number values) if and only if ℝ^ℕ/U ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ^ℕ/U, where variables can have hyperreal number values).

In other words: ℝ and ℝ^ℕ/U are elementary equivalent.

So, how will we prove this? Well, we will use induction: "if something being true for all m < n implies it being true for n itself, then it must be true for all n (where m and n are natural numbers)". Specifically, we will use induction on the length of formulas: we will show that, if the above statement holds for all formulas ψ shorter than φ, then it must also hold for φ.

However, we won't use the exact statement above. Instead, we will use the following:

Given a formula φ(...) and hyperreal numbers x₁,...,xₖ, ℝ^ℕ/U ⊧ φ(x₁,...,xₖ) if and only if {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large.

Now, why does this imply the original statement? Well, when k = 0, {i | ℝ ⊧ φ} can only be ∅ or ℕ. It being ∅ is equivalent to φ being false in ℝ and, if the statement is true, also equivalent to φ being false in ℝ^ℕ/U. And it being ℕ is equivalent to φ being true in ℝ and, again, if the statement is true, it is also equivalent to φ being true in ℝ^ℕ/U. We thus have that φ being true in ℝ is equivalent to φ being true in ℝ^ℕ/U.

Note: M ⊧ φ simply means that the formula φ is true when interpreted in M.

Now, why do we need this stronger statement? Well, it makes induction a lot easier: given that this statement holds for all ψ shorter than φ, it's easier to prove it also holds for φ.

Now, we can actually do the induction.

First, if φ ≡ "x = y", then we need to show that (1) ℝ^ℕ/U ⊧ φ(x,y) iff (2) {i | ℝ ⊧ φ(x(i),y(i))} is large. This follows immediately from the definition of equality in ℝ^ℕ/U, the same holds for "<".

Now, if φ(x₁,...,xₖ) ≡ "ψ(x₁,...,xₖ) ∧ ξ(x₁,...,xₖ)", we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i)) ∧ ℝ ⊧ ξ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} ∩ {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))}. Since {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} is large iff ψ(x₁,...,xₖ) is true in ℝ^ℕ/U, and {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))} iff ξ(x₁,...,xₖ) is true in ℝ^ℕ/U, and U is closed under intersections, we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large iff φ holds in ℝ^ℕ/U. A similar argument works for ∨.

If φ(x₁,...,xₖ) ≡ "¬ψ(x₁,...,xₖ)", then we can just use the ultraness of the ultrafilter.

If φ ≡ "∃y ψ(y,x₁,...,xₖ)", then {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i))} = {i | ∃y ∈ ℝ. ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} = ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))}. We have that the set {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} for y ∈ ℝ is large iff ℝ^ℕ/U ⊧ ψ(j(y),x₁,...,xₖ). If this set is large for some y ∈ ℝ, and thus if ℝ^ℕ/U ⊧ φ(x₁,...,xₖ), then ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is larger than that set, so it is large as well. For the converse direction, if ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is large, then we can create a hyperreal z where ψ ⊧ ψ(z(i),x₁(i),...,xₖ(i)) for all i for which ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i)), and we have ℝ^ℕ/U ⊧ ψ(z,x₁(i),...,xₖ(i)), and thus ℝ^ℕ/U ⊧ φ(x₁(i),...,xₖ(i)). Again, a similar argument works for ∀.

(Sorry if you couldn't follow along, I'm not good at explaining these things in an intuitive way.)

This result can be extended to show that M^κ/U is elementary equivalent to M for every structure M, every set κ and every ultrafilter U on κ.

Now, this result might be surprising, as we have a new number ω in ℝ^ℕ/U. Surely, there is a formula that states the existence of this number, right?

Well, it turns out, such a formula does not exist! You can try something like "there is no natural number n so that 1+...+1 w/ n 1's is greater than ω", but ω+1 is a natural number in the hyperreals, so such a natural number does exist. Similarly, any formula you can come up with, as long as it is created using the rules above (using conjunction, disjunction, negation, qauntification, etc), cannot state the existence of an infinite number ω.

But if ℝ^ℕ/U and ℝ are seemingly indistinguishable, might there already be an undetectable infinite real number in ℝ? Well, maybe~ :3 But it's undetectable anyways, so you don't have to worry about it.

Before I end this blog-post, I want to give some more intuition on what filters & ultrafilters actually are. To me, ultrafilters, and filters in general, are like "limits of sets". The principal filter ↑X has X as limit, while non-principal filters and ultrafilters have limits that aren't really sets, but look like ones. For example, you might have the set of prime numbers in your filter, and then the limit of that filter will be a "set" in which all numbers are prime numbers. And if your ultrafilter is non-principal (so for every n, there is a set A ∈ U in the filter that does not contain n), then the limit of that ultrafilter will be a "set" in which all numbers don't actually exist. In the case of filters, this "set" can be any "set" (though it still isn't really a set), but in the case of ultrafilters, this limit looks like a singleton set (i.e. it only has one "element": ω).

I don't know if my intuition of filters and ultrafilters will help anyone, tho, but I think it's cool!

That's all I had to say.

Bye!~ Have a nice day.

[wouldtheybecomeafearavatar]

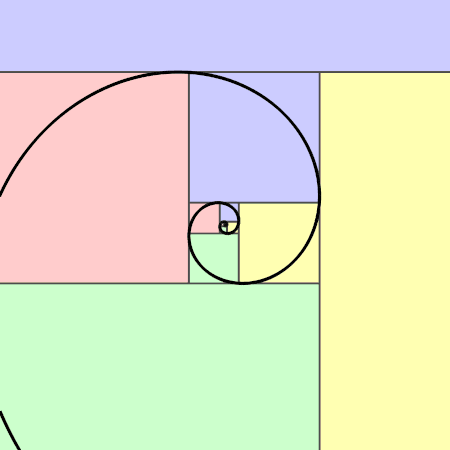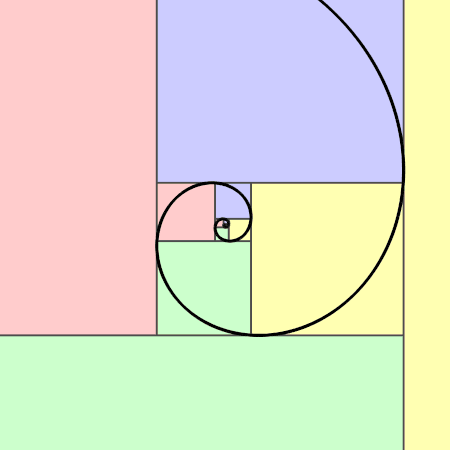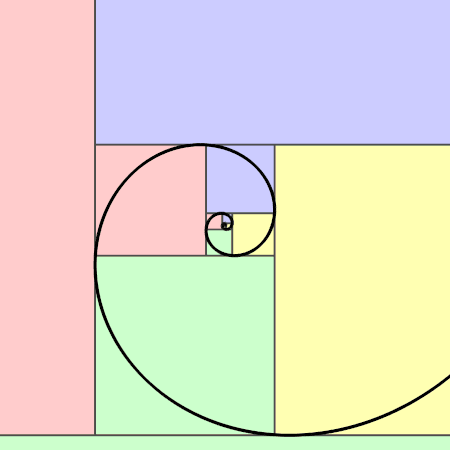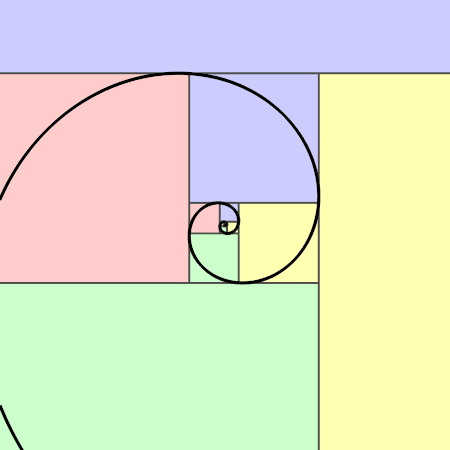
Would Fibonacci's spiral be a manifestation of the spiral?

Propaganda: besida it being a literal spiral, I FUCKING HATE IT WHY IS IT EVERYWHERE, THERE IS NO ESCAPE FROM IT SOMEBODY SAVE ME BEFORE IT'S TOO LATE

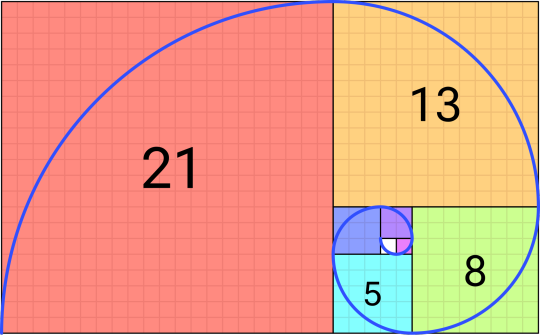
This is not exactly the same as, but approximates the Golden Spiral and becomes closer and closer to being identical as it approaches infinity.

[monkabonka1]

I MADE A NEW MODEL

just a fun little thing i did in about 6 hours instead of sleeping lol

some expression demos

and a bonus one for the fellow stans

Heres the link for the model (credit me if you plan to use it)

[pv1isalsoimportant]

(Semi-regularly updated) list of resources for (not only) young mathematicians interested in logic and all things related:

Igor Oliveira's survey article on the main results from complexity theory and bounded arithmetic is a good starting point if you're interested in these topics.

The Complexity Zoo for information on complexity classes.

The Proof Complexity Zoo for information on proof systems and relationships between them.

Computational Complexity blog for opinions and interesting blog posts about computational complexity and bunch of other stuff.

Student logic seminar's home page for worksheets on proof complexity, bounded arithmetic and forcing with random variables (great introduction for beginners).

Eitetsu Ken's list for resources on proof complexity, computational complexity, logic, graph theory, finite model theory, combinatorial game theory and type theory.

Jan Krajíček's page is full of old teaching materials and resources for students (click past teaching) concernig logic, model theory and bounded arithmetic. I also recommend checking out his books. They are basically the equivalent of a bible for this stuff, although they are a bit difficult to read.

I also recommend the page of Sam Buss, there are downloadable versions of most of his articles and books and archive of old courses including resources on logic, set theory and some misc computer science. I especially recommend his chapters in Hnadbook of Proof Theory.

Amir Akbar Tabatabai's page for materials on topos theory and categories including lecture notes and recordings of lectures.

Andrej Bauer's article "Five stages of accepting constructive mathematics" for a funny and well-written introduction into constructive mathematics.

Lean Game Server for learning the proof assistant Lean by playing fun games.

[trembling-amber]

the Wistful Fabulist, during the time when they were still somewhat new to the Neath, when they were known as the Saccharine Balladeer, roughly 21 and with eyes like two ambers.

[numinoussssss]

"Do you believe in fate, doctor? Our paths carved before us, guided by an invisible hand."

[art-of-mathematics]

Icosahedron

Today I improved the thread connections.

[ro-botany]

How Big Is Grima, Really?

It’s a question as old as Awakening. We all know the fell dragon is fucking gigantic; but no one’s measured them to find out exactly how gigantic they are.

As an enthusiastic dragon biologist, I feel it’s my duty to set the record straight.

TL;DR

Through careful measuring of character models ripped directly from the files of Engage, I determined the Chrom's height in centimeters. Then, using those measurements along with character models ripped from Awakening, I measured the true size of Grima as they appear in the endgame.

According to my measurements, Grima:

Is ~726.8 m (2384 ft) long from snout to tail tip.

Is ~349.7 m (1147 ft) long from snout to vent.

Has an ~815.6 m (2676 ft) wingspan (middle pair of limbs)

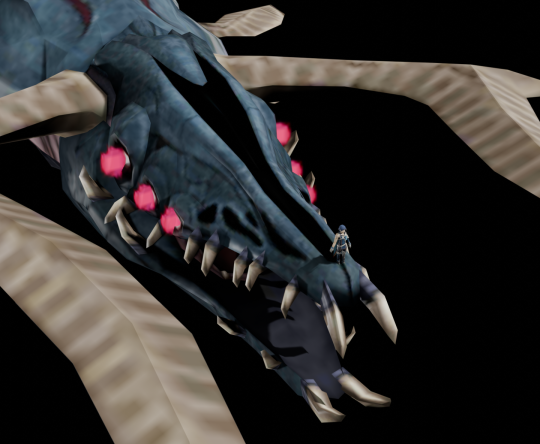
(Look at how small Chrom looks compared to them, good grief)

Want a more in-depth look at how I determined this? My entire process is documented in detail below the cut.

(Also, consider this an invitation: if there's any character from the 3DS fire emblems or engage that you want to know the size of, send me an ask and I might be able to measure them for you.)

---

Preparations

Finding a way to measure Grima is difficult due to the simple fact that nothing and nobody in Awakening can reliably be used as a ruler. We’re not given precise sizes for any objects, and no characters have canonical heights.

Luckily for us, Awakening is not the only game which features its own characters! Several members of its cast are featured in Engage as emblems. This is important because the non-emblem characters in Engage – and the Three Houses emblems also kicking around – all have canonical heights! That means that we can use them as rulers to find the height of any character in the game who doesn’t have one. And once we have a height measurement for one of Awakening’s cast members, we can use their original Awakening model as a ruler to measure the model of Grima themself.

So, I decided to use Byleth and Fogado as rulers with which to measure Chrom, who would then go on to be the ruler for measuring Grima with.

I personally ripped all models used in this experiment directly from (...legally obtained...) ROMs of Awakening and Engage. This was done to ensure the relative sizes of models from the same game remained consistent with how they appear in-game. Any rips available for download online may have been edited or scaled any number of ways, you can’t trust em.

I also, in all cases, had to perform some surgery on the models; but I did my utmost to put them back together as precisely as possible.

-

Finding Chrom’s Height

As I just mentioned, on the Engage side I decided on Chrom as my ruler, and decided to use Byleth and Fogado to measure him.

Engage’s character models are all patterned off a base model – one for female characters and one for male characters. For each character these base models are sculpted slightly, and then scaling factors are applied to various bones in the rigging to give them their unique proportions – these affect the length and thickness of the torso, arms, legs, head, etc.

For all three of my chosen characters, I:

Ripped their head, hair, skin, and clothing models, along with their rigging, from Engage, and imported them into blender.

Applied basic textures to them so they’re easier to see.

Carefully stitched all the component models back together and onto the rigging.

Carefully stitched the legs and feet of the base model back onto the finished character models. This removes any margin of error we would get from including the soles/heels of their shoes in their measurements.

Ripped each character’s scaling factors from Engage’s data files and applied each factor to the appropriate bones on the rigging. I also compared to screenshots from the game to double-check that everything looked correct.

Used blender’s MeasureIt add-on to measure the distance between the highest point on the top of their heads to the lowest point on the bottom of their left heel, in ONLY the Z axis (which is up and down in blender).

The result is this:

(Ignore their weird eyes, Engage's eye textures are a pain in the ass to replicate and I gave up for now)

Using these measurements, and the canonical heights for Fogado and Byleth, we can come up with conversion factors for translating engage blender units (henceforth called “ebu”) to centimeters.

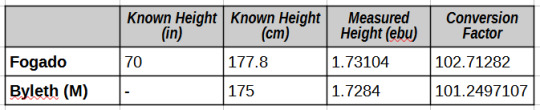
Fogado is canonically 5’10”, i.e. 177.8 cm (source). So, according to his measurements, 1 ebu = 102.713 cm.

Byleth (male) is canonically 175 cm tall (source). So, according to his measurements, 1 ebu = 101.25 cm.

You may notice those are slightly different numbers when, if these character heights were truly consistent, you would expect them to be the same!

Well, I’m chalking that up to the heights from 3H being in less precise units, and the developers probably not being quite as gung-ho about consistent character heights as I’m being right now. It would probably be smart to use another non-emblem Engage character with more of a height difference than these two to get another conversion factor and see how three data points compares, but... I’m so tired from putting these three bozos’ models together, y’all. I’m done. This is just what we get.

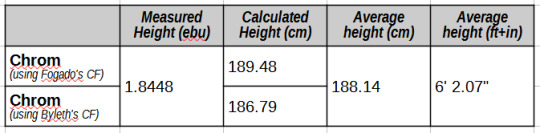
Our two conversion factors give us two possible heights for Chrom. Either he’s about 189.48 cm tall, or he’s 186.79 cm tall. I’m going to take the average of those numbers and use that for Chrom’s height.

We have now found Chrom to be 188.14 cm tall, i.e. 6’ 2”.

...He’s tall! He’s taller than I thought he was, honestly.

-

Measuring Grima

The next step is to take what we know about Chrom, and repeat this process with Chrom and Grima’s models from Awakening.

One frustrating thing about this is that Grima’s in-game model is almost certainly scaled smaller relative to the people than his CG model. And I can’t get the CG models, because those are locked in some vault at IntSys headquarters, and not included in the game files; and there are zero frames in any of the CGs that can be used for this kind of measuring.

But you know what? I spent too long in the Engage ripping mines to give up over CG Grima's differences. In-engine Grima is still ridiculous and I want to know about them.

Awakening’s character models are composed of several parts: A main body (which for humans is class-based, not character-based), in most cases one each of a character-specific head and hair model, and up to two accessory models. Each character also has one scaling value; a multiplier on their model’s overall size. (Tragically you can’t have fun fucking up their proportions like you can Engage characters)

So for each of these two, I:

Ripped all their component models from the game. For Chrom this was the lord class body and his head (which, unlike other characters, also includes his hair). For Grima this was their full-body model and their two accessory models, the upper and lower halves of their mask.

Applied basic textures to them

Carefully stitched their component models together; which effectively was positioning their heads back on their bodies.

For Chrom, I also borrowed a generic head model from another character and aligned it with his regular head; this is so that I could measure his height from the top of his head instead of his hair.

Checked their scaling factors; in this case, I couldn’t find a scaling value for Grima and Chrom had the default value of 1.0, so nothing needed to be done.

Used blender’s MeasureIt add-on to measure them. On Chrom, I measured the z-axis (up-down) distance between the highest vertex on his skull and the lowest vertex on his left heel to get his height. On Grima, three measures were taken; snout-vent (as in snout to the end of their body/base of their tail), snout to tail, and wingspan; each only measured in one relevant axis.

The measurements ended up being this, in what I will henceforth call awakening blender units, or “abu”

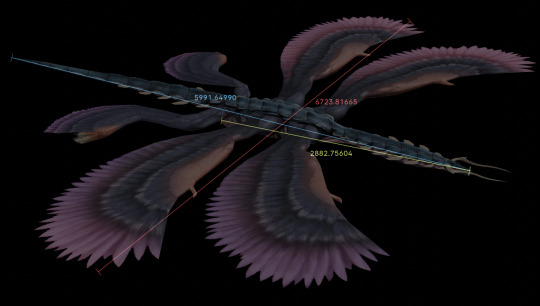
Using our estimated height for Chrom from Engage, we calculate our conversion factor; 1 abu = 12.13 cm.

And then we can finally convert Grima's measurements to useful units!

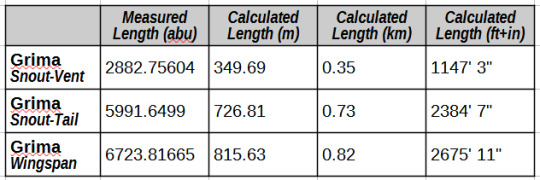
Conclusions

Holy fuck that dragon is large.

[unnonexistence]

one of my friends is a biologist & i was really amused hearing some of her stories yesterday because they put into context just how believable newt's kaiju drift is as Shit A Biologist Would Do. like my friend has personally met both a guy who got infected with a botfly larva and didn't do anything to remove it (because he just didn't mind), and another guy who identified a tapeworm species by intentionally exposing himself to it (he had it narrowed down to 2 species and needed to know if it was the one that would infect humans) (it was)

[cabeswaterdrowned]

Adam is turned on by being taught Latin (Ronan) and History (Gansey) by powerful rich hot brunette men with nice cars so ofc Greenmantle scores points with him.

[not-kamenx]

“…Why am I in a studio with low quality lighting in this outfit?”

don’t repost

I was doodling in my sketchbook feeling so awful and sad and WHATEVER emotions blah blah unimportant then I made him

Here he is in the sketchbook

I did a few wrongs in the digital but it’s okay at least he’s colored and I can improve later

IDK random design idea just came outta nowhere

[pv1isalsoimportant]

Professors will skip a nontrovial part of a proof and then write this

like thank's for reminding me of what \aleph_0^+ is i guess.

[filoo]

Mirror Anomaly sfN / sNr+N = P What you see is just a shadow of what you should see

Instagram , Twitter , Tiktok , Behance