#math resource
Explore tagged Tumblr posts
Text
(Semi-regularly updated) list of resources for (not only) young mathematicians interested in logic and all things related:
Igor Oliveira's survey article on the main results from complexity theory and bounded arithmetic is a good starting point if you're interested in these topics.
The Complexity Zoo for information on complexity classes.
The Proof Complexity Zoo for information on proof systems and relationships between them.
Computational Complexity blog for opinions and interesting blog posts about computational complexity and bunch of other stuff.
Student logic seminar's home page for worksheets on proof complexity, bounded arithmetic and forcing with random variables (great introduction for beginners).
Eitetsu Ken's list for resources on proof complexity, computational complexity, logic, graph theory, finite model theory, combinatorial game theory and type theory.
Jan Krajíček's page is full of old teaching materials and resources for students (click past teaching) concernig logic, model theory and bounded arithmetic. I also recommend checking out his books. They are basically the equivalent of a bible for this stuff, although they are a bit difficult to read.
I also recommend the page of Sam Buss, there are downloadable versions of most of his articles and books and archive of old courses including resources on logic, set theory and some misc computer science. I especially recommend his chapters in Hnadbook of Proof Theory.
Amir Akbar Tabatabai's page for materials on topos theory and categories including lecture notes and recordings of lectures.
Andrej Bauer's article "Five stages of accepting constructive mathematics" for a funny and well-written introduction into constructive mathematics.
Lean Game Server for learning the proof assistant Lean by playing fun games.
#math#mathblr#mathematics#maths#logic#computational complexity#proof complexity#bounded arithmetic#topos theory#category theory#lean#math resource#studyblr#finite model theory#complexity theory
82 notes
·
View notes
Text
24,unsorted




























#blinkies#carrd graphics#web graphics#flash warning#carrd resources#da stamps#stamps#space#cat#static#socks#tw bright colors#dividers#Christmas#eyes#the simpsons#ned flanders#Bart Simpson#video games#asteroids#frogger#2025#new year#years#alien#aromantic#trans#gravity falls#cool math games#favicons
505 notes
·
View notes
Text
back to basics


mostly free resources to help you learn the basics that i've gathered for myself so far that i think are cool
everyday
gcfglobal - about the internet, online safety and for kids, life skills like applying for jobs, career planning, resume writing, online learning, today's skills like 3d printing, photoshop, smartphone basics, microsoft office apps, and mac friendly. they have core skills like reading, math, science, language learning - some topics are sparse so hopefully they keep adding things on. great site to start off on learning.
handsonbanking - learn about finances. after highschool, credit, banking, investing, money management, debt, goal setting, loans, cars, small businesses, military, insurance, retirement, etc.
bbc - learning for all ages. primary to adult. arts, history, science, math, reading, english, french, all the way to functional and vocational skills for adults as well, great site!
education.ket - workplace essential skills
general education
mathsgenie - GCSE revision, grade 1-9, math stages 1-14, provides more resources! completely free.
khan academy - pre-k to college, life skills, test prep (sats, mcat, etc), get ready courses, AP, partner courses like NASA, etc. so much more!
aleks - k-12 + higher ed learning program. adapts to each student.
biology4kids - learn biology
cosmos4kids - learn astronomy basics
chem4kids - learn chemistry
physics4kids - learn physics
numbernut - math basics (arithmetic, fractions and decimals, roots and exponents, prealgebra)
education.ket - primary to adult. includes highschool equivalent test prep, the core skills. they have a free resource library and they sell workbooks. they have one on work-life essentials (high demand career sectors + soft skills)
youtube channels
the organic chemistry tutor
khanacademy
crashcourse
tabletclassmath
2minmaths
kevinmathscience
professor leonard
greenemath
mathantics
3blue1brown
literacy
readworks - reading comprehension, build background knowledge, grow your vocabulary, strengthen strategic reading
chompchomp - grammar knowledge
tutors
not the "free resource" part of this post but sometimes we forget we can be tutored especially as an adult. just because we don't have formal education does not mean we can't get 1:1 teaching! please do you research and don't be afraid to try out different tutors. and remember you're not dumb just because someone's teaching style doesn't match up with your learning style.
cambridge coaching - medical school, mba and business, law school, graduate, college academics, high school and college process, middle school and high school admissions
preply - language tutoring. affordable!
revolutionprep - math, science, english, history, computer science (ap, html/css, java, python c++), foreign languages (german, korean, french, italian, spanish, japanese, chinese, esl)
varsity tutors - k-5 subjects, ap, test prep, languages, math, science & engineering, coding, homeschool, college essays, essay editing, etc
chegg - biology, business, engineering/computer science, math, homework help, textbook support, rent and buying books
learn to be - k-12 subjects
for languages
lingq - app. created by steve kaufmann, a polygot (fluent in 20+ languages) an amazing language learning platform that compiles content in 20+ languages like podcasts, graded readers, story times, vlogs, radio, books, the feature to put in your own books! immersion, comprehensible input.
flexiclasses - option to study abroad, resources to learn, mandarin, cantonese, japanese, vietnamese, korean, italian, russian, taiwanese hokkien, shanghainese.
fluentin3months - bootcamp, consultation available, languages: spanish, french, korean, german, chinese, japanese, russian, italian.
fluenz - spanish immersion both online and in person - intensive.
pimsleur - not tutoring** online learning using apps and their method. up to 50 languages, free trial available.
incase time has passed since i last posted this, check on the original post (not the reblogs) to see if i updated link or added new resources. i think i want to add laguage resources at some point too but until then, happy learning!!
#study#education resources#resources#learning#language learning#math#english languages#languages#japanese#mandarin#arabic#italian#computer science#wed design#coding#codeblr#fluency#online learning#learn#digital learning#education#studyinspo#study resources#educate yourselves#self improvement#mathematics#mathblr#resource
788 notes
·
View notes
Text
I really do fail to understand how people are able to justify this genocide at all even after 'claiming' to know the narratives of both the sides?
How can you remain neutral in face of mass murder?
All that privilege must be real nice. Getting to sleep in your beds, safe from this living hell, while justifying genocide must be real nice. Shame on you! Shame on you! Shame on you!
And I'm sorry to the Palestinians. I'm sorry the world's humanity is conditional. I'm sorry that we have failed you.
#palestine#free palestine#genocide#someone literally argued with me about being blinded by Palestine's side of the story because I'm too emotionally invested#and I provided verified resources to support whatever I had posted#I literally did math and supported it with verified data to prove the quarter of a nuclear bomb claim#and I was enfuriated by the lack of empathy#I really am sorry that we have failed you#I am sorry that you have to prove everything even when you are the victim here#I'm sorry I cannot do more#auroras thoughts#free gaza#gaza strip#gazaunderattack#save gaza
1K notes
·
View notes
Note
Heyo, can you do Radio Scramble and/or Psycho Math (Both from Crashbox) themed borders? (doing only one of them is okay)




🎙️Radio Scramble Dividers🎙️



📊Psycho Math Dividers🧮
please like, reblog, & credit if you use!
[DIVIDER REQUESTS ARE OPEN!]
DNI: TERFS, endo, proship, pro ana, nazi, MAPs, zoophiles
tag list: @ghostboneswrites2 @savanaclaw1996 @lordhavemercyyyyy @bloodythornsandskulls
@und3ad-mutt @ribbed-scythe @idkwhatto-namethis @nothers @yourlocaltrasheater
@ang3l-d1nn3r @puppy-monst3r @orisaspirin @bunnyb0yy @blindweb
@worstwolverinesbf @wardenofbanland @weirdest-worlds
[if you’d like to be on the tag list for dividers, please leave a message in my inbox]
#sister lucifer’s dividers#dividers#aesthetic#aesthetic dividers#crashbox#radio scramble#psycho math#rentry graphics#rentry resources#rentry decor
93 notes
·
View notes
Text
This is stupid:
buuuut it still works cause tangle is awesome :] i direct you to issue 37, where tangle does this:

at face value, heck yeah!! using her tail as a pulley system to tie up the boat?? so clever :) (and being able to wrap her tail around all that after the boat starts falling, before it loses much height - that’s very fast, accurate tail extension! what if she’d accidentally bonked her tail into any of those metal beams down there instead of going between them? she wouldn’t have made it in time if she did bonk!)
but you look closer… and it might not be that clever. in fact, it looks like a mistake.

(at the dark purple question mark, her tail’s path isn’t very clear. i went with ‘repeating the pattern’ around a part of the boat we couldn’t see in blue, which would then wrap around at the angle you see her tail stretch left, out from the question mark.)
it’s wrapped around the whole boat, so where’s the problem…?
the problem is: leverage (or whatever the word is for pulleys & ropes).
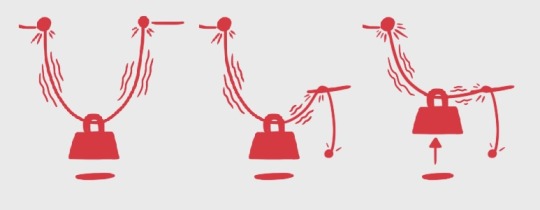
in the leftmost diagram, we see the dots - the anchor points of the rope - are at equal height. at a resting point, they will both hold the weight up with their own material integrity; that is, it will stay at the resting height unless the material breaks.
in the middle diagram, the ‘anchor point’ for the right rope has moved lower; the bar it holds the weight up towards is far lower, and the excess is wrapped over to tie to the ground. again, at resting position, it will remain there while the material holds.
in the right diagram, the rope arrangament is the same as the middle one, but now we’re applying pull force to bring the weight upwards. at this level, due to where the right rope is ‘anchored’ on the bar, no matter what force is applied, it cannot raise the weight any higher than that bar - only the rope on the left could pull it higher, or support its weight in a higher position.
applied to this situation:

the blue sections are parts where tangle’s tail can support the boat just by wrapping around and staying in place, pretty much; it’s a net woven around that just needs to not slip. the orange sections are where the only provable anchor point above the boat is tangle herself! (and i will note that the way she’s holding her tail here, her tail is almost certainly not the limb doing most of the pulling - for it to angle so much before and after her grip on it, it can’t be tensed. to better clarify - if you have long hair, and something pulls on your hair, it pulls your scalp. unless you grab your hair with a hand and pull it closer to your scalp, and then all the active tension is redirected through your arms.)
which means that for the boat to stay where it is - above the ‘blue level’ - tangle is actively pulling it higher! pulling the entire weight of the boat up.
so how hard is this - how heavy is the boat? in this panel, it looks like a relatively small boat; maybe a dinghy? dinghies can have those ribbed sides, and are generally round, and it could weigh somewhere between 100-200lbs, and be a little tough to carry…
nope! it is some type of motor boat (perhaps a skiff). you can see a propeller under the ‘cinch’, so it has a motor… and if you look at the rest of the page, it has at least 7 seats (presumably 8), so it has to be large enough to hold at least 7 people!


i’m not acquainted with boats so i had to do some digging - and most of the ones i found at first had consoles/raised walls/less seats than this one, which weren’t exactly a fair weight comparison. i also didn’t want to try to calculate precisely how long this boat is, since the angles are off and hard to calculate from this perspective.
so, instead i looked at a few different types of boat to get rough estimated of weights, and then i’d roughly downsize that based off estimates of how much smaller a boat for ~3ft people needs to be!
i went through a handful of similar motorboats (mostly 1-4 people, but with added physical features to add weight) and found weights between 1,000lb to 2,000lb depending on length (18-22+ feet). a yamaha 195S is 19’5” long, and 2,509lb - but a nitro z18 is 18’8” and 1,700lb. the only good visualizers i found were charts for what motor horsepower to use for what length and weight:

so it was super hard to get a good estimate of the weight here!! like super hard!! so i’m just doing a vague whatever conservative estimate and someone else can do proper math!!!
if you half the length to a presumed 10ft long - which i’m not sure is properly long enough for this boat, i’d guess somewhere between 12-15ft - and then quarter the 20ft weight to try to account for the square-cube law, you get a guesstimate of a boat weighing about 500lb. if you’re conservative with it, maybe 400lb?
which, to keep from tipping out away from the metal cradle, lowering to the level of tangle’s tail wrapped around underneath, & be held upright as tangle is doing, has to be fully supported - and as noted earlier, without real assistance from tangle’s tail’s strength, this is just her arms.
now, you could assume tangle simply wrapped that mystery segment of tail around the cradle bar she’s standing on, and this would allow much more of the boat’s weight to be supported by her tail’s structure… but it’d have to be an awkward angle for her tail to do that and it to not be visible next to her feet or in the empty space to the right, which would also put some more of the strain on her arms/body instead of her tail, so she’d stil be doing a lot!
and especially if you estimate the boat closer to 12-15ft, which is closer to 600-750lb, that gets crazier…
PLUS the fact that she had to hold that weight up for at LEAST as long to ask them to hurry & tie the boat up, AND as long as it took for the others to actually work something up/fix the cradle to hold the boat and relieve tangle of it.
conclusion: this is canon

#tangle the lemur#analysis#sonic idw#idw sonic#as soon as i noticed her tail’s hand was at the bottom grabbing on i was like ‘wait thats stupid.-#-shes holding the entire boat up without using her tail to pull’ and then all i needed to do was figure out how heavy the boat was#anyways. to any whispangle fans: tangle can absolutely scoop whisper up effortlessly. do with this what you will#i also DID NOT have any proper heavy resources or references for the exact boat. so if anyone can correct me on the math#please do correct me & share with the class thatd be so fun
78 notes
·
View notes
Text











⿻ The Second Coming Stamps ⿻
♯ F2U with or without credits! Reblogs and likes appreciated
↳ Self Indulgent ⨾ no reposts ×
« Art Credits: Official Art »

#⸝⸝⸝ paws in the stars⨾ 𓃦⟡ ݁₊ .#carrd graphics#rentry graphics#carrd resources#carrd decor#rentry resources#rentry stuff#rentry inspo#carrd stuff#rentry#web decor#blog decor#page decor#sntry decor#rentry decor#stamps#rentry stamps#alan becker#the second coming#animation vs animator#animation vs minecraft#animation vs math
40 notes
·
View notes
Note
hey! I'm a 4th year math undergrad in the States and I am astounded by your knowledge of algebra. it's my favorite branch of math and I know a lot more than my peers but not nearly as much as you. where did you learn? any textbook recommendations?
keep up the great mathematics and posts!
haha, well, I don't know that much algebra to be honest (me using a fancy word in a joke means i have heard of it before, not that I actually know how to work with it!)
But yknow I could give out some resources, so here they are (so far I have mostly learned from classes but yknow i'm at that point where i'm starting to need to transition from listening to someone ramble to reading someone's ramblings and then rambling myself)
For basic linear algebra I didn't learn through a textbook, but I have heard good things about Sheldon Axler's Linear Algebra Done Right and it seems similar to what the classes I had did (besides the whole hating on determinants part, though I kinda get it).
For some introductory group theory, I also had a class on it, but the lecture notes are wonderful. I would happily give the link to them here but since they're specifically the lecture notes of the class from my uni I would be kinda doxxing myself. Also they're in French. I will give out some of the references my prof gave in the bibliography of the lecture notes (I have not read them, pardon me if they're actually terrible and shot your dog): FInite Groups, an Introduction by Serre (pdf link), Linear Representations of Finite Groups also by Serre (pdf link), Algebra by Serge Lang (pdf link). Since our prof is a number theorist he sometimes went on number theory tangents and for that there's Serre's A Course in Arithmetic (pdf link). I'm starting to think our prof likes how Serre writes.
For pure category theory and homological algebra I have read part of these lecture notes. I think a good book for category theory is Emily Riehl's Category Theory in Context (pdf link). For homological algebra, a famous book that I have read some parts of is Weibel's An Introduction to Homological Algebra (pdf link). Warning: all pdfs I found of it on the internet all have some typographygore going on. If anyone knows of a good pdf please tell me.
For commutative algebra, A Term of Commutative Algebra by Altman and Kleinman (pdf link). I haven't read all of it (I intend to read more as I need more CA) but the parts of it I read are good. It also has solutions to the exercises which is neat.
For algebraic geometry (admittedly not fully algebra), I am currently reading Ravi Vakil's The Rising Sea, and I intend on getting a physical copy when it gets published because I like it. It tries to have few prerequisites, so for instance it has chapters on category theory and sheaf theory (though I don't claim it is the best place to learn category theory).
For algebraic topology (even less fully algebra, but yknow), I have learned singular cohomology and some other stuff using Hatcher. I know some people despise the book (and I get where they're coming from). For "basic" algebraic topology i.e. the fundamental group and singular homology I have learned through a class and by reading Topologie Algébrique by Félix and Tanré (pdf link). The book is very good but only in French AFAIK.
For (basic) homotopy theory (does it count as algebra? not fully but what you gonna do this is my post) I have read the first part of Bruno Vallette's lecture notes. I don't know if they're that good. Now I'm reading a bit of obstruction theory from Davis and Kirk's Lecture Notes in Algebraic Topology (pdf link) and I like it a lot! The only frustrating part is when you want to learn one specific thing and find they left it as a "Project", but apart from that I like how they write. It also has exercises within the text which I appreciate.
For pure sheaf theory, a friend recommended me Torsten Wedhorn's Manifolds, Sheaves and Cohomology, specifically chapter 3 (which is, you guessed it, the chapter on sheaves). I only read chapter 3, and I think it was alright (maybe a bit dry). I also gave up at the inverse image sheaf because I can only tolerate so much pure sheaf theory. I will come back to it when I need it. The whole book itself actually does differential geometry, but using the language of modern geometry i.e. locally ringed spaces. I have no idea how good it is at that or how good this POV is in general, read at your own risk.
Also please note I have not fully read through any of these references, but I don't think you're supposed to read every math book you ever touch cover to cover.
thanks for the kind comments, and I hope at least one of the things above may be helpful to you!
#ask#algebraic-dumbass#math#mathblr#math books#math resources#math textbooks#algebra#category theory#sheaf theory#algebraic topology#algebraic geometry#homotopy theory#group theory#linear algebra
49 notes
·
View notes
Text
things which, while not universally hated, are often treated with disdain by some ttrpg players:
pvp
dungeon crawls
resource tracking
unwinnable fights/situations
metagaming
gm not preparing the adventure details beforehand
things am trying to put in my games
pvp
dungeon crawls
resource tracking
unwinnable fights/situations
metagaming
gm not preparing the adventure details beforehand
#algie might make ttrpgs#bcos i LIKE these when used well#admittedly the resource tracking in my current in progress game is not super crunchy#u have a number. u can use em for advantage on rolls or lose em when things break bad.#but also that's partly bcos time is weird in this setting soooooo#(also it is bcos i. have brain bad. and math is hard.)#im trying to make a dungeon crawl game but the mechanics are sorta simplified#idk how much can be left up to gm's discretion tho we'll see how it playtests#i WANT to believe that 'give a greater effect for actions that do something Clever#like targeting a revealed weakness or building on what someone else did'#would be. clear info for the gm. and easy to implement.#buuuuut we'll. see
140 notes
·
View notes
Text
Physics and Mathematics Resources (plus some Chemistry):
I will update this because I know I have more recommend textbooks somewhere in my files, I'm just too tired to look right now. Latest update: 5/13/25
Physics:
The Science Spot--Mostly lesson plans for teaching kids
The Physics Classroom Tutorial--Has interactive online activities and models. Some videos and also some chemistry stuff.
HyperPhysics--Quite possibly the best resource I've ever seen because it shows how all concepts are linked together. The site isn't loading for me but it says it's up. There is a downloadable version on the Internet Archive (though it doesn't look as nice and clean). EDIT: I found a GitHub that lets you clone and download the html so you can click through it offline and it works! If people are interested I can make a tutorial, it was very easy.

PhET--A ton of demonstrations and tutorials. Also has some for mathematics and chemistry.
Paradigms Physics Notes--this was the curriculum that was used in my junior and senior classes. A lot of stuff here. If you are interest about teaching physics using this method, you can read more here.
Quantum Mathamatica Add-on--Useful for calculations.
The Hypertextbook--uhh lots here. Problems, solutions, explanations, etc.
oPhysics--interactive physics software.
MiniPhysics--more demonstrations and interactive software.
Michel van Biezen--really clear work-throughs of many subjects (algebra, calculus, chemistry, physics). He actually has a tumblr but has been active in like a decade @ilectureonline
Mathematics:
Paul's Online Math Notes--Got my whole class through junior and senior year
Calculator Soup--a lot of different kinds of calculators
3Blue1Brown--Very interesting youtube channel that shows a lot of calculus and linear algebraic principals visually or in intuitive ways.
Mathologer--more interesting advanced mathematical concepts.
General:
OpenStax--Free textbooks, legally
#physicsgoblinthoughts#resources#physics#math#mathematics#chemistry#learning resources#textbooks#school
29 notes
·
View notes
Note
Can you make some stamps of the coolmathgame “Run 3” please? I’ve been playing it recently and it tickles my brain
Haiiii ofc!! Hope you like these!!






#my graphics#request#cool math games#run 3#blog resources#carrd resources#carrd stuff#neocities#carrd graphics#rentry graphics#da stamps#rentry graphic#rentry resources#rentry stuff#rentry gif#rentry#web graphics#graphics#early internet
45 notes
·
View notes
Text


wow I wonder what could have happened around 2013 to cause this
#which the article doesn't mention at all of course#look. i can only speak to 1) math instruction 2) on the elementary school level#and middle school level#and only in the districts ive worked with#but ive said this before and I'll say it again. the current way math is taught has the same problems that balanced literacy did#kids who are naturally good at math will figure it out no matter how its taught#in fact they probably ARE benefiting a lot from being exposed a variety of strategies and conceptual thinking#the sort of stuff that would typically be reserved for a pull-out gifted/discovery/links class#but the kids who struggle with math? this does NOT help them#they dont just 'pick up' addition and multiplication facts#the ~more conceptual~ strategies dont actually lead to more conceptual understanding for them. its just a different (more complicated!)#algorithm for them to memorize#and because it doesn't come easily to them#they aren't given the necessary practice (which yes. involves repetition!!) to master any strategy#kids who can't struggle to make big conceptual leaps shouldn't be denied access to basic math skills#and i will die on the hill of 'its easier to think about complex probel#*problems and think conceptually if you aren't devoting mental resources to trying to figure out 8*7 by repeated addition
15 notes
·
View notes
Text
Fun fact: if I am having trouble with how to draw a certain angle of Vox’s head, I use a Rubix cube to figure it out.
#telly txt#I bought it with the intent of drawing; not for Vox specifically but to practice boxes#but it has a lovely secondary use now lol#it takes a bit of mental math since his head is thin#but it’s a great resource and I recommend it 👍
14 notes
·
View notes
Text
I swear the rest of my work for this semester of education is going to be done purely out of spite. I am going to write sentences like I'm writing my novel just to get up to word count goals. This class was feeling pointless and directed mainly at multi-subject majors before I decided to drop the edu load and now that feeling has doubled. None of this will be useful. But. My gpa
#Starlight Does Uni#No seriously making vocab posters isn't really going to work long term in the college math classroom I don't know what to tell you#I don't think they'd even be really useful in the AP Calc classroom that was my original plan tbh#Aside from the first few days of concept learning#Because honestly if you're having to rely long-term on a poster in order to be able to do derivation and integration#You're not going to do well on the AP exam#And that's like. the point of the class#I get scaffolding is good and everything. Like I understand that#But like. For the AP classroom. There's a very particular goal that they're trying to reach.#And too much long-term scaffolding of the basics will actually hinder rather than help.#I honestly feel like my AP Calc class didn't do as well as they could have#Because my teacher didn't set limits on what we were allowed to use on exams until the month before the big one#So I was the only one holding myself to exam pacing (finishing in the exam period) and doing my best to not rely on the formula sheet#And I was one of the only people to get a 5#Like absolutely there should be resources for ELLs#But I don't think this is something that would work quite like they're saying it should at the 12th grade level idk#Because what's being suggested is essentially that formula sheet on the walls.#And. No.
8 notes
·
View notes
Text
anyways, everyone should know about KodyTools.
it's a website with a collection of online tools; everything from math, finance, writing/text, science, coding, date/time, et cetera. and not just one or two for each category either! there are over 200 tools on this website. it's just absolutely fantastic; it's also an easy website to navigate + it's really simple to use all the tools! they also explain each one~
also it's free + there is only one singular ad, as far as i can tell, just the single banner at the top of the page. so you won't have to deal with annoying ad pop ups constantly.
i actually found it because of their text tools, specifically their combination generator + their sort lines generator (it's actually how i got all the combinations for my TF picker wheel)! i also recently found their empty lines remover which has been a lifesaver~
some (but not all) other ones they have:


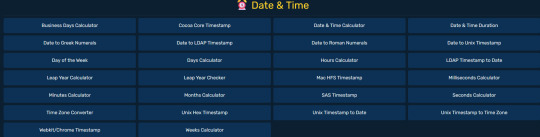


#resources#references#generators#writing generators#useful#helpful#writing#math#science#coding#development#web development#kodytools#kody tools#; save#; favorite#; mine#FREE TO REBLOG#ENCOURAGED TO REBLOG
7 notes
·
View notes
Photo









Floorplans my beloved
#Minecraft#Damned#WPVG#WPMC#Oooooh you wanna tour the Institute soooo baaaddd#Lol#So some quick stats - I believe I'm currently making this at 3/5ths scale on some loooooose math#At a glance - if the floor plan is To Scale (which tbh I don't think it is lol) the institute itself is ~330x620ftsq#Tho it's weirdly shaped so honestly it's a bit hard to tell lol#There's only one given square footage on the entire map and it's an awkward 14'x16' in the Activities Shed (not featured here - yet)#So approximating in 10' blocks from there I've been putting down two Minecraft block per approximate 10'#Which if each block is a meter then two meters is a little over 6' - 6' to 10' - thus 3/5ths scale#I /think/ I am not a math gay I just have the mental illness that makes me want to walk around fictional mental asylums#It's honestly so fun to see it come together :D#Fun to walk those halls!#It's also been very meditative to lay walls and floors and ceilings and lights and the outer shell one block at a time haha#Probably the most cerebral part has been the alternating pattern in the bathrooms haha#Funnily enough this was actually inspired by some papercraft - saw some paper buildings and got The Urge#I want some kind of physical object of the institute so baaaad#Digital effigy isn't a bad alternative tho#And there's a level of exactness that can't be achieved in like - the Sims for example#(The Sims Institute my deeply deeply beloved been pulling much inspiration thank you Alana <3)#Tho the Sims /does/ have the advantage of painting one side of a wall one colour and the other side a different colour hgh#Doubling up wall thickness has been killer on keeping the internal/external sizing consistent#I've managed so far! But I am still only on the first floor#Well - the shell of the lower floor will require restrictions either way it's fine#I'm having a lot of fun with it! And also ow my wrist lol#I think it'll be a fun resource to have :) And I mean hey - it's easier to make something physical with a 3D rendering to work from yeah?#Ignoring how Minecraft doesn't have to abide by physics lol#Institute dollhouse with modular rooms and floors...... Hh..............
6 notes
·
View notes