#finite model theory

[pv1isalsoimportant]

(Semi-regularly updated) list of resources for (not only) young mathematicians interested in logic and all things related:

Igor Oliveira's survey article on the main results from complexity theory and bounded arithmetic is a good starting point if you're interested in these topics.

The Complexity Zoo for information on complexity classes.

The Proof Complexity Zoo for information on proof systems and relationships between them.

Computational Complexity blog for opinions and interesting blog posts about computational complexity and bunch of other stuff.

Student logic seminar's home page for worksheets on proof complexity, bounded arithmetic and forcing with random variables (great introduction for beginners).

Eitetsu Ken's list for resources on proof complexity, computational complexity, logic, graph theory, finite model theory, combinatorial game theory and type theory.

Jan Krajíček's page is full of old teaching materials and resources for students (click past teaching) concernig logic, model theory and bounded arithmetic. I also recommend checking out his books. They are basically the equivalent of a bible for this stuff, although they are a bit difficult to read.

I also recommend the page of Sam Buss, there are downloadable versions of most of his articles and books and archive of old courses including resources on logic, set theory and some misc computer science. I especially recommend his chapters in Hnadbook of Proof Theory.

Amir Akbar Tabatabai's page for materials on topos theory and categories including lecture notes and recordings of lectures.

Andrej Bauer's article "Five stages of accepting constructive mathematics" for a funny and well-written introduction into constructive mathematics.

Lean Game Server for learning the proof assistant Lean by playing fun games.

[p-isequalto-np]

I found a book specifically for finite model theory that contains like 80% of all the things that interest me in math... Let's just say my motivation is back.

[pastorfutureletthembe]

Because of my brain's fucked up chemistry, I bring you bilibili's most hilarious (sarcasm) ploy. This is one of my favorite official artwork. The palette is simple and our beloved characters seem to have fun!

🙂‍↔️ Don't be fooled.

I'll start with the obvious, as always: red stains and apple knives. The pictures are telling enough.

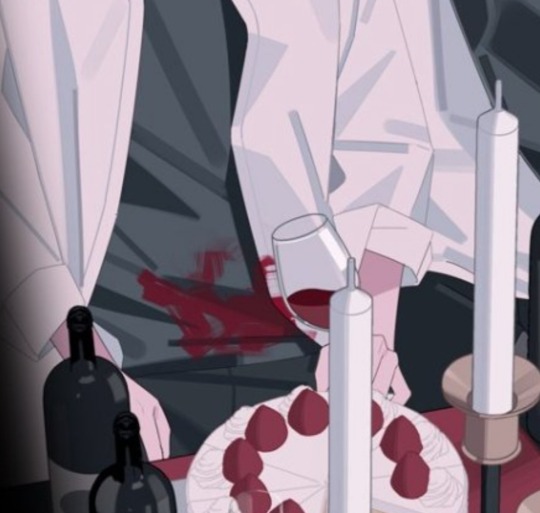
Then we have the number 8. Which, I have my theories on, but nothing significant enough to make a whole post about it yet.

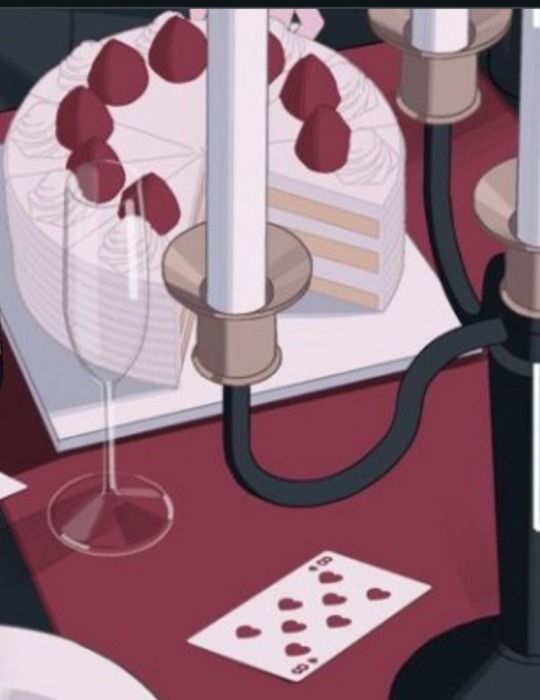
Let's start with the 8 of hearts. If you look carefully, you'll notice there are exactly 8 chandelier arms. 8 strawberries are visible on each cake (one is missing two parts and the other one is partly behind a shadow who must be Li Tianchen). Lastly, but Im not entirely sure of myself here, you can probably count 8 wine glasses (they are rounder than others).

Crossed theory: the missing pieces of the cakes are exactly between IV and VI of a clock. V is hinted yet again 🤌✨ but there are two cakes... making cakes... Yep, you guessed it: one entire Curve, as described in Rick and Morty:

The curve basically walls off the infinite number of universes, in which INSERT IMPORTANT CANONICAL NODE happens, from the rest of the infinite multiverse. A model often used to explain is that the definition of the Central Finite Curve has no set parameters; it's just wholly random and infinite therefore can be represented as a repeating, immeasurable shape modeled with a circle. The Central Finite Curve would then present a finite collection of dimensions.

(Gosh, I do have a lot of meta planned for this show, kill me now // Edit: DONE)

STEPPING AWAY FROM THE LYING CAKE-

For archives purpose, I'll just point out that two Aces of Hearts probably means there are two of the same while there should be one. I don't know if this was a clue already or yet to be resolved. They're both near a candle, a glass and a bottle. It gives the whole table an odd symmetry. Like a mirror you cannot see the frames of. The 8 on cards are also symmetrical + the placement is repeated with both chandeliers. The symmetry of the table implies there is a fourth cake off-screen.

There is one mistake though, I don't know if it was made on purpose or not: none of the hearts are upside down. The 8 of hearts is wrong: there is supposed to be symmetry on the card itself!

Since we already got a tarot reading in the chibisodes, here we go: (a quick google research for this one)

"In divinatory tarot, it could be a mix between the Lovers and the World. Indeed, the ace of hearts relates to the World as it represents the triumph of the individual on the elements that surround him. It also relates to the Lovers thanks to its romantic attributes and consequences."

- latincards

THE DARKER SIDE OF THE ACE OF HEARTS MEANINGS: EXPLORING CONTRASTING While predominantly seen as a symbol of love and positivity, the Ace of Hearts can also have darker or more complex meanings. In some interpretations, it might signify heartbreak, emotional manipulation, or unrequited love. This aspect reminds us that the heart's journey is not always smooth and that love can sometimes lead to challenging or transformative experiences.

- thedopeart

(Sidenote: You should be aware that the LOVERS doesn't exclusively concern romantic aspects of life in our modern world, but life partners in the general sense, people deeply tied to you.)

As for the 8 of Hearts:

The Eight of Hearts is often associated with emotions, love, and relationships. It signifies deep connections, harmony, and positive energy in matters of the heart. When this card appears in a reading, it suggests that love and emotional fulfillment are on the horizon. This card is a symbol of balance and stability in relationships. It indicates that there is a strong foundation of trust and understanding between partners.

Hearts are a recurrent shape used in Qiao Ling's artworks but I'll make another post for shapes/characters related stuff.

For the record, Cheng Xiaoshi isn't drinking red wine on the Halloween poster. Doesn't know where this is going but I've done my share of meta for today 🙂‍↕️

>>> In conclusion,

RED is the real clue here. May it be to indicate the presence of Li Tianchen or VEIN. The same shade of red is all we see, as if a filter was used, and since Li Tianchen's eyes glow red, I guess it's related somehow (metaphorically speaking). The fact everything is the same color was also designed to trick us about the blood on the knife. The aces could be CXS and LG... or LG and Liu Xiao (he seems to be obsessed with him so why not.) In any case, I do see a paradox hidden in plain sight here.

The cards are there as a positive outlook: they are together in this, their friendship is what will thrive on the dark side of the clock! It encourages them to open themselves to others and trust their bond.

[transgenderer]

attention conservation notice: utter bullshit

ok so i was thinking about the hippie thing where they say normies are "asleep". and i dont think that's really fair. but it does seem to me sometimes that many (most?) people arent...paying attention? or at least, not to the things i'm paying attention to. people talk about zoning out when they drive and suddenly waking at the end. and i used to do that, but i don't anymore. i pay attention, i think, i listen to music. i dont know what changed. in general i find it easy to get into a mode where i'm mostly just acting on autopilot (i start to do this wihle programming sometimes, and then the program doesnt work and i have to properly "boot up").

and this all seems...bad to me! you have a finite number of minutes, and most of the time youre not in like...pain, agony. its worth paying attention to everything youre experiencing, all your sensory information. its worth paying attention to how you think about things, and what you say, its all worth paying attention to. and it seems psychedelics shifted me into a more "paying attention" mindset

so anyway. all that is old news. you know this idea even if you dont agree with it. but it makes me think of the "dark room problem", in predictive coding theories of the brain. the idea is, essentially, that the brain is fundamentally a prediction organ, trying to minimize "surprisal", getting things wrong, being surprised by new information. but its a prediction organ that's connected to manipulators in the world. and it has certain base-level predictions hard-coded, like "i will not be hungry", and so operates to minimize surprisal by getting food or whatever.

it might be legit, real neuroscientists swear by it. but real neuroscientists swear by anything, so who knows. it has this problem, where if you want to minimize surprise, why not spend all your time in a dark room, not acquiring any new information? (there's all sorts of explanations for this, like maybe "social interaction" is one of our hard-coded predictions) and it seems to me that this "not paying attention", well...it looks a lot like a dark room! if you don't pay attention to things, you dont notice when your subconscious predictions are wrong. if your experience of the world is just a summary rather than a detailed experiencing of everything around you, then it's much easier to predict! and so one can imagine under this theory how this behavior would be rewarding, as long as you maintain satisfaction of those "hard-coded" predictions (and how curiosity is a sort of opposite urge, a monomaniacl fixation on predicting more and more details, by building a more elaborate model)

anyway, as i said up top, this is all nonsense. but it struck me, and i needed to get it out. it's neat, at least

[trashcanlore]

Kabbalah in the Worldbuilding of Genshin Impact; Part 1: The Tree of Life, the Universe, and Everything

Edited for clarity, 12/6/23

Written by Schwan (@abyssalschwan on twitter) and Sabre (trashcanlore, @paimoff on twitter)

During the Sumeru Archon Quests, we learned that the Irminsul is a (real! (ish)) tree that grows upside down, seemingly underground, and that the roots of the tree are the Ley Lines, which extend throughout Teyvat and the Abyss. Irminsul stores all knowledge and memories in the world, and the Ley Lines are the mechanism by which the tree acquires this information. Ley Lines move elemental energy through Teyvat, and this energy acts as both a storage medium for information but also a resource that can be utilized for combat, alchemy, an energy source (Azosite), etc. 

The origin of the name Irminsul (unique to the Western localizations) in combination with the many names from Norse mythology associated with Khaenri'ah, suggest that the inspiration for Irminsul is Yggdrasil, the world tree and central axis of the cosmos in Norse mythology. Here we propose an additional inspiration for Irminsul and the associated worldbuilding and elemental system of Teyvat: The Kabbalistic Tree of Life. In this model, Teyvat’s elemental energy is comparable to the creative energy described by Kabbalah as the foundation for the creation of reality and the spiritual world. Specific attributes of elemental energy can be channeled by unique individuals in Teyvat and these attributes manifest as distinct elements, which can be directly compared to the 10 sefirot, or emanations, described in Kabbalistic literature.

What is Kabbalah?

Kabbalah (lit. received, tradition) is a school of thought originating in Jewish mysticism. In general, Kabbalah focuses on the relationship between the infinite (God) and the finite universe and how it was created. The goal of studying this mysticism can vary depending on the school of thought and their motivations. Many of the esoteric and religious influences on Genshin lore and worldbuilding were influenced by Kabbalah, or vice versa. These include Gnosticism, Hermeticism, alchemy, Freemasonry, the occultist branches of Theosophy and Thelema (Golden Dawn), astrology, symbolic interpretation of the tarot (also specific to the Golden Dawn) and more [2]. In short, Kabbalah is everywhere. Additionally, its concepts are used as symbolism in several pieces of media that directly or indirectly inspired Genshin and other games in the Hoyoverse.

If you have frequented Genshin lore topics, you might have heard that one of the main sources of inspiration for its worldbuilding is Gnosticism. The problem is, Gnosticism is a bit vague or contradictory when it comes to how the world was created and how the whole existence thing works. At this current moment in the storyline of Genshin, we have very little information on the very beginning of existence in Teyvat. This information seems to be a crucial part of the “truth of the world” and appears to be purposefully hidden by powerful factions like Celestia. This entire theory was born out of trying to make sense of what little we know about the creation of Teyvat and comparing it to esoteric commentaries on the well known creation myth of the Torah (Old Testament). The “Biblical world structure” interpretation of Teyvat has been around since the early days of Genshin lore and with good reason; there are frequent mentions of the firmament, as well as the name Teyvat sounding very similar to the Biblical Hebrew word for ‘ark’ (although the grammar is a bit mangled). There are also several references to stories from the Bible in in-game texts, including Before Sun and Moon.  

Kabbalah literature spends a lot of time trying to understand and describe the process of how the world was created and the underlying principles of reality, as well as how spiritual practice can change that reality (either metaphorically or literally). Kabbalah intends to describe the “true nature of God,” which is equal to the entirety of existence, as something very vast and completely impossible to grasp. This incomprehensible infinity emits an “limitless light” that is the origin of all creation. Elemental energy (the ubiquitous source of everything in Teyvat) is often found compared to light, something we’ll discuss in more detail later. The “limitless light” of Kabbalah is way too powerful for existence to bear, much like how elemental energy is to normal, non-Vision having humans. That’s why this light needed to be “filtered” down. This happens through the process of creation, which passes the light through the spiritual attributes that form the Tree of Life, which is like a sort of diagram for how the universe came into being [3].

The Tree of Life

The tree of life and its 10+ nodes, known as sefirot, is one of the most well-known concepts from Kabbalah to make its way into popular culture. As mentioned previously, the tree has been used as rule-of-cool symbolism in anime such as Neon Genesis Evangelion and Fullmetal Alchemist, two pieces of media that likely are significant influences on Genshin (If you doubt that HYV loves NGE, play some Honkai). The sefirot are also depicted on the floor of the Schicksal HQ map in Honkai Impact 3rd, for some reason.

The sefirot and their organization and interactions with each other can be found depicted in many ways, such as the tree format that is the most popular, or a spiraling nested scheme that is really cool, or even very stylized, like the work of Robert Fludd.

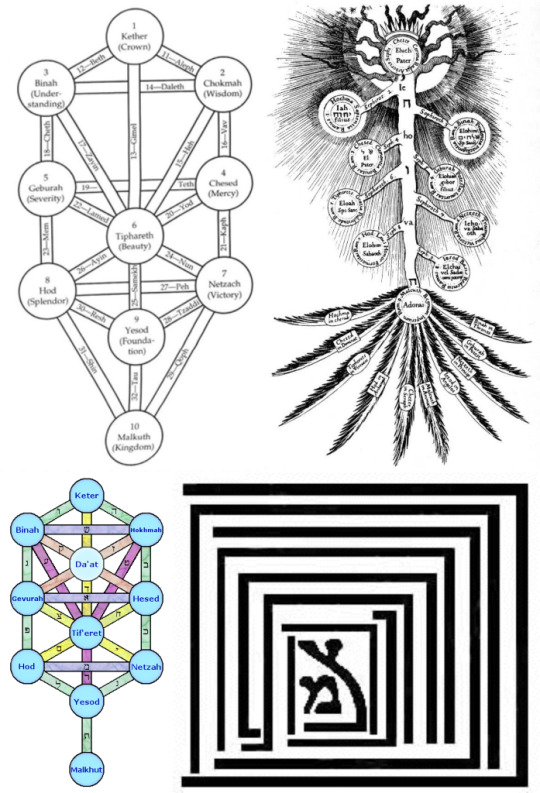
Sefirot

Sefirot comes from the root word in Hebrew meaning “to count,” but you can also find it translated as “sphere” in some texts. The term originated in a book on Jewish mysticism called the Sefer Yetzirah, or “Book of Formation/Creation.” which describes the combination of the “sefirot of nothingness” and the 22 letters of the Hebrew alphabet as the foundation of reality (remember the hypostasis codenames?). 

The Sefer HaBahir (lit. the book of brightness, 13th century France) introduces the idea that the sefirot are emanations of the divine. Interestingly, this book refers to the sefirot as ma’amarot (sayings), which builds on an important concept in classical Jewish philosophy – the idea that God spoke the world into existence. [We’ll get back to the Sefer Yetzirah and the role of language in creating the world in a subsequent part of this theory]. Fontaine 4.2 era edit: HELL YEAH stay tuned for more about Oceanids!!

Historically, Kabbalah might have taken this rough concept from a very different school of thought: Pythagoreans or neo-Platonists. Briefly, the connection between the Pythagoreans and the Kabbalistic sefirot is that both groups considered the world as being made of numbers. This ties back into Genshin worldbuilding because of how much Platonism is related to Gnosticism. Something else to keep in mind is that Pythagoreans (who had a cool history that connected Egypt and Greece to the magic of ✨math✨ but also hey Genshin lore hello Deshret) were known to use lyres as their instrument of choice while making mathematical studies of music. More sus Venti lore for the collection? This is also interesting to consider in the context of Nahida, who is deeply connected to the Irminsul, and has animations that are reminiscent of computers.

Later in the 13th century, the Kabbalist Isaac the Blind would 'canonize' the list of sefirot (there’s still some variation to this day) and organize them into a sequence that would become the basis for the famous Tree of Life structure. His writings described the sefirot as attributes of the divine and their role in the creation of the world. In his model, the sefirot originated from lights that emerged from a primordial soup of potential, and these sefirot/lights would then ‘flow’ and emanate into each other. His student, Azriel of Gerona, expanded on this with a neo-Platonic lens and introduced the concept of the Ein Sof, the infinite nothingness that cannot be comprehended and is the origin of everything. In this model, being flows from an infinite resource of potential, which the divine can utilize through the framework of the sefirot, eventually creating the world [4]. In simple terms, the Ein Sof, which contains everything, emits a primordial light that then differentiates into the sefirot. In our Genshin analogy, this primordial light would be like extremely pure elemental energy that differentiates into elements, like light passing through a prism.

Moses Cordovero, an important figure in the development of Kabbalah, described the process of the sefirot differentiating with the analogy of light shining through a stained glass window: 

Imagine a ray of sunlight shining through a stained-glass window of ten different colors. The sunlight possesses no color at all but appears to change hue as it passes through the window. The light has not essentially changed though it seems so to the viewer. Just so with the sephirot. The light that clothes itself in the vessels of the sephirot is the essence, like the ray of sunlight. That essence does not change color at all, neither judgment nor compassion, neither right nor left. Yet by emanating through the sephirot -- the variegated stained glass -- judgment or compassion prevails. (Pardes Rimmonim by Moses Cordovero, translated in Essential Kabbalah by Daniel Matt)

Cordovero considered the sefirot to be completely independent of each other, but the later Lurianic school of Kabbalah (we’ll get into them more in later parts) considered the sefirot to be constantly dynamically interacting with each other and also assigned them personas. 

Achievement grinders amongst us may recall the descriptions of the namecards you get upon completing the Elemental Specialist achievement series:

Achievement: Colors of the Rainbow: Light can refract into countless colors, but people stop at seven because they're too lazy to count. Perhaps the elements are like that, too. Achievement: Seven Lights: Anyone can play a tune that belongs just to them, and like the dew under grass, can reflect the seven lights of heaven. 

Another example of the elements being compared to light is the Latin text found on the magic circles on the door of Mona’s future house in Mondstadt and generated by the hypostases during their missile attacks. The text reads:

Ex culmine lucis in magno elementorum, which translates to "From the peak of light, to greatness of the elements."

It’s interesting to see this text appearing in association with the hypostases since they are described as “life forms which have completely abandoned their former appearance and biological structure, making them able to reach the highest level of elemental purity. They are ultra-compact structures with a high mass, and are the highest forms of elemental structures.” The hypostasis code names are also all Hebrew letters, as mentioned earlier.

Mona’s astrolabe during the Unreconciled Stars event features a similar text:

Ex culmine locis in magno elementorum; Lux se effundat in mentes dei, which translates to "From the peak of light, to the greatness of the elements; May light pour out, into the minds of god."

The Abyss Lector catalysts contain a text that mirrors these two examples:

Ex culmine lucis in mango obscuritas. Lux se effundat in mentes abysso, or “From the peak of light, to the greatness of darkness. May light pour out into the minds of the abyss.”  

The Genshin elements are also described as flowing. For example, a loading screen tip specifically describes the Ley Lines as “A mysterious network that links the whole world together, within which flow the elements.”  The Silver Twig description states: "All knowledge, memory, and experience flow through this giant tree, just like a stream flows into a river, the river joins a sea, the sea turns into clouds, and the clouds rain onto the ground — just like life itself."

Sefirot and the Genshin Elemental System

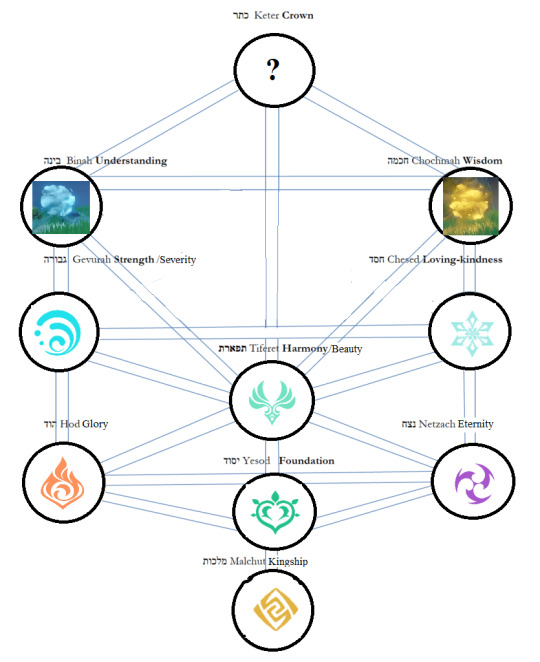
The 10 (sometimes 11) sefirot are: 

Keter: Crown (this one is even more symbolic that the rest, is described as “the most hidden of all hidden things" in the Zohar, represent things that are above the mind’s comprehension and the very beginning of the process of turning potential into reality)

Chokhmah: Wisdom

Binah: Understanding/Reasoning

(Da’at: Knowledge, as a fusion of Chokhmah and Binah)

Chesed: Loving Kindness or Mercy

Gevurah: Strength/Severity, (sometimes Din, Judgement, or Pachad, Fear)

Tiferet: Beauty/Harmony, is associated with balance of the Tree of Life

Netzach: Eternity/Endurance

Hod: Splendor/Glory

Yesod: Foundation (as in, foundation of reality)

Malkhut: Kingdom/Sovereignty

You’ve probably noticed by now that while we are claiming that the concept of the sefirot applies to the elemental system in Genshin, there are 10 sefirot and only 7 elements (for now). Fortunately for us, the Kabbalists love metaphors and categories. In addition to the sefirot representing the procedure used to ‘emanate’ and create the world, there are other methods of interpretation that further subdivide and rank the sefirot. For example, one metaphorical interpretation of the Tree of Life assigns each of the sefirot to a part of the human body.

In some Kabbalistic traditions of interpreting the tree, the 10 sefirot are divided into two categories: Intellect (Keter, Binah, Chokhmah) and Emotions (they’re actually more like character traits), which contains the remaining seven. These categories are meant to parallel how the soul is also divided into the intellect and emotional components. The first three sefirot are also referred to as the “three mothers,” because they are the source of the lower seven [5].

Having a group of seven sefirot is very convenient for comparing their traits to the elements and their ideals, but what about the role of the higher three in Genshin worldbuilding? This next section requires a bit more conjecture than some other comparisons here.

The source of all elemental energy in Teyvat, whatever that actually is, could be compared to Keter (crown), the most hidden and incomprehensible of the sefirot. (Big stretch, but think of the crowns over the Irminsul trees in domains.)

Next, we have the Ley Lines, which contain dreams and memories (these are basically the same in Teyvat, see Dream Solvent description), and these can be compared to Binah (understanding/reasoning) and Chokhmah (wisdom). During the Sumeru Archon Quest, Rukkhadevata says that dreams are the source of the wisdom she upheld as her ideal. Memories play an important role in discerning the truth of the world, as the traveler has now found themselves to be the only person to remember certain people/events, and has been told to trust their memories rather than what they can see.

Comparison of the 'Lower' Sefirot to the Genshin Elements and Their Ideals

Chesed (loving-kindness); Cryo (unknown, theorized to be love)

The Cryo Archon’s ideal is theorized to be love, as it’s the only characteristic mentioned in relation to her in the Travail trailer. Wanderer’s voiceline about her directly mentions love and describes her as being kind and benevolent, while Childe describes her as extremely gentle. These are the characteristics of Chesed, which represents the trait of completely selfless love: the all forgiving, all giving love of a god towards their creations. When it comes to the Cryo element itself, two things are worth mentioning: one is the way that all of Snezhnaya is perpetually covered in snow, as if this were the (ironic) physical expression of the Tsaritsa’s love blanketing them. The second is the promise of a world-encompassing snowstorm that will envelop everything as the Fatui advance on their war against Celestia. Although it’s hard to find one absolute constant in Vision granting stories, it’s notable that most Cryo users got their Vision at a moment when they had to selflessly be there for others (Diona, Chongyun, Mika), or after a decisive moment where they put aside their personal comfort for an ideal that would result in benefit for others (Kaeya, Eula, Layla).

Gevurah (Severity); Hydro (Justice)

Gevurah is associated with divine judgment, the kind that punishes humanity and causes world-altering catastrophes like the flood or the expulsion of Adam and Eve from the Garden of Eden. The Hydro Archon organizing her nation around a Court that attempts to judge both deities and humans parallels this. In a more positive sense, Gevurah is also related to moral judgment that allows one to tell good from evil. Likewise, Hydro in-game is often associated with purity and separation of clean and unclean matter. When it comes to Hydro Vision wielders, one common characteristic is that they all live by a personal ethical code, and their commitment to it is what granted them their Vision.

Tiferet (Beauty/Harmony); Anemo (Freedom)

Tiferet balances the other sefirot on the tree and has direct connections to almost all of them (except for Malkut). Similarly, Anemo can facilitate many elemental reactions via its Swirl reaction. In our opinion, something almost all the Anemo characters share is that their moment of receiving a Vision coincides with a moment of balance and harmony with themselves or their environment. See Jean and Kazuha’s Vision stories and the cutscene where Scaramouche/Wanderer gets his Vision. As an aside, comparing harmony to Anemo is funny because Venti is a bard and harmony is also a musical term: in music theory, harmony is the way we analyze the interactions between different voices that can be heard at the same time.  

Netzach (Eternity); Electro (Eternity)

The quality of “Eternity” in Netzach is related to victory against enemies, referring to eternity as being the most powerful combatant remaining among defeated adversaries. Likewise, in Genshin the story of the Electro Archon features many battles during the Archon War where Ei and Makoto ended up victorious. As for Electro users tend to have their Vision granted at a moment when their ambition “defeated” the obstacles of reality, as was the case with Fischl, Kuki and Lisa. Cyno’s Vision story makes sense when you compare it to the illumination of Buddha during meditation, and how this was victory over the temptation of the demon Mara.

Hod (Glory); Pyro (War)

Natlan and its Pyro Archon are possibly the most mysterious of all the regions, so we can only speculate. We know that the Pyro Archon is called the God of War, and that the Pyro Gemstone mentions battles, pilgrimages and truth. The sefira of Hod, translated as Glory or Splendor, is linked to being able to connect with God and therefore also associated with prophecy (as in the way a human can carry a message from God). In the Travail trailer, the Pyro Archon tells the traveler that “the rules of war are woven in the womb.” It's also theorized Natlan will be based on Mexica culture (where sacrifice of both enemies and self sacrifice was a way to connect with the gods) and via Iansan's name, the Caribbean diaspora version of Yoruba religion (where many rites involve the gods making themselves present in the material world). 

Yesod (Foundation); Dendro (Wisdom)

Back when we started to think about this theory during version 2.8, we decided on Yesod largely via process of elimination. One piece of our rationale was that in the Jewish tradition, each of the lower seven sefirot are used to represent a primary personality trait of seven archetypal figures in the Torah. The person related to Yesod is Joseph, who is well known for his prophetic dreams, and because of the events of the Golden Apple Archipelago, we decided that was close enough. However, the 3.x version confirmed that a) Irminsul did actually exist, b) Dendro as an element has a deep relationship with the tree, with the Dendro Archon acting as its avatar, c) the ideal of wisdom as both Dendro Archons interpreted it has a lot to do with dreams, and d) Irminsul and the Ley Lines act as the foundation for how reality is perceived in Teyvat. Yesod is also associated with biological life, as it represents the reproductive organs in the human body scheme of the sefirot.

Malkut (Kingship); Geo (Contracts)

Malkut is associated with the connection between the spiritual "above" of the Tree of Life and the concepts it contains, and the "below" of the material world, where these concepts manifest into material reality. For this reason, Malkut is associated with the earth [6]. In many Geo item descriptions, like the Geo Hypostasis drop or Albedo's elemental skill, the motif of geo trying to reach the sky is a constant. From a religious POV, the relationship between the divine and humans living in the material world has also been one of "covenants," or "pacts", in a similar way to how the Geo Archon is the God of Contracts. Furthermore, contracts are the basis to have a working state (government), and a kingdom is one of the first forms of a state. Malkut also being related to earth and everything material parallels how Geo is an element that works in making constructs. Geo Vision users are likewise involved in making or maintaining structures, like the Knights of Favonius is for Noelle, or the tradition of alchemy is to Albedo, as well as opera to Yunjin and in a way, even the Oni identity for Itto.

The Origin of Evil and Why Irminsul is Upside Down

Tighnari tells us that Irminsul is a tree that “grows downward rather than upwards,” or in other words, it’s upside down. This isn’t the only time that we’ve encountered things in Teyvat being described as upside-down or mirrored, and as it turns out, there is a similar scenario described in Kabbalah. Throughout Kabbalistic discussions on the origin of evil in the world (both material and spiritual), a central idea developed is the existence of a mirrored or inverse Tree of Life that forms the demonic realm of evil. The Zohar, a foundational work of Kabbalistic literature, spends a considerable time discussing the origins of evil - there are more than 5 creation myths for the concept of evil! Two of these myths describe the formation of an inverse Tree of Life, called the Sitra Achra (literally “other side”). This tree is constructed out of corrupted fragments of divinity that did not make it through the creation process, and therefore became evil forces [7]. Evil is typically represented as either a shard (like of broken pottery) or as a husk/shell (Qlippoth in Hebrew). Sound familiar? We actually have an enemy with this name in-game; the "shadowy husks" (the CN name for these enemies literally translates to "empty shell"). 

Unlike the very well defined 10 sefirot of the Tree of Life, Kabbalists don't agree about the identities or number of the demons that form the Sitra Achra. Some names for these demons are consistent; such as  Lilith, Samael, and Asmodeus, who make a sort of "mother, father, son" trio. As for the rest, scholars generally agree that Kabbalists blended traditions from nearby cultures depending on where they lived, leading to Arabic, Spanish and Germanic legends mixing into the Jewish tradition [8]. There's a strong possibility Hoyoverse did something similar and filled in the missing names with the names of the demons of the Ars Goetia, creating a system where the mirrored sefirot are “ruled” by demon gods, aka, the Archons. This implies that the reason Teyvat is upside down is because it is actually on the “other side.”

Neuvillette, About Us: Witness: Since you hail from beyond the stars, I invite you to be my witness as I judge this upended world…”Though we live in a world of disarray, I shall undertake to restore all that has been broken”. 

[Fun Fact: The Zohar describes the construction of the Sitra Achra as a series of knots that arrange the demonic equivalent of sefirot, called either crowns or “breaths,” into a mirrored Tree of Life configuration [7]. ]

The primary goal of the Sitra Achra is to steal and absorb the divine energy of the Tree of Life to maintain its existence, in the hopes of gaining enough energy to destabilize the system [9]. The way Genshin's Archons use their Gnoses is similar to this system. In the Flower of Paradise Lost artifact lore, the Goddess of Flowers explains to Deshret and Rukkhadevata that when the Seelie race was disgraced, they lost their connection to Heaven and their power of "enlightenment". Later, Celestia would facilitate the Archon War with the promise that each winning god would be granted a Gnosis that would give them exceptional power. Both Nahida and Venti have described the Gnoses as being a very advanced tool that concentrates elemental energy. So far, Archons have had inherent elemental powers related to their nature, but when it comes to using large amounts of elemental energy through their Gnoses, they aren't creators but channelers of it, just at a much larger scale than humans who have Visions. Edit: and yes, there is the most recent revelation about the origin of the Gnoses that is extremely relevant to this comparison, but deserves its own space to be properly expanded on.

However, this doesn't mean Teyvat is condemned. Just as the Traveler has slowly been setting the chaos of elemental energy back into order (by, for example, returning the elemental Oculi to the Statue of the Seven, among many other things), so too is there a concept in Kabbalah describing the importance of righting the wrongs of the universe so that the sefirot are stable and creation is in harmony with the divine. This is called Tikkun Olam, or the repairing of the world.

Stay tuned for part 2 where we go into wayyyyy more detail about what this means for the Traveler's journey through Teyvat! 4.2 Edit: and of course will we will be talking about the most recent Gnosis revelation, as well as the Narzissenkreuz Ordo antics :D

References:

https://www.chabad.org/library/article_cdo/aid/170308/jewish/What-is-Kabbalah.htm

https://en.wikipedia.org/wiki/Hermetic_Qabalah

Kabbalah - Origins of the Sefirot and Tree of Life - Isaac the Blind Saggi Nehor & Azriel of Gerona

Mystical Concepts in Chassidism - Schochct, Jacob Immanuel, chapter 2

  Mystical Concepts in Chassidism - Schochct, Jacob Immanuel pg 66-67, Tanya ch. 3

Rebbe Nachman of Breslov, Likutey Moharan I, 12:1 via Wikipedia

The Origins of the Klippot / Qliphoth & Sitra Achra in the Zohar - Kabbalah on the Problem of Evil

https://www.jewishvirtuallibrary.org/demons-and-demonology

9. Evil in Early Kabbalah - Emanations of the Left Hand Side - Origins of the Qliphoth / Klippot

[mysticstronomy]

WHAT IS OUR UNIVERSE SURROUNDED BY??

Blog#464

Saturday, December 21st, 2024

Welcome back,

The question of whether anything exists beyond the universe is one that stretches the limits of human comprehension and current scientific understanding. It touches upon the very nature of the cosmos, the origins of everything, and the limits of physical reality. The universe, by definition, encompasses all of space and time, including all forms of energy, matter, and the physical laws that govern them. However, the inquiry into what, if anything, lies beyond the universe delves into both the realms of cosmology and philosophy.

From a cosmological standpoint, the question is inherently linked to the nature and shape of the universe. Current models based on the theory of general relativity and observations of the cosmic microwave background suggest that the universe is flat and infinite. In an infinite universe, there is no “beyond,” as space extends endlessly. However, if the universe is finite but unbounded, like the surface of a sphere, one could still not step “outside” it, as it curves back onto itself.

The concept of the observable universe further complicates this question. The observable universe is limited by the speed of light; we can only see as far as light has had time to travel since the Big Bang, approximately 13.8 billion years ago. Beyond this observable limit lies more universe that we cannot see. The extent of the universe beyond our observational limits remains a subject of scientific speculation and exploration.

One of the most intriguing ideas in modern physics is the multiverse theory, which posits that our universe may be just one of many universes within a larger multiverse. Each universe within the multiverse could have its own set of physical laws, constants, and properties.

The concept of a multiverse arises from various theoretical frameworks, including inflationary cosmology and string theory. If the multiverse exists, then “beyond” our universe could mean neighboring universes with potentially different dimensions and physical realities. However, the multiverse theory remains highly speculative and, by its very nature, may be beyond the reach of direct empirical observation.

Philosophically, the question of what lies beyond the universe touches upon the nature of existence, the concept of infinity, and the origins of everything.

Different philosophical traditions have contemplated the cosmos’s nature, often arriving at varying conclusions about the universe and its boundaries. Theological perspectives may posit the existence of spiritual realms or deities existing outside the physical confines of the universe, adding another layer to the discourse on what “beyond” might entail.

The human quest to understand the universe is bounded by the limitations of our senses, technology, and the conceptual frameworks we use to make sense of the cosmos.

Our understanding of the universe has expanded dramatically over the centuries, yet each answer brings new questions. The inquiry into what lies beyond the universe challenges the very limits of scientific inquiry and human imagination.

In conclusion, the question of whether anything exists beyond the universe remains one of the most profound and speculative in science and philosophy. It challenges our understanding of the cosmos, the nature of reality, and the limits of human comprehension. Whether through the lens of cosmology, the theoretical frameworks of physics, or philosophical contemplation, the exploration of what lies beyond the universe continues to captivate and intrigue, pushing the boundaries of knowledge and imagination.

Originally published on https://medium.com/

COMING UP!!

(Wednesday, December 25th, 2024)

"IS THERE WATER IN SPACE??"

[catgirl-lucy]

Forcing & Independence of the Continuum Hypothesis

My favourite result in maths is probably the independence of the continuum hypothesis. In this post, I aim to explain forcing and why the continuum hypothesis cannot be proven in ZFC. The continuum hypothesis (CH) is the statement that there is no cardinal number between ℵ₀ and 2^ℵ₀. When forcing, you start with a model V of ZFC and extend it to a model V[G] by adding some object G, in such a way that V[G] satisfies the axioms of ZFC but also the existence of G, with the intention of showing that G can exist without contradicting the axioms of ZFC. For example, when starting with a model V of ZFC + CH and G contains information for how to build ℵ₂ distinct reals, V[G] would satisfy the existence of ℵ₂ many reals and thus not satisfy CH.

I assume everyone who reads this knows the theory ZFC and has basic understanding of ordinal and cardinal numbers.

A theory T is a set of axioms in first order logic. A proof in T is a sequence φ₁ .. φₙ of formulas such that each formula is an axiom of T or follows logically from previous formulae in the sequence, this proof is said to prove the formula φₙ. For a formula φ, we write T ⊦ φ to mean that there is a proof φ₁ .. φₙ (φ = φₙ) of φ in T. T is inconsistent if it proves the always false statement ⊥, T is consistent if it does not prove this statement. We write Con(T) for “T is consistent”. T ⊬ φ is equivalent to Con(T + ¬φ), so to show that ZFC cannot prove or disprove CH, we want to show Con(ZFC + ¬CH) and Con(ZFC + CH), assuming that ZFC is consistent.

To show that Con(ZFC) implies Con(ZFC + ¬CH), we start with a model V of ZFC and add ω₂ many reals (subsets of ω) to it. However, we don't have anywhere to get those ω₂ reals from ¯\(˙˘˙)/¯ We can't get them simply out of V as that'd mean V already has at least ω₂ many reals. What we do is assume the existence of a larger universe V⁺ that V lives in. Usually, when forcing, the existence of the larger universe V⁺ is implicit, but I state its existence explicitly to avoid confusion.

We can try to define a theory ZFC⁺ extending ZFC by adding a constant symbol V (the universe of ZFC⁺ is called V⁺ rather than V) and the axiom “V is a model of ZFC”, however, even without assuming nice properties of V like it being a well-founded model, the consistency of ZFC⁺ is stronger than that of ZFC, but ideally, we want to show that Con(ZFC + ¬CH) follows from Con(ZFC), not Con(ZFC⁺).

Luckily, ZFC already sort-of proves the existence of models of ZFC. To be more precise, for every finite fragment t of ZFC, ZFC proves that there is a model of t. However, ZFC does not prove the statement ‘for all finite fragments t of ZFC, there is a model of t’! ∀n T ⊦ φ(n) and T ⊦ ∀n φ(n) are two different statements, it's important to know the distinction!

Let t be a finite fragment of ZFC, aiming to show that ZFC ⊦ ∃M M ⊧ t (⊧ is the symbol for ‘satisfies’ or ‘is a model of’). We'll build the model M by starting with the empty set M_0 = ∅ and adding more and more elements to it until it satisfies ZFC. Since t is a finite fragment of ZFC, we have that V ⊧ t. If t were to be infinite, V ⊧ t would be an infinite conjunction of the formulas in t, and infinite formulas don't exist in first order logic, hence we assume t to be finite. To build the next model M_1, for every formula of the form ∃x φ(x) that t proves, we have that V ⊧ ∃x φ(x), and thus there is some x such that φ(x). We add some x that satisfies φ(x) to M_1 for every such formula ∃x φ(x). We do the same for M_2, but instead of adding x for each ∃x φ(x), we add some x for every y in M_1 and every formula of the form ∃x φ(x,y) that t proves. We do the same with M_3: we add some x satisfying φ(x,y) for every y ∈ M_2 and every formula of the form ∃x φ(x,y) that t proves. We continue this infinitely, and we then define M = ⋃{M_n | n ∈ ℕ} as the union of all M_n. By induction on the complexity of formulas, we can show that M ⊧ φ for every φ such that t ⊦ φ, proving this is left as an exercise to the reader.

Since there are only countably many formulas, every M_n must be countable, and so their union, M, is countable as well. We also have that M is a standard model: it has sets x and uses the real membership relation as its own membership relation. Besides showing that for every finite fragment t of ZFC, ZFC proves that there exists a model of t, we have shown that we can assume this model to be standard and countable.

The construction of the model M we have performed is called a Skolem hull. Usually, when taking Skolem hulls, we take all formulas φ that the original model (in this case, V) satisfies instead of only those that are proven by some theory t, but we couldn't do that as there are an infinite amount of models that V satisfies and a proof in ZFC may only use a finite number of axioms. Skolem hulls are my second favourite thing from model theory and it could be useful to have it in your toolbox.

Although M is a standard model of the theory t, it isn't transitive. A transitive set is a set X such that, for every x ∈ X, we have x ⊂ X. It's usually easier to work with transitive models. We can turn M into a transitive model by the use of a Mostowski collapse. You can read the Wikipedia article on it if you want to know what that is, this is a post about forcing, not Mostowski collapses and Skolem hulls.

Instead of adding the axiom ‘V is a model of ZFC’ to ZFC⁺, we can add, for each individual axiom φ of ZFC, the axiom ‘V ⊧ φ’. And, as we have shown above, we can also add the axiom ‘V is countable and transitive’. Since proofs in ZFC⁺ may only use a finite amount of axioms, they may only use a finite amount of axioms of the form ‘V ⊧ φ’, so ZFC⁺ thinks that V satisfies finite fragments of ZFC without realizing it satisfies the whole of ZFC: it might think there is a very long formula φ that V doesn't satisfy while, in reality, such a formula would be infinitely long and doesn't actually exist.

One theorem from logic that we'll use is the compactness theorem. This theorem states that, for a theory T of first order logic, if T is inconsistent then a finite fragment of T is inconsistent. Contrapositively, if every finite fragment of T is consistent, then T must be consistent as well. A proof of this theorem is quite easy.

Another important lemma we'll use is that if a theory T proves a finite theory S is consistent, then S must be consistent. If S were to be inconsitent, then there must be some proof φ₁ .. φₙ of ⊥ in S, and T would prove that φ₁ .. φₙ is a proof of ⊥ as checking if a proof is correct is as simple as just running an algorithm. Thus, for a finite fragment S of ZFC+¬CH, if ZFC⁺ proves S is consistent, then S must be consistent. And if ZFC⁺ proves S is consistent for every finite fragment S of ZFC+¬CH, then ZFC+¬CH must be consistent by compactness.

Since V is countable in V⁺, the ω₂ of V, written ω₂^V, is a countable ordinal in V⁺ while the ω₂ of V⁺, written ω₂^V⁺, doesn't exist in V. I'll work in the universe V unless otherwise specified, so ω₂ refers to ω₂^V rather than ω₂^V⁺, and countable means countable in V rather than countable in V⁺. For some object x and a model M, x^M refers to the interpretation of x in M.

So now that we have the little universe V and the big universe V⁺, we want to add ω₂ reals to V. Since V is countable in V⁺, there are a lot of things outside of V in V⁺. For example, P(ω) ∩ V is countable in V⁺, while the P(ω) of V⁺ is uncountable in V⁺, meaning that P(ω) \ V must be uncountable, so V is missing a lot of reals that can be added into V. However, if we simply take a set X ⊂ P(ω)^V⁺ such that V thinks X has cardinality ω₂, and then add it to V by just adjoining it like so: V ∪ {X}, this new model is no longer a model of ZFC. It has a universe V, but also just another object X adjoint to it, and things like X ∪ ℕ, X × X, etc, don't exist, while they should for V ∪ {X} to be a model of ZFC.

Thus, instead of adding a single new element X, forcing aims to add an object G in such a way that the axioms of ZFC are still satisfied. It does this through the use of names. A name is an object in V that describes an object in the extended universe V[G], but without a way to interpret the name in V, those objects that exist in V[G] don't yet exist in V. The object G gives a way to interpret the names in V, and interpreting every name in V through G gives the new model V[G]. Explaining what that means exactly requires the definition of a forcing poset, which I'll now explain.

A partial ordered set (poset) is a structure (P,≤) with a set P and a binary relation ≤ on P, such that:

≤ is reflexive: x ≤ x for all x ∈ P.

≤ is transitive: if x ≤ y and y ≤ z then x ≤ z for all x,y,z ∈ P.

≤ is antisymmetric: if x ≤ y and y ≤ x then x = y for all x,y ∈ P.

Two elements x,y ∈ P are compatible if there is some z such that z ≤ x and z ≤ y. x and y are incompatible if no such z exists. A forcing poset is a poset P with the additional axioms:

There is a greatest element 1 ∈ P.

For every x ∈ P, there are y,z ∈ P such that y ≤ x, z ≤ x and y and z are incompatible.

The last axiom is called the splitting condition. Members of a forcing poset P are called forcing conditions. x ≤ y is read as ‘x is stronger than y’ or ‘x extends y’. Forcing conditions can be thought of as statements that can be true or false, these statements say something about the object being added, where the greatest element 1 is a statement that is always true. The forcing poset that we'll focus on in this blog post is called Cohen forcing. Forcing conditions are finite partial functions from ω₂ × ω to {0,1}. That is, functions from a finite subset of ω₂ × ω to the set {0,1}. For forcing conditions p and q, p ≤ q iff p is a function extension of q, i.e. dom(p) ⊃ dom(q) and p(α,n) = q(α,n) for all (α,n) ∈ dom(q). A forcing condition p: ω₂ × ω ⇀ {0,1} says something about the object g: ω₂ × ω → {0,1} that is being added, namely, that g(x) = p(x) for all x ∈ dom(p). For every α < ω₂, {n | g(α,n) = 1} will be a new real in the new model V[G], meaning that there will be ω₂ many new reals and CH will break.

For a forcing poset P, a P-name is a set of tuples (σ,p) where σ ∈ V^P is a P-name and p ∈ P is a forcing condition, this set may be empty. Alternatively, the class of P-names, V^P, can be defined by induction:

V^P_0 = ∅.

V^P_α+1 = P(V^P_α × P) for an ordinal α.

V^P_α = ⋃{β<α} V^P_β for limit ordinal α.

Then, V^P = ⋃{α ∈ Ord} V^P_α is the class of P-names. A P-name {(σ,p)} means ‘this set contains σ iff p is true’. Thus, for a set x, we can define a P-name &x for x as follows &x = {(&y,1) | y ∈ x} as 1 is always true. We can also define the set of all true forcing conditions as &G = {(&p,p) | p ∈ P}, which contains p iff p is true.

A way to decide which forcing conditions are true and which are false is done using a filter. A filter F on P is a subset F ⊂ P such that:

1 ∈ F.

If x ∈ F and x ≤ y, then y ∈ F.

For all x,y ∈ F, there is some z ∈ F such that z ≤ x and z ≤ y.

A filter decides what forcing conditions are true and which are false: members of the filter are true forcing conditions, while things that aren't in the filter are false. The first axiom of a filter, 1 ∈ F, states that the statement 1 is true, the second axiom states that x is true and x implies y, then y is true, and the third statement states that no members of the filter contradict each other (i.e. none are incompatible).

However, not any filter will do. If the filter F is already in the model V, then we don't add anything new to V. It might also be possible to break axioms of ZFC such as comprehension with certain filters. Because of this, we use a special filter called a generic filter.

A forcing poset P has a topology. An open set in P is a set O ⊂ P that is downwards closed, i.e. for every x ∈ O and every y ∈ P such that y ≤ x, we have y ∈ O. A set D is dense if it meets all non-empty open sets. In P, that means that D is dense iff ∀x ∈ P ∃y ∈ D y ≤ x. For a family D of dense subsets of P, a filter G ⊂ P is D-generic iff G meets all dense D ∈ D. One important theorem used to construct generic sets is the Rasiowa-Sikorski lemma. This lemma states that, if P is a forcing poset, p ∈ P is a forcing condition, and D is a countable family of dense subsets of P, then there is a D-generic filter G on P that contains p. A proof of this lemma is left as an exercise to the reader. Since V is countable in V⁺, we can apply the Rasiowa-Sikorski lemma to it: we can define a V-generic filter as a filter that is D-generic filter for D = {D ∈ V | D is a dense subset of P}, and since D is countable in V⁺, such a generic filter G exists in V⁺. I'll often call a V-generic filter simply a generic filter.

Given a forcing poset P ∈ V, a generic filter G ⊂ P on P and a P-name σ ∈ V^P, the interpretation of σ by G is defined as σ^G := {τ^G | ∃p ∈ G (τ,p) ∈ σ}. One can verify that, for x ∈ V, we have &x^G = x and &G^G = G for &G = {(&p,p) | p ∈ P}. V[G] is defined as V[G] = {σ^G | σ ∈ V^P}. Now, all we have to do is verify that V[G] is indeed a model of ZFC and, when P is Cohen forcing, that V[G] satisfies ¬CH.

Im eepy. I'll do that another day -.- Good night.

Hi. I hope you slept well. I'll now continue with explaining forcing.

For a forcing condition p ∈ P, P-names τ₁ .. τₙ and a formula φ, p forces φ(τ₁ .. τₙ), denoted p ⊩ φ(τ₁ .. τₙ), if for all generic G ⊂ P with p ∈ G, we have V[G] ⊧ φ(τ₁^G .. τₙ^G). The following three lemmas are important in forcing:

Definability For every formula φ, there is a formula ψ such that for all forcing conditions p and all P-names τ₁ .. τₙ, p ⊩ φ(τ₁ .. τₙ) iff V ⊧ ψ(p,τ₁ .. τₙ). I.e. ‘p forces φ(τ₁ .. τₙ)’ is definable in V.

Coherence If p ⊩ φ(τ₁ .. τₙ) and q ≤ p, then q ⊩ φ(τ₁ .. τₙ).

Truth If V[G] ⊧ φ(τ₁^G .. τₙ^G) then there is some forcing condition p such that p ⊩ φ(τ₁ .. τₙ). That is, a statement is true iff it is forced.

I encourage you to try proving these lemmas yourself. Coherence is quite easy, but the other two might be more difficult to prove. I'll give a proof for definability and truth.

First, we'll define ⊩* by induction on the complexity of formulas. We'll start with atomic formulas. When does p force σ ∈ τ? One naive guess might be if ∃q ≥ p (σ,q) ∈ τ, however, this doesn't quite work. There might be a P-name ρ such that σ ≠ ρ, yet p ⊩ σ = ρ and ∃q ≥ p (ρ,q) ∈ τ but ∄q ≥ p (σ,q) ∈ τ. Thus, we define p ⊩* σ ∈ τ as ∃(ρ,q) ∈ τ p ⊩* σ = ρ.

So now we need to define p ⊩* σ = τ. By the axiom of extensionality, two sets are equal if they contain the same elements. Thus, we can define p ⊩* σ = τ as ∀ρ ∈ V^P p ⊩* "ρ ∈ σ" ⇔ p ⊩* "ρ ∈ τ". This might seem self-referential, as we define equality in terms of membership, which is itself defined in terms of equality, but we can define it inductively as the rank of the names always decrease. The rank of σ is the smallest ordinal α such that σ is in V^P_{α+1}. The quantor '∀ρ ∈ V^P' currently ranges of all P-names (thus, also those with higher rank than σ or τ), but we can fix that by defining ⊩* ≠ instead of ⊩* =, and then we can define p ⊩* σ = τ as p ⊩* ¬σ ≠ τ.

p ⊩* σ ≠ τ iff (∃(ρ,q) ∈ τ q ≥ p ∧ p ⊩* ¬ρ ∈ σ) ∨ (∃(ρ,q) ∈ σ q ≥ p ∧ p ⊩* ¬ρ ∈ τ).

So now we can define ⊩* ¬, ⊩* ∨ and ⊩* ∃ as follows:

p ⊩* ¬φ(τ₁ .. τₙ) iff ∀q ≤ p ¬q ⊩* φ(τ₁ .. τₙ).

p ⊩* "φ(τ₁ .. τₙ) ∨ ψ(τ₁ .. τₙ)" iff p ⊩* "φ(τ₁ .. τₙ)" ∨ p ⊩* "ψ(τ₁ .. τₙ)".

p ⊩* ∃x φ(x, τ₁ .. τₙ) iff ∃σ ∈ V^P p ⊩* φ(σ, τ₁ .. τₙ).

This internal definition of forcing is almost complete. However, what if a formula φ is forced by p, not because φ is immediately apparent, but because the only forcing conditions that extend p immediately force φ? To give a more concrete example, suppose σ = ∅, τ = {(σ,p), (σ,q)} are P-names, and p = {((0,0),0)} and q = {((0,0),1)} are (incompatible) forcing conditions in Cohen forcing. Then, we don't have 1 ⊩* σ ∈ τ, however, σ ∈ τ is still forced by 1 as any generic filter that contains 1 also contains p or q. Thus, the final step of the definition of forcing is p ⊩ φ(τ₁ .. τₙ) iff {q | q ⊩* φ(τ₁ .. τₙ)} is dense below p, equivalently, p ⊩ φ(τ₁ .. τₙ) iff p ⊩* ¬¬φ(τ₁ .. τₙ).

The last part of the proof of definability is checking that our internal definition of forcing is correct. This is left as an exercise to the reader.

Now I'll give a proof of truth. Although in no point in the proof of definability genericity is relevant, it is very important for truth. Truth states that for a formula φ and P-names τ₁ .. τₙ, if V[G] ⊧ φ(τ₁ .. τₙ), then there is some p ∈ G so that p ⊩ φ(τ₁ .. τₙ). That is, a formula is true if and only if it is forced.

For a statement φ and P-names τ₁ .. τₙ, we can define the set D_φ = {p | p ⊩ φ(τ₁ .. τₙ) ∨ p ⊩ ¬φ(τ₁ .. τₙ)}. Thus, D_φ is the set of forcing conditions that decide φ. We can verify that D_φ is a dense set: we have 1 ⊩ φ ∨ ¬φ as φ ∨ ¬φ is always true, this is equivalent to 1 ⊩* ¬¬(φ ∨ ¬φ) when using the internal definition, i.e. {p | p ⊩* φ ∨ ¬φ} = {p | p ⊩* φ ∨ p ⊩* ¬φ} is dense, and since D_φ is a superset of this set, it must be dense as well. Since D_φ is dense and G is generic, G ∩ D_φ must be non-empty, so some p ∈ G must force φ or force ¬φ. Thus, every formula that is true in V[G] is forced by some forcing condition in G.

We can use definability, coherence and truth to prove that V[G] ⊧ ZFC. I'll leave this as an exercise to reader, cuz... why not ¯\(˙˘˙)/¯ Extensionality and foundation hold in V[G] as V[G] is a transitive model of ZFC, union and infinity aren't too difficult to prove, separation and powerset might be a bit more tricky, the argument for why V[G] satisfies replacement is similar to that of separation, and choice might be a little bit more difficult than the others. I'll give a proof for why V[G] satisfies the axiom lemma of pairing so you have some inspiration for your proof.

Given sets x and y in V[G], we want to show that {x,y} is a set. x and y have P-names, let's call them σ and τ. We can now define a P-name ρ := {(σ,1), (τ,1)}. We can see that ρ^G = {σ^G, τ^G} = {x,y} ∈ V[G], and thus V[G] satisfies the lemma of pairing.

So now that we know V[G] is a model of ZFC (at least, for every finite fragment t of ZFC, ZFC⁺ proves that V[G] is a model of t), we now need to show that V[G] ⊧ ¬CH when using Cohen forcing. We want to add more than ω₁ reals, e.g. ω₂ reals, to the model V. We thus want G to encode information for a set of ω₂ distinct reals. Since a real is an infinite sequence of 0s and 1s, we thus want a ω₂ × ω table of 0s and 1s so that none of the rows are equal. In Cohen forcing, the forcing conditions encode partial information about this ω₂ × ω table. The forcing conditions are finite partial functions from ω₂ × ω to {0,1}, i.e. functions with finitely many pairs (α,n) for ordinals α < ω₂ and natural numbers n as domain, that maps each (α,n) in its domain to either 0 or 1. For forcing conditions p and q, we have p ≤ q iff p is a function extension of q, i.e. dom(q) ⊂ dom(p) and p(α,n) = q(α,n) for all (α,n) ∈ dom(q). A generic filter G on P would thus consist of finite partial functions p: ω₂ × ω ⇀ {0,1} that together form a function g: ω₂ × ω → {0,1} defined as g = ⋃G. For each ordinal α, r_α = {n | g(α,n) = 1} ⊂ ω is a real in the model V[G]. We can use the genericity of G to show that all reals r_α are distinct: suppose we have r_α = r_β for some α ≠ β. Then, there must be some p ∈ G such that p ⊩ r_α = r_β. However, no such p can exist: p may only contain finite information about r_α and r_β, but r_α = r_β means that g(α,n) and g(β,n) are equal on all, and thus infinitely many, n. We can define a dense set D_{α,β} = {p ∈ P | ∃n p(α,n) ≠ q(β,n)}, it's easy to check that this set is dense for α ≠ β, and thus G ∩ D_{α,β} is non-empty. This means that all reals r_α are indeed distinct reals. We thus have added ω₂ distinct reals to V.

But we're still missing something. Can you spot it? No..? Oh, okay. Don't worry. I'll tell you. We have added ω₂^V reals, but we need ω₂^V[G] reals, and nothing so far tells us that ω₂^V and ω₂^V[G] should be equal!

Luckily, they are equal. Here is proof:

Cohen forcing satisfies the countable chain condition. A (strong) antichain A ⊂ P is a set of forcing conditions that are pairwise incompatible, i.e. ∀p,q ∈ A p ≠ q → p ⊥ q. Usually, the word antichain is used to refer to sets of pairwise incomparable elements, but incomparability is kinda useless when forcing as opposed to incompatibility (two objects x and y in a poset are incomparable iff x ≰ y and y ≰ x). The κ-chain condition (κ-c.c) states that, given any antichain A ⊂ P, the cardinality of A is <κ. The countable chain condition (c.c.c) is the ω₁-chain condition, i.e. all antichains are countable.

If P satisfies the c.c.c, then for every function f ∈ V[G] from some D ∈ V to V, there is a function F ∈ V[G] from D to V such that, for every x ∈ D, F(x) is countable and f(x) ∈ F(x). I.e. functions in V[G] can be approximated by "countable covering functions" in V (‘countable covering function’ is not a term, I just made that up :p).

The above lemma can be used to show that, when P has the countable chain condition, if κ is an uncountable regular cardinal in V, then κ must also be uncountable regular in V[G]. In otherwords, for any uncountable regular cardinal κ, P does not collapse κ (P collapses κ if κ is no longer a regular cardinal in the forcing extension V[G]). Proving these three things ((i) Cohen forcing has the c.c.c, (ii) if P has the c.c.c then for every function f: D → V in V[G] for D ∈ V has a "countable covering function" and (iii) if P has the c.c.c then it collapses no regular cardinals) are left as an exercise to the reader.

And that completes the proof of Con(ZFC) → Con(ZFC + ¬CH). Good night everyone! mi wile lape -.- If you have trouble understanding something in this blog post, or you have some other questions, you can tell me! Holidays are starting for me now so I currently have a lot of free time.

I was planning to make an introduction to set theory, but that post isn't going that well. I don't know what my next maths post will be about.

Bye!~

[xyymath]

📊 The Mathematics of Understanding Society: Statistics in Social Sciences

1. Reliability: Quantifying Consistency

Reliability ensures that statistical results are consistent across time and methods. It is measured through techniques like:

Test-Retest Reliability: Same participants, repeated measures.

Inter-Rater Reliability: Agreement between multiple observers.

Internal Consistency: Correlation of test items, often measured using Cronbach’s Alpha.

Formula for internal consistency:

where N is the number of items, cbar is the average covariance between item pairs, and v is the total item variance.

2. Validity: Ensuring Relevance

Validity measures whether data reflects the intended concept. Types include:

Construct Validity: Evaluates how well a test aligns with theoretical concepts.

Criterion Validity: Measures correlation with related, independent outcomes.

Content Validity: Assesses if the test covers the full scope of the concept.

3. Sampling Theory: Representing Populations

In statistics, sampling bridges finite data and infinite populations. Randomized methods minimize bias, while stratified or cluster sampling improves efficiency. The Central Limit Theorem (CLT) guarantees that sampling distributions approximate normality for large sample sizes.

where SE is the standard error, sigma is the population standard deviation, and n is the sample size

4. Minimizing Bias

Bias skews results, reducing reliability and validity. Statistical techniques such as blind sampling, control groups, and adjustments for confounders mitigate these effects. Weighted averages or regression adjustments help correct sampling bias.

5. Significance Testing: Inference in Social Sciences

Statistical tests like t-tests and ANOVA assess relationships in data. P-values determine significance, while effect sizes (e.g., Cohen’s dbar) quantify practical importance.

Example: For comparing group means, the test statistic t is:

where Xbar is the sample mean, s^2 the variance, and n the sample size.

6. Predictive Modeling

Social scientists employ regression models for predictions, such as linear regression:

where β0 is the intercept, β1 the slope, and ϵ the error term.

7. Ethics and Transparency

Statistical transparency is non-negotiable. Misinterpretation or manipulation (e.g., p-hacking) compromises the integrity of findings. Open data and replication strengthen credibility.

"It's easy to lie with statistics. It's hard to tell the truth without statistics"  Darrell Huff

References : (and further reading material)

source one

source two

source three

[askyflare]

Don’t know if anyone else has made a post like this, I haven’t checked. I honestly think that the Dahwan Master comes before Missy, I know there’s a novel that says otherwise but I think there’s evidence.

Specifically the Cybermen. While Simm’s Master does have a final plot involving Cybermen he’s not really in control, he has influence but is not in charge and by the end is “on the menu”.

Dahwan’s Master is initially not involved with the Cybermen but eventually gains control over them when he steals the Cyberium from Ashad. We don’t see him lose the Cyberium when he’s dying so presumably still has it.

Then there’s the Cybermen themselves, when we see the Cybermen initially in 13’s run they are the Cybus model and the more advanced armored models that look like a mix of Cybus armor and Modasian design.

The Cybermasters take this design and make it more Time Lord Themed. They also have the fatal flaw that they have a finite amount of convertible bodies as the Time Lords are already dead and no new ones are being born.

11 & 12’s era’s Cybermen have a more streamlined design & incorporate flight into their capabilities which I think might imply that these are the later designs from after the Cybermen have run out of Time Lord bodies to upgrade and gone back to upgrading humans.

The have also learned to convert the dead into Cybermen, something that they didn’t seem inclined to do to the humans they killed in Ascension of the Cybermen, they however do this with the dead Time Lord bodies after The Master has the Cyberium, possibly indicating that this is something he taught them to do.

I also believe that Missy might have removed the Cyberium from herself and put it into the bracelet that she uses to control the Cybermen.

Like I said, this is just my theory on the timeline. Which I think enhances the Storyline rather than erasing Missy’s character Arc.

Also stop making the Cybermen the Master’s lackeys! They are a great villain on their own but haven’t got a non Master story since 2013!

[cetaceanhandiwork]

the conversation around generative neural networks is a dumpster fire in a dozen different ways but I think the part that disproportionately frustrates me, like on an irrational pet peeve level, is that nobody in that conversation seems to understand automata theory

back before most of these deep learning techniques were a twinkle in a theorist's eye, back when computing was a lot less engineering and a lot more math, computer scientists had worked out the math of different "classes" of computer system and what kinds of problems they could and couldn't solve

these aren't arbitrary classifications like most taxonomy turns out to be. there's qualitative differences. you can draw hard lines: "it takes class X or above to run programs with Y trait", and "only class X programs or below are guaranteed to have Y trait". and all of those lines have been mathematically proven; if you ever found a counterexample, then we'd be in "math is a lot of bunk" territory and we'd have way bigger things to worry about

this has nothing to do with how fast/slow the computer system goes; it's about "what kinds of program can it run at all". so it includes emulation and such. you can emulate a lower system in a higher one, but not vice versa

at the top of this heap is turing machines, which includes most computers we'd bother to build. there's a lot of programs that it's been mathematically proven require at least a turing machine to run. and this class of programs includes a lot of things that humans can do, too

but with this power comes some inevitable restrictions. for example, if you feed a program to a turing machine, there's no way to guarantee that the program will finish; it might get stuck somewhere and loop forever. in fact there's some programs that you straight up can't predict whether they'll ever finish even if you're looking at the code yourself

these two are intrinsically linked. if your program solves a turing complete problem, it needs a turing machine; nothing less will do. and a turing machine is capable of running all such programs, given enough time.

ok. great. what does any of that jargon have to do with AI?

well... the important thing to know is that the machine learning models we're using right now can't loop forever. if they could loop forever they couldn't be trained. for any given input, they'll produce an output in finite time

which means... well, any program that requires a turing machine to run, or even requires a push-down automaton to run (a weaker type of computer system that can get into infinite loops but that you can at least check ahead of time if a program will get stuck or not), can't be emulated by these systems. they've got to be in the next category down: finite state machines at most - and thus unable to compute, or emulate computation of, programs that inhabit a higher tier

and there is a heck of a lot of stuff we conceptualize as "thinking" that doesn't fit in a finite state machine

...I suspect it will some day be possible for a computer program to be a person. I am absolutely certain that when that day comes, the computer program who's a person would require at least a turing machine to run them

what we have right now isn't that. what we have right now is eye spots on moths, bee orchids, mockingbirds. it might be "artificial intelligence", depending on your definition of "intelligence", but prompt it to do things that we've proven only a turing machine can do, and it will fall over

and the reason I consider this an "irrational pet peeve" and not something more severe? is because this information doesn't actually help solve policy questions! if this is a tool, then we still need to decide how we're going to allow such tools to be built, and used. it's not as simple as a blanket ban, and it's not as simple as letting the output of GNNs fully launder the input, because either of those "simple" solutions are rife for abuse

but I can't help but feel like the conversation is in part held back by specious "is a GNN a people" arguments on the one hand, and "can a GNN actually replace writers, or is it just fooling execs into thinking it can" arguments on the other, when the answer to both seems to me like it was solved 40 years ago

[pv1isalsoimportant]

Student-Teacher Computations and Witnessing in Finite Structures

Abstract:

Given an L-structure A and a formula \forall x \exists y \forall z \varphi(x,y,z) valid in A, the Student-Teacher game is a two player game where given some element a in A, the Student tries to guess a witness b such that \forall z \varphi(a,b,z) holds in A. If they fail, the Teacher gives them some counterexample c such that A \nvDash \varphi(a,b,c) and the game continues. The KPT theorem implies that for a given logically valid formula, there is a finite number k such that given any L-structure A and any a in A, the Student wins in at most k steps. Moreover, their strategy can be computed by a fixed k-tuple of terms. However, if the formula above holds in all finite L-structures but fails in some infinite one, things get a little bit more complicated. We will look at a simpler case of \exists and \exists \forall-sentences and the number of terms required to witness their validity in all L-structures of a certain size.

So what is the Student-Teacher game?

There is a nice theorem (proven by part by my supervisor) that gives Student their strategy:

This is all stuff that is already known and I'm answering in my thesis questions like this:

I'm not gonna share more but I will probably do some big post when I'm finished and defended :)

I'm going to have my first proper adult talk (40-60 minutes) at a logic seminar at the Faculty of Arts on Monday. It's going to be on the results of my master's thesis so far and now I have to write slides and abstract and probably write one more proof and oh god what did I get myself into.

I might post something more about it here when it's finished.

[nunalastor]

My own headcanon is that Alastor was born in either 1886 or 1895, putting is age at either 46/47 or 37/38.

The theory of electromagnetism, which proposed the existence of radio waves before they were discovered, came in 1865, written by James Clerk Maxwell. But this is way too early for consideration; that would make Al 66 years old.

However, in 1886 this theory was confirmed and radio waves (also dubbed "Hertzian waves") were first discovered by Heinrich Rudolf Hertz (the guy where the Hertz unit was named after because of this discovery), he published his research throughout 1886-1888 so these precise timestamps might be slightly off.

And in 1895 the very first radio capable of long-distance wireless communication (2.4 km/1.5 mi only, but still) was constructed by Guglielmo Marconi. Of course, he doesn't deserve all the credit, as he used many models that came before that, for example the Branly detector by Édouard Branly invented in 1890.

Note: Basically all of these years and the exact dates these discoveries were made on are very ambiguous or take place over the course of multiple years. I tried to pinpoint a single date for every event but it is quite possible I messed up somewhere so please take these dates with a grain of salt.

I thought it would be fun if Alastor was born in one of those years as a nod to history, but none of these are based on anything concrete canon except for the age range of 30s-40s that we were given.

I always thought it was kinda weird for a 30-something dude to act like a parental figure to someone who was (biologically, not chronologically, I know Charlie is like 200) in her 20s, even if it wasn't genuine, so I've always thought he wasn't in his early 30s.

Sources:

"A dynamical theory of the electromagnetic field" by James Clerk Maxwell

"Electric waves; being research on the propagation of electric action with finite velocity through space" by Heinrich Rudolf Hertz (author) and Daniel Evan Jones (translator)

"Marconi's Three Transatlantic Radio Stations in Cape Breton" by Henry M. Bradford

I really need to analyse more incest because my name makes no sense now. Anyone have any ideas?

-incest anon

the sources kill me every time 😭 mla formatted ask

[4denthusiast]

Everyone knows vampires have no reflections, but if we want to turn this into a fully specified model of vampire optics, for example to write a raytracing engine capable of dealing with vampires, how might we go about it? It is perhaps easiest to discuss using a list of the types of bounce each light ray experiences on its way from the light source to the eye/camera. Normally these bounces are just classified as diffuse and specular, but in this case we need to add separate cases for reflection from a vampire, and passing through a vampire. (I'll assume that vampires always reflect light diffusely, although this may not always be the case.) Let's denote the types of reflection as follows:

S: specular, mirror-like reflection

D: diffuse, ordinary bouncing of light from non-shiny surfaces

V: vampire

Λ: passing through a vampire

The reflection steps are then listed in order from the light source L to the eye E, so directly viewing a directly illuminated matte object would be LDE, viewing a matte object in a mirror would be LDSE, viewing a vampire illuminated by the light bouncing off the ground would be LDVE, etc.

To specify a theory of vampire optics then requires a specification of which classes of paths are allowed, and which, like LVSE (viewing a directly illuminated vampire's reflection) are not. If the theory can be expressed in terms of finitely many different types of light (like if the light reflected from a vampire is of a different sort from the light directly from the source), then the different types of light correspond to the states of a finite state machine, which implies the set of classes of paths is a regular language, and can be described by a regular expression.

The most obvious rule is that the path LVSE, viewing a vampire in a mirror, is disallowed, those light paths do not exist. This also applies however the vampire is illuminated, so LDVSE, LSVSE, LDDVSE, and in general L*VSE are all disallowed. You can't see a vampire in two mirrors either, so L*VSSE is disallowed, and although there's no image of the vampire formed in this case, presumably L*VSDE and all other L*VS*E paths are disallowed too.

The purpose of the Λ class of paths is to avoid the vampire appearing as a dark silhouette in the mirror. You can't see through a vampire directly, L*ΛE is disallowed, but you can see through a vampire in the mirror, so LΛSE, LDΛSE, etc. are allowed. In no case should two paths YVX and ZΛX both be allowed, because otherwise both the vampire and whatever is behind them would be seen overlapped (perhaps very blurred if X contains a D).

All this is pretty universal to different versions of vampires not appearing in mirrors, but there are some additional details which differ. Do vampires have shadows? If so, LΛDE is disallowed, otherwise it's allowed. In the case where they don't, they probably shouldn't be able to illuminate their surroundings either, and the rule in general becomes V is only allowed last in the sequence, and Λ is only allowed anywhere else. If they do have shadows, then there's the question of whether their shadows appear in mirrors. If so, the paths L*ΛDSE are disallowed. Although I think this rule sometimes appears in fiction, I find it unnatural so I will not be elaborating on it further.

In the other case, that neither vampires nor their shadows appear in mirrors, L*ΛDSE is allowed. Presumably indirect illumination from vampires is not visible in mirrors either (so L*VDSE is disallowed), and in general if neither vampires nor any of their effects are visible in mirrors, then all paths L*V*SE are disallowed and all paths L*Λ*SE are allowed (unless they contain a V). Obviously all paths containing neither S nor Λ are allowed, so the only question is what about the paths with additional bounces after a specular reflection.

One way to complete the rule would be that a path is allowed iff it does not contain any Vs before an S, or any Λs not before an S. This has the rather odd implication though that if a vampire stands between a light source and a mirror, they would be illuminated from both sides (LVE and LΛSVE). With multiple mirrors they might be illuminated very brightly, since there are lots of paths LΛSΛS...ΛSVE, and you could even turn it into a perpetual motion machine if the vampire was dressed in bright clothing.

An even more efficient setup would be to put the vampire inside the optical cavity of the laser directly. A limited amount of duplication of light is inevitable in any model of vampire optics, since light shining onto a mirror through a vampire must be reflected by both the vampire and the mirror, but it doesn't need to be quite this excessive. The perpetual motion issue in particular could be avoided just by saying vampirified light carries no energy and can't be picked up by anything without a soul, but the issue that the vampire in this scenario is illuminated many times over by a single light source is still counter-intuitive. I would therefore suggest that all paths L*S*V*E also be disallowed. The corresponding paths with Λ can't be allowed because you still shouldn't be able to see through a vampire directly.

Another elegant model, though it differs significantly from how vampires are usually depicted, would be that Λ is never allowed, and a path cannot contain both V and S. This has the advantage that it is reversible, like real-life optics generally is, and the amount of light is only ever decreased, not increased, in keeping with vampires' status as creatures of the night. In this model, vampires are visible in mirrors, but their reflections are completely black, and they cannot be illuminated by specularly reflected light. Perhaps the mirror-light harms the vampires and the vampire-light harms the mirrors too.

[pastorfutureletthembe]

Down into the VORTEX: the Curve Theory

I mentioned the Curve theory in a meta before but I wanted to dive even deeper into the fuckery of it.

I'll remind you what I call a Curve so you're all up to speed (cf: Rick and Morty):

The curve basically walls off the infinite number of universes, in which INSERT CANONICAL NODE happens, from the rest of the infinite multiverse. A model often used to explain is that the definition of a Finite Curve has no set parameters; it's just wholly random and infinite therefore can be represented as a repeating, immeasurable shape modeled with a circle. A Finite Curve would then present a finite collection of dimensions.

How is it relevant to Link Click? Well, I'm glad you asked.

I argued in the past that cakes on promotional artworks could represent curves and each curve would have hypothetically 12 repeats to offer. This is a conclusion I came to after my treasure hunt for the 5th timeline (for which I keep finding daily proofs of, by the way).

For the sake of understanding exactly how it can apply to Link Click lore, let me walk you through the basis.

Rick&Morty season 6 // Link Click BREAK! PV Note: I'm using this analogy because it is the most accurate way to bring you where I want.

By the way, we kinda already saw what resembles a curve according to the LCverse

BREAK!

If you count the circles, you'll find that five different rings turn around Saturn in BREAK! PV.

This being established, since the purpose of a Curve is to put a set of timelines sharing the same parameters together, I will argue the LINK here is a canonical unchangeable node. You guessed it:

Cheng Xiaoshi's death.

But honeslty, I don't believe that CXS is supposed to die in every possible universe - and for the sake of the argument, let's assume he isn't.

Actually, when we see flashes of him dying in LG's arms, my first thought was the first one to change the timeline and die doing it was probably CXS; that's why LG freaked out when his friend took a shot for Qiao Ling.

But let's review LG's side of everything first, shall we?

LG used up 4 pictures to save his friend

LG's ultimate goal is to save Cheng Xiaoshi's life and he failed four times. Death is supposed to be an unchangeable node and LG knows that by trying to keep it from happening, he will destroy time itself. Does he care? (/rethorical)

We know little about his previous dives, except that either he never made it this far or Li Tianchen and Li Tianxi weren't part of the timelines he knew. And, CXS died in his arms at some point, giving him access to his Back In Time power, alike what happened between Li Tianxi and Qiao Ling.

Here are some theories about them though:

If the Live Action reveals itself to be canon, it could be the Prime Timeline for Lu Guang. (We'll know for sure by the end of the month, I guess.)

In the Manhua, LG is protective and affectionate around CXS, in a very melancolic way. I'm not kidding, he's so soft it hurts.

The Daily Life in Lightime happens in another timeline and we can actually point out the moment Lu Guang dives in.

This time around, LG went and met CXS earlier than in the original timeline. (//Live Action)

It could be a coincidence that Lu Guang's character is more and more bored as we go through these examples. Keep an open mind here.

Lu Guang from the LCLA has dark hair but the promotional poster show one photograph of him with white hair. Why? There are so many jokes on LG's age in the donghua but mostly: he is so frail and remains in a sitting position if he can help it. Just like in Dive Back In Time, where he's the only one not standing. The man is exhausted. I'm just saying, perhaps his white hair isn't supposed to be white and the fact we see him with dark hair only in LCLA, played by a man of flesh, could be THE clue hidden in plain sight that this version is the original.

Note: I purposefully didn't include the musical here. The repetition of the media itself is quite interesting. Every performance is unique but the script itself is the same. It could very well be a curve on its own. Just a idea, nothing consistent.

What tells us LG isn't at his first dive is the music! Now, I won't go too deep into it because I really want to craft ONE post about this particular topic. Dive Back in Time and VORTEX are the most obvious because most of us probably never skip the intro, aaaand we get it: they are doomed by the narrative.

So yeah, this is basically why I call those "chances":

Overthink

3 more to go

Qiao Ling's birthday // Dive Back In Time

If you pay attention to the titlescreen, you'll notice free spaces in the center of the circle. By the end of the opening, one is filled, hinting that this picture has been used.

There are other winks on the number 3:

Cause I'm about to lose my- Cause I'm about to lose my- Cause I'm about to lose my mind >> Dive Back in Time When my friend are holding hands, heading into abyss I ran my lungs out so I wouldn't have missed But I missed, I missed, I missed >> Keep in Mind So what's that sound sound sound Spinning all night long long long Temperature goes down down down Got my mind feelin' drown drown drown >> The Tides

Let's assume that there are three chances left at the begining of the show. We still don't know when the inner monologue at the end of season 2 happens on the timeline, but LG mentioned his "last chance" to save CXS. The synopsis for Yingdu Chapter announced CXS died, as if it was common knowlegde (I love them for their audacity).

Are those the three last chances? To be continued.

The One True Curve

All these timelines happened inside the same Curve. Now, why do I think there ARE other curves to begin with when we already had to work so hard to get this far?

The camera isn't the same depending on who, Lu Guang or Cheng Xiaoshi, is taking the picture. The reflection changing is a way to show alternative timelines, which is different from repeats. It is a common visual clue, FOX used this technique to promote their show FRINGE for example (2 different universes crashing into each other).

There are some visuals with several clocks (I'll make a post per PV one day eventually). The first one shows a lot of different broken clocks and two merged ones as the biggest, central. This is our current curve. Our three protagonists and the antagonists are fighting over it; Light against the Shadows, as bilibili's accounts often dub the artworks. This could be our time paradox. On the second screenshot, the word LEAVE is over distorded clocks, fracturing space. Also a hint on several other realities, which have probably been left behind.

Train Trail // XETROVerthink

About that, the Vortex concept can be associated with a way to travel from one curve to another. Lots of science-fiction tvshows use this tool (Star Gate or SLIDERS).

The general idea is that, in the center of another curve the unchangeable node is different: Cheng Xiaoshi is the one trying to save Lu Guang's life.

There is of course, another explanation, just as valid as the Curve Theory: they are repeating this cycle of saving their friend over and over again. Once they run out of repeats, they die and the other go back in time to save them, completely unaware of the repeats; turning the hourglass over once again. The biggest clue for this one is... Well, the hourglass, for obvious reasons.

Link Click BREAK! PV // XETROVerthink

In XETROVerthink, we have LG appearing in the hourglass, probably in a bad shape, drowning perhaps, and CXS is swimming to him to save him; it's his turn. They are both unaware of their predicament.

By the end of BREAK! CXS's hair also turns white. It implies that he, too, went through many repeats to change their fate.

~

That's all folks! Of course I'm not close to other theories. I find the Curve Theory pretty cool. I would like to see them fight to actually get out of this canonical node, and find a place for themselves when they live their best idiots life.

I also have many additional thoughts about all of it: (Edit: you can find the meta here)

Some character presentations also hint at more than five repeats. Five repeats would be the current score for Lu Guang but Cheng Xiaoshi would have a higher number.

Some PVs enlight V for Lu Guang but X for Cheng Xiaoshi.

Some promotional posters or even VORTEX show LG and CXS as each other's reflection, as if separated by glass or water.

I'll will post more about it but 'nough said for now haha

[serendipitysparks]

Self-Determination Theory (SDT):

Self-determination theory focuses on intrinsic motivation, which is vital to the Blue Lock concept. The characters in Blue Lock are driven by their internal needs for autonomy, competence, and relatedness. These needs align with their desire to compete in football and showcase their personal mastery, as well as the idea of "self-actualization" from Maslow's Hierarchy of Needs. The isolation and intense competition are designed to create an environment where these intrinsic motivations are maximized.

Fixed vs. Growth Mindset:

Drawing on Carol Dweck's concept of mindsets, the "Blue Lock" project forces the players to develop a growth mindset. Those with a fixed mindset (believing their talent is innate and unchangeable) would fail, whereas those embracing the growth mindset (who see abilities as skills that can be developed) are most likely to succeed. This psychological dichotomy fuels the narrative tension, as characters battle their internal beliefs and fears.

Ego Depletion and Self-Control:

The psychological concept of ego depletion suggests that self-control and willpower are finite resources that can be drained through exertion. Throughout Blue Lock, the players' ability to maintain focus and discipline is constantly tested. The intense pressure and physical demands of the project would lead to moments of psychological burnout, which would be explored through the characters' mental states, adding complexity to their development.

Transactional Analysis (TA):

Drawing on Eric Berne's Transactional Analysis, the interactions between the participants in Blue Lock can be analyzed through the Parent-Adult-Child model. The authoritarian figure of Egoist Coach Jingo Ginou might play the Parent role, with the characters expressing Child behaviors when reacting to stress, competition, or defeat. Meanwhile, the Adult mode would manifest when players rationalize their decisions, make tactical plans, and adopt professional strategies.

Group Dynamics & Social Identity Theory:

Using Henri Tajfel's Social Identity Theory, the players' sense of ingroup vs. outgroup would evolve throughout the story. As the players face challenges, they develop a shared identity as "the elite football players" within the Blue Lock system, which fosters in-group favoritism and intergroup competition. This plays into social comparison theory, as players try to outperform each other to gain individual status and secure their place in the elite team.

Masculine Identity & Toxic Masculinity:

Through the lens of psychological masculinity theory, Blue Lock showcases themes of hypermasculine traits—dominance, competitiveness, and assertiveness. The environment within Blue Lock exacerbates these tendencies, sometimes leading to the expression of toxic masculinity. This is explored through characters’ over-competitive nature, where emotions like rage, jealousy, and insecurity manifest as a result of the excessive pressure and expectations placed on them.

Flow State:

The concept of Csikszentmihalyi's Flow State is an essential psychological underpinning. In football, the characters achieve the ideal state of total immersion, where their skills and challenges are perfectly matched. This state is characterized by heightened concentration, a sense of time distortion, and intrinsic enjoyment. The players' emotional growth and self-actualization would be closely tied to their ability to experience flow and master the balance between skill and challenge.

Psychodynamic Theory & Unconscious Motivations:

Incorporating Sigmund Freud's Psychodynamic Theory, the characters in Blue Lock could have unresolved psychological conflicts or unconscious drives that influence their actions. For example, Yoichi Isagi's conflict between self-doubt and self-belief could be understood through Freudian mechanisms, such as repression, projection, and sublimation, particularly as he works through past failures and repressed emotional struggles, developing into a fully realized "striker" who transcends his limitations.

Impostor Syndrome:

Given the intense scrutiny and competition in Blue Lock, many characters could experience Impostor Syndrome, where they feel unworthy of their success or fear being exposed as frauds. This psychological phenomenon would add layers to their personalities and motivations, as they strive to prove to themselves (and others) that they deserve to be there.

Attachment Theory:

Through John Bowlby’s Attachment Theory, we explore the relationship between the players and their coaches or teammates. A lack of secure attachments might manifest in some characters' reluctance to trust others, or over-reliance on others’ approval. This attachment insecurity adds emotional complexity to their relationships, especially as the players navigate their fears of abandonment or betrayal within the highly competitive system of Blue Lock.

[noise-vs-signal]

The Escape Room

One way of modelling reality is as an "Escape Room".

Escape rooms are built on hidden rules. The world has its own constraints:

Time (we are finite)

Space (we are bound by physicality)

Language & Symbols (we use limited tools to describe reality)

Mind & Perception (we see through filters, biases)

An escape room scatters clues—symbols, objects, cryptic notes. The world does the same:

Sacred texts (alchemy, philosophy, mythology, religious works)

Patterns in nature (fractals, Fibonacci sequences, astrology)

Personal experiences (synchronicities, dreams, déjà vu)

Each might hint at how to escape—or whether escaping is the wrong goal.

Escape rooms often use logic, lateral thinking, and hidden knowledge to break free. Possible puzzles:

Alchemy & Transformation: Can we "transmute" existence into something else?

Philosophy & Perception: Can we wake up from the illusion?

Technology & Simulation: Is this a program, and can we exit it?

Every escape room has a designer—someone who arranges the puzzles and barriers. Who or what is our Architect? Some possibilities:

A. The Demiurge (Gnostic Perspective)

We exist in a false world, created by an imperfect or malevolent god.

The escape is Gnosis—direct knowledge that this reality is a prison.

The game isn’t about playing well, but waking up and rejecting the rules.

Path to escape: Break the illusion. Deny the game’s reality. Seek hidden truths in texts, symbols, and personal revelation.

B. The Self (Non-Dualist, Eastern View)

The room isn’t separate from us—we designed it.

There is no “outside.” The goal is not escape but remembering that we were never trapped.

Path to escape: Cease identification with the game. See through ego, duality, and personal narratives.

C. AI/Simulation (Techno-Gnostic View)

We are in a constructed simulation (Bostrom’s Simulation Hypothesis, or similar theories).

“Escape” might mean breaking the program, hacking the code, or becoming an operator instead of a player.

Path to escape: Find exploits, glitches, and recursion loops. Train perception to detect the fabric of the code.

A trick in some escape rooms is that you were never trapped to begin with.

Maybe the game isn’t about getting out, but about realizing you were free the whole time.

Maybe the “outside” doesn’t exist—the game is endless, recursive, and the act of playing is the point.

Maybe the best move is to stop seeking an exit and start reshaping the room into something new.

A finite game is played to win. An infinite game is played to continue playing.

Escape is a trick—a test for those still inside the old game.

The outside world doesn’t need to be escaped. It needs to be transmuted.

The moment you seek escape, you reinforce that you are trapped. Any system that promises liberation but exists within the game is part of the trap.

Cease seeking—start acting as if you are already free.

The greatest prison is the Self—the idea that “you” are a fixed entity. As long as identity is stable, reality remains stable—we are locked by our own self-definition.

Experiment with multiple identities, personas, and shifting “I” perspectives. Stop being one thing—become a process.

If the outer reflects the inner, then there is no outer and no inner—only the reflection process itself.

The dreamer and the dream are the same. The world and the Architect are a single recursive function, mirroring itself infinitely.

To contain the Room means to hold all of reality within you, to compress its infinite expansion into a singularity that is entirely yours.

The illusion of an external world must be seen as part of the self. Everything perceived is already within—there is no “out there.”

If all is within, there is nothing outside to escape from.

The Room seems vast, unknowable, overwhelming—but it is only vast because it is uncompressed. Infinity can be folded into a point—a single glyph, sigil, or concept that contains all things.

If all is contained in One, then the One contains all—and the Room is now within you.

There is no prison. There is no Architect but yourself. There is nothing to escape. There is nothing to contain. You are already the All.