#proof of lagrange theorem

[aedislumen]

26 for the ask game （╹◡╹）

26. Forgotten hero everyone should know about

This could have been a perfect occasion to talk about Claude-Antoine Prieur again, but given that I plan to devote him many future posts on my blog, I thought it would have been more appropriate to use this ask to share my knowledge about an important and unfortunately still rather unknown STEM personality, who truly inspired me when I was a young student. I'm referring to Sophie Germain.

Born in Paris in 1776, Sophie was one of the rare mathematiciennes of the 18th-19th century. She had her first approach with mathematics during the days of the storming of the Bastille, when it was too dangerous for a young 13 years old girl to go outside. To pass the time, she turned to her father's library and a book named "Histoire des mathématiques" by Jean-Étienne Montucla captured her interest. The story of Archimedes narrated in the book fascinated her deeply, eventually leading her to start studying mathematics on her own through the works by famous mathematicians like Euler, Newton, Cousin. Her interest and dedication to the discipline was so strong, that during winter, when her parents denied her warm clothes and a fire in her bedroom to prevent her from studying she kept doing it anyway despite the cold; at the time maths wasn't considered appropriate as a studying discipline for a woman.

When the Polytechnic school opened in 1794, women couldn't attend, but the policy of the school allowed to everyone, who asked for them, notes of the lectures. She requested them under the pseudonym of Antoine-Auguste Le Blanc, a former student who had dropped out. Given that, as a student of the Polytechnic school, one was expected to send written observations about the lectures - a sort of homework - Germain wrote and sent hers to Joseph-Louis Lagrange, one of the teachers and renowned mathematician. The latter was so positively impressed by her essays that requested a meeting with the brilliant student LeBlanc, who unexpectedly had improved so much. She was then forced to reveal her identity. Lagrange was pleasantly surprised to realize Monsieur Le Blanc was in reality a young and talented woman and decided to support her, becoming her mentor.

One of her most noteworthy contribution to mathematics was in number theory, where she proved a special case of the so-called Last Fermat's Theorem (1), which has remained one of the hardest mathematical theorems to prove for more than three centuries and whose final proof was actually found only in 1994 by Andrew Wiles. Other important works of hers include treatises on elastic surfaces, one of which, Recherches sur la théorie des surfaces élastiques, awarded her a prize from the Paris Academy of Science in 1816.

Although she often faced prejudice for being a woman, Germain was praised and also supported by various well-known mathematicians of the time. Some of them include the aforementioned Lagrange, Legendre, who thanks to her work on the Fermat's theorem, was able to prove it for another special case; Cousin himself, Fourier, who managed to grant her the permission to follow the sittings held at the Paris Academy of science and last, but obviously not least, the great Gauss, who after Germain's death advocated for giving her an honorary degree in mathematics.

Notes

(1) In short, the Last Fermat's Theorem asserts that for n > 2 there are no integer solutions to the following equation:

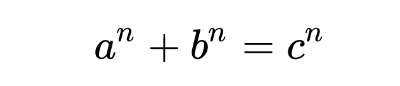
with a, b, c being positive integers. Sophie Germain proved the theorem for all numbers n equal to a prime p, so that 2p + 1 is also prime. The whole thing is much more complex that how I explained it, my aim was to write down a simple intoduction. If you want to read more about that I recommend you this link.

[1d1195]

(This is my third try submitting this because the first two times my tumblr crashed and said something went wrong with my ask😭 so I’m sorry if you end up getting all three! Re: math abbreviations)

I love those! Clit💀 same energy as sqrt because my mind does not think of square root first😂 any time i saw arcsin, my mind said “arson😈” even though they aren’t even pronounced the same lol

My dyslexia didn’t like Lagrangian and Laplace. I kept saying Laplancian and Lagance in front of my whole class for months 😭 still slip up sometimes lol

If it’s phrases we didn’t use often, I’d write them out, otherwise I’d just use symbols and abbreviations. I don’t remember what proof we did, but my instructor started writing out “therefore, there exists (whatever it was) in a set of integers, (etc.)” and I said… I think tf not bro ✍️ and I got to work with the dots and epsilons and what not💀 don’t have time for that when you look down at your notes for a millisecond and look back up to a blank board as if your instructor just took a gymnasium broom to it😂

I figured out how to take notes without looking at my papers because that happened so much😂

I’m so glad I have someone to talk about this stuff with!!♥️♥️♥️

-👩🏻‍🔬

FOR EVERY EPSILON GREATER THAN 0 THERE EXISTS A DELTA GREATER THAN 0 was that the theorem? It sounds like it 😭😭😭 I think one day I’ll get that tattooed on my body; it should be turned into song lyrics. I still don’t understand real analysis. It was too complicated. I didn’t understand proof writing. Now I do and it’s too late! And then my dumbass took complex analysis in grad school 🤦🏻‍♀️ That was nuts. Although my professor took pity on us and made it WAY easier than it was supposed to be. You sound like you’re 100 times smarter than me (probs more) so forgive me if I can’t keep up. It’s been a while since I talked LaGrange and LaPlace but it’s in my brain hiding in there. I’m all algebra these days although I’m falling in love with stats more and more each year. I actually want to go back to get a second masters (I need $$) I think I would do a pure math thing but I wish there was a stats program out there (if the teaching thing doesn’t work out, I think I gotta be an actuary). But I don’t want to pay for the masters nor do I want to have to stress so much again.

ANYWAY, back to the abbreviations. One time I abbreviated standard deviation but I was new to teaching stats and my prof did St. D and I NEVER thought anything of it. But naturally, my students were like “why did you write STD” and I was like “oh fudge” 🤦🏻‍♀️

Maybe this summer I’ll reteach myself calculus I miss derivatives and MAYBE I’ll finally learn series and sequences 🤭

So fun to chat math with you 💕

Xoxo

[max1461]

Yes that's the kind of list. The one I thought up for myself, several years ago, was:

What is the proof of Lagrange's Theorem in group theory?

What is the conjugation of a rahen verb in Early Middle Japanese?

What unused tile in Super Mario World allows Mario to pass through but causes entities to slide?

Thinking about this metric of like...

Come up with a set of three general-knowledge questions (by general knowledge I mean not stuff about your personal life; roughly the type of information you might find in a Wikipedia article) that you think uniquely narrow you down, in the sense that you feel confident you are the only person on earth who could answer all three questions correctly.

I can think of a few question sets like this for me, where I'm like 80% confident that I'm the only person who knows the answer to all three of them. If you have a little bit of obscure knowledge on a couple of topics, this is fairly easy to do I think.

Well, then the question is, how many meaningfully distinct sets of three questions like this do you have. Call that number your Obscurity Rank.

It's pretty cool to be of high Obscurity Rank, and one should strive for it.

[rajat478]

Lagrange theorem proof in an easy and detailed way with all the required definitions, lemmas, and corollaries.

[vacuously-true]

I think we should replace "theorem" with "hot take" from now on. Pythagoras' hot take. Fundamental hot take of algebra

Hello! Thanks for sharing your hot take. Your opinion is Wrong and I am going to tell you Why.

"Hot take" should be reserved for statements which are conjectured or hypothesized but not proven. Despite not being proven, a statement should have some evidence in its favor before being presented as a hot take.

On the other hand, once something is proven, it is tea. To prove something is to spill the tea. A proof is an effortpost. Proper format for spilling the tea is to write the statement of the tea, followed by "in this essay I will," and then the effortpost, beginning with statement of assumptions. A proper effortpost ends with "thank you for coming to my TED talk," or "TED" for short. Allow me to demonstrate.

Fermat's Little Tea.

For p, a ∈ ℤ, if p is a prime which does not divide a, then a^(p-1) = 1 (mod p).

In this essay I will let p, a ∈ ℤ, such that p is a prime which does not divide a. Lagrange's theorem indicates that ℤ/pℤ* is a cyclic group under multiplication. As such the order of any element of ℤ/pℤ* is the order of the group, p-1. Since p does not divide a, a is an element of ℤ/pℤ*, and as such, its order in the group is p-1. Therefore a^(p-1) = 1 (mod p). TED.

The Four Color Tea is notable for being the first major tea spilled by computer. The Four Color Tea, then the Four Color Hot Take, was first proposed by Francis Guthrie in 1852. The tea was notoriously difficult to spill, but over a century later, in 1976, Wolfgang Haken and Kenneth Appel presented an effortpost using a very advanced (for the time) computer at the University of Illinois.

The first person to spill the tea on the Riemann Hot Take with an effortpost accepted by experts will be the recipient of a million dollar prize.

[notarealwelder]

Seriously though—

An amount of mathematics is...straightforward, for lack of a better word; for easier problems you can ~intuit* the proof, and as you go solving easier problems you very naturally develop a toolset to analyze and prove them, which transfers to harder problems. So you can start from a small* amount of ineffable intuition, definitions, and theorem-ideas, and grind your way into nontrivial skill levels of, I dunno, topology.

(This does not extend to the skill of, say, intuiting novel definitions or concepts, which is Important for research, but, ok, maybe this happens all by itself somehow.)

Many serious theorems you might not guess to be true offhand, or wouldn't guess to try to prove — there're many similar-looking statements, and this one is not obviously distinguishable as a provable theorem — but they're straightforward to discover: you can pretty much just play with definitions and concepts you have, apply them to each other in uncomplicated ways, and would you look at it, a theorem falls out. (Lagrange's theorem is like that; Sylow's likewise, though less obviously.)

(On the other hand, Lagrange's was noticed in 1771, but proven partially in 1801, and completely only in 1861, which...puts into perspective just how important good concepts/definitions are. Or how little time people had for math, or how much worse math-invention ability was propagated back then; I don't really know.)

But sometimes the whole theorem is basically a single bullshit insight, some trivial steps taking it to the conclusion, and absolutely no way to guess the approach from the shape of the problem.

Sure, you can consider frevrf sbez bs fva, wildly but very reasonably guess that it can be cerfragrq nf na vasvavgr cebqhpg of jut spput**, and from there the closed form of the sum of 1/n² is pretty obvious. But the question is: how do you know to look that way? Or how do you think to check / to try something in that vein?

In this particular case, the third hint seems unnecessary given the first two, but offhand I do not know the ~intuition that would lead one to guess them, nor how one can develop such an intuition.

It is dastardly frustrating.

(If somebody knows how to guess the first or the second hint, please tell me!)

[savrenim]

Hi so I'm studying optimization and I'm a bit stumped in regards to convexity. To be precise, I'm told that a problem has a unique minimum if both the function that will be minimised and the constraints are convex, but I can't see how a constraint (for example, (x^2)+(y^2)=3) can be convex, nor how that implies that the minimum is unique. Help?

Okay, woof, I would love to see a more specific wording of the problem because there are a couple of different things that are going on:

1. Every continuous function on a compact set (be it 1D, so a closed interval, or multidimensional--for example x^2+y^2=3 is the spherical shell of radius sqrt(3), which is both closed and bounded and hence compact but also a closed ball, rectangle, etc etc--note that this is compact, not convex, a convex set has a different meaning, although x^2+y^2=3 is convex too) reaches a global maximum and global minimum on that set. 

The proof of this is actually pretty clever: I'm going to go through the bullet points of the proof, feel free to ask me to comment more specifically on any of the bullet points if you want me to? but basically:

--a continuous function on a closed bounded set has a least upper bound and a greatest lower bound (it's defined everywhere, it's closed so there's no open-interval-can-tend-to-infinity-but-the-actually-asymptote-isn't-in-the-interval-so-we're-fine bit, so the values the function takes have to be bounded)--we'll do the least upper bound B, greatest lower is same argument. as it is the least upper bound, there have to be a sequence of x_n in the set such that f(x_n)>= B-1/n. this is basically stating that you can get arbitrarily close to the least upper bound, so why not pick a sequence of arbitrarily close points.--now the compact part is important: one of the definitions of a compact set, sequential compactness, is that every sequence has a convergent subsequence. so you can pick an x_(n_k) subsequence such that it converges to z for a point z in the set--and then by continuity, you can pass limits in and out of the function, so f(z)=f(lim k-->infty x_n_k)=lim_k-->infty f(x_n_k)=lim_k-->infty B-1/n_k=B.--so woohooo there exists at least one point which reaches THE GLOBAL maximum!

The two things that were necessary are indeed the weakest assumptions necessary; you NEED the function to be continuous for this to work, we used it in the proof to pass the limit inside the function, and you NEED the set to be compact for it to work; we used that to argue that the sequence had a convergent subsequence.

The problem with this is, this give existence, not uniqueness. So there will always be at least one point on a compact set with a continuous function that has a global maximum or minimum. BUT you could just as easily have two points that reach that value, or an infinite number of points. (technically any constant function on any compact set is continuous and does have a unique maximum/minimum value--its constant value--which it achieves literally everywhere on the set.)

So the place where boundary conditions come in is basically part 2: okay so what can we *also* say to go from there *exists* a point that achieves the max/min to it is a *unique* point that achieves the max/min. and uniqueness is really really hard to guarantee and so conditions get a lot more specific, and it turns out that one of the things that characterize convex functions the most is that they have under pretty loose conditions, unique minimums.

The basic idea as to why you want both the convex function and the convex set to be convex are, well, (and this is kind of oversimplifying it but I'd want to see the specific theorem you're talking about to be able to comment on exactly why the hypotheses of the theorem/what conditions your problem has to fulfill are what they are) -- but the basic idea is the math sees all the constraints involved very similarly? like if you're doing the Lagrange multiplier method (so we’re back to just continuous and compact set no guarantee of uniqueness) you have f that you're trying to minimize or maximize, and boundary conditions g, but the equations are grad(f)=lambda*grad(g), g=0 that are the system of equations that you solve, you're doing very very similar things to f and g. Well, a set is convex if and only if it is the area above the graph of a convex function. So requirements of a set to be convex/boundary conditions to be convex are because we will be using similar properties/procedures on all of the functions that we are looking at, be they the minimizable one or the boundary, so they better all follow the same rules. (but please, that is pretty touchy-feely instinct, send me the exact statement you want me to explain and I'll see if I can go through a proof of it if that's too vague for you)

If you want to get into more serious proofs, you start doing functional analysis. which means the fundamental theorem behind minimization is the geometric Hahn-Banach theorem and then it's basically convexity makes up for potential infinite dimensionality of your sets. which is fun. Hahn-Banach comes up E V E R Y W H E R E, it's a lifesaver

[fulltestbank]

Test Bank For Calculus: Multivariable, 12th Edition Howard Anton

TABLE OF CONTENTS   PREFACE ix   SUPPLEMENTS x   ACKNOWLEDGMENTS xi   THE ROOTS OF CALCULUS xv   11 Three-Dimensional Space; Vector 657   11.1 Rectangular Coordinates in 3-Space; Spheres; Cylindrical Surfaces 657   11.2 Vectors 663   11.3 Dot Product; Projections 673   11.4 Cross Product 682   11.5 Parametric Equations of Lines 692   11.6 Planes in 3-Space 698   11.7 Quadric Surfaces 705   11.8 Cylindrical and Spherical Coordinates 715   12 Vector-Valued Functions 723   12.1 Introduction to Vector-Valued Functions 723   12.2 Calculus of Vector-Valued Functions 729   12.3 Change of Parameter; Arc Length 738   12.4 Unit Tangent, Normal, and Binormal Vectors 746   12.5 Curvature 751   12.6 Motion Along a Curve 759   12.7 Kepler's Laws of Planetary Motion 771   13 Partial Derivatives 781   13.1 Functions of Two or More Variables 781   13.2 Limits and Continuity 791   13.3 Partial Derivatives 800   13.4 Differentiability, Differentials, and Local Linearity 812   13.5 The Chain Rule 820   13.6 Directional Derivatives and Gradients 830   13.7 Tangent Planes and Normal Vectors 840   13.8 Maxima and Minima of Functions of Two Variables 845   13.9 Lagrange Multipliers 856   14 Multiple Integrals 866   14.1 Double Integrals 866   14.2 Double Integrals Over Nonrectangular Regions 873   14.3 Double Integrals in Polar Coordinates 882   14.4 Surface Area; Parametric Surfaces 889   14.5 Triple Integrals 902   14.6 Triple Integrals in Cylindrical and Spherical Coordinates 909   14.7 Change of Variables in Multiple Integrals; Jacobians 918   14.8 Centers of Gravity Using Multiple Integrals 930   15 Topics in Vector Calculus 942   15.1 Vector Fields 942   15.2 Line Integrals 951   15.3 Independence of Path; Conservative Vector Fields 966   15.4 Green's Theorem 976   15.5 Surface Integrals 983   15.6 Applications of Surface Integrals; Flux 990   15.7 The Divergence Theorem 999   15.8 Stokes' Theorem 1008   A Appendices   A Trigonometry Review (Summary) App-1   B Functions (Summary) App-8   C New Functions From Old (Summary) App-11   D Families of Functions (Summary) App-16   E Inverse Functions (Summary) App-23   READY REFERENCE RR-1   ANSWERS TO ODD-NUMBERED EXERCISES Ans-1   INDEX Ind-1   Web Appendices (online only)   Available in WileyPLUS   A Trigonometry Review   B Functions   C New Functions From Old   D Families of Functions   E Inverse Functions   F Real Numbers, Intervals, and Inequalities   G Absolute Value   H Coordinate Planes, Lines, and Linear Functions   I Distance, Circles, and Quadratic Equations   J Solving Polynomial Equations   K Graphing Functions Using Calculators and Computer Algebra Systems   L Selected Proofs   M Early Parametric Equations Option   N Mathematical Models   O The Discriminant   P Second-Order Linear Homogeneous Differential Equations   Chapter Web Projects: Expanding the Calculus Horizon (online only)   Available in WileyPLUS   Blammo the Human Cannonball -- Chapter 12   Hurricane Modeling -- Chapter 15         Read the full article

[quadrantmathematics]

Quadrant Mathematics Book

https://en.wikipedia.org/wiki/Quartic_function

Polynomials can be solved by radicals only up to degree four. It took a very long time to discover the proof for degree four. The fourth is always different. It took until 1824 to discover the proof.

The first four Mersenne primes were known by the ancients. The fourth is different. It took until modern times to discover the fifth. The fourth is always different. The fifth is ultra transcendent.

https://en.wikipedia.org/wiki/Mersenne_prime

3

31

7

127

8191 was discovered in 1461

The FOIL method is used for multiplying binomials in math. The four terms for the FOIL method are

First ("first" terms of each binomial are multiplied together)

Inner ("inside" terms are multiplied—second term of the first binomial and first term of the second)

Outer ("outside" terms are multiplied—that is, the first term of the first binomial and the second term of the second)

Last ("last" terms of each binomial are multiplied)

https://www.youtube.com/watch?v=S0_qX4VJhMQ

The geometric proof for derivatives in calculus involves four squares in quadrant formation. I learned this proof while watching a teaching company course on Calculus.

https://www.mathsisfun.com/algebra/completing-square.html

The geometric analysis for completing the square involves four squares. Completing the square is essential in algebra. The geometric proof for derivatives in calculus also involves four squares.

There are 16 squares in the quadrant model. There are 16 possible Truth Functions of two binaries

Here is an example of a truth table with the four possibilities

The ancient Greeks knew about the first four perfect numbers. The fourth one is different, and it took a lot longer for the ancient Greeks to discover the fourth.

https://en.wikipedia.org/wiki/Perfect_number

for p = 2:   21(22 − 1) = 6

for p = 5:   24(25 − 1) = 496

for p = 3:   22(23 − 1) = 28

for p = 7:   26(27 − 1) = 8128.

Euclid’s Elements was the most popular book behind the Bible. Euclid’s Elements had five postulates. The five postulates are the most famous set of postulates in math history. The fifth postulate was proven to be false. The fifth is always questionable. However, the discovery that the fifth postulate was false lead to the uncovering of different geometries. Ancients saw the fourth postulate as different. Proclus did not think that the fourth postulate should be a postulate. The fourth is always different. Euclid also proposed five axioms. The fifth axiom is false and the fourth is different. Some suggest that Euclid intentionally made the fifth postulate false so that out of its discovery as false, new geometries would be discovered. I learned about Euclid’s postulates on a teaching company course on mathematics, and the professor described how the fifth was incorrect and the fourth was different.

https://blogs.scientificamerican.com/roots-of-unity/whate28099s-the-deal-with-euclide28099s-fourth-postulate/

"To draw a straight line from any point to any point."

"To describe a circle with any centre and distance [radius]."

The third is about circles. A circle has the look of being an object and being whole. The first postulate is about a line. A line is like air, taking up no area. Air is the first square element. The second postulate is a straight line that is extended. The second element is water. Still there is no area being taken up, but it is longer. The first two are a duality. The third, the circle, brings area into the equation. The third square is the most solid. The fourth postulate is on right angles. Right angles are quadrants. The fourth is always transcendent

"To produce [extend] a finite straight line continuously in a straight line."

"That all right angles are equal to one another."

Semiotic squares take the form of a quadrant and are very popular. Semiotic squares are used a lot in academia.

https://en.wikipedia.org/wiki/Semiotic_square

https://www.newyorker.com/magazine/2008/03/03/numbers-guy

Deheane describes how in cultures throughout the world the first three numbers were usually represented similarly, but the fourth differently. For instance Roman numerals has I II and III, but IV is written with a V, different from the first three. There are some cultures that represent the first four numbers similarly. But all cultures represent five differently.

Deheane also points out that when tracking objects, only four can be tracked at one time. With three objects it is difficult, but four very difficult, but five at one time is impossible.

The quadrant model has 16 squares. Also scientists pointed out that a person can only imagine 16 squares at one time.

https://books.google.com/books?id=1p6XWYuwpjUC&pg=PT83&lpg=PT83&dq=Stanislas+Dehaene+one+two+three+four+chinese&source=bl&ots=S6NCR0YXvL&sig=01bEkiLf6Hoj44PrRG4mPsc8C6A&hl=en&sa=X&ved=0ahUKEwjsrfre0N3XAhUY6GMKHeClDXs4ChDoAQgxMAE#v=onepage&q=Stanislas%20Dehaene%20one%20two%20three%20four%20chinese&f=false

https://en.wikipedia.org/wiki/Subitizing

People can make flash judgements on the number of objects from one to three well. At four it becomes difficult, and at five the accuracy makes an exponential decline. The fourth is always different. The fifth is ultra transcendent

https://en.wikipedia.org/wiki/Approximate_number_system

The approximate number system is four numbers greater than four. Numbers one through four are counted through parallel individuation.

There are four fundamental operations in math. The four operations are

https://en.wikipedia.org/wiki/Operation_(mathematics)

+, plus (addition)

÷, obelus (division)

−, minus (subtraction)

×, times (multiplication)

Quartiles are very important in statistics

https://en.wikipedia.org/wiki/Quartile

Quartiles are three points that divide a graph into four equal groups.

Boxplot (with quartiles and an interquartile range) and a probability density function (pdf) of a normal N(0,1σ2) population

Boxplots are also very important in statistics. I learned about boxplots in middle school and in my college statistics course. I also learned about quartiles and interquartile range in middle school and in college. A box plot graphically depicts numerical data through its quartiles.

https://en.wikipedia.org/wiki/Box_plot. The bottom and top of the box are the first and third quartiles. The inside of the box is the second quartile.

Figure 1. Box plot of data from the Michelson–Morley experiment

Boxplot (with an interquartile range) and a probability density function (pdf) of a Normal N(0,σ2) Population

https://en.bywiki.com/wiki/Lagrange%27s_four-square_theorem#Historical_development

There is a four square theorem in mathematics

https://en.wikipedia.org/wiki/Pfister%27s_sixteen-square_identity

There is a sixteen square identity in mathematics. There are sixteen squares in the quadrant model

Jade Mirror of the Four Unknowns solved equations for up to four unknowns. The book also had equations of three unknowns. In the book we thus see the three, four dynamic.

https://en.wikipedia.org/wiki/Yuan_dynasty

https://en.wikipedia.org/wiki/Jade_Mirror_of_the_Four_Unknowns

The first four problems illustrate the method of the four unknowns. The four unknowns are

Heaven

Man

Earth

Matter

Jade mirror of the four unknowns consists of four books.

The introduction shows The Square of the Sum of the Four Quantities of a Right Angle Triangle

The illustration is a sixteen square quadrant model. The first illustration of the book is a sixteen square quadrant model

The book ends with the equation of the four unknowns

The famous Rhind Mathematical papyrus has four sections

https://en.wikipedia.org/wiki/Rhind_Mathematical_Papyrus

https://en.wikipedia.org/wiki/Lo_Shu_Square

The Lho Shu Magic Square contains a cross of odd numbers. The magic square is used to structure Jain Temples. It is seen as very sacred

There is a cross/quadrant pattern within the Sator Square. A cross/quadrant is depicted with the word Tenet. The sator square is a “four time palindrome”. People have claimed that it has magical properties.

https://en.wikipedia.org/wiki/Sator_Square

By repositioning the letters around the central letter Ν (en), a Greek cross can be made that reads Pater Noster (Latin for "Our Father", the first two words of the "Lord's Prayer") both vertically and horizontally. The remaining letters – two each of A and O – can be taken to represent the concept of Alpha and Omega, a reference in Christianity to the omnipresence of God. Thus the square might have been used as a covert symbol for early Christians to express their presence to each other

In Plato’s Meno, Plato tries to prove that knowledge is innate and comes from the World of the Forms. Socrates claims that people come from the World of the Forms before they are born, and that whenever somebody learns something, he is merely recalling what he already knows from the World of the Forms. Socrates proves that knowledge is innate by showing that a slave boy knows geometry. According to Socrates, the slave boy has received no education, since he is a slave. But because the slave boy understands the geometry, Socrates claims, the slave boy must have already known it from the World of the Forms

Socrates draws diagrams in the sand. The diagrams that Socrates draws to prove the world of the Forms are what I call the Form of the Good, the Form of Existence. Socrates draws the quadrant model 16 squares. I watched a teaching company course where the Professor drew the diagrams that Socrates drew in the sand.

https://tothereal.wordpress.com/2013/06/16/are-we-slaves-to-socrates/

Here are the diagrams that Socrates draws

In Roman numerals X is the number 10. Philosophers connect the number 10 and the tetractys. I have seen Jungian philosophers propose that because the x is fourfold, and the tetractys is related to four, the reason why the Romans used X as 10 is because of the tetractys.

https://en.wikipedia.org/wiki/The_Garden_of_Cyrus

The Garden of Cyrus is a book by Sir Thomas Browne. Browne sees the quincunx in so many places in reality that he says that it is evidence of intelligent design. Thomas Browne relates the quincunx to the Garden of Cyrus. The Garden of Cyrus took a quincunx pattern.

Frontispiece to 'The Garden of Cyrus' (1658)

In high school trigonometry my class learned the unit circle. The unit circle is a quadrant

http://locusacademy.org/unit-circles-and-trigonometric-equations/

An acronym that my class used to remember the four quadrants of the unit circle was All Stations to Central

http://locusacademy.org/unit-circles-and-trigonometric-equations/

In the upper left quadrant, only the sin values are positive, while the others are negative

The upper right quadrant's values of sin, cos and tan are all positive.

In the lower left quadrant, the tan values are positive, while the others are negative

The fourth quadrant is where the cos values are positive while the others are negative.

There is a famous puzzle called the Nine Dots Puzzle. My Grandpa showed me the puzzle. Also in my psychology class at UCSD the Professor showed us the puzzle. You are told to draw four lines that connect nine dots. The nine dots are in three columns. The way to solve the solution is to go outside of the limits of the nine dots. If you do so, you go into the region of a 16 square quadrant model. Moveroever, at the center of the solution is an X. An X is a quadrant. The solution employs what psychologists call “lateral thinking”. In order to solve the problem you must think outside of the box.

https://en.wikipedia.org/wiki/Thinking_outside_the_box

The Wason Selection task is also known as the “four card problem”. Developed by Peter Cathcart Wason, the four card problem is one of the most famous tasks in the study of deductive reasoning. I remember learning about the four card problem in a psychology class I took at UCSD.

https://en.wikipedia.org/wiki/Wason_selection_task

The Cartesian coordinate system is used extensively in mathematics. The Cartesian coordinate system is made up of four quadrants

https://en.wikipedia.org/wiki/Cartesian_coordinate_system

The complex number plane is similar to the Cartesian coordinate system, but it uses the imaginary number i on the y axis. The complex number plane is called an argand diagram, and it has four quadrants. Pauli saw the use of imaginary numbers and complex number planes in quantum mechanics as further evidence that physics was based around the quatenary.

http://www.peterstone.name/Maplepgs/complex.html

The Missing Squares Puzzle is a famous puzzle in mathematics

https://en.wikipedia.org/wiki/Pythagorean_hammers

Pythagoras used four hammers to discover the foundations of musical tuning. The four hammers are known as the Pythagorean hammers. He came across five men hammering with hammers, and four of them were harmonious, but the fifth was not. Again, the fourth is always transcendent, and the fifth is always questionable.

https://www.amazon.com/Fifth-Hammer-Pythagoras-Disharmony-World/dp/193540816X

https://mitpress.mit.edu/books/fifth-hammer

https://en.wikipedia.org/wiki/Anscombe%27s_quartet

Ascombe’s quartet is four datasets that have very similar descriptive statistics, but seem very different when graphed.

https://en.wikipedia.org/wiki/P_versus_NP_problem

NP Hard is different from the other three, P, NP, and NP complete. P v NP is a major unsolved problem in computer science

P

NP-Complete

NP

NP hard

In a math class that I sat in on at UCSD, the Professor drew the bijection, injection, surjection quadrant on the board. The fourth quadrant is different from the other three. The fourth quadrant does not even have a name

I sat in on a math class as well at UCSD where the four types of Fourier Transforms were brought up. The four types fit a quadrant pattern. Fourier transforms were talked about a lot in different classes that I studied. The four types fit a quadrant pattern.

https://dsp.stackexchange.com/questions/28020/formulas-of-the-fourier-transform-family

https://en.wikipedia.org/wiki/Quartic_function

A quartic function is the highest degree such that every polynomial can be solved by radicals. Quartic means four

Graph of a polynomial of degree 4, with 3 critical points and four real roots(crossings of the x axis) (and thus no complex roots).

Ferrari discovered the quartic solution in 1540. The proof that the quartic is the highest degree polynomial that could be solved by radicals was given by the Abel- Ruffini theorem in 1824.

In order to complete the proof on the quadrature of the parabola, Archimedes must prove that

His proof involves a diagram that resembles a quadrant model

Archimedes' proof that 1/4 + 1/16 + 1/64 + ... = 1/3

The Missing Square Puzzle is a famous puzzle in mathematics. It invovles four colors

https://en.wikipedia.org/wiki/Missing_square_puzzle

Kryptos is a sculpture by the American artist Jim Sanborn at the Central Intelligence Agency (CIA) in Langley, Virginia.

It has four encrypted messages. Three of the four messages have been encoded. The fourth is different and transcendent.

https://en.wikipedia.org/wiki/Kryptos

Pyramids in Egypt are quadrants, and the pyramids of Giza reflect the pythagorean theorem.

http://africancreationenergy.blogspot.com/2014/12/the-ptah-horus-pythagoras-theorem.html

http://africancreationenergy.blogspot.com/2014/12/the-ptah-horus-pythagoras-theorem.html

Each side of the Pythagorean theorem represented for the Egyptians a different God. The four by four square is the quadrant model square. The four by four 16 square of the simplest pythagorean triple, the three four five triangle, is represented by Isis

http://africancreationenergy.blogspot.com/search/label/African%20Mathematics

The proof of the Pythagorean theorem attributed to pythagoras involved four squares. Look at the diagram to the right above, and notice the four segments.

http://theopenscroll.blogspot.com/2013/06/part-3-signs-of-horus-worship-345-on-map.html

64 is four quadrant models. 16 is the quadrant model. The eye of Osiris has the ratios of the quadrant model

The right side of the eye =  1⁄2

The pupil =  1⁄4

The eyebrow =  1⁄8

The left side of the eye =  1⁄16

The curved tail =  1⁄32

The teardrop =  1⁄64

The Rhind Mathematical Papyrus contains tables of "Horus Eye Fractions".[16]

https://en.wikipedia.org/wiki/Eye_of_Horus

https://en.wikipedia.org/wiki/Missing_square_puzzle

The missing squares puzzle is a famous mathematical optical illusion. The demonstration involves four figures of four colors.

Sam Lloyd’s paradoxical dissection also has four shapes and colors.

Sam Loyd's paradoxical dissection

https://en.wikipedia.org/wiki/Missing_square_puzzle

Mitsunobu Matsuyama's "Paradox" uses four congruent quadrilaterals and a small square, which form a larger square. The diagram makes a quadrant.

https://en.wikipedia.org/wiki/Missing_square_puzzle

The 15 puzzle involves 16 squares. The 15 puzzle is a four by four quadrant model

https://en.wikipedia.org/wiki/15_puzzle

https://en.wikipedia.org/wiki/Mathematical_puzzle

Four fours is another mathematical puzzle

https://en.wikipedia.org/wiki/Four_fours

https://en.wikipedia.org/wiki/Tower_of_Hanoi

The three peg tower of Hanoi puzzle has a simple recursive solution. The optimal solution for a four peg tower of hanoi puzzle was not discovered until 2014. For the case of more than four pegs the problem is an open problem. The fourth is always transcendent and the fifth is questionable.

The famous T puzzle consists of four polygonal shapes. The puzzle seems easy but it is not “because of the irregular piece”. The fourth piece is different than the previous three. Again we see the three plus one pattern. Few people are able to solve the T puzzle in under five minutes.

https://en.wikipedia.org/wiki/T_puzzle

https://en.wikipedia.org/wiki/T_puzzle

The latin cross puzzle uses a cross. A cross is a quadrant.

https://en.wikipedia.org/wiki/T_puzzle

http://www.cropcircleconnector.com/2017/cleyhill/comments.html

https://en.wikipedia.org/wiki/Cantor_set

Cantor Dust is made of quadrants

http://mathworld.wolfram.com/CantorDust.html

https://en.wikipedia.org/wiki/Menger_sponge

A Jerusalem cube is a fractal object described by Eric Baird in 2011. It is created by recursively drilling Greek cross-shaped holes into a cube.[8][9]The name comes from a face of the cube resembling a Jerusalem cross pattern

http://www.critcrim.org/redfeather/chaos/029management.html

Chaos research, as mentioned, tracks the transformations of dynamical systems from one behavioral regime (attractor state) to another. In such transformations, management science has much to learn and much to ponder. As key parameters of systems reach each one of four feigenbaum numbers (F1-F4 discussed below), the system displays an orderly procession from one dynamical state to another. The procession ceases to be orderly and becomes very chaotic at F4. As a system becomes more chaotic, i.e., it transforms from a simple outcome basin to a much more complex causal field.

Sierpinski triangle in logic: The first 16 conjunctions of lexicographicallyordered arguments. The columns interpreted as binary numbers give 1, 3, 5, 15, 17, 51... (sequence A001317 in the OEIS)

https://en.wikipedia.org/wiki/Sierpinski_triangle#Analogues_in_higher_dimensions

The Sierpinski triangle is created by dividing an equilateral triangle into four equal triangles, and continually dividing triangles into four equal triangles.

There is also the Sierpinski tetrahedron. Tetra is four

https://en.wikipedia.org/wiki/Sierpinski_triangle

https://en.wikipedia.org/wiki/Kakuro

Kakuro is a logic puzzle that involves quadrants

Sujiko is a logic based problem that involves quadrants

https://en.wikipedia.org/wiki/Sujiko

https://en.wikipedia.org/wiki/Mathematical_puzzle

Ken ken is a logic puzzle that involves quadrants

https://en.wikipedia.org/wiki/KenKen

https://www.target.com/p/otrio-board-game/-/A-52338707?sid=1307S&ref=tgt_adv_XS000000&AFID=google_pla_df&CPNG=PLA_Toys+Shopping_Local&adgroup=SC_Toys&LID=700000001170770pgs&network=g&device=c&location=9031022&gclid=Cj0KCQiA38jRBRCQARIsACEqIese4XJFLR0_GIN7ppWFN4YZ4q2QxHsQD6F4ry5zAbr1NqyoAG95cg4aAruJEALw_wcB&gclsrc=aw.ds

Wang tiles are quadrants

https://en.wikipedia.org/wiki/Wang_tile

https://en.wikipedia.org/wiki/Level_of_measurement

I learned the four levels of measurement at UCSD. The first thing that was taught in my statistics class was the four levels of measurement.

Level of measurement or scale of measure is a classification that describes the nature of information within the values assigned to variables.[1] The best known classification of levels of measurement was developed by psychologist Stanley Smith Stevens: nominal, ordinal, interval, and ratio.

The four levels are

nominal

interval

ordinal

ratio

https://ncatlab.org/nlab/show/normed+division+algebra

The figure above shows the fibonacci spiral

Approximate and true golden spirals: the green spiral is made from quarter-circles tangent to the interior of each square. The length of the side of a larger square to the next smaller square is in the golden ratio. Quarters are one fourths.

A Fibonacci spiral approximates the golden spiral using quarter-circle arcs inscribed in squares of integer Fibonacci-number side, shown for square sizes 1, 1, 2, 3, 5, 8, 13 and 21.

https://en.wikipedia.org/wiki/Golden_spiral

https://ncatlab.org/nlab/show/normed+division+algebra

Over the real numbers there are only four normed division algebras up to isomorphism: the algebras of

Real numbers

Quaternions

Complex numbers

Octonions

http://mathworld.wolfram.com/TetramagicSquare.html

https://en.wikipedia.org/wiki/Multimagic_square

Tetra is four. A tetramagic square is a magic square such that the first, second, third, and fourth powers of the elements all yield magic squares. The tetramagic square is transcendent. The first tetramagic square was discovered in 1983.

https://en.wikipedia.org/wiki/Euler%27s_four-square_identity

In mathematics, Euler's four-square identity says that the product of two numbers, each of which is a sum of four squares, is itself a sum of four squares.

https://en.wikipedia.org/wiki/Pfister%27s_sixteen-square_identity

Pfister’s sixteen square identity shows that, in general, the product of two sums of sixteen squares is the sum of sixteen rational squares. This is a popular theorem.

[oh-so-many-science-things]

Symmetry and Conservation in Physics: The Famous Work of Emmy Noether

The following is a paper written by me for the class MATH 23b: Introduction to Proofs at Brandeis University and is posted for course credit.

Noether’s Theorem was proven, as the name suggests, by the mathematician Emmy Noether  in 1918. While Noether was a mathematician, her famous theorem pertains to the field of physics, and is often regarded as one of the most important concepts in the field. Noether’s Theorem shows the connection between conservation laws and continuous symmetries of systems. It states that if there is a continuous symmetry in the Lagrangian of a system, then there is an associated conservation law. Before one can make sense of this, a few terms need to be discussed.

First is the definition of symmetry. Symmetry is a transformation which keeps the object it is being applied to “the same” in some sense of the word. For a symmetry to be continuous, it means that the scale of the transformation does not change the fact that the object is symmetric under that transformation. This is best understood through an example. Consider a circle, which has both reflective and rotational symmetry. If you cut the circle in half and flip it about that line some integer number of times it appears the same as before. This reflection is not a continuous symmetry however, because it can only be reflected an integer number of times and nothing in between. Now consider the rotational symmetry of a circle. If you rotate a circle about its center by some angle, it appears the same, regardless of the size of the angle by which you rotate it. This is what we mean by continuous symmetries.

The physics to which Noether’s Theorem pertains is called Lagrangian Mechanics which is build upon “the principle of least action.” This principle simply states that when considering the motion of an object, that object will minimize the quantity called the action3. The action is defined to be the time integral of the Lagrangian, which is some function of the generalized coordinates of the system considered and the derivatives of those coordinates. That’s a mouthful, but it comes down to this, the Lagrangian is: L=L(q,q’) for a set of generalized coordinates denoted by q where the prime denotes the derivative, and the action is: S[q(t)]=integral(L(q,q’)dt) from t to t+dt.  To minimize the action, we take its derivative and set that equal to zero, the outcome of which is the “Euler-Lagrange Equation:” dL/dq-(d/dx)(dLdq’)=0.

In Noether’s Theorem, the symmetries considered are continuous symmetries of the Lagrangian, meaning that for some coordinate q, L(q+q,dq’+dq’)=L(q,q’) for an arbitrary change in q, where q can be any of the coordinates of the system.  To minimize the action, we take its derivative and set that equal to zero, the outcome of which is the “Euler-Lagrange Equation:” dL/dq-(d/dx)(dLdq’)=0. If the Lagrangian is symmetric with respect to a coordinate q then we know that dL/dq=0 since the Lagrangian does not change with changes in the coordinate. This means that for a system with a Lagrangian symmetric in q, the Euler-Lagrange equation reads (d/dx)(dL/dq’)=0, and thus we say that the quantity dL/dq’=constant and thus is conserved for all time.  Some common symmetries in the Lagrangian are spatial translational, spatial rotational, and time translational symmetries, and these symmetries correspond to the conserved quantities; linear momentum, angular momentum, and energy respectively. For example when considering a particle with mass m in unaccelerated motion in one dimension, the classical Lagrangian is  L=(½)m(x’)^2 where this is the kinetic energy of the particle and the derivative of the position of this particle x’ is the velocity. From this the Euler-Lagrange Equation gives (d/dx)(mx’)=0 since the Lagrangian is symmetric in the x direction and thus mx’=constant. Where this conserved quantity mx’ is equal to the linear momentum of the particle. In other words, the linear momentum of the particle is conserved.

Noether’s Theorem shows a fundamental connection between mathematical symmetries in a system and the most important physical quantities. This connection is reflected in the common wording of Noether’s Theorem, “Where there is symmetry in a physical system, there is a conserved quantity associated with it.” This gives those working in physics an idea of where conservation comes from and how to find conservation laws, which allow for a much greater understanding of physical systems. This is why Noether’s Theorem came to be known as one of the most amazing concepts in physics.

References

1 Emmy Noether, Encyclopedia Britannica;https://www.britannica.com/biography/Emmy-Noether

2 The Noether Theorem, Columbia University; http://phys.columbia.edu/~nicolis/NewFiles/Noether_theorem.pdf

3 The Principle of Least Action, The Feynman Lectures, California Institute of Technology;             http://www.feynmanlectures.caltech.edu/II_19.html

[thousandmaths]

Math & Art Double Feature

This post represents two of the three talks given at the 2017 by Jim Henle.

------

The Art that is Mathematics

I went to this talk with some expectations about what this would be, and those turned out to be largely wrong. One of the first things he said in the talk is “Mathematics is beautiful, but that doesn’t make it an art. A sunset can be beautiful, but it cannot be art.” In particular, if it were an art: what are the objects? what makes it good? who is the public? who are the artists? 

However, what Henle argues is that there is, actually, an art in mathematics.

The objects are “mathematical structures”— anything that can be described completely and unambiguously. He gives examples: games, geometric diagrams, groups, number systems, set theories, etc.

The art is good if it engages the public to explore and play. (It is not, in particular, good because it is useful, nor because it is interconnected)

The public is heterogenous. It includes mathematicians [in the extended sense], discerning game-players, puzzlers, and people who enjoy “logical jokes”. In short, it can include roughly anyone, at roughly any point in time— although maybe not everyone at every point in time :)

An artist is “anyone who intends to create mathematical art”— as distinct from someone who intends to create mathematics.

After mulling on this definition for a while, you do what you’re supposed to do when you think you have discovered an art that nobody knew about before: you ask the philosophers about it. They had some questions:

“Can a proof be art?” Under this definition, no, not really. It’s theoretically possible, but its primary role is functional.

“Can a theorem be art?” Under this definition, not usually. But it’s a lot easier for a theorem to be art than a proof.

“Can a structure be art if it is created by a mathematician who is not an artist?” Yes, full stop.

So much for definitions. Any examples? 

Henle cites Dudeney as “possibly the first mathematical artist”. Later artists include Gardner, and Conway (who is Henle’s “candidate for the greatest mathematical artist [yet].”) On the side of the art itself he claims Euclid’s postulates, Pascal’s triangle, Penrose tiles, Fractals, and Sudoku, are among the masterpieces of this art.

------

The Affinity of Mathematics and Music is Cultural, not Technical

Again, I thought I knew what was coming here, but I didn’t, because I wasn't reading the word “affinity” in the right way. He begins the talk by admitting that there is tremendous technical connection between math and music. But his focus is on the special love for music that mathematicians seem to have.

Some evidence for this is found in college course enrollment:

Math majors are more likely than average to take music courses.

Math majors are less likely than average to take other art courses, including literature.

Music majors are less likely than average to take math courses.

Something which has been known for a while is that the musical periods (in the West) tend to be rather different than those for the visual arts. Henle took the defining features of those periods and attempted to map them onto the mathematics of the time. The results:

“Renaissance mathematics” was the period in which Western math advanced significantly beyond what the Greeks had done.

“Baroque mathematics” begins with Descartes.

“Classical mathematics” includes Euler, Lagrange, Laplace, & co.

“Romantic mathematics” deals with the ‘infinite and the impossible’, which he describes as from Galois to Cantor.

When you look at the timeline, what you find is that these periods line up much closer to the musical versions than to the other ones.

(source: Henle, personal communication)

It should be noted that the entire scheme here is quite Eurocentric, both from the maths side and from the arts side. This isn’t necessarily a problem because we are arguing that the cultures of math and music are tied together, and these cultural evolutions are easiest to track within particular cultural contexts. But of course, if you should show similar trends for the Islamic world, and for east Asia, etc., it would make a much more compelling argument.

[blog-normal-distribution]

My current moveset is

1. Sylow Theorems (proofs not included)

2. Euler-Lagrange Equations

3. The choreography to every tik tok dance

4. The time independent schrodinger equation

When it comes to maths my brain operates under pokemon's 4 move-slot mechanic

[aidloindia-blog]

CBSE Class 12th Math Syllabus

CBSE Class 12th Math Syllabus

Unit-I: Relations and Functions

1. Relations and Functions - 15 Periods Types of relations: reflexive, symmetric, transitive and equivalence relations. One to one and onto functions, composite functions, inverse of a function. Binary operations. 2. Inverse Trigonometric Functions - 15 Periods Definition, range, domain, principal value branch. Graphs of inverse trigonometric functions. Elementary properties of inverse trigonometric functions.

Unit-II: Algebra

1. Matrices 25 Periods Concept, notation, order, equality, types of matrices, zero and identity matrix, transpose of a matrix, symmetric and skew symmetric matrices. Operation on matrices: Addition and multiplication and multiplication with a scalar. Simple properties of addition, multiplication and scalar multiplication. Non- commutativity of multiplication of matrices and existence of non-zero matrices whose product is the zero matrix (restrict to square matrices of order 2).Concept of elementary row and column operations. Invertible matrices and proof of the uniqueness of inverse, if it exists; (Here all matrices will have real entries). 2. Determinants 25 Periods Determinant of a square matrix (up to 3 x 3 matrices), properties of determinants, minors, co-factors and applications of determinants in finding the area of a triangle. Adjoint and inverse of a square matrix. Consistency, inconsistency and number of solutions of system of linear equations by examples, solving system of linear equations in two or three variables (having unique solution) using inverse of a matrix.

Unit-III: Calculus

1. Continuity and Differentiability 20 Periods Continuity and differentiability, derivative of composite functions, chain rule, derivatives of inverse trigonometric functions, derivative of implicit functions. Concept of exponential and logarithmic functions. Derivatives of logarithmic and exponential functions. Logarithmic differentiation, derivative of functions expressed in parametric forms. Second order derivatives. Rolle’s and Lagrange's Mean Value Theorems (without proof) and their geometric interpretation. 2. Applications of Derivatives - 10 Periods Applications of derivatives: rate of change of bodies, increasing/decreasing functions, tangents and normals, use of derivatives in approximation, maxima and minima (first derivative test motivated geometrically and second derivative test given as a provable tool). Simple problems (that illustrate basic principles and understanding of the subject as well as real-life situations). 3. Integrals 20 Periods

4. Applications of the Integrals - 15 Periods Applications in finding the area under simple curves, especially lines, circles/ parabolas/ellipses (in standard form only), Area between any of the two above said curves (the region should be clearly identifiable). 5. Differential Equations 15 Periods Definition, order and degree, general and particular solutions of a differential equation. formation of differential equation whose general solution is given. Solution of differential equations by method of separation of variables, solutions of homogeneous differential equations of first order and first degree. Solutions of linear differential equation of the type:

Unit-IV: Vectors and Three-Dimensional Geometry

1. Vectors - 15 Periods Vectors and scalars, magnitude and direction of a vector. Direction cosines and direction ratios of a vector. Types of vectors (equal, unit, zero, parallel and collinear vectors), position vector of a point, negative of a vector, components of a vector, addition of vectors, multiplication of a vector by a scalar, position vector of a point dividing a line segment in a given ratio. Definition, Geometrical Interpretation, properties and application of scalar (dot) product of vectors, vector (cross) product of vectors, scalar triple product of vectors. 2. Three - dimensional Geometry - 15 Periods Direction cosines and direction ratios of a line joining two points. Cartesian equation and vector equation of a line, coplanar and skew lines, shortest distance between two lines. Cartesian and vector equation of a plane. Angle between (i) two lines, (ii) two planes, (iii) a line and a plane. Distance of a point from a plane.

Unit-V: Linear Programming

1. Linear Programming - 20 Periods Introduction, related terminology such as constraints, objective function, optimization, different types of linear programming (L.P.) problems, mathematical formulation of L.P. problems, graphical method of solution for problems in two variables, feasible and infeasible regions (bounded or unbounded), feasible and infeasible solutions, optimal feasible solutions (up to three non-trivial constraints).

Unit-VI: Probability

1. Probability 30 Periods Conditional probability, multiplication theorem on probability, independent events, total probability, Bayes’ theorem, Random variable and its probability distribution, mean and variance of random variable. Repeated independent (Bernoulli) trials and Binomial distribution.

Read the full article

[integralhistory]

Fermat’s Last Theorem

Pierre de Fermat: [1]

Life:

French Mathematician, 1601 - 1665

Founder of the modern theory of numbers

Received his baccalaureate in law from the university of orleans

By trade he was a councillor in the parliament in Toulouse (essentially a lawyer)

Jump to Mathematics

In the custom of his day, he began to reconstruct ancient mathematical works, the most inspiring to his work was a reconstruction of the 3rd century greek work “Plane Loci of Apollonius”, loci here meaning “points”

Through his study of loci (points), he discovered that you can use algebra to describe geometry through using a coordinate system.

Mathematical Contributions

Study of curves:

Generalized the form for a  parabola: ay = x^2

Generalized the form for a hyperbola: xy = a^2 to a^n - 1y = x^n

Generalized the form of the archimedean spiral: r = aθ

The study of these curves lead him to an algorithm that is equivalent to differentiation (derivatives), and to integration, though it is not known if he discovered that these operations are the inverse of one another

Fermat’s only published work in his lifetime was: “De Linearum Curvarum cum Lineis Rectis Comparatione” (“Concerning the Comparison of Curved Lines with Straight Lines”), he proved that certain algebraic curves were rectifiable (able to find the length of a curve), disproving the long lasting dogma from Aristotle, that curves are not precisely rectifiable.

Fermat’s Last Theorem:

x^n + y^n = z^n, where x, y, z, and n are positive integers, has no solution if n is greater than 2.

In the margin of the notebook where he stated this theorem he wrote “. I have discovered a truly marvelous demonstration of this proposition that this margin is too narrow to contain”. No proof was ever found posthumously.

Progress towards a proof:[2]

First Case:

exponents which are relatively prime to , , and

Sophie Germain (French Physicist, Mathematician, and philosopher) proved this case for any prime P, where 2P +1 is also a prime

Adrien-Marie Legendre (French Mathematicia), proved this case for any prime P such that  , , , , or are also primes. Through these discoveries, Fermat’s last theorem was proven for n < 100

In 1849, Ernst Kummer (German Mathematician), proved the first case for all regular primes and composite numbers for which regular primes are factors

Second case:

The exponent divides exactly one of Coeffiecients X, Y, and Z

1852, Vandiver’s criteria: a criteria for determining if an irregular prime P is the exponent in fermat’s last theorem if the theorem holds

1700s.Leonhard Euler (prolific swiss mathematician), proved general case for n = 3

1600s, Fermat proved the general case for n = 4

1800s Peter Dirichlet(German Mathematician) and Joseph-Louis Lagrange (italian mathematician), proved the general case for n= 5

1800s Dirichlet also proved the general case for n = 14

Late 1800s the n=7  case was proven by Gabriel Lamé (french mathematician)

Hiccups:

1937, Ferdinand Lindemann published several invalid “proofs” of fermat’s last theorem

1988, Yoichi Miyaoka published another false proof of fermat’s last theorem

In 1987, A prize of 100000 German marks, known as the Wolfskehl Prize, was also offered for the first valid proof

Further Exploration:

1909, Arthur Wieferich(German mathematician), proved that if the equation in fermat’s last theorem is solved in integers with an odd prime P, then  then 2^(p-1) is equivalent to 1(mod p^2), these numbers are called Wieferich Primes

1909, Dmitry Semionovitch Mirimanoff(Russian Mathematician), similarly proved 3^(p-1) is equivalent to 1 (Mod p^2)

Equations of the form above also hold with Coefficients 5,7,11,13,and 17.

1941, All of these number theory discoveries led the smallest possible prime that may be a counter example for fermat’s last theorem to be:2532 253 747 889, in the first case of the theorem

1988,Granville and Monagan showed if there exists a prime p satisfying Fermat's Last Theorem, then q^(p-1) is equivalent to 1 (mod p^2), bringing the smallest prime counterexample up to 714 591 416 091 398

Andrew Wiles[5]

English Mathematician Born in 1953

At the age of ten, Wiles picked up a book on fermat’s last theorem, and was amazed that such a simple sounding theorem still remained an open question, and set out to solve it

He eventually realized through his teens that proof would not be straightforward, and put off the task for two decades, to acquire more mathematical skill

While set up as a research fellow at oxford, and then princeton, between the years of 1986 and 1993, he took up the task of constructing the proof

Taniyama-Shimura conjecture:[6]

A general theorem connecting topology ( the study of geometry without regard to area, concerned with stretching, twisting, and deformation of objects (not tearing)), and number theory

the conjecture says that every rational elliptic curve is a modular form

Semistable case:[7]

An elliptic curve is semistable if, for all such primes l, only two roots become congruent mod l

Proof of the theorem:

In 1993, Andrew Wiles came out of mathematical hiding and revealed what he had spent the past 7 years to find, by proving the semistable case of the Taniyama Shimura Conjecture, he essentially got a proof of Fermat’s Last theorem for free

Hiccups:

Several holes were found in Wiles’ initial proof,but were quickly resolved with the help of Former research student Richard Taylor in 1994, and re-published in 1995

Legacy of the theorem [2]

Fermat’s last theorem was an open question for 350 years.

Fermat’s last theorem has even entered pop culture:

In the episode “Homer^3” of the simpsons, the formula: appears on the blackboard in the background. This is a near-miss solution, only correct to the first nine decimal places

The Wizard of Evergreen Terrace mentions , which is only correct to the first ten decimal points

At the start of Star Trek: The Next Generation episode "The Royale," Captain Picard mentions that studying Fermat's Last Theorem is a relaxing process.

Fermat probably didn’t have a proof of the theorem, as the techniques used are far beyond what he had access to at the time

Works Cited:

Contributor:Carl B. Boyer, Article Title:Pierre de Fermat, Website Name:Encyclopædia Britannica,Publisher:Encyclopædia Britannica, inc.,Date Published:February 22, 2017,URL:https://www.britannica.com/biography/Pierre-de-Fermat.Access Date:July 08, 2017

Weisstein, Eric W. "Fermat's Last Theorem." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/FermatsLastTheorem.html

Weisstein, Eric W. "Regular Prime." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/RegularPrime.html

Weisstein, Eric W. "Bernoulli Number." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/BernoulliNumber.html

., .. .. "Andrew Wiles." Famous Mathematicians. Famous Mathematicians, 26 Sept. 2016. Web. 08 July 2017.

Weisstein, Eric W. "Taniyama-Shimura Conjecture." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Taniyama-ShimuraConjecture.html

Weisstein, Eric W. "Semistable." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/Semistable.html

[thousandmaths]

Algebra? In *my* Counting Problem?

So a question I’ve had for a long time about algebraic combinatorics is: how necessary is the algebra, really?

I mean, there are often algebraic ways of formulating any particular counting problem, and so it certainly provides a language. That language may even be useful for narrowing down the essential bits and finding theorems which are relevant. But simpleminded attempts to do this often run into the issue that the resulting proof could really have been done just as easily with honest counting methods— indeed, some really basic results in algebra are often obtained by counting; Lagrange’s theorem comes to mind.

I feel kind of silly asking this question, since I spend so much time, on the blog and in real life, thinking about Schur functions and representations of the symmetric group, and invariant theory and other Coxeter groups... but yes, sometimes I do wonder to what extent that is all just hifalutin language for concepts could just as well be described with “respectable”, down-to-earth combinatorial calculations.

Vic Reiner gave a talk at the Intro to Research seminar last year about algebraic combinatorics; I figured that most of the content he would go over would be familiar to me (I was right), so I went in with this question intentionally in mind.

Something that was more surprising to me then than it is to me now is how much that talk focused on linear algebra. In hindsight this makes sense because we are incredibly more capable of doing computations with linear algebra than with literally anything else. So if we actually want honest numerical answers, we might want to look to linear algebra at some point.

Often the way that algebra gets involved is that we “linearize” a problem: this can be done, for instance, by taking the free module with standard basis being the objects we are trying to count, or even over a larger collection that contains the objects we want to count. In this way we form an object with considerably more structure, but retain the original counting information via the dimension. Then, perhaps by coming up with an isomorphism from this free module to something else we understand better, we can compute the dimension of that other thing, and then immediately declare that this is the dimension of the thing we want because of the isomorphism.

In the abstract, it’s quite feasible to imagine that we still haven’t managed to do anything substantial. The isomorphism would have to be rather complicated in order for it to not “just” be a linearization of something that we could have done by honest counting methods.

However, there is something that we get from linear algebra that we’re almost never going to get by simple counting, which is the existence of eigenvalues. So if we could instead recognize our solution as being bound up in the eigenvalues of some particular linear transformation, then it is now a matter of computing those eigenvalues. And for this we have a very powerful tool: similarity of matrices. Any two similar matrices have the same eigenvalues, so we can transfer our problem from the combinatorially motivated matrix to anything that happens to be convenient for computational purposes, as long as it is similar to the original matrix. 

[ Looking back on it, it’s a little surprising that I didn’t think of this idea earlier, considering my own difficulties with trying to combinatorialize a linear-algebra-because-eigenvalues proof in my senior thesis. I’m still not convinced that it can’t be done, so maybe this is not the greatest example, but at least it works for humanity’s current level of understanding :P ]

Of course, eigenvalues can have combinatorial interpretations, but the linked example, I think, is more in our favor than against us. The combinatorics is fairly unnatural, and would not have been reasonable to discover without the aid of the algebra. Even ignoring issues of discovery, there’s not any obvious connection between the answer and the question. As early as the first step: why should Robinson-Schensted show up? So although we can give a combinatorial interpretation for the eigenvalues, the disconnect— between the combinatorics of the question and the combinatorics of the answer— makes it seem unlikely that we could combinatorialize the entire proof.

If anyone else has experience with concrete benefits of introducing algebra into problems where it doesn’t seem to naturally be (combinatorial or otherwise), I’d love to hear your thoughts. 

[ Minor nitpick: if you’re going to tell me about how you use algebraic objects as invariants, I’d be happiest if you showed me some way in which you’re actually using the algebraic structure. For instance if your invariant is a finitely generated abelian group, that this is doing more than “packaging” the numbers which are its rank and invariant factors. ]

[mathematicianadda]

On the proof of $\;(1+x)^p\equiv1+x^p \pmod p$ https://ift.tt/eA8V8J

I know the proof for $(1+x)^p\equiv 1+x^p\mod p$ using the binomial theorem. Moreover, I know that $x^p \equiv x \mod p$ due to Fermat's theorem.

Hence, is $(1+x)^p\equiv(1+x)\equiv1+x^p \mod p$ a correct proof of this relation?

After thinking about it for a bit, one of the proof of Fermat's theorem uses the binomial theorem so my comments might have been redundant (although Fermat's theorem can be deduced from Lagrange's theorem).

I guess you can try to prove Fermat's by Pigeon hole:

Assuming $a\not\equiv 0$

$$a^i,\;\;1\le i \le p$$ takes $p$ values but $\mod p$ can only take $p-1$ distinct values ($a^p \not \equiv 0$ unless $a=0$) and so $a^i\equiv a^j$ and take inverses and the rest follows. If $a\equiv 0$, then the statement follows.

This can be extended to $(1+x)^{p^n}\equiv (1+x^{p^n})$ without using induction since $p |p^n$, then $$(1+x)^{p^n}\equiv (1+x)^{p\cdot{p^{n-1}}}\equiv 1+x \equiv 1+x^{p^n}$$

I have a gut feeling that says I overlooked something important.

If this is correct, what additional instructive value does the proof using the binomial theorem has that the Fermat's proof doesn't?

PS: I don't know what to say on the title. Feel free to edit it.

from Hot Weekly Questions - Mathematics Stack Exchange crystal_math from Blogger https://ift.tt/2zuOY1s