#spherical projection mapping

[dramatic-dolphin]

I looked it up once, and there is actually no real reason why north is up and south is down. A south-up map is just as easily readable, and throughout history there have been so many kinds of maps. In the medieval Middle East they usually made maps with south-up, mesieval European maps were often east-up, and there were also maps with no real orientation, with words and labels in all directions.

The actual reason seems that the colonization-era European cartographers who made the first world maps were basing the maps off the work of 2nd century Hellenic Egyptian cartographer Ptolemy, who, for some reason lost to us, put the north upwards. ....And that's it. It's really just one of many choices that got enshrined as tradition.

Also, the nothern hemisphere objectively having more land and people is SO true. I really like the polar equidistant projections for showing how weirdly north-heavy the current distribution of continents is (except for Antartica obviously). In a north pole-centered map, Australia is the worst off, getting squashed a little too much, but the other continents (except Antarctica. obviously.) keep their shape, even with Africa and South America becoming wider. In a south pole-centered projection, Asia, Europe, and North America are just... smeared all over the edge.

maps being "misleading" about the size of countries and continents is not a global conspiracy to make you think western countries are more important (bc size = importance obvs), it's because you can't accurately depict a sphere in 2d. it's literally not that deep.

[mysticstronomy]

WHY ARE THE MAPS OF THE COSMOS ALWAYS OVAL - SHAPED??

Blog#495

Welcome back,

Wednesday, April 9th, 2025.

The Universe is a vast and expansive place. From any location, you have total freedom to look in any direction you like: up or down, left or right, and near or far, to any distance in any direction that you choose. (Well, so long as there isn’t anything nearby in the way of a more distant object that you want to observe.) It’s like you have a buffet, an omnidirectional buffet, of targets to choose from.

You can even imagine observing it all: not just the half of the sky you can see by lying down in a field on a clear night, but in all directions all at once, like if you had an array of lenses that looked around in all 360° at once (plus the ability to view 90° up and down from the horizontal), that gathered light from all possible angles simultaneously.

And yet, when we show images of the cosmic microwave background — whether from COBE, WMAP, Planck, or a different mission — they’re almost always shown as oval-shaped. What does that oval shape actually show us, and why do astronomers make that specific visualization choice? That’s what Ed Matzenik wants to know, writing in to ask:

“I don’t understand the projections we see of the CMB. They are usually a circle or an oval. Is that the whole sky or just a section? If I was looking at a sphere from inside I don’t know how I’d represent it on a flat sheet…hope you can clear up this mystery for me.”

Honestly, the first time I encountered them — and remember, I’m a professional cosmologist who first encountered them in graduate school — I suffered from almost exactly the same puzzlement. Let’s begin with something we’re much more familiar with in order to get started: planet Earth.

This is going to sound obvious, but the first thing you have to realize about planet Earth is that, to a first approximation, its shape is spherical. The most accurate tool we use to model and represent planet Earth is a three-dimensional structure: a globe. A globe, after all, is spherical in shape, and when you see land masses and watery regions, the globe does an excellent job of displaying things accurately in a wide variety of ways.

Originally published on https://bigthink.com

COMING UP!!

(Saturday, April 12th, 2025)

"WHAT IF THE UNIVERSE IS ALIVE AND CONSCIOUS??"

[tanadrin]

Pr and the Mniw

Pr is a minor planet orbiting the millisecond magnetar MMR CHA J1712-2901 ("Ast"), about a thousand light years from Earth, in the constellation Sagittarius. Ast has four major planets: Wsjrhp, Hrw, Mnw, and Bstt. Hrw has one moon, Jmstj. There are five large minor planet in eccentric orbits within 3 AU, Jrb, Bjr, Rrj, Zr, and Pr.

Planetoid

Pr is a large asteroid with a rotation period of about two hours; its average density is less than 4 g/cm^3, but its internal composition is highly variable. About 40% of its solid material is composed of massive diamond fragments fused together at seams formed of carbon glass, and the interior of the planet contains a large irregular cavern roughly 250 kilometers in radius. This cavern is sufficiently enclosed to retain an envelope of water and air with minimal outgassing. Due to the very high rotation speed of the planetoid, the surface of the cavern, at its lower levels, experiences a centrifugal force about 1-2% of Earth's gravity. The axis of Pr's rotation is nearly perpendicular to its orbit.

No complete model of the formation of the Ast system has yet been offered, but several hypotheses have been suggested to account for some of its more unusual features. The formation of a protoplanetary disk may be due to the disruption of a stellar companion, or fallback from the supernova that formed Ast in the first place; the diamond fragments which make up Pr may have originated in a disrupted carbon-rich planet or planetoid, or gas giant. The interior atmosphere of Pr is perhaps due primarily to biological processes releasing volatiles into the cavern.

Deliberate planetary engineering has been mooted as a possibility, but the crew of the DSE Scholiast, the only vessel to survey the system so far, has not yet found evidence of such engineering by other civilizations, and the indigenous inhabitants of Pr are likely incapable of such undertakings at this time.

[Map of Pr, with some regions and bodies of water labelled, plus many major settlements. The relief of the cavern interior is very great; the large plateaus have scarps tens or hundreds of kilometers high. Note that the equilibrium potential at the interior surface of a rotating body is cylindrical, not spherical, and this projection is adjusted accordingly, and so shows true shapes near the poles. The nature of the geological processes that have shaped Pr's interior are not fully understood at this time. The total land area visible here is roughly equivalent to Texas or the Iberian Peninsula.]

Biology and Ecology

Pr's internal heat is maintained by the radiation from Ast, which is converted to thermal energy in Pr's crust. Thinner regions of the crust, particularly near the equator, have higher heat flow from the exterior; the high axial tilt of Pr also means that the northern and southern hemispheres can experience somewhat different heat flows throughout the year. Much more important to Pr's seasons, however, is the variability of Ast's magnetic field created by the eccentricity of Pr's orbit. When Pr is closest to Ast, organisms can extract energy from the magnetic field, as Pr's rotation allows them to create selective ion gradients whose diffusion provides energy, or to directly extract mechanical energy from electrically charged cilia. (Induced current is much too weak to be a useful source of biological energy).

As on Earth, the native lifeforms can be broadly classified into producers and consumers, but even the consumers on Ast obtain a significant portion of their energy budget from autotrophy, using heterotrophy only to supplement this budget. A minority of producers are also radiotrophs, who extract energy from the radioactive elements in Pr's crust.

Pr biology does not use DNA and is highly resistant to radiation. It also does not seem to experience Darwinian genetic drift. Instead, cells seem able to adapt their own internal machinery in response to certain kinds of stress, and to disseminate these changes throughout the organism, or even to conspecifics. The nature of this process and how it could have evolved is still a mystery, nor can they apparently account for all of the different forms observed among the native life.

The interior of Pr is dim, but not dark. Some plant species have evolved to emit light as a form of signaling, incentivizing some animal species to evolve eyes in response.

Because of the energy inefficiency of pure heterotrophy, to say nothing of pure heterotrophy that involves predating on other heterotrophs, no carnivorous animals are known on Pr.

[Above, the Mniw. The upper Mni has a fully-grown set of skin-plates; the lower Mni has either shed or removed hers, possibly as a cosmetic choice. The dark patches of skin shown are the rough beds from which the skin-plates grow.]

The Mniw

The Mniw (singular Mni) are the indigenous inhabitants of Pr. They are 12-18 centimeters long, with tough gray skin, and usually found with a mineralized defensive covering that grows out from the skin. They have a single sex, and reproduce via parthenogenesis. However, they still engage in a form of sexual intercourse, which is divorced from reproduction: instead, sex among the Mniw exists as a means of facilitating horizontal gene transfer, which then alters the nature of the offspring they bear. It can also allow a limited sharing of experiential memory. In addition to sight, hearing, and the other usual senses, the Mniw have the ability to sense the weak induced electrical currents in Pr's crust, which helps them perceive their environment better.

Mniw hatch from eggs and are generally raised in family units; they do not make sex-based distinctions, but do make social distinctions based on relationships. A mwt is the Mni who laid the egg; all other adults in the same household involved in childrearing are jtw; the sntw are siblings who share a mother, while other children raised in the same house are snw. Children from one's own eggs are srtw, while children from one's partner(s) are mnw.

As in humans, Mni adolesence is marked by gradual sexual maturity; reproductive fertility comes later in life, however, around the age of 30. Past 50, fertility declines slowly, as does the capacity to engage in horizontal gene transfer, though the capacity for sexual intercourse remains. Past 65 or so, Mniw enter their equivalent of "old age," but Mni do not experience a sudden collapse in their physiological health late in life, and can in principle life forever so long as they are not felled by accident, violence, or disease. In practice, lifespans are around 130-200 years, with a great deal of variability.

Mniw have many social elements, like hierarchy and emotions and social roles, that would not be entirely alien to humans, but they have no direct analogue to human sex roles or orientations. Instead the major cleavage in Mni society historically is between Mniw who tend to be primarily exogamous, preferring to mate and rear children with Mniw from distant communities, vs Mniw who tend to be primarily endogamous, with about 85% of Mniw being primarily endogamous; these traits perhaps evolved in the context of horizontal gene transfer to take advantage of different patterns of dissemination of useful traits.

Mniw can survive outside of Pr, but without a strong, moving magnetic field must consume a large amount of food; and the food they are normally adapted for will not grow at all absent such a field. An Earth-standard gravitational field would render them totally immobile, and would be extremely unpleasant, though probably not fatal, and it's possible given their unique physiology that they could eventually adapt to such an environment.

Mniw generally inhabit large, almost hive-like cities that are built out in three dimensions; historically, these could be strongly fortified against attack in a way that made wars of conquest nearly impossible until the invention of gunpowder. Mniw have had writing for about 5,000 years, and the first confederate states emerged around 3-4,000 years ago. The dissemination of gunpowder weapons 1,500 years ago radically altered politics and society on Pr, but the absence of easy paths to industrialization has caused a certain degree of stagnation since.

Modern Pr is divided into about a dozen large states, in an area of roughly 750,000 kilometers square, with a fair amount of diversity in languages, cultures, and social systems, given the small size of Pr. A very loose framework of international diplomacy is carried out through a series of councils called the Jaw Mwad, and on the occasion of the Scholiast's arrival, the Mniw convened a great council, a Wr Jaw Mwad, for the first time in over a century to open formal channels of communication.

[pseuddamntired]

Hmmm okay I have my shitty python script most of the way there. Basically, you know those stereographic projection sculptures Henry Segerman did? The 3d printed ones?

These:

https://youtu.be/lbUOScpu0ws?si=L0CtMawBZNWuzfdm

I want to do that with a lace sphere. Problem 1: map the intended shadow to a sphere.

Problem 2: project the spherical coordinates such that I can make the needlelace flat, with minimal distortion of the spherical image.

I got both of those figured out. So I can convert from the left photo below to the right photo below. Or. I can convert from a given photo to a maybe-not-too-distorted approximation of a flattened globe (I’m using an interrupted sinusoidal projection; if anyone even sees this and has suggestions for a better projection to use for this purpose, I would very much appreciate hearing about it. I got sick of reading about map projections very quickly).

The right image below would (hopefully, if I did it right) be the pattern that creates a sphere that will project the target image. It’s supposed to a tiling of abstract lotuses based on Greek pottery but. I don’t think they read very clearly. And they ended up upside down because I was checking that the coordinates were right by plotting them instead of converting them to an image. So. That’s a thing. I’ll fix it when I’m not tired of staring at my computer.

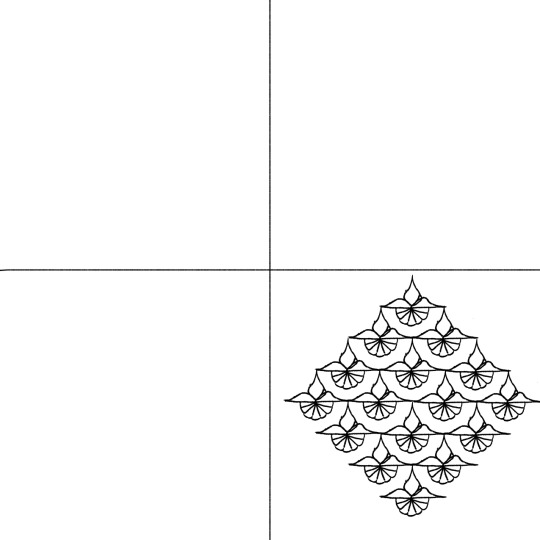
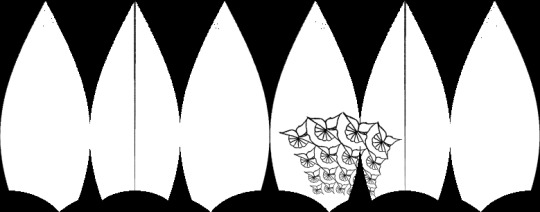
It will take forever to actually make a design I’m happy with and then execute it with thread, but I at least have the ability to make my computer do the projection for me now. Still have some things to work out regarding what maximum resolution i can use for the final image, but if need be I can fuss with the arguments until it’s a doable pattern.

[jymwahuwu]

Mini! reader x Aventurine + Ratio + Jade !! Various miniature cuteness <3 🫣😚

Mini! You live on a planet that is smaller than the average planet, and the people on it are as mini as you. This is what a normal body shape is for you. The residents of your planet once had dreams of trading, communicating and making friends. However, all this was overturned after the era of space travel - you found that people on other planets were taller and bigger than you, just like giants!! You... are only the size of their hands. Their maps, transportation, and all public facilities are not designed for your size… You are already climbing hard just to go down the stairs…

But, you want to run your business and don’t want to give up. You heard that IPC is openly recruiting stall owners to participate in the exhibition. You drive a pocket spaceship and knock on the door of IPC headquarters with samples. After arriving at the door, you parked the spaceship in the parking lot as required, and then used all your strength to open the door. Just as you pulled out a gap, someone stopped in front of you and looked at you condescendingly. You glared at him before continuing to push the door open and walk into the lobby.

The lobby of IPC is so luxurious that even the walls are decorated with money. The light shines softly on the information desk. On the ceiling is a huge spherical projection light, with golden and white as the main colors. There is also a statue of the famous Aeon Qlipoth.

Ugh, I really want to sleep already. That’s all for writing today...😴😴😴

[spacetimewithstuartgary]

X-Ray Imaging and Spectroscopy Mission unveils black hole and supernova remnant surroundings

The X-Ray Imaging and Spectroscopy Mission (XRISM) has revealed the structure, motion and temperature of the material around a supermassive black hole and in a supernova remnant in unprecedented detail. Astronomers presented the first scientific results of the new X-ray telescope today, less than a year after the telescope's launch.

What do a gigantic black hole and the remains of a massive, exploded star have in common? These are both dramatic celestial phenomena where extremely hot gas produces highly energetic X-ray light that XRISM can see.

In its first published results, XRISM, a mission led by the Japan Aerospace Exploration Agency (JAXA) with participation from ESA, shows its unique capabilities to reveal the speed and temperature of sizzling hot gas, called plasma, and the three-dimensional structures of material surrounding a black hole and an exploded star.

The research is published on the arXiv preprint server.

"These new observations provide crucial information in understanding how black holes grow by capturing surrounding matter, and offer a new insight into the life and death of massive stars. They showcase the mission's exceptional capability in exploring the high-energy universe," says ESA XRISM Project Scientist Matteo Guainazzi.

Supernova remnant N132D

In one of its "first light" observations, XRISM focused on N132D, a supernova remnant located in the Large Magellanic Cloud about 160 000 light-years from Earth. This interstellar 'bubble' of hot gas was expelled by the explosion of a very massive star approximately 3000 years ago.

Using its Resolve instrument, XRISM uncovered the structure around N132D in detail. Contrary to prior assumptions of a simple spherical shell, scientists found out that the remnant of N132D is shaped like a doughnut. Using the Doppler effect, they measured the speed (velocity) at which the hot plasma in the remnant is moving towards or away from us, and established that this is expanding at the apparent speed of around 1200 km/s

Resolve also revealed that the remnant contains iron that has an extraordinary temperature of 10 billion degrees Kelvin. The iron atoms were heated during the supernova explosion through violent shock waves spreading inwards, a phenomenon that had been predicted by theory, but never observed before.

Supernova remnants like N132D hold important clues into how stars evolve and how (heavy) elements that are essential to our life, like iron, are generated and spread out in interstellar space. Yet, previous X-ray observatories have always had difficulty revealing how the plasma's velocity and temperature were distributed.

Supermassive black hole in galaxy NGC 4151

XRISM has also shed new light on the mysterious structure surrounding a supermassive black hole. Focusing on the spiral galaxy NGC 4151, located 62 million light-years away from us, XRISM's observations offer an unprecedented view of the material very close to the galaxy's central black hole, which has a mass 30 million times that of the sun.

XRISM captured the distribution of the matter circling and ultimately falling into the black hole over a wide radius, spanning from 0.001 to 0.1 light-years, that is from about a distance comparable to the sun–Uranus separation to 100 times that.

By determining the motions of iron atoms from their X-ray signature, scientists mapped out a sequence of structures surrounding the giant black hole: from the disk 'feeding' the black hole all the way out to the doughnut-shaped torus.

These findings provide a vital piece of the puzzle in understanding how black holes grow by gobbling up surrounding matter.

Although radio and infrared observations have revealed the presence of a doughnut-shaped torus around black holes in other galaxies, XRISM's spectroscopic technique is the first, and currently only way to track down how the gas near the central 'monster' is shaped and moves.

Looking ahead: Future observations and discoveries

In the last months, the XRISM science team has diligently worked on establishing the instruments' performance and refine the data analysis methods by observing 60 key targets. In parallel,104 new set of observations were selected from the over 300 proposed submissions from scientists worldwide.

XRISM will conduct observations based on the successful proposals over the next year; thanks to its exceptional performance in orbit, surpassing even initial expectations, this promises many more exciting discoveries to come.

TOP IMAGE: This image shows JAXA’s XRIMS X-ray telescope observation of supernova remnant N132D. This supernova is the result of a stellar explosion approximately 3000 years ago in the Large Magellanic Cloud, 160 000 light-years away from Earth. At the top of the image, the supernova remnant is shown in X-ray light. The yellow circle depicts the area where XRISM’s instrument Resolve measured extremely hot iron (10 billion degrees Kelvin). The pink line shows the rim of the remnant, where the blast wave interacts with the interstellar medium, and the hot gas (plasma) is cooler (around 10 million degrees Kelvin). The spectrum shows many chemical elements that are present in N132D. XRISM can identify each element by measuring the energy of the X-ray photon specific to different atoms. The label 'keV' on the x-axis of the graph refers to kiloelectronvolts, a unit of energy. The ‘energy resolution’ of XRISM, that is its capability to distinguish X-ray light with different wavelengths, is ground-breaking. With 30 times the resolution of its predecessors, XRISM’s advanced spectroscopic capabilities enable scientists to measure the motion and temperature of the hot plasma with unprecedented precision. Credit: JAXA

CENTRE IMAGE: JAXA’s XRISM X-ray telescope captured the distribution of matter falling into the supermassive black hole in galaxy NGC 4151 over a wide radius, spanning from 0.001 to 0.1 light-years. By determining the speed of the iron atoms from their X-rays signature, scientists have mapped out a sequence of structures surrounding the central ‘monster’: the disk closest to the black hole (in blue) where gas moves at a speed a few percent of the speed of light, followed by a transition region where gas is moving at speed of thousands of km/s and which astronomers call “the broad line region (BLR)” (in orange) , and finally the doughnut-shaped torus (in red). Credit: JAXA

LOWER IMAGE: XRISM will study the Universe in X-ray light with an unprecedented combination of light collecting power and energy resolution – the capability to distinguish X-rays of different energies. The mission will provide a picture of the dynamics in galaxy clusters, the chemical make-up of the Universe and the flow of matter around accreting supermassive black holes (Active Galactic Nuclei or AGN), among many other topics. Credit: European Space Agency

[seradae]

I think I just solved a huge problem that's been plaguing me for over a year. Finally. In short: where do you put a set of orbital rings around the Earth in order to maximize the number of people who can make use of them? I've tried a dozen different approaches but they've all boiled down to two basic techniques: pick two cities, connect them with an orbital ring, see how many people are within range of it; or pick a random ring orientation, see how many people are within range of it. Both of these are computationally expensive as hell (the more cities you're checking, the slower it is), and are unlikely to give you anything close to an optimal solution, especially since you need to drastically reduce the number of population centers you're checking in order to make it work ... Basically at all. I could only test about 70% of the world's population, unless I wanted to let it run for weeks.

I've known there had to be a better solution, but this is a novel problem and I couldn't put the pieces together. Typically when you're trying to solve a hard problem in math, it's best to find a new way of looking at it, which reduces the complexity and/or transforms it to a known problem. Today, I finally managed to do that.

Instead of looking at the earth as a sphere with cities on it, I can use a gnomonic projection. This is a projection that's utterly useless for most cases, because it doesn't preserve area, distances, or anything like that -- but it does make all great circles into straight lines, and all lines are great circles. (Great circles are what you get when you have a plane cutting through the center of a spherical body -- they neatly define the orientation of an orbital ring, but are also used for flight planning since they give you the shortest path.)

So I can start with an empty (and very large) image and for each population center, draw the radius around it that represents the distance a tether could reach from an orbital ring. Transform that into the gnomonic space (we can invert the southern hemisphere to do a single map), and draw it into that image. Instead of writing the population into the image, you have an ID that represents which city or cities are in that "pixel" of the map, so that you know which population centers are being touched, without overcounting them.

Once you've computed that map, all you have to do is draw lines on it and see which line has the highest total population. Because we have a fuck-off huge map, this would also be expensive, but we can do it in passes: start with downsampled versions of the map to get rough estimates, then refine iteratively. This will greatly speed it up.

It's completely independent of the number of population centers you have to work with -- the performance is 100% determined by the resolution you're using in gnomonic space. Depending on how you find the line of best fit, you're not guaranteed an optimal solution, but you're likely to get very very very close. I suspect that my original estimate of a single equatorial ring + 15 additional rings will be able to cover over 90% of the world's population; I'm curious how correct I am when I implement this.

This will be a huge step towards showing the efficacy of my design, if I'm right 🥹 C'mon space trains!

[shilohta]

Not yet it's final evolution but finished enough for the requirements of this week's course, I present "And While The Fires Are Burning, Let's Make A Bunch More Gasoline (with apologies to Geoff Berner's Super Subtle Folk Song)" aka my "the oceans are full of plastic and the world is on fire" piece.

Needle punched on wool fabric with strips of reusable Walmart bags (from some of my instacart customers), and blue yarn (75% acrylic 25% wool, originally from Zellers), continents of wet felted wool that was ripped with a seam ripper to pull up the wisps of fire. Wooden safety matches.

Below are some of the challenges of constructing this piece. Cutting the felt open with a steak knife (because I was too lazy to go back to my desk for my scissors/ knew that if I got my scissors I would forget them in the dye kitchen and stress about having lost them in my messy desk). Testing various plastic strips (realizing the project would go faster if I paired the plastic with acrylic yarn). The plastic recycling bag that wrapped around the cutting blade. My pile of cut walmart worms. Using a drop spindle to ply the Walmart worms with the yarn (also showing off the Oxford punch needle the instructor brought in). Figuring out how to assemble the globe (I stapled 5 of the seams and did a ladder stitch to close the final seam. I should have hand stitched all of them but there's no way I could have machine stitched it, especially turning it inside out). And then mapping out the continents onto a spherical surface. That took a fair bit of time and troubleshooting. I made paper templates so I could test proportions before committing to cutting them out of my felt. I tried to add more detail to North America but it ended up quite wonky. Eurasia was a struggle but I ended up piecing it together with smaller sections, which also created mountain ranges.

Future plans: this is my contribution to the interdepartment collaboration on the theme of Nature and the Environment. I could add more handstitching and embellishment to the continents. I would like to refine my matches placement and create charms of oil and gas company logos to hang from the matches (likely using embroidery on water soluble material so they're light and airy).

I think I will abandon my dream of having actual fire on this piece, for safety reasons. However for the exhibition I think it would be fun to freeze ice onto the poles and let it slowly melt, as a sort of performance piece.

[michaeldswanson]

Apple’s Mysterious Fisheye Projection

If you’ve read my first post about Spatial Video, the second about Encoding Spatial Video, or if you’ve used my command-line tool, you may recall a mention of Apple’s mysterious “fisheye” projection format. Mysterious because they’ve documented a CMProjectionType.fisheye enumeration with no elaboration, they stream their immersive Apple TV+ videos in this format, yet they’ve provided no method to produce or playback third-party content using this projection type.

Additionally, the format is undocumented, they haven’t responded to an open question on the Apple Discussion Forums asking for more detail, and they didn’t cover it in their WWDC23 sessions. As someone who has experience in this area – and a relentless curiosity – I’ve spent time digging-in to Apple’s fisheye projection format, and this post shares what I’ve learned.

As stated in my prior post, I am not an Apple employee, and everything I’ve written here is based on my own history, experience (specifically my time at immersive video startup, Pixvana, from 2016-2020), research, and experimentation. I’m sure that some of this is incorrect, and I hope we’ll all learn more at WWDC24.

Spherical Content

Imagine sitting in a swivel chair and looking straight ahead. If you tilt your head to look straight up (at the zenith), that’s 90 degrees. Likewise, if you were looking straight ahead and tilted your head all the way down (at the nadir), that’s also 90 degrees. So, your reality has a total vertical field-of-view of 90 + 90 = 180 degrees.

Sitting in that same chair, if you swivel 90 degrees to the left or 90 degrees to the right, you’re able to view a full 90 + 90 = 180 degrees of horizontal content (your horizontal field-of-view). If you spun your chair all the way around to look at the “back half” of your environment, you would spin past a full 360 degrees of content.

When we talk about immersive video, it’s common to only refer to the horizontal field-of-view (like 180 or 360) with the assumption that the vertical field-of-view is always 180. Of course, this doesn’t have to be true, because we can capture whatever we’d like, edit whatever we’d like, and playback whatever we’d like.

But when someone says something like VR180, they really mean immersive video that has a 180-degree horizontal field-of-view and a 180-degree vertical field-of-view. Similarly, 360 video is 360-degrees horizontally by 180-degrees vertically.

Projections

When immersive video is played back in a device like the Apple Vision Pro, the Meta Quest, or others, the content is displayed as if a viewer’s eyes are at the center of a sphere watching video that is displayed on its inner surface. For 180-degree content, this is a hemisphere. For 360-degree content, this is a full sphere. But it can really be anything in between; at Pixvana, we sometimes referred to this as any-degree video.

It's here where we run into a small problem. How do we encode this immersive, spherical content? All the common video codecs (H.264, VP9, HEVC, MV-HEVC, AVC1, etc.) are designed to encode and decode data to and from a rectangular frame. So how do you take something like a spherical image of the Earth (i.e. a globe) and store it in a rectangular shape? That sounds like a map to me. And indeed, that transformation is referred to as a map projection.

Equirectangular

While there are many different projection types that each have useful properties in specific situations, spherical video and images most commonly use an equirectangular projection. This is a very simple transformation to perform (it looks more complicated than it is). Each x location on a rectangular image represents a longitude value on a sphere, and each y location represents a latitude. That’s it. Because of these relationships, this kind of projection can also be called a lat/long.

Imagine “peeling” thin one-degree-tall strips from a globe, starting at the equator. We start there because it’s the longest strip. To transform it to a rectangular shape, start by pasting that strip horizontally across the middle of a sheet of paper (in landscape orientation). Then, continue peeling and pasting up or down in one-degree increments. Be sure to stretch each strip to be as long as the first, meaning that the very short strips at the north and south poles are stretched a lot. Don’t break them! When you’re done, you’ll have a 360-degree equirectangular projection that looks like this.

If you did this exact same thing with half of the globe, you’d end up with a 180-degree equirectangular projection, sometimes called a half-equirect. Performed digitally, it’s common to allocate the same number of pixels to each degree of image data. So, for a full 360-degree by 180-degree equirect, the rectangular video frame would have an aspect ratio of 2:1 (the horizontal dimension is twice the vertical dimension). For 180-degree by 180-degree video, it’d be 1:1 (a square). Like many things, these aren’t hard and fast rules, and for technical reasons, sometimes frames are stretched horizontally or vertically to fit within the capabilities of an encoder or playback device.

This is a 180-degree half equirectangular image overlaid with a grid to illustrate its distortions. It was created from the standard fisheye image further below. Watch an animated version of this transformation.

What we’ve described so far is equivalent to monoscopic (2D) video. For stereoscopic (3D) video, we need to pack two of these images into each frame…one for each eye. This is usually accomplished by arranging two images in a side-by-side or over/under layout. For full 360-degree stereoscopic video in an over/under layout, this makes the final video frame 1:1 (because we now have 360 degrees of image data in both dimensions). As described in my prior post on Encoding Spatial Video, though, Apple has chosen to encode stereo video using MV-HEVC, so each eye’s projection is stored in its own dedicated video layer, meaning that the reported video dimensions match that of a single eye.

Standard Fisheye

Most immersive video cameras feature one or more fisheye lenses. For 180-degree stereo (the short way of saying stereoscopic) video, this is almost always two lenses in a side-by-side configuration, separated by ~63-65mm, very much like human eyes (some 180 cameras).

The raw frames that are captured by these cameras are recorded as fisheye images where each circular image area represents ~180 degrees (or more) of visual content. In most workflows, these raw fisheye images are transformed into an equirectangular or half-equirectangular projection for final delivery and playback.

This is a 180 degree standard fisheye image overlaid with a grid. This image is the source of the other images in this post.

Apple’s Fisheye

This brings us to the topic of this post. As I stated in the introduction, Apple has encoded the raw frames of their immersive videos in a “fisheye” projection format. I know this, because I’ve monitored the network traffic to my Apple Vision Pro, and I’ve seen the HLS streaming manifests that describe each of the network streams. This is how I originally discovered and reported that these streams – in their highest quality representations – are ~50Mbps, HDR10, 4320x4320 per eye, at 90fps.

While I can see the streaming manifests, I am unable to view the raw video frames, because all the immersive videos are protected by DRM. This makes perfect sense, and while I’m a curious engineer who would love to see a raw fisheye frame, I am unwilling to go any further. So, in an earlier post, I asked anyone who knew more about the fisheye projection type to contact me directly. Otherwise, I figured I’d just have to wait for WWDC24.

Lo and behold, not a week or two after my post, an acquaintance introduced me to Andrew Chang who said that he had also monitored his network traffic and noticed that the Apple TV+ intro clip (an immersive version of this) is streamed in-the-clear. And indeed, it is encoded in the same fisheye projection. Bingo! Thank you, Andrew!

Now, I can finally see a raw fisheye video frame. Unfortunately, the frame is mostly black and featureless, including only an Apple TV+ logo and some God rays. Not a lot to go on. Still, having a lot of experience with both practical and experimental projection types, I figured I’d see what I could figure out. And before you ask, no, I’m not including the actual logo, raw frame, or video in this post, because it’s not mine to distribute.

Immediately, just based on logo distortions, it’s clear that Apple’s fisheye projection format isn’t the same as a standard fisheye recording. This isn’t too surprising, given that it makes little sense to encode only a circular region in the center of a square frame and leave the remainder black; you typically want to use all the pixels in the frame to send as much data as possible (like the equirectangular format described earlier).

Additionally, instead of seeing the logo horizontally aligned, it’s rotated 45 degrees clockwise, aligning it with the diagonal that runs from the upper-left to the lower-right of the frame. This makes sense, because the diagonal is the longest dimension of the frame, and as a result, it can store more horizontal (post-rotation) pixels than if the frame wasn’t rotated at all.

This is the same standard fisheye image from above transformed into a format that seems very similar to Apple’s fisheye format. Watch an animated version of this transformation.

Likewise, the diagonal from the lower-left to the upper-right represents the vertical dimension of playback (again, post-rotation) providing a similar increase in available pixels. This means that – during rotated playback – the now-diagonal directions should contain the least amount of image data. Correctly-tuned, this likely isn’t visible, but it’s interesting to note.

More Pixels

You might be asking, where do these “extra” pixels come from? I mean, if we start with a traditional raw circular fisheye image captured from a camera and just stretch it out to cover a square frame, what have we gained? Those are great questions that have many possible answers.

This is why I liken video processing to turning knobs in a 747 cockpit: if you turn one of those knobs, you more-than-likely need to change something else to balance it out. Which leads to turning more knobs, and so on. Video processing is frequently an optimization problem just like this. Some initial thoughts:

It could be that the source video is captured at a higher resolution, and when transforming the video to a lower resolution, the “extra” image data is preserved by taking advantage of the square frame.

Perhaps the camera optically transforms the circular fisheye image (using physical lenses) to fill more of the rectangular sensor during capture. This means that we have additional image data to start and storing it in this expanded fisheye format allows us to preserve more of it.

Similarly, if we record the image using more than two lenses, there may be more data to preserve during the transformation. For what it’s worth, it appears that Apple captures their immersive videos with a two-lens pair, and you can see them hiding in the speaker cabinets in the Alicia Keys video.

There are many other factors beyond the scope of this post that can influence the design of Apple’s fisheye format. Some of them include distortion handling, the size of the area that’s allocated to each pixel, where the “most important” pixels are located in the frame, how high-frequency details affect encoder performance, how the distorted motion in the transformed frame influences motion estimation efficiency, how the pixels are sampled and displayed during playback, and much more.

Blender

But let’s get back to that raw Apple fisheye frame. Knowing that the image represents ~180 degrees, I loaded up Blender and started to guess at a possible geometry for playback based on the visible distortions. At that point, I wasn’t sure if the frame encodes faces of the playback geometry or if the distortions are related to another kind of mathematical mapping. Some of the distortions are more severe than expected, though, and my mind couldn’t imagine what kind of mesh corrected for those distortions (so tempted to blame my aphantasia here, but my spatial senses are otherwise excellent).

One of the many meshes and UV maps that I’ve experimented with in Blender.

Radial Stretching

If you’ve ever worked with projection mappings, fisheye lenses, equirectangular images, camera calibration, cube mapping techniques, and so much more, Google has inevitably led you to one of Paul Bourke’s many fantastic articles. I’ve exchanged a few e-mails with Paul over the years, so I reached out to see if he had any insight.

After some back-and-forth discussion over a couple of weeks, we both agreed that Apple’s fisheye projection is most similar to a technique called radial stretching (with that 45-degree clockwise rotation thrown in). You can read more about this technique and others in Mappings between Sphere, Disc, and Square and Marc B. Reynolds’ interactive page on Square/Disc mappings.

Basically, though, imagine a traditional centered, circular fisheye image that touches each edge of a square frame. Now, similar to the equirectangular strip-peeling exercise I described earlier with the globe, imagine peeling one-degree wide strips radially from the center of the image and stretching those along the same angle until they touch the edge of the square frame. As the name implies, that’s radial stretching. It’s probably the technique you’d invent on your own if you had to come up with something.

By performing the reverse of this operation on a raw Apple fisheye frame, you end up with a pretty good looking version of the Apple TV+ logo. But, it’s not 100% correct. It appears that there is some additional logic being used along the diagonals to reduce the amount of radial stretching and distortion (and perhaps to keep image data away from the encoded corners). I’ve experimented with many approaches, but I still can’t achieve a 100% match. My best guess so far uses simple beveled corners, and this is the same transformation I used for the earlier image.

It's also possible that this last bit of distortion could be explained by a specific projection geometry, and I’ve iterated over many permutations that get close…but not all the way there. For what it’s worth, I would be slightly surprised if Apple was encoding to a specific geometry because it adds unnecessary complexity to the toolchain and reduces overall flexibility.

While I have been able to playback the Apple TV+ logo using the techniques I’ve described, the frame lacks any real detail beyond its center. So, it’s still possible that the mapping I’ve arrived at falls apart along the periphery. Guess I’ll continue to cross my fingers and hope that we learn more at WWDC24.

Conclusion

This post covered my experimentation with the technical aspects of Apple’s fisheye projection format. Along the way, it’s been fun to collaborate with Andrew, Paul, and others to work through the details. And while we were unable to arrive at a 100% solution, we’re most definitely within range.

The remaining questions I have relate to why someone would choose this projection format over half-equirectangular. Clearly Apple believes there are worthwhile benefits, or they wouldn’t have bothered to build a toolchain to capture, process, and stream video in this format. I can imagine many possible advantages, and I’ve enumerated some of them in this post. With time, I’m sure we’ll learn more from Apple themselves and from experiments that all of us can run when their fisheye format is supported by existing tools.

It's an exciting time to be revisiting immersive video, and we have Apple to thank for it.

As always, I love hearing from you. It keeps me motivated! Thank you for reading.

[bad-dagon]

riemann spheres as a fundamental type, pt.1 basics

ive been thinking on and off about riemann spheres for a while now, a couple weeks really, and so far i think there's some utility to them as a building block of a type system of some kind for a joke/toy computer language

background: riemann spheres are a neat tool in complex analysis where we imagine a sphere whose equator intersects the complex plane, and every number on the complex plane is representable by a point on the sphere such that a line is projected from the north pole and through that point onto the complex plane. naturally, this means that the north pole is P(∞) and the south pole is P(0). see below how that would look like with other unit points of the complex numbers

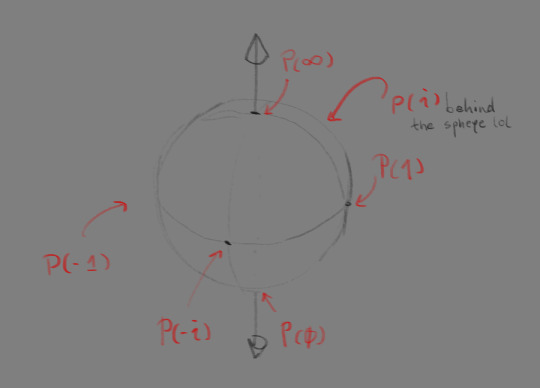
a neat thing the riemann sphere allows us is to define meaningful division by zero so now z/0 = ∞ clean and simple! and also its inverse, z/∞ = 0 is well behaved as well. this simplifies doing complex analysis but stereographic projection is an absolute bitch to work with turns out, and doing arithmetic on points on the sphere is a mess because it's not a linear mapping (it's continuous though so that's fine)

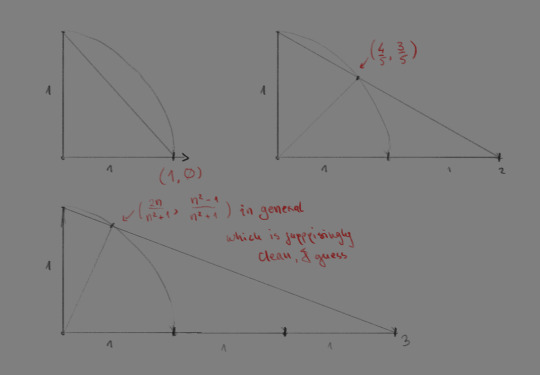
if we're dealing with ONLY real numbers in relation to a circular slice of the riemann sphere, it already starts looking like a mess; for any number n∈R its projective cognate on the circle is located at (2n/n²+1, n²-1/n²+1). on the real riemann sphere though? zoo wee mamma

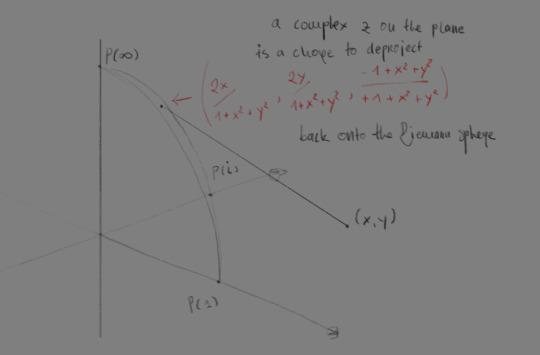
an arbitrary z∈C, represented as a point (x,y) on the complex plane, has to walk through a rather ugly mapping (related to the previous one) to find its point on the sphere; more accurately, given the coordinates (x,y) of the point on the plane, the point on the sphere is located at (2x/1+x²+y², 2y/1+x²+y², -1+x²+y²/1+x²+y²), which is godawful in spherical-to-polar coordinate terms, this is much simpler; for a polar pair (r,θ) the point on the unit sphere representing it is (φ,ξ) = (2*arctg 1/r, θ); and conversely projecting from the riemann sphere is also dead simple, given the zenith-azimuth pair (φ,ξ), (r,θ) = (ctg φ/2, ξ). of course, translating from polar to real coordinates is ALSO dead simple; x = r * cos θ, y = r * sin θ. if a computer system were to store complex numbers (or any coordinate on a 2d plane really), it makes sense to store them in terms of spherical coordinates of a riemann sphere, since this makes infinity well-behaved as a unit (zenith = 0, azimuth = literally who gives a fuck) and is surprisingly efficient. knowing that the zenith is ∈[0,π] and azimuth ∈[0, 2π] can allow for some formidably dumb optimisations that can save on space and ensure granularity. compared to storing them as 2d cartesian or polar coordinates, this provides the benefit of having neither number be larger than like 6.3, so an underlying/backing type that can offer great precision in this small range would be more efficient numerically than, say, floating points which have insane baggage and gaps

or iunno i'll look into that one a bit later, i'm just kind of furious right now that i rederived stereographic projection on my own when the formulas were right fucking there if id only just googled for them

[thisnameisnotspokenfor]

The Kingdom of the Stars Chapter 4: The Proposition

((ooc: Merry Christmas to all of my tumblr followers/readers!))

Previous: Chapter 3

Next: Chapter 5

 They made their way down the hallway, as several servants stopped to bow to their passing king.

It wasn’t until Asha recognized the familiar sight of the west wing’s door did she began to feel nervous. 

He wasn’t going to take her down here, was he?

With a simple gesture, she watched the doors open themselves for the king as he stepped through. For a moment she hesitated, but after a minute or so of reassurance, she quietly followed the king through the doors. 

Why was he taking her here? She wondered as she hesitantly followed him past the doors into another quiet room where there were three doors. All like the doors before had strange markings engraved into their frames. Runes, perhaps? She wasn’t sure, but something about them felt…different, even ominous.

Beside her, the king stopped, only to spare her a brief look before he said, “Do you know why you’re here Asha?”

“Not exactly your highness,” she confessed. Part of her was hoping that it hadn’t been to unleash whatever secret magical creature he’d hidden down here on her as punishment for her treason.

She held her breath as she watched him push the door open, revealing a large room that was thankfully absent of any mythical creature. Quietly, she followed him toward the room’s center. A sense of awe filled her as she took in the architecture of the room. Its tall windows in combination with the beautiful starry sky that had been painted on the ceiling left her feeling breathless. 

“Does it look familiar?” he asks, a grin appearing on his face. 

“This…this was one of my first star maps,” she breathed. “I made it back when my father was still here, and he’d take me stargazing.”

“I could tell. You remember showing it to us don’t you?” he asked as she gave him a brief nod. “It was always one of Amaya’s favorites. So, we were thinking that it was only fair that our apprentice of 5 years got to see the wish room, especially when we’d made her maps one of the more…permanent additions.”

“The wish room?” she repeated, feeling stunned as the glowing orbs came into view overhead. 

He nods, as she watches the glowing, spherically shaped wishes of various colors slowly descend towards them. Some were bigger than others she noted, as the faint outlines of shapes and figures materialized as they neared. She could hear them, the sounds of laughter and voices talking as the wishes began to surround them. They’d looked just as she’d seen them in the wishing gardens, where people went to distribute their wishes to the king. 

To anyone such a sight would’ve evoked a sense of wonder and beauty, but to Asha, she couldn’t help but feel… Skeptical? Disappointed? Maybe even angry? 

She wasn’t sure how to explain it as she frowned, and quickly stepped out of the way of another wish that had begun to float towards her. 

This hadn’t been her first time seeing a wish, as she’d remembered asking the king about her Saba’s wish a few years ago. It’d been his birthday and she’d wondered whether or not the king would grant his wish that he’d kept for years. So, after mustering up what little courage she could, she’d asked him, and to her surprise, he’d patiently answered. He’d selected her grandfather’s wish before promptly telling her that he wouldn’t grant it. Of course, she’d been a bit tempted to argue, but the arguments had immediately died down when she’d seen what said wish was.

At first, it depicted her Saba cheerfully playing his mandolin. Something that she’d deemed quite harmless. Then it’d shown her Saba cheerfully playing said mandolin while riding a fire-breathing dragon. Alright, so maybe his wish hadn’t been that harmless. She’d unfortunately conceded that point to the king.

Not all wishes were meant to be granted.

The sounds of the smaller wishes filled her ears as she could hear a middle-aged man wishing for someone to help him with his garden, and an elderly woman wishing for company.

She cast a glance in Magnifico’s direction, taking note of the serene yet happy expression his face held as he gently examined the wish in his hand. It was at moments like these that Magnifico truly resembled the king she’d read of in fairy tales. The ruler who fought the stars to protect the wishes of his people.  The man whom her father had befriended and admired. A man who she too, could fully respect.

She could tell that these wishes had meant everything to him, and with his dying breath, he’d ensure that they would always be protected. 

Quietly, he began to hum as the sounds of a gentle lullaby made itself known. One that felt so melancholic yet comforting at the same time.

“I’m truly honored Your Highness,” she softly says with a curtsy. 

“As you should be. With the dawn of a new era upon us, there will be no time to be stuck dwelling in the past. We should all be moving forward as the best way to prevent history from repeating itself is to understand and know your future. Do you understand?”

“Yes Your Highness,” she nodded, although she’d felt that his words had been more of a command than a question. 

“Good,” she watched as the wish slowly distanced itself from his fingers as he turned to her. “This is why we must move on- to protect what is important from those who would seek to destroy it at all costs.”

She nodded, and a brief image of the monsters he’d fought from the murals came to mind.

Part of her thought that such creatures were nothing more than exaggerations of past foreign enemies.

After all of her studies, Asha was confident that stars weren’t real monsters. She believed stars were nothing more than distant wonders of nature. 

Nothing more and nothing less. 

“Where are these wishes from?” she asked, glancing around at the wishes that surrounded them. 

“They’re from Banquo.” the king answered, sounding a tad bit distracted. 

The western part of Rosas, she noted, was just where the girl’s wish had been from as well. 

 “But speaking of Banquo, that reminds me. I have a proposition for you, something that I think you’d be interested in.” 

“What…sort of proposition?” Asha asked, feeling her nerves begin to take hold of her once more.

“Well think of it like this, you want time off, correct? And I want you to stay around to help with the Astral Ball. So, I’ve devised a compromise of sorts. I will give you the day of the Astral Ball off- if , and only if   you can finish the tasks I’ve given you by tomorrow nightfall.”

“Really? Well, what sort of tasks would you like me to do, your highness?”

He chuckled. Uh oh. “Well I’m glad you asked,” he says before withdrawing an extensively long scroll from thin air. Oh no . “I’m going to need you to oversee the decorations of the western and eastern markets, ensure all the shipments have arrived and are in their proper places,  and -,”

“And?” Asha squeaked, nearly giving into despair.

“I will need you to tell my nephew that his presence is requested for the ball.”

Asha nearly choked when she heard that. 

His nephew? 

Prince Ignacio?

He hadn’t been seen or heard from in months! No one knew where he was! How was she supposed to find him and convince him to come home in less than a day?! 

“Do you think you can do all of that?” he says while giving her a look that said he most definitely knew she could not. Missing royal nephew aside, getting the markets dressed to the nines in time would be impossible- how was she going to travel the island in less than a day?! 

“W-well, I-,” she begins.

“You know what?” he called, looking way too amused at her hesitation. “ I’m feeling generous today, so I’ll even throw in this offer. If you get all of these things done on time, not only will I grant you time off, but I’ll even consider funding one of your little projects! How does that sound?”

Oh, he definitely didn’t think she could do this on time, but the offer of funding for one of her projects sounded too good to pass up. It could be the solution she’d long since dreamed of- a way out of all of the dead ends of frustrations she’d been feeling lately!

“Well, I have been doing some work on my boat models, and I really think we could-,”

“Yes, yes, that’s lovely,” the king interrupted with a wave of his hand. Now he looked impatient. “But are you going to accept my proposal or not?”

‘This was a lot to do for a well-deserved vacation and some consideration,’ Asha thought, while hesitantly glancing out of the window. But consideration was a lot more than the usual firm, no, and it did give her a good excuse to travel where the girl who’d wished for the dresses had been…Not to mention that if she could do it, then she’d finally be able to see her Saba and mother again, both of whom she was starting to miss terribly. If only they could know what their hero, the king, was putting her through to see them again, she thought. She wondered if it would change their perception of him. Maybe they’d finally start to listen to her about not indulging in the magic of Rosas, for once-

“The clock is ticking Asha. So what will it be?”

Determined not to look as panicked or uncertain as she felt, Asha straightened her posture, “of course! I will do my best, your highness. I will have everything finished by tomorrow nightfall!”

“Excellent,” he says, sounding a little too smug for her liking as she watches the scroll place itself into her hands. With a flicker of his hands, the wishes begin to ascend towards the ceiling once more before completely disappearing without a trace. “I’ll check in on you tomorrow at the eastern market. I wish you luck on all of your tasks, Asha,” Magnifico calls, as she begins to follow him out.

'Him and me both,' Asha thought, as she quickly jotted down the tasks from the scrolls onto a spare piece of paper she kept in her satchel before placing the scroll down on a nearby table. 

She had scurried past the entrance to the west wing when she saw him again. “Oh and another thing,” he calls to her as she sees the door to the west wing close themselves. “Could you please fix the lock on the library door for me? It’s been broken since last night.”

“Yes your Highness,” she bows as she hears him chuckle once more. The familiar taste of disappointment filled her mouth as she heard him chuckle again before walking off.

Thirty minutes later, Asha found herself feeling determined to make the king regret his proposition. She was quite certain that said proposition was nothing more than a lesson to teach her about inconveniently asking for time off. However, she’d felt that the king had sorely underestimated her if he’d decided to call victory so soon. 

Fixing the lock on the library had expectedly taken her a total of three minutes to do. Such a banal task had been familiar to her as she’d had a history of repairing broken non-magical locks all over the castle. It was just one of the many trivial tasks as an apprentice that Magnifico usually assigned for her due to her lack of magical ability.

But as soon as she’d finished said task, she’d rushed as quickly as she could back to her quarters. She’d written several messages, all to the people she’d spoken to for the ball’s arrangements, calling for them to meet her this evening. She’d done it before, and she was quite confident she could do it again.

“It’s at times like these when I begin to realize exactly why democracy is on the rise in some countries. Why is it that I have to do a herculean task just to get him to even consider some of my projects? He could have just said no like he always does! But, if he thinks I’m going to pass up this opportunity, well he’s got another thing coming and I don’t think he’s going to like it!” Asha whispered to Valentino as he followed her through the dark passages to the castle courtyards. The castle courtyards were always in impeccable shape, she thought as she saw the beautiful limestone statues above the bushes of blooming crimson roses and lemon-colored tulips. 

Had it not been for the arduous amount of tasks she had to do, Asha would’ve gladly stopped to enjoy the sweet scent and sights of the brilliant flowers that surrounded her. But alas, she knew better. The flowers served as nothing more than one of the king’s many beautiful distractions to the people of Rosas. 

Navigating through the mazes of well-trimmed green bushes, marble fountains, and smaller flowers, she finally made her way to the small wooden birdhouse that had been neatly tucked out of sight.

She’d built this birdhouse a year ago after she’d saved a few birds from the royal couple’s nefarious cat. Although said deed had earned her the eternal ire of the royal cat, she’d quickly found herself forming a small friendship with the birds, as their numbers quickly began to grow.

“I’m back!” she sang, watching as a few dozen colorful birds emerged from their birdhouse flying over to greet her. She let out a small laugh as she watched many of them land near her feet as she withdrew a piece of bread from her pocket.

Kneeling to the ground she called out, “Hello Adelina, Alejandro, Carmen,” she grinned as a scarlet-colored bird perched on her sleeve, brightly chirping to her as she gently petted it. “I missed you too Abril. How has everyone been doing?” she asked, as the birds responded with a choir of chirps and song. “I’ll take that as a ‘very good’. Are you guys ready for lunch?” 

The birds replied with a variety of chirps before eagerly hopping towards her. “I’ll take that as a yes as well,” she grinned as she began to toss the pieces of food to them.  They eagerly gobbled it up, before she withdrew another piece of bread from her pocket.  “I hope you guys have been doing well- the cat wasn’t after you again was he?” she asked, as the birds continued to coo and chirp. “I’ll take that as a no.” She began to tear the bread into smaller pieces as she watched Valentino happily chase some of the birds who always flew out of reach. 

“Look, I need to ask you guys a quick favor,” she said to the birds that had stilled near her feet. “My Saba’s birthday is coming up soon, and I need to take time off. So the king agreed to give me time off, if and only if I could complete a certain amount of tasks on time. It’s a lot to do, and I was wondering if you could lend me a hand, er, wing, please? I’ll give you guys a surprise if you help me out,”

That seemed to do the trick as she saw a few bluebirds flap their wings in excitement. 

“I knew you’d see it my way,” she grinned. “Now I’m going to need 10, or maybe 12 of you, to fly to the landmarks we learned and deliver these messages. Ok?”

The birds nodded, twelve hopping towards her as she began to gently tie her messages to their feet. After a few minutes of simple instructions, they began to fly off toward the directions she’d assigned them. “Stay safe!” She called as she watched their figures sail off into the distance. 

“Ok, that’s one task down.” She muttered to herself as she began to pace. Several remaining birds had joined Valentino to curiously watch her.

“If they all reach their destination then I should be able to meet with everyone today which will be perfect.” She glanced towards the sky. Her mind fervently racing against the clock. “There’s still time, so I should be able to make my way towards the western market and Banquo. If I can oversee that I’ll be able to take care of other affairs-,” she paused mid-step as she glanced at the animals who’d still been curiously watching her.

“Right right and then I’ll have to hunt down the prince. The same prince who literally disappeared off the face of the earth three years ago, but I’ll have to find him. In less than a day,” she groaned as Valentino bleated. “It was a figure of speech, Valentino no one can just disappear off of the face of the earth. Especially a prince. Someone has to know something, but who-,” She paused mid-stride as an idea made its way into her head and she grinned. “I think I just got an idea.”

Now Valentino looked curious, as Asha bid the rest of her birds farewell and began to make her way through the courtyard. 

She’d nearly reached the entrance to the secret passage when a sudden figure stepped into her view.

“Y-your Highness!” she stammered as she clambered into a curtsy. 

“Asha,” the queen had said with a small smile as she held a small single crimson rose. “I hope I wasn’t disturbing anything?”

“Of course not Your Highness,” Asha replied. “How may I be of service to you?”

The queen paused, shooting a glance around the garden before she stepped forward. She quietly took Asha’s hands into her own as she whispered, “I only come to ask you of something. It won’t be much because I know he’s given you a lot to worry about, but please- when you find Ignacio, tell him that there will always be a place here for him, regardless of what his uncle says…” Asha nodded, a bit taken aback by the grief and sadness that had washed over the queen’s face. “It’s been three years,” she murmured. “Please tell him to come home.”

“I will do my best to see to his return,” Asha promised, before giving the queen a small bow. 

“Thank you,” the queen said, withdrawing her hands before departing.

Asha wasted no time packing everything she’d need for the trip which was a short list that included: clothes, her storybook, her emergency kit, her drawing book, her apprentice papers, a few star maps along with a traditional map of Rosas, and her father’s old astrolabes.  

The only thing she needed now was food.

Quickly using the secret passages, she entered into the kitchen where Dahlia was now working.

“Dahlia!” she cried.

“Let me guess you need some food for your trip?” the girl had asked while wiping her hands on the apron.

“Yes! Wait…how did you figure that out? No, no let me guess- he was monologuing on his way to his study again, wasn’t he?”

“Yep,” Dahlia nodded. “He had a whole musical number with it.”

“Was it catchy?”

“Very.” 

“Great, now I guess I know what song everyone will be running into the ground for the next week,” Asha groaned.

Dahlia grinned, walking towards her with a bag of food. “Here you go,” she said as she handed it to Asha. “You’ll be needing it. I packed some stuff for Valentino as well.”

“Thank you,” Asha said, grateful for the assistance. “I’ll pay you back for this.”

“You don’t need to pay me back for this,” Dahlia replied as her voice grew quiet. “Just bring Ignacio back, please.”

“I’ll see what I can do,” Asha promised. 

“And when you do, could you tell him?” Dahlia paused, her voice trailing off as she watched her cast a wary glance towards the door. ‘It was probably where the other apprentices were, Asha thought, as she placed the bag of food in her satchel. Then with a defeated shake of her head, Dahlia sighed, “Never mind. Just stay safe out there ok?”

“I will,” Asha said, offering her a small smile. “I’ll be back soon, and I’ll bring him home. I promise.”

“Thank you,” Dahlia said, before quietly taking her place next to the oven. The warm fire of the oven cast a soft glow on her features, as she closed her eyes. The wonderful scent of lemon cakes and croissants began to reach Asha, as she briefly took in the quiet serenity of the kitchen.

A lot of things had been left unsaid between them, she thought as she made her way to the stable. Things that she wasn’t sure if she’d regret not hearing before she’d embark. She’d known that out of the two markets, the more affluent one would be the more sensible and easy one to tackle with her remaining hours of daylight. Then tomorrow, she’d figured that she’d focus all of her energy on both the eastern market and the missing prince if she hadn’t found him before the night had ended.

She admitted that she’d been making a lot of promises lately. Promises she hadn’t been certain she could keep. But she’d try, if not for her own sake, then for the sake of the queen, Dahlia, and her family.

She’d made her way to the stable before she ran into two other apprentices- Bazeema and Safi. 

“You should take Sebastian,” Safi sniffled while pointing to the black horse. “He’s the fastest horse we have.” 

“Thanks,” Asha said. She was quite certain that he’d been more familiar with the horses here than her. When he wasn’t busy working with the king or the castle’s chickens, he’d often spend his time out here in the stables.

“Be careful out there,” Bazeema said softly as her dark eyes filled with worry. 

“I will,” Asha promised, trying to hide her surprise at their help. It wasn’t that she didn’t appreciate the gesture, but part of her felt that it was done more out of concern for their friend than her. 

But Bazeema’s next words quickly put those thoughts to rest when she said, “If you go west…Try- try not to go into the forests ok?”

“What’s wrong with the forest?” Asha asked, actually halting as she looked at the girl curiously.

“W-well the last time I went out there, it felt different- but maybe that was just me.”

“The forests are always unpredictable,” the boy nodded. “Especially on the eastern side.”

That was to be expected, Asha thought. The eastern side of Rosas hosted the biggest wish garden- a place where people would go to send their wishes to the king. From there all were sent to the castle where a selected few would make their way forward, purely by chance, as the king had promised, to him. 

But the look of concern and fright on Bazeema’s face seemed so sincere that for a second Asha really began to consider whether or not it was a good idea to go.

Of course, it was, she nodded to herself.

She had to go if she wanted to be home for her Saba’s birthday, or help the people get their wishes granted or even get her project funded!

She was so close and she would not let anyone or anything get in the way of that. Magic or not.

Steeling her nerves, She’d carefully settled herself on the horse’s saddle, looking over everything as she made sure that Valentino was properly secured. 

“I’ll be back soon with the prince,” she told them. “You can count on it.”

“Good luck out there!” Safi said before sneezing into his elbow.

“Stay safe!” Bazeema called as they rode out from the stable. 

The wind whistled as it whipped through her hair, the warm breeze felt welcoming as she took in the sounds of the distant city. 

“Ready?” she asked the young goat, who’d bleated excitedly, and with that, she’d taken off, blissfully unaware of the trouble that soon awaited her.

[tanadrin]

There's a very cheap trick you can pull to get landmasses in a game world to distort correctly near the poles on a 2D map projection, and that's just to sample 3D noise on the surface of a sphere. You're still only going to get very basic, blobby landmasses, but you will at least get the correct amount of visual "stretching" near the poles. But if you then implement base movement costs that scale inversely with latitude, becoming very cheap near the poles, you've basically got a game on a spherical world for free, projected onto two dimensions for your convenience.

This is important because I think if you're lobbing nuclear missiles at your opponent a la Civilization, they should follow great circle routes over the poles if necessary.

[suemillerauthor]

His body reassembled under an overcast sky at a crossroads midway between the destroyed southern gate into the ruins of Hyrule Castle Town and the northern gate of the fort-style enclosure that had cropped up around the Sacred Ground Ruins, which had been labeled New Castle Town on the map. He was also practically straddling one gangly metal leg of a Guardian Stalker. “Shit!” He grabbed both his sword and shield and immediately whacked at the metal appendage. Dark and unoccupied as it was, though, the blade failed to take the limb all the way off on the first hack and the Guardian both moved away and turned its eye toward him, firing up its targeting mechanism. “Midna!” The imp appeared with a yawning stretch to blink balefully at him, but almost immediately perked up as she noticed the danger at hand. “Ooh, a challenge!” A flash of turquoise near his knee brought the sword in his hand to life— but its glow had morphed into a deep blood red and the new jewel shone with a steady light. Confidence surged through him. He turned and brought his shield up just in time to deflect the Guardian’s laser beam right back at itself, scoring a hit to the base of one of the legs, shearing it clean off and sending the mechanical monster reeling wildly, parts flying like shrapnel. The Stalker landed on its side, remaining metal limbs flailing madly and exposing a large, glowing blue spot on its vulnerable underside. The sword’s light intensified and the handle gave a distinct shake in his hand. He drew back and stabbed directly into the metal belly of the Guardian, the brightness of the blade waning as the energy shot from it into the machine, overwhelming its capacity and shorting it out.  It sputtered and died as it lay, spitting out a small pile of various parts, some he recognized and some Navi identified for him. As he was bent over to grab a glowing spherical object Navi called a giant Ancient core, he heard the telltale sounds of another Guardian’s targeting system and turned to find a second Stalker bearing down on him from the southeast. As he was setting himself to deflect the shot with his shield, however, he heard yet another targeting mechanism fire up and turned his head back to find that a decayed Stalker, partially buried in the dirt near the decrepit wall guarding what was left of the old town, had been awakened by the ruckus. “Fuck.”

[nevernoneart]

DAY 5: MAP - This is the Dahlia “Mercator”. The Mercator projection is a geographical chart where a spherical globe is flattened into a two dimensional map, presented by geographer and cartographer Gerardus Mercator in 1569. The dahlia is a large cactus dahlia with red stripes radiating out of the centre, resembling its namesake.

I should mention that this is the flower that made me realise that I could link plants to each prompt. Thank you to @farmergracy for the inspiration!

[sandgame]

Faking a spherical Age for the sake of KI coordinates

Heyo Tumblr, been a while!

Although I haven't used this blog lately, I have still been screwing around with this thing in the background of my life, because at this point I've basically accepted that semi-theorizing about how to make Better Uru is just my pastime.

Anyway. As a result of something else I was contemplating for this bizarre project of mine, I realized that because of how KI coordinates work, game worlds which allowed players to wander sufficiently far from the Age's Maintainer's Mark would need to implement some form of fakery in order to properly simulate the effect of walking around on a sphere while using a cylindrical coordinate system.

The "obvious" solution of just making the game world a sphere is… not really smart, though, so what's a game dev who is overcommitted to the concept of realism in this game to do?

Well, first let's finish defining the problem.

As you walk away from the Zero point of an Age, your elevation coordinate will decrease (generally; local surface geometry like mountains notwithstanding) until you reach the Zero’s exact antipode, because walking across the surface of the sphere will always send you "down" relative to the placement of the Maintainer's Mark. It should then increase back to 0 as you proceed back toward the Zero point across the other half of the planet.

But because game worlds are flat, this effect would have to be simulated for sufficiently large maps.

To do this, we have to know the following values:

The average radius of the planet

The distance traveled from the Zero point

The Zero point’s elevation relative to the planet’s average radius

The player’s local elevation relative to the planet’s radius

Using the equation for the length of a circular arc, we can reverse engineer the angular distance traveled:

L = θ * r

Or

θ = L / r

Where L is the length of the arc travelled (how far from the zero point the player is in a straight line), and r is the planet’s radius. 

NOTE: The math in the next part assumes you never travel more than 90 degrees around the planet, which I think is generally acceptable for the purposes of this hypothetical, but just be aware that what's presented here is not a completely comprehensive solution.

Solving for θ lets us construct a right triangle whose hypotenuse is the planet’s radius plus the player’s current elevation above that radius, and whose long leg is the planet’s radius minus the vertical distance the player has travelled away from the Zero point. We find the length of the leg with this function:

a = c × sin(θ)

Once we have a, we subtract it from the planet’s radius to get the elevation KI coordinate.

It may be necessary to make adjustments to certain values going into the equation solving for a in cases where the player has moved more than 90 degrees around the planet from the Zero point. 

The distance coordinate is calculated using the following formula to get the horizontal “opposite” leg of the right triangle formed by the radius of the planet and the angle the player is away from the Zero axis—which extends straight through the center of the planet, or:

b = c × cos(θ)

The value of b is our horizontal distance from the axis of the Zero point. (I should point out that we can't just use the XZ vector distance between the player and the Zero point for this measurement, as the player's travel is being treated as an arc for the purposes of simulating a sphere, and the arc's length would be greater than the actual absolute linear distance traveled if the map were actually spherical.)

The angle coordinate is the simplest to calculate, as it’s simply the player position’s angle from the vector of the Zero point (the “line” of the Zero), converted to torantee. 

In addition to faking the KI coordinates, a shader may also be used to post-process the geometry of the scene such that it falls over a false “horizon”, much like Animal Crossing New Horizons’ island terrain does (though the effect would be far less dramatic in this case). 

[spacetimewithstuartgary]

FAST detected 90% circular polarization in a repeating fast radio burst

Fast radio bursts (FRBs) are a kind of energetic cosmic radio burst. Though their duration is usually at millisecond scale, their energy (estimated isotropically) reaches 10^36 ～10^41 erg, equivalent to the energy release of the sun in minutes to months. Some FRB sources emit bursts repeatedly, releasing even more energy in total. Since the discovery in 2007, the physical mechanism for such bright radio emission has become atrending topic in astrophysics. The polarization of electromagnetic wave is usually thought to carry key information of the astrophysical sources, e.g. the linear polarization usually traces the geometric configuration of magnetic fields in the radiation zone and circular polarization probes both intrinsic radiation mechanisms and propagation effects. The “China Sky Eye” Five hundred meter Aperture Spherical radio Telescope (FAST) is the largest single dish radio telescope in the world. With its superb sensitivity and polarimetry precision, FAST has many important discoveries in the field of FRB observation.

FRB 20201124A is an FRB repeater discovered on 2020 November 24 by the Canadian Hydrogen Intensity Mapping Experiment (CHIME) telescope. During its first active episode in 2021 March-May, radio telescopes around the world including FAST achieved rich observational results. This FRB repeater entered another short but fierce active episode in late September 2021, during which the highest event rate recorded by FAST exceeded 500 bursts per hour.

Recently, the FAST key science project fast radio burst searches and multi-wavelength observations analyze the FAST data of the second active episode of FRB 20201124A in 2021 September, in which the scientists find a fast radio burst with 90% circular polarization. Such high degree of circular polarization is both unprecedented in FRB observations, and also unpredicted in theoretical models. In addition, rapid variation and jumps are also found in the observational data. These findings may provide new constraints and clues for the theoretical research on the radiative mechanism of FRBs. The research team have measured the polarization of more than 500 fast radio bursts in four FAST observation session between 2021 September 25 and 28. Among them, the average or peak circular polarization fraction of 32 bursts exceed 50%. The highest degree of circular polarization reaches 90.9%, which is the new record in FRB observation. Rapid variation in polarization fraction and position angle, sign reversal of circular polarization, and orthogonal jump of position angle due to orthogonal polarization modes (OPMs) are also found in the observation. These findings are recently published in National Science Review, with title “Ninety percent circular polarization detected in a repeating fast radio burst”. The corresponding authors are Prof Kejia Lee from Peking University, Prof. Weiwei Zhu from National Astronomical Observatories, Chinese Academy of Sciences (NAOC, CAS) and Prof. Bing Zhang from University of Nevada, Las Vegas (UNLV). Jinchen Jiang and Jiarui Niu of NAOC and Jiangwei Xu of Peking university are the first authors.

There are currently two categories of emission mechanisms for FRB repeaters. The gamma-ray burst (GRB) like models presume that relativistic shocks from a compact central engine stimulate masers in the outer medium, while in the pulsar-like models the FRBs are generated in the pulsar magnetosphere. In the early days, the FRB observations generally show linearly polarization with constant direction, which can be explained by both kinds of models.

Thus, the two types of models cannot be tested. The polarization observational results of FRB 20201124A challenges both kinds of models. For GRB-like models, the high degree of circular polarization can only be observed at the edge of the emission beam generated by relativistic particles, where the emission should be fainter compared with the beam center.

However, such brightness difference is not significant in observation. The rapid variation of linear polarization is also difficult to explain under GRB-like models. It’s more convenient to explain the observation using pulsar-like models, though the observed circular polarization fraction curves also limit the geometric parameters of the magnetosphere.

IMAGE: Polarimetric results of a selected sample of bursts with high degrees of circular polarization or abrupt jumps in the linear polarization position angle. Credit ©Science China Press