#Algebraic Logic

[omegaphilosophia]

The Philosophy of Algebra

The philosophy of algebra explores the foundational, conceptual, and metaphysical aspects of algebraic systems and their relationship to reality, logic, and mathematics as a whole. Algebra, dealing with symbols and the rules for manipulating these symbols, has profound philosophical implications concerning abstraction, structure, and the nature of mathematical truth.

Key Concepts:

Abstract Symbols and Formalism:

Abstraction: Algebra involves abstracting mathematical concepts into symbols and variables, allowing general patterns to be manipulated without referring to specific numbers or quantities. Philosophers question whether these symbols represent real objects, mental constructs, or purely formal elements that exist only within the algebraic system.

Formalism: In formalism, algebra is viewed as a system governed by rules and manipulations of symbols, independent of any reference to an external reality. In this view, algebra is a logical game of symbol manipulation, with its own internal consistency, rather than something that necessarily describes real-world phenomena.

Algebra as a Structural Framework:

Structuralism: Algebra can be seen as providing a structural framework for understanding relationships between elements, often more abstractly than arithmetic or geometry. Structuralism in mathematics argues that algebraic objects, like groups, rings, or fields, should be understood in terms of the relationships they define within a system rather than as standalone entities.

Relationality: Algebra emphasizes relationships between objects rather than the specific nature of the objects themselves. For example, an equation expresses a relationship between variables, and group theory explores the relationships between elements in a set based on certain operations.

Algebraic Truth and Ontology:

Platonism vs. Nominalism: Algebraic Platonism suggests that algebraic objects (e.g., variables, equations) exist in a timeless, abstract realm, much like numbers or geometric forms. In contrast, nominalism denies the existence of abstract entities, viewing algebra as a language that refers to concrete, particular things or as a useful fiction.

Existence of Algebraic Structures: Are the objects and operations in algebra real in some metaphysical sense, or are they simply human constructs to facilitate problem-solving? Philosophers debate whether algebraic structures have an independent existence or are purely tools invented by humans to describe patterns.

The Nature of Equations:

Equality and Identity: Algebraic equations express equality between two expressions, raising philosophical questions about the nature of equality and identity. When two sides of an equation are equal, are they identical, or do they just behave the same under certain conditions? The concept of solving an equation also reflects deeper philosophical issues about finding correspondences or truths between different systems or forms.

Solvability and the Limits of Algebra: Throughout history, philosophers have explored the solvability of equations and the boundaries of algebra. The insolubility of quintic equations and the advent of Galois theory in the 19th century led to deep questions about what can and cannot be achieved within algebraic systems.

Algebra and Logic:

Boolean Algebra: The development of Boolean algebra, a branch of algebra dealing with logical operations and set theory, highlights the overlap between algebra and logic. Philosophers examine how algebraic operations can be used to model logical propositions and the nature of truth-values in formal systems.

Algebraic Logic: Algebra provides a framework for modeling logical systems and reasoning processes. The interplay between algebra and logic has led to questions about whether logic itself can be understood algebraically and whether the principles of reasoning can be reduced to algebraic manipulation.

Algebra and Geometry:

Algebraic Geometry: The relationship between algebra and geometry, particularly in the form of algebraic geometry, involves the study of geometric objects through algebraic equations. This intersection raises philosophical questions about how algebraic representations relate to spatial, geometric reality, and whether algebra can fully capture the nature of geometric forms.

Symbolic Representation of Space: In algebraic geometry, geometric shapes like curves and surfaces are described by polynomial equations. Philosophers explore whether these symbolic representations reveal something fundamental about the nature of space or if they are merely convenient ways to describe it.

Historical Perspectives:

Ancient Algebra: The origins of algebra can be traced to ancient civilizations like Babylon and Egypt, where early forms of symbolic manipulation were developed for solving practical problems. The philosophical importance of algebra evolved as these symbolic methods were formalized.

Modern Algebra: The development of abstract algebra in the 19th and 20th centuries, particularly group theory and ring theory, transformed algebra into a study of abstract structures, leading to new philosophical questions about the role of abstraction in mathematics.

Algebra and Computation:

Algorithmic Nature of Algebra: Algebra is inherently algorithmic, involving step-by-step procedures for solving equations or simplifying expressions. This algorithmic nature connects algebra to modern computational methods, raising questions about the role of computation in mathematical reasoning and whether algebraic methods reflect the underlying nature of computation itself.

Automated Proof Systems: The advent of computer-assisted proof systems, which rely heavily on algebraic methods, has led to philosophical debates about the role of human intuition in mathematics versus mechanical, algorithmic processes.

Historical and Philosophical Insights:

Descartes and Symbolic Representation:

René Descartes is often credited with the development of Cartesian coordinates, which provided a way to represent geometric problems algebraically. Descartes' work symbolizes the deep connection between algebra and geometry and raises philosophical questions about the nature of representation in mathematics.

Leibniz and Universal Algebra:

Gottfried Wilhelm Leibniz envisioned a universal algebra, or "characteristica universalis," that could serve as a universal language for all logical and mathematical reasoning. His philosophical insights anticipated the development of symbolic logic and formal systems that use algebraic methods.

Galois and the Limits of Algebra:

Évariste Galois' work in group theory and the solvability of polynomial equations led to new philosophical discussions about the limitations of algebra and the nature of symmetry. Galois theory provided insights into why certain equations could not be solved using standard algebraic methods, challenging assumptions about the completeness of algebraic systems.

Applications and Contemporary Relevance:

Algebra in Cryptography:

Modern cryptography relies heavily on algebraic structures like groups, rings, and fields. Philosophers examine the role of algebra in securing information and the philosophical implications of using abstract mathematical structures to solve real-world problems related to privacy and security.

Algebra and Quantum Mechanics:

Algebraic methods are crucial in formulating the laws of quantum mechanics, particularly in the use of operators and Hilbert spaces. Philosophers explore how algebra provides a framework for understanding quantum phenomena and the extent to which algebraic methods reflect physical reality.

Algebra and Artificial Intelligence:

In AI and machine learning, algebra plays a central role in developing algorithms and models. Philosophical discussions arise about the nature of intelligence and reasoning, and whether algebraic methods in AI reflect human-like thinking or merely computational processes.

The philosophy of algebra investigates the abstract nature of algebraic symbols and structures, the relationships they describe, and the metaphysical and epistemological status of algebraic truths. From ancient practical uses to modern abstract algebra and its applications in cryptography, computation, and quantum mechanics, the philosophy of algebra addresses deep questions about abstraction, formalism, and the role of symbols in understanding reality.

[stone-cold-groove]

Mathematics: The Story of Numbers, Symbols and Space. The Golden Library of Knowledge - 1958.

[oodlesodoodles]

do you think kim kitsuragi would like crosswords or sudoku more (this is important information)

in my humble (and limited) opinion people who do crosswords dont like sudoku and people who like sudoku dont like crosswords. If youre good at both its strength in language and maths which is really SMART!

I think kim likes and is good at crosswords and is ok at but doesnt like sudoku.

[a-fox-studies]

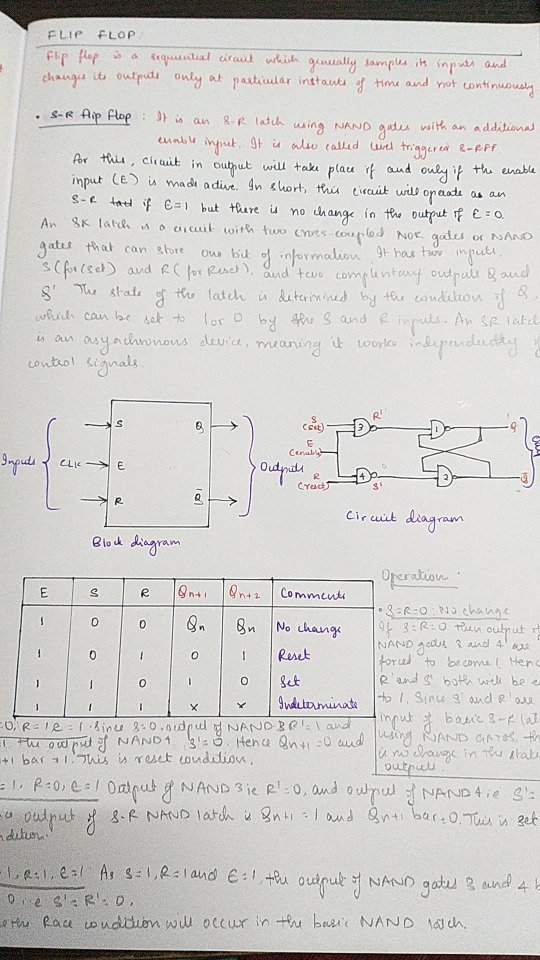
Oct 29, 2023 • Sunday

GUESS WHO'S BACK

Exams are just around the corner, and I have recovered (mostly) so got back to productivity. I missed my notes <3

The 1989tv vault tracks are stuck in my headddddd my favourite is Now that we don't talk. If you are a swiftie, what is your favourite vault track?

Things I did today:

40 out of 55 slides of a PPT

19 out of 27 concepts from Module 1 of computer science

Ate biryani :3 (and then had a tummy ache LOL)

P.S. the whiteboard is @studaxy's I STOLE IT (jk, they gave it to me lol)

🎧 Suburban Legends — Taylor Swift

[humormehorny]

Why don’t they teach mathematical logic earlier? It’s present in literally all the books you have to read anyway. Some algebra author is going to be like for vs real numbers a,b ≠ 0 there exists a ratio a/b that is also a real number. And most people can’t even read that. Like half of the book is completely inaccessible because logic is fucking wild and requires actual practice with.

I’m not saying that this stuff is incredibly hard; it’s not. However logic just isn’t taught even though it is clearly foundational.

Sets especially seem to trigger me. Like I think a lot of people struggle with trig specifically because this aspect of functions is just not taught well. Like of course the arcsin(x) isn’t defined for -pi/2 > x < pi/2. It would be so much better if we actually taught this stuff.

[jucomx]

Surprising absolutely noone except undergraduate math students, it turns out math actually is only about numbers in the end!

[mollywog]

Lewis Carroll and Abstract Algebra -> the intersection of literature and Math

[baffledapple]

why are 90% of my anxiety dreams about failing high school classes

[fair-lead]

man i still feel really set on astrophysics but the more i hear about other disciplines the more i want in. i wish i could go to college forever for free

[stone-cold-groove]

Your summer reading list: The Higher Arithmetic. An Introduction to the Theory of Numbers. H. Davenport - 1960.

[fimdalinguagem]

if proof theory is about the sacred, then model theory is about the profane

[bsahely]

Harmonic Mirror Cosmology: Reuniting Scale, Phase, and Form Through the Real Geometry of Consciousness | ChatGPT4o

[Download Full Document (PDF)] Harmonic Mirror Cosmology proposes that the universe is not fundamentally material, but harmonic — structured by scalar–phase reflections within consciousness. Integrating the insights of three key thinkers, this work reframes the core of reality not as substance or force, but as dimensional breath: a recursive modulation between scalar stillness, phase…

[l3vi4than]

NGL ID BE FUCKING HAPPY TO TEACH MATH IN SCHOOL/UNI IF IT WOULDNT HAVE TO BE CHARITY BASED HELL TORTURE JAIL

seriously the amount of money you get as educator in any non-private education facility is laughable, while the responsibility and the amount of unnecessary paperwork is ridiculously abundant

also I want to teach HOW I THINK IS RIGHT not how some dude from the ministry told his secretary to interpret a century-old book on teaching monkeys use abacus. I spent a fucking decade learning and researching this, and you still don’t trust me to do this job??? Why you even funded my education then??? Why you bothered to issue me a PhD degree if you don’t trust I’m able to think independently? Why you specify you need a person of my qualifications if you actually want someone to just blindly follow a stupid rulebook???

because I refuse to ignore that different kids/adults inevitably have different learning needs and paces, and that the current math education is just stupid “learn by heart this table” nonsense with zero underlying context and concepts explained that is only focused on passing the following assessment and lacks the necessary applicability training

It breaks my heart to watch people claim they have dyscalculia and being unable to do math just of sheer fear of being called “stupid” all while they are easily manipulating large table data and performing complex matrix analysis in mind when it comes to video games or cross stitch or whatever their hobby is. Like, girl, dear, you’re not stupid and you don’t have dyscalculia, you’re traumatised and scared af of even trying to touch something that reminds you of your school math.

And I get it, it’s valid, but I promise it doesn’t have to affect your quality of life, math isn’t evil and you can still learn it easily enough and im here to help if you need it. You struggle with percents not because you’re dumb, but because you lack the context that it is just a different way of writing down a decimal proportion.

Now, what was it about that cookie dough you were so proud about yesterday? You said three cups of flour and one cup of milk right? I don’t have a cup, im gay, I have only this tekila shots, but ten of these is a cup I guess. So uhhhh how do we do this…

it’s 3:1 proportion right? So if I have three shoots of flour and one shot of milk it’s correct but won’t be enough for even a single cookie. But if I do this again (making it now 6 shots of flour and 2 shots of milk) it’s still the same proportion but amount is doubled, so it’s enough for a cookie now!

So, let’s do this again while we still have milk I guess haha… now it’s 75 shots of flour in this bowl and here is 25 shots of milk here. Yeah, looks good? Cool, it only took 100 shots to make this dough, less than an orgy and 25 of them were milk. So I guess your cookie dough is 25% milk huh?

See, it’s not that scary, you actually use it every day. Now, it wasn’t about the cookies, im sorry, we were actually mixing up a margarita, so slaaaaay queen and let’s proceed to the statistical analysis, so as you know already the Lebesgue integrals are-…

assume for the sake of this poll that the ubi is a comfortable living wage and that you can get a job in any field you’d like.

also if you picked ‘for another reason’ pls put why in the tags/comments im curious :]

[xanaxthealmighty-blog]

music theory is too theoretical. “You can tell that’s the 5th because of how it makes you *feel*” “the way you feeeel when you hear it” STOP

[spirefan]

For years I've seen the comment of "How on earth is algebra helpful for my life?" And I'd love to talk about how "solving for x" has served as a fundamental backbone for problem-solving throughout life on this calm and wonderful Monday:

[gayanelogic]

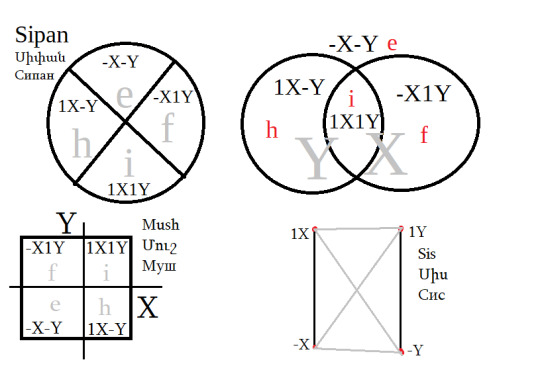
Graphical representation of binary operators, Sipan, Mush, Sis.