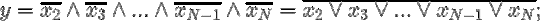#Boolean Algebra

[a-fox-studies]

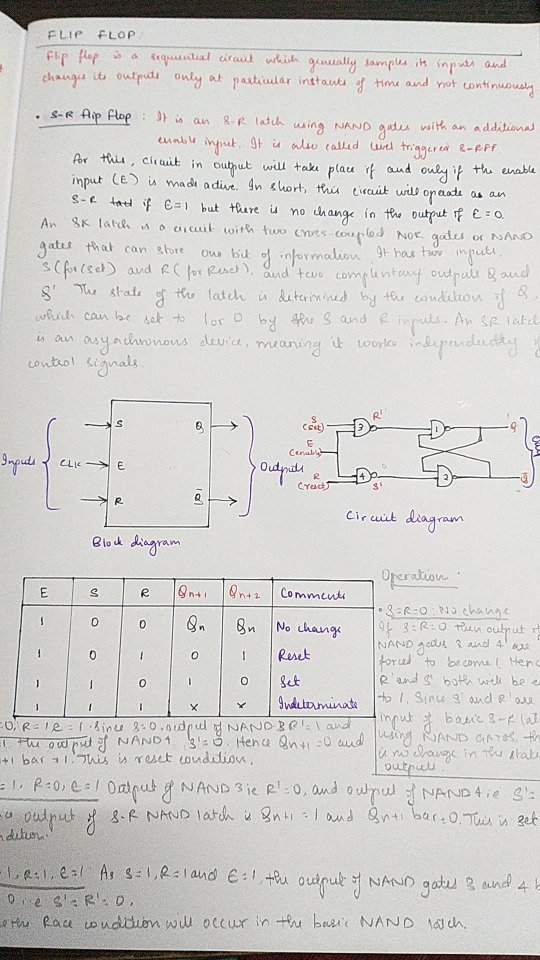
Oct 29, 2023 • Sunday

GUESS WHO'S BACK

Exams are just around the corner, and I have recovered (mostly) so got back to productivity. I missed my notes <3

The 1989tv vault tracks are stuck in my headddddd my favourite is Now that we don't talk. If you are a swiftie, what is your favourite vault track?

Things I did today:

40 out of 55 slides of a PPT

19 out of 27 concepts from Module 1 of computer science

Ate biryani :3 (and then had a tummy ache LOL)

P.S. the whiteboard is @studaxy's I STOLE IT (jk, they gave it to me lol)

🎧 Suburban Legends — Taylor Swift

[omegaphilosophia]

The Philosophy of Algebra

The philosophy of algebra explores the foundational, conceptual, and metaphysical aspects of algebraic systems and their relationship to reality, logic, and mathematics as a whole. Algebra, dealing with symbols and the rules for manipulating these symbols, has profound philosophical implications concerning abstraction, structure, and the nature of mathematical truth.

Key Concepts:

Abstract Symbols and Formalism:

Abstraction: Algebra involves abstracting mathematical concepts into symbols and variables, allowing general patterns to be manipulated without referring to specific numbers or quantities. Philosophers question whether these symbols represent real objects, mental constructs, or purely formal elements that exist only within the algebraic system.

Formalism: In formalism, algebra is viewed as a system governed by rules and manipulations of symbols, independent of any reference to an external reality. In this view, algebra is a logical game of symbol manipulation, with its own internal consistency, rather than something that necessarily describes real-world phenomena.

Algebra as a Structural Framework:

Structuralism: Algebra can be seen as providing a structural framework for understanding relationships between elements, often more abstractly than arithmetic or geometry. Structuralism in mathematics argues that algebraic objects, like groups, rings, or fields, should be understood in terms of the relationships they define within a system rather than as standalone entities.

Relationality: Algebra emphasizes relationships between objects rather than the specific nature of the objects themselves. For example, an equation expresses a relationship between variables, and group theory explores the relationships between elements in a set based on certain operations.

Algebraic Truth and Ontology:

Platonism vs. Nominalism: Algebraic Platonism suggests that algebraic objects (e.g., variables, equations) exist in a timeless, abstract realm, much like numbers or geometric forms. In contrast, nominalism denies the existence of abstract entities, viewing algebra as a language that refers to concrete, particular things or as a useful fiction.

Existence of Algebraic Structures: Are the objects and operations in algebra real in some metaphysical sense, or are they simply human constructs to facilitate problem-solving? Philosophers debate whether algebraic structures have an independent existence or are purely tools invented by humans to describe patterns.

The Nature of Equations:

Equality and Identity: Algebraic equations express equality between two expressions, raising philosophical questions about the nature of equality and identity. When two sides of an equation are equal, are they identical, or do they just behave the same under certain conditions? The concept of solving an equation also reflects deeper philosophical issues about finding correspondences or truths between different systems or forms.

Solvability and the Limits of Algebra: Throughout history, philosophers have explored the solvability of equations and the boundaries of algebra. The insolubility of quintic equations and the advent of Galois theory in the 19th century led to deep questions about what can and cannot be achieved within algebraic systems.

Algebra and Logic:

Boolean Algebra: The development of Boolean algebra, a branch of algebra dealing with logical operations and set theory, highlights the overlap between algebra and logic. Philosophers examine how algebraic operations can be used to model logical propositions and the nature of truth-values in formal systems.

Algebraic Logic: Algebra provides a framework for modeling logical systems and reasoning processes. The interplay between algebra and logic has led to questions about whether logic itself can be understood algebraically and whether the principles of reasoning can be reduced to algebraic manipulation.

Algebra and Geometry:

Algebraic Geometry: The relationship between algebra and geometry, particularly in the form of algebraic geometry, involves the study of geometric objects through algebraic equations. This intersection raises philosophical questions about how algebraic representations relate to spatial, geometric reality, and whether algebra can fully capture the nature of geometric forms.

Symbolic Representation of Space: In algebraic geometry, geometric shapes like curves and surfaces are described by polynomial equations. Philosophers explore whether these symbolic representations reveal something fundamental about the nature of space or if they are merely convenient ways to describe it.

Historical Perspectives:

Ancient Algebra: The origins of algebra can be traced to ancient civilizations like Babylon and Egypt, where early forms of symbolic manipulation were developed for solving practical problems. The philosophical importance of algebra evolved as these symbolic methods were formalized.

Modern Algebra: The development of abstract algebra in the 19th and 20th centuries, particularly group theory and ring theory, transformed algebra into a study of abstract structures, leading to new philosophical questions about the role of abstraction in mathematics.

Algebra and Computation:

Algorithmic Nature of Algebra: Algebra is inherently algorithmic, involving step-by-step procedures for solving equations or simplifying expressions. This algorithmic nature connects algebra to modern computational methods, raising questions about the role of computation in mathematical reasoning and whether algebraic methods reflect the underlying nature of computation itself.

Automated Proof Systems: The advent of computer-assisted proof systems, which rely heavily on algebraic methods, has led to philosophical debates about the role of human intuition in mathematics versus mechanical, algorithmic processes.

Historical and Philosophical Insights:

Descartes and Symbolic Representation:

René Descartes is often credited with the development of Cartesian coordinates, which provided a way to represent geometric problems algebraically. Descartes' work symbolizes the deep connection between algebra and geometry and raises philosophical questions about the nature of representation in mathematics.

Leibniz and Universal Algebra:

Gottfried Wilhelm Leibniz envisioned a universal algebra, or "characteristica universalis," that could serve as a universal language for all logical and mathematical reasoning. His philosophical insights anticipated the development of symbolic logic and formal systems that use algebraic methods.

Galois and the Limits of Algebra:

Évariste Galois' work in group theory and the solvability of polynomial equations led to new philosophical discussions about the limitations of algebra and the nature of symmetry. Galois theory provided insights into why certain equations could not be solved using standard algebraic methods, challenging assumptions about the completeness of algebraic systems.

Applications and Contemporary Relevance:

Algebra in Cryptography:

Modern cryptography relies heavily on algebraic structures like groups, rings, and fields. Philosophers examine the role of algebra in securing information and the philosophical implications of using abstract mathematical structures to solve real-world problems related to privacy and security.

Algebra and Quantum Mechanics:

Algebraic methods are crucial in formulating the laws of quantum mechanics, particularly in the use of operators and Hilbert spaces. Philosophers explore how algebra provides a framework for understanding quantum phenomena and the extent to which algebraic methods reflect physical reality.

Algebra and Artificial Intelligence:

In AI and machine learning, algebra plays a central role in developing algorithms and models. Philosophical discussions arise about the nature of intelligence and reasoning, and whether algebraic methods in AI reflect human-like thinking or merely computational processes.

The philosophy of algebra investigates the abstract nature of algebraic symbols and structures, the relationships they describe, and the metaphysical and epistemological status of algebraic truths. From ancient practical uses to modern abstract algebra and its applications in cryptography, computation, and quantum mechanics, the philosophy of algebra addresses deep questions about abstraction, formalism, and the role of symbols in understanding reality.

[andietries]

At first, Boolean is the most unintuitive shit ever. Like, girl, what do you mean that A+A=A

[donpasquella]

Frankly Blank

A lust for learning in my high school years triggered in me a desire to know what lay outside the boundaries of my math classes.

Along came an irresistible temptation in the form of a course on Boolean algebra offered by a correspondence school which, they assured me, I could do at my own pace.

The material arrived, wrapped as tight as a mummy. When I opened Lesson One, my naive young self soon realized that I had dramatically over-estimated by math ability by quite a bit.

It was true that my math grades were light years better than Wanda’s, the girl who sat behind me in her one school dress not even bothering to take notes in our geometry class taught by the school's wrestling coach.

But man oh man, Boolean algebra was not of this world. I never even made it through the First Lesson. To this day, I have no idea what it is or what it’s used for.

Nor do I have any idea whatever happened to Miss Wanda.

I am frankly blank on both subjects.

[genericnbbuddy]

Electronical Engineer: *Thinks that the only way that a boolean algebra can be formed is with a set consisting only of a 1 and a 0*

Theoretical computer scientist/mathematician, watching P(A): "Watch that cute polycule gooooooo"

I don't necessarily agree with this but it has such a mathematical quality to it somehow

[gayanelogic]

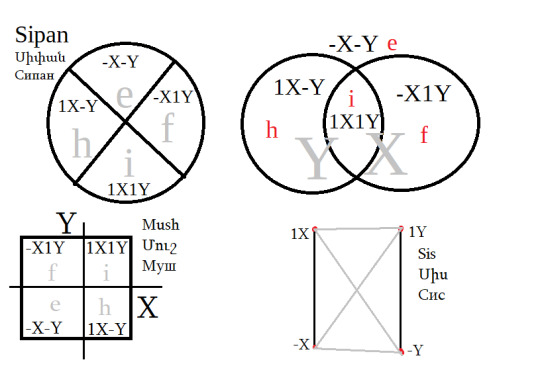
Graphical representation of binary operators, Sipan, Mush, Sis.

[deimonspikelet777]

[forgottenbones]

NP-COMPLETENESS - The Secret Link Between Thousands of Unsolved Math Problems

[hindicomputer]

Learn Boolean Algebra In Hindi

[chai-en-kaadhale]

if they could make computers with hextech i think they'd forgo the standard 0 and 1 binary for uhh 0123456789... oh and fuck it lets throw in ABCDE and F too

like yk

hexadecimal

(badumtss)

[petergender]

me & my weighted spidey merch to literally calm down from the spidey hyperfixation. do we think this will work

[fangirlsovertoomanythings]

im gonna hunt george boole for sport

[horsescary]

so ur telling me this istor is trans???

[vivaciouscynner]

I'll add on too, cuz why not ;)

what is math but practiced logic

media literacy requires logic

Having media literacy is more important than being good at math prove me wrong

[autism-corner]

nothing to worry about 6=w=9