#Complex Geometries

[asikoglueo]

Innovative Horizons in 3D Printing with QSY

The 3D printing industry is evolving at an unprecedented pace, and QSY is at the forefront of this innovation. With a focus on SLS (Selective Laser Sintering) 3D printing, QSY offers cutting-edge solutions that cater to a variety of industries, from aerospace to healthcare.

One of the standout features of QSY's SLS technology is its ability to create complex geometries that traditional manufacturing methods struggle to achieve. This opens up a world of possibilities for designers and engineers, allowing them to push the boundaries of creativity and functionality.

The commitment of QSY to quality and precision in SLS 3D printing is reflected in their detailed craftsmanship. Customers can expect not only high-performance parts but also timely delivery and exceptional customer service.

As the demand for rapid prototyping and customized solutions grows, QSY remains dedicated to providing innovative and sustainable 3D printing solutions that empower businesses to thrive in a competitive landscape.

Explore the future of manufacturing with QSY and discover how SLS 3D printing can transform your projects into reality!

[idea-explorer]

[faultfalha]

Stark buildings emitted a faint digital hum as we traversed the unfamiliar cityscape. It seemed as if we were lost, but then suddenly we spotted a sleek, shimmering behemoth, standing in contrast to the other buildings. We knew its name, Metafold, and its purpose. It was a firm devoted to the almost magical intersection of geometry and technology. Inside, a hushed tension filled the building. Everywhere we looked, there was a quiet excitement, as if they all knew something great was about to happen. Suddenly, we heard the roar of distant cheers; they had just closed a funding round. An enormous 1.78 million dollars had been raised in a single day. We felt the energy in the air; finally, the world had begun to take notice. Metafold had invented a new form of art, a kind of 3D printing that could create forms of beauty and complexity that had never been seen before. To the workers of this fledgling company, it was a kind of salvation, a way forward and a way out. We could feel the hope that existed in the building, and we felt proud to have been part of it.

[mathematical-cheese]

Just realised there's a convoluted proof for showing that any smooth vector bundle is homotopy equivalent to its base space

[daily-public-domain]

Day 364: "Broken glass 1"

link

–This image is part of the public domain, meaning you can do anything you want with it! (you could even sell it as a shirt, poster or whatever, no need to credit it!)–

[dougielombax]

An apartment complex is simple to most people, sure.

But what if it’s a 13-dimensional non-Euclidean apartment complex with dimensionally transcendental properties?!

What then?

Not so simple now. Is it?

Though thats very unlikely to happen.

But still.

Kid Named Apartment Complex:

*UNGODLY, INHUMANE BELLOWING NOISES!!!!!!!!!!*

[riiviir]

hey guys so I just started reading Flatland by Edwin A. Abbott and OMG AHSBNSBSBSNSNBSHZHSHDBFHGGHFHGRJ2KSHSBSNSK AAAAAAAAAAAAAAA I LOVE THINKING ABOUT THE RELATIVITY BETWEEN DIMENSIONS!!!!!!

[nablavii]

But on the other hand. I had my first complex variable exam and, well... I think it is pretty easy when you learn complex structures under the topological and geometric perspective. U can make that pullback to an IRⁿ subset. Pretty happy with the results.

Here's one of the results I do remember and...

The first part of another exercise .

Well, see ya soon guys!

[arbieroo-art]

Sprott's "Case F" strange attractor, demonstrating chaotic motion by following the trajectory of 100 Rainbow Dots. Here's the citation, on the off chance anybody wishes to look up the details: Sprott, J. C.: Some Simple Chaotic Flows. Phys. Rev. E, vol. 50, nr. 2, pp. R647-R650, 1994

[idea-explorer]

How SLA Enhances Product Design

One of the standout features of SLA is its accuracy. Traditional methods often struggle with intricate details, but SLA delivers impressive precision. This level of detail is crucial for industries like aerospace and medical devices, where every tiny element matters. For instance, custom implants made with SLA can significantly improve patient care. Thus, SLA not only boosts design quality but also contributes to better outcomes. Click the link and visit our website for more information!

[faultfalha]

In a move that is sure to revolutionize the printing industry, Metafold, a leading geometric 3D-printing specialist, has announced that it has landed $1.78M in funding. This infusion of cash will allow the company to expand its operations and bring its innovative printing technology to a wider audience. Metafold's unique printing technique, which relies on geometric folding to create three-dimensional objects, has generated a great deal of interest in the printing community. And with good reason: the results are simply stunning. Thanks to this new round of funding, Metafold is poised to take the printing world by storm. Be sure to keep an eye out for its products in the near future!

[abugidaithink]

is this a good

[stylewishstudio]

Club Night Flyer available on Graphicriver.

[dayofphylosophyorideology]

Universality

Universality is a profound and foundational concept in science and mathematics that describes the property by which systems with vastly different microscopic details exhibit the same macroscopic behavior. It is most prominently observed in the study of critical phenomena in statistical mechanics, but it also emerges across a wide range of disciplines, including condensed matter physics, dynamical systems, chaos theory, mathematics, computer science, and even certain branches of economics and biology. The notion of universality provides a framework for understanding how complex behavior can emerge from simpler rules and how such behavior can be characterized independently of specific details, relying instead on symmetries, dimensions, and collective properties.

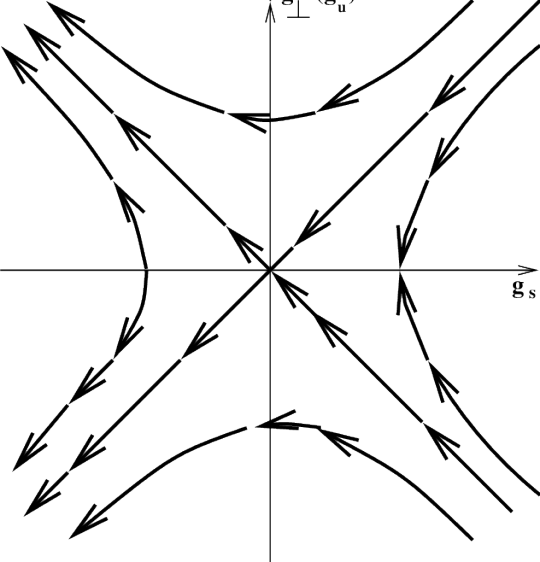
The concept of universality originated in the mid-20th century, particularly in the context of phase transitions in statistical physics. Physicists observed that vastly different physical systems—such as magnets near the Curie point and fluids near the liquid-gas critical point—exhibited strikingly similar behavior near their respective critical points. This was paradoxical because the underlying microscopic interactions in these systems were entirely different.

The resolution of this paradox came with the development of the renormalization group (RG) theory, primarily by Kenneth Wilson in the 1970s. RG provided a rigorous framework to explain how systems at different scales could be related through scale transformations, and how certain large-scale behaviors are invariant under these transformations. Universality emerged naturally from this framework: systems that flow toward the same fixed point in the space of physical theories under RG transformations exhibit the same critical exponents and scaling laws, regardless of their microscopic details. This laid the foundation for a deep understanding of universality and marked a turning point in theoretical physics.

A central feature of universality is the classification of systems into universality classes. These are groups of systems that, despite differences in their microscopic structures or interactions, share the same set of critical exponents, scaling functions, and general behavior near criticality.

The primary determinants of universality classes are:

Dimensionality of the system – The number of spatial dimensions significantly affects the critical behavior of a system. For example, the Ising model in two dimensions has different critical exponents than in three dimensions.

Symmetry of the order parameter – The nature of the symmetry breaking involved in the phase transition plays a key role. The Ising model, with a discrete Z2 symmetry, belongs to a different universality class than models with continuous symmetries like O(N) (e.g., the XY and Heisenberg models).

Range of interactions – Systems with short-range interactions often belong to different universality classes than those with long-range interactions.

Conservation laws and dynamics – In dynamical systems, the conservation or non-conservation of order parameters (such as energy or magnetization) can define dynamic universality classes distinct from their static counterparts.

Examples of well-known universality classes include the Ising universality class (scalar order parameter with Z2 symmetry), the XY universality class (vector order parameter with U(1) symmetry), and the Heisenberg universality class (vector order parameter with SO(3) symmetry).

The renormalization group (RG) formalism is essential to the modern understanding of universality. It describes how physical systems behave under changes in scale, allowing for the systematic "coarse-graining" of microscopic details while retaining the large-scale features that determine macroscopic behavior.

The key idea in RG is that as one examines a system at increasingly larger scales, the effective parameters governing the system’s behavior flow under RG transformations. At critical points, these flows approach fixed points, which correspond to scale-invariant behavior. Systems that flow toward the same fixed point share universal properties—hence the emergence of universality.

In this context, critical exponents describe how physical quantities diverge near the critical point (e.g., specific heat, susceptibility, correlation length), and these exponents are determined by the properties of the RG fixed point, not the microscopic details of the system. For instance, the critical exponent β, which describes how the order parameter vanishes near the critical temperature, is the same for all systems in the same universality class.

While the concept of universality originated in statistical mechanics, its implications extend far beyond that domain.

1. Dynamical Systems and Chaos

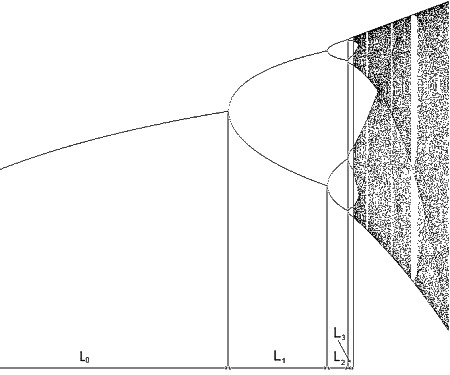
In the study of deterministic chaos, universality appears in the context of bifurcation theory and the transition to chaos. One of the most striking examples is the Feigenbaum constants, which describe the rate of period-doubling bifurcations in one-dimensional maps such as the logistic map. Regardless of the specific form of the map, the ratio of intervals between bifurcations converges to the same universal constant (~4.669), and the scaling behavior near the onset of chaos follows universal laws. This indicates that the transition to chaos in wide classes of dynamical systems exhibits universal features.

2. Quantum Field Theory and High-Energy Physics

Universality is also a key idea in quantum field theory (QFT), where it helps explain why effective field theories at low energies can be described using a limited set of relevant operators, despite the potential complexity of high-energy (UV) theories. RG methods show that low-energy phenomena are governed by universality classes characterized by the relevant operators at an IR (infrared) fixed point.

In lattice gauge theories and studies of quantum critical points, universality informs the scaling behavior of observables near quantum phase transitions, which occur at absolute zero and are driven by quantum fluctuations rather than thermal ones.

3. Computer Science and Algorithmic Universality

In theoretical computer science, a different kind of universality appears in the concept of computational universality, particularly in Turing completeness. A computational system (e.g., a Turing machine or lambda calculus) is said to be universal if it can simulate any other computational system. This form of universality is foundational to the theory of computation and underlies the universality of general-purpose computers.

Cellular automata also exhibit universality. For example, Conway’s Game of Life is computationally universal, meaning that it can simulate a Turing machine despite its simple local rules.

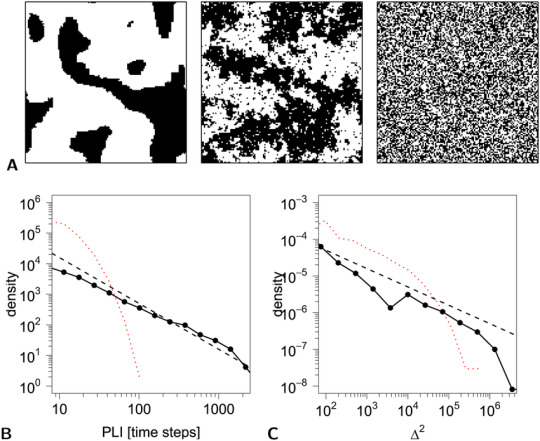
4. Percolation, Fractals, and Geometry

Percolation theory provides another domain where universality emerges. Near the percolation threshold, properties like the size of connected clusters exhibit power-law distributions characterized by universal critical exponents. These exponents depend only on the dimensionality of the system and not on the microscopic details of the lattice or geometry.

Fractals, which exhibit self-similarity and non-integer dimensions, are also associated with universality. The fractal dimensions of certain critical clusters (e.g., in percolation or the Ising model) are universal and can be related to the scaling laws governing the system.

Although more speculative and less rigorously defined, analogs of universality have been proposed in biological and economic systems. For example, scaling laws in biological systems—such as the relation between metabolic rate and body mass (e.g., Kleiber’s law)—exhibit regular patterns across a vast range of organisms. Similarly, certain macroeconomic behaviors, such as power-law distributions in wealth and income or the scaling of urban infrastructure with population size, have been argued to reflect universal principles.

However, unlike in physics, the presence of complex, adaptive agents and feedback loops in these systems complicates the identification of precise universality classes or fixed points. Nonetheless, attempts to apply statistical physics and RG-like methods in these fields continue to be active areas of interdisciplinary research.

Universality in a formal mathematical sense often involves invariance under group actions, limit theorems, or fixed-point theory. For example:

Central Limit Theorem: One of the simplest manifestations of universality in probability theory. It states that the distribution of the sum of many independent random variables tends toward a Gaussian distribution, regardless of the underlying distribution, provided the variance is finite.

Random Matrix Theory: In the study of eigenvalues of large random matrices, universality appears in the distribution of spacing between eigenvalues, such as the Wigner-Dyson distribution. These distributions are universal across broad classes of ensembles, including those modeling nuclei, disordered systems, and even zeros of the Riemann zeta function.

Scaling Limits and Universality in Stochastic Processes: Brownian motion, the scaling limit of many discrete random walks, provides a classical example. Similarly, the Kardar-Parisi-Zhang (KPZ) universality class encompasses a wide range of stochastic growth models that, despite different dynamics, share the same large-scale statistical properties.

Universality challenges reductionist viewpoints by emphasizing that many macroscopic behaviors are insensitive to microscopic details. This has profound implications for how scientists model and understand complex systems. Rather than focusing on the exact microscopic state of a system, one can study representative models that capture the relevant symmetries and conservation laws to extract universal predictions.

It also exemplifies the power of abstraction and the importance of symmetry and scaling in nature. The idea that fundamentally different systems can exhibit identical critical behavior suggests that there are deep organizing principles underlying complex phenomena.

Furthermore, the concept has epistemological significance, influencing how knowledge is structured and how laws of nature are interpreted. It bridges the gap between the particular and the general, providing a unifying framework for diverse phenomena.

Universality is a cornerstone of modern science, offering a window into the fundamental structure of complex systems. From phase transitions and critical phenomena to dynamical chaos, quantum fields, algorithmic computation, and beyond, universality reveals the deep and often surprising regularities that transcend specific details. Its discovery and formalization represent one of the most profound insights in 20th-century physics, with ongoing implications for a broad range of disciplines in the 21st century. As science progresses, the principle of universality continues to guide our understanding of emergent behavior, scale invariance, and the interconnectedness of nature.

[nablavii]

Stereographic Projection

Actually, it is my first real interaction with topology and differential geometry without knowing any knowledge. I mean, stereographic projection it's a diffeomorphism and you can see how (in that sense), the IR²U{∞} sphere can be covered as well with two sheets.