#Euler angles

[microqwavve]

fuckin da USB port but i gotta rotate 180 degrees on the z axis cuz it wont go in then rotate another 180 degrees on the z axis because the previous try also wouldnt go in then figuring out i just wasnt aiming straight the first time i tried it and the whole thing is just kind of stupid

[cubsha]

if you dont learn to lurp n slurp your gimbles are gonna get LOCKED bro

[storymaker14]

Bizzaro Right Triangles

Okay, we all know that, if you have a right triangle with sides a and b and hypotenuse c, that means a^2 + b^2 = c^2, right?

So you can have 3-4-5 right triangles, and 5-12-13, and 7-24-25, etc.

And technically, a 1-i-0 right triangle follows this pattern, too, which has made the rounds in the math meme community.

But I found something better and weirder. I found a whole family of better and weirder.

I'm gonna skip a bit of the beginning and start here:

cos x = (e^ix + e^-ix) / 2

That follows from Euler's formula; if you need a walkthrough, I can provide, but I want to start with the above. So then, it follows that:

cos (i*lnx) = (x + 1/x)/2 = (x^2 + 1)/2x

Which means that an angle of (i*lnx) radians in a right triangle will have an adjacent side of (x^2 + 1) and a hypotenuse of 2x. By Pythagoras, then, the opposite side must be (x^2 - 1)*i.

But please note: if x is odd, then the lengths of all three sides will be even, and thus can be divided by 2.

Which means -- are you holding onto your hats and shoes?!? -- means that the proportions of the right triangle with angle i*ln(3) radians... are 5-4i-3.

And for i*ln(5) radians, they are 13-12i-5.

And so forth, with all the familiar Pythagorean triplets sqrt(2n+1)-n-(n+1) showing up, just with one side imaginary and the hypotenuse and remaining side swapped -- so, (n+1)-n*i-sqrt(2n+1). They still fulfill Pythagoras, every single one.

Which I think is, pardon my directness, fucking terrific. But just as a little bonus, please note that this means the triangle with angle i*ln(2) radians, the proportions are 5-3i-4, which is just delightful IMHO.

[xds369]

"If you're tired, why don't you escape and relax with me?"

After painting, it looks like Euler eloped to the Angle of view (……)

[bootleghellokitty16]

it’s been a years long journey but I thank mathblr, my parents, friends, and ofc the queer community for getting me to a place where I have some hope. Before I was 2 squared to do anything (bad pun I know) but now that I’ve gotten to where I am I’d need something longer than a Euler to show how far I’ve come. (Another bad pun). Anyway thank you tumblr for transing my gender I’m sorry for posting abt it so much it’s just new and exciting I don’t have set theory (haha) on how to go abt everything yet but I think I’m approaching it from the right angle (teehee)

[squareallworthy]

Triangle Tuesday 3: The orthocenter, the Euler line, and orthocentric systems

Previously, we have looked at two different ways to mark a point in a triangle. First, we drew cevians (lines from the vertices) to the midpoints of the sides and found that they all cross at a point, which is the centroid. Then we tried drawing perpendiculars to the sides from the midpoints, and those all met at the circumcenter. And you could do this with any point on the side of a triangle -- draw a cevian to it, or a perpendicular from it, and see what happens.

This time, though, we're going to do both. That is, we're going to work with the cevians that also form perpendiculars to the sides. These are the altitudes, which run from a vertex to the nearest point on the opposite side, called the foot of the altitude. The three altitudes all meet at a point H, and that's the orthocenter. (The letter H has been used to mark the orthocenter since at least the late 19th century. I believe it's from the German Höhenschnittpunkt, "altitude intersection point.") Anyway, let's prove that the orthocenter exists.

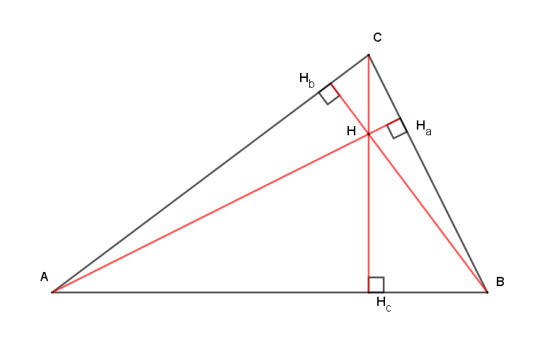
Theorem: the three altitudes of a triangle coincide.

Here's a very simple proof that the three altitudes coincide. It relies on the existence of the circumcenter, which we already proved before. Given a triangle ABC, draw a line through A parallel to the opposite side BC. Do the same at B and C. These lines cross at D, E, and F and form the antimedial triangle (in blue).

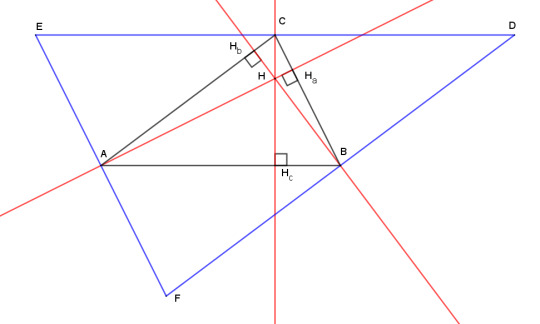
Then the altitudes of ABC are also the perpendicular bisectors of DEF. We proved before that perpendicular bisectors all meet at a point, therefore altitudes do as well.

That was easy. Let's do it again, but in a different way. It's not quite as simple, but it includes a large bonus.

Theorem: the three altitudes of a triangle coincide at a point colinear with the circumcenter and centroid, and GH = 2 GO.

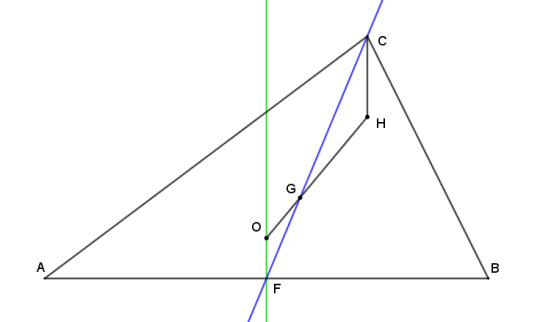
Let's take triangle ABC, and let F be the midpoint of side AB. Then mark two points that we already know, the circumcenter O and the centroid G. We'll also draw the median (green) and the perpendicular bisector (blue) that run through F, leaving the other ones out to avoid cluttering the picture.

We already know from our look at the centroid that G cuts segment FC at a third of its length, so GC = 2GF. Let's extend segment OG in the direction of G by twice its length out to a point we'll label H, so that GH = 2GO.

Now consider the two triangles GOF and GHC. By construction, their two blue sides are in the ratio 1:2, and the same for their two black sides. They also meet in vertical angles at their common vertex G. So by side-angle-side, the triangles are similar, and it follows that HC is parallel to OF, and therefore perpendicular to AB. So H lies on the altitude from H to side AB.

By analogous construction, we can show that H also lies on the other two altitudes. So not only have we proved that the altitudes coincide, but also that O, G, and H all lie on a line, and furthermore that G is located one third of the way from O to H, in any triangle.

This proof is due to Leonard Euler, and the line OGH is called the Euler line. Not only these three points but many others as well fall on this line, which we will get to later on.

Let's look at some more properties of the orthocenter and the feet of the altitudes. I'm just going to look at the case of an acute triangle for now, and show how this extends to the obtuse case later.

Theorem: two vertices of a triangle and the feet of the altitudes from those vertices are concyclic.

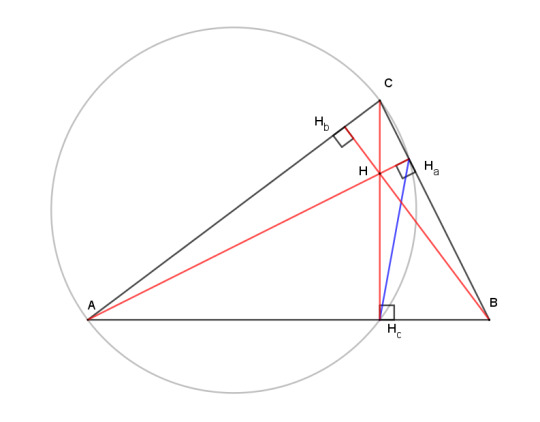
Proof is easy: the two right triangles AHcC and AHaC share segment AC as a hypotenuse. Therefore AC is a diameter of the common circumcircle of AHcC and AHaC (following from Thales's theorem).

(Incidentally, look at the angle formed by the blue segment and the altitude CHc. It subtends the same arc as angle CAHa, so (by the inscribed angle theorem again) they must be equal. That's not a part of this theorem, so just tuck that fact away for a moment.)

Theorem: a vertex, the two adjacent feet of the altitudes, and the orthocenter are concyclic.

Same idea, but now the right triangles are AHcH and AHbH, and AH is the diameter of the common circumcircle.

(And incidentally, look at the angle formed by the new blue line and the altitude CHc. It subtends the same arc as HbAH, which is same angle as CAHa. So those angles must be equal too. Since both angles between a blue line and the altitude CHc are equal to the same thing, they are equal to each other. Again, not a part of this theorem, just something I wanted to note.)

So those are some interesting concyclicities, but now let's look at the pedal triangle of the orthocenter, which is called the orthic triangle.

Oh, hey, it's made up blue lines, just like the ones we were talking about. And we proved that the two longest blue lines make equal angles with the altitude between them. By symmetry, we can prove the same thing about all the angles made by the blue lines. So that means

Theorem: two sides of the orthic triangle make equal angles with the altitude between them.

Another way to say this is that the altitudes are the angle bisectors of the orthic triangle. And I admit that was kind of a roundabout way to introduce the orthic triangle, but I think it makes the proof of this property easier to follow.

Two other properties of the orthic triangle immediately follow from this:

In an acute triangle, the inscribed triangle with the shortest perimeter is the orthic triangle

and

In an acute triangle, the orthic triangle forms a triangular closed path for a beam of light reflected around a triangle

which are two ways of saying the same thing.

But those two properties only hold for acute triangles. What happens to the orthic triangle in an obtuse triangle? Let's push point C downward to make triangle ABC obtuse and see what happens. To make things clear, I'm going to extend the sides of ABC and the altitudes from line segments into lines. Here's the before:

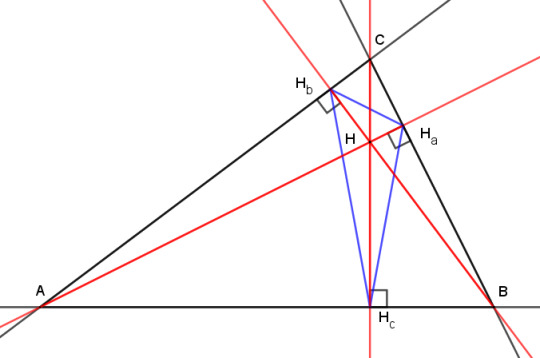
And here's the after:

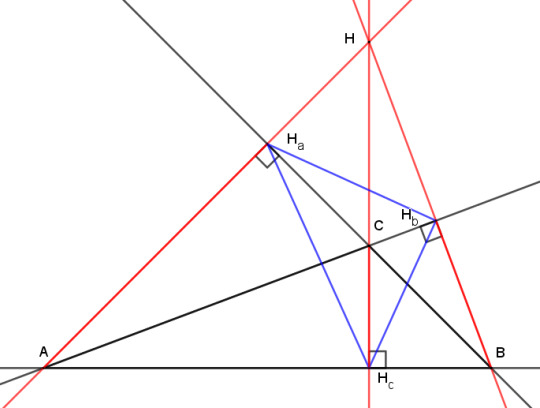
The orthocenter has moved outside of triangle ABC, and two of the altitudes have their feet on extensions of the sides of ABC rather than on the segments AC and BC. The orthic triangle now extends outside ABC, and certainly isn't the inscribed triangle with the shortest perimeter any more.

But look at it another way. We now have an acute triangle ABH, and the line HHc is an altitude of both the obtuse triangle ABC and the acute triangle ABH. Meanwhile, lines AC and BC have become altitudes of ABH.

So what we have is essentially the same acute triangle with two swaps: point C trades places with H, and Ha trades places with Hb. That means that our two theorems about concyclic points morph into each other as triangle ABC switches between acute and obtuse. Here's an animation to show the process:

And this is why I didn't bother with the obtuse case above -- each theorem of concyclicity is the obtuse case of the other.

So if we can just exchange the orthocenter with one of the vertices, what does this mean for their relationship? If you are given a group of vertices and lines, how can you tell which one is the orthocenter and which one are the vertices? Well, you can't.

Theorem: Given an acute or obtuse triangle ABC and its orthocenter H, A is the orthocenter of triangle BCH, B is the orthocenter of ACH, and C is the orthocenter of ABH.

The proof comes from consulting either of the "before" and "after" figures above. Take any three lines that form a triangle, red or black. The other three lines are then the altitudes of that triangle. The three feet are where a red and black line meet perpendicularly, so they are the same for all four possible triangles, which means all four share the same orthic triangle.

(Of course, if ABC is a right triangle, then we get a degenerate case, as you can see from the gif at the moment when C and H meet.)

Such an arrangement of four points is called an orthocentric system. Of the four points, one is always located inside an acute triangle formed by the other three, and it's conventional to label the interior one H and the others ABC.

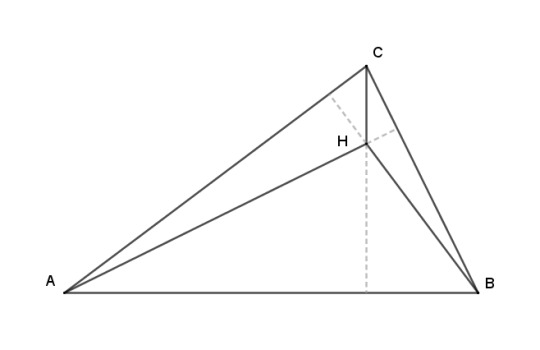
Orthocentric systems pop up all over the place in triangles, so expect to see more of them as we go along. Now, let me do one little lemma about altitudes, and then I'll show something cool about orthocentric systems.

Lemma: the segment of an altitude from the orthocenter to a side of the triangle is equal to the extension of the altitude from the side to the circumcircle.

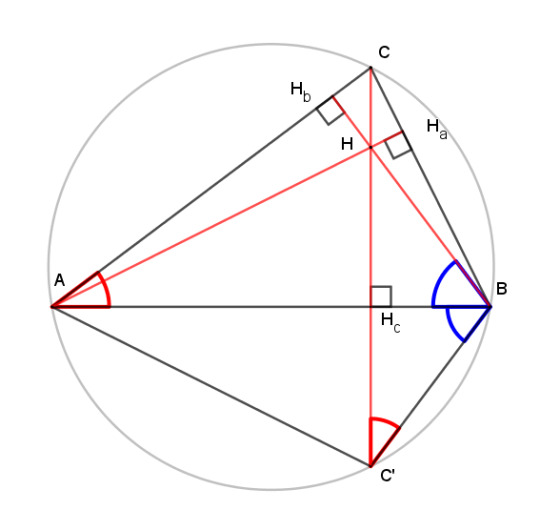
We can show this with just a little shuffling of angle identities. Extend altitude CHc to meet the circumcircle at C'. The angles CAB and CC'B, labeled in red, subtend the same arcs, so they are equal. Triangle ABHb is a right triangle, so angle HbBA, in blue, is complementary to it. The same is true for the right triangle C'BHc, so the two angles labeled in blue are equal. Then by angle-side-angle, triangles BHcH and HHcC' are congruent, and segment HHc = HcC'.

By the same argument, we can show that triangle AHHc is congruent to AC'Hc, which leads us into the next bit.

Theorem: all the circumcircles of the triangles of an orthocentric system are the same size.

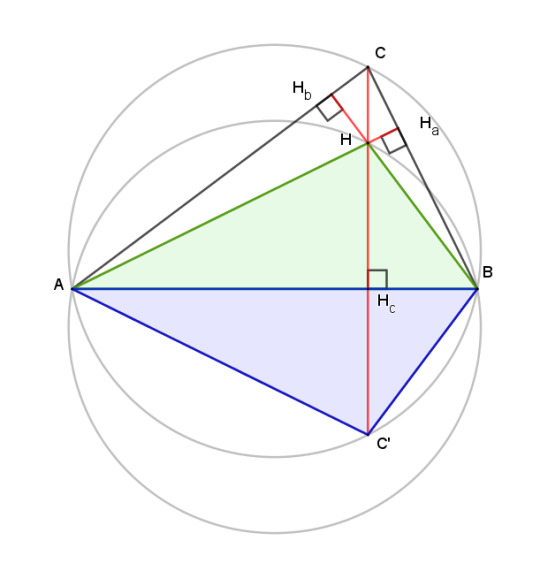
The blue triangle has the same circumcircle as triangle ABC. From the foregoing, the blue and green triangles are congruent. Therefore their circumcircles are the same size as well. The same argument works for ACH and BCH.

So here is an orthocentric system with its four circumcircles.

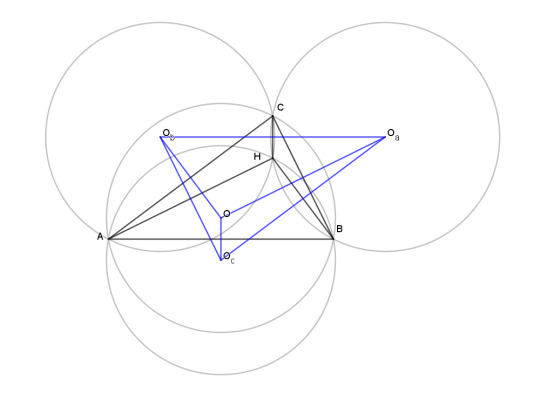
The four circumcenters O, Oa, Ob, and Oc form another orthocentric system, congruent to the first one.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[utopicwork]

i have a few Bread3D questions

how are rotations done in Bread3D? quaternions/rotors (marctenbosch.com/quaternions is a pretty good resource), or rotation matrices, or euler angles? axis-angle?

do you compose all the transformations into a single 4x4 view matrix? (most 3d engines i know of use this technique)

how do you do hidden surface elimination? zbuffer? face sorting? backface culling (insufficient for nonconvex shapes)?

will the rendering primitive be triangles or will it be able to handle other shapes as well? (e.g. true sphere)

also, one of the interesting side effects of rendering to low resolution is that per-pixel operations (like fragment shaders) are less painful.

Rotations are done with euler angles at the moments but I want to have a manipulable axis of rotation so I'll do it with quaternions after I've done some reading (thank you for the link I'll add that to my reading list)

The visual output uses some rather simplistic division operations that I'm going to work into something better as I go

Hidden faces get drawn over at the moment Ive been working on automatic face sorting though

Currently rendering primitives are just whatever face polygons are requested but that'll change. Though I am trying to keep it pretty low resource intensity

And yeah! I like rendering to a low resolution because of that and because Pillow is very snappy at low resolutions

[nhaneh]

just occurred to me that gimbal lock issue with euler angles might make a lot more sense if you think about the pitch/heading axes less as rotations and more as latitude/longitude angular coordinates on the surface of a sphere.

I mean, if you were to stand at a latitude of either 90 or 180 degrees - ie. on the north or south pole - then it makes sense that trying to move left or right along the equatorial longitudal axis would just having you spinning around in place in a banking rotation rather than actually going anywhere.

[booz1995]

Tatsumaki. Generated on Stable Diffusion. 17.12.2023.

Promts:

(best quality, masterpiece, perfect face, beautiful and aesthetic:1.2, colorful, dynamic angle, highest detailed face) alone girl girl posing in front (night tokyo :1.1), full body, Tatsumaki, arched back, (black long fitt-tight dress:1.1), (lush ass:1.1), (thin weist:1.2), (lush hips:1.1), (small breast:1.1), (short culry green hair:1.1), bright green eyes <lora:tatsumaki:1.3>, emotional face, detailed eyes

NP:

easynegative

Steps: 23, Sampler: Euler a, CFG scale: 7, Size: 512x712, Model: forgottenmixAnimation_v10, VAE: vaeFtMse840000Ema_v100.pt, Denoising strength: 0.35, Clip skip: 2, Hires upscale: 2, Hires upscaler: Latent, Lora hashes: "tatsumaki: 2ac93c82c950", Version: v1.6.0

[coraniaid]

top 5 mathematical identities :)

I wish Tumblr supported LaTeX.

OK, not trying to overthink this too much.

There are lots of fun identities involving binomial coefficients (or their q-analogs), or related integer sequences like the Catalan numbers and Motzkin numbers. But I think I have to go with the Chu-Vandermonde identity: who doesn't like a good convolution formula?

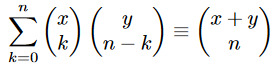
Of all the trigonometric identities I've ever had to learn, this is certainly not the most useful in practice or the hardest to prove or, arguably. the most inherently interesting either. I think the half-angle formula for tan is surprisingly pretty though.

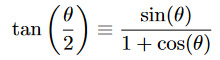
Let S be a finite set of real numbers. The maximum-minimums identity relates the largest element of this set to the smallest elements of every (non-empty) subset of S.

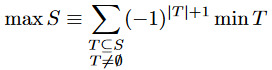
or, more concretely,

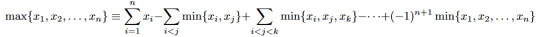
Perhaps not classically beautiful, but certainly enormously useful, the Sherman-Morrisson-Woodbury identity in linear algebra gives a formula for computing the inverse of a rank-k update of an invertible matrix by doing rank-k updates of the inverse of that original matrix. It's valid whenever the matrices are suitably conformable and when both the required inverses exist.

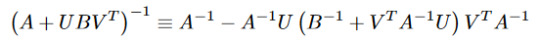
I feel like I have to include something due to Euler here, but -- rather than one of the famous ones involving π or anything to do with topology -- I'll go with some analytic number theory. The pentagonal number theorem gives a series expansion of the Euler function, valid for any complex x in the unit circle.

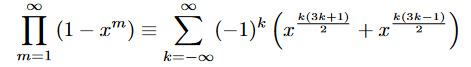
or, expanding both sides,

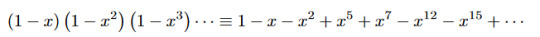
That takes us into the world of q-series and we can generalize it further to get Jacobi's triple product formula or various identities due to Ramanujan or MacDonald's identities for affine root systems or other increasingly exotic and strange things ... but this identity is the prototype for all of them.

[manyblinkinglights]

Okay SquashStretch is "working," there's still mystery Inspector problems but if you bull through, it results in a correct avatar so. whatever. Now for forefoot pickup.

I think I'll expose all three local euler angle rotations of one of the pickup thigh transforms (and use it to mirror the other). Then people can manually point their foreleg until it matches their arm angle. THEN I'll expose all three local euler angle rotations of the pickup foot and pickup toe. Then people can manually point their pawbs until they match their hand angle.

[seradae]

I want to get new tattoos and I think I'm going to design out all the mathematical identities and formulas I commonly use for my left arm for easy reference.

Euler's Formula: e^(iθ) = cos θ + i sin θ

2d rotation: x' = x cos θ - y sin θ; y' = x sin θ + y cos θ

Cartesian to polar: r = |(x,y)|; θ = atan(y/x)

Polar to Cartesian: x = r cos θ; y = r sin θ (this one is just a special case of 2d rotation where you plug in (r, 0) though, so probably leave this one off)

Angle between vectors: θ = acos(||a|| • ||b||)

... Goddamn I'm a nerd.

[scramble-crossing]

Euler's Identity

Chapter 1: After the Sermon, Before the Wake

Rating: M

Characters: Sho Minamimoto, Neku Sakuraba, Shiki Misaki, Daisukenojo "Beat" Bito, Rindo Kanade, Tosai "Fret" Furasawa, Nagi Usui, Shoka Sakurane

Pairings: Sho Minamimoto & Neku Sakuraba, Sho Minamimoto & Rindo Kanade & Tosai "Fret" Furasawa & Nagi Usui, Implied Neku Sakuraba/Shiki Misaki/Daisukenojo "Beat" Bito

Warnings: Implied/Referenced Suicide and Self-Harm

Summary:

It happened again

As it has happened before

And as it will happen a hundred times more

After yet another attempt at the Composer's seat leaves Minamimoto critically wounded, he's forced to seek refuge in the only place left that will have him: his old home, WildKat. But it's come under new management since he's seen it last. Proprietor Neku Sakuraba has been dealing with his own ghosts since reclaiming the life he should have lived after the Long Game, though he's able to find comfort in his friends as they help him, and the cafe, get back on their feet. Maybe they can do the same for Minamimoto, when the Wicked Twisters reach out to him with an offer of reconciliation...

Sometimes all it takes is a little deviation

Read on Ao3

(And also a playlist here!)

My fic for the @subasekabang 2023! Had a blast participating alongside my Bang partners @starocide and @awanderingserena. Make sure to check out their works!

Preview under the cut

Morning broke, and from within it spilled a city untouched by rapture.

The gentle, lapping water of the Shibuya River blushed indigo, reflective of a sky that fell like a silken curtain over towers buttoned here or there with a warm yellow light, a few windows stirring, blinking sleepily open. Little moved and all was quiet. Well, quiet as it ever could be. Washed in a dusky lowlight burnt only at the very edges by the dayish gold of a still-rising sun, most of Shibuya was still dreaming as Sho Minamimoto emerged from the dark tunnel’s maw, greeted only by the rumble of far-off cars like a cat’s amused purr.

He breathed fresh air. It was tinged with the familiar scents of scathed asphalt and smoke and filled whatever mimicry of lungs he had left in his chest. Notes of citysong danced in his ears. He heard birds chitter, saw airplanes pull white-tufted tails behind them, both swimming the sky’s murky depths, and him, standing inside of it all, a part of it all, was as alive as a dead man like him could ever be.

…But he wasn’t supposed to.

‘Incongruent.’

This time was different than before.

‘Why am I…?’

Sho staggered. A searing pain tore down through his stomach like a knife plunged in and twisted, blood bursting in his head, filling his sight with a pulsing red haze, ruby dark, growing darker. He shut his eyes. Fumbled in blackness. His legs trembled like that of an infant still fresh to the earth; it took all he had left just to keep himself from collapsing into the embrace of concrete beneath his feet.

He would not fall. No, he would hurt and he would ache, he would fracture into pieces, but he would not let himself go wholly and with quiet humiliation into a storm that had since vanished.

And so he started walking.

Shadows of the overpass criss-crossed his path as Sho dragged himself over the gutter’s sloped ridge, keeping low along the city’s underbelly. They were long and soft in the surrounding dimness. Easy to slide into. He knew someone who would’ve loved them (Who? That was lost somewhere in memory), but for him the angles were too stretched, too obtuse, the encroaching sunlight giving too little space to hide. He would have to keep moving. Even as exhaustion weighed heavily on him, sucking at his heels like torrent water and making him think for one wild, confused moment that it was the river wanting him back.

He tried to shake it off, clean his mind of the clinging, gurgled whispers whose voices he couldn’t tell from his own. It was all the same, anyways. A reprise on unfinished business.

You lost

‘I lost.’

He never stood a chance.

When he flexed his hands to make sure he could still feel them, his fingers pressed with splintered nails into palms that hadn’t once brushed the fantastically inhumane coldness of divinity. They were hot and slicked with sweat and dirt from the ground he’d crawled across. His eyes were not reverent, nor were they holy. They were pained by the light that had filled them. Even when they were closed he felt no relief, the image of His split-grinning face twin tattoos on the insides of his eyelids.

White.

‘No’

Teeth.

‘Stop’

Cherubim faces, child’s hands.

Great shafts of light like sterile dreams.

He grasped his hair, tugged hard until it screamed.

Peach lips. Apple cheeks. Fruit of the Lord, piercing his still-warm core.

(It didn’t help)

Him. Him in the center of it all, when the omnipotent hymns of gold and saintly frequencies fell silent, and he met his violet, ice-chip eyes.

‘It hurts’

When he smiled.

‘It hurts.’

When he laughed.

‘It hurts’

When he saw himself in a smear across the floor, everything he ever was or ever could have been left as a stain on God’s front porch.

+ some bonus shitposts

[arbieroo-art]

[machine-saint]

i use the trig double angle identities infrequently enough that i never bother memorizing them, i just derive them from euler's formula

like, cos(2x)? well, letting z=e^(ix), that's just (z^2+z^(-2))/2, and cos(x) is (z+z^(-1))/2, so cos^2(x) = (z^2+2+z^(-2))/4, so double that and subtract 1. done

[squareallworthy]

Triangle Tuesday 8: the nine-point circle, the deep lore, and did I say nine? I meant, like, fifty-six.

Today we are looking at the nine-point circle, a famous construction with connections to other triangle geometry that we've looked at before. But first, I'd like to re-introduce the centers that we've met so far. You should imagine that they're members of a super team each with their own little sequence that the cartoon always shows when they go into action.

And imagine that they're appearing with one of these dramatic cartoon backgrounds like this. I would go ahead and do that, but it would look really messy on the little screen you're staring at. It will look better in your imagination.

Anyway, here we go. Here they are, now each with its own thematic color.

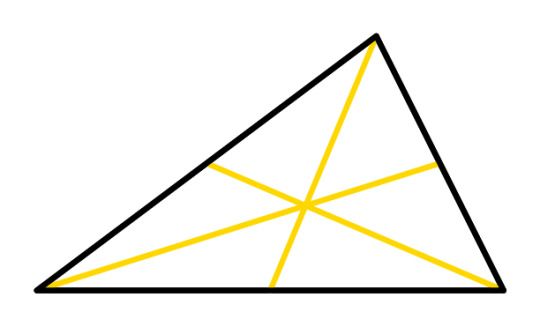
G, the Centroid!

Secret origin: intersection of the medians

Trilinear coordinates: 1/a : 1/b : 1/c

Affiliations: Euler line, isogonal conjugate of the symmedian point

Super powers: center of gravity of triangle area • center of gravity of triangle vertices • divides triangle into equal parts ABG, BCG, and ACG • divides medians 2/3 of the distance from vertex to midpoint

O, the Circumcenter!

Secret origin: intersection of the perpendicular bisectors

Trilinear coordinates: cos A : cos B : cos C

Affiliations: Euler line, isogonal conjugate of the orthocenter

Super powers: center of circumcircle • circumcircle is locus of points with degenerate pedal triangles • relates to incenter via Euler's theorem in geometry

H, the Orthocenter!

Secret origin: intersection of the altitudes

Trilinear coordinates: sec A : sec B : sec C

Affiliations: Euler line, isogonal conjugate of the circumcenter

Super powers: constitutes an orthocentric system along with the vertices • incenter of orthic triangle • sides of orthic triangle are antiparallel to sides of reference triangle • concyclic with a vertex and two adjacent feet of altitudes

I, the incenter!

Secret origin: intersection of the angle bisectors

Trilinear coordinates: 1 : 1 : 1

Affiliations: entourage of excenters

Super powers: center of the incircle • isogonally self-conjugate • forms orthocentric system along with excenters • relates to circumcenter via Euler's theorem in geometry • always lies in interior of orthocentroidal disc

K, the symmedian point!

Secret origin: intersection of the symmedians

Trilinear coordinates: a: b: c

Affiliations: isogonal conjugate of centroid

Super powers: perspector of reference and tangential triangles • parallels through K intersect sides in six concyclic points • antiparallels through K intersect sides in six concyclic points, with K at the center of the circle • circles through K and two vertices intersect sides in six concyclic points • lines joining midpoints of altitudes and sides pass through K • centroid of its own pedal triangle • just very pretty

So now that we've got the super team together, it's time to introduce them to someone new. I know, you're thinking we've got this established cast of characters, and they relate to each other in so many varied and intimate ways. How could a new triangle fit into these relationships? Wouldn't it feel like a superfluous add-on at this point in the show?

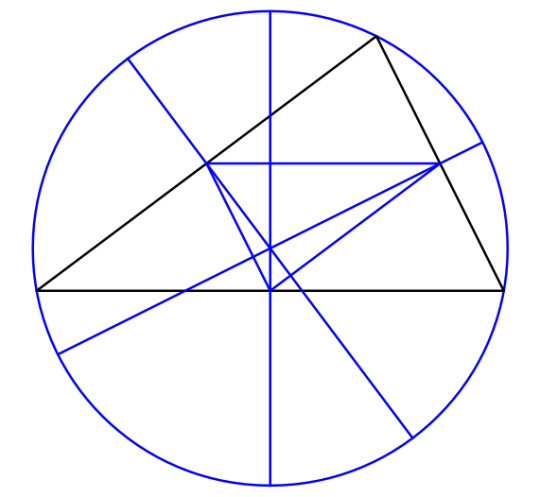
Well, let's see. Let's go back and look at the midpoints of the sides. We find the midpoints by drawing perpedicular bisectors on each side. Those lines meet at the circumcenter, which makes the midpoints the feet of the circumcenter. The triangle formed by the midpoints is the pedal triangle of the circumcenter.

Any three points also determine, naturally, a circle. The circle formed by the feet of a point is called the pedal circle of the point. And every point has a pedal circle with respect to a given triangle.

The orthocenter, for instance, has a pedal circle defined by the feet of the altitudes, and guess what? It's the same circle! What's more, this circle bisects the segments that join the orthocenter with the vertices. For this reason, the circle is called the nine-point circle, and its center is the nine-point center, N. Let's prove that it exists.

Theorem: in any triangle the midpoints of the sides, the feet of the altitudes, and the midpoints of the segments connecting the orthocenter to the vertices lie on a common circle.

Here's our triangle ABC, with midpionts of sides Ma, Mb, Mc, feet of the altitudes Ha, Hb, Hc, and midpoints of segments joining H and the vertices Sa, Sb, Sc. We will rely on the fact that a line segment joining the midpoints of two sides (a midline) is parallel to the third side and half as long.

In green we have horizongal segments MbMa, a midline of ABC, and SaSb, a midline of ABH. Both of these midlines are parallel to side AB and half its length, so they are parallel to each other and equal. Vertical green segments MbSa and MaSb are midliness of ACH and BCH respectively, so they are also parallel and equal. Therefore the green segments form a rectangle.

In the same way, the blue segments also form a rectangle. These two rectangles have a common diagonal MbSb, and so have the same circumcircle. And McHcSc is a right triangle, and its hypotenuse McSc is also a diagonal of the blue rectangle. Therefore Hc is on the same circle, and by analogous argument so are Ha and Hb.

Since now we can be sure the nine-point circle and its center exist, it should get its own introduction scene and signature color.

N, the nine-point circle!

Secret origin: pedal circle of circumcenter and orthocenter

Trilinear coordinates: cos(B-C) : cos(C-A) : cos(A-B)

Affiliations: Euler line

Super powers: passes through nine points • many many others which we will get to next

So those are some nice ways that connect the nine-point circle to the circumcenter and orthocenter. And it's cool that this new character N has some connections to the established characters O and H, but what about the other points? Can we find some connections there?

Yes, we can, because it turns out the nine-point center is connected to everything. Would you like to see some of them?

(This is me right now.)

Because there are kind of a lot.

The nine-point circle is tangent to the incircle and the excircles. If you are keeping track, that's now 13 points of interest on the nine-point circle.

The radius of the nine-point circle is half that of the circumcircle. This is easy to see, because the circle is the circumcircle of the medial triangle, which is half the size of the reference triangle.

The nine-point center lies on the Euler line midway between the circumcenter and the orthocenter. The centroid is one-third of the way from the circumcenter to the orthocenter. These positions give the orthocenter and centroid special status with regard to the nine-point circle.

The nine-point circle bisects any line segment from the orthocenter to the circumcircle, making the fact that it bisects the tops of the altitudes into a special case of a general property.

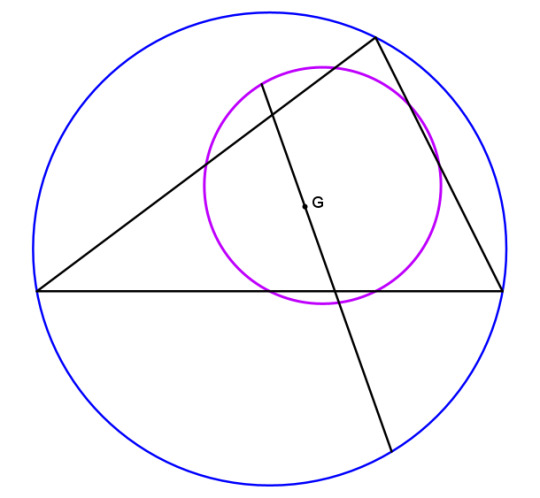
The centroid trisects any line segment extending from a point on the nine-point circle through G and on to the circumcircle. Another way of saying this is that G is a center of dilation between the circumcircle and nine-point circle with scaling factor -1/2. In triangle geometry, this particular dilation through G is called taking the complement of a point, so a third way of describing this relationship is to say that the nine-point circle is the complement of the circumcircle.

The nine-point center is also the center of gravity of A, B, C, and H.

As we have seen previously, the vertices and the orthocenter form an orthocentric system, meaning that any one of the points A, B, C, and H is the orthocenter of the other three. For all four of the triangles ABC, ABH, ACH, and BCH, the feet of the altitudes are the same, so they all share the same orthic triangle and the same nine-point circle.

But each of these four triangles has its own incircle and set of excircles, and the nine-point circle is tangent to all of them, making sixteen points of tangency. That's now 29 points of interest on the nine-point circle.

The incenter and the excenters form another orthocentric system, and the nine-point center of this system is the circumcircle of the original triangle. The reference triangle ABC is the orthic triangle of the excentral triangle JaJbJc.

And speaking of the orthic triangle, it defines three other triangles in the corners that are similar to the reference triangle. The Euler lines of these corner triangles coincide at a point on the nine-point circle. That brings us to 30 points of interest on the nine-point circle.

Let's go back to pedal triangles, and remember that if a point is on the circumcircle, its feet are colinear and its pedal triangle has collapsed to a line segment, called a Simson line. The envelope of these line segments form a shape called the Steiner deltoid.

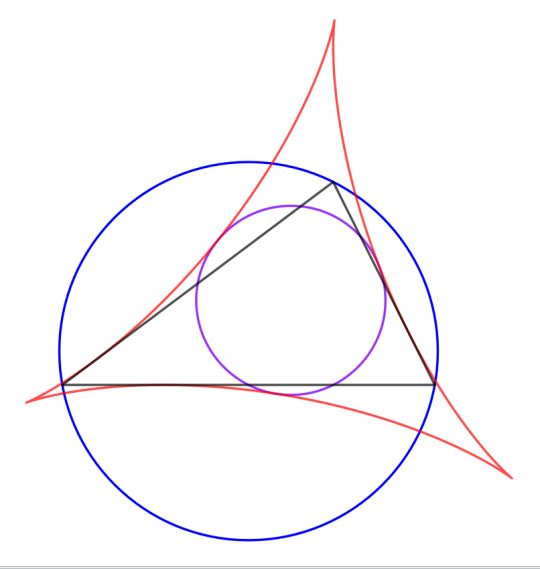
The nine-point center is also the center of the Steiner deltoid, and the circle is tangent to the deltoid at three points. There are four different circumcircles in an orthocentric system, so there are twelve points of tangency in all, so we now have 42 points of interest on the nine-piont circle.

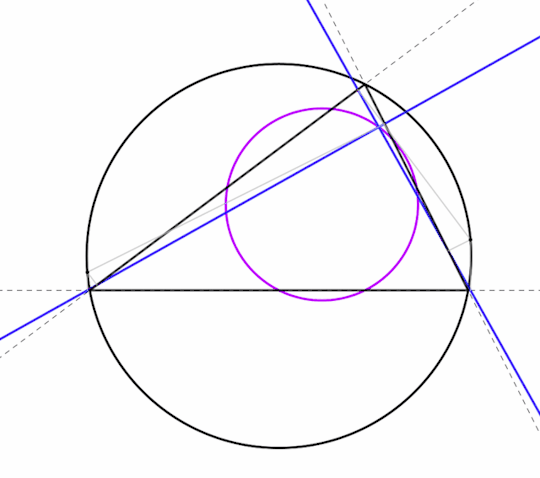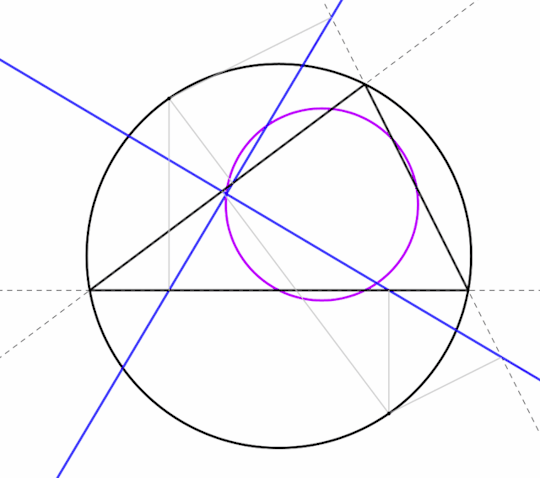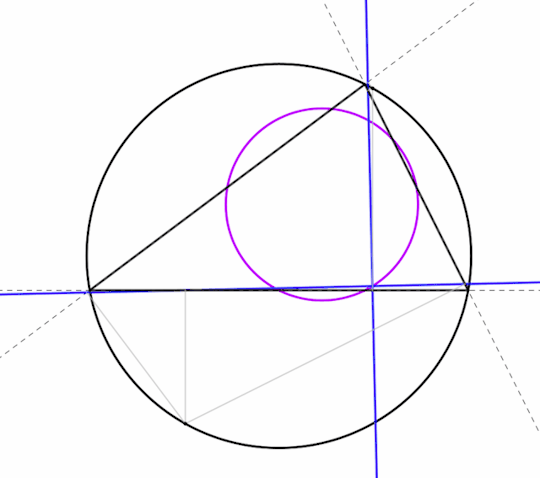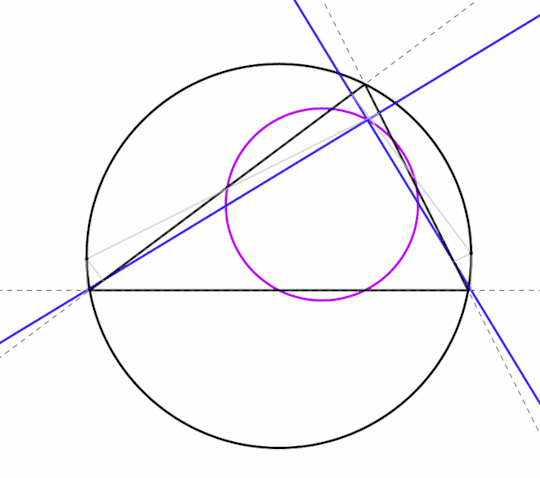
The Simson lines of two opposite points on the circumcircle intersect perpendicularly on the nine-point circle.

You may have noticed that in citing all these connections I haven't mentioned the symmedian point K so far. As far as I can tell, K is just not that very strongly connected to N. However, here's one: the circle through K, N, and O is orthogonal to the circle with diameter GH (the orthocentroidal circle). That's five members of our super team tied into one relation. But that's all I've got. Sometimes members of a team don't interact that much.

And this is the kind of thing you look for in a successful series, right? You have an established cast of characters, with a rich, dense lore linking them all together in various ways. Then, as the story develops and someone new is introduced, new retlationships make the lore even richer. That that's why I'm in the triangle fandom.

With that, I think the only question left to answer is "Hey, Square, do you happen to have a group portrait of the whole team together in one clear and not at all confusing picture?" And of course I do.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.