#no euler angles here

[cubsha]

if you dont learn to lurp n slurp your gimbles are gonna get LOCKED bro

[storymaker14]

Bizzaro Right Triangles

Okay, we all know that, if you have a right triangle with sides a and b and hypotenuse c, that means a^2 + b^2 = c^2, right?

So you can have 3-4-5 right triangles, and 5-12-13, and 7-24-25, etc.

And technically, a 1-i-0 right triangle follows this pattern, too, which has made the rounds in the math meme community.

But I found something better and weirder. I found a whole family of better and weirder.

I'm gonna skip a bit of the beginning and start here:

cos x = (e^ix + e^-ix) / 2

That follows from Euler's formula; if you need a walkthrough, I can provide, but I want to start with the above. So then, it follows that:

cos (i*lnx) = (x + 1/x)/2 = (x^2 + 1)/2x

Which means that an angle of (i*lnx) radians in a right triangle will have an adjacent side of (x^2 + 1) and a hypotenuse of 2x. By Pythagoras, then, the opposite side must be (x^2 - 1)*i.

But please note: if x is odd, then the lengths of all three sides will be even, and thus can be divided by 2.

Which means -- are you holding onto your hats and shoes?!? -- means that the proportions of the right triangle with angle i*ln(3) radians... are 5-4i-3.

And for i*ln(5) radians, they are 13-12i-5.

And so forth, with all the familiar Pythagorean triplets sqrt(2n+1)-n-(n+1) showing up, just with one side imaginary and the hypotenuse and remaining side swapped -- so, (n+1)-n*i-sqrt(2n+1). They still fulfill Pythagoras, every single one.

Which I think is, pardon my directness, fucking terrific. But just as a little bonus, please note that this means the triangle with angle i*ln(2) radians, the proportions are 5-3i-4, which is just delightful IMHO.

[squareallworthy]

Triangle Tuesday 3: The orthocenter, the Euler line, and orthocentric systems

Previously, we have looked at two different ways to mark a point in a triangle. First, we drew cevians (lines from the vertices) to the midpoints of the sides and found that they all cross at a point, which is the centroid. Then we tried drawing perpendiculars to the sides from the midpoints, and those all met at the circumcenter. And you could do this with any point on the side of a triangle -- draw a cevian to it, or a perpendicular from it, and see what happens.

This time, though, we're going to do both. That is, we're going to work with the cevians that also form perpendiculars to the sides. These are the altitudes, which run from a vertex to the nearest point on the opposite side, called the foot of the altitude. The three altitudes all meet at a point H, and that's the orthocenter. (The letter H has been used to mark the orthocenter since at least the late 19th century. I believe it's from the German Höhenschnittpunkt, "altitude intersection point.") Anyway, let's prove that the orthocenter exists.

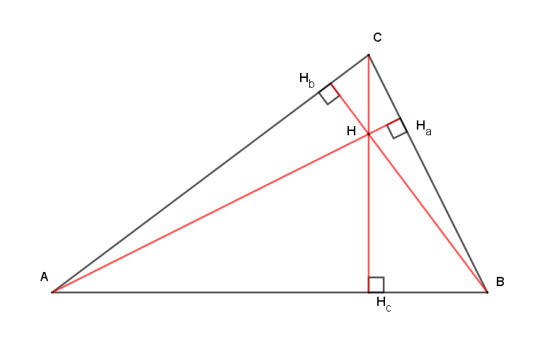
Theorem: the three altitudes of a triangle coincide.

Here's a very simple proof that the three altitudes coincide. It relies on the existence of the circumcenter, which we already proved before. Given a triangle ABC, draw a line through A parallel to the opposite side BC. Do the same at B and C. These lines cross at D, E, and F and form the antimedial triangle (in blue).

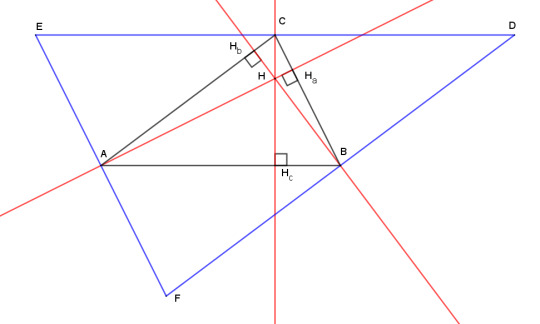
Then the altitudes of ABC are also the perpendicular bisectors of DEF. We proved before that perpendicular bisectors all meet at a point, therefore altitudes do as well.

That was easy. Let's do it again, but in a different way. It's not quite as simple, but it includes a large bonus.

Theorem: the three altitudes of a triangle coincide at a point colinear with the circumcenter and centroid, and GH = 2 GO.

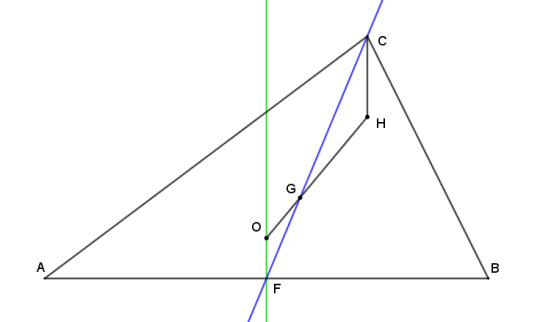
Let's take triangle ABC, and let F be the midpoint of side AB. Then mark two points that we already know, the circumcenter O and the centroid G. We'll also draw the median (green) and the perpendicular bisector (blue) that run through F, leaving the other ones out to avoid cluttering the picture.

We already know from our look at the centroid that G cuts segment FC at a third of its length, so GC = 2GF. Let's extend segment OG in the direction of G by twice its length out to a point we'll label H, so that GH = 2GO.

Now consider the two triangles GOF and GHC. By construction, their two blue sides are in the ratio 1:2, and the same for their two black sides. They also meet in vertical angles at their common vertex G. So by side-angle-side, the triangles are similar, and it follows that HC is parallel to OF, and therefore perpendicular to AB. So H lies on the altitude from H to side AB.

By analogous construction, we can show that H also lies on the other two altitudes. So not only have we proved that the altitudes coincide, but also that O, G, and H all lie on a line, and furthermore that G is located one third of the way from O to H, in any triangle.

This proof is due to Leonard Euler, and the line OGH is called the Euler line. Not only these three points but many others as well fall on this line, which we will get to later on.

Let's look at some more properties of the orthocenter and the feet of the altitudes. I'm just going to look at the case of an acute triangle for now, and show how this extends to the obtuse case later.

Theorem: two vertices of a triangle and the feet of the altitudes from those vertices are concyclic.

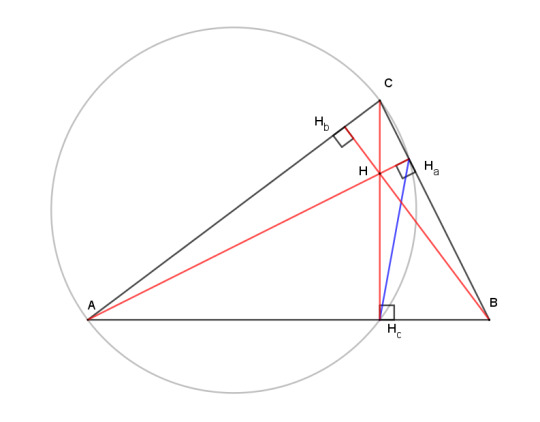
Proof is easy: the two right triangles AHcC and AHaC share segment AC as a hypotenuse. Therefore AC is a diameter of the common circumcircle of AHcC and AHaC (following from Thales's theorem).

(Incidentally, look at the angle formed by the blue segment and the altitude CHc. It subtends the same arc as angle CAHa, so (by the inscribed angle theorem again) they must be equal. That's not a part of this theorem, so just tuck that fact away for a moment.)

Theorem: a vertex, the two adjacent feet of the altitudes, and the orthocenter are concyclic.

Same idea, but now the right triangles are AHcH and AHbH, and AH is the diameter of the common circumcircle.

(And incidentally, look at the angle formed by the new blue line and the altitude CHc. It subtends the same arc as HbAH, which is same angle as CAHa. So those angles must be equal too. Since both angles between a blue line and the altitude CHc are equal to the same thing, they are equal to each other. Again, not a part of this theorem, just something I wanted to note.)

So those are some interesting concyclicities, but now let's look at the pedal triangle of the orthocenter, which is called the orthic triangle.

Oh, hey, it's made up blue lines, just like the ones we were talking about. And we proved that the two longest blue lines make equal angles with the altitude between them. By symmetry, we can prove the same thing about all the angles made by the blue lines. So that means

Theorem: two sides of the orthic triangle make equal angles with the altitude between them.

Another way to say this is that the altitudes are the angle bisectors of the orthic triangle. And I admit that was kind of a roundabout way to introduce the orthic triangle, but I think it makes the proof of this property easier to follow.

Two other properties of the orthic triangle immediately follow from this:

In an acute triangle, the inscribed triangle with the shortest perimeter is the orthic triangle

and

In an acute triangle, the orthic triangle forms a triangular closed path for a beam of light reflected around a triangle

which are two ways of saying the same thing.

But those two properties only hold for acute triangles. What happens to the orthic triangle in an obtuse triangle? Let's push point C downward to make triangle ABC obtuse and see what happens. To make things clear, I'm going to extend the sides of ABC and the altitudes from line segments into lines. Here's the before:

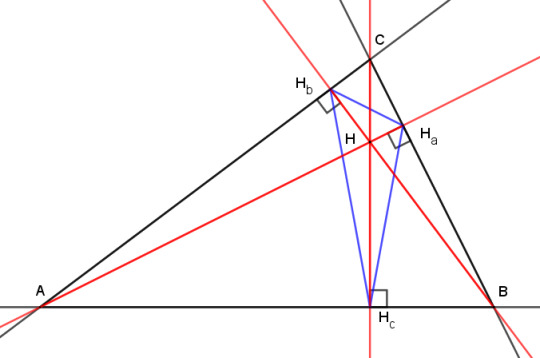
And here's the after:

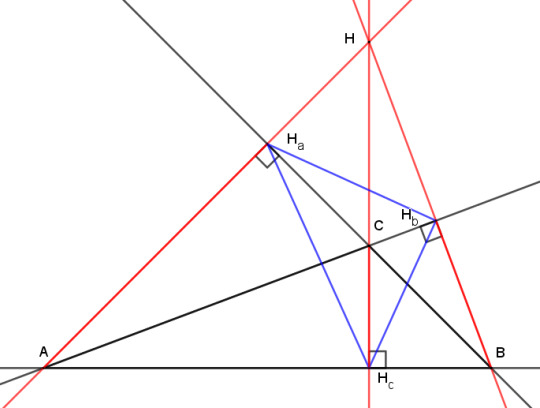
The orthocenter has moved outside of triangle ABC, and two of the altitudes have their feet on extensions of the sides of ABC rather than on the segments AC and BC. The orthic triangle now extends outside ABC, and certainly isn't the inscribed triangle with the shortest perimeter any more.

But look at it another way. We now have an acute triangle ABH, and the line HHc is an altitude of both the obtuse triangle ABC and the acute triangle ABH. Meanwhile, lines AC and BC have become altitudes of ABH.

So what we have is essentially the same acute triangle with two swaps: point C trades places with H, and Ha trades places with Hb. That means that our two theorems about concyclic points morph into each other as triangle ABC switches between acute and obtuse. Here's an animation to show the process:

And this is why I didn't bother with the obtuse case above -- each theorem of concyclicity is the obtuse case of the other.

So if we can just exchange the orthocenter with one of the vertices, what does this mean for their relationship? If you are given a group of vertices and lines, how can you tell which one is the orthocenter and which one are the vertices? Well, you can't.

Theorem: Given an acute or obtuse triangle ABC and its orthocenter H, A is the orthocenter of triangle BCH, B is the orthocenter of ACH, and C is the orthocenter of ABH.

The proof comes from consulting either of the "before" and "after" figures above. Take any three lines that form a triangle, red or black. The other three lines are then the altitudes of that triangle. The three feet are where a red and black line meet perpendicularly, so they are the same for all four possible triangles, which means all four share the same orthic triangle.

(Of course, if ABC is a right triangle, then we get a degenerate case, as you can see from the gif at the moment when C and H meet.)

Such an arrangement of four points is called an orthocentric system. Of the four points, one is always located inside an acute triangle formed by the other three, and it's conventional to label the interior one H and the others ABC.

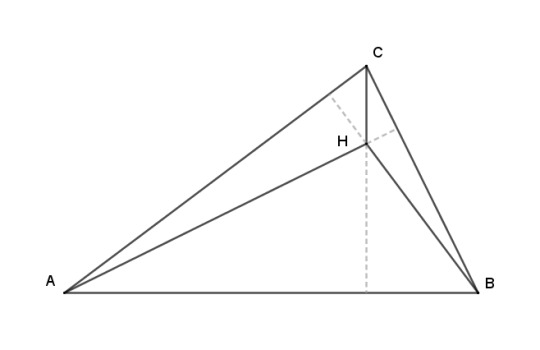
Orthocentric systems pop up all over the place in triangles, so expect to see more of them as we go along. Now, let me do one little lemma about altitudes, and then I'll show something cool about orthocentric systems.

Lemma: the segment of an altitude from the orthocenter to a side of the triangle is equal to the extension of the altitude from the side to the circumcircle.

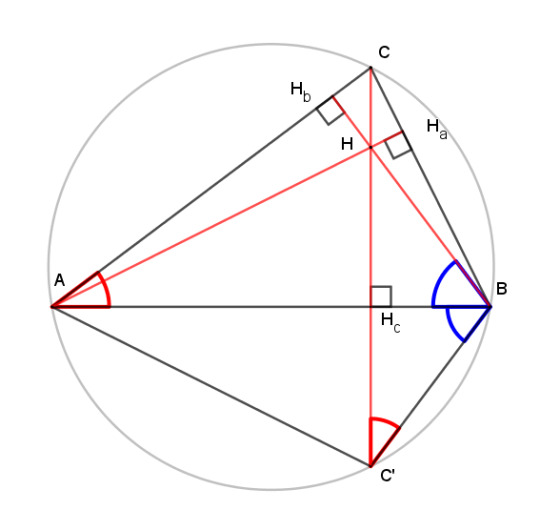
We can show this with just a little shuffling of angle identities. Extend altitude CHc to meet the circumcircle at C'. The angles CAB and CC'B, labeled in red, subtend the same arcs, so they are equal. Triangle ABHb is a right triangle, so angle HbBA, in blue, is complementary to it. The same is true for the right triangle C'BHc, so the two angles labeled in blue are equal. Then by angle-side-angle, triangles BHcH and HHcC' are congruent, and segment HHc = HcC'.

By the same argument, we can show that triangle AHHc is congruent to AC'Hc, which leads us into the next bit.

Theorem: all the circumcircles of the triangles of an orthocentric system are the same size.

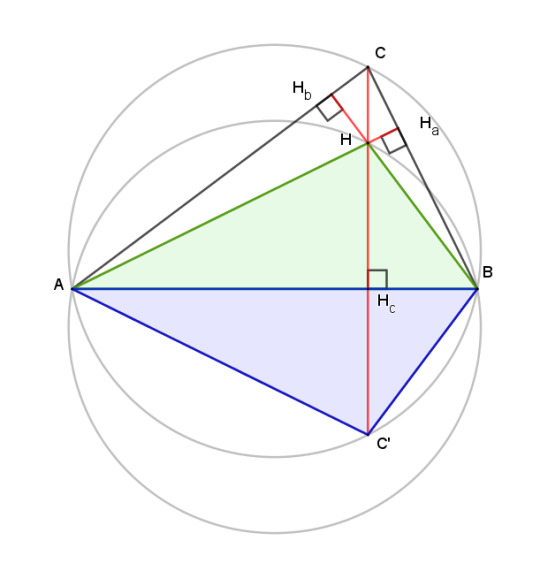
The blue triangle has the same circumcircle as triangle ABC. From the foregoing, the blue and green triangles are congruent. Therefore their circumcircles are the same size as well. The same argument works for ACH and BCH.

So here is an orthocentric system with its four circumcircles.

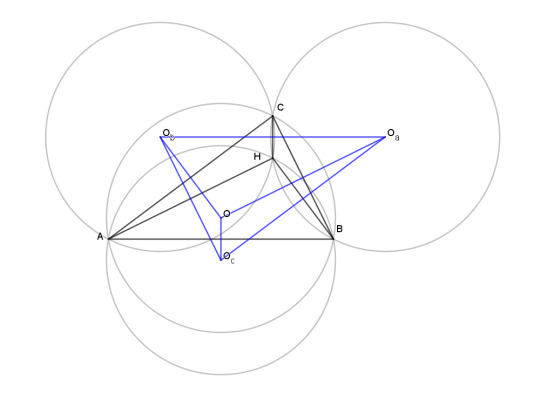
The four circumcenters O, Oa, Ob, and Oc form another orthocentric system, congruent to the first one.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[coraniaid]

top 5 mathematical identities :)

I wish Tumblr supported LaTeX.

OK, not trying to overthink this too much.

There are lots of fun identities involving binomial coefficients (or their q-analogs), or related integer sequences like the Catalan numbers and Motzkin numbers. But I think I have to go with the Chu-Vandermonde identity: who doesn't like a good convolution formula?

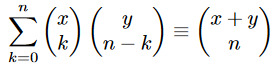
Of all the trigonometric identities I've ever had to learn, this is certainly not the most useful in practice or the hardest to prove or, arguably. the most inherently interesting either. I think the half-angle formula for tan is surprisingly pretty though.

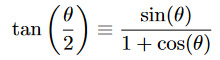
Let S be a finite set of real numbers. The maximum-minimums identity relates the largest element of this set to the smallest elements of every (non-empty) subset of S.

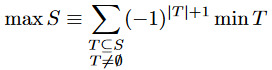
or, more concretely,

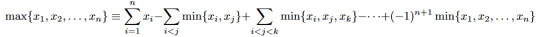
Perhaps not classically beautiful, but certainly enormously useful, the Sherman-Morrisson-Woodbury identity in linear algebra gives a formula for computing the inverse of a rank-k update of an invertible matrix by doing rank-k updates of the inverse of that original matrix. It's valid whenever the matrices are suitably conformable and when both the required inverses exist.

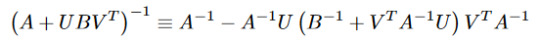
I feel like I have to include something due to Euler here, but -- rather than one of the famous ones involving π or anything to do with topology -- I'll go with some analytic number theory. The pentagonal number theorem gives a series expansion of the Euler function, valid for any complex x in the unit circle.

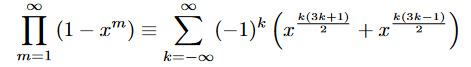
or, expanding both sides,

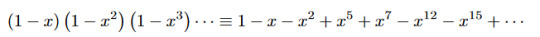
That takes us into the world of q-series and we can generalize it further to get Jacobi's triple product formula or various identities due to Ramanujan or MacDonald's identities for affine root systems or other increasingly exotic and strange things ... but this identity is the prototype for all of them.

[scramble-crossing]

Euler's Identity

Chapter 1: After the Sermon, Before the Wake

Rating: M

Characters: Sho Minamimoto, Neku Sakuraba, Shiki Misaki, Daisukenojo "Beat" Bito, Rindo Kanade, Tosai "Fret" Furasawa, Nagi Usui, Shoka Sakurane

Pairings: Sho Minamimoto & Neku Sakuraba, Sho Minamimoto & Rindo Kanade & Tosai "Fret" Furasawa & Nagi Usui, Implied Neku Sakuraba/Shiki Misaki/Daisukenojo "Beat" Bito

Warnings: Implied/Referenced Suicide and Self-Harm

Summary:

It happened again

As it has happened before

And as it will happen a hundred times more

After yet another attempt at the Composer's seat leaves Minamimoto critically wounded, he's forced to seek refuge in the only place left that will have him: his old home, WildKat. But it's come under new management since he's seen it last. Proprietor Neku Sakuraba has been dealing with his own ghosts since reclaiming the life he should have lived after the Long Game, though he's able to find comfort in his friends as they help him, and the cafe, get back on their feet. Maybe they can do the same for Minamimoto, when the Wicked Twisters reach out to him with an offer of reconciliation...

Sometimes all it takes is a little deviation

Read on Ao3

(And also a playlist here!)

My fic for the @subasekabang 2023! Had a blast participating alongside my Bang partners @starocide and @awanderingserena. Make sure to check out their works!

Preview under the cut

Morning broke, and from within it spilled a city untouched by rapture.

The gentle, lapping water of the Shibuya River blushed indigo, reflective of a sky that fell like a silken curtain over towers buttoned here or there with a warm yellow light, a few windows stirring, blinking sleepily open. Little moved and all was quiet. Well, quiet as it ever could be. Washed in a dusky lowlight burnt only at the very edges by the dayish gold of a still-rising sun, most of Shibuya was still dreaming as Sho Minamimoto emerged from the dark tunnel’s maw, greeted only by the rumble of far-off cars like a cat’s amused purr.

He breathed fresh air. It was tinged with the familiar scents of scathed asphalt and smoke and filled whatever mimicry of lungs he had left in his chest. Notes of citysong danced in his ears. He heard birds chitter, saw airplanes pull white-tufted tails behind them, both swimming the sky’s murky depths, and him, standing inside of it all, a part of it all, was as alive as a dead man like him could ever be.

…But he wasn’t supposed to.

‘Incongruent.’

This time was different than before.

‘Why am I…?’

Sho staggered. A searing pain tore down through his stomach like a knife plunged in and twisted, blood bursting in his head, filling his sight with a pulsing red haze, ruby dark, growing darker. He shut his eyes. Fumbled in blackness. His legs trembled like that of an infant still fresh to the earth; it took all he had left just to keep himself from collapsing into the embrace of concrete beneath his feet.

He would not fall. No, he would hurt and he would ache, he would fracture into pieces, but he would not let himself go wholly and with quiet humiliation into a storm that had since vanished.

And so he started walking.

Shadows of the overpass criss-crossed his path as Sho dragged himself over the gutter’s sloped ridge, keeping low along the city’s underbelly. They were long and soft in the surrounding dimness. Easy to slide into. He knew someone who would’ve loved them (Who? That was lost somewhere in memory), but for him the angles were too stretched, too obtuse, the encroaching sunlight giving too little space to hide. He would have to keep moving. Even as exhaustion weighed heavily on him, sucking at his heels like torrent water and making him think for one wild, confused moment that it was the river wanting him back.

He tried to shake it off, clean his mind of the clinging, gurgled whispers whose voices he couldn’t tell from his own. It was all the same, anyways. A reprise on unfinished business.

You lost

‘I lost.’

He never stood a chance.

When he flexed his hands to make sure he could still feel them, his fingers pressed with splintered nails into palms that hadn’t once brushed the fantastically inhumane coldness of divinity. They were hot and slicked with sweat and dirt from the ground he’d crawled across. His eyes were not reverent, nor were they holy. They were pained by the light that had filled them. Even when they were closed he felt no relief, the image of His split-grinning face twin tattoos on the insides of his eyelids.

White.

‘No’

Teeth.

‘Stop’

Cherubim faces, child’s hands.

Great shafts of light like sterile dreams.

He grasped his hair, tugged hard until it screamed.

Peach lips. Apple cheeks. Fruit of the Lord, piercing his still-warm core.

(It didn’t help)

Him. Him in the center of it all, when the omnipotent hymns of gold and saintly frequencies fell silent, and he met his violet, ice-chip eyes.

‘It hurts’

When he smiled.

‘It hurts.’

When he laughed.

‘It hurts’

When he saw himself in a smear across the floor, everything he ever was or ever could have been left as a stain on God’s front porch.

+ some bonus shitposts

[janmisali]

Here is a tiny fraction of the reasons why 2 is special and why 2 MUST WIN:

Euler’s Formula about planar graphs has the constant 2

2 appears in formulas everywhere, especially around tau and pi

2!=2

2+2=2*2=2^2=2^^2=...

Normal distribution has z^2/2 in it

First prime number

truth values have 2 possibilities

Powerset has size 2^n

Infinitely many platonic solids in dimension 2

Completing the square is sososo important

Conic sections are the most complicated well behaved curves, and they come from order 2 polynomials

Lorentz transform is 2ish

F=1/r^2 makes planets travel in ellipse

x.dx=0 -> |x|^2=r^2

Mandelbrot set is all about raising things to the power of 2. And things escape the set if their modulus goes > 2

The sum of inverse powers of 2 is 2.

Groups come from 2-ary operations

Asymmetric objects have 2 possible chiralities

= is a 2-ary relation

Highest order of differential equation that cannot be chaotic

Can split any angle into 2, or any line segment into 2 with simple construction. Can construct sqare root, but not any other roots.

2 used to prove bound on iterated totient function

Biggest group with trivial automorphism group

Dimension of C over R

Antipodal map is null-homotopic in iff the sphere's dimension is not a multiple of 2

Highest moment needed for CLT

Every nontrivial finite degree subfield of an algebraically closed field is degree 2

Fermat primes come from the number 2

Wilson’s theorem is about elements of order 2

Every element order 2 implies Abelian and vector space

Reflection is order 2 symmetry

Every ring except in characteristic 2 has 2nd root of unity

The Euclidean norm is the only norm with continuous rotational symmetry, and it's analytic, with derivative 2x. It also gives the circle parameterised by e^i\theta

It's the dimension in which shapes first appear

It's the smallest possible number base

.

[allofmymaths]

i = 1

I saw something today that asserted i = 1 and the proof went like this: 

i = i^1

= i^(4/4)

= (i^4)^(1/4)

= 1^(1/4)

= 1

At first this seems legitimate, but clearly there is something wrong. It can be hard to spot what the problem is exactly, but it becomes a lot more obvious with this similar proof that -1 = 1

-1 = (-1)^1 

= (-1)^2/2

= ((-1)^2)^(1/2)

= 1^(1/2)

= 1

Here it becomes clearer thanks to the last step, that the assertion that (-1)^2/2 = ( (-1)^2 )^(1/2) is incorrect, and likewise in the i = 1 example. 

The problem is that there are two things that square to give 1 (1 and -1) but only one of them is defined to be the square root of 1 (i.e. 1^(1/2)) and that would be 1.

In the i = 1 example, there are 4 complex numbers that when raised to the power of 4 become 1 and they are 1, -1, i, and -i. But similarly, only one of them is defined to be the 4th root of 1 (i.e. 1^(1/4)) and that would be 1.  If this isn’t a good enough reason for you, you can consider the polar form.

Instead of using x, y coordinates to describe a point in 2-D space, you can consider instead r, the shortest distance from the point to the origin, and t, the angle between this shortest distance line and the positive x-axis, with positive angles being measured in the anti clockwise direction. 

Complex numbers may then be represented as re^(it) where e is Euler’s Constant. With this form, and supposing that r = 1, we can see that if we take some complex number e^(it) and we take ( e^(it) )^4 then we get e^(4it) Therefore you can see the angle changes from t to 4t, meaning that this new complex number has an angle 4 times larger than the original. 

You can then think for complex numbers z that are on the unit circle that (z^4)^(1/4) is taking a complex number z and multiplying the angle by 4 and then dividing by 4 again. 

Finally, we can use the fact that for i, the angle t would be pi/2 radians which is the equivalent of 90 degrees. Therefore, scaling this by 4 gives 2pi radians or 360 degrees, which is the problem. 360 degrees would be equivalent to 0 degrees and if you were to divide 0 degrees by 4, you would get 0 degrees. 

This is why this process won’t get you back to the original complex number: because the angle for the original complex number was large enough that multiplying it by 4 made it wrap around back to zero.

This does however mean that if instead we’d written (i^(1/4))^4 then we’d be perfectly fine. But of course, i = i isn’t exactly groundbreaking and probably wouldn’t go viral. 

[hypnoticwinter]

Down the Rabbit Hole part 17 (nsfw elements)

I keep telling myself that it’s enough to have gotten this far, this is an adequate demonstration of bravery, that I should be impressed that I kept my nerve enough to even get to this point in the tunnel, but even though my heart quails and I’m shaking lightly, a kind of mixed blend of anxiety and terror at the prospect that something might be stalking me down here, I stay where I am as though my feet had grown roots.

For there in front of me, just as Makado had said there would be, is the puckered, anus-like entrance to a ballast bulb. Only took me roughly twenty minutes of crawling through a tight, suffocating, pitch-black venterial canal, all manner of slime and scum and filth caking around my face and arms. My suit will be an absolute mess but nobody will know the difference, most likely; after this first day all of the pristine and immaculate dull orange suits have become equally dirty - mine will just be a little fresher.

Getting out of the camp was surprisingly easy. I had crept by Joker with some trepidation, half expecting him to spring into life and go after me without Euler holding his leash, but all that happened was that the machine’s head had risen slightly as I had moved past and then settled down again.

I guess that after Makado and I had left to return to my hotel room and retrieve my gear, the team had asked Euler to showcase some of Joker’s other features and he’d activated some sort of autonomous mode. It had taken him some thirty minutes to set up, Elena had informed me, the back of Joker’s cranium hinged open and Euler poking around in there, but afterwards they’d lead him over to some sort of obstacle course Elena had called a ‘kill house’ and let him loose and the results had been so impressive and entertaining that they’d had Joker repeat the course four times before Euler had begged off, citing some sort of instability in the machine’s logical pathways…whatever that means. We hadn’t seen either of them for the rest of the day up until the party; Euler had explained, briefly, that he’d been working with the Engineering department to get radio tags working with Joker’s system so that while we were down here he know who was and wasn’t part of the team. Don’t go walking around without your suit, they’d warned us. Otherwise, if for some reason we do let him operate on his own, he might not know who’s who. Might act unpredictably.

Shades of Terminator, of Robocop. But I rolled my eyes at myself and brushed past him, let my hand press lightly against his burnished chestplate for just a moment – you can never be too superstitious – and then squeezed my way into the tunnel. There were no tents clogging its entrance on account of it being so small. I had to go on my hands and knees most of the way, except for a little bulbous bit in the middle where it widened up and I was able to stand.

I don’t know how I made myself go through it. I kept getting a prickling feeling along the back of my scalp, like something was stalking up behind me, but whenever I curled over and looked back there was nothing there, just the ribbed walls of the passage, like I was inside of a giant esophagus.

I had a panic attack halfway through. I don’t know what brought it on; I’m not prone to panic attacks, normally. I made it to a section where the tunnel dropped down a couple of feet, a sort of rough 45-degree angle, and I just started crying. I wanted fervently to be back at home in bed waking up from the crazy dream I’d been having. I wanted to go and listen to We Didn’t Start the Fire by Billy Joel and follow along to the lyrics and not hear anything odd or unusual, just have my mind skip over everything like normal and have it all be okay. I wanted –

I don’t know what I wanted.

But at the end of it I rolled over onto my back and closed my eyes, and then I sat up and smoked a cigarette from the pack I’d smuggled in with me. Just one cigarette, and then I crushed the pack in my hand and threw it away. I kept the lighter, though; you never know when something like that will come in handy.

Then I got back on my knees and pulled my way through the tunnel and now here I am, nose still clogged and runny, but feeling better.

I have a knot at the base of my stomach the size of a baseball and I keep looking behind me, frightened that something’s going to grab me and eat me and that I’ll never see anybody – especially Elena – ever again. I’m afraid that I’ll drink this stuff and that’ll be a wrap for me, the Pit will have gotten its claws in me and I’ll be different, I’ll be changed somehow.

“Fuck it,” I mutter under my breath. The cigarette had calmed my nerves a little and, to tell the truth, I’d been craving one after a few days without. A momentary pang of regret few through me on ghostly wings; I thought for a moment about going back and finding the pack I’d discarded but then my lip curled at the thought of myself grubbing around in the muck looking for it. I’m not that pathetic.

Getting the bulb’s entrance dilated enough for me to crawl through is tough work. I’m buried up to my elbows in the thing, feeling vaguely nauseated at the wrinkled folds of flesh just a few inches from my face. There’s some sort of sphincter-like muscle there banding around the opening like steel cord, but the more I press and lever with my elbows opposed the more it relaxes. Soon it’s large enough for my head, then for my shoulders, but I keep going to make sure that I can fit through with the added bulk of the suit.

The smell is intensely strange. I had thought for a while that it might remind me of a Coke Heartthrob, especially with memories of the last one I’d had still relatively fresh in my mind, but the smell is completely different, more…earthy and spicy and invigorating. It smells like…like vanilla. There is a distinct odor of vanilla. There’s still the same disgusting organic undertone to the air that pervades everywhere in the Pit, but it mixes with the drooling sweat odor pouring from the orifice in front of me to form something new and strange and…appealing. Appealing in the same way that a mixture of sweat and men’s deodorant can be appealing, appealing in the same way that –

I shake my head, try to clear it. Easy, girl. You’re just going to crawl in there, drink some of this stuff – I can feel my gorge rising again but I shut my eyes and count to five and breathe through my mouth and the feeling dissipates – and then crawl back out and go back to Elena and fall back asleep. That’ll be all.

The Pit groans, a little noise of stress and tension, and I jump.

“Fuck it,” I murmur again, and then I clamber into the orifice, feel it suck at my thighs and calves and feet as it tightens behind me, and then I slip down a slick, slippery surface of flesh and fall face-first into about three or four feet of murky, milk-white ballast. It takes me a moment to find a purchase on the rubbery flesh at the bottom of the pool but I do, finally, and then I come up sputtering, trying to clear my eyes. I haven’t drank any of it; some instinct screwed my mouth shut as soon as my head went under and I couldn’t force myself to open it for all that I tried.

I open my eyes and look round. The inside of the bulb is red and fleshy and membranous; there is a long rind-like deposit of something stretching between the ceiling and the floor, just a little off-center of the middle of the room, thick as a tree trunk. There are little curling wisps of some sort of vapor rising from the surface of the ballast; that must be what gives it such a strong smell. The odor’s grown even more intense here, inside the thing, and I can –

Huh.

I can feel something happening on my face, my hands, pretty much every piece of exposed skin that had gone under when I lost my balance and fell down the side of the bulb face-first. It’s hard to pin down at first, but then it resolves from an indistinct feeling to a light and pleasant tingling a little like the breathy feeling you get when someone’s been tickling you for a very long time and then they suddenly stop. I wait for a moment, cringing inwardly, but it doesn’t resolve into burning pain or – or whatever I expected, it just stays light and tingling and pleasant.

No wonder people liked to bathe in this stuff.

I raise my hand to my cheek hesitantly. The skin on my face feels softer somehow. Gentler, as though I hadn’t been baking in the West Texas sun for the last week or so. The same’s happened to my hands, I realize on closer inspection; the hard nubby calluses on either wrist, just above that little bone on the edge of the wrist, gained from hours spent working at a desktop typing, are now little more than suggestions of their former selves.

I spend a long while there, staring at my wrist, the detached headlamp clutched in my teeth. What the hell is this stuff going to do to me if I drink it?

But the tingling feeling is already abating, and it isn’t as though it took my skin off, didn’t disfigure me. Most likely, anyway. I probably look a couple of years younger. I prod at my forehead experimentally; it feels a little tighter.

“Fuck it,” I say again, and then I cup my hands and dip them into the pool of ballast at my feet, and then raise it to my lips and drink.

The taste is surprisingly mild and savory. The texture, though – it’s thick, thicker than water. It feels as though I’m drinking some kind of oil and for a moment it’s enough to make me gag, but I force down a couple of swallows and then, almost as soon as it hits my stomach, I feel a heat building there, the same kind of warm, pleasant one gets after they’ve eaten a large meal and want to do nothing other than lay down somewhere and not think for a while, just without the accompanying sensation of fullness. This dissolves after a moment into the same sort of tingling that I’d felt on my hands and face, only a dozen times stronger, and it turns into a sort of burning, fizzing sensation that races through my body, and I double over with the force of it but I’m grinning, I’m grinning so hard, because I’ve never felt so good –

And then I move wrong and I nearly scream at the sudden jolt of pleasure so intense that I initially mistook it for stabbing pain. It takes me a moment, frozen, eyes wide, to identify what happened, and then, cautiously, I isolate my chest and move it gently, trying to brush against the inside of the suit, and it sweeps through me again and even though my knees grow weak and I hear a low animal moaning echoing in the bulb, it takes me a disconcertingly long time for me to realize that it’s issuing from my mouth.

When I had moved my nipple had brushed up against the coarse fabric on the inside of the suit and I had almost came just from that. I flop against the side of the bulb and feel my breast through the suit carefully; it feels larger than usual, swollen somehow, and taut and sensitive, the nipple hard enough to cut glass. I look down and I can see it actually poking through the suit.

I get shakily to my feet, trying hard to avoid any other accidentally brushes like that, and I realize that I am incredibly, almost discomfortingly, wet. There’s a throbbing in my groin like a heartbeat and a warmth that quickly turns into an ache, a need for something to fill me. I shake my head again, trying to clear it, but it doesn’t do anything to help. I glance back down at the innocuous milky ballast; did I drink enough? Two cupped handfuls – not that much. But if it’s already doing this to me, can I handle more?

My hand, I realize, has gravitated to my crotch, and I’ve started rubbing myself through the suit. “Goddam it,” I hiss out loud, pulling my hand back like it was burned, my body aching for it to come back.

I can feel a small trickle run down my leg and I feel my lip curl, first in disgust, then it curls further into a lascivious grin. I think for a moment about undoing the bottom of the suit and just masturbating there, thinking I might get the demon off of my shoulders and out of my head with an orgasm or three, but while my hand is idly massaging my breast through the suit I think of Elena and such a surge of lust goes through me that for a moment I can’t even breathe. I squeeze at my chest through the suit until I feel pain and that wakes me a little, and then, still grinning, I rise and start to make my way back to the orifice, head filled with all of the things I’ll do to Elena when I get back to the tent, hands quivering lightly with anticipation. I find the light and fumble with it clumsily for a moment before I click it on and angle it up towards the opening so I can make my way out, but then when I see what the light is shining on I almost scream again and it is only the sudden presence of mind that makes me clap my hand to my mouth that stops me from shrieking.

For there, at the mouth of the bulb, is a pale human arm, stuck elbow-deep inside the orifice, and gradually wrenching it open!

I click the light off and drop into a low crouch and then slowly creep backwards, taking care not to make too much noise with the wet ballast up to my knees. I make it to the pillar-like deposit of – of whatever the hell it is in the center of the bulb and skirt behind it just as I hear the soft groan of the bulb’s sphincter giving up the fight against whoever is trying to make their way in here.

I scarcely dare to breathe. I can feel my heart thumping a million miles an hour and I can feel terror gnawing at me, trying to get its fangs in, but for the moment I’ve mastered myself. Whoever it is, they have a much more powerful light than I do, but they don’t seem to have spotted me; the light sweeps once, twice, around the inside of the bulb and then I hear a sliding sound of something heavy and then a definitely male grunt as whoever it is splashes into the ballast. I hear him set the light down and then indeterminate splashing, but at the very least he doesn’t seem to suspect I’m here.

Now that the immediate danger is over my body is urgently reminding me how horny I am. I bite my lip and bear it; if anything the feeling seems to be intensifying rather than falling off, especially since I’m not doing anything about it. If I don’t consciously think about it and stop myself I find my hands gravitating back to my breasts, to my groin, little twinges of pleasure making me bite my lip, suck in soft breaths. Finally I end up just putting my hands on my cheeks and keeping them there, to hell with whatever aching neediness I feel between my legs. I feel a little stupid, but if my hands are on my face I can keep track of them more easily.

I shift a little to the left and peek around the waxy deposit growing out of the ceiling and my mouth drops open; I see Crookshank’s ruddy cheeks and unruly sideburns, his powerful barrel chest heaving as he scoops handfuls of ballast from the pool and rubs it on his arms, his cheeks, his face. He’s undone his suit, the halves of it flopping around his waist, and as I watch he slaps the liquid on his bare chest, rubs it in like lotion.

This continues for another few minutes before he kneels and takes a great gulp of the fluid, and I gasp lightly, for he lapped up so much more than I had, and even though he is much bigger than I am and perhaps the same principle as alcohol applies, perhaps he can handle much more of it, I shudder to think of what that much of the fluid would have done to me.

He stands there for a long while, leaned against the wall, eyes shut, his cheeks slowly growing even redder, and then he zips his suit down further and starts to jerk himself off. I lean back around the deposit and force myself not to think about it but I can’t help it, I can’t get the image out of my head, I can’t stop myself from salivating over it, from thinking of the way it’d feel inside of –

No. Stop. He’s going to jerk off and then he’ll leave and then you can get out of here and never talk about this ever again.

But if that’s the case, goddam it, why am I fucking touching myself, why is it so much easier to peek my head around the corner like this and watch him and rub myself through the suit. He’s not even hot, he isn’t my type, fuck, I wouldn’t have thought twice about him, but with this – with this drug in my body I can’t stop myself from thinking about him taking a fistful of my hair and bending me over and then forcing himself into –

Stop.

I crouch there in the dark, reeking of ballast, listening to Crookshank grunt rhythmically as he fucks his hand, and then finally he lets out a louder grunt and I swear, I swear I can hear it hit the ballast. I’m crying, I realize again, something’s short-circuited inside of me and all I can do is cry and rage at the stupid animal cage I’m trapped in, the stupid animal cage that wants to get bent over and fucked and used. I don’t want to have to think, I don’t want to have to be like this, I don’t want to -

Crookshank leaves and I finally let out a shaky breath. I’m still unbearably, agonizingly horny. I think about touching myself, about just getting it over with, but again I think of Elena, and I think of Crookshank, of goddam motherfucking Crookshank grunting like a bear in heat, and suddenly I feel as though doing it here would make me vomit. I don’t want to see this place again, I don’t want to even think about it. I want to just go back and crawl into the tent and let Elena hold me and wake up clean. Except…

I eye the murky surface of the ballast.

What if the amount I drank isn’t enough? What if I should have drank more, what if if I leave now I’ll be throwing away the only chance I get? I doubt we’ll have time for me to sneak back here on the return trip, and even if we did I don’t want to take my chances running into Crookshank or whoever else.

But Christ, if the small amount I drank is doing this to me…

I reach down and cup a small amount in my hand. I raise it to my mouth and then stop, then I squeeze my eyes shut and drink it down. I stand there and sway and shudder as the heat intensifies. I put my arms around myself and clutch and just hold my ribs tight until I feel as though I can move, and then I make my way to the orifice and force my way out of it. It’s easier going out than in, although I still have to squeeze. I nearly shriek again as it presses against my breasts unexpectedly, and the sudden pressure and the burning jolt of pleasure makes me buck my head, momentarily lost in the sensation, but I claw my way out, manage to clear my head somehow and keep moving. The smell of ballast has become sickening, and as I crawl my way down the long ventricular canal back to the camp I feel as though it’s clinging to me and I’ll never be able to get it off, no matter how many showers I take, no matter how hard I scrub myself.

I happen upon my discarded pack of cigarettes and laugh to myself even as I ache to see if any of them escaped destruction, but I keep my dignity and pass it by. Well, some of my dignity; I’m so horny now that even the soft rubbing together of my thighs, a motion forced by the tight quarters where I have to go on my hands and knees, is becoming unbearable. I keep arching my back and imagining filthy things and pawing at myself, but somehow I manage to keep enough of my mind from crumbling in on itself to make my way back to the camp. I squeeze past Joker again, trailing my fingers along his shoulders, the cool dull spark of the metal on my fingertips seeming newly sensitive to my revitalized fingers. It’s late, it’s so late, but I feel agonizingly awake. I find the tent, slip out of the suit as quickly as I reasonably can, leave it crumpled on the fleshy floor next to Elena’s neatly folded suit, and then I unzip the tent and clamber in.

Elena’s eyes are tracking me there in the dark, little glittering jewels glinting at me. She rolls over as I move fully into the tent and I am so unspeakably happy to see her that for a moment I can do nothing more than squat there on my haunches with an idiot grin plastered all over my face before she smiles at me softly.

“Hi,” she says, her voice grown innocent, still heavy with sleep.

I breathe her name like it’s a prayer and then I am kissing her and she kisses me back, a laugh bubbling in her throat as she does, and I can’t stand it any more, I have to be closer to her, I want all of her, I want everything, and while she makes little delighted sounds of amusement and disbelief at how insatiable I am I kiss my way all over her, grinding against her thigh as I do, and when she reaches up for me and finds my breasts I shudder and arch my back inwards, trying to press more of myself against her.

“Missed me?” she asks, her thumbs working in slow circular motions. She has a smug little smile on her face. I’m panting I want her so bad. I don’t trust myself to speak so I just nod. Her hand trails upwards from my breast and I let out a little whining moan. It fixes around my throat, squeezes lightly, and I swallow. Her other hand tracks down my stomach and I can feel my hips buck gently as I know what’s coming, and I grin at her, but she stops just before where I want her to, tangles her fingers in my pubic hair, massages me there, and though I try to angle my hips forward and slide her fingers against me, wet and slick and willing, she stays agonizingly still.

“Why do you smell like ballast, Roan?” she asks, cocking her head at me. Her eyes have gone cold and calculating and her grip on my neck has become very, very strong. I want to fuck so badly that the well of fear bursting in my gut is something I can barely recognize, barely react to. I open my mouth and let out another little moan.

“Elena,” I groan, “I don’t –“

“Oh, don’t lie,” she murmurs. I see her eyes flick down to my nipple and then she darts forward and latches onto it with her mouth, eyes still fixed on mine, at least until she brings her teeth together extremely gently and I shudder, starbursts blossoming in my vision. Then she lets me go with a wet pop that I find incredibly, unspeakably lewd. I feel as though my cheeks are on fire.

“Your name isn’t Merriweather either, is it?” she asks me.

“Elena,” I say again. It’s all I can say. I can’t summon the breath for anything more complicated.

“See,” she says, “after you left I thought I’d stay awake until you got back. But you took a long, long time. So then I started thinking,” she says, punctuating the statement with a sharp gesture downwards with her finger, just brushing against me, and it feels like heaven.

“Y-you can’t,” I start, giving her a pleading look, but she’s enjoying this too much. The torture will end when she wants it to.

“Then I looked up your personnel file, cause I wanted to creep on you. Only guess what?”

I shut my eyes.

“Right,” she says, squeezing my throat a little tighter. “You don’t have one.”

“Elena,” I say very carefully, trying to keep my voice from pitching upwards into a moan, “I can explain.”

“I’m sure you can,” she says. When I crack my eyes open she’s looking at me with something resembling sympathy. “But I don’t care about that right now.”

“You don’t?”

She moves her hand downward, lets go of my throat. I gasp slightly, and then when she inclines her middle finger slowly upwards and brushes against me I gasp harder. “Tell me this is real,” she says.

“W-what?”

“Tell me,” she repeats slowly, “that this is real. That you aren’t using me to get down here, that there’s not some ulterior motive at play. Tell me it’s real, Roan.”

Her finger presses inside of me and I collapse against her, bury my face into her neck, kiss her again and again, leave a trail of bite marks in my wake. “It’s real,” I moan into her ear, and then she fits another finger into me and all I can see is her wide grin growing wider before the night dissolves into a parade of sensual enjoyments, of flesh and reactions and noises burned indelibly into my frantic, pleasure-drunk brain.

 * * *

 When we’re done finally and whatever effect the ballast had on me is fading, Elena curls me into her arms and I kiss her softly. My mouth and tongue are still a little tired but it was infinitely worth it. We stay like that in fuzzy oblivion for only a moment before Elena inclines her head and nuzzles at my forehead with her nose.

“So who are you really?” she asks me. “What’re you doing here?”

“Oh,” I groan. “It is a long story.”

Elena laughs quietly. “Well, we’ve got nothing but time.”

“It must be so late,” I tell her. “Shouldn’t we get to sleep?”

“It’s midnight.”

”What?”

“See?” she asks, twisting around a little to show me her watch. It’s a huge clunky tactical-looking thing. I almost laugh at it. “Down here the name of the game is early to bed, early to rise. I know Sarge will get us going later though, cause of you and Euler. You won’t be used to it.”

“Well,” I say, not knowing what else to. Elena holds me tighter.

“So tell me,” she says simply, and so I tell her.

She handles it well, but it’s not a very difficult story. It even makes sense in places, I think. I skirt around the main issue for a while but eventually seize on it and just tell her. When she doesn’t react I glance up at her, meet her level gaze. “It’s only transmitted through blood-to-blood contact,” I say quickly. “So we don’t have to worry about –“

“I know how it works,” she tells me. “Still sort of the thing you ought to tell someone about before you fuck them.”

I feel myself flush; Elena sees too. She takes my chin in her hands, looks down at me. “It’s okay,” she tells me. “I get why you didn’t.”

“I’m sorry.”

“I said it’s okay.”

“I’m sor-“

“Shh.”

We lay there in silence for a while longer. “They told you you were allergic?” she asks. “At the hospital?”

“Uh. Yeah.”

“That’s what they said? Verbatim?”

I can feel everything shrinking into myself. “Yes,” I say quietly. “I think so, I – yes.”

“Or did they say it was like you were allergic?”

“No, they – well. I don’t know. You’re making me doubt myself.”

“Medicine can go off,” she says. “It can go bad. If it did and they didn’t know and used it anyway, if it had been mislabeled, you might have gone into shock, you might have –“

“I don’t want to –“

“Shh,” she says again, holding me to her. I try to pull away but she doesn’t let me. More than anything I want her to stop asking questions, I want her to just hold me here and not judge me, not say anything. I feel fragile, I feel like a thousand needles are poking in at me just millimeters from my skin and if I make one motion they’ll stick –

“I’m sorry,” I whisper, and she laughs.

“What the hell are you sorry for?” she says. She runs a hand through my hair and try as I might not to like it, I like it. I like the way it feels. “What else were you going to do?” she asks. “You were scared, you didn’t know any better. You wanted to run from it and not confront it, I don’t think there’s shame in that. And then you found out about this place and everything just fell like dominoes.”

“Yeah,” I agree in a small voice.

“Fucking cruel of Veret to send you down here, though.”

“I asked for it,” I say. “She didn’t want to.”

Elena grunts.

“You don’t like her much, do you?” I ask.

“I think,” Elena says after a long time, “that after 2007 she should have gotten as far away from this place as she could and found something that made her happy.”

“I don’t understand –“

“Makado made it her mission to make sure the Pit could never hurt anybody ever again,” she tells me, “when she got Head of Sec. But that’s impossible, you know. The thing’s so large, there’re so many ways in, so many ways out, you can’t do anything about it. She lets it eat her up.”

“You didn’t call her ‘Veret’ just then,” I point out. Elena looks at me.

“I don’t hate her. I just think that she isn’t suited for the job.”

“You really don’t care that I lied to you?” I ask her.

“About who you are? No. In the same circumstances I’d have lied to you.”

Elena has been kneading my hipbone gently with her thumb for the past five minutes, and the rhythmic motion is going to put me to sleep soon. I kiss her again, near her collarbone, and shut my eyes. Elena holds me tighter, there in the dark, and for a moment I’m able to not worry.

Just as I’m about to drift off, all wrapped up and warm and happy, still basking in the afterglow, I feel her thumb stop.

“But if I find out that you’re lying about this being real…” she murmurs, very softly, clearly thinking that I’ve fallen asleep, and there is such a knife-edge of menace in her voice that I lay there for a long, long time in her arms, even after her breathing has become low and regular and even, trying to will myself to fall asleep.

Continue with Part 18

Back to Table of Contents

[tricky-pockets]

🌌 ⚡a gob grimoire ⚡ 🌌

i keeps my calculus formula sheets in here ⭐🌙🕯️🔮📜

To any who may find this volume and fail to return it to one Samwise the Canny at 26 of the street of cherries, chamber 205: May the dread spirits of Newton and Leibniz eat thy ass, and may thou be cursed with a thousand mandatory iterations of the Cubic Formula

L: Anti-Derivation: minor abjurations

R: Euler’s Excellent Unraveler

The eyeball guy 👾 holds the pages open for me. His name is Jimothy.

Seal of Angles

Oscillations of the Pythagorean Rune Functions, plus some more basic trig

It's a work in progress - the goal is to get all of my formula sheets and guides into one Thing instead of a thousand index cards and sheets of scrap paper.

[thequirkdetective]

Investigation 13: Elasticity – Danjuro Tobita

It’s almost the Christmas holidays as I write this, as well as being exactly halfway through December. Hopefully during the holidays we can catch back up to schedule, so this should be the last upload that isn’t on time. Let’s not dwell on it. Shall we?

Danjuro Tobita, better known as Gentle Criminal, has the quirk of elasticity. This allows him to make anything he touches elastic (in the sense of property, rather than material). I only learned when researching this quirk that his name is in fact a pun of the quirk in Japanese, where the standard Japanese kanji for ‘elasticity’ also translates as ‘gentleman’. This has nothing to do with the investigation, I just thought it was a cool fact.

The first problem we run into is that elasticity isn’t a set property at the molecular level. Different materials are elastic for different reasons, mostly due to the different ways the atoms and molecules within the substance are bonded together. For example, rubber is elastic because of its complex interlinked polymers that align when stretched. Most other substances deform elastically due to uniform deformation of their atomic structure. Which brings us to our second problem…

Nothing is perfectly elastic. Rubber and other elastomers are ‘elastic’ up to a point (around 10x their original length), but other materials can only deform slightly before they become plastic. Plasticity, in opposition to elasticity, is the property of a substance that retains its new shape when deformed, while elastic materials return to their original shape.

These two factors together make the effects of Gentle’s quirk highly irregular. To explain them, we first have to look at elasticity in more depth. So-called ‘perfect elasticity’ is described by Hooke’s Law, which states the force required to stretch or extend a material is directly proportional to the distance it is to be stretched or extended. This means to compress a spring to a quarter its length, one must apply twice the force required to halve its length, and so forth. This is (practically) true for all materials to a point. After that point, known as the yield point, the material stops being perfectly elastic, and begins deforming plastically. There are other stages between this and the material breaking, but these are unnecessary to discuss since no material that has been affected by the quirk has ever reached its yield point.

Let’s begin, as always, with the largest use of the quirk, here being the material that underwent the largest force and still remained elastic. The answer would of course be the air trampolines that redirected Izuku’s pellet of air[1], but the physics behind this interaction is possibly the most gratuitous and bloody murder of sense in the anime. I usually shy away from criticising the anime on its science, primarily because it’s a work of fiction about superheroes, but also because its purpose is a source of entertainment, and I bring the burden of applying science to it upon myself. In this instance however, I am allowing myself a small fracture in my usual composure to discuss why this scene is absolutely nonsensical.

Firstly, Izuku cannot create a bullet of air. To flick his finger is to create a pressure wave that spreads out from the point of creation at the speed of sound. No faster, no slower. If the finger is to move at a supersonic speed, the resultant pressure wave would create a sonic boom, and still travel at only the speed of light, still in a dissipating wave. Due to the properties of waves, their amplitude decreases with the square of the distance from the source. Thus Deku’s blast wave would not need aiming, and would also be barely a light breeze at such a distance as it is used.

Additionally, and most grievously, Gentle cannot create trampolines of air in the air. This is for the simple (yet often misquoted) fact of Newton’s Third Law. The classic, profound, smart-guy quip version is “every action has an equal opposite reaction”, but this is most likely only because the full answer is far more bloated. The law is in fact “when body A exerts a force on body B, body B exerts a force on body A that is of equal magnitude, opposite direction, identical type, and in the same line, as the force of body A on body B”. Quite a mouthful, but there’s a lot of subtle and important detail missing from the first, I’m sure you’ll agree. The problem here is that the created trampoline must exert a large force of Gentle to cause such acceleration (see Newton’s Second Law of Motion), and thus Gentle exerts a force on the trampoline, that causes an accelerate in the same proportion to the acceleration of Gentle as the ratios of their respective masses. Since air is a lot less dense than Gentle, and his quirk does not appear to add mass to a system, the trampoline would be accelerated backwards considerably fast before Gentle could gain any significant acceleration. It would be like trying to push yourself backwards by punching a balloon. Sure, the balloon is elastic, but it does not have enough mass to exert the required force. The only way this could work is if the trampolines were connected to the earth (thus the mass of the system is increased), but the only way this could occur is via more elasticated air. This does not happen because a) it is not seen – the elasticated air becomes slightly opaque (possibly a stylistic effect to show the action of the quirk) and there are no opaque structures visible, just a single floating disc, and b) these structures would be elasticated, and thus the system would be too flexible to exert such force over such distance.

Right, after that little rant, lets get back to the matter at hand. During the fight with Gentle and Deku there is a scene within a construction site that gives a lot of valuable information. This comes in the form of gratuitous quirk use, as well as an explicit statement of the quirk’s features: it cannot be turned off at will, and instead fades over time. This is odd when compared to almost all other quirks (if you need any examples, every other quirk investigated save one can be both activated and deactivated at will) and so it is likely it ties into the mechanism of the quirk’s action.

The scene contains two key uses of elasticity. Firstly, multiple steel girders are made elastic, and secondly a crane arm is made elastic. The former is useful because it is used by Gentle for movement, so the force on it and thus a lower limit for the yield point can be garnered. The second is useful because it showcases the flexibility of elasticated materials by how much the crane arm bends.

The steel beam bends about 1m each side of its equilibrium, which seems to be relatively unaffected by the quirk. The beam seems around 10m long, but thankfully the beams look like Universal Beams, which have standardised measurements including each type’s flange thickness, root radius, and most importantly, mass by metre and elastic modulus in each axis. Unfortunately there are almost 100 types, each of subtly different dimensions and properties. After downloading a spreadsheet and sifting through all types, I can confidently say the distinction does not matter, as the differences are all within the margin of error that arises upon attempts to measure the on-screen girder.

Let’s start with some maths. There’s no escaping it, and this time it’s back with a vengeance. Assuming the girder bends to approximate an arc (a section of a circle’s circumference) we can use some geometry to figure out the length of the original and stretched girders, and thus how much longer the latter is than the former. The unstretched we already know is around 10m long, and the centre bends ~1.5m from equilibrium. Since the ends are fixed, we know the chord subtending the arc is 10m long, and the distance bent (1.5m) is the distance between the arc and the centre of the chord. I won’t bore you with the details, but it turns out that the steel only increases length by 60cm, or one 60th its original length.

There isn’t much clear data on how elastic metals are (illustrated by the fact that a cursory search of “how far do metals stretch” gets 10 results in before some very different and nsfw questions come up instead, no points for guessing what they are) but there is an incredibly useful dataset courtesy of engineering toolbox, containing the ultimate tensile strength, yield strength or Young’s Modulus of almost every material you can think of. I’m not sure which engineer would need to compare the elasticity of compact and spongy bone, but I’m sure some day I’ll be glad the entry is there. For now we’ll look at the structural steel values, and thankfully all three are available. Let’s take a moment to discuss what they mean.

Young’s Modulus is the ratio of stress against strain, and has a fixed value for each material. Stress is the force per unit of cross-sectional area applied to the material, and the strain is the stretched length sure to such stress over the original strength. Yield strength is the minimum stress required to deform the material plastically, and ultimate tensile strength is the stress required to snap the material. Structural Steel has a Young’s Modulus of 200, so for every 200 MN of force per square metre of cross-sectional area, the beam will double in length. Sadly, these simple calculations are only applicable when the force and extension lie on the same line. In our case, the deformation is complex, non-shear, and therefore cannot be described at an angle relative to the force. In this case, we must apply the terrifyingly named Euler-Bernoulli Beam Theory. It contains some fittingly terrifying equations, included variable functions based on beam material, and second derivatives against two separate nested variables. However, in our scenario, the beam is supported at both ends (known as a simply supported beam) and we’ll assume it is uniform in density, elasticity, etc. Therefore we get an equation that looks like this: σmax = ymax F L / (4 I) where σmax is maximum stress at a given point, ymax is the distance from the point to the neutral axis, F is the force applied to the centre of the beam, L is double the length of the beam, and I is the ‘area moment of inertia of the cross section’. I have almost no idea what that last one means, but thankfully I managed to find an equation for it given different dimensions of a symmetrical I-shaped cross-section. There are two pieces of bad news. 1, it looks like this: Iy = (a^3 h / 12) + (b^3 / 12) (H - h), and 2, we now need to play a game of universal-beam ‘Guess Who’ to gain the correct dimensions.

The beam in the anime seems to be less than 500mm in depth, so that removes 47 possible types. Less than 500mm in width sadly doesn’t remove any more. However, we do know the beam is roughly larger than 150mm, since it larger than Deku’s hand span, which removes another 23. Averaging the rest gives us some dimensions we can use as an approximation of the beam. Thankfully, there exists a table of standard UK I beam dimensions and their respective area moment of inertia of the cross section. Comparing our values to the closest standard gives a value of 7440. Plugging this into the max strain equation, we find the maximum strain on the beam to be 0.79N per square metre. A strangely low number that says to me something must be wrong. The problem is we don’t know the value of F, and since I just used Gentle’s weight the formula treats the beam as incredibly flexible, since it bent so much under such little load. This is a problem, only solved by using a formula involving the Young’s Modulus E  of the beam rather than F. Such a formula is even more complex than those already seen, and is at such a level that I cannot understand how to apply it to the above scenario. Indeed, this post is already much over its due posting date at time of writing, and we have not talked at all about the quirk’s mechanism. Beam theory being as complicated as it is, and having spent now a good few days failing to apply it, I believe it is best we approach the problem from a different angle.

It’s safe to say the metal becomes not just more elastic, but more flexible, when the quirk takes effect. It takes a very large force to bend metal to the extent shown, and that metal would snap or at least bend plastically before that point is reached (sadly I cannot say which would occur). Therefore something about the molecular structure of the metal must change.

As previously discussed, metals and polymers bend differently at the molecular level, and this is because their very structures are different. Metal atoms bond by delocalising their outer electrons, creating positively charged ions attracted to a sea of negatively charged delocalised electrons. This is why metals shine – the electron sea is incredibly smooth, sub atomically so. Polymers bond via covalent bonds and inter-molecular bonds, creating discrete polymers that weakly attract each other. Gentle’s quirk must somehow make both these structures, and others, elastic in the same fashion.

The first answer is to weaken the inter-molecular forces within the structures, allowing polymers/molecules/any base elements to more easily move past each other within the material. Sadly, this just makes the material more ductile, which is the ease with which the material can be elongated via tensile force. To make something more elastic, the forces holing the molecules together must be made, for want of a better word, springier. Essentially, they must be able to act over a longer distance in order to pull the material back into shape after deformation. To do this simply would be to make the bonds stronger, but this would also make the material less flexible and denser. Instead, the force must somehow be spread across some distance profile, maintaining its magnitude at the standard distance of molecules from each other, but fall off slower as distance increases. The way to do this while retaining the other featured of the material is essentially fictional, and would even break thermodynamics (again) by being able to increase the Helmholtz Free Energy within a closed system. Since we’re now changing the mechanism by with one of the four fundamental forces of the universe functions, we can suppose the quirk changes the quirk in such a way ass to create perfectly elastic materials, since they already seem to have ridiculously high yield points.

Supposing this is the case, the question immediately arises – so what? The answer is that perfectly elastic materials have immense uses within many scientific circles. If a material returns to exactly the same state after deformation as it was in before, then it has the same energy. This means any object that hits it rebounds with the same kinetic energy as it started with, a phenomenon known fittingly as a perfectly elastic collision. Every other collision loses energy as heat, save for collisions that stretch the term for physics reasons, such as two orbiting objects. In our case purely elastic collisions have as many uses as elastic materials do, and possibly more. To have any material possible suddenly, even though temporarily, gain perfect elasticity will have material scientists drooling, and although I do not have the intelligence to think of any novel applications of such, asking one of them would I’m sure give you myriad answers.

Another fun application is heat-proofing. A material becomes liquid when the inter-molecular forces are partially overcome by kinetic energy, and gasses when the forces are broken completely. Since these forces are unlimited in distance, the objects would never be able to become gaseous, and would have very high cohesion (surface tension) when liquid. I’m again not sure of the applications of this, but it is cool nonetheless.

To conclude, Gentle Criminal’s quirk affects any material he touches, and changes the effect of the electrostatic forces within it, making them act across any distance, with a slight reduction in magnitude with distance. This works by having the force pull the molecules together from any distance, until they become close enough to be repelled by the electrostatic repulsion of the atoms. Any force applied may overcome the electrostatics for a distance, but will never cause yielding.

[1] Season 4 episode 85: School Festival Start!!

I hope you enjoyed this investigation! It’s almost Christmas as I post this, and as I’m sure you’re aware this post should have ben released on the 1st. I’m also sure you’re aware this has become a trend, and I’m sure you know reasons behind it. It is therefore with a heavy heart I announce we will be taking a hiatus for an undefined length of time. We have decided it is better to write a few posts as backup and prepare for posting, rather than desperately writing posts weeks after they’re due and apologising. We don’t have an idea of when we will be back, but we will. In the mean time, go have a Merry Christmas/Happy Holidays, and a happy new year. We’ll see you some time in 2021.

[rbrooksdesign]

“PRIMES on the BIM (formerly “PTOP on the BIM): PART IV: #31”

In Part III, we combine and simplify everything from the Part I & II including:

SYMMETRY, STEPS, EVENS, EVENS/2, PPsets, PRIME SEQUENCE FRACTALS, ISOSCELES & EQUILATERAL TRIANGLES, INVERSE SQUARE LAW, PYTHAGOREAN TRIPLES; ALL ON THE BIM.

~~~~~~

These PPsets are formed from the Horizontal and Vertical AXIS numbers that intercept those BLUE circle values. The PRIMES Sequence (PS)—3,5,7,11,13,17,19,23,...— determines the pattern. Notice that the PPsets ALSO fall exactly on the same BIM/24 Active ROWS (PURPLE Bands) as do the PPTs and PRIMES

BIM: Part III becomes significant when one finds that the NPS of those PPsets falls on exactly the SAME Active Rows that previously ALL PRIMES and ALL PPTs were found to occupy on the BIM! No small coincidence and quite easily seen when, the actual PPset values are overlaid on those LD values. The PS fractals along the Horizontal and Vertical AXIS intercept at these points on the BIM. They form the NPS of the PTOP directly on the BIM! It is no longer hidden!

The PRIMES Sequence Fractal—3-5-7-11-13-17-19-23-29-31-…—found along each AXIS, together forms the PPsets = EVENS = Goldbach Conjecture Proof.

The PPset TRAILS (Rows) ALWAYS INCREASE FASTER than the PRIME Gaps ensuring that the PPsets = EVENS = Goldbach Conjecture Proof.

One could say, that by definition, ALL EVENS are indeed formed from the OVERLAPPING PS Fractal TRAILS of PPsets = EVENS = Goldbach Conjecture Proof.

~~~

The NPS holds true for ALL PPsets that together define any given EVEN!

Like shining a light at a sculpture in the dark, each angle reveals a new “look,” yet it is just one sculpture. That’s what we are doing here. Hopefully, the BIM: Part III look will give us the simplest, most direct and informative view of just how EVERY EVEN IS MADE OF SYMMETRY AND PS FRACTAL ENDOWED PPsets IN THE FORM OF THEIR OVERLAID PPset TRAILS. Euler’s Strong Form of the Goldbach Conjecture simply falls out from this builtin relationship between the ISL, the PPTs and PRIMES as seen on the BIM.

~~~

2020, Reginald Brooks

PRIMES Index

PRIMES on the BIM ebook

[lthmath]

Recently we have been reorganizing our LThMath Book Club. The whole idea behind it is to read and discuss books with other people. We are happy that the Goodreads Club grew to 278 people. We have created a Facebook Group with the same idea as the Goodreads one. After the first months we have reached 377 members in the group and we have some really great book recommendations. Hope you all enjoy the idea.

Due to this change, we cannot do just a Goodreads poll for the bi-monthly book. Therefor, we decided to do a survey (created using Google forms). In this way more people can vote for the book. If you want to vote, you need to do it HERE.

“A Beautiful Mind” by Sylvia Nasar*

Economist and journalist Sylvia Nasar has written a biography of Nash that looks at all sides of his life. She gives an intelligent, understandable exposition of his mathematical ideas and a picture of schizophrenia that is evocative but decidedly unromantic. Her story of the machinations behind Nash’s Nobel is fascinating and one of very few such accounts available in print.

We are very interested in this book due to the movie “A Beautiful Mind”*. It is an incredible, emotional and interesting movie about the life of John Nash. If this book was chosen, we believe it would be a great idea to watch the movie after we read the book. What do you think?

“Things to Make and Do in the Fourth Dimension: A Mathematician’s Journey Through Narcissistic Numbers, Optimal Dating Algorithms, at Least Two Kinds of Infinity, and More” by Matt Parker*

In the absorbing and exhilarating Things to Make and Do in the Fourth Dimension, Parker sets out to convince his readers to revisit the very math that put them off the subject as fourteen-year-olds. Starting with the foundations of math familiar from school (numbers, geometry, and algebra), he takes us on a grand tour, from four dimensional shapes, knot theory, the mysteries of prime numbers, optimization algorithms, and the math behind barcodes and iPhone screens to the different kinds of infinity―and slightly beyond. Both playful and sophisticated, Things to Make and Do in the Fourth Dimension is filled with captivating games and puzzles, a buffet of optional hands-on activities that entice us to take pleasure in mathematics at all levels. Parker invites us to relearn much of what baffled us in school and, this time, to be utterly enthralled by it.

“Lost in Math: How Beauty Leards Physics Astray” by Sabine Hossenfelder*

Whether pondering black holes or predicting discoveries at CERN, physicists believe the best theories are beautiful, natural, and elegant, and this standard separates popular theories from disposable ones. This is why, Sabine Hossenfelder argues, we have not seen a major breakthrough in the foundations of physics for more than four decades. The belief in beauty has become so dogmatic that it now conflicts with scientific objectivity: observation has been unable to confirm mindboggling theories, like supersymmetry or grand unification, invented by physicists based on aesthetic criteria. Worse, these “too good to not be true” theories are actually untestable and they have left the field in a cul-de-sac. To escape, physicists must rethink their methods. Only by embracing reality as it is can science discover the truth.

Looking at the general description, this sounds more like a book about physics but we are still interested to see how the author deals with the bondary between mathematics and physics. Also, this book was released in 2018.

“The Indisputable Existence of Santa Claus: The Mathematics of Christmas” by Hannah Fry and Thomas Oléron Evans*

How do you apply game theory to select who should be on your Christmas shopping list? Can you predict Her Majesty’s Christmas Message? Will calculations show Santa is getting steadily thinner – shimmying up and down chimneys for a whole night – or fatter – as he tucks into a mince pie and a glass of sherry in billions of houses across the world?

Full of diagrams, sketches and graphs, beautiful equations, Markov chains and matrices, Proof That Santa Exists brightens up the bleak midwinter with stockingfuls of mathematiccal marvels. And proves once and for all that maths isn’t just for old men with white hair and beards who associate with elves.

“The Music of the Primes: Why an unsolved problem in mathematics matters” by Marcus du Sautoy*

Prime numbers are the very atoms of arithmetic. They also embody one of the most tantalising enigmas in the pursuit of human knowledge. How can one predict when the next prime number will occur? Is there a formula which could generate primes? These apparently simple questions have confounded mathematicians ever since the Ancient Greeks.

In this breathtaking book, mathematician Marcus du Sautoy tells the story of the eccentric and brilliant men who have struggled to solve one of the biggest mysteries in science. It is a story of strange journeys, last-minute escapes from death and the unquenchable thirst for knowledge. Above all, it is a moving and awe-inspiring evocation of the mathematician’s world and the beauties and mysteries it contains.

“A Brief History of Infinity” by Brian Clegg*

Infinity is a concept that fascinates everyone from a seven-year-old child to a maths professor. An exploration of the most mind-boggling feature of maths and physics, this work examines amazing paradoxes and looks at many features of this fascinating concept.

“Gamma: Exploring Euler’s Constant” by Julian Havil*

Among the many constants that appear in mathematics, π, e, and i are the most familiar. Following closely behind is y, or gamma, a constant that arises in many mathematical areas yet maintains a profound sense of mystery.

In a tantalizing blend of history and mathematics, Julian Havil takes the reader on a journey through logarithms and the harmonic series, the two defining elements of gamma, toward the first account of gamma’s place in mathematics.  Sure to be popular with not only students and instructors but all math aficionados, Gamma takes us through countries, centuries, lives, and works, unfolding along the way the stories of some remarkable mathematics from some remarkable mathematicians.

“Proofiness: The Dark Arts of Mathematical Deception” by Charles Seife*

“Proofiness,” as Charles Seife explains in this eye-opening book, is the art of using pure mathematics for impure ends, and he reminds readers that bad mathematics has a dark side. It is used to bring down beloved government officials and to appoint undeserving ones (both Democratic and Republican), to convict the innocent and acquit the guilty, to ruin our economy, and to fix the outcomes of future elections. This penetrating look at the intersection of math and society will appeal to readers of Freakonomics and the books of Malcolm Gladwell.

“Tales of Impossibility: The 2000-year quest to solve the mathematical problems of Antiquity” by David S. Richeson*

Tales of Impossibility recounts the intriguing story of the renowned problems of antiquity, four of the most famous and studied questions in the history of mathematics. First posed by the ancient Greeks, these compass and straightedge problems–squaring the circle, trisecting an angle, doubling the cube, and inscribing regular polygons in a circle–have served as ever-present muses for mathematicians for more than two millennia. David Richeson follows the trail of these problems to show that ultimately their proofs–demonstrating the impossibility of solving them using only a compass and straightedge–depended on and resulted in the growth of mathematics.

We hope this helped you decide what book you would like to read in August – September with us. Hope you liked this post. Have a great day. You can find us on Facebook,  Tumblr, Twitter and Instagram. We will try to post there as often as possible.

Lots of love and don’t forget that maths is everywhere! Enjoy!

*This post contains affiliate links and I will be compensated if you make a purchase after clicking on my links.

December – January Book Choice Recently we have been reorganizing our LThMath Book Club. The whole idea behind it is to read and discuss books with other people.

[squareallworthy]

Triangle Tuesday 8: the nine-point circle, the deep lore, and did I say nine? I meant, like, fifty-six.

Today we are looking at the nine-point circle, a famous construction with connections to other triangle geometry that we've looked at before. But first, I'd like to re-introduce the centers that we've met so far. You should imagine that they're members of a super team each with their own little sequence that the cartoon always shows when they go into action.

And imagine that they're appearing with one of these dramatic cartoon backgrounds like this. I would go ahead and do that, but it would look really messy on the little screen you're staring at. It will look better in your imagination.

Anyway, here we go. Here they are, now each with its own thematic color.

G, the Centroid!

Secret origin: intersection of the medians

Trilinear coordinates: 1/a : 1/b : 1/c

Affiliations: Euler line, isogonal conjugate of the symmedian point

Super powers: center of gravity of triangle area • center of gravity of triangle vertices • divides triangle into equal parts ABG, BCG, and ACG • divides medians 2/3 of the distance from vertex to midpoint

O, the Circumcenter!

Secret origin: intersection of the perpendicular bisectors

Trilinear coordinates: cos A : cos B : cos C

Affiliations: Euler line, isogonal conjugate of the orthocenter

Super powers: center of circumcircle • circumcircle is locus of points with degenerate pedal triangles • relates to incenter via Euler's theorem in geometry

H, the Orthocenter!

Secret origin: intersection of the altitudes

Trilinear coordinates: sec A : sec B : sec C

Affiliations: Euler line, isogonal conjugate of the circumcenter

Super powers: constitutes an orthocentric system along with the vertices • incenter of orthic triangle • sides of orthic triangle are antiparallel to sides of reference triangle • concyclic with a vertex and two adjacent feet of altitudes

I, the incenter!

Secret origin: intersection of the angle bisectors

Trilinear coordinates: 1 : 1 : 1

Affiliations: entourage of excenters

Super powers: center of the incircle • isogonally self-conjugate • forms orthocentric system along with excenters • relates to circumcenter via Euler's theorem in geometry • always lies in interior of orthocentroidal disc

K, the symmedian point!

Secret origin: intersection of the symmedians

Trilinear coordinates: a: b: c

Affiliations: isogonal conjugate of centroid

Super powers: perspector of reference and tangential triangles • parallels through K intersect sides in six concyclic points • antiparallels through K intersect sides in six concyclic points, with K at the center of the circle • circles through K and two vertices intersect sides in six concyclic points • lines joining midpoints of altitudes and sides pass through K • centroid of its own pedal triangle • just very pretty

So now that we've got the super team together, it's time to introduce them to someone new. I know, you're thinking we've got this established cast of characters, and they relate to each other in so many varied and intimate ways. How could a new triangle fit into these relationships? Wouldn't it feel like a superfluous add-on at this point in the show?

Well, let's see. Let's go back and look at the midpoints of the sides. We find the midpoints by drawing perpedicular bisectors on each side. Those lines meet at the circumcenter, which makes the midpoints the feet of the circumcenter. The triangle formed by the midpoints is the pedal triangle of the circumcenter.

Any three points also determine, naturally, a circle. The circle formed by the feet of a point is called the pedal circle of the point. And every point has a pedal circle with respect to a given triangle.

The orthocenter, for instance, has a pedal circle defined by the feet of the altitudes, and guess what? It's the same circle! What's more, this circle bisects the segments that join the orthocenter with the vertices. For this reason, the circle is called the nine-point circle, and its center is the nine-point center, N. Let's prove that it exists.

Theorem: in any triangle the midpoints of the sides, the feet of the altitudes, and the midpoints of the segments connecting the orthocenter to the vertices lie on a common circle.

Here's our triangle ABC, with midpionts of sides Ma, Mb, Mc, feet of the altitudes Ha, Hb, Hc, and midpoints of segments joining H and the vertices Sa, Sb, Sc. We will rely on the fact that a line segment joining the midpoints of two sides (a midline) is parallel to the third side and half as long.

In green we have horizongal segments MbMa, a midline of ABC, and SaSb, a midline of ABH. Both of these midlines are parallel to side AB and half its length, so they are parallel to each other and equal. Vertical green segments MbSa and MaSb are midliness of ACH and BCH respectively, so they are also parallel and equal. Therefore the green segments form a rectangle.

In the same way, the blue segments also form a rectangle. These two rectangles have a common diagonal MbSb, and so have the same circumcircle. And McHcSc is a right triangle, and its hypotenuse McSc is also a diagonal of the blue rectangle. Therefore Hc is on the same circle, and by analogous argument so are Ha and Hb.

Since now we can be sure the nine-point circle and its center exist, it should get its own introduction scene and signature color.

N, the nine-point circle!

Secret origin: pedal circle of circumcenter and orthocenter

Trilinear coordinates: cos(B-C) : cos(C-A) : cos(A-B)

Affiliations: Euler line

Super powers: passes through nine points • many many others which we will get to next

So those are some nice ways that connect the nine-point circle to the circumcenter and orthocenter. And it's cool that this new character N has some connections to the established characters O and H, but what about the other points? Can we find some connections there?

Yes, we can, because it turns out the nine-point center is connected to everything. Would you like to see some of them?

(This is me right now.)

Because there are kind of a lot.

The nine-point circle is tangent to the incircle and the excircles. If you are keeping track, that's now 13 points of interest on the nine-point circle.

The radius of the nine-point circle is half that of the circumcircle. This is easy to see, because the circle is the circumcircle of the medial triangle, which is half the size of the reference triangle.

The nine-point center lies on the Euler line midway between the circumcenter and the orthocenter. The centroid is one-third of the way from the circumcenter to the orthocenter. These positions give the orthocenter and centroid special status with regard to the nine-point circle.

The nine-point circle bisects any line segment from the orthocenter to the circumcircle, making the fact that it bisects the tops of the altitudes into a special case of a general property.

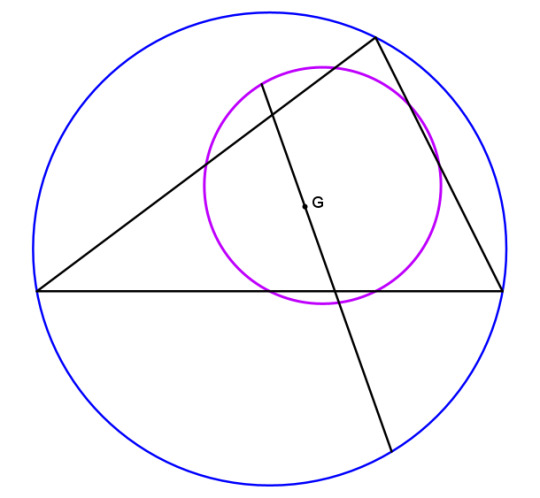
The centroid trisects any line segment extending from a point on the nine-point circle through G and on to the circumcircle. Another way of saying this is that G is a center of dilation between the circumcircle and nine-point circle with scaling factor -1/2. In triangle geometry, this particular dilation through G is called taking the complement of a point, so a third way of describing this relationship is to say that the nine-point circle is the complement of the circumcircle.

The nine-point center is also the center of gravity of A, B, C, and H.

As we have seen previously, the vertices and the orthocenter form an orthocentric system, meaning that any one of the points A, B, C, and H is the orthocenter of the other three. For all four of the triangles ABC, ABH, ACH, and BCH, the feet of the altitudes are the same, so they all share the same orthic triangle and the same nine-point circle.

But each of these four triangles has its own incircle and set of excircles, and the nine-point circle is tangent to all of them, making sixteen points of tangency. That's now 29 points of interest on the nine-point circle.

The incenter and the excenters form another orthocentric system, and the nine-point center of this system is the circumcircle of the original triangle. The reference triangle ABC is the orthic triangle of the excentral triangle JaJbJc.

And speaking of the orthic triangle, it defines three other triangles in the corners that are similar to the reference triangle. The Euler lines of these corner triangles coincide at a point on the nine-point circle. That brings us to 30 points of interest on the nine-point circle.

Let's go back to pedal triangles, and remember that if a point is on the circumcircle, its feet are colinear and its pedal triangle has collapsed to a line segment, called a Simson line. The envelope of these line segments form a shape called the Steiner deltoid.

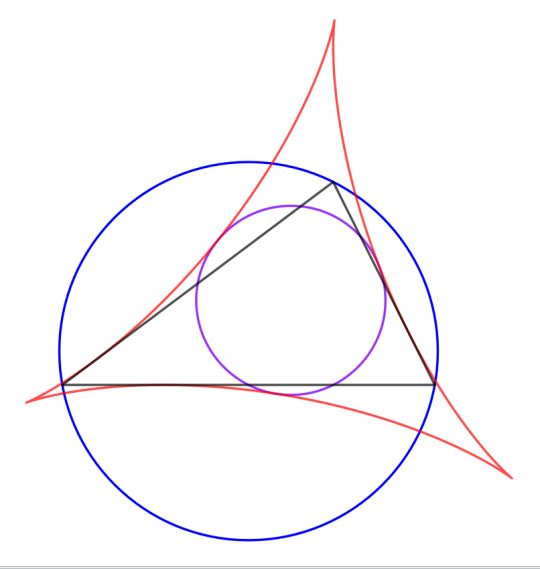
The nine-point center is also the center of the Steiner deltoid, and the circle is tangent to the deltoid at three points. There are four different circumcircles in an orthocentric system, so there are twelve points of tangency in all, so we now have 42 points of interest on the nine-piont circle.

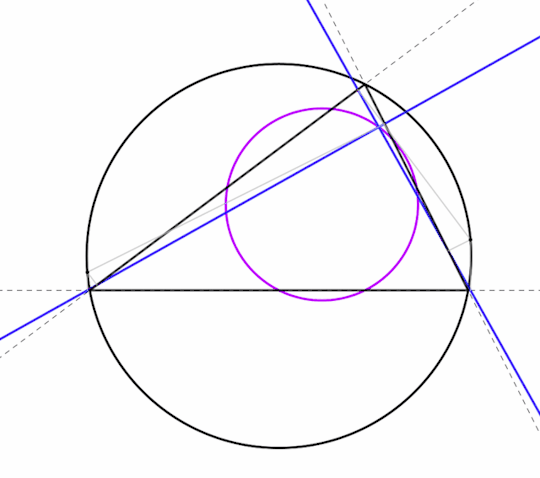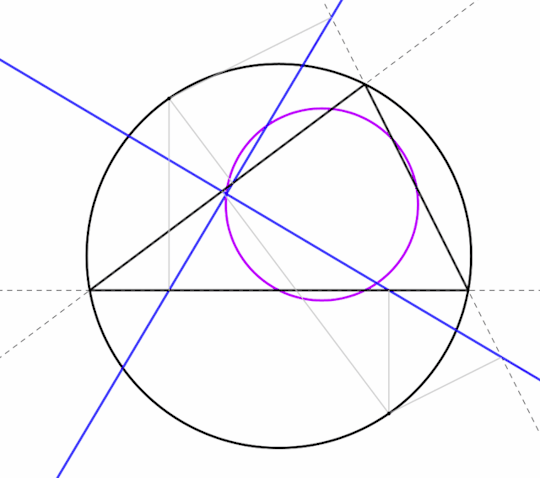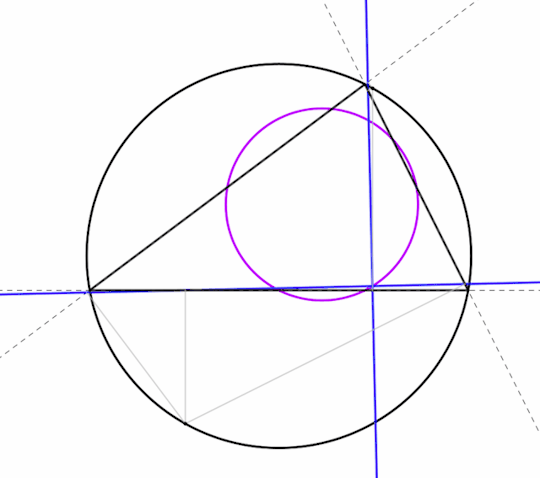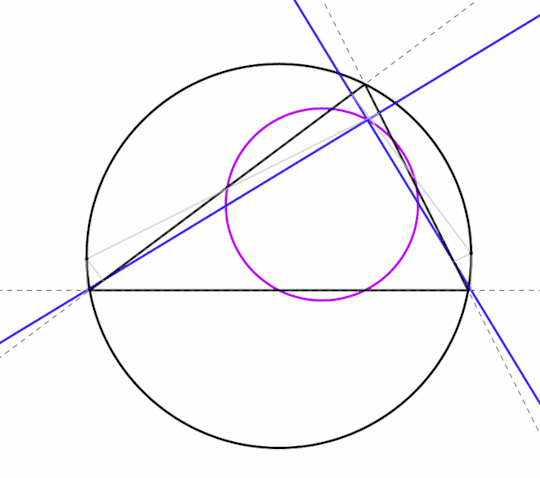
The Simson lines of two opposite points on the circumcircle intersect perpendicularly on the nine-point circle.

You may have noticed that in citing all these connections I haven't mentioned the symmedian point K so far. As far as I can tell, K is just not that very strongly connected to N. However, here's one: the circle through K, N, and O is orthogonal to the circle with diameter GH (the orthocentroidal circle). That's five members of our super team tied into one relation. But that's all I've got. Sometimes members of a team don't interact that much.

And this is the kind of thing you look for in a successful series, right? You have an established cast of characters, with a rich, dense lore linking them all together in various ways. Then, as the story develops and someone new is introduced, new retlationships make the lore even richer. That that's why I'm in the triangle fandom.

With that, I think the only question left to answer is "Hey, Square, do you happen to have a group portrait of the whole team together in one clear and not at all confusing picture?" And of course I do.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.

[nuka-nuke]

| Jack Euler |

Name: Jack Philip Lee Euler

Nickname: None

Age: 31

Birthday: August 23, 2046 (Virgo) 

Height: 6’

Weight: 190~ lbs

Specials: Str 10 - Per 4 - End 10 - Cha 3 - Int 1 - Agi 10 - Luck 1

Eyes: Hazel blue

Hair: Dark brown and very long, always kept in a ponytail because he gets overwhelmed by it getting all over the place.

Body type: Lanky and skinny with broad shoulders and huge feet.

References: Here

Status Pre-War: A mechanic working for a local garage, married to the love of his life who was the more successful out of the two with her job as a lawyer. He moved to Boston for her, originally being from rural Pennsylvania.

Status Currently: An agent with the Railroad struggling to find his way in the wasteland.

Relationship Status: Widower

Spouse(s)/Partners: Vivia Loreña-Euler (deceased)

Sexuality: Heterosexual

Gender: Male

Ethnicity: American

Family:

Vivia Loreña-Euler, wife (deceased)

Jerri-Lynn Kristiana Euler-Oliver, sister

-Roscoe Oliver, brother-in-law

Bianca Oliver, niece

Marina Oliver, niece

Roscoe Oliver Jr., nephew

Jolene Mari-Ella Euler-Wilson, sister

-Ezra Wilson, ex-brother-in-law

Lorna May Ellis Wilson, niece

Aberdeen Lora-Jo Euler, sister

Rosanna Cecila Ophelia Euler, sister

Josephine Arlandria Penelope Euler-Slonina, sister

-Waylon Slonina, brother-in-law

Quentin Leyton Slonina, nephew

Woodrow Reggis Slonina, nephew

Sam Christopher Slonina, nephew

Francis (Ford) Lee Albert Euler, brother

Philip Albert Stanley Euler, father (deceased)

Luanne Georgina Euler, mother (deceased)

Languages: English 

Disabilities/Illnesses/Injuries: None, he is fairly hardy. Mild PTSD from his time in the war and social anxiety which sometimes gives him panic attacks.

Allergies: None

Scars: He has a long scar crossing from the bridge of his nose down and under his right eye, an injury acquired during combat in the war when he was bashed in the face with an enemy rifle, breaking his nose in the process. The man who inflicted the damage was then beaten to death before his eyes by one of his platoon members, which was the first time he had ever witnessed the murder of another person. Jack always feared the inner monster a person could become under trauma from that point forward and hoped to never see himself become that.

Other facial scars include a long scar below his left eye which crosses down his cheek and over his lips. He was working in the garage cutting exhaust pipe with a cut off wheel on an angle grinder, negligently not using a face shield, when the wheel shattered and a piece broke off and embedded into his face. Luckily Ford was there and was able to get him to the hospital, and saved the heckling until after they ensured he wasn’t going to die. He never lived that one down for as long as he and Ford worked on cars together.

He has countless smaller scars on his hands and wrists from mechanic work over the years. Notably he has a large burn on his left elbow which mangles one of his tattoos, from accidentally leaning on a weld seconds after finishing welding something. Various other scars all along his knees and shins (from being clumsy and falling over his giant feet all the time) and one gnarly puncture wound on his left shoulder from a Red Widow bloodbug which he hit with his bat just a few moments too late.

Physical traits: Jack has a birth mark on his forehead that is mostly obscured by the amount of freckles he has all over his face, which continue all over the rest of his body as well. He has an American traditional style eagle tattoo across his chest and a sleeve of random flash-sheet kind of American traditional tattoos all over his left arm, acquired from his time living out of his car and traveling all over the states and adding a tattoo from every town he stayed in. He has wrinkles between his eyebrows from years working in the sun and focusing way too hard, and often looks exhausted due to the creases around his eyes. He has a scruffy beard and extremely perfect eyebrows that always made his sisters jealous.

Voice: Jake Gyllenhaal, but only as Jack Twist.

Clothing: Pretty much hasn’t changed out of his vault suit since leaving Vault 111. Like ever. He added a coat, though. Also he always wears his holotags from the military, his wedding ring, and his pipboy which is painted red.

Fashion Style/Lifestye: His fashion sense is pretty much “how long can I get away with wearing the same disgusting, dirty outfit before Bambi finally requests that I change and do laundry.”

Weapon of Choice: “The Fuck ‘Em Up”, a chain wrapped baseball bat, also painted red, or a bladed tire iron.

Skills: Strength, combat, situational awareness (in nonsocial situations), mechanics, artistic

Weaknesses: Easily stressed out in social situation, has a hard time explaining himself, can be kind of slow, spaces out a lot and daydreams. Very scatterbrained. Often sees things way too literally.

Poor skills: Computer technologies, verbal communication, stealth (too clumsy).  

Affiliations: The Railroad, Acadia

Former Affiliations: None

Enemies: The Institute

Neutral Affiliations: The Brotherhood of Steel, the Minutemen, Nuka World Raiders

Religion: Agnostic

Likes: Cars, working on cars, collecting random trinkets, drawing and writing in his journal (mostly to Vivia), digging through junkyards and scrap and planning how to build a new Corvega one day. Also enjoys cooking and making new recipes for the various types of wasteland animals he kills.

Dislikes: Pre-war food, Nuka Cola Quantum (the radiation makes him extremely sick), most sweets 

Hates: Spiders, radscorpions, insects of any variety. Vivia was the bug killer of their household.

Friends: Deacon, Piper Wright

Acquaintances: Ilya Valle (pre-war), Nataniel Valle (pre-war)

Former friends: None

Enemies: None that he is aware of, maybe there are some out there. Don’t know.

Pets: Sometimes junkyard dogs hang out with him at Hub City. But really none.

Fallout OC friends/family: Brook Cecil, Benjamin Reese, Andre Torres, Bambi (Beth), Sirius Tillinghast, Katherine Vance

Personality: Jack is overall pretty laid back. There isn’t much that can make him lose his temper, and even if he does, he ends up feeling bad about it and apologizing later. He is terrible in social situations and uses his awkward sense of humor to try to bridge conversations, which sometimes works, as in the case of how he scored Vivia’s phone number.

Favorite color: Green

Favorite foods: Radstag jerky, mirelurk cakes, literally everything his mother cooked when he was a kid.

Favorite drinks: Vim!, Vim! Quartz, Gwinnett Lager

Favorite Sweets: If anything, he might have some gum. Overall, not a fan of sweets. 

_____________________________________

Thanks to @madddraws for letting me use their character profile layout!

[logicxonomy]

Euler’s Theorem and Euler’s Inequality (Proof)

It is used to find the distance between the incenter and circumcenter of a triangle. Let a triangle ABC in which I is the incenter and O is the circumcenter, the length of the inradius and circumradius are r and R respectively.

Draw lines AN, BI, and CI as given in the figure.

∠IAB= ∠IAC= A/2 ∠ABI= ∠CBI= B/2 (I is the intersection point of angle bisectors) ∠NBC= ∠NAC= A/2 (Angles, subtended by the same chord NC) ∠BIN= ∠IBA+∠IAB= (A+B)/2 (External angle of the triangle) In the △NBI, ∠NBI= ∠NIB

So, BN=IN …………(i)

Intersecting chord theorem, AI×IN=LI×IM AI×IN=(R-d)×(R+d) …….(Circumradius=R) AI×BN=R²-d² ………….(ii) (From equation i, BN=IN)

Draw ID⟂AB, so ID=r (Inradius) NQ is the diameter so ∠NBQ=90° (Theorem) Now, △NBQ ~ △IDA (Similar triangles) ID/BN=AI/QN r/BN=AI/2R

AI×BN=2Rr R²-d² =2Rr d²=R×(R-2r)

— — — — — — — — — —

Euler’s Inequality: R≥2r

For more details, Click the link given below:

Join us on Telegram at ‘Logicxonomy’ for regular updates.

[thestillnessandthedancing]

November 7th 2018

Catching up with the freshest blends from around the globe. Here’s a wonderful set of sounds to drift to.

-hour1- Stray Theories - Begin (from.. All that Was Lost - 2018 - n5MD) Josh Alexander - Cirrus (from.. Hiareth - 2018 - Moderna Records) CEEYS - Union (from.. Waende - 2018) Mitch Labrosse - Sanctuary (from.. Points of Lights - 2018) Chihei Hatakeyama - Wilderness (from.. Afterimage - 2018 - White Paddy Mountain) Exist Strategy - September 22nd (from.. Singles - 2018) The Green Kingdom - Snowd (from.. Ephemera - 2018 - Rusted Tone Recordings) Sound Awakener & Tyson Swindell - Merging With the Shadows (from.. Two Haunted Pianos - 2018 - Rusted Tone Recordings) dramavinile - II (from.. Fall - 2018 - Sounds Against Humanity) Ian William Craig - And Therefore the Moonlight (from.. Thresholder - 2018) Niall Byrne - Beaubost (from.. Nightsongs - 2018) Hedia - wearedissolved (ST - 2018 - Pyramid Blood Records)

-hour2- Dino Spiluttini - The Strength to Hold Me (from.. Ceremony - 2018 - ACR) Pimmon - Shadow Catch You Tiring (from.. The Oansome Orbit - 2011 - Room40) Andrew Heath - Artefact (Tape Fragment) (from.. Evenfall - 2018) Precession - Unknown Origin p1 (from.. Euler Angle - 2018) Field Works/Benoît Pioulard) - The Source (from.. Pogue’s Run - 2018 - Temporary Residence Ltd.) Field Works/Rafael Anton Irisarri) - Into the White (from.. Pogue’s Run - 2018 - Temporary Residence Ltd.) Field Works/Julien Marchal) - Industry (from.. The Fair State - 2018 - Temporary Residence Ltd.) Lung cycles - Cammal (from.. ST - 2018 - Lily Tapes & Discs) Eefje harings - vi (from.. Being back in the house where i found myself - 2018)

*Photo the cover for Dino Spiluttini's Ceremony out now on ACR Recordings