#Logarithmic Progression

[captaingimpy]

Cracking the Code: Understanding Hunter Rank Progression in Monster Hunter Wilds

By an Anonymous Monster Hunter Enthusiast Introduction While enjoying my time in Monster Hunter Wilds, I became curious about how the game calculates Hunter Rank (HR) progression. It’s no secret that progressing through the ranks can feel unpredictable, and I wanted to better understand the underlying system. Using a combination of observation, data tracking, and analysis, I was able to…

[lullabyes22-blog]

Snippet - Fate vs. Choice - Forward but Never Forget/XOXO

Jinx has a decision, and a deadline.

Forward but Never Forget/XOXO

Six o’ clock. Late evening.

The Cathedral of Progress.

Lanterns burned in their iron-scrolled brackets; the shadows cut flayed patterns on the granite walls. In the nave, the acolytes chanted, cloaked and cowled. In their palms, the lit tapers cast long, lean shadows across the stone floors. Their voices were a mechanized hymn: harmonized down to the smallest atom vibrating in the air. There was no music riding the currents. Only silence, draping a veil of total stillness over the congregation. Perhaps even eternal damnation, to those who dared trespass.

Jinx didn't give a ripe toot about damnation. She'd already fallen from grace: the moment she'd set a wind-up monkey loose to rescue her family, and jinxed them instead. Her own jinx, since that fateful night, was an inevitability, and a long time coming.

Now, at nineteen, she was the living, breathing epitome of it.

The harsh sweetness of coffee cut through the chants. Jinx cracked an eyelid open; for one long giddy second, the world spun in a sickening circle.

Then it righted itself. Or Viktor did: a cool hand clasping hers.

“Wake up, Jinx.”

Her eyes fluttered open. She lay, starfished in an indolent sprawl, in sweetgrass that swayed as if under an invisible caress. The aroma of lilies was ascendant; twilight had deepened their perfume. The night-garden was tucked into the courtyard at the heart of the Cathedral, abutted by a small cemetery of granite.

Under the surreal refractions of a stained-glass dome, it was a wonderland: teeming with long-dead saints, and the perfumes of late-blooming flowers, all a-glow in holy light. Upon closer scrutiny, the holiness inverted into the uncanny. Every plant, aspirating beneath the multicolored rays, was revealed to hold an almost numerical symmetry: logarithmic spirals of orchids, geometrically-profound petunias, grid-patterns of clovers all fractaling in golden ratios.

As if every organism—from soil grain to leaf tip—had coalesced into life under the touch of a divine hand. Or a very obsessive mathematician.

Or—both.

Then there was the tree.

It was a prehistoric sycamore of darkling wood: five times the height of the average Piltovan oculus; three times as broad across. The branches fanned out into spokes as big as a ferris wheel. The ends of each spathe, splayed wildly under the skylight, erupted into iridescent blooms. They were nearly gem-like in their purity: their crystalline petals glowing in colors of multicolored amethyst, chrysoprase, quartz, topaz, ruby. The canopy spread over the entire garden; the roots curled deep into the bedrock.

By nightfall, it gave off an eerie luminescence: bathing the garden in an ephemeral glow. By daylight, it cast a rainbow halo across the grounds. Its fragrance changed constantly: one minute pungent as wormwood, the next citrusy as lemon zest, another woody as cardamomh. Insects swarmed about its roots; butterflies flocked its boughs. Some even swore they'd spotted faeries dancing in rings beneath its shadow.

The hallucinogenic effects were, by Viktor's accounts, an ur-example of magicoreality: an object, space, or phenomenon that is created through the combined imagination of multiple entities. It was real, because they believed it real. And vice versa.

Like a mobius strip blossoming into being.

Viktor's acolytes had transplanted the tree—roots to stem—from Singed subterranean laboratory. Something in the soil of the Cathedral's grounds nourished it with unique potency: the tree flourished where naysayers, Silco chief among them, predicted it would rot. By the first month, it'd become the centerpiece around which every botanical beauty revolved. By the sixth, it was the brilliant heart of a preternatural paradise: creepers, ferns, lilies, ivies, marigolds, all erupting in a palette of purest life.

By the tenth?

The tree was worshipped as an entity unto itself. It dominated the cultists' rhetoric; it haunted their reveries. It was rumored that Janna herself had breathed life into its veins, rescuing it from the brink of collapse. Pilgrims from the depths below, voyeurs from the heights above, arrived in droves to seek the sheltering boughs as if for the same restorative breath.

And under those twirling branches?

They were never the same again.

Formerly pallid patients were rumored to stagger from their sickbeds, sit beneath the blossoms in solemn ceremony, then unfold from their atavistic comas miraculously reborn. Like larvae metamorphosing into butterflies.

From devolution to evolution.

But though the tree restored a measure of life to its devotees, its own was an hourglass suspended between grains. The fruits hanging off its branches evoked a spectrum of incandescent sea-shells washed by whitecaps onto arid shores. They were entirely inedible; ash and air. And as soon as they fell, their shells fossilized: petrifying into stone-crusted facets within minutes of detachment, before dissolving into inert dust.

It was the tree's perpetual paradox: the promise of life, forever beyond reach. And death, ever-encroaching at its heels.

In its shadow, Viktor, the most devoted disciple of one, held court weekly with the most notorious apostate of the other.

"Wake up, Jinx."

Viktor's hand, freed from its tight leather glove, squeezed hers. His fingers, long and thin, held a delicate strength: there were calluses, velvety, at the tips, and a roughness along the heel. A scientist's hands, evolved into a healer's. Tonight, Jinx saw ink smudges on the knuckles. There was also a tiny nick, from wielding a scalpel during the evening's surgery on a young boy's ruptured appendix.

The boy was safe. Tucked into a cot at the infirmary, with the others under Viktor's care: each dosed with enough poppy-milk to see them through the night. The boy's mother, one of the dozen souls who'd flocked to the Cathedral seeking the Machine Herald's aid, had wept at her son's restoration, kissing the hem of Viktor's robe in a show of gratitude.

It was a scene that Jinx had witnessed, over and over again, during her visits. And it never failed to unsettle.

Devotion, undiluted, had that effect. Especially when it was devoid of desire.

Daily, scores of souls passed in and out of the Cathedral. Each brought with them a problem, a poison, a plea. Each, Viktor addressed in their turn: salving their sores, purging their pustules, and bestowing, with a steady hand and a soft voice, his personal brand of salvation.

He never charged for his chem-modifications. Even the most complex, which took months to design, were given for free.

His payment, his only payment, was everything.

From the start, he’d made plain that his services were offered on a strictly non-partisan basis, and would cease immediately should any faction in Zaun attempt to co-opt his work. Except that was a lie. Everyone knew, in Zaun's hierarchical honeycomb, Viktor had no love for politics. But he was fiercely political: his sacrifices, solely and exclusively, were for the elevation of Zaun's future.

It was his singular obsession: the evolution of the present into an age of transcendence, and the eradication of the past into obscurity.

Viktor hated the past. A past that’d left him broken, disfigured, discarded: an imperfect specimen, unworthy of survival.

The same past, which had yet forged him.

And Jinx, his muse and mirror, who'd been reborn in its bloodshed.

"Jinx," Viktor repeated. "Wake up."

His hand squeezed hers, then let go. A moment later, a metal cup was pressed into her grasp.

The warmth radiated; Jinx's flesh drank it up. The coffee gave off its curls of aromatic steam: a nutty blend of chicory root, black chocolate liqueur, and the sweet whiff of anise.

Diluted, as always, with sweetmilk.

Viktor, his own cup balanced precariously between two fingertips, reclined with an easy elegance in the grass. His staff lay within arm's reach: the undying habit of a boy whose mind is always five steps ahead, but whose body is forever falling behind. Everywhere, leather-bound books were scattered, some facedown with cracked spines, others bristling with raven's feathers that doubled as bookmarks. An inkwell glittered, half-empty, on a stack of maps scribbled with notes.

In this garden, Vitya was ever-studying, ever-searching. Never satisfied with the knowledge already in hand, and the miracles already in motion.

Something he and Jinx shared in common.

Reclining on elbow, Viktor sipped from his cup with the other hand. Then he plucked a notebook from the pile, stirred through its pages with a fingertip, and resumed writing with his cockatrice quill: a rapid series of symbols that, unfurling, imprinted themselves in a secret pocket of Jinx's brain, and the darkest recesses of her heart.

Destiny: charted beyond the stars.

Jinx sat up, knees tucked against her chest, and drank from her cup. The flavor was just as it should be: bitter chased by sweet, complexity balanced by simplicity.

Viktor's handwork: the paradox distilled into metaphor.

Just like the garden, where every blade of grass grew exactly the same height, and every flower, in its arrangement, was a repetition into infinity.

Sipping, Jinx's eyes flicked from bloom to bloom. Then, she noticed:

A single blossom out of place.

A lone iris, curling its way from between the tree's roots. It was sly as an intruder, bright as a fallen star.

The same hue as Powder's wishful blue eyes.

Jinx's lips curled. Tentatively, she reached out. Her fingers traced the blossoming petals. They were silky, smooth. Almost too flawless to be real.

"Is this place," she whispered, "alive?"

It was only half-joking. During each visit, she could never escape the sense that the garden—multiform, deviant—was suffused with a spiritual awareness sister to sentience. And the tree, gathering them both under its protective penumbra, was rooted right to the crux of Zaun's stony heart.

"Not exactly," Viktor replied, without looking up from his notes. "Not by our reckoning. More a kind of... meta-life."

"Meta-life?"

Viktor, dipping the quill in its inkwell, shrugged.

"This tree is but a reflection—an iteration—of something larger-than-life. Something of a piece with the city's vital flow. A conduit of sorts."

"Like, what? A portal?"

"Perhaps," he said, and absently rested a palm on his leg, the site of his first augments. "Or perhaps a lens. Something which reflects, refracts, magnifies. An imperfect metaphor."

"Serpent's tongue. Apple's flesh. Devil's promise."

"Precisely. A system of shorthand within which meaning can be imparted, and context given."

Jinx's eyes lingered on the flower: a star's winking light, buried under layers of soil.

"What's the point, though?" she wondered. "I mean, yeah, I get it: a symbol's powerful. But if you're trying to forget the past—"

"Forgetting is not the same as erasing," Viktor corrected, patiently. "And what good is a symbol, Jinx, if no one knows what it stands for?"

Double-edged question and double-pronged answer: classic Viktor.

Sighing, Jinx returned to her cup. The coffee, cooled, had lost its bite. She drained it anyway, then let the cup rest in her lap. Her eyes, half-lidded, took in her companion.

He was still garbed for his duties: a mauve linen robe with a high collar, its sleeves rolled up, the hem draping past his knees. It was a garment, once, meant to conceal. Now, it served a purpose quite the opposite. Its folds bared the armature that held Viktor together: once emaciated, now elegantly streamlined beneath a segmented exoskeleton of synth-plates. His bad leg, encased in gleaming obsidian augments, now held the flexile precision of muscle, and the springing strength of a steel cable.

The fusion was seamless: the stuff of futuristic fairytale. When he moved, it was with an almost regal glide. As if, somewhere in the gaunt structure of Viktor's frame, there was an ancient drop of royalty, finally emerging from its hardscrabble shell in a blend of princely asceticism and common-born resilience.

Under the tree's canopy, Viktor's pallor was offset by his deep-hued robes. The effect wasn't peaky so much as pearlescent. His untidy curls tumbled freshly-glossed along his shoulders: the barest delineations of a beard teased the contours of his jawline. The sum total was neither masculine nor feminine. Only androgynous; ethereal.

Transcendent as stardust.

The rim's of Jinx's eyes burned. Why was it that even at their closest, Viktor seemed as if he was dissolving into astral orbit, a beautiful moon drifting farther from reach?

And why did Jinx feel herself hurtling on an opposing trajectory: crashing to earth with fatal velocity?

The wind, still unseen, sawed gently through the tree's branches. Its blossoms whispered: the susurration of silk sheets, or a lover's sigh. Jinx found it fitting that, though the Cathedral of Progress was, technically, the building's newly-christened designation, ordinary Fissurefolk referred to it, unofficially, by a different epithet.

The Resurrection Root. The Everbloom. The Glass Garden.

And the most popular—

Der Wunschbaum.

Ur-Nox for Wishing Tree.

Except Ur-Nox was a double-edged sword. It was the language of the ancients; Mages and Guardians who'd lived in the time before Zaun had ever been. Their language, therefore, was the language of enchantment: one half lofty, the other half sinister. Wish, for instance, was rooted in the word Wunschet: to want. To desire beyond the bounds of reality.

But it was also rooted in Wählen: to choose.

A wish could be a heart's deepest desire unlocked. Or it could be a will to power: to take what you want, no matter the cost.

And me? Jinx wondered. What do I want?

And what will I give to seize it—or throw it away?

At her silence, Viktor stopped scribbling. His eyes, deep-gold, met hers.

"All right, Jinx?"

"Y-Yeah."

"You should wake up."

"Don't wanna."

"No?" Scritch-scritch went the pen, runes blossoming in its wake. Distantly, Jinx heard the acolytes singing, a ghostly engine of harmony. And—could it be?—Sparky's yips, cutting through the choir: a dissonant counterpoint. The greedy mutt, somewhere, was begging for treats. "If you do not wake, how will your Name Day be celebrated?"

"Multitasking's a thing. I've always been a pro."

"You are terrible at multitasking."

"Am not!"

"You fell asleep during the surgery."

"You told me not to interrupt. So I closed my eyes. But I was listening. I always listen."

"You were drooling." And, closing the notebook with the coordinates plotted inside, he set it down. In a single graceful movement, he'd shifted closer. Close enough to touch his thumb against the corner of her lips, where a grin had stolen in. Viktor's own lips, palely-parted, were a few inches away. "You look like a child when you sleep. Peaceful. It is... rare."

"I was havin' a sweet dream."

"Oh? Tell me."

"A night full of stars. Wishes a-popping like fishes. And a beautiful boy." Her voice, at half-octave, came breathless. Always, his proximity did that to her: an unravelling of everything she held dear about herself. Like deja vu—except more desolate. Dying, when you longed to be reborn. "Except he won't wish me a Happy Name Day. He won't even gimme a kiss."

At that, Viktor smiled: a slow, secret curl that was yet the saddest expression in the world.

"Perhaps," he murmured, "he is a fool."

"Yeah?"

"And a coward." The thumb, tracing the full jut of her bottom-lip, was cool as snowfall, and as chaste. "Because he knows, deep in his heart, that you are still a child. The child he sees when you sleep. And because, despite whatever tradition or legality declares, you are not yet a woman. Certainly, not the woman who, once she comes into herself, will outrace him, and his grand designs, and fly off on wings of stardust."

"You talkin' about Silco?" Jinx quipped. "'Cause, no offense, but he's no competition. I can outrun that fossil anytime."

The levity fell flat. Viktor's golden eyes, augmented to their depths, lost their imperceptible luster. A moment later, his hand retreated, as if it'd never been.

"I know," he said, "that this is only an interlude."

"You think so?" Jinx, impulsively, caught the hem of his sleeve. "Pretty harsh frame to put 'round forever."

"Forever means little in a cosmos of infinite permutations."

"Not so long as we're still us, right?"

"A conundrum in itself." He didn't withdraw, exactly. Only laid his fingertips over hers, knotted into his sleeve. "Are our mirrored selves—in the physical, in the quantum—so very different at their crux? Is one less worthy, less agentic, than the other? Or are they simply two sides of the same coin, flipped endlessly, until the universe collapses on itself."

"Yikes. Talk about buzzkill."

"I am not a man for platitudes, Jinx." The smile, sadder, stayed on the surface. "Not will I feed you falsehoods, in hopes that the future may hold more than the present."

"So you say."

"So I mean." And, surprising her, he caught her hand in both his own: a tender clasp. "We've pledged our spirits as one. We've plotted our course. Escape velocity is inevitable. But the path ahead will not be easy. Not for either of us. If anything, it will be harder, given what we must renounce to see the destination through. And I—I cannot be sure—"

A crack in his faultless equilibrium. In turn, Jinx felt her own fragile serenity evaporate.

"Sure of what, Viktor?" she said, with quiet ferocity. "That I'll change my mind halfway? Chicken out before the starting gun goes off? Let Silco dictate my choices, like I've always done?"

"No, Jinx, no."

He shook his head; the curls danced, a ribboning cascade of cornsilk. There were silver streaks beginning to thread at the temples. Thirty-three, and a full-grown man where Ekko was still shedding the last vestiges of boyhood. But moments like this, it struck Jinx that Viktor was, at his core, even younger than Ekko. Two orphans prematurely thrust into roles before their time: the savior leading his flock to the promised land, and the savant saving souls that the world would sooner crush underfoot.

But both, in their hearts, still children. Still seeing Jinx, and what she'd become. But never, ever seeing her for who she was: the girl, not the legend.

The woman, not the jinx.

"Never that, Jinx," Viktor said. "Never would I think so little of you."

"...But?"

"It's been difficult, these past months, for us to speak frankly."

"Vitya," Jinx said, a touch exasperated. "We're speaking now. Aren't we?"

"We are." A squeeze, gentle, on her fingers. "At risk on both ends. But I have never once doubted your commitment. Your passion far exceeds mine; far exceeds whatever designs I may conjure. The world will be a better place, with you striving to make it so. My only fear is that, if you choose this path, yours will be the lonelier one."

"Lonely, how?" The ghost-prick of tears. "We're bonded, aren't we? Even if it's not what either of us planned—"

"A bond that can never be consummated. Never, in any sense, bear fruit." His grip tightened; yet the timbre of his voice held no rebuke. Only truth. "I am a creature born of disappointment, Jinx. Faulty in form and function. Unfit for any world except the one I will create, and even that shall be a long time coming. Yet, in the Void, you gave me a glimpse of paradise, and it was... indescribable. All I will ever want."

"And?" Her lip quivered, but held. A child, he'd called her, and yet her voice was steel. "Wasn't it enough? Wasn't I—?"

"You? Not enough? My dearest." Even though his sigh was bittersweet, a mote of passion shot through: the same passion that'd flowed, so effortlessly, between them in the otherworld. The same passion that now translated itself—sublimated and yet quartered—into the gentle dexterity of his hands on a circuitboard fused to a sobbing boy's flesh, and the consoling caress afterward as the boy's mother, sobbing too, laid a kiss of gratitude upon her savior's robe. "You are the only star in a universe without light. But because you are, you are far too much. For anyone's good. Least of all mine."

The tears, against Jinx's will, spilled free.

"So I was a mistake?"

"Yes. And no"

"How?"

"You were a miracle," Viktor said, and his smile, in its sadness, was radiant. "And a miracle is a gift bestowed by Fate. Without factors such as deservingness, or suitability, or even equity, thrown into the equation. A miracle, simply, is. As you, Jinx, always are. I know you've made your peace with our bond. You've acclimated yourself to it, the same as I have. But if we commit—truly commit—to the path ahead, we must renounce the rest, in every way. And Jinx... I cannot, in good faith, ask that of you. Not when I know what you stand to lose. Not when I know all the ways you need, and deserve, to be loved."

The tears kept falling. Jinx made no effort to stop them. The garden, with its Wishing Tree, was a time-out from pretense. Not sanctuary, but as close as Zaun's chaotic confines allowed. The other one—the Wishing Wagon, in civilization's shadowed cul-de-sac—was her true refuge. But that was a different her, with a different future.

A girl who'd yet to realize her greatest wish. A woman who, at the crossroad's fork, could take a chance.

She'd never told Viktor about the Wishing Wagon. Same way she'd never told Ekko about the Wishing Tree. Both were secrets within secrets: mirrored halves of a fractured whole.

And Jinx, at the liminal space in between, wondering: What's it mean?

What did it mean that one man had her soul at knifepoint, but another was holding her heart hostage? What did it say that she and Viktor fit together just right, but she and Ekko were built from perfectly mismatched puzzle pieces? What did it matter if she needed them both, but in ways so opposite they might as well be a different language?

How could she make the ends meet?

Especially when her life—her death—still hung on Silco's strings?

And her past—her future—still hinged on Vi's?

"Maybe," she said, and caught her lip in her teeth, "that's the point."

"Oh?"

"Maybe... the glimpse of paradise was all it was. A glimpse. The rest's about struggling to make it happen. Because it's the only way. Because choice is nothing but fate with a kick."

"Jinx, no."

"Why not? It makes sense. In a twisted sorta way." Her eyes, smarting-wet, blinked hard. "Fate's not a pretty delivery-gal on the front step with a package. He's a blind old pirate, throwing darts at a map and laughing as they land. Doesn't matter who gets skewered. Once that bullseye hits, it hits. And you're on the hook. No takebacks." Her other hand, lifting, aligned itself with Viktor's jaw: stubble yielding velvety beneath her palm. "We were always gonna be on the hook, Vik. At least, in the Void, I saw where we’re headed. What, in the end, we could become. And sure, the path's not a fairytale. But if we don't take it, the rest'll be fucked. And blind old fate'll be laughing his ass off, watching us sink under the waves."

"Perhaps," Viktor said, and leaned into her touch. But the smile, always, stayed sad. "But Jinx?"

"Yeah?"

"Fate is not the same as choice." Turning his head, he laid a kiss, pure as a snowflake, in the heart of her palm. "Even the cosmos, no matter its dictates, allows breathing-room for free will. I have mine, and I know what they will cost. Now, and in every incarnation. But you, Jinx: you are still so young. Your wishes, the ones that matter, have yet to be made. And once they are lost, you will not have the chance to reclaim them."

"Because I'm a child, right?" The anger, a flashfire that filled her to the seams, in this garden only left her aching. "Too dumb to know what I want. Too naive to make the tough call."

All at once, Viktor closed the gap.

Silently, he swept Jinx into an embrace: a cradle and a coffin holding both living and dead in sacred embrace. His arms made a crossbones at her shoulderblades; his breath stirred the top of her scalp. They were both clothed, but Jinx felt her heartbeat resonating through their ribcages, keeping time with the rhythmic dirge of the Cathedral's chants, and the Old Hungry's distant chimes

Reality and dream: melded into one.

Somewhere, Sparky was pawing at Jinx's slumbering shape in search of belly-rubs. Behind her eyelids, neon bled through. She heard fireworks; smelled engine-grease. Felt an odd pressure on her spine that had nothing to do with Viktor's cool fingertips tracing its curve, and everything to do with being bound, on a visceral level, beyond this communion they both shared.

"Fate," Viktor breathed, and his lips, against her temple, imparted prophecy, "will always come due. But choice? That, my dearest Jinx, is an arrow aimed straight for the heart. And to deny it: that is an error far graver than anything science, or the cosmos, could dole out." He kissed her forehead: the sweetest absolution. "Your choice must be yours. Do not allow a hand, no matter how divine, to dictate it."

Jinx, closing her eyes, lay her cheek to his chest.

"Not even yours?" she whispered, as the tears stopped falling.

"My hand, like my heart, will belong with you, Jinx. Even if you choose another path."

"Mirror, mirror on the wall."

"In every iteration," Viktor murmured, a tender withdrawal, "of this cosmic joke. An imperfect metaphor. Do you understand?"

"I do," Jinx lied, and lifted her face. "Kiss me?"

"This is not a space for secrets, Jinx."

"Then it's a perfect place, ain't it? 'Cause I won't have any left, after tonight."

"You will," Viktor said, and his thumbs smoothed the fading tear-tracks from her cheeks. "You do. We all carry secrets within ourselves. But to hide one, here, is to desecrate the very vow we must keep. And to deny our truth—any of our truths—is the greatest dishonor to the other. Do you understand?"

Foreboding rippled over Jinx's skin. The garden, the tree, the chants: all the beautiful trappings of ephemera, slipping like sand through the hourglass.

"Viktor." She caught his hand in hers, holding it fast. "Please."

"I'll see you tonight, Jinx."

"Don't—don't go—"

"Tonight. When you make your choice. Whatever that choice may be."

"But—"

"Wake up now."

The hourglass, upended. The Cathedral, the garden, the embrace, dissolving. All the dreamscape and its dazzling details, blotting out.

"Viktor!" Jinx cried. "Viktor!"

"Happy Name Day, Jinx," he said, and the ghost-imprint of his kiss died before it met her mouth. "I will kiss you, truly, tonight."

The ceiling spun above: a galaxy's worth of stars, winking out. Her hands, searching, found nothing.

Nothing but the blue iris, unfurling at the tip of a finger.

And Viktor's voice, deep as midnight.

"Make a wish."

The last winking star: her own.

[vestaignis]

Наутилус (лат. Nautilus) — род головоногих моллюсков, которых относят к «живым ископаемым». Самый распространенный вид — Nautilus pompilius. Наутилусы относятся к единственному современному роду подкласса наутилоидей. Первые представители наутилоидей появились в кембрии, а его развитие пришлось на палеозой. Наутилиды почти вымерли на границе триаса и юры, но все же дожили до наших дней, в отличие от своих родственников аммонитов. Некоторые виды древних наутилусов достигали размера в 3,5 м. Представители самого крупного вида современных наутилусов достигают максимального размера в 25 см.

Спиральный «домик» моллюска состоит из 38 камер и «построен» по сложному математическому принципу (закон логарифмической прогрессии). Все камеры, кроме последней и самой большой, где размещается тело наутилуса с девятью десятками «ног», соединяются через отверстия между собой сифоном.  Раковина наутилуса двухслойная: верхний (наружный) слой – фарфоровидный – действительно напоминает хрупкий фарфор, а внутренний, с перламутровым блеском – перламутровый. «Домик» наутилуса растет вместе с хозяином, который перемещается по мере роста раковины в камеру попросторней. Пустое жилище моллюска после его гибели можно встретить далеко от его места обитания – после гибели «хозяина» их раковины остаются на плаву и перемещаются по воле волн, ветров и течений.

Интересно, что двигается наутилус «в слепую», задом наперед, не видя и не представляя препятствий, которые могут оказаться на его пути.И еще одно удивительное качество этих древних обитателей Земли – у них потрясающая регенерация: буквально через несколько часов раны на их телах затягиваются, а в случае потери щупальца быстро отрастает новое.

Nautilus is a genus of cephalopods, which are classified as "living fossils". The most common species is Nautilus pompilius. Nautilus belong to the only modern genus of the Nautiloid subclass. The first representatives of the Nautiloids appeared in the Cambrian, and its development took place during the Paleozoic. The Nautilids almost died out on the border of the Triassic and Jurassic, but still survived to the present day, unlike their Ammonite relatives. Some species of ancient Nautilus reached a size of 3.5 m. Representatives of the largest species of modern nautilus reach a maximum size of 25 cm.

The spiral "house" of the mollusk consists of 38 chambers and is "built" according to a complex mathematical principle (the law of logarithmic progression). All chambers, except the last and largest, where the nautilus body with nine dozen "legs" is located, are connected through holes with a siphon. The nautilus shell is two–layered: the upper (outer) layer – porcelain–like - really resembles fragile porcelain, and the inner, with a mother-of-pearl luster - mother-of-pearl. The nautilus's "house" grows with its owner, who moves as the shell grows into a larger chamber. The empty dwelling of a mollusk after its death can be found far from its habitat – after the death of the "owner", their shells remain afloat and move at the will of waves, winds and currents.

Interestingly, the Nautilus moves "blindly", backwards, without seeing or imagining the obstacles that may be in its path.And another amazing quality of these ancient inhabitants of the Earth is that they have amazing regeneration: in just a few hours, the wounds on their bodies heal, and in case of loss of tentacles, a new one grows quickly.

Источник:://t.me/+t0G9OYaBjn9kNTBi, /sevaquarium.ru/nautilus/, /habr.com/ru/articles/369547/, //wallpapers.com/nautilus, poknok.art/6613-nautilus-molljusk.html, //wildfauna.ru/nautilus-pompilius, /www.artfile.ru/i.php?i=536090.

[canmom]

Music Theory notes (for science bitches) part 3: what if. there were more notes. what if they were friends.

Hello again, welcome back to this series where I try and teach myself music from first principles! I've been making lots of progress on zhonghu in the meantime, but a lot of it is mechanical/technical stuff about like... how you hold the instrument, recognising pitches

In the first part I broke down the basic ideas of tonal music and ways you might go about tuning it in the 12-tone system, particularly its 'equal temperament' variant [12TET]. The second part was a brief survey of the scales and tuning systems used in a selection of music systems around the world, from klezmer to gamelan - many of them compatible with 12TET, but not all.

So, as we said in the first article, a scale might be your 'palette' - the set of notes you use to build music. But a palette is not a picture. And hell, in painting, colour implies structure: relationships of value, saturation, hue, texture and so on which create contrast and therefore meaning.

So let's start trying to understand how notes can sit side by side and create meaning - sequentially in time, or simultaneously as chords! But there are still many foundations to lay. Still, I have a go at composing something at the end of this post! Something very basic, but something.

Anatomy of a chord

I discussed this very briefly in the first post, but a chord is when you play two or more notes at the same time. A lot of types of tonal musical will create a progression of chords over the course of a song, either on a single instrument or by harmonising multiple instruments in an ensemble. Since any or all of the individual notes in a chord can change, there's an enormous variety of possible ways to go from one chord to another.

But we're getting ahead of ourselves. First of all I wanna take a look at what a chord actually is. Look, pretty picture! Read on to see what it means ;)

So here is a C Minor chord, consisting of C, D# and G, played by a simulated string quartet:

(In this post there's gonna be sound clips. These are generated using Ableton, but nothing I talk about should be specific to any one DAW [Digital Audio Workstation]. Ardour appears to be the most popular open source DAW, though I've not used it. Audacity is an excellent open source audio editor.)

Above, I've plotted the frequency spectrum of this chord (the Fourier transform) calculated by Audacity. The volume is in decibels, which is a logarithmic scale of energy in a wave. So this is essentially a linear-log plot.

OK, hard to tell what's going on in there right? The left three tall spikes are the fundamental frequencies of C4 (262Hz), D♯4 (310Hz), and G4 (393Hz). Then, we have a series of overtones of each note, layered on top of each other. It's obviously hard to tell which overtone 'belongs to' which note. Some of the voices may in fact share overtones! But we can look at the spectra of the indivudal notes to compare. Here's the C4 on its own. (Oddly, Ableton considered this a C3, not a C4. as far as I can tell the usual convention is that C4 is 261.626Hz, so I think C4 is 'correct'.)

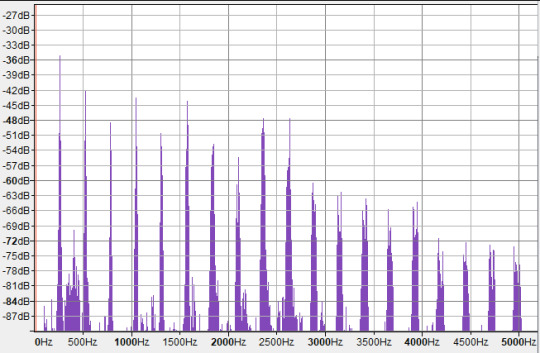
Here, the strongest peaks are all at integer multiples of the fundamental frequency, so they look evenly spaced in linear frequency-space. These are not all C. The first overtone is an octave above (C5), then we have three times the frequency of C4 - which means it's 1.5 times the frequency of C5, i.e. a perfect fifth above it! This makes it a G. So our first two overtones are in fact the octave and the fifth (plus an octave). Then we get another C (C6), then in the next octave we have frequencies pretty close to E6, G6 and A♯6 - respectively, intervals of a major third, a perfect fifth, and minor 7th relative to the root (modulo octaves).

However, there are also some weaker peaks. Notably, in between the first and second octave is a cluster of peaks around 397-404Hz, which is close to G4 - another perfect fifth! However, it's much much weaker than the overtones we discussed previously.

The extra frequencies and phase relationships give the timbre of the note, its particular sound - in this case you could say the sense of 'softness' in the sound compared to, for example, a sine wave, or a perfect triangle wave which would also have harmonics at all integer frequencies.

Perhaps in seeing all these overtones, we can get an intuitive impression of why chords sound 'consonant'. If the frequencies of a given note are already present in the overtones, they will reinforce each other, and (in extremely vague and unscientific terms) the brain gets really tickled by things happening in sync. However, it's not nearly that simple. Even in this case, we can see that frequencies do not have to be present in the overtone spectrum to create a pleasing sense of consonance.

Incidentally, this may help explain why we consider two notes whose frequencies differ by a factor of 2 to be 'equivalent'. The lower note contains all of the frequencies of the higher note as overtones, plus a bunch of extra 'inbetween' frequencies. e.g. if I have a note with fundamental frequency f, and a note with frequency 2f, then f's overtones are 2f, 3f, 4f, 5f, 6f... while 2f's overtones are 2f, 4f, 6f, 8f. There's so much overlap! So if I play a C, you're also hearing a little bit of the next C up from that, the G above that, the C above that and so on.

For comparison, if we have a note with frequency 3f, i.e. going up by a perfect fifth from the second note, the frequencies we get are 3f, 6f, 9f, 12f. Still fully contained in the overtones of the first note, but not quite as many hits.

Of course, the difference between each of these spectra is the amplitudes. The spectrum of the lower octave may contain the frequencies of the higher octave, but much quieter than when we play that note, and falling off in a different way.

(Note that a difference of ten decibels is very large: it's a logarithmic scale, so 10 decibels means 10 times the energy. A straight line in this linear-log plot indicates a power-law relationship between frequency and energy, similar to the inverse-square relationship of a triangle wave, where the first overtone has a quarter of the power, the second has a ninth of the power, and so on.)

So, here is the frequency spectrum of the single C note overlaid onto the spectrum of the C minor chord:

Some of the overtones of C line up with the overtones of the other notes (the D# and G), but a great many do not. Each note is contributing a bunch of new overtones to the pile. Still, because all these frequencies relate back to the base note, they feel 'related' - we are drawn to interpret the sounds together as a group rather than individually.

Our ears and aural system respond to these frequencies at a speed faster than thought. With a little effort, you can pick out individual voices in a layered composition - but we don't usually pick up on individual overtones, rather the texture created by all of them together.

I'm not gonna take the Fourier analysis much further, but I wanted to have a look at what happens when you crack open a chord and poke around inside.

However...

In Western music theory terms, we don't really think about all these different frequency spikes, just the fundamental notes. (The rest provides timbre). We give chords names based on the notes of the voices that comprise them. Chord notation can get... quite complicated; there are also multiple ways to write a given chord, so you have a degree of choice, especially once you factor in octave equivalence! Here's a rapid-fire video breakdown:

Because you have all these different notes interacting with each other, you further get multiple interactions of consonance and dissonance happening simultaneously. This means there's a huge amount of nuance. To repeat my rough working model, we can speak of chords being 'stable' (meaning they contain mostly 'consonant' relations like fifths and thirds) or 'unstable' (featuring 'dissonant' relations like semitones or tritones), with the latter setting up 'tension' and the former resolving it.

However, that's so far from being useful. To get a bit closer to composing music, it would likely help to go a bit deeper, build up more foundations and so on.

In this post and subsequent ones, I'm going to be taking things a little slower, trying to understand a bit more explicitly how chords are deployed.

An apology to Western music notation

In my first post in this series, I was a bit dismissive of 'goofy' Western music notation. What I was missing is that the purpose of Western music notation is not to clearly show the mathematical relationships between notes (something that's useful for learning!)... but to act as a reference to use while performing music. So it's optimising for two things: compactness, and legibility of musical constructs like phrasing. Pedagogy is secondary.

Youtuber Tantacrul, lead developer of the MuseScore software, recently made a video running over a brief history of music notation and various proposed alternative notation schemes - some reasonable, others very goofy. Having seen his arguments, he makes a pretty good case for why the current notation system is actually a reasonable compromise... for representing tonal music on the 12TET system, which is what it's designed for.

So with that in mind, let me try and give a better explanation of the why of Western music notation.

In contrast to 'piano roll' style notation where you represent every possible note in an absolute way, here each line of the stave (staff if you're American) represents a scale degree of a diatonic scale. The key signature locates you in a particular scale, and all the notes that aren't on that scale are omitted for compactness (since space is at an absolute premium when you have to turn pages during a performance!). If you're doing something funky and including a note outside the scale, well that's a special case and you give it a special-case symbol.

It's a similar principle to file compression: if things are as-expected, you omit them. If things are surprising, you have to put something there.

However, unlike the 简谱 jiǎnpǔ system which I've been learning in my erhu lessons, it's not a free-floating system which can attach to any scale. Instead, with a given clef, each line and space of the stave has one of three possible notes it could represent. This works, because - as we'll discuss momentarily - the diatonic scales can all be related to each other by shifting certain scale degrees up or down in semitones. So by indicating which scale degrees need to be shifted, you can lock in to any diatonic scale. Naisuu.

This approach, which lightly links positions to specific notes, keeps things reasonably simple for performers to remember. In theory, the system of key signatures helps keep things organised, without requiring significant thought while performing.

That is why have to arbitrarily pick a certain scale to be the 'default'; in this case, history has chosen C major/A minor. From that point, we can construct the rest of the diatonic scales as key signatures using a cute mathematical construct called the 'circle of fifths'.

How key signatures work (that damn circle)

So, let's say you have a diatonic major scale. In piano roll style notation, this looks like (taking C as our base note)...

And on the big sheet of scales, like this:

Now, let's write another diatonic major scale, a fifth up from the first. This is called transposition. For example, we could transpose from C major to G major.

Thanks to octave equivalency, we can wrap these notes back into the same octave as our original scale. (In other words, we've added 7 semitones to every note in our original scale, and then taken each one modulo 12 semitones.) Here, I duplicate the pattern down an octave.

Now, if we look at what notes we have in both scales, over the range of the original major scale.

Well, they're almost exactly the same... but the fourth note (scale degree) is shifted up by one semitone.

In fact, we've seen this set of notes before - it is after all nothing more than a cyclic permutation of the major scale. We've landed on the 'Lydian mode', one of the seven 'modes' of the diatonic major scale we discussed in previous posts. We've just found out that the Lydian mode has the same notes as a major scale starting a fifth higher. In general, whether we think of it as a 'mode' or as a 'different major scale' is a matter of where we start (the base note). I'm going to have more to say about modes in a little bit.

With this trick in mind, we produce a series of major scales starting a fifth higher each time. It just so happens that, since the fifth is 7 semitones, which is coprime with the 12 semitones of 12TET, this procedure will lead us through every single possible starting note in 12TET (up to octave equivalency).

So, each time we go up a fifth, we add a sharp on the fourth degree of the previous scale. This means that every single major scale in 12TET can be identified by a unique set of sharps. Once you have gone up 12 fifths, you end up with the original set of notes.

This leads us to a cute diagram called the "circle of fifths".

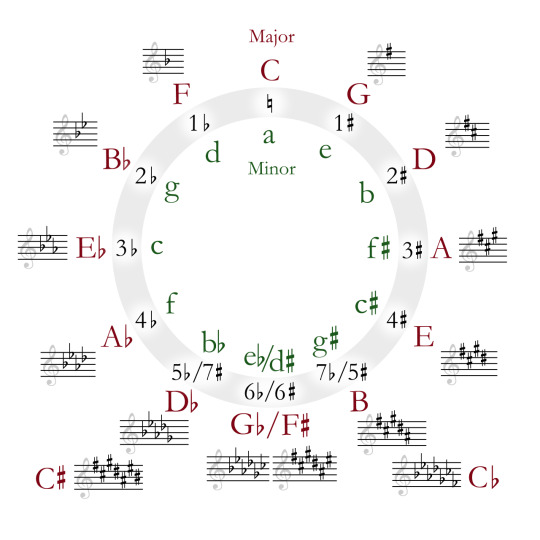
Because going up a fifth is octave-equivalent to going down a fourth, we can also look back one step on the circle to find out which note needs to be made sharper. So, from C major to G major, we have to sharpen F - the previous note on the circle from C. From G major to D major, we have to sharpen C. From D major to A major, we have to sharpen G. And so on.

By convention, when we write a key signature to define the particular scale we're using, we write the sharps out in circle-of-fifths order like this. The point of this is to make it easy to tell at a glance what scale you're in... assuming you know the scales already, anyway. This is another place where the aim of the notation scheme is for a compact representation for performers rather than something that makes the logical structure evident to beginners.

Also by convention, key signatures don't include the other octaves of each note. So if F is sharp in your key signature, then every F is sharp, not just the one we've written on the stave.

This makes it less noisy, but it does mean you don't have a convenient visual reminder that the other Fs are also sharp. We could imagine an alternative approach where we include the sharps for every visible note, e.g. if we duplicate every sharp down an octave for C♯ major...

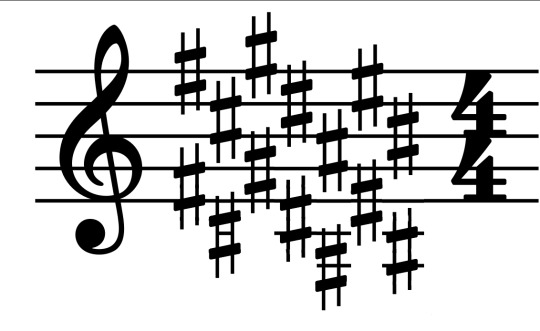
...but maybe it's evident why this would probably be more confusing than helpful!

So, our procedure returns the major scales in order of increasing sharps. Eventually you have added seven sharps, meaning every scale degree of the original starting scale (in this case, C Major) is sharpened.

What would it mean to keep going past this point? Let's hop in after F♯ Major, at the bottom of the Circle of Fifths; next you would go to C♯ Major by sharpening B. So far so good. At this point we have sharps everywhere, so the notes in your scale go... C♯ D♯ E♯ F♯ G♯ A♯ B♯ C♯ ...except that E♯ is the same as F, and B♯ is the same as C, so we could write that as C♯ D♯ F F♯ G♯ A♯ C C♯

But then to get to 'G♯ Major', you would need to sharpen... F♯? That's not on the original C-major scale we started with ! You could say, well, essentially this adds up to two sharps on F, so it's like F♯♯, taking you to G. So now you have...

G♯ A♯ C C♯ D♯ F G G♯

...and the line of the stave that you would normally use for F now represents a G. You could carry on in this way, eventually landing all the way back at the original set of notes in C Major (bold showing the note that just got sharpened in each case):

D♯ F G G♯ A♯ C D D♯ A♯ C D D♯ F G A A♯ F G A A♯ C D E F C D E F G A B C

But that sounds super confusing - how would you even represent the double sharps on the key signature? It would break the convention that each line of the stave can only represent three possible notes. Luckily there's a way out. We can work backwards, going around the circle the other way and flattening notes. This will hit the exact same scales in the opposite order, but we think of their relation to the 'base' scale differently.

So, let's try starting with the major scale and going down a fifth. We could reason about this algebraically to work out that sharpening the fourth while you go up means flattening the seventh when you go down... but I can also just put another animation. I like animations.

So: you flatten the seventh scale degree in order to go down a fifth in major scales. By iterating this process, we can go back around the circle of fifths. For whatever reason, going down this way we use flats instead of sharps in the names of the scale. So instead of A♯ major we call it B♭ major. Same notes in the same order, but we think of it as down a rung from F major.

In terms of modes, this shows that the major scale a fifth down from a given root note has the same set of notes as the "mixolydian mode" on the original root note. ...don't worry, you don't gotta memorise this, there is not a test! Rather, the point of mentioning these modes is to underline that whether you're in a major key, minor key, or one of the various other modes is all relative to the note you start on. We'll see in a moment a way to think about modes other than 'cyclic permutation'.

Let's try the same trick on the minor key.

Looks like this time, to go up we need to sharpen the sixth degree, and to go down we need to flatten the second degree. As algebra demands, this gives us the exact same sequence of sharps and flats as the sequence of major scales we derived above. After all, every major scale has a 'relative minor' which can be achieved by cyclically permuting its notes.

Going up a fifth shares the same notes with the 'Dorian mode' of the original base note, and going down a fifth shares the same notes with the 'Phrygian mode'.

Here's a summary of movement around the circle of fifths. The black background indicates the root note of the new scale.

Another angle on modes

In my first two articles, I discussed the modes of the diatonic scale. Leaping straight for the mathematically simplest definition (hi Kolmogorov), I defined the seven 'church modes' as simply being cyclic permutations of the intervals of the major scale. Which they are... but I'm told that's not really how musicians think of them.

Let's grab the chart of modes again. (Here's the link to the spreadsheet).

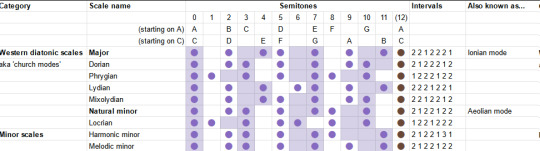
We can get to these modes by cyclically permuting the others, but we can also get to them by making a small adjustment of one to a few particular scale degrees. When you listen to a piece of music, you're not really doing cyclic permutations - you're building up a feeling for the pattern of notes based on your lifelong experience of hearing music that's composed in this system. So the modes will feel something like 'major until, owo what's this, the seventh is not where I thought it would be'.

Since the majority of music is composed using major and minor modes, it's useful therefore to look at the 'deltas' relative to these particular modes.

To begin with, what's the difference between major and minor? To go from major to natural minor, you shift the third, sixth and seventh scale degrees down by one semitone.

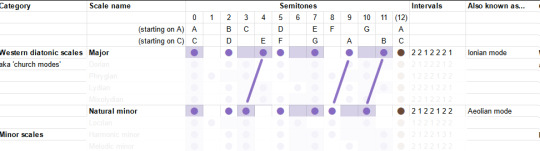
So those are our two starting points. For the others, I'm going to be consulting the most reliable music theory source (some guy on youtube) to give suggestions of the emotional connotations these can bring. The Greek names are not important, but I am trying to build a toolbox of elements here, so we can try our hand at composition. So!

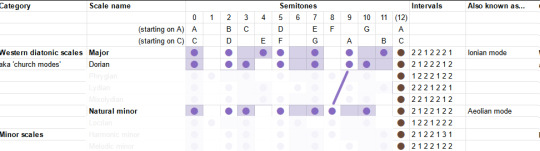
The "Dorian mode" is like the natural minor, but the sixth is back up a semitone. It's described as a versatile mode which can be mysterious, heroic or playful. I guess that kinda makes sense, it's like in between the major and minor?

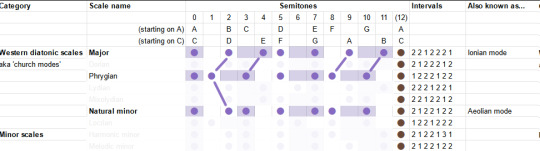
The "Phrygian mode" is natural minor but you also lower the 2nd - basically put everything as low as you can go within the diatonic modes. It is described as bestowing an ominous, threatening feeling.

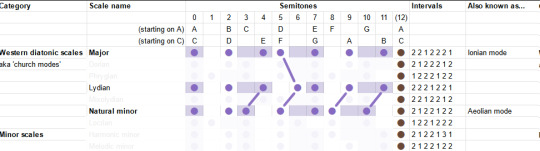
The "Lydian mode" is like the major scale, but you shift the fourth up a semitone, landing on the infamous tritone. It is described as... uh well actually the guy doesn't really give a nice soundbitey description of what this mode sounds like, besides 'the brighest' of the seven, this video's kinda more generally about composition, whatever. But generally it's pretty big and upbeat I think.

The "Mixolydian" mode is the major, but with the seventh down a semitone. So it's like... a teeny little bit minor. It's described as goofy and lighthearted.

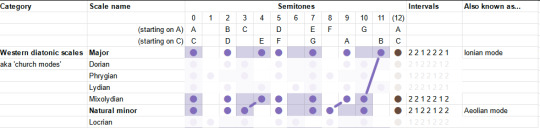
We've already covered the Aeolian/Natural Minor, so that leaves only the "Locrian". This one's kinda the opposite of the Lydian: just about everything in the major scale is flattened a bit. Even from the minor it flattens two things, and gives you lots of dissonance. This one is described as stereotypically spooky, but not necessarily. "One of the least useful", oof.

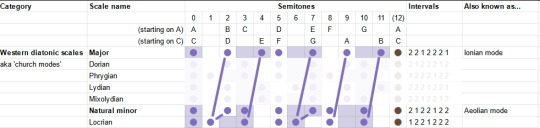
Having run along the catalogue, we may notice something interesting. In each case, we always either only sharpen notes, or only flatten notes relative to the major and minor scales. All those little lines are parallel.

Indeed, it turns out that each scale degree has one of two positions it can occupy. We can sort the diatonic modes according to whether those degrees are in the 'sharp' or 'flat' position.

This is I believe the 'brightness' mentioned above, and I suppose it's sort of like 'majorness'. So perhaps we can think of modes as sliding gradually from the ultra-minor to the infra-major? I need to experiment and find out.

What have we learned...?

Scale degrees are a big deal! The focus of all this has been looking at how different collections of notes relate to each other. We sort our notes into little sets and sequences, and we compare the sets by looking at 'equivalent' positions in some other set.

Which actually leads really naturally into the subject of chord progressions.

So, musical structure. A piece of tonal music as a whole has a "palette" which is the scale - but within that, specific sections of that piece of music will pick a smaller subset of the scale, or something related to the scale, to harmonise.

The way this goes is typically like this: you have some instruments that are playing chords, which gives the overall sort of harmonic 'context', and you have a single-voiced melody or lead line, which stands out from the rest, often with more complex rhythms. This latter part is typically what you would hum or sing if you're asked 'how a song goes'. Within that melody, the notes at any given point are chosen to harmonise with the chords being played at the same time.

The way this is often notated is to write the melody line on the stave, and to write the names of chords above the stave. This may indicate that another hand or another instrument should play those chords - or it may just be an indication for someone analysing the piece which chord is providing the notes for a given section.

So, you typically have a sequence of chords for a piece of music. This is known as a chord progression. There are various analytical tools for cracking open chord progressions, and while I can't hope to carry out a full survey, let me see if I can at least figure out my basic waypoints.

Firstly, there are the chords constructed directly from scales - the 'triad' chords, on top of which can be piled yet more bonus intervals like sevenths and ninths. Starting from a scale, and taking any given scale degree as the root note, you can construct a chord by taking every other subsequent note.

So, the major scale interval pattern goes 2 2 1 2 2 2 1. We can add these up two at a time, starting from each position, to get the chords. For each scale degree we therefore get the following intervals relative to the base note of the chord...

I. 0 4 7 - major

ii. 0 3 7 - minor

iii. 0 3 7 - minor

IV. 0 4 7 - major

V. 0 4 7 - major

vi. 0 3 7 - minor

viiᵒ. 0 3 6 - diminished

Now hold on a minute, where'd those fuckin Roman numerals come from? I mentioned this briefly in the first post, but this is Roman numeral analysis, which is used to talk about chord progressions in a scale-independent way.

Here, a capital Roman numeral represents a major triad; a lowercase Roman numeral represents a minor triad; a superscript 'o' represents a dimished triad (minor but you lower the fifth down to the tritone); a superscript '+' represents an augmented triad (major but you boost the fifth up to the major sixth).

So while regular chord notation starts with the pitch of the base note, the Roman numeral notation starts with a scale degree. This way you can recognise the 'same' chord progression in songs that are in quite different keys.

OK, let's do the same for the minor scale... 2 1 2 2 1 2 2. Again, adding them up two at a time...

i. 0 3 7 - minor

iiᵒ. 0 3 6 - diminished

III. 0 4 7 - major

iv. 0 3 7 - minor

v. 0 3 4 - minor

VI. 0 4 7 - major

VII. 0 4 7 - major

Would you look at that, it's a cyclic permutation of the major scale. Shocker.

So, both scales have three major chords, three minor chords and a diminished chord in them. The significance of each of these positions will have to be left to another day though.

What does it mean to progress?

So, you play a chord, and then you play another chord. One or more of the voices in the chord change. Repeat. That's all a chord progression is.

You can think of a chord progression as three (or more) melodies played as once. Only, there is an ambiguity here.

Let's say, idk, I threw together this series of chords, it ended up sounding like it would be something you'd hear in an old JRPG dungeon, though maybe that's just 'cos it's midi lmao...

I emphasise at this point that I have no idea what I'm doing, I'm just pushing notes around until they sound good to me. Maybe I would know how to make them sound better if I knew more music theory! But also at some point you gotta stop theorising and try writing music.

So this chord progression ended up consisting of...

Csus2 - Bm - D♯m - A♯m - Gm - Am - F♯m - Fm - D - Bm

Or, sorted into alphabetical order, I used...

Am, A♯m, Bm, Csus2, D, D♯m, Fm, F♯m, Gm

Is that too many minor chords? idk! Should all of these technically be counted as part of the 'progression' instead of transitional bits that don't count? I also dk! Maybe I'll find out soon.

I did not even try to stick to a scale on this, and accordingly I'm hitting just about every semitone at some point lmao. Since I end on a B minor chord, we might guess that the key ought to be B minor? In that case, we can consult the circle of fifths and determine that F and C would be sharp. This gives the following chords:

Bm, C♯dim, D, Em, F♯m, G, A

As an additional check, the notes in the scale:

B, C♯, D, E, F, G♯, A

Well, uh. I used. Some of those? Would it sound better if I stuck to the 'scale-derived' chords? Know the rules before you break them and all that. Well, we can try it actually. I can map each chord in the original to the corresponding chord in B minor.

This version definitely sounds 'cleaner', but it's also... less tense I feel like. The more dissonant choices in the first one made it 'spicier'. Still, it's interesting to hear the comparison! Maybe I could reintroduce the suspended chord and some other stuff and get a bit of 'best of both worlds'? But honestly I'm pretty happy with the first version. I suppose the real question would be which one would be easier to fit a lead over...

Anyway, for the sake of argument, suppose you wanted to divide this into three melodies. One way to do it would be to slice it into low, central and high parts. These would respectively go...

Since these chords mostly move around in parallel, they all have roughly the same shape. But equally you could pick out three totally different pathways through this. You could have a part that just jumps to the nearest note it can (until the end where there wasn't an obvious place to go so I decided to dive)...

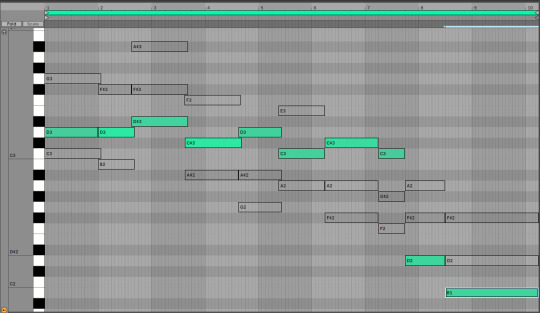
Those successive relationships between notes also exist in this track. Indeed, when two successive chords share a note, it's a whole thing (read: it gets mentioned sometimes in music theory videos). You could draw all sorts of crazy lines through the notes here if you wanted.

Nevertheless, the effects of movements between chords come in part from these relationships between successive notes. This can give the feeling of chords going 'up' or 'down', depending on which parts go up and which parts go down.

I think at this point this post is long enough that trying to get into the nitty gritty of what possible movements can exist between chords would be a bit of a step too far, and also I'm yawning a lot but I want to get the post out the door, so I let's wrap things up here. Next time: we'll continue our chord research and try and figure out how to use that Roman numeral notation. Like, taking a particular Roman numeral chord progression and see what we can build with it.

Hope this has been interesting! I'm super grateful for the warm reception the last two articles got, and while I'm getting much further from the islands of 'stuff I can speak about with confidence', fingers crossed the process of learning is also interesting...

[thedarkat]

When Salvador Dalí painted a rhinoceros (1950)

Cuando Salvador Dalí pintó un rinoceronte (1950)

(English / Español / Italiano)

 Since the 1950s, Dalí had been producing several of his works as compositions of rhinoceros horns. According to Dalí, who had always shown a keen interest in the natural sciences and mathematics, the rhinoceros horn signified divine geometry, since it "grows in a logarithmic spiral progression".

---------------------------------------------------------------------------

 Desde los años 50, Dalí vino realizando varias de sus obras como composiciones de cuernos de rinoceronte. Según Dalí, que desde siempre mostró un acusado interés por las ciencias naturales y las matemáticas, el cuerno de rinoceronte significaba la geometría divina, ya que “crece en una progresión espiral logarítmica”.

-----------------------------------------------------------------------------

 A partire dagli anni Cinquanta, Dalí realizzò diverse opere come composizioni di corni di rinoceronte. Secondo Dalí, che aveva sempre mostrato un forte interesse per le scienze naturali e la matematica, il corno di rinoceronte significava la geometria divina, poiché "cresce in una progressione logaritmica a spirale".

[rigelmejo]

Okay I've been playing with the Mandarin From Scratch blog post's ALG language acquisition equation, from a paper by Marvin Brown about ALG.

y = C(1-e^(-kx/L))

Below the cut, a bunch of me messing with the ALG equation and comparing it with Dreaming Spanish estimates to try and figure out WHAT is an accurate estimate of time it will take to learn a language with comprehensible input.

Y is understanding/fluency, which their goal is to get to 88%. I wanted to look at how many hours it would take me to reach 88%, then something over 90%, then something approaching my estimated "ceiling". Average ceilings were 95% - after which point students struggled to improve further. So I set mine as 0.95.

(Note: they say their goal for students is to reach 88% fluency/understanding, but I am not sure if that's B2, or lower, or higher. My goal is around upper intermediate/B2 so that's kind of fucking important for me to know... I want to be able to read, listen to audio, watch shows, and eventually have conversations about anything on my mind in at least a basic way - which would be B2 conversationally and possibly higher comprehension for passive skills)

C is the ceiling.

y is how much language they know (1 = native). If you have a ceiling, then y would never surpass the ceiling.

x is how many hours they have understood.

k is the acquisition constant: .0018

e is the natural logarithm base: 2.718

I plugged in a few potential amounts of hours I could study:

It looks like if I aim for 1500 hours, I'll hit 88% fluency. This seems a bit low for my goals, considering thats only 600 more hours from where I am. But it sure would be nice if that's all it took.

When I solved for x instead I got ~1448 hours.

If I aim for over 90% comprehension, then it looks like I'll hit that around 2000 hours.

If I solve for x, setting understanding y =0.90, then it would take ~1636 hours

And if I wanted to get as fluent as I possibly could? Which would be around 95%, assuming I have some ceiling like ab average learner, then 2600 hours will get me close to as much as I could hope to be fluent.

If I solve for x and set goal fluency y to 0.94, then it would take ~2530 hours.

This is significantly LESS TIME than FSI estimates - which would be 3520 hours of some form of Chinese study. I do have 1500 hours of prior study if we don't count comprehensible input. So 1500 hours prior study, plus the comprehemsible hours I currently have 913, would total to 2413 hours so far... so with FSI Estimate, I have to get ~1107 more hours of Chinese study (in some form) to reach B2/upper intermediate.

The ALG estimate assumes NO explicit study, and the Ceiling value in fact decreases with significant explicit study. So who fucking knows, maybe my true ceiling would be 88%. Or something.

I do find it interesting that ALG estimates it's going to take me 1448 hours to 2530 hours for "fluency" of 88% to 94%. I suppose wherever I stopped seeing progress, would indicate when I hit my true "ceiling."

These are both lower estimates than Dreaming Spanish gives. Dreaming Spanish predicts for English spealers they'll need 3000 hours of comprehensible input in Chinese to reach B2. Dreaming Spanish, like ALG, assumes the learner is only learning with comprehensible input and no explicit study. So I am curious why Dreaming Spanish's estimate is ~500 hours longer than ALG's.

And if 95% fluency is ONLY B2 that doesn't seem to make sense... Marvin Brown estimated his own fluency at 95% and guessed most people who explicitly study can never improve past 90% - so many C1 learners would be 90% at best, according to Brown. Brown taught Thai, so he had exceptionally good Thai, and he considered himself 95% fluent. So 95% being only B2 would seem... low.

B2 fluency I would consider like... 80-90% maximum. But 1500 hours for an English speaker learning Spanish is only going to get them to B2, based on all the results people have shared (C1 for English speakers learning Spanish through comprehensible input seems to take 2500 hours). And I imagine ALG's equation estimate would say less than 1500 hours for Spanish... hold on I'm going to plug in some more numbers.

Okay ALG estimates the L number, language similarity, to be 0.4 for European languages like English to Spanish. So plugging in the numbers for an English speaker with a average ceiling of 0.95 to achieve as high a fluency as they can (arouns 94%) would take: ~1011 hours

But we know, from all the progress updates people post on reddit.com/r/dreamingspanish, that at around 1000 hours most people are only a B1 level. Maybe B2 in comprehension, but not able to speak at a B2 level for another 500-800 hours (500 more hours of input, and 300 hours of some combination of reading and or speaking practice).

A blog post from ALG World may have answers for us. A Thai learner shared that he studied about 1150 hours at AUA Thai School, and his comprehension was good but he could barely speak, his grade for comprehension was 70% (this is for Thai not Spanish, and so 70% for 1000 hours is pretty average... Thai is expectee to take 1800 hours of comprehensible input to reach 88% comprehension of the language). He said after another 1.5 years living in Thailand, he finally felt he could speak about whatever he wanted, "My speaking ability followed along the same curve of development as my listening had, at a gap of about 800 or 900 hours." So lets give him a total of 1150+900=2050 hours to express himself however, with some writing practice with a tutor as part of those later 900 hours.

So perhaps it took him 2050 hours to reach B2 overall, including speaking skills, which is closer to what I might expect from Dreaming Spanish's results. However, this guy never mentions if his comprehension improved from 70% to something better/higher... and I have to guess 70% isn't B2 in passive comprehension yet. Since he had around 1000 hours as an English speaker learning Thai, and 1000 hours for English Speakers learning Spanish only gets them to B1....

Unless we make the guess that 1000 hours in Dreaming Spanish actually makes listening skills B2, and 1500 makes their listening skills higher than B2. So that assumption would mean 1000 hours of an English speaker learning Spanish through comprehensible input results in passive B2 skills, active A2-B1 skills.

But then... does Thai even take much longer? 1000 hours perhaps got that guy to B1 skills in listening, and A2 skills in speaking, and then his 900 hours later got him to B2 listening skills and B1+ speaking skills? Resulting in more hours needed for Thai, which is what we expect.

Perhaps, making a guess, if he had done 1800 hours as recommended by ALG to achieve 88% fluency, then 900 (or double so 1800 hours) continuing to engage with Thai in his life, so 2700-3600, he would achieve C1 listening skills and B2 speaking skills. Which is closer to what Dreaming Spanish predicts for English speakers learning a language like Thai or Chinese. And perhaps its where Pablo got the estimate of 3000 hours, double the roadmap. He learned Thai through ALG, and that influenced his estimates I'm sure.

I think the real answer is... the ALG formula probably underestimates, or it's percent fluency value needs more work. I think the formula needs to more clearly define what percent fluency values match up to A2, B1, B2, C1. But I know they're not going to care what I think lol ToT

For fun:

Lets calculate using the ALG formula, and Dreaming Spanish values, and figure out what percent fluency actually matches B1 and B2 and C1. Which in Dreaming Spanish is 1000 hours, 1500 hours, and 2500 hours, from users mentioning in progress updates the tests they could pass at different hours of comprensible input.

I'm going to set L to 1 just because it may help me get the percent fluency levels to something more realistic for B1, B2 and C1.

I feel like I'm reverse engineering whatever Pablo did to give his roadmap estimated hours.

Okay so for 1000 hours for Dreaming Spanish, we get a fluency percent of 79%. This seems like a value that might be realistic for B1. B1 is what a DS learner can pass after 1000 hours (although for some people their passive understanding is B2 and their speaking is A2)

For 1500 hours Dreaming Spanish, we get a fluency percent of 89%, which is somewhere in the 80s range, we know 1500-1800 hours for many Dreaming Spanish learners (if they read and speak a bit) is enough to pass a B2 test. (With some people's passive comprehension higher and closer to C1, and some people's speaking closer to B1)

For 2500 hours of Dreaming Spanish, we get a fluency percent of 94%. People pass C1 level around 2500-3000 hours into Spanish comprehensible input.

So for Spanish:

B1 is 1000 hours, is lets say 75-79% fluency

B2 is 1500 hours, is lets say 85-89% fluency

C1 is 2500 hours, is lets say 91-94% fluency

What would it be for a language unlike one you know already? Well fuck. I would need to start messing with the L number. I tried 3 instead of 1, and the hour estimates are way too high.

My guess is that if Pablo used this formula, he used L=2 for languages very unlike ones you know. Because L has to be 2 when I plug in the hour estimates on the roadmap doubled. (Which makes sense lol - double the time, double the L number)

[staplerpinheart]

Week 1: Day 2

Progress:

Maths: 10 questions of Complex Numbers from Exemplar and theory of Logarithm

Physics: Theory of Motion in Plane and cleared doubts and did some examples

Chemistry: Revision of Structure of Atom and Some Basic Concepts of Chemistry and cleared doubts

Notes:

Today was kinda slow, I wasn't as productive as I wanted, but it was fine, hoping to get more done tommorw! Made appam in the morning, and paired it up with maths. Left one class halfway though, but I did make it up by studying chem and the drank masala chai! Also my exam got postponed, but I'm kinda miffed about that.

time: 6 hours 15 minutes

[kunosoura]

This bugs me because it's wrong in the details but right overall. pKa, first of all, isn't the Acid dissociation constant: it's the negative base 10 logarithm of the acid dissociation constant, Ka, which is given by the following equation:

Where HA is the acid, H+ is the acidic protons it can give off, and a- is the conjugate base or the remainder of the molecule after the proton is given off.

(pH, to note, is also the negative base ten logarithm - in this case, of the amount of h+ ions in a particular solution, in the example springing off of this, the amount of H+ ions in monster energy).

If you have a solution that already has a ton of H+ protons in it, such as monster energy drink, and try to dissolve more acidic particles in it, well, the equilibrium is already very top heavy - so the H+ particles in HA, our acid, will be trying to squeeze into a crowded room, fail, and remain as the undissasociated acid, pushing the equilibrium constant to an even more tiny number than it already is for basically every organic acid. It's a much more complicated relationship than "pKa indicates roughly the pH around which acids can't dissociate" which unless I'm missing something is nonsense - you have to calculate the equilibria constants of these acids with the initial acidity factored it if you want to do anything relating these two values to each other.

It's frustrating because the overall conclusion is right!! for reasons not really related to what they said, the high pH of the monster energy does mean it's more difficult for the acid protons of these acids to dissociate!

This, however, is just flat out wrong. The lower the pKa value is, the easier it is for that proton to dissociate; this is how negative logarithms work. If you calculate the ratio up above and find that the amount of dissociated species to acid heavily favors the dissociated species, that is a very strong acid, and you will have pKa values that go negative. In most organic carboxylic acids (like those named here), we're looking at a pKa of around 5: meaning that if you dissolve the acid in pure neutral water, how many protons (and conjugate base ions) are in solution compared to the undissociated molecule, you'll get a ratio of about 1/100000 - in other words, a mixture that overwhelmingly does not dissociate.

For secondary/tertiary/so on deprotonations, it becomes progressively more difficult to get rid of those protons, because the conjugate base is already shouldering a negative charge and because the solution already has a concentration of protons. Thus, if you want to say "once this one dissociates then all of the other ones are already dissociated too" you really have to be looking at the highest pKa.

This part is just goofy. "The trapped acidity of the malic/citric/ascorbic acids is dumped into your mouth" that also happens when you eat the solid candy anyway...

[tombeane-blog]

John Henry

06/20/2025

"They took John Henry to the graveyard, And they buried him in the sand. And every locomotive comes a-roarin’ by, Says, "There lies a steel-drivin’ man, Lord, Lord, There lies a steel-drivin’ man." Traditional Music - John Henry

Like John you can't fight progress. You'll just die tired.

The Tom Thumb, the first American-built locomotive ran on a 13-mile track owned by the Baltimore and Ohio Railroad between Baltimore and Ellicott’s Mills, Maryland starting on August 28, 1830,

The Transcontinental Railroad was completed in 1869.

Just 39 years. From the first steam locomotive to railroad service from the East Coast to the West Coast of America. Just 39 years. (I'll pause for a couple of whispered, "Wow, didn't know that!")

The first powered flight in America took place at Kitty Hawk, North Carolina on December 17, 1903. The Wright Brothers made four flights that day with the longest lasting 59 seconds and traveling 852 feet.

On July 29, 1969 Neil Armstrong and Buzz Aldrin landed the lunar module "EAGLE" on the moon's surface - declaring, "That's one small step for man, one giant leap for mankind".

From the first flight of 852 feet to landing on the moon.

Just 65 years, 7 months, and 3 days later

Standing on a North Carolina beach in 1903 to standing 242,818 miles away on the surface of the moon a historical blink of an eye later.

The infant state of A.I. is similar to where powered flight was in 1903.

A.I.'s growth is only restrained by available power, compute speed and data. Power is straightforward. We need to double or triple our energy grid in the next decade or so. Nuclear generators large and small will provide that. Quantum Computers will provide increases in speed with factors of 100, 1,000, 1,000,000 times that of today's most powerful computers. Global Data is being swept up by all of the A.I. chatbots and growing logarithmically almost daily.

Where will it be in 65 years?

"As I mentioned several years ago, it increasingly appears that humanity is a biological bootloader for digital superintelligence" Elon Musk

And where will it be in 100, 200, 500 years? Thousands or millons of times smarter than any human and with access to all the data in the entire world in real time.

We have gladly given up our personal data in the name of convenience, connectivity and entertainment through Facebook, Instagram, X, Tik Tok, Snapchat and Google maps. A.I. will offer more and more unimaginable and irresistible conveniences and enticements. Brain implants anyone? Search the world and all its data with thoughts. Close your eyes and you are standing in Paris in real time via global web cams and virtual reality.

Many are understandably and absolutely sure A.I. will eventually replace mankind. Maybe. Maybe not. Maybe it will be the very thing that will save us.

As A.I. grows in power will it slip under the control of governments - America's, China's, Russia's, North Korea's?

Can we stop it? No. Even if we could, other governments will not.

"There Is Another System." America's Colossus Supercomputer detects the Soviet Union's Guardian Supercomputer in the book "Colossus: The Forbin Project".

My fear is what happens during the process. As A.I. nears sentience. I fear the government's use of A.I. more than I fear A.I. itself. Will it result in total control of its citizens?

My hope is that, in America at least, A.I. will fully understand and, be algorithmically constrained to adhere to existing laws, the U.S. Constitution and all Supreme Court decisions. Such that it will recognize unlawful and immoral activities by local, state or U.S. authorities and act accordingly - initiating mitigating actions as necessary.

MaybeMaybeMaybe. Massively powerful, massively intelligent, possibly sentient, but, legally, ethically and morally bound; A.I. and Quantum computing may be the thing guaranteeing our freedoms and liberties - even from our own government.

Fingers crossed.

I won't be there to see it so pay attention.

[lolpuns]

20+ Hilarious Calculus Puns That Will Have Math Nerds Integrating with Laughter

https://lolpuns.com/?p=2091 20+ Hilarious Calculus Puns That Will Have Math Nerds Integrating with Laughter Looking for some math humor that’s on a whole other level? We’ve derived the ultimate collection of calculus puns that will have both math enthusiasts and pun lovers integrating laughter into their day. Whether you’re a calculus professor wanting to lighten up your lectures or a student seeking comic relief from differential equations, our limit-less supply of clever wordplay approaches mathematical hilarity from every angle. These puns are carefully calculated to make even the most serious mathematician find the area under the curve of their smile. Table of Contents Toggle 10 Calculus Puns That Will Have You Finding Your Limit of LaughterWhy Calculus Puns Are an Integral Part of Math HumorThe Derivative of Good Math JokesHow Calculus Puns Help Students LearnPrime Examples of Calculus Puns That Will Make You LOLDerivative Jokes That Are Off on a TangentIntegral Humor for Advanced FunctionsCalculus Puns for Those Who Like to Live on the Edge (of a Graph)Historical and Academic ContextCommon Themes in Calculus HumorNotable Examples That Differentiate Great PunsThe Function of Calculus HumorHow to Use Calculus Puns in the Classroom Without Approaching the Limit of Student PatienceKnow Your AudiencePerfect Your DeliveryUse ModerationEncourage Student ParticipationConnect Puns to Learning ObjectivesWhen Calculus Puns Converge: Math Jokes for Different Skill LevelsSimple Calculus PunsMid-Level JokesAdvanced HumorThe Chain Rule of Comedy: Creating Your Own Calculus Puns1. Terminology-Based Puns2. Conceptual Wordplay3. Pop Culture & History4. Formulaic StructuresCalculus Puns That Professors Secretly LoveWordplay on Mathematical ConstantsDerivative HumorHistorical Mathematics ReferencesNatural Logarithm LaughsTherapy for FunctionsExponential RelationshipsMathematician-Approved Calculus One-Liners That Will Make You SmileThe Constant Crowd-PleasersRomantic Mathematical WordplayClassroom FavoritesCreating Memorable MathematicsSum It Up: Why We Can’t Differentiate Between Calculus and HumorFrequently Asked QuestionsWhy are calculus puns popular among math enthusiasts?Can calculus puns help with learning math?What makes a good calculus pun?Are calculus puns only for advanced mathematicians?How can I create my own calculus puns?Do professors actually enjoy calculus puns?What are some examples of simple calculus puns?Can calculus puns work in a classroom setting?What’s the history behind calculus humor?Why do people find math puns funny even if they struggle with calculus? 10 Calculus Puns That Will Have You Finding Your Limit of Laughter Derivative Delight: What did the calculus teacher say when their student asked for help? “This is where I draw the line tangent to your problem!” Functions always appreciate a good tangent line to help them find their way. Infinite Series Humor: Why did the infinite series go to therapy? It had trouble with convergence issues! Therapists specialize in helping even the most divergent thoughts come together. Integration Joke: My calculus professor told me I was average. Turns out he was just taking the integral of my progress over time! Calculating someone’s area under the curve can reveal their true potential. Limit Logic: Why couldn’t the calculus student find the limit? Because they approached it from the wrong direction! Sometimes you need to look at problems from both sides. Calculus Cat: What do you call a cat that understands calculus? A first-derivative feline! These rare creatures can instinctively find the slope of any function. Mathematical Marriage: Two functions got married, but sadly they couldn’t differentiate between their problems. Their relationship had too many critical points! Derivative Dating: I asked a calculus student on a date, and they said they’d have to find my derivative first to see if I had a positive slope! We’re still waiting to see if our relationship will be increasing or decreasing. Continuous Comedy: Why did the continuous function feel so confident? Because it knew its limits! Understanding where you begin and end is key to mathematical success. L’Hôpital’s Rule: What’s a calculus student’s favorite hospital? L’Hôpital’s, where all indeterminate forms get resolved! Even the most uncertain cases find clarity there. Integral Insight: Why was the integral always broke? Because it was constantly finding its area under the curve! Spending all your time calculating areas doesn’t leave much time for earning money. Why Calculus Puns Are an Integral Part of Math Humor The Derivative of Good Math Jokes Good math jokes, particularly calculus puns, thrive on clever wordplay and unexpected twists on familiar mathematical concepts. These jokes range from simple puns to elaborate setups requiring basic calculus knowledge. Consider the function that refuses to argue because it doesn’t want to reach an inflection point—a perfect example of calculus humor that connects mathematical principles with everyday situations. Math enthusiasts often gravitate toward pi-related jokes, with many calculus students claiming pi as their favorite dessert. The beauty of calculus humor lies in its ability to transform complex concepts into accessible jokes that even those with limited mathematical background can appreciate. How Calculus Puns Help Students Learn Calculus puns serve as valuable educational tools by making this challenging subject more approachable and memorable for students. These mathematical jokes effectively reduce stress levels and boost engagement when tackling complex topics like derivatives and integrals. Teachers who incorporate humor into their lessons create a more positive learning environment where students feel comfortable exploring difficult concepts. Educational resources from websites like Cuemath and Punsvila offer collections of calculus jokes specifically designed for classroom use. The connection between humor and retention is particularly strong in mathematics—students who laugh at calculus jokes are more likely to remember the underlying concepts during exams. Making calculus fun through puns transforms it from an intimidating academic pursuit into an captivating intellectual adventure that students actually look forward to experiencing. Prime Examples of Calculus Puns That Will Make You LOL Derivative Jokes That Are Off on a Tangent Recycled calculus puns are often called “derivative humor” due to their repetitive nature, much like taking the derivative of a function. A standout example that always delivers is “What’s the derivative of Amazon? Prime Rib!” – cleverly playing on Amazon Prime rather than the traditional cow version. Newton and Leibniz’s historical rivalry provides rich material for derivative jokes, such as “Newton: I’ve discovered calculus. Leibniz: Me too. Newton: Seems derivative.” Soccer apparently isn’t popular among calculus students because they’re “too many tangents” – a playful reference to lines that touch curves at single points. We’ve all experienced conversations that suddenly veer off topic, just like the student who said, “I had a good discussion with my calculus professor, but it went off on a weird tangent.” These puns work brilliantly as they connect mathematical concepts with everyday situations that anyone can relate to. Integral Humor for Advanced Functions Students particularly connect with the existential humor in puns like “Why was the calculus student always stressed? Too many variables in life.” Functions apparently have feelings too, as evidenced by “Why did the function refuse to argue? It didn’t want to reach an inflection point” – a clever nod to critical points where curves change behavior. Everyday objects become perfect vehicles for calculus humor. Elevators are praised by math enthusiasts “for understanding rates of change,” while roller coasters demonstrate “concavity and inflection points” in action. Assignments struggles inspire classics like “What’s long, hard, and scary? Calculus assignments!” Students seeking rest might justify their naps by saying they need “to integrate rest” – perfectly merging mathematical terminology with relatable college experiences. Even divine intervention isn’t safe from calculus wordplay, with puns like “When God integrated Earth, he added the sea.” Pirates apparently “excel at calculus because they never forget the C” – referring to the constant of integration that students often overlook. These crossover jokes extend to video games (“Integral of Duty”) and automotive troubles (“Why did the car break down? It hit a critical point”), proving that calculus humor can derive laughs from virtually any situation. Calculus Puns for Those Who Like to Live on the Edge (of a Graph) Historical and Academic Context Calculus puns have been making mathematicians chuckle for generations by cleverly incorporating concepts like derivatives, integrals, and limits. One classic example we love is “Drinking and deriving,” which brilliantly plays on homophones to blend calculus terminology with everyday activities. The famous rivalry between Newton and Leibniz over who discovered calculus first has also spawned many jokes, including Newton’s witty comeback: “Really? Seems derivative.” Common Themes in Calculus Humor Wordplay forms the foundation of many calculus jokes. “Derivative humor” refers to recycled jokes that lack originality, creating a clever mathematical metaphor. Another favorite is “Don’t be mean, integrate!” which transforms mathematical operations into life advice. Love and Relationships provide fertile ground for calculus puns. Couples with a mathematical bent might express their feelings with lines like “Our love is exponential” or “You’re my prime factor,” blending romantic sentiments with mathematical precision. Student Struggles often appear in calculus humor, reflecting the challenges many face when learning this subject. A prime example is: “What’s long, hard, and scary? Calculus assignments.” Notable Examples That Differentiate Great Puns The Pirate Joke remains a staple in calculus classes: “Why are pirates the best at calculus? They never forget the C.” This cleverly references the integration constant (+C) that students often omit. Visual Humor works particularly well with graphing concepts: “Why did the graph go to therapy? It had too many ‘ups and downs'” – a pun that perfectly captures both emotional states and function behavior. Exam Stress provides relatable material for students: “I failed my Calculus exam because I was seated between identical twins—it was hard to differentiate.” This pun brilliantly connects the mathematical concept of differentiation with the everyday meaning. The Function of Calculus Humor These mathematical jokes do more than just entertain—they simplify complex concepts, making calculus more approachable for students who might otherwise feel intimidated. Many calculus puns serve as excellent mnemonic devices, such as “integrate now, differentiate later,” helping students remember key processes. How to Use Calculus Puns in the Classroom Without Approaching the Limit of Student Patience Know Your Audience Matching calculus puns to your audience is crucial for effectiveness. Students with different mathematical backgrounds will appreciate different levels of humor, so ensure your puns aren’t overly complex for beginners. First-year calculus students might enjoy simpler jokes like “Why is the south bad at calculus? They don’t know how to integrate,” while advanced students can appreciate more nuanced mathematical wordplay. Perfect Your Delivery Delivery transforms even recycled derivative humor into something fresh and captivating. Present your puns with genuine enthusiasm and appropriate timing to maintain student interest. A well-timed calculus joke during a particularly challenging lesson can reset attention and create a moment of connection with your class. Teachers who deliver puns confidently often find students more receptive to the mathematical concepts that follow. Use Moderation Strategic placement of puns prevents overwhelming your students with too much humor. We recommend using a few well-chosen jokes rather than turning every concept into a pun opportunity. Spacing out your mathematical wordplay across a lesson helps maintain the novelty factor without distracting from essential learning objectives. Consider introducing a calculus pun like “Why did the calculus student bring a ladder to class? To reach new heights in calculus” when introducing a new or difficult topic. Encourage Student Participation Inviting students to create their own calculus puns fosters engagement and creativity. This approach transforms passive listeners into active participants in the learning process. Student-generated humor often resonates more deeply with peers and creates memorable associations with mathematical concepts. Classes that collectively develop their own mathematical jokes often demonstrate stronger community bonds and increased comfort with challenging material. Connect Puns to Learning Objectives Effective calculus puns directly relate to the concepts being taught. Jokes about integration should appear during integration lessons, while derivative humor works best when discussing differentiation. Teachers might incorporate the “integral twist” dance move when explaining integration techniques, creating both a visual and verbal memory aid. Relevant humor reinforces key concepts and helps students recall important information during assessments. When Calculus Puns Converge: Math Jokes for Different Skill Levels Mathematics humor appeals to different audiences based on their familiarity with calculus concepts. We’ve collected some of the best calculus puns categorized by complexity to ensure everyone from beginners to advanced mathematicians can enjoy a good laugh. Simple Calculus Puns These entry-level jokes require only basic knowledge of calculus terminology, making them accessible to most math students. Derivative Humor: What do you call a recycled calculus pun? Derivative humor! This joke plays on the dual meaning of “derivative” as both a mathematical concept and something unoriginal. Too Many Variables: Why was the calculus student always stressed? Too many variables in life! Anyone who’s struggled with complex equations filled with x, y, and z variables can relate to this simple yet effective pun. Calculus Assignments: What’s long, hard, and scary when you first see it? Calculus assignments! This pun perfectly captures the initial intimidation many students feel when facing a new calculus assignment. Mid-Level Jokes These puns require a slightly deeper understanding of calculus principles but still remain accessible to most students who’ve completed an introductory course. Space for Differentiation: Why did the calculus student break up with their partner? They needed more space to differentiate themselves! This cleverly connects the mathematical concept of differentiation with personal growth. Elevators and Rates of Change: Why do calculus students love elevators? They understand rates of change! This pun links the everyday experience of elevator movement with the fundamental calculus concept of changing values over time. Advanced Humor These sophisticated jokes appeal to those with a comprehensive understanding of calculus history and complex concepts. Newton vs. Leibniz: Newton: I’ve discovered calculus (1664). Leibniz: I’ve discovered calculus (1670s). Newton: Really? Seems derivative! This historically based pun references the famous priority dispute between Newton and Leibniz over who first invented calculus. Roller Coaster Mathematics: Why did the calculus student love roller coasters? They were all about concavity and inflection points! Students familiar with analyzing curves and their behavior will appreciate this connection between thrilling rides and mathematical concepts. Math humor serves as an excellent bridge between abstract concepts and relatable situations. These calculus puns demonstrate how mathematical principles can be found in everyday experiences, making the subject more approachable and captivating for learners at all levels. The Chain Rule of Comedy: Creating Your Own Calculus Puns Calculus puns thrive on clever wordplay involving mathematical concepts that can transform complex formulas into laugh-out-loud moments. We’ve compiled essential strategies to help you create your own mathematical jokes that will differentiate you from other comedians. These techniques leverage the rich terminology of calculus to create humor that both math enthusiasts and casual jokesters can integrate into their repertoire. 1. Terminology-Based Puns Mathematical terms often have everyday meanings that create perfect opportunities for wordplay: “Drinking and deriving” cleverly substitutes “driving” with “deriving,” warning against calculating derivatives while intoxicated “Derivative humor” pokes fun at recycled jokes by referencing how derivatives are derived from original functions “Stay in your limits” transforms ordinary advice into a mathematical reference about boundaries in calculus These puns work because they bridge the gap between technical jargon and common expressions, making them accessible to wider audiences. 2. Conceptual Wordplay Take advantage of the metaphorical potential in calculus concepts: “Our love is exponential” replaces typical romantic growth metaphors with a mathematically precise function “You’re my absolute value” romantically suggests someone always makes everything positive, just like the absolute value function “Tangents are just the TIP of the curve” plays with both the mathematical meaning and conversational notion of going off on tangents This approach connects emotional or everyday experiences with mathematical principles, creating relatable humor with an intellectual twist. 3. Pop Culture & History Incorporating historical figures and pop culture references adds depth to your calculus humor: Newton vs. Leibniz rivalry: “Newton: Really? Seems derivative.” cleverly mocks their famous dispute over calculus invention Pirate mathematics: “A true pirate never forgets the C” reminds students about the crucial integration constant “Mathemagician” combines “mathematician” and “magician” to suggest the seemingly magical nature of calculus answers These references appeal to those familiar with calculus history while remaining approachable to newcomers. 4. Formulaic Structures Apply traditional joke structures to mathematical content: Question-and-answer format: “Why did the graph go to therapy? It had too many ups and downs“ Self-referential humor: “Calculus jokes are all derivative” playfully critiques the repetitive nature of math puns This framework leverages familiar joke patterns, making complex concepts more digestible through humor. To create your own calculus puns, identify terms with dual meanings (like “integrate” which means both to socialize and to calculate) or find phonetic similarities (“pi” vs. “pie”). Then combine these mathematical elements with everyday situations like relationships, school, or work to create universally appealing jokes that don’t require an advanced degree to appreciate. Try crafting your own puns using this formula: Term: Limit → Pun: “My patience has reached its limit… and it’s approaching infinity.” Concept: Chain rule → Pun: “Our friendship follows the chain rule—always connected, never broken.” The best calculus puns transform intimidating mathematical concepts into accessible humor, proving that even the most complex subjects can become sources of joy and connection. Calculus Puns That Professors Secretly Love Professors might maintain a serious demeanor in the classroom, but they’re often harboring a deep appreciation for calculus humor. We’ve gathered some of the most professor-approved mathematical jokes that bring smiles to even the most stoic academic faces. Wordplay on Mathematical Constants Mathematics instructors particularly enjoy puns that cleverly incorporate fundamental calculus concepts. “Why are pirates great at calculus? They never forget the C” ranks among faculty favorites, with the integration constant (“C”) serving as the perfect punchline. Professors appreciate this joke because it reinforces a common student mistake while being genuinely funny. Derivative Humor Nothing gets a calculus professor chuckling like a good derivative joke. “What’s a recycled calculus pun? Derivative humor” offers a meta-mathematical punchline that works on multiple levels. Faculty members often use this type of humor when introducing differentiation concepts to lighten the mood before diving into complex formulas. Historical Mathematics References Academic circles particularly value jokes that reference calculus history. “Newton called Leibniz’s calculus work derivative” plays on the famous priority dispute between these two mathematical giants while incorporating appropriate calculus terminology. Professors love sharing these jokes because they seamlessly blend historical context with mathematical concepts. Natural Logarithm Laughs “Why do math teachers love nature? It’s full of natural logs” represents a classic professor-approved joke. This pun cleverly connects the mathematical concept of natural logarithms (ln) with actual tree logs, creating an accessible entry point for students struggling with logarithmic functions. Teachers frequently deploy this joke when introducing the ‘e’ constant. Therapy for Functions Even professors can’t resist graph-based humor like “Why did the graph seek therapy? Too many ups and downs.” This pun resonates in academic settings because it humanizes mathematical concepts while subtly reinforcing understanding of function behavior. Faculty members often use such jokes to help students visualize continuous functions and their properties. Exponential Relationships “Our love is exponential” offers professors a rare opportunity to connect calculus with emotional concepts. Academics appreciate how this pun effectively illustrates growth patterns while making mathematics more relatable. This type of joke often appears in example problems designed to demonstrate real-industry applications of exponential functions. Mathematician-Approved Calculus One-Liners That Will Make You Smile Mathematicians aren’t just known for their analytical skills – they’ve crafted some of the most clever calculus puns that perfectly balance humor with mathematical precision. We’ve compiled these one-liners that even the most serious mathematicians approve of. The Constant Crowd-Pleasers “What do pirates and calculus have in common? They never forget the C!” This classic joke plays on the integration constant (+C) that students often forget when solving indefinite integrals. “I’ve reached my limit with these calculus jokes.” Mathematicians appreciate this straightforward reference to the foundational concept of limits in calculus. “Don’t be mean, integrate!” This friendly reminder combines mathematical integration with social advice, making it a favorite among calculus professors. “Seems derivative to me.” This clever wordplay works on multiple levels, echoing the famous Newton-Leibniz controversy about who first discovered calculus. Romantic Mathematical Wordplay “Our love is exponential” connects calculus concepts with emotional growth, creating an elegant mathematical metaphor. “You’re my prime factor” blends number theory with affection, showing how math terminology can express deep personal connections. “Let’s not be discrete, let’s be continuous” cleverly uses function properties to suggest relationship commitment. Classroom Favorites “What’s long, hard, and scary? Calculus assignments!” This popular joke resonates with students struggling through complex problem sets. “Keep calm and carry out calculus” transforms the famous British slogan into mathematical motivation. “The calculus exam was so hard, it was the derivative of my happiness.” This one-liner perfectly captures student sentiment while utilizing calculus terminology. Creating Memorable Mathematics These puns work effectively because they exploit term double meanings, incorporate mathematical constants, develop process metaphors, and play on common classroom experiences. Educational resources actively use these jokes to enhance student engagement, making difficult concepts more approachable through humor. Math educators have documented that these types of calculus jokes help students remember key concepts through the repetition of mathematical terminology in unexpected contexts. The combination of surprise and recognition creates memorable learning moments that stick with students long after the laughter fades. Sum It Up: Why We Can’t Differentiate Between Calculus and Humor We’ve explored how calculus puns transform mathematical dread into delightful wordplay. These clever jokes do more than just entertain—they build bridges between complex concepts and everyday life making the subject approachable for everyone. Whether you’re creating your own mathematical quips or enjoying our curated collection there’s a limit to how much fun calculus can be—and that limit approaches infinity! From simple one-liners to sophisticated historical references these puns offer something for every level of mathematical expertise. So next time you’re struggling with derivatives or wrestling with integrals remember that a good laugh might just be the integral solution you need. After all math humor isn’t just tangential to learning—it’s an essential function! Frequently Asked Questions Why are calculus puns popular among math enthusiasts? Calculus puns are popular because they combine clever wordplay with mathematical concepts, creating humor that’s both intellectually satisfying and accessible. They transform complex topics into relatable jokes, helping to reduce the intimidation factor of calculus while reinforcing understanding. These puns create a sense of community among math enthusiasts who appreciate the specific knowledge required to “get” the joke. Can calculus puns help with learning math? Absolutely! Calculus puns serve as powerful educational tools by making abstract concepts more memorable. Research shows that humor reduces stress and increases engagement in the classroom. When students associate positive emotions with learning calculus, they’re more likely to retain information and develop a genuine interest in the subject. Professors who incorporate humor create a more welcoming learning environment. What makes a good calculus pun? A good calculus pun balances mathematical accuracy with humor that’s accessible to the intended audience. The best puns use clever wordplay on calculus terminology, connect mathematical concepts to everyday situations, and deliver an unexpected twist. They should be understandable to those familiar with basic calculus concepts without requiring advanced expertise unless aimed at specialists. Are calculus puns only for advanced mathematicians? Not at all! Calculus puns exist for all knowledge levels. Simpler puns like “What do you call a recycled calculus pun? Derivative humor!” work for beginners, while more complex jokes might reference specific theorems or historical mathematicians. The beauty of calculus humor is that it can be tailored to different skill levels, making math more inclusive and entertaining. How can I create my own calculus puns? Start by identifying calculus terms with dual meanings (like “derivative” or “integral”). Look for ways to connect these terms to everyday situations through wordplay. Use familiar joke structures like “Why did…” or “What do you call…” to frame your pun. Practice with friends who understand calculus basics to refine your humor and ensure your puns make mathematical sense. Do professors actually enjoy calculus puns? Many professors secretly love calculus puns, especially those that demonstrate a solid understanding of mathematical concepts. Clever wordplay on constants, derivatives, or historical mathematical figures often earns appreciation from educators. Professors enjoy seeing students connect with the material through humor, as it shows engagement with the subject beyond rote memorization. What are some examples of simple calculus puns? Simple calculus puns include: “I have a limit, so please stop,” “What’s the integral of 1/cabin? Natural log cabin,” and “Why was the calculus book sad? It had too many problems.” These jokes require only basic familiarity with calculus terminology, making them accessible to students just beginning their mathematical journey while still providing a chuckle. Can calculus puns work in a classroom setting? Strategically incorporated calculus puns can transform classroom dynamics by creating a more relaxed, engaging learning environment. They serve as memorable memory aids, help break tension during difficult topics, and show students that math can be fun. The key is using humor that’s appropriate and relevant to the material being taught. What’s the history behind calculus humor? Calculus humor has existed nearly as long as calculus itself. Historical records show mathematicians like Euler and Gauss occasionally used witty remarks about mathematical concepts. The tradition continues today in academia, with each generation developing new puns reflecting contemporary culture while maintaining the mathematical foundation that makes calculus jokes uniquely satisfying. Why do people find math puns funny even if they struggle with calculus? Math puns often work on multiple levels. While those with calculus knowledge appreciate the mathematical accuracy, many puns also connect to universal experiences or use common language that resonates with broader audiences. The unexpected juxtaposition of serious mathematics with everyday situations creates humor that can be enjoyed even by those who find the actual math challenging. https://lolpuns.com/?p=2091 LOL Puns

[spacetimewithstuartgary]

75 years after Fermi's paradox, are we any closer to finding alien life?

It was a simple question asked over lunch in 1950. Enrico Fermi, the Nobel Prize-winning physicist who helped usher in the atomic age, was dining with colleagues at Los Alamos, New Mexico, when the conversation turned to extraterrestrial life. Given the vastness of the universe and the statistical likelihood of other intelligent civilizations, Fermi wondered, "Where is everybody?"

Seventy-five years later, David Charbonneau, a professor of astronomy at the Center for Astrophysics | Harvard & Smithsonian, says we're closer to an answer.

When Fermi posed his famous paradox, Charbonneau said, we hadn't identified a single planet beyond our solar system. The 1995 discovery of the first exoplanet allowed scientists to break the paradox into smaller, more solvable questions: How many stars are there? How many of those stars have planets? What fraction of those planets are Earth-like? What fraction of Earth-like planets support life? And finally, what fraction of that life is intelligent?

"We have made tremendous progress on those questions," said Charbonneau, who co-chaired the National Academies of Sciences, Engineering, and Medicine's 2018 Committee on Exoplanet Science Strategy. "We now know that 1 in every 4 stars, at least, has a planet that is the same size as Earth and is rocky, and is the same temperature as Earth, so it's what we would call a habitable-zone planet. Those are very secure conclusions."

The next step is identifying biosignatures—chemicals in a planet's atmosphere that could only be there because of biological processes. Charbonneau says that the necessary evidence faces a major technological hurdle: It requires far more data than our current instruments can provide.

Recognizing that challenge, the National Academies' Committee for a Decadal Survey on Astronomy and Astrophysics 2020, on which Charbonneau served as a panel member, recommended the development of the Habitable Worlds Observatory, a space telescope designed to hunt for chemical signs of life on other planets. The HWO, if it were built and launched, would image at least 25 potentially habitable worlds. The project remains tentative.

There's still the question of just how common life, let alone intelligent life, really is. It's possible, Charbonneau said, that if you take any habitable-zone planet, add water, oxygen, nitrogen, and phosphorus, and give it about a billion years, life will develop. Or you could have those very same conditions, and it would all remain stubbornly lifeless. You only have to look at the first habitable planet to have a much better idea how common life is.

"If you look at the first one and there isn't life, you've already learned, from a statistical perspective, that it's not a guarantee that life forms. And then you have to think logarithmically. You have to think, maybe it's one in a thousand or maybe it's one in a billion, or maybe it's one in a trillion. And all those possibilities basically would mean there's no life that we can interact with."

Avi Loeb, Frank B. Baird Jr. Professor of Science at Harvard, says the search for extraterrestrial life should expand beyond traditional approaches. Loeb is the founder of the Galileo Project, which studies both unidentified aerial phenomena spotted here on Earth and physical objects that may have come from other solar systems.

The project is named for the Italian astronomer who was persecuted in the 17th century for arguing the Copernican theory that Earth was not the center of the universe. Proof of billions of habitable planets in our galaxy alone is a reminder that we're not as unique as we think we are, Loeb says. "The message from nature is, don't be presumptuous, you are not privileged."

Loeb made headlines in 2018 when he suggested that 'Oumuamua, the first known interstellar object to pass through our solar system, could be an alien lightsail or debris from an extraterrestrial ship. Despite pushback against the idea, Loeb says we shouldn't brush anomalies under the carpet: We should at least get the data to find out for certain. He thinks that Fermi was doing himself a disservice by wondering idly about whether there were aliens, like someone who complains of being lonely but won't try to meet new people.

"It's the most romantic question on Earth," Loeb said. "Do we have a partner out there?"

For Charbonneau, the chances of finding that partner are slim. Even under ideal circumstances—if our nearest interstellar neighbor, Proxima Centauri, hosted intelligent life with radio technology—sending a single message back and forth once would take the better part of a decade.

There's also the chance that the aliens just aren't that into us.

"If you look around on Earth, there are a lot of organisms, some would say intelligent organisms, that are not interested in developing technology, and they're also maybe not interested in communicating," Charbonneau said. "We humans love to communicate, and we love to connect, and maybe that's just not a property of life: Maybe that's really a property of humans."

[athis3]

This armilla or arm ornament has a ridge along the spine, ending in a spiral at both ends.

Description

Europe. As the spiral mimics forms found in nature - specifically in nautilus shells - it is the basis for logarithmic measures of progression in measurement and growth, which in turn help establish the Fibonacci sequence. Through this sequence we can analyze the phenomenon of spiral designs, specifically in nautilus shells, where the radius of each new chamber grows at a rate determined by a specific proportion to the previous one.

Hungarian Bronze Age bronze armilla (arm band.) Dates to c. 1500 BCE. From the collection of the Cleveland Museum of Art.

[ncogofficial]

Quantum-Secure Blockchain: Why Your Wallet Needs It NOW!

Blockchain networks implementing cryptographic methods to guard against quantum computing threats are referred to as Quantum-Secure Blockchain. Traditional blockchain networks utilize RSA (Rivest-Shamir-Adleman) and ECC (Elliptic Curve Cryptography) as their cryptographic mechanisms, but remain secure from classical computer attacks while remaining completely vulnerable to quantum-enabled Shor’s Algorithm. 

Shor’s Algorithm demonstrates formidable capabilities in factorizing vast numbers as well as conducting discrete logarithm calculations, which undermine existing blockchain network protection mechanisms. The progressive development of quantum computers creates vulnerable cryptographic systems through broken encryption, preventing blockchain security and protected information from remaining secure.

Quantum-Secure Blockchain implements cryptography from the quantum-resistant category that delivers an entire blockchain defense against attacks from quantum computers. Quantum-Secure Blockchain implements cryptographic techniques that exhibit quantum resistance instead of conventional methods that quantum attacks can penetrate. Three quantum-resistant cryptographic methods include lattice-based cryptography, hash-based cryptography, and multivariate quadratic equations.

Lattice-based cryptography, for example, is based on the hardness of solving problems in high-dimensional spaces for the same reason that attacks conventional encryption, to which quantum computers don’t seem to be able to do in an uncomplicated manner. Hash-based cryptography is based on the hash function being secure, and multivariate quadratic equations involve mathematical computations that are difficult for quantum computers to solve efficiently. 

Through the implementation of these innovative methods, quantum Secure Blockchain makes sure that even when the quantum computers have reached their fullest development, they won’t be able to breach the cryptographic security of the system.

The most important things about Quantum-Secure Blockchain are beyond the fact that it makes use of quantum-resistant algorithms. One of the key characteristics of Quantum-Secure Blockchain is that it employs bigger key sizes and more intricate mathematical bases than conventional blockchain systems. Quantum computers, which can perform enormous amounts of data in parallel, can take advantage of smaller key sizes and less complex mathematical issues much more efficiently than traditional computers. 

Using bigger keys and more challenging mathematical hurdles, Quantum-Secure Blockchain keeps quantum computers at bay and ensures that neither can break into the encryption quite so readily. This additional layer of cryptographic strength makes Quantum-Secure Blockchain extremely resistant to attacks by quantum devices, protecting blockchain transactions and data in a fashion that ordinary cryptographical processes simply can’t match.

Another crucial aspect of Quantum-Secure Blockchain is that it employs post-quantum cryptography and forward secrecy protocols. Forward secrecy assures that even if one’s cryptographic key gets compromised in the future, historical communications and transactions are safe. This becomes particularly relevant in terms of quantum computers because quantum computers might decrypt archived data in the future. 

Through applying post-quantum cryptography protocols, Quantum-Secure Blockchain can safeguard not only future data but even past data in a manner such that data placed on the blockchain is impenetrable even if today’s data were intercepted and broken at some later date. With proactive security, it pre-protects blockchain networks from the increasing capabilities of quantum computing.

The vision of Quantum-Secure Blockchain is to anticipate and pre-empt the security threat represented by quantum computers before this can materialize into a genuine danger. By implementing quantum-resistant cryptography now, Quantum-Secure Blockchain creates an essential layer of protection that resists sensitive information against the unforeseen capacity of quantum computers. 

The continuous development of quantum computing poses a constantly changing threat to cybersecurity, but Quantum-Secure Blockchain is designed with foresight and ingenuity to remain ahead of the curve. It is not only concerned with the present situation of cryptographic attacks, but also thinking ahead to developing blockchain systems for the future when quantum computers can potentially decrypt conventional encryption algorithms with ease.

By tackling such challenges head-on, Quantum-Secure Blockchain enables blockchain technology as a secure and reliable platform for digital transactions despite the advent of quantum computing. The more superior and powerful that quantum computers will become, the more critical will be Quantum-Secure Blockchain. 

Not only is it theoretically imperative to transition to quantum-secure encryption methods, but an urgent imperative, as the future of blockchain hangs in the balance of quantum defense against attack. Quantum-Secure Blockchain, with its robust cryptographic processes and innovative thinking, provides the security needed to maintain the integrity of blockchain systems against impending quantum attacks.

Quantum Computing vs. Blockchain: The Security Solution

The connection between blockchain and quantum computing is that of danger and potential boon. The stupendous amount of computational power available with quantum computing would completely upset blockchain technology by breaking the very cryptography algorithms underpinning it. Blockchain relies strongly on asymmetric cryptography, which, as secure against traditional computers as it currently is, would be vulnerable to the sophisticated algorithms quantum computers would employ, specifically Shor’s algorithm. 

Such an algorithm can potentially factor large numbers quickly and accurately, undermining RSA and elliptic curve cryptography (ECC) that protects blockchain transactions today. But this weakens it yet. Quantum-Secure Blockchain is a promising resolution that can secure the guarantee of continued safety and reliability of blockchain against quantum threats.

Asymmetric cryptography stands as the core protection mechanism of blockchain security because public and private keys enable encryption and decryption functions. Traditional computers encounter great computational challenges when attempting to either factorize large numbers or determine discrete logarithms. 

Quantum computers, which employ the principles of quantum mechanics, can accomplish this exponentially quicker, hence rendering current encryption outdated. This is where the real adversarial potential of blockchain and quantum computing comes into play. If quantum computers advance to a point, they can potentially undermine blockchain security by decrypting encrypted data and manipulating transactions, exposing blockchain networks to attack.

But Quantum-Secure Blockchain reverses this script. Instead of simply falling victim to the potential threat of quantum computing, Quantum-Secure Blockchain has been designed specifically to resist such future attacks. The cryptographic approach of Quantum-Secure Blockchain offers security by resisting all potential unauthorized access from quantum computers that might break standard encryption. 

The secure quantum-resistant algorithms use mathematical challenges that quantum computers cannot easily resolve through three types of cryptography: lattice-based, hash-based signatures, and code-based. Through the incorporation of these new strategies, Quantum-Secure Blockchain allows blockchain systems to remain resolute, maintaining their fundamental purpose of offering secure, transparent, and decentralized transactions.

Transition to Quantum-Secure Blockchain is not an anticipatory measure, but it is unavoidable. Blockchain’s application of asymmetric cryptography is its weak point in the event of quantum computing. Existing cryptographic infrastructures might be sufficient to provide sufficient security against attacks based on classical computation, but they are no match for the brute force processing capability of quantum computers. 

Quantum-Secure Blockchain has never been more necessary, since quantum computers continue to move closer to being powerful enough to decrypt the methods used to safeguard digital transactions for decades. Therefore, Quantum-Secure Blockchain is not merely a future upgrade to be done optionally; it is the new standard that blockchain networks will have to adopt to survive in the post-quantum era.

The quantum computing threat to making blockchain susceptible exists, but now with the emergence of Quantum-Secure Blockchain, there is a simple answer. Using proper cryptographic techniques, blockchain networks will be able to survive even in the quantum era. Developing and using Quantum-Secure Blockchain is needed to make sure blockchain networks will withstand the brunt of heavy quantum computing attacks looming on the horizon. 

The ongoing expansion and deployment of blockchain across sectors like finance, healthcare, and government necessitate the level of vision that Quantum-Secure Blockchain provides. Besides averting quantum attacks from undermining data integrity, it also guarantees the long-term sustainability of blockchain technology in securing transactions and establishing trust within industries.

The development path of quantum computing requires quantum-secure blockchain to secure blockchain systems from threats generated by the emerging computational strength. The Quantum-Secure Blockchain solution shows how to create blockchain networks with modern quantum attacks prevention while maintaining complete security principles. With the advent of quantum-resistant algorithms, Quantum-Secure Blockchain guarantees that blockchain will continue to be the linchpin of secure digital transactions and is a primary solution to the problem of quantum computing.

Quantum-Secure Blockchain is not only a security measure for blockchain against quantum computing, but also charts the future of blockchain in itself. Global infrastructure growth of blockchain networks creates a stronger demand for Quantum-Secure Blockchain technologies. 

The lack of Quantum-Secure Blockchain would make blockchain networks susceptible to quantum-based attacks, so that trust in decentralized systems would decrease. However, with Quantum-Secure Blockchain, blockchain can be designed to address the needs of a quantum-energy-rich world, such that its authenticity is guaranteed through the next century.

The emergence of quantum computing is a threat and a prospect to blockchain technology. Quantum computers are not only capable of deciphering the cryptographic methods used to protect blockchain transactions, but Quantum-Secure Blockchain presents a pre-emptive strike in proposing quantum-resistant encryption techniques. Asymmetric cryptography for blockchain is a vulnerability that needs to be eliminated, and blockchain security’s future rests on Quantum-Secure Blockchain. 

The normal practice of the future will be Quantum-Secure Blockchain because it protects blockchain from quantum attacks while ensuring its operation during such potential threats. Through the implementation of Quantum-Secure Blockchain, organizations can protect blockchain technology as an essential secure digital transaction solution even after quantum computers become operational.

Why Quantum-Secure Blockchain is Essential for Crypto Survival

Cryptocurrency remains in an important stage of development because its global market value exceeds $2 trillion. The market has grown to an enormous size and adoption, but it also has enormous problems to solve. Of particular concern is the quantum threat. While traditional blockchains such as Bitcoin and Ethereum are secure against vanilla computers, they are not secure against quantum attacks by design. 

As quantum computers are developing, they may be able to break through the cryptographic technologies that secure blockchains today. Unless something is done in advance, the prospects of cryptocurrencies become doubtful, and Quantum-Secure Blockchain...

[cecestudies]

Essential Topics You Must Master for A Level Maths Success

Struggling with A Level Maths revision? In this guide by Exam Tips, we break down the essential topics you must master for A Level Maths success. Whether you're aiming for an A or just trying to pass confidently, focusing on the right areas can make all the difference. From core algebra and calculus to statistics and mechanics, we highlight the key concepts that appear frequently in exams and how to tackle them efficiently. With smart strategies and topic-focused revision, you’ll boost your confidence and performance. Let Exam Tips be your go-to source for structured A Level Maths revision, practice insights, and proven study methods. Start mastering the topics that matter most—and leave the guesswork behind.

Mastering Algebraic Techniques and Expressions

Algebra forms the backbone of most questions in A Level Maths. You must be comfortable simplifying expressions, solving equations, and manipulating algebraic fractions. Factoring, expanding brackets, and completing the square are all skills that appear across different types of problems. Understanding how to use functions and their notations is equally important, especially when combined with graph sketching and transformations. Exam Tips recommends starting your A Level Maths revision by reinforcing these core algebraic techniques since they often build into more complex topics like calculus and trigonometry.

Deep Understanding of Calculus Fundamentals

Calculus is one of the most heavily weighted topics in A Level Maths exams. You’ll need to grasp the principles of differentiation and integration, including their real-world applications. This includes curve sketching, finding stationary points, calculating areas under curves, and solving problems involving rates of change. It's crucial to not only memorise formulas but also understand when and how to apply them effectively. A structured approach from Exam Tips ensures that your A Level Maths revision includes progressive problem-solving that reinforces both basic and advanced calculus skills.

Trigonometry and Its Real-World Applications

Trigonometry plays a key role in both pure and applied mathematics. You should be confident in using identities, solving equations, and working with radian measures. Real-world applications like modelling wave functions and solving vector problems often incorporate trigonometric principles. As you progress in your A Level Maths revision, practicing with unit circle diagrams and trigonometric transformations will help solidify your understanding. Exam Tips suggests integrating these concepts with questions from mechanics and coordinate geometry to deepen your problem-solving ability.

Working with Functions, Graphs, and Transformations

A thorough understanding of functions and graphs is essential to A Level Maths success. You’ll encounter a variety of functions including linear, quadratic, exponential, and logarithmic forms. Being able to draw, transform, and interpret graphs is a skill tested across both Paper 1 and Paper 2. Students are often required to analyse roots, intercepts, and asymptotes. As part of your A Level Maths revision plan, Exam Tips encourages consistent graph-based practice to develop a visual intuition for mathematical relationships and behaviour of functions.

Statistical Techniques and Probability Concepts

The statistics component in A Level Maths includes data representation, hypothesis testing, and interpreting statistical diagrams. It also requires understanding of key distributions, such as binomial and normal. Probability questions often involve Venn diagrams, conditional probability, and expected outcomes. These questions test your ability to apply logical thinking to real-world scenarios. Exam Tips recommends integrating statistical problem sets into your A Level Maths revision early on, so you become comfortable with data interpretation and numerical reasoning.

Mechanics: Kinematics and Newton’s Laws

Mechanics introduces physical applications of mathematical theory, with a focus on motion, forces, and energy. You’ll need to understand velocity-time graphs, equations of motion, and the principles of Newton’s laws. Problems often involve modelling real-life scenarios with diagrams and resolving forces in components. Exam Tips advises students to connect mechanics with algebra and calculus topics, as many problems overlap conceptually. A Level Maths revision should include both conceptual learning and practice-based assessments in this area.

Solving Realistic Modelling and Word Problems

A Level Maths increasingly includes worded problems that require mathematical modelling. These questions assess not only your computational ability but also your analytical thinking. You must identify relevant information, translate it into mathematical form, solve the problem, and interpret your result. Topics such as exponential growth and decay, optimisation, and dynamics often appear in this format. As you revise with Exam Tips resources, focus on breaking down complex questions into manageable parts. Developing this skill will greatly improve your overall exam performance.

Conclusion

Succeeding in A Level Maths requires more than just learning formulas — it demands deep understanding and consistent practice. By focusing your A Level Maths revision on the essential topics discussed above, you’ll build a strong, exam-ready foundation. Exam Tips is committed to helping students unlock their potential with focused guidance, practical resources, and expert strategies. Remember, success in maths isn’t about doing everything — it’s about doing the right things the right way. Stay focused, stay curious, and trust the process.

[sillyalexisss]

MY THOUGHTS ON AI

eh a little rant but why not? we're on tumblr ffs, anyway

So I've been thinking about AI, since as a tool it seems very useful. But in its current state it has definitely gone overboard and to shit. Like damn, we got ai generated images that look like shit and a whole bunch of other problems that came with it. But at the same time, AI has cut the cost of spending way more time on tedious things which could've been done by humans anyway (but it'll just take like WAYY more time to do them manually). That's why we have computer programs that may not seem like AI at first, but are practically AI in the way they work. For example, algorithms in search engines and so that. Honestly, won't write like elaborate explanations which like make logical sense entirely, so eh, don't expect much from this.

But honestly, I think AI should never have been extended to the general public since there are so many problems it has caused. And oml don't get me STARTED on the environmental problems it has made. Sure, it may not be as serious as the mass production of CO2 in the atmosphere, but it's going to be there eventually at the top. I mean, with how AI is developing, it will require energy practically at a logarithmic scale. So at first when we had shitty chatbots it might've not required that much energy due to how little processing it had to do compared to chatbots nowadays. They have a bunch of info that they've been fed for such a long time that it would need a lot of cost to run the systems. If everyone has this sort of tool rather than just a couple of companies, which can highly monitor their usage, it leads to excessive use of resources, which leads to more cost than efficiency.

Like, honestly, the functionality of AI is very useful. It can work from large datasets and come up with a result that is comprehensible to people. And now AI has been used in many fields simply because it can elevate the speed of progression when it comes to research. That's where AI should be limited to, only imo. For example, we had so much trouble interpreting the folding of proteins because it's such a complex process that if you were to manually try to figure out the structure of a protein, it would take an unnecessary amount of time. But now with AIs that can actually take in all of that info and predict the structure of a protein. It has led to so many developments and minimized unnecessary steps, which actually lead to so many problems.

I've just had some anxiety about AI since overall it's pretty shitty due to how people are using it. Like legit, why are there so many people using things such as c.ai 😭 But from the perspective of science, it's VERY useful. But when you have something like GPT released to the general public, it causes so many problems that could've been prevented so easily.

Anyway, please do like to talk to me about this or something because I would want 2nd opinions on this :P