#bijective

[arcsin27]

if youre bisexual youre also insexual and sursexual

[nontrivialproof]

I have three siblings and so a time-honored group activity is sorting ourselves into any other group of four. And since Thanksgiving I have been intermittently thinking about when we were doing this for The Beatles and my older brother said with zero hesitation, "Well, Raina is definitely Paul." What did he mean by that. It's not a compliment.

[nicholasandriani]

Mastering Isometric & Isomorphic Game Design: A Quickstart Guide to Unlocking 3D Potential in 2D Worlds

We say that: “oh I love that Baldur Gate, let’s crack out an isometric.” Or, “oh, digging this Final Fantasy Tactics stuff, let’s do that sideways angle thing.” But what does that mean? Let’s break it down mathematical. T:(X,∥⋅∥X)→(Y,∥⋅∥Y) is a isometric isomorphism if it is a linear isomorphism, and it is an isometry, that is ∥T(x)∥Y=∥x∥X∀x∈X; T:(X,∥⋅∥X)→(Y,∥⋅∥Y) is a topological…

[cleverusername01]

pride month is getting to be a little much this year. I mean love is love and everything but what the FUCK is “bijective”

[despondent-beauty]

Tfw you believe you've somehow created an ordered list of every single real number even though such a thing contradicts its own existence and you back this up by raging about how everyone who disagrees is just spewing what they were taught at school because you can't deal with the fact that you've spent 15 years of your life failing to prove something in a field you don't understand.

God, I love bringing you topical content.

[fazedlight]

Awakening (Kara character study, small part supercorp softness)

“But why can’t I be matched to Tali, mom? She’s my best friend!”

Alura turned to Kara, her jaw tensed with frustration with the stubborn child. “Kara, you know better than this. Stable matching can only be achieved if there is a true bijection between disjoint sets-”

“We don’t even have a true bijection because the population is constantly changing, we don’t sort according to all possible preferences, we don’t even have-” “It is not in our nature, Kara,” Alura said, with a dangerous tone in her voice. “We are not Daxamites.”

“But-” 

“The answer is no.”

---

Kara is thirteen Earth years the first time she’s called “dyke.” She doesn’t know what it means. She had only been to school for a couple of weeks. Before that, the only substantial English she had spoken was the couple months with Eliza, Jeremiah, Alex, and Kal. 

Clark, not Kal. Saying “Kal” would put her baby cousin- her older cousin- her cousin in danger.

Alex’s face flushes, and her eyes almost burn with anger, as she shoves Jake Howell against a locker. Kara could do it easily herself, but showing her newfound strength to humans would put her in danger too, somehow. Kara doesn’t think asshole is a nice word, given how Alex growled it. But she suspects dyke isn’t a nice word either.

That night after dinner, Eliza sighs, and hugs Kara gently - and Kara resolves to never get called dyke again.

---

“She’s gorgeous, she’s smart, she smells nice. Hell, I want to date her.” Kara flushed with discomfort, as the words came unbidden from her lips. But Alex didn’t remark on the odd statement, and Kara shoved the thought away.

Just weeks later, awkwardness would turn to tension as Lucy growled. “You and Hank, why do you all lie?”

“When you are an alien,” Kara choked, “You’re willing to sacrifice anything, everything, betray your fundamental instincts - just to fit in.” Something tugged in Kara’s soul at that moment. That she had always tried to fit in, long before she became an alien. But there simply hadn’t been time to linger.

It was only weeks later, when Lucy was saying her goodbyes before leaving National City to rejoin the military, that Kara felt the uncomfortable spike again. “I do know what it’s like to hide,” Lucy confessed.

Kara tilted her head, questions like why? and what do you mean? floating through her mind. But she thought it would be kinder not to ask. “I hope someday, you can be all that you are.”

Lucy gave a small smile. “Me too.”

---

She hadn’t expected meeting Lena to feel like lightning in her veins. The younger Luthor was quick-witted, and beautiful, and playful. Kara felt herself flush with the gentle teasing during their first coffee, and found herself marveling at never quite having a friendship like this before. 

---

“So… so she’s gay?” Kara asked, the word heavy in her throat. “And are you saying, you’re gay too?”

Alex sighed and paced in front of Kara, her frustration just as apparent as her confusion. How can you not know if you’re gay?, Kara wondered, at the same time feeling strangely allergic to the conversation. Wouldn’t it be obvious? “What’s changed?” Kara asked.

---

Yeah, he was… immature. Irresponsible. But they connected - orphans of a lost planet, who spoke the same tongue, who had the same bewilderment in their first moments on an alien planet with newfound powers. And if being in his bed brought her pleasure, it was only proof of their connection, that a good relationship could come of it.

Sometimes there were those flashes - Mon-El had been confused by Alex’s coming out, not understanding the concept. The more the merrier would ring in Kara’s head, and she’d chase away the image of Lena’s face.

---

“I couldn’t have done it, Kara.”

Kara’s chest heaved as she gazed down at Lena, hearing Kal’s words flash through her mind. Lena clung to Kara’s arm as Kara hovered above the reservoir, and some corner of Kara’s mind knew that she should go land, that the danger was over. That Lena was safe. That the city was safe.

But she could only stare down at Lena, whose heart hammered in her chest, whose panting breaths from her climb had not yet slowed. I almost lost her, Kara thought, forlorn. I couldn’t lose her…

It was that moment that her world came crashing down, that realization made her feel like she was drowning. That romantic love wasn’t merely a combination of friendship and lust. That shared experience didn’t mean a shared connection. There was something that ran deeper.

She was in love with Lena, and she could no longer deny it.

---

It was a drunken movie night, after Lena’s breakup with James, when Kara heard I love you fall from Lena's lips.

“It was always you,” Lena confessed, her words slightly slurred from the alcohol as Kara finished pulling the covers over her. “I just wanted to be close to you.”

Kara stood back, feeling her heart pound as she watched Lena slip into slumber. I wish I had told you, Kara thought, her mind flashing to a moment long ago in a forest. I wish I had told you, before…

Kara spent a fitful night trying to sleep on her couch, and Lena’s eyes flashed with shame the next morning as she woke. But they left for Noonan’s, leaving the conversation behind.

---

It felt impossibly brief, that window of time after Kara had revealed her secret, where everything felt almost right with the world. Maybe someday, she and Lena could finish that conversation.

But she found herself in a kryptonite shell.

The universe ended soon after, and even magic couldn’t fix how they had broken. Until the day Kara finally found her hands in Lena’s, vowing together to take down her brother, and Kara felt again that hopeful wonder of what a future with Lena could hold.

And then she found herself in the Phantom Zone again, the words ringing in her head, I wish I had told you.

---

Sleep had eluded Kara in the weeks back from the Phantom Zone. So she was already wide awake at 2am, when she heard Lena’s heart begin to hammer. 

Kara tensed, rushing to her window and ears tuning in as she prepared to fight off an assassination attempt or catch Lena as she fell.

But as she shot into the sky, she nearly tumbled when she realized that Lena wasn’t in distress. The shaky breaths and small laughs caused Kara’s chest to tighten in anguish. She’s fine, Kara thought, feeling tears prick the edges of her vision. She’s fine. 

---

“Are you okay?” Lena said, when she finally found Kara in the Tower, sitting on a step. “Alex said she couldn’t find you - you were in the Fortress?”

Kara glanced up from the steps. “I just, um. I was reading in the Fortress, I fell asleep there.” It had the benefit of being true. The Fortress was far enough to drown the sound of Lena’s heart out.

Lena shuffled next to Kara, taking a seat. “I don’t remember seeing any beds there.”

“I float in my sleep,” Kara shrugged, staring at her hands as she let silence fall.

Lena shifted, uncomfortable with the quiet. “Are you okay?”

Yeah, Kara almost said, but something stopped her this time. Perhaps it was the poor sleep. Perhaps it was the litany of I wish I had told you that would replay in her mind.

How many more times am I going to do this?, Kara thought. How many more times am I going to carry that regret? “I love you,” Kara said finally, sensing Lena tense up next to her. “I know… I know that door is closed. But I love you. I should’ve told you so long ago.”

“You… you heard me last night,” Lena wondered softly. “So you went to the Fortress?”

Kara grimaced. “I stopped listening as soon as I realized,” Kara said, fighting a panic. Will she be angry? “I never meant to- to invade your privacy. I’ll be more careful.”

“The door isn’t closed,” Lena said. “If you don’t want it to be.”

Those words made Kara brave enough - or maybe just confused enough - to finally tilt her head up to meet Lena’s gaze. “But- last night-”

“I’ve been trying to get over you. Not very successfully,” Lena added, with a wry grin.

“Really?” Kara smiled.

“Really.” 

---

The matching laws had been long dismantled by the time a smiling Alura officiated their marital rites. Kryptonians didn’t have concepts like best man or matron of honor, but that didn’t stop the two women from inviting Alex and Kelly to stand at each of their sides as they said their vows.

Kara never imagined that it’d be a woman’s wrist she’d place her wedding bracelet on. Though she supposed she never imagined marrying on an asteroid of her father’s creation, or marrying for romantic love, or marrying someone her people would call Hero of Argo for the creation of a black rock.

She never imagined finally telling Lena her secret. She never imagined Lena’s forgiveness. She never imagined the feel of Lena’s lips pressed against her own, hands tugging at her robes, as she whispered zhao against Lena’s lips.

And she never imagined being the one to make Lena’s heart race.

[boycritter]

is this function bisexual i mean bijective

[bubbloquacious]

Okay so to get the additive group of integers we just take the free (abelian) group on one generator. Perfectly natural. But given this group, how do we get the multiplication operation that makes it into the ring of integers, without just defining it to be what we already know the answer should be? Actually, we can leverage the fact that the underlying group is free on one generator.

So if you have two abelian groups A,B, then the set of group homorphisms A -> B can be equipped with the structure of an abelian group. If the values of homorphisms f and g at a group element a are f(a) and g(a), then the value of f + g at a is f(a) + g(a). Note that for this sum function to be a homomorphism in general, you do need B to be abelian. This abelian group structure is natural in the sense that Hom(A ⊗ B,C) is isomorphic in a natural way to Hom(A,Hom(B,C)) for all abelian groups A,B,C, where ⊗ denotes the tensor product of abelian groups. In jargon, this says that these constructions make the category of abelian groups into a monoidal closed category.

In particular, the set End(A) = Hom(A,A) of endomorphisms of A is itself an abelian group. What's more, we get an entirely new operation on End(A) for free: function composition! For f,g: A -> A, define f ∘ g to map a onto f(g(a)). Because the elements of End(A) are group homorphisms, we can derive a few identities that relate its addition to composition. If f,g,h are endomorphisms, then for all a in A we have [f ∘ (g + h)](a) = f(g(a) + h(a)) = f(g(a)) + f(h(a)) = [(f ∘ g) + (f ∘ h)](a), so f ∘ (g + h) = (f ∘ g) + (f ∘ h). In other words, composition distributes over addition on the left. We can similarly show that it distributes on the right. Because composition is associative and the identity function A -> A is always a homomorphism, we find that we have equipped End(A) with the structure of a unital ring.

Here's the punchline: because ℤ is the free group on one generator, a group homomorphism out of ℤ is completely determined by where it maps the generator 1, and every choice of image of 1 gives you a homomorphism. This means that we can identify the elements of ℤ with those of End(ℤ) bijectively; a non-negative number n corresponds to the endomorphism [n]: ℤ -> ℤ that maps k onto k added to itself n times, and a negative number n gives the endomorphism [n] that maps k onto -k added together -n times. Going from endomorphisms to integers is even simpler: evaluate the endomorphism at 1. Note that because (f + g)(1) = f(1) + g(1), this bijection is actually an isomorphism of abelian groups

This means that we can transfer the multiplication (i.e. composition) on End(ℤ) to ℤ. What's this ring structure on ℤ? Well if you have the endomorphism that maps 1 onto 2, and you then compose it with the one that maps 1 onto 3, then the resulting endomorphism maps 1 onto 2 added together 3 times, which among other names is known as 6. The multiplication is exactly the standard multiplication on ℤ!

A lot of things had to line up for this to work. For instance, the pointwise sum of endomorphisms needs to be itself an endomorphism. This is why we can't play the same game again; the free commutative ring on one generator is the integer polynomial ring ℤ[X], and indeed the set of ring endomorphisms ℤ[X] -> ℤ[X] correspond naturally to elements of ℤ[X], but because the pointwise product of ring endomorphisms does not generally respect addition, the pointwise operations do not equip End(ℤ[X]) with a ring structure (and in fact, no ring structure on Hom(R,S) can make the category of commutative rings monoidal closed for the tensor product of rings (this is because the monoidal unit is initial)). We can relax the rules slightly, though.

Who says we need the multiplication (or addition, for that matter) on End(ℤ[X])? We still have the bijection ℤ[X] ↔ End(ℤ[X]), so we can just give ℤ[X] the composition operation by transfering along the correspondence anyway. If p and q are polynomials in ℤ[X], then p ∘ q is the polynomial you get by substituting q for every instance of X in p. By construction, this satisfies (p + q) ∘ r = (p ∘ r) + (q ∘ r) and (p × q) ∘ r = (p ∘ r) × (q ∘ r), but we no longer have left-distributivity. Furthermore, composition is associative and the monomial X serves as its unit element. The resulting structure is an example of a composition ring!

The composition rings, like the commutative unital rings, and the abelian groups, form an equational class of algebraic structures, so they too have free objects. For sanity's sake, let's restrict ourselves to composition rings whose multiplication is commutative and unital, and whose composition is unital as well. Let C be the free composition ring with these restrictions on one generator. The elements of this ring will look like polynomials with integers coefficients, but with expressions in terms of X and a new indeterminate g (thought of as an 'unexpandable' polynomial), with various possible arrangements of multiplication, summation, and composition. It's a weird complicated object!

But again, the set of composition ring endomorphisms C -> C (that is, ring endomorphisms which respect composition) will have a bijective correspondence with elements of C, and we can transfer the composition operation to C. This gets us a fourth operation on C, which is associative with unit element g, and which distributes on the right over addition, multiplication, and composition.

This continues: every time you have a new equational class of algebraic structures with two extra operations (one binary operation for the new composition and one constant, i.e. a nullary operation, for the new unit element), and a new distributivity identity for every previous operation, as well as a unit identity and an associativity identity. We thus have an increasing countably infinite tower of algebraic structures.

Actually, taking the union of all of these equational classes still gives you an equational class, with countably infinitely many operations. This too has a free object on one generator, which has an endomorphism algebra, which is an object of a larger equational class of algebras, and so on. In this way, starting from any equational class, we construct a transfinite tower of algebraic structures indexed by the ordinal numbers with a truly senseless amount of associative unital operations, each of which distributes on the right over every previous operation.

[svndaysaweek]

e^(iπ)+1=0 — {Feat. Minnie}

1.3k words

A/N: I've been studying math so hard that I came up with this... I don't know if all readers can understand this, so I recommend googling the inclined terms(which are mathematical ones). Also know that e^(iπ)+1=0 is the most beautiful formula in mathematics,,

p.s: Why is eˣ okay but e^(iπ)+1=0 not? Tumblr mysteries..

Tags: Math(?), Choking, Creampie, Loving Sex

******

Minnie is like the eˣ function to you. The way her consistency fills up your heart—eˣ differentiated is still eˣ—, her always positive character—its domain is always positive number—, her out-of-this-world beauty—e^(iπ)+1=0—, and–

The way her back forms an exponential arc in front of you.

"F-fuck,"

On her knees Minnie is taking your pounding, with her entire body. Her back arcs upward to meet you face to face, as she turns her head back to you and into a blissful kiss.

You draw the sin x graph with your tongue inside her mouth. Up and down, up and down, corresponding to her tongue that draws a cos x graph, intertwined with yours completely—but following the exact same period of 2π.

You push her down to the mattress, and now you can see the hyperbolic curve of her waist. You grab on the narrow valley of it and continue pounding.

What you are doing to Minnie is distorting the perfectness of her body, although it's your way of worshiping it. The circular dark orbs in her elliptical eyes disappear into her head.

You choke her from behind. The amount of air getting in her lungs converges to zero, while the pleasure diverges to infinity.

Her fingers dig into the mattress as you pace up. You feel her walls pulse like sin x. Instant grips and loosenings of her pussy indicate that she is now close. You contribute the last drop of your patience for her orgasm—the maximum, when the derivative of her pleasure hits the X axis.

"I'm cummi–"

Minnie cums with a scream silenced by your grip around her neck. You for a moment regret restraining her voice, but no. You can just make her cum again, again, and again.

You flip her around to face you and resume the race. The race of which finish line you all are aware of obviously.

You kiss her again, this time drawing infinity with your tongue. It of course doesn't mean that it'll last forever, but you feel like it lasts as long as eternity itself. Rather, it would mean the neverending high you two are sharing right now.

Integral. Integrity. You and Minnie in bed together can't be counted as two. Undivided pleasure travels your connected, shared body. No boundaries are found between you and Minnie as you are pulled into a tight hug by her. You can feel how smooth her skin is, how soft her breasts are like it's your body—forget about the breasts, maybe.

Actually, it sounds quite right because it is your body—it's been so long since you lost count how many times you two told each other "You're mine,". Minnie moaning beneath you is yours. Yours to savor, yours to please, yours only to love.

Yes, yours only, and vice versa. You two are bijective functions. Each of your factors matches each of hers, without duplicity.

Again, you're hers only. Minnie is here, taking your cock to define you, to differentiate you, to integrate you. Minnie is moaning underneath your body, to be your proof, to be your solution, to be your answer.

"Are you close, babe?"

You were just about to say that you were, but you are so predictable a problem—Minnie knows the exact formulae to use when dealing with you.

"I am,"

Go ahead, she eyes you. You crook your neck to nibble on her ear and whisper,

"I fucking love you, Minnie,"

The moment you cum inside her, you are sent out of this world. The real world means nothing to you. Imaginary sensations feel more real than the real ones. Like you're feeling the i itself—the imaginary number.

1×1=1. You and Minnie just can't get separated. When it comes to you two, it's not the concept of addition or subtraction. You two love each other so it's 1×1=1. When you two are away from each other, you're still one, because 1÷1=1. Being 2 means you and Minnie are two 1s, which makes you two different individuals—right now, and of course always, you'd disprove that proudly.

You already came about half a minute ago, but you don't pull out. You see Minnie's heaving back and it's perfectly symmetrical—her erector muscles being the perfect axis for it.

It's an even function —f(x)=f(-x)— that you get visual, psychological satisfaction from. That way you could split her perfectly into two halves.

Your hands softly rub on her back. She still is in the middle of recovery, as you can feel her bumping heartbeats on your palm.

"Y-you feel so warm, baby,"

Minnie slightly lifts her limp head from the bed and murmurs with such a low tone. You then pull out and lie down next to her. Turning your body to her side you brush her hair behind her ears. She looks at you and gives you a satisfied, satisfying smile that could literally melt anything, everything.

Minnie's hand comes up to touch your face and–

It hits your still hard dick and she looks at it.

"Wanna go for another round?"

Minnie asks you, sitting up and getting on your thighs. It's a question with only one answer, it's another function that defines you two—a constant function, no matter what she says your answer is yes, undeniably.

Minnie grabs it, strokes it softly, and you feel your lust being recharged. Seems like she doesn't even look for your answer, anyway.

"Holy–"

You're inside her. Right after insertion Minnie starts to ride you out fast. You can only gasp at the feeling of her already-fucked inside, which is what you do every fucking time. Minnie kneeling, each of her knees are next to your both sides as she waves her hip and waist on you.

"Ah, fuck… You can last longer, right?"

She again asks you a question, locking fingers with you. Just like before, your answer is undoubtedly yes. Minnie then brings your hands to her lower waist and leans down forward, completely relying her weight on you. She lets your head into her embrace and whispers into your ear.

"Warm me up again, baby."

Your hands go down to grab on her hips and you begin fucking her upward with pace. As soon as your thrusts start to fuck your previous cum deeper into her womanhood, she moans beautifully into your ear.

Her arms tighten around your head, but the only tightness you can recognize is that of what's around your cock. She nibbles on your ear. Hot breaths tickle your ear, and her teeth on it motivates you to go even faster, rougher, and harsher. That's what loving sex is to her, and of course, to you too.

Your right hand detaches from her ass and gets on the back of her head. Minnie then lifts her head slightly up to fall into a dirty kiss. This time, you review the whole session beforehand.

You are drawing sin x, cos x, and infinity randomly with your tongue. Her back begins to arc exponentially, so you strengthen your hand on her head to keep her body tangent to yours. Your fingers on her ass rubs on her another hole, to make her pleasure diverge to infinity.

And everything you're doing earns her uncontrolled scream of ecstasy, as if she's trying to make an auditory definition of orgasm.

She again closes in to lock lips with you, and soon she cums. On your still-moving cock she cums hard, and in your mouth she lets the orgasmic sound out. It travels through your body fast, reverberates in your skull, sending you over the edge in no time.

You push deep into her for the last time before violently cumming inside her again.

It's explosive, you would term it. Minnie's entire body reacts to every spurt you shoot inside her.

"Holy fuck…"

You let out a sigh of words.

"Baby, that was…"

On top of her lungs she says, only to pause for breathing.

That was awesome, yeah. You know that, because you feel just like her too.

You look into her eyes, and find the excellence itself, the perfect, absolute beauty—e^(iπ)+1=0 .

[lipshits-continuous]

Topological Spaces 1: Introduction and Metric Spaces

Welcome to the first of several posts about general topology! The goal of these posts is to give an overview and introduction to key concepts in topology. I will try to give intuitions about definitions and results so that even if you're not as aquainted with formal mathematics you can still get something from this. Whilst there aren't any prerequisties per say (for the reason above), for those who are interested in the moral formal aspects it will be helpful to be familiar with real analysis. Some familiarity with linear algebra is also helpful in this post though probably won't play a role going forward.

Topology is such a broad subject that assigning one goal is quite hard. One early goal is to generalise the notion of continuity and other familiar notions, which we shall do. Topology certainly doesn't stop there. One large goal is to find properties which are invariant under homeomorphism (bijective continuous maps whose inverse is also continuous). We shall see some examples of this as we go further!

The goal of this post is to give context to the definitions of topological spaces and continuity via the study of metric spaces. The definition of a topological space can seem quite dry and like it's been plucked out of thin air when just presented without motivation. In this sense, metric spaces are the bridge between familiar concepts in real analysis and the more general setting of topology.

1.1: Metric Spaces:

As the name might suggest, metric spaces are sets with an appropriate notion of distance between points in the set. For the real numbers, we have an intuitive sense of distance between two numbers: the absolute value of their difference. From this, we can immediately get three desirable properties we'd want a notion of distance to have:

Positivity: |x-y|≥0

|x-y|=0 if and only if x=y

Symmetry: |x-y|=|y-x|.

These are desirable because this says, in order, that distance is always positive, two points are the same only when the distance between then is 0, and the distance beween x and y is the same as the distance between y and x.

The last property is not as immediately obvious from the definition but is still a fairly intuitive property that we'd expect a notion of distance to have: the triangle inequality. Formally, for any x,y, and z real number we have |x-y|≤|x-z|+|z-y|. This just says that the distance between two points is always shorter than the distance achieved by adding an intermediate point. The name comes from visiualising this with lengths of a triangle! The proof that this holds for the absolute value can be found here.

You might ask whether there are any more properties we'd like but it turns out that this is enough to generalise a lot of concepts in real analysis in an appropriate way. That is, we still maintain a lot of nice results without requiring too many rules. So let us finally see the definition!

Definition 1.1:

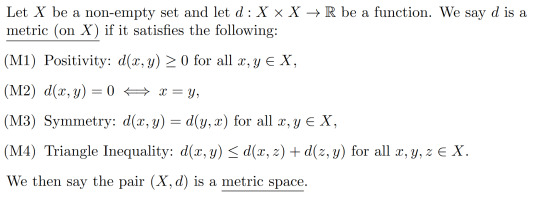
Note: It's common to combine the first two axioms together but for the sake of clarity, I have separated them.

Examples 1.2:

The details of why each of these is a metric can be found in this post.

A result of the second example is that metric spaces are also an appropriate generalisation of normed vector spaces. The fact they are a generalisation is seen from the fact that the discrete metric cannot be seen as the result of a norm and isn't restricted to vector spaces.

1.2: Continuity:

Intuitively, continuous functions are ones that don't have gaps or sudden jumps. In the case of functions from the real numbers to itself, we can view this as "we can draw its graph without lifting the pencil". This can be restated as "points that are close to each other remain close to each other after the function is applied". But how does one formalise "closeness"? With distances of course!

Definition 1.3:

Remark: Continuity departs on the metrics. A function that is continuous in one metric isn't necessarily continuous in another.

Examples 1.4:

Now I'd like to prove a fairly common result to further demonstrate continuity.

Proposition 1.5:

1.3: Open Sets in Metric Spaces

Now we shall see the first aspects of topology creeping in. One way to think about open sets which don't have any points "at the edge". This is immediately clear in the definition we will give below but when we generalise the notion of an open set, we will seemingly lose this. However, we will see that this intuition will still hold!

Definition 1.6:

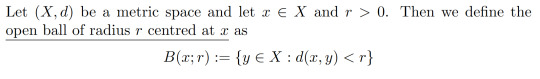
Example 1.7:

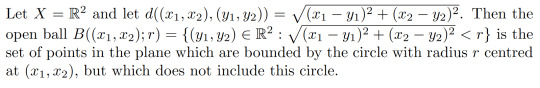
We will now define the notion of an open set using these open balls.

Definition 1.8:

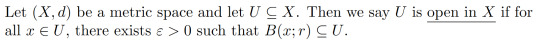
This does indeed formalise "no points at the edge" since for open sets, all points close enough to x are always in U.

Remark: Openness depends on the metric. For example, {0} is open in the real numbers with the discrete metric but not with the absolute value metric.

Now, "open ball" would be a silly name for it if they weren't indeed open in the sense of definition 1.8 but luckily they are!

Proposition 1.9:

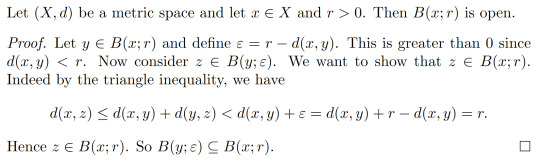
Example 1.10:

Open intervals of real numbers are indeed open with respect to the absolute value. If we have the open interval I=(a,b) for finite a<b, we may view I as an open ball by setting x=(b+a)/2 and r=|b-a|/2. Then I=B(x;r).

Now we shall prove a very important result about open sets that lets you build new open sets out of old opens but will also be the foundation upon which we generalise the notion of open sets!

Lemma 1.11:

Proof:

Remark: Finiteness is important for 3. If we consider the real numbers with the absolute value metric then (-1/n,1/n) is open for all (non-zero) natural numbers. However their intersection over all n is {0} which is not open in this metric.

Typically, courses would usually talk about closed sets now. However, since the discussion doesn't vary much between metric spaces and topological spaces, we will hold off for now.

1.4: Continuity in terms of open sets

This is a very important step in our journey in generalising continuity. This section with along with the next section will suggest that open sets are actually the structures we'd like to study!

Lemma 1.12:

Before we prove this, I'd like to just comment on why this still alligns with our intution about continuity. The right hand side is saying that points end up close together in Y must've been close together in X.

Remark: It is important to note that U open in X does not necessarily imply f(U) is open in Y when f if continuous. For example, take f(x)=x² in ℝ with its usual notion of continuity, then (-1,1) is open but f((-1,1))=[0,1) which is not open. Maps for which open sets are mapped to open sets are called open maps.

We will see examples of how to use the property on the right hand side in the next post!

1.5: Equivalent Metrics

The goal of this section is to see that sometimes different metrics will give rise to the same open sets!

Definition 1.13:

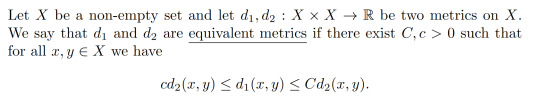
Example 1.14:

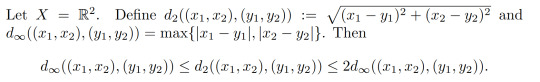
I will omit the details of the proof for brievity. Not that the 2 on the right hand side comes from the fact we're in ℝ² and isn't related to the 2 in the metric.

Remark: Not all metrics are equivalent. The discrete metric and d₂ are not equivalent metrics.

Proposition 1.15:

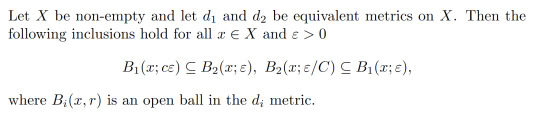
Corollary 1.16:

This ultimately means that some metrics generate the same open sets. Then Lemma 1.12 tells us that equivalent metrics give the same continuous funcitons since we can view continuity in terms of open sets. This suggests that what really matters here is which sets are open. This is what we shall exploit to generalise continuity even further! But that shall have to wait til the next post!

[bagalois]

lecture notes today

i was assigned topology hw0 today and i completed it today. it was two proofs, one of which was more or less trivial (discrete topology is a topology) and the other one which we had shown in class (finite complement topology is a topology).

i dont say that to diss the professor or anything. it's common for math classes to start out this way and then escalate to extreme levels of difficulty (subjective) after just a few weeks.

our analysis lecture today covered an intuitive understanding behind the proof reasoning for theorem that states, if X and Y are sets, that if there exists an injection from X->Y and an injection from Y->X then there exists a bijection between the two. it was some pretty neat reasoning, but it wasn't required to understand for the class so i didnt write it down in my notes. if anyone is interested though i'll post it; the intuitive reasoning isn't too hard once you overcome the difficult notation (which appears to be a common point of all analysis).

[max1461]

Let G be a group. For any g in G, let f_g : G -> G be the map defined by f_g(x) = gx. For any x and y in G, if f_g(x) = f_g(y) then gx = gy by definition. Cancelling (multiplying on the left by g^{-1}) yields x = y. So f_g is injective. For any x in G, notice that f_g(g^{-1}x) = x, so f_g is surjective. Therefore, each f_g is a bijection and lies in S_G.

Consider the map φ : G -> S_G defined by φ(g) = f_g. Notice that for any g and h in G and any element x, we have f_g(f_h(x)) = f_g(hx) = ghx = f_{gh}(x). Thus, f_g ∘ f_h = f_{gh}, Since multiplication in S_G is composition of maps, this means that for any g and h in G we have φ(g)φ(h) = f_g ∘ f_h = f_{gh} = φ(gh), so φ is a homomorphism. Furthermore, suppose that φ(g) = φ(h). Then f_g = f_h, so g = f_g(e) = f_h(e) = h. Thus, φ is injective. Therefore φ is an embedding of G into S_G, and so G can be embedded as a subgroup of a symmetric group.

This is Cayley's Theorem.

[as-if-and-only-if]

so, coding challenge! what’s the quickest way (in a real, normal computer—ok, a very quick way) to generate all and only all length-N sequences of bits such that:

among all bit sequences equivalent to each other under cyclic permutation, only the lexicographically minimal one is generated.

For example:

if N = 4, we only want to wind up with

0000

0001 (equivalent to: 0010, 0100, 1000)

0011 (equivalent to: 0110, 1100, 1001)

0101 (equivalent to: 1010)

0111 (equivalent to: 1110, 1101, 1011)

1111

They don’t need to be generated in lexicographic order, though. Output order is irrelevant.

Also, I’m willing to sacrifice lexicographic minimality for simply generating a single element of each equivalence class if need be—the core of the problem is generating these representatives without redundancy!

If somehow it happens to be convenient, we can even exclude ones that are periodic (like 0000 and 0101, i.e. with nontrivial stabilizer under the cyclic permutation action) if we like. (Doing so is technically better for my application, but only very very slightly, so it’s not necessary in practice.)

Bonus points for an approach that is lazy and parallelizable, e.g. one that bijectively maps integers up to some known quantity to sequences directly; it would be good to sample randomly from things here. Even more bonus points if you can specify N, k, i, and get out the i’th bit sequence of length N (not necessarily in any particular order) that has exactly k 1’s in it! But speed is more important than both of these.

N should be able to be, like, pretty big. At least 25.

Does this problem have a name? Has someone figured this out already?

Note: this is equivalent to generating all lists of integers that sum to N and, similarly, choosing a representative from each orbit-under-cyclic-permutations which is lexicographically maximal among those in the orbit: just look at all runs of the form 0…01 for nonzero bit sequences after rotating the sequence at hand so that it ends with a 1 (e.g. 100011010 ↦ 010001101 = (01)(0001)(1)(01) ↦ [2,4,1,2]; we would not generate this one, and instead generate [4,1,2,2]). (fun exercise: prove this makes sense!)

[spectrallysequenced]

Use of Hilbert's Hotel in Set Theory

I'm helping out some freshmen in their mathematics fundamentals course, and this wonderful argument came up:

Suppose that I have an infinite set, where the definition of infinite we are using is that contains a countable (i.e. bijective to the naturals) subset. This definition assumes the axiom of choice (don't worry about it), but if you'd like, replace the general set in the rest of this post by the real numbers, which we know contain the natural numbers as a countable subset. Let X be an infinite set, and {x_0,x_1,x_2,....} be a countable subset. Suppose we want to add a point to x. The context that this came up in was constructing a bijection from the half- closed ray [-2,inf) to the real numbers. You might know that if this were an open interval (-2,inf) then a bijection would easily be given by R->(-2,inf), x|-> (e^x)-2. Its inverse is log(x+2). We want to "hide" the point, get rid of it somehow. In other words, we add a point * to our set which is disjoint from it, and we want to construct a bijection X u {*} -> X, thereby hiding the point. In the case of the problem, this is a bijection [-2,inf)->(-2,inf), and our point * would be -2. You might know of Hilbert's Hotel, which has infinitely many rooms numbered 1,2,3,.... and is fully occupied. A new guest requests a room, so to accomodate them, the guest at room 1 moves to room 2, the guest at room 2 to room 3, and so on, so all the guests still have a room, but now we have room 1 for our new guest! We employ the same idea here, defining a function by:

f(x) = x_0 if x=*

x_{n+1} if x=x_n,

x otherwise

Then f is a bijection X u {*} -> X (Check!). We "made room" for our new point * by moving our countable set up an index, just as in Hilbert's Hotel!

In the case of our bijection [-2,inf)->(2,inf), we use the natural numbers, so we map -2 to 0, 0 to 1, 1 to 2 etc, and all other points to themselves.

Now we can compose our bijection with the bijection (-2,inf)->R we described earlier to show that [-2,inf) is in bijection with R.

Even basic set theory is cool

[emmy-noethers-rings]

With all the talk about girl math, I think it’s worth understanding the concept. To that end, we have discovered the following results of note:

Proposition 1.1: there exists and isomorphism between girl math and math.

Proof:

Let t:girl math-> math be a set valued “forgetful” function, with t(x) = x.remove(Girl). t is clearly an embedding of girl math in math, thus we get for free that it is injective. Consider the codomain of t and consider Im(t) = { m : m ∈ math}.

We suppose Im(t) to be nonempty. Thus, consider m ∈ Im(t) ⇒ ∄ g ∈ girl math: t(g)=m. However, ∀ m ∈ Im(t), girl m ∈ girl math, a contradiction. Thus t is bijective.

Consider t(m*n)= m*n.remove(Girl)= m.remove(Girl)*n.remove(Girl)=t(m)*t(n). Thus t is structure preserving. Thus, it is an isomorphism. □

Proposition 1.2: the isomorphism between girl math and math is the “girl function” (really it’s better to formalize as the girl functor but that’s neither here nor there) e. As the astute reader may recall, e(x) = e.add(Girl)

Proof:

Left as an excercise to the reader □