#euler's totient

[passion8alot]

I'm working on a proof for my assessment and I am a stage where I need to prove that the function is multiplicative in order for my next argument to be true but in order for my next argument to be true I need to prove that the function is multiplicative.

Its a closed circuit of P(x) -> Q(x), Q(x) -> P(x), and I am trying so hard to get in between them and break up the party, or at least access the playlist that's blasting over the speakers.

[javascript-official]

They say ogre is stupid and it's true!!!! Ogre is studying abstract group theory and can only understand surface level connections between modular group composition and the Euler totient function without grasping more complicated theorems like prime ideals of polynomial rings and it's use in the fast Fourier transform ,..,.. at this rate ogre will never understand the unsolvability of the quintic and Galois theory.,..,. :(((((

:((((((

[timeflow]

for the ask game!

n where n = inf A and A := {j∈ ℤ+ : ¬∃k ∈ℤ+ s.t. φ(k) = j}

assuming φ is euler totient function then I can check the cardinality of the multiplicative group of ℤ/kℤ and just go through the positive integers since I suspect it's probably either a really small number or it doesn't exist or it's an unsolved problem (either of these 2 cases would lead to me calling you names). φ(k)=1 and φ(k)=2 are obviously possible for k=2 and k=3 respectively, so I suppose φ(k)=3. 1,-1∈(ℤ/kℤ)* and 1≠-1 (since this would be k=2 which has φ(2)=1) so for the third element a such that (ℤ/kℤ)*={1,-1,a} you'd need a*a = 1, but since a is coprime with k you also need -a∈(ℤ/kℤ)*. this gives either -a∈{1,-1} at which point a∈{1,-1} which is a contradiction, or a=-a and 2a=0 which implies a divides k which is again a contradiction. so inf(A)=3, which means you have asked me:

3. Ever done any drugs?

no and I don't really intend to either

[magnet-lattice]

Some of the notes have brought to my attention that the relevant context for this post is a mix of fairly old videos with recent enough streams that there are not relevant edited YouTube videos available yet, so I will add some clips for explanations and context. (Transcripts below the cut.)

S3 (Ashswag's edited video):

S5 (MinuteTech's abyss arc finale stream):

Clip 1 (S3, Ashswag's issues with Zam's elevator):

Ash, voiceover, accompanied by footage of Ash pressing a button and then lagging and falling through the floor of the redstone elevator as it rises: This elevator has been discriminating against me for several months now. You see, it runs on some really fancy slime-honeyblock redstone that my internet cannot keep up with. Ash, in the footage: I'm gonna get my revenge on this elevator, one way or the other.

Clip 2 (S5, Ashswag learns Bacon wrote the math problem wrong):

Minute: (okay we're back we're back, chat)

Ash: And you know what the worst part is? Bacon-- I just asked Bacon and he said, "oh, yeah I'm sorry, I didn't know that was the symbol for determinants." I swear when I see this guy at VidCon, I swear, somebody hold me back.

Minute: Oh my gosh, oh my gosh.

Ash: When I see this kid at VidCon, somebody hold me back.

Minute: Oh my god.

Ash: It's absolute value. He-- you know what absolute value is, Minute?

Minute: Yeah, yeah--

Ash: Absolute value is if you get a negative number, it's just the number, it's just the positive version, and-- and this kid didn't know that it's the symbol for determinants, he didn't know it's a symbol for magnit[ude]--

Clip 3 (S5, Ash reacting to Bacon's math error with Minute pre-event):

Ash: I hope someone in chat feels my pain. I genuinely do, I don't know how-- I'm lost for words right now. I've played on this server three years: never been this angry. And he's being so like stuck up about it, chat, you don't know--

Minute: Okay, whatever. What do we get, though, what do we get now?

Ash: This is the-- hold on, one second, let me vent for a second.

Minute: Okay.

Ash: This is like the culmination of weeks and weeks of them being like, "oh, why don't you guys just solve the puzzles", "oh why're you guys just complaining, obviously we're going to stall", being like stuck up about their stupid holier-than-thou mission. They're trying to void spawn and they're trying to make us seem like the crazy people. Never let anyone gaslight you into thinking that you're not worth it, chat. That's my advice for today.

Clip 4 (S5, Ash confronts Bacon about the math errors):

Ash: No, Bacon, not a shred of-- you know how much-- bro. I got called a clown in my math gc. I want you to know that. Because you wrote the question wrong.

Bacon: That's so funny. Okay, wait, what did I write wrong? What did I write wrong, I'm actually curious.

Minute: Bro, I don't wanna fucking talk about it, bro, let's just do our epic finale, please! Let's do our epic finale now, please!

Ash: 23^7819, you wrote "2^37819", it's not possible to solve modular arithmetic when the highest common denominator between 26 and 2 is 2, the Euler's totient formula just doesn't work. It just doesn't work. And also the fucking absolute value thing you did? Boy do I have-- dude, matrices? That symbol is for determinant. And you just-- bro--

Bacon: Yeah, no, actually, I'm remembering this now, I haven't done matrix-- I only did, it was like a year ago.

Ash: (Oh my f--) I'm making-- I don't care, you're gonna get hate comments. I'm saying all of this in the video, I'm--

Zam (background): Oh my god.

Bacon: Wait, wait! No, this isn't my fault, though! This is Meep's fault!

Ash: I don't care.

Minute (background, overlapping): Whatever bro, whatever bro, whatever bro, it's done, it's done, it's done, it's done, let's do our cool--

Bacon: The determinant thing was my fault, but unfortunately the other thing is Meep's fault.

♠️.

[afactaday]

#aFactADay2022

in commemoration of five hundred beautiful facts, today is a double issue, containing twice the facts, twice the fun and for only 2.5x the price!!

Week #20: Hedges! huh, its also week 20.

#500: if you took all the hedges in england and layed them end to end, they would stretch to the moon and... most of the way back... in the 30s it would have been able to do 3 and a half trips to the moon but unfortunately for all the hedgehogs, the government thought it was more efficient to have fewer, larger fields for growing stuff in, so the majority of hedges were torn down. nowadays we understand the full ramifications of hedge-removal :)

#500 part two! 500 is the smallest Strong Achilles Number. an achilles number is a powerful number that is not a perfect power - in other words, the square every prime factor of an achilles number is also a factor. for example, 108 = 2 * 2 * 3 * 3 * 3, therefore the prime factors are 2 and 3. the squares of these prime factors (4 and 9 respectively) are also divisible into 108, but 108 is itself not a square number. the smallest pair of consecutive achilles numbers is 5425069447 (7^3 * 41^2 * 97^2) and 5425069448 (2^3 * 26041^2). now 500 is extra special because it is a strong achilles number, which means φ(500) is also an achilles number. φ(n) is Euler's Totient Function and i cant be bothered to explain it in simple terms so have this definition from wikipedia: Euler's totient function counts the positive integers up to a given integer n that are coprime to n. and φ(500) is 200 which is also an achilles number, making 500 a strong achilles number. try it yourself :D

[nofatclips]

Why do prime numbers make these spirals?

[janmisali]

Here is a tiny fraction of the reasons why 2 is special and why 2 MUST WIN:

Euler’s Formula about planar graphs has the constant 2

2 appears in formulas everywhere, especially around tau and pi

2!=2

2+2=2*2=2^2=2^^2=...

Normal distribution has z^2/2 in it

First prime number

truth values have 2 possibilities

Powerset has size 2^n

Infinitely many platonic solids in dimension 2

Completing the square is sososo important

Conic sections are the most complicated well behaved curves, and they come from order 2 polynomials

Lorentz transform is 2ish

F=1/r^2 makes planets travel in ellipse

x.dx=0 -> |x|^2=r^2

Mandelbrot set is all about raising things to the power of 2. And things escape the set if their modulus goes > 2

The sum of inverse powers of 2 is 2.

Groups come from 2-ary operations

Asymmetric objects have 2 possible chiralities

= is a 2-ary relation

Highest order of differential equation that cannot be chaotic

Can split any angle into 2, or any line segment into 2 with simple construction. Can construct sqare root, but not any other roots.

2 used to prove bound on iterated totient function

Biggest group with trivial automorphism group

Dimension of C over R

Antipodal map is null-homotopic in iff the sphere's dimension is not a multiple of 2

Highest moment needed for CLT

Every nontrivial finite degree subfield of an algebraically closed field is degree 2

Fermat primes come from the number 2

Wilson’s theorem is about elements of order 2

Every element order 2 implies Abelian and vector space

Reflection is order 2 symmetry

Every ring except in characteristic 2 has 2nd root of unity

The Euclidean norm is the only norm with continuous rotational symmetry, and it's analytic, with derivative 2x. It also gives the circle parameterised by e^i\theta

It's the dimension in which shapes first appear

It's the smallest possible number base

.

[natural-blogarithm]

euler's totient function my beloved!!!

talking about GCD and the euclidean algorithm with my high schoolers today :3

[smallblueandloud]

15 people, 15 questions

i was tagged by @everythinghappens-love! thank you!

nickname(s): essbie or blue!

zodiac: stars?

height: 5′1″

last thing googled: euler’s totient function!

sung stuck in my head: “the dismemberment song” by the blue kid because it’s a REALLY good song. cw for blood and... dismemberment, lmao.

number of followers: two hundred something? i try not to think about it too hard lmao

amount of sleep i got: last night, 7.5 hours? or thereabouts? probably less, because it takes me awhile to fall asleep, and also i’m always SUPER groggy in the mornings.

lucky number: 5!

favorite song: “gravity” by sara barielles, forever and always! but right now, “samson” by regina spektor.

favorite instrument: the piano will always, always be my favorite instrument, but i have a very soft spot for the clarinet, which was my instrument for two years

dream job: anything that’s interesting and also actually stops when i clock out

aesthetic: hmm... short, stocky, loud, passionate, joyous, nerdy....... essentially a dwarf. i usually wear jeans and a t-shirt (ideally something space related) so like, a modern day dwarf? it’s hard to appreciate my aesthetic sometimes but tbh i never feel as happy as when i’m wearing jeans, my nasa shirt, and my hair is down and cared-for. oh my god i’m genuinely a dwarf aren’t i.

favorite author: douglas adams probably?

favorite animal noise: purring cat of course. nothing more comforting

random: i pulled my back earlier and now my spine HURTS but that’s nothing new!

i’m tagging anyone who sees this! i always worry about forgetting people so here, if you’re reading this this is for you.

[alukaforyou]

To be honest I would be kind of interested in seeing the paper that you have written for your math prof back then (you mentioned it somewhere (some time?) on Tumblr and on Instagram as well). I'd be interested in your opinion on math in general because I never would have thought that an amazing artist like you majored in math, it's very interesting to me. (Ignore if this all seems weird, LOL! I hope I haven't bothered you in any way.)

i didnt write a math paper i translated eulers e271 which was originally written in latin. it was abt one of fermat’s theorems and the totient function u can see the pdf here but its only in latin or a german translation! 

also im not majoring in math i go to an arts uni LOL i was just asking on insta story cuz i wanted to kno if any of my followers were math majors! i wanna say im good at certain kinds of math my mental arithmetic isnt too fast but idk if u explain it well i think i can do p okay. the prof who taught the course who i did the e271 for was soo amazing i understood everything!!

[comp6841]

Midterm - Past Paper 2017

=== Question 0 === (3 Marks)

What is the most important property for a cryptographic hash function to have to make it as resistant as possible to birthday attacks?

.[A] Preimage resistance .[B] Collision resistance .[C] Confidentiality .[D] Symmetry .[E] Second-preimage resistance .[F] Non-determinism

The whole idea behind the “birthday paradox” is that given a room of people it “seems more likely than you think” that any two people will have the same birthday. The key part here is “any” - the idea of being able to find “any” 2 hashes for a function is a collision attack; hence the answer is B.

=== Question 1 === (3 Marks)

You are a developer of opensource fake-news software called "The trumpet shall sound", or "Trumpet" for short. You wish to use a cryptographic algorithm to generate a 64 character "digital fingerprint" of the "Trumpet" binary, which you will display on your web site so that people can check that they have downloaded a legitimate and unaltered copy of "Trumpet".

What is the most important property for this cryptographic fingerprint algorithm to have?

.[A] Preimage resistance .[B] Collision resistance .[C] Confidentiality .[D] Symmetry .[E] Second-preimage resistance .[F] Non-determinism

If someone is trying to make an illegitimate document, they are essentially trying to fake the hash which means it must be either A, B or E. Since they are looking to find another x’ (i.e. fake document) such that h(x) = h(x’) where x is the original document, the answer is clearly second-preimage resistance - E.

=== Question 2 === (3 Marks)

A MAC is designed to provide .[A] Neither Integrity nor Authentication .[B] Authentication but not Integrity .[C] Integrity but not Authentication .[D] Integrity and Authentication .[E] A Very Fashionable Device

A MAC is a hash of a message and a key - the purpose of hashing this is to ensure the data is not modified (i.e. integrity) and that the other individual knows the key (i.e. authentication) so they can verify the MAC code. Therefore the answer is clearly D.

=== Question 3 === (3 Marks)

You have a password file of 1,000 password hashes. Assuming that 50% of the passwords used were weak passwords which can be found in a dictionary of 1,000,000 common passwords, and that hashing a password takes 12 bits of work on average, roughly how many bits of work would it take to discover all these 500 or so weak passwords?

Note: only enter DIGITS in your answer (or else the automarker will mark it wrong.) _____

The easiest way to do this problem is to firstly hash all the dictionary passwords and put them in a table.

Work = 1,000,000 * 2^12 = 2^20 * 2^12 = 2^32

If you have them in a hash map, you can pretty much do an O(1) (constant time) lookup. This is comparatively very small compared to the computation required to compute a hash function, so we can ignore this. (i.e. we don’t need to worry about the 50% being weak at all here really) So the answer is 2^32 bits of work.

=== Question 4 === (3 Marks)

As for Question 3 but now assume that each password is appended to a different 32 bit number (a salt) before the hash was computed, and that the salt number for each password hash is stored, unencrypted, next to the hash in the password file.

Roughly how many bits of work would it take to discover all the 500 or so weak passwords in this case?

Note: only enter DIGITS in your answer (or else the automarker will mark it wrong.)

Now we actually have to consider the assumption that 50% of the given 1000 passwords are weak. This is actually a generalised birthday problem (except 1/2 for weak instead of 1/365 for birthdays) - i.e. given a room of 1,000 people, what is the value of n such that the probability that n people (0 <= n <= 1000) have a birthday on the same day is 0.5? I think solving this is well beyond the scope of this course - so in this question, I will make the assumption there is instead a 50% chance for any ‘given password’ to be weak. This means that on average your expectation would be that you need to check all the passwords to see if they are weak - the actual answer to the generalised birthday problem is not that far off 1,000 so I would argue we may be overestimating the amount of work by 2^0.5.

For each of the passwords we need to check, we will need to calculate the hash with the given salt for each of the common passwords. Now remember, around half of them are weak; this means on average we will only need to hash half the password list for the ones which are weak. The normal passwords we will end up wasting our time on the entire list:

So our answer based on our assumption would be 41.5 bits of work; I would argue that once you take the unintended generalised birthday problem into account it is probably closer to 41 bits of work.

=== Question 5 === (3 Marks)

Below are six lists of expenses submitted by six politicians. Sadly 3 of the politicians are dishonest and submitted made-up fake expense claims, not costs that they really incurred. :(

{{{ Albus Bert Carl Dave Egon Fred

269 6,296 543 1,137 503 206 1,428 3,217 220 638 4,195 74 3,840 520 3,080 696 5,780 257 2,163 456 5,070 543 7,774 350 165 111 108 113 986 50 2,701 2,176 8,078 145 884 426 339 476 7,963 313 6,530 3,226 64 2,607 68 236 50 108 942 824 2,457 701 9,801 94 17 10 7,952 422 5,717 17 423 112 5,332 5,723 29 158 37 13 5,705 964 3,933 609 723 9,048 8,851 750 6,122 5,769 172 295 99 7,905 91 19 498 165 6,424 9,953 89 275 5,583 3,008 48 491 19 898 56 1,396 8,339 2,675 758 506 158 19 1,945 8,212 427 3,467 1,244 238 916 897 8,503 9,217 2,445 51 3,618 392 3,617 26 866 921 4,219 941 338 1,349

}}}

Correctly identify the status of each politician.

==== 5.1 Albus ==== .[A] Honest .[B] Dishonest

==== 5.2 Bert ==== .[A] Honest .[B] Dishonest

==== 5.3 Carl ==== .[A] Honest .[B] Dishonest

==== 5.4 Dave ==== .[A] Honest .[B] Dishonest

==== 5.5 Egon ==== .[A] Honest .[B] Dishonest

==== 5.6 Fred ==== .[A] Honest .[B] Dishonest

Had to look up a bit about datasets to find out that this was utilising Benford’s law (on Wikipedia) - an observation regarding the frequency of leading digits in real-world datasets. Basically the idea is they should occur fairly closely to the distribution in the image below:

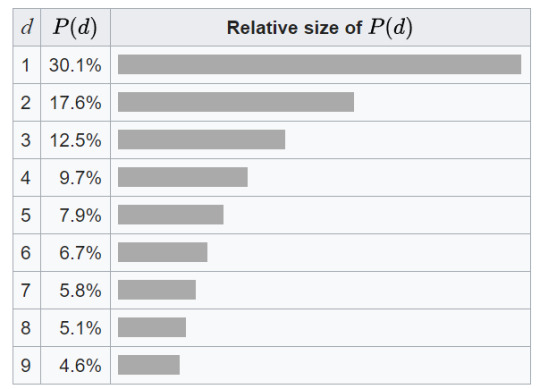
So what you need to do in the above dataset is count the number of 1′s for each of the politicians as leading digits and the percentage they represent in each column. I did this and got A - 29%, B - 33%, C - 10%, D - 14%, E - 5% and F - 24%. You can clearly see that A, B and F more closely resemble real-world data and are more likely the honest politicians (you can also check this with 2′s as well). Therefore the dishonest politicans are likely C, D and E.

=== Question 6 === (10 Marks)

What is the 5th word in the plaintext for the ciphertext below?

{{{ HHPET IAESR DTEHN SRAKA UASMI UEOYR CNWOK FNERA TRONE TNYLO SOENO OHDAS RYUSW DONUR BNSGI STLAU HTTOO DSAHE EWSYO SRTEC IFHWO EHNOC TIHGM AENUB EAERW DEYRV EYHTA OUGNS WSODE ROEVN HLTLA ESSEE SRTEC ONSDA YVREE SNIEO ENHTI IAKRD WOENN AYROA EOHTN OIYFR SAERU TNABU IIGNH RAAPN IFROK NSATN TEUBC OODUY NOKTN AWHTO CAOLT AECDK TIENB RSUBI IEFDI ETFYF NTEBE YAHTE LUBRO TNEKA YHNET EURAO ENHTI EAKRD HETNV YUHGO EURAO COATN LULAT HITNY KDRAE }}}

THEPE 

My immediate idea was that this was a transposition cipher because it would be kinda cruel otherwise since we aren’t given any word spacing information or punctuation. The first word I saw was “THE” at the start, so I figured it must mean something - I attempted assembling with key length 3 however this didn’t make sense (neither did a length of 4). When I tried a length of 5, I got “THEPH” -> “RASEI” -> “NTHED” -> "ARKAS” (i.e. “THE PHRASE IN THE DARK AS”). This seemed to make sense and checking it a bit further, this seemed to be the correct mapping which is (1,2,3,4,5) -> (5,2,4,3,1) - this means the 5th word is “DARK”.

=== Question 7 === (20 Marks)

Suppose we convert letters and other characters into numbers in the range 1..54 using the following table and then separately encipher each of these numbers using RSA with a public encryption key of 23 and a modulus of 55.

{{{ 1 <         21 L       41 4 2 >         22 M     42 5 3 ?         23 N      43 6 4 /         24 O      44 7 5 :         25 P       45 8 6 ;         26 Q      46 9 7 “         27 R      47 ( 8 '         28 S       48 ) 9 @       29 T      49 * 10 A      30 U     50 + 11 B      31 V      51 , 12 C      32 W     52 - 13 D     33 X       53 . 14 E      34 Y       54 / 15 F      35 Z 16 G     36 SPACE 17 H     37 0 18 I      38 1 19 J      39 2 20 K     40 3 }}}

For example the plaintext ":)" would be converted into 5,48, and then each of these numbers would be individually encrypted using RSA to produce the cipertext 15,42.

The remainder of this question has been encrypted using RSA with an encryption key of 23 and a modulus of 55.

{{{ 24,18,49,16,48,49,33,10, 2,12, 52,49,48,16,19,20,16,24,18, 2, 7,16,31,50,49, 7,24, 2,19,12, 16,18,10, 7,16,11,49,49,12,16, 49,12,23,48,34, 5,24,49,52,16, 50, 7, 2,12,26,16,48, 7,10,16, 43, 2,24,18,16,10,12,16,49,12, 23,48,34, 5,24, 2,19,12,16,25, 49,34,16,19,20,16,29,35,16,10, 12,52,16,10,16,33,19,52,50,21, 50, 7,16,19,20,16, 3, 3,47,16, 16,24,18,49,16,10,12, 7,43,49, 48,16,23,19,52,49,43,19,48,52, 16, 2, 7,16,53,53,53,53,53,53, 53,53. }}}

What is the answer codeword?

If you read a little about RSA you would know that you pick 2 primes (p and q) at the beginning of the algorithm which multiply together to give you your modulus. Since we have a modulus of 55, then p = 5 and q = 11. This means Euler’s totient = (5 - 1)(11 - 1) = 40. For the public key it is clear that 23 has been chosen as it doesn’t share any factors with 40. To determine the decryption key we can solve d * e (mod ϕ) = 1. We will do this via Extended Euclidean algorithm:

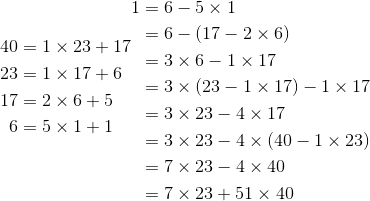
Therefore our private key is (d = 7, n = 40). We can use this to decrypt the answer if we want rather quickly; to save time you could probably just calculate the stuff near the end - for example once you calculate 53 ^ 7 (mod 55) you unlock quite a few bits of the text. An easy way to do this is to realise that 53 (mod 55) = -2 (mod 55) and -2 (mod 55) = -128 (mod 55) = 37. Anyway I got lazy and just dumped it all in a script:

So the codeword is ‘00000000′.

[seb-sec-blog]

RSA activity

This activity took me on a wild journey to make my own RSA keys. Naturally being a cyber actor I created uncrackable keys.

First, we must select 2 prime numbers, p & q. I chose 5 & 7, which we multiply together to get the number n = 35.

We then calculate Euler’s totient, which is represented by phi and given by  ϕ(n) = ( p-1 ) * ( q-1), which for us is 24.

Then we select a number e between 3 and  ϕ(n) which is relatively co-prime with  ϕ(n), that is, e doesn’t share any factors with  ϕ(n)- 17 works.

e and n now form our public key:(e=17, n=35)

We must now choose a value d that satisfies  (e * d mod ϕ = 1). Lets pick 17 since the website doesn’t seem to like large numbers. This number now completes our private key: (d=17, n=35) (pretend this isn’t also our public key, that might be a bad practice in real life)

We now have two keys we can use to encrypt and decrypt messages by doing the following: 

 c = me mod n, where c is the encrypted value of the ascii leter m, and e and n are from our public key. If we choose the letter ‘A’ (ascii value 65), we get a c value of 25.

To decrypt this, we apply a similar formula:

m = cd mod n , with d and n from our private key. Applied to a c value of 25, we get back 65=A

To summarise: We form a public key starting from two prime numbers and can use this key to encrypt a message. We form a private key that satisfies the given formula and can use this to decrypt a message encrypted by the public key. We can release our public key to the world and people can encrypt messages to us using this key. We keep our private key secret and can use it to read those messages.

[raymondsecurityadventures]

Lecture 3

Risk Evaluation and the Folly of Mankind 

It’s not uncommon for low risk, high impact events to be grossly underestimated or grossly overestimated. It’s in human nature to think this way, as some events are so highly unlikely to occur that we never see it occur hence we don’t tend to think about them. And so, security features that protect against such events are often given less consideration than they should otherwise deserve.  On the flip side, threats that are relatively low impact (compared to say the human cost of drink driving) such as terrorism are very visible and the response by governments to such attacks are often very kneejerk-type reactions, with the world’s governments tripling defence spending since 9/11 and implementing incredibly tight airport security controls. This works to assuage our ‘relatively’ unfounded fear of acts of terror, fund the military industrial complex and provide an excuse to introduce repressive legislation that causes more harm to society than multiple 9/11 attacks.

Another example mentioned was the Challenger disaster, wherein the official investigations exploring the possible causes simply stated that it was a freak occurrence that the O ring failed and that it would never happen again. One Richard Feynman however, in following the chain of authority down to the lowest level engineers found that the NASA executives’ publicised probabilities of failure were totally incorrect and that each lower link in the chain of authority provided a higher estimate to the risk of failure than their superior.  This was explained as an example of the tendency for humans to underestimate low risk events, with each manager in the hierarchy exaggerating their inferior’s claims. 

And so Richard preaches that we shouldn’t follow in the footsteps of our governments and managers and when thinking in the scope of security engineering we should always seek to verify the necessity and resources of introducing risk countermeasures. 

Countering the effects of conflicting interest

Introduce as many third parties - as partial as possible and with opposing interests - to help observe any possible risks and contribute them to the risk register.  This will serve to minimise the effects of conflicting interest by setting parties, whose interests lie in opposite directions, to the task and assuming that both parties will act in their own self-interest and balance one another out. 

Compliance Culture 

Is quite useful in that it prevents stupid mistakes from occurring, however, can be dangerous when people assume that merely compliance is enough to prevent risks.  Instead, compliance to a policy should be merely the minimum standard for threat annulment. 

Dealing with Risk:

1. Devote resources and develop countermeasures 2. Eat it (forgot point 2 hehe) 3. Give it to someone else e.g. an insurance company  4. Take it when it’s unavoidable 

Centralisation and its Issues:

Centralisation is the process of consolidating all power of a structure under a single authority. This process, as mentioned in our discussion of the Bell LaPadua model, will have the issue of a single point of failure but will also be less subject to the constraints of bureaucracy and in general, the opinions of the masses. 

Work Factor and its role in preventing attacks: 

Much of cryptography breaks down to the asymmetric information problem and that an attacker would be required to do a prohibitive amount of work in order to break a cipher, while messengers A and B will enjoy access to information which allows them to decipher text far more quickly. 

Insider Attacks: 

Are considered far more effective than most forms of attack as they’re more insidious in nature, difficult to uncover and depending on the insider’s level of access, potentially more impactful. In fact, it is often only when other insiders that have been captured/caught reveal the identities of an organisations malicious insiders that, that these attacks are able to be prevented. 

However, they appear to be under-considered by many companies and other organisations of the world and Richard believes it is because many simply refuse to acknowledge that anyone working under them would be corruptible.

The Key Problem: 

A wants to talk to 10000 people, but to talk to 10000 people safely A will require 10,000 keys. A is struggling to manage 10,000 keys, when suddenly another 10,000 people want to join and suddenly A is swamped with more keys. Enter public key cryptography.

Public Key Cryptography

Fixes this problem by making everyone’s keys public, however, this public key is simply used to identify the actual private key required to decode the message. So there will not be 10,000 keys floating around that need to be managed, everyone just has their own public key and, depending on the system, either a list of keys. 

RSA 

1. Large Prime Number Generation: generate 2 large primes, p and q, preferably of size 1024

2. Multiply them to generate a large composite number, n. This is the foundation of RSA’s security, as composite numbers are difficult to be decomposed into ints prime factors

3. Calculate Euler’s totient (phi) which is simply (p-1) * (q-1)

4. Determine a public key, e, which is simply a prime between 3 and phi paired with n.

5. We determine the inverse of the public key which is the private key, d, with phi, using the Extended Euclidean algorithm or brute force. Meaning that e * d mod (phi) = 1. We pair d with n as well. 

To encrypt a message ‘m’, we convert it to a large number and calculate m^e mod n = c, where c is the cipher text. 

To decrypt it, we simply apply the same calculation but using the cipher text and the private key. 

[comparecheapssl]

RSA Algorithm: A Trusted Method for Encrypting and Securing Data

The RSA algorithm is a commonly used method for secure data transmission in the field of cryptography. It is a type of public-key encryption, which means that it uses two different keys for the encryption and decryption process: a public key and a private key. The public key is used to encrypt the data, while the private key is used to decrypt it.

What is the RSA algorithm?

The RSA algorithm is a powerful encryption method that is widely used to protect sensitive information. It is a type of public-key encryption, which means that it uses two different keys for the encryption and decryption process: a public key and a private key. The public key is used to encrypt the data, while the private key is used to decrypt it.

RSA was first introduced in 1977 by Ron Rivest, Adi Shamir, and Leonard Adleman, and since then it has become the de facto standard for secure data transmission. It is based on the mathematical properties of large prime numbers, making it one of the most secure encryption methods currently in use.

The RSA algorithm works by first generating two large prime numbers, p and q. These prime numbers are used to calculate a third value, n, which is the product of p and q. The value of n is used as the modulus for both the public and private keys.

Read about – Cheap Code Signing Certificate

Why is the RSA algorithm used?

The RSA algorithm is used for secure data transmission because it provides both confidentiality and authenticity. It uses a pair of public and private keys to encrypt and decrypt messages, ensuring that only the intended recipient can read the message and that the message has not been tampered with. It is widely used for secure communications such as email, file transfer, and VPNs, and for digital signatures, software protection, and secure online transactions.

How does the RSA algorithm work?

The RSA algorithm is a method for secure data transmission. It is widely used in electronic commerce and other communications. The algorithm is based on the mathematical properties of large prime numbers and the difficulty of factoring the product of two large prime numbers.

The basic steps of the RSA algorithm are:

Select two large prime numbers, p and q.

Compute n = pq, where n is used as the modulus for both the public and private keys.

Select a public exponent e, where 1 < e < φ(n) (φ is the Euler’s totient function) and e is relatively prime to φ(n).

Compute the private exponent d, where d = e^-1 mod φ(n).

The public key is the pair of values (n, e) and the private key is the pair of values (n, d).

To encrypt a message, the sender uses the recipient’s public key (n, e) and raises the message to the power of e (mod n). To decrypt the message, the recipient uses their private key (n, d) and raises the encrypted message to the power of d (mod n).

Read About – SSL Certificate

Because the encryption and decryption keys are related by the properties of large prime numbers and modular arithmetic, it is computationally infeasible to determine the private key based on knowledge of the public key. This ensures that only the intended recipient can decrypt the message.

Example of RSA encryption algorithm

Here is an example of how the RSA encryption algorithm can be used to encrypt a message:

Select two large prime numbers, p = 61 and q = 53.

Compute n = pq = 61 * 53 = 3233, which will be used as the modulus for both the public and private keys.

Compute φ(n) = (p-1)(q-1) = (61-1)(53-1) = 3120.

Select a public exponent e, such as e = 17. (e is relatively prime to φ(n) = 3120)

Compute the private exponent d, using the extended Euclidean algorithm. We find that d = 2753.

The public key is the pair of values (n, e) = (3233, 17) and the private key is the pair of values (n, d) = (3233, 2753).

Read more

[starling-the-whore]

eulers testicular totient function

[softlifesofttech]

Cryptographic involves maths, funny that

Cryptography is the means by which data is stored and transmitted securely so that only the intended recipient can read or process it. In order to facilitate data encryption (the conversion of plaintext into ciphertext), computational algorithms underpin the process (Munir, 2005). 

A subfield within cryptography includes asymmetric encryption processes. This system makes use of both a public-key, primarily used for encryption and a private-key for decryption. Most often encryption is rooted in applying mathematical operators to produce ‘random’ numbers. This method is particularly secure as it is nearly impossible to calculate the decryption key even with knowledge of the encryption key (Evans, 2013). 

A notable algorithm used for asymmetric encryption is the RSA (Rivest-Shamir-Adleman) algorithm. The RSA algorithm utilises two large prime numbers between 100 and 200 digits to generate the public key. The nature of prime numbers and the limited factors are key to the success. The underlying principle is that multiplying large numbers are easy, but factoring large numbers presents a more challenging and lengthy process (Munir, 2005). 

The mathematical processes that underpin RSA are modular arithmetic, Euler’s theorem, and Euler’s totient function. Modular arithmetic provides a one-way function as opposed to a two-function that is easy to revert (Reges, n.d.). It has however been noted that the RSA algorithm may not be sustainable in the long term (Sullivan, 2013) and researchers have explored additional mathematical based solutions, for example, the elliptic curve. An elliptic curve refers to a curve that satisfies all the points of an equation, y² = x³+ax+b (Kat et al, 2016). This cryptosystem requires that a prime number be assigned as maximum for the curve equation and public point (Knutson, 2018). The idea is that a vertical line can intersect the curve at multiple points to find a new point (dot function). From this new point you can go up or down the axis. Dotting initially is fairly easy but to reverse the process is more challenging.