#formula for binomial theorem

[etcetraetcetra]

•12.11.23• D-15/30•

Maths is next! I love doing maths but the syllabus is too huge. We need to complete revising 12 chapters. But we also have a long gap of 5 days. So far I have completed revising 6, 6 more to go! Recently I have started following James Scholz from YouTube. Although after the 11.5 hrs he studies, when it ends, I become completely burnt out (which is generally not the case when studying alone), I have started to enjoy studying with him. It’s less distracting and I have a structured schedule about when to take a break and when to study. Hope I do good in maths!

Things I did today-

Study theory of Permutation and Combinations

Practice solving problems on PnC

Studied theory of Binomial Theorem (I literally forgot everything about it. Took up a huge chunk of my time)

Practice solving problems on Binomial Theorem

Revise the formula of Trigonometry

________________________________________________________

PS- I am going to my Bio tuition after an entire month. I was suffering from pox for which I didn’t go there for 2 weeks and then the exams on the exact class timings prevented me from going for another week. I missed 2 tests and my teacher once asked my mom about it. Although she was told by my mom I had pox and I was absent, it’s kinda scary to go again today. She already removed 7 people from the group chat coz they didn’t attend for a week. I am absolutely fucked I think.

[coraniaid]

top 5 mathematical identities :)

I wish Tumblr supported LaTeX.

OK, not trying to overthink this too much.

There are lots of fun identities involving binomial coefficients (or their q-analogs), or related integer sequences like the Catalan numbers and Motzkin numbers. But I think I have to go with the Chu-Vandermonde identity: who doesn't like a good convolution formula?

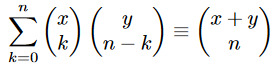
Of all the trigonometric identities I've ever had to learn, this is certainly not the most useful in practice or the hardest to prove or, arguably. the most inherently interesting either. I think the half-angle formula for tan is surprisingly pretty though.

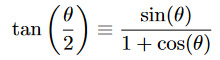
Let S be a finite set of real numbers. The maximum-minimums identity relates the largest element of this set to the smallest elements of every (non-empty) subset of S.

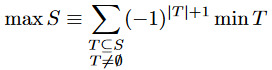
or, more concretely,

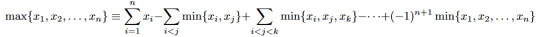
Perhaps not classically beautiful, but certainly enormously useful, the Sherman-Morrisson-Woodbury identity in linear algebra gives a formula for computing the inverse of a rank-k update of an invertible matrix by doing rank-k updates of the inverse of that original matrix. It's valid whenever the matrices are suitably conformable and when both the required inverses exist.

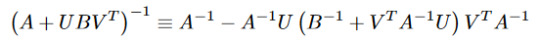
I feel like I have to include something due to Euler here, but -- rather than one of the famous ones involving π or anything to do with topology -- I'll go with some analytic number theory. The pentagonal number theorem gives a series expansion of the Euler function, valid for any complex x in the unit circle.

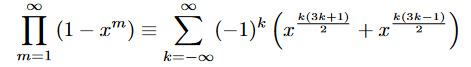
or, expanding both sides,

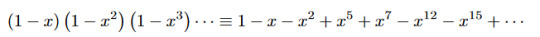
That takes us into the world of q-series and we can generalize it further to get Jacobi's triple product formula or various identities due to Ramanujan or MacDonald's identities for affine root systems or other increasingly exotic and strange things ... but this identity is the prototype for all of them.

[jessecmckeown]

Whence Fabulous Faulhaber?

should I promise not to make this a habit?

Dear Mr. Haran, I'm grateful to you and correspondent Eischen (and Conway) for putting the name of Faulhaber on a calculation which heretofore I'd only known quoted, without attribution, by Heinrich Dörrie in Triumf der Mathematik---(which I've only read in translation). However, I'm most frustrated that neither Dörrie nor Eischen give any satisfying motivation for why the postulate should work.

For bystanders still catching up, this postulate is that if one defines a sequence of numbers $B_k$ "by expanding" $$(B-1)^{k+1} = B^{k+1}$$ and transcribing exponents to subscripts... one finds that the differences $$ (n + B)^{k+1} - B^{k+1} $$ similarly treated are equal to cumulative power sums, $$(k+1) \sum_{j \leq n} j^k$$

So the calculation is doable. My Beef is Dilemmimorphic: Either the notational abuse of $(n + B)^k$ suggests that $B$ should be Some Kind Of Linear Operator, in which case what is it? Or else there's an Amazing Coincidence being Overlooked!

It's a comparative Triviality that the power sums $\sum_1^N n^k$ should be polynomials of $N$, and that the leading term be $\frac{1}{k+1} N^{k+1}$ , so indeed it is perfectly reasonable to consider coefficients $B_{k,j}$ defined by $$ \sum_1^N n^k = \frac{1}{k+1} \sum \binom{k+1}{j} B_{k,j} N^{k+1-j} $$ BUT WHY SHOULD WE ASSUME that in fact $B_{k,j}$ depends only on $j$? That's STAGE MAGIC, and the fact that indeed it somehow works does not explain "where it comes from" (Eischen's favourite phrase on the matter).

So, in my customary way of starting with the actual problem and throwing at it what seems to me the minimum of thought, let's first explicate that "comparative triviality": the sequence of polynomials $p_k(j) = \binom{j+k}{j}$ are integral generators for the Integral-valued polynomials, and are recursively definable as iterated cumulative sums of the constant polynomial $p_0 \equiv 1$: $$\binom{j+k+1}{j} = \binom{j+k}{j} + \binom{j+k}{j-1}$$. Hence, cumulative sums of any polynomial, written in the binomial basis, can be obtained just by incrementing: $$\sum_{j=1}^N \sum a_n p_n(j) = \sum a_n p_{n+1}(N)$$

Next, cumulative sums are themselves defined by induction: $"\sum_{j=1}^0" P(j) = 0$ and $\sum_{j=1}^{N+1} P(j) = P(N+1) + \sum_{j=1}^N P(j)$, or said differently, by the Difference equation $$ SP(N+1) - SP(N) = P(N+1).$$ In other words we are trying to solve the Difference Equations $$ S_k(N) - S_k(N-1) = N^k,$$ but in the basis of Monomials $N^j$ instead of Binomials $p_j(N)$.

The binomial theorem, $$ (x+y)^k = \sum \binom{k}{j} x^{k-j} y^j $$ makes the Taylor-MacLaurin formula a Theorem for polynomials $$ (x+y)^k = \sum y^j \frac{1}{j!} \frac{d^j}{dx^j} x^k $$ which is fruitfully abbreviated $$ P(x+y) = e^{y\\, d/dx} P(x) $$ the Backwards Difference, then, is similarly $$ P(x) - P(x-1) = (1 - e^{- d/dx}) P(x) $$

Shall we say, The kernel of the Backward Difference is reasonably well understood? The differential operator is the retract of the Integral operator $\int_0$, so the Taylor-MacLaurin formula provides us also a section for the Forward Difference operator, $$ 1-e^{-x} = \frac{d}{dx} + A\frac{d^2}{dx^2} $$ where, for now, the main point is that the unbounded-degree differential operator $A$ commutes with $d/dx$, so that, for example $$ (1 - e^{-d/dx}) \left(\int_0 \sim dx - A + A^2 \frac{d}{dx} - A^3\frac{d^2}{dx^2} + - \cdots \right) P(x) = P(x)$$

Of course, there are various paths to the power series, other than via expansion of the powers of $A$, but there is a (Laurent) power series $$ \frac{1}{1-e^{-t}} = \frac{1}{2}\coth(\frac{t}{2})+\frac{1}{2} = \frac{1}{t} + \sum \frac{B_j}{j!} t^{j-1} $$ where $B_j$ are the faBulous Bernoulli numbers.

In any case, applied to simple powers, $$ \left( \int_0 \sim dx + \frac{1}{2} + \sum_{j=2}^{\infty} \frac{B_j}{j!} \frac{d^{j-1}}{dx^{j-1}} \right) x^k = \frac{1}{k+1} x^{k+1} + \sum_{j=1}^{k} \frac{k!}{j!(k-j+1)!} x^{k-j+1} B_j \\\\ {} = \frac{1}{k+1} \sum_{j=0}^{k} \binom{k+1}{j} B_j x^{k+1-j} $$ Finally, the power sum polynomials $S_k$ vanish both at zero (formally an empty sum) and at $-1$ (since $S_k(0) - S_k(-1) = 0^k$), so that in particular, $$ \sum_{j=0}^k \binom{k+1}{j} B_j (-1)^{k-j} = 0$$ THAT'S WHERE THIS IS COMING FROM.

[mitchi-witch]

"Pure mathematics is, in its way, the poetry of logical ideas." — Albert Einstein, German theoretical physicist

ABOUT ME

Hola! It's me, Mitzi from PSHS-CARC! Another quarter had ended and I am here again to share with you my insightful journey of Mathematics 3 for the 4th quarter in which I would never get tired of doing! :>

How would you describe your Math 3 fourth quarter learning journey?

I would describe my learning journey in Math 3 for this quarter as quite complex. For me, this quarter is slower than the previous quarters. However, I had troubles at first because I thought I was doing the right solutions. As time goes by, I learned by my mistakes and I strived` for the better. Although I would describe the topics as easy, for me, the first Long test in this quarter under this subject is a bit complex. Moreover, this quarter served as a path for improvement and it is fun.

Which topic did you find most enjoyable? What made it enjoyable for you? Provide clear images of your solutions to sample problems or exercises on the topic.

Hmmm? This is quite hard since I have two favorite topics but if I were to choose one, I would choose Arithmetic Sequences as my favorite. It is enjoyable since it is quite easy you just have to familiarize yourself with the formulas. What made it more easy is practice which really helped me familiarize myself with them.

What concepts did you find easy to learn? What do you think made them easy for you?

As I said earlier, Arithmetic Sequences is the most enjoyable topic for me because of the reason that it is easy. I had also narrated earlier how and why it was easy for me. Additionally, Geometric Sequences are also easy and the reasons why it was easy is almost the same as those of Arithmetic Sequences.

What concepts did you find most interesting/inspiring? Why do you think so?

The concept I found interesting is the Binomial Theory, which I think would be considered as the hardest topic in this quarter. For me, it is interesting because it was more complex than the others which made me explore it more to learn it.

What concepts have you mastered most? Why do you think so? Provide clear images of your solutions to sample problems or exercises on the topic.

I have mentioned a lot that the easiest topics were Geometric Sequences and Arithmetic Sequences which was easy mainly because of practice. So, for me these are also the topics that I have mastered the most since I had practiced a lot for it which also made them easy.

What concepts have you mastered the least? Why do you think so? Provide clear images of your solutions to sample problems or exercises on the topic.

For me, the concept I have mastered the least is Binomial Theorem primarily the combination parts. It is still easy but it's still my least mastered concept. I think that it's the least mastered since I didn't have a lot of time to learn about it and practice problems.

Honestly, have you developed a better appreciation for mathematics? What lessons, or discussions related to your topics, will you be able to retain throughout your life?

In all honesty, yes. Mathematics 3 had taught me to appreciate concepts to understand things better. It offered me real-life problems that highlighted it's importance in various fields. For me, the topics that I will retain throughout my life are the exponential growth and depreciation rates because I will always remember it when investing into things and it will help me not to get scammed and save more money.

What quick notes do you have for:

i. Teacher:

For the whole year of being my instructor, I could say that he is very consistent and hands-on to his students!! He is really approachable and kind. He doesn't let his students feel left out from the topic. Overall, I could say that he is passionate about his job and he loves his students.

ii. Your Classmates:

I couldn't really say that much about them but one thing's for sure; I hope that they become what they deserve in life. I wish that they could be more independent. I mean, there's nothing wrong for asking for help but just don't do it all the time and also try to do it yourself.

iii. Myself:

I would say that I'm really proud of myself for surviving this year. I have no grudge to myself 'cause keeping some would be really dumb since I can't even change anything about my past. The only Thing I can change is the future and I ought to myself that I will strive for the better and most improved version of myself not only in this subject but also in general. (˶˃ ᵕ ˂˶)

[mathlearningjourney]

My Math 3 Fourth Quarter Learning

Hello again! In this blog, I’ll be reflecting on my Math 3 Fourth Quarter learning journey! This time, we explored Sequences and Series, including Arithmetic Sequences, Geometric Sequences, and the Binomial Theorem. It was a mix of challenging and satisfying moment but overall, I enjoyed seeing how everything was connected.

❔How would you describe your Math 3 Fourth Quarter learning journey?

It was a little bit easy, but I had some trouble with Pascal’s Triangle. Some concepts felt familiar and smooth, while others—especially the Binomial Theorem—required more focus and practice.

❔Which topic did you find most enjoyable? What made it enjoyable for you?

The most enjoyable topic for me was Arithmetic Sequences. I liked how it had a simple and formula:

aₙ = a₁ + (n - 1)d

It felt easy because I just had to plug in the values and solve. It gave me confidence because it was consistent and easy to follow. Even solving for missing terms or the number of terms in a sequence was fun!

❔What concepts did you find easy to learn?

I found both Arithmetic and Geometric Sequences pretty easy to learn, especially once I understood their formulas. You just had to input the values:

aₙ = a₁ + (n - 1)d aₙ = a₁ × rⁿ⁻¹

Also, identifying whether a sequence was increasing or decreasing based on the common ratio was very straightforward.

❔What concepts did you find most interesting or inspiring?

The most interesting concept for me was definitely the Binomial Theorem. It felt very "math-magical" how you could expand something like (a + b)ⁿ using a formula and patterns from Pascal’s Triangle. Even though it was harder than the others, I liked how it brought together exponents, combinations, and patterns.

It made me realize how beautiful and organized math can be when you look closely.

❔What concepts have you mastered most?

I’ve definitely mastered Arithmetic Sequences the most. After doing lots of practice problems and understanding the formula clearly, I feel very confident using it. I can solve for any term, find the common difference, and even compute the sum of terms without much confusion.

❔What concepts have you mastered the least?

Honestly, the Binomial Theorem is still a bit tricky for me. I mean, I kind of get Pascal’s Triangle... but. I still need more practice to feel more comfortable with it. It is also very long.

❔Have you developed a better appreciation for mathematics?

Yes, I think I have! This quarter helped me appreciate math. I also learned that even if something is hard at first, I can improve with effort and practice.

📝 Quick Notes:

To my teacher: Thank you for explaining each step clearly and giving us time to practice. You helped me stay motivated even when I got stuck.

To my classmates: Congrats on finishing Math 3! Continue striving for great things in the future.

To myself:

Practice makes perfect.

🌈 Final Reflection

This quarter showed me that math has a rhythm and structure that you can learn to follow. Some topics were tricky, but every small improvement felt like a win. I’m proud of what I’ve learned and excited to keep improving in the next chapter of my math journey.

Thanks for reading! :D

[piatosniathenie]

MATH REFLECTIONS (the last one!!(for this sy))

After last quarter’s disaster with logarithmic functions and my very well known struggle of keeping up with the lessons, I was pleasantly surprised with the last lessons for this school year since it was sequencing, a topic I’ve been familiar with since the second grade.

Learning about binomial theorem was a different story however because while I do have prior knowledge of it from the fifth and seventh grade, I wasn’t that familiar with the lesson as I have less practice with it than what I had with sequences. My former math teacher ensured that the ability of recognising patterns and figuring out the common differences between terms was drilled into me by the time I was eight, so I suppose I should thank her for that since it would most especially help me in the coming years like it did just this quarter. Being taught them again was fairly easy for me aside from the fact that I often had to look at the book for formulas to reinforce my current knowledge of the topic. Meanwhile with the binomial theorem, it was a matter of remembering Pascal’s Triangle, the patterns associated with it, and basic algebra. I had to do some extra practice with it and solve a good chunk of problems from the book to get the hang of it until I eventually did understand it. For some reason, the entire quarter in Math 3 felt like a haze in all honesty with the lack of the usual difficulty I felt from the previous quarters. Sequencing in general was easy for me due to it already being familiar, but more specifically it was arithmetic sequencing I found the easiest. As mentioned earlier, it was the one I was most familiarised with and anyone who does anything knows that the difficulty of things has a direct correlation with practice and experience. I guess finding the common difference was the easy portion and everything else clicked in place soon after dissecting the formulas as explained by my teacher and consulting former math coaches. With the additional topics I learnt over the last quarter and the practice questions I’ve been doing over the years, I feel like this is the topic I’ve also mastered the most out of the four. I was more thoroughly fascinated by the implications of Pascal’s Triangle after seeing the many patterns found in it like how it’s connected to the fibonacci sequence which then connects it to the golden ratio or how the patterns inspire artworks like Sierpinski’s Triangle. I also learnt along the way that this can be used in combinatorics where it’s used to calculate the combinations of successes and failures. I don’t know, but to me it’s amazing what one triangle full of numbers can do. Unfortunately, the binomial theorem was also the lesson I mastered the least since it was the lesson I had the least amount of experience on, considering the only practice I had with it was doing binomial expansions and nothing more. Math 3 has certainly opened my eyes to the subject after everything that has happened and I will be taking it as a warning for what’s coming soon in the following school years. Honestly, I value math the same as I did five years ago and felt like it was another round of ‘Try, Try, and Try Again Until the Lesson is Embedded in Your Psyche’. All I know is that my grade isn’t going anywhere until I revert back to my old ways (hyper studying math until I’m on the verge of burning out). Oh well, after everything is said and done, I’ve gotta admit that I’m thankful that the ninth grade is over. Thank you to Sir Joseph for putting up with our batch for so long and for the stories you’ve told us over the quarters. As well as teaching us whenever we’re stuck on difficult problems ( which is most of the time) because, I think our batch (most especially me) is clueless half of the time. 

To my classmates, congratulations for making it out of grade 9! Pia, go back to being an academic weapon, please. Balik ka na sa pagiging ‘Sophia’, nagmamakaawa po ako. a favorite quote of mine because it's me on an everyday basis: "I know what it's like to be afraid of your own mind." - Spencer Reid

[gmax-steelsurge]

Hello, other version of Rose. How advanced truly are math lessons? I only hear complaints from my dear chosen regarding math.

- Xolo, from @shadowshock094

Other Version? I teach year thirteen (12 grade) math, so that's algebra and numbers; measurement; relations and functions; trigonometry; and permutations, combinations and binomial theorem.

I'm also an IB teacher, so id say its pretty advanced. at least for most students who aren't interested in math.

Math is based on algorithms, patterns and formulas. its all about personally ability and how much time your willing to put into practice and learning the subject. I'm sure your chosen just isn't fond of the subject, most aren't.

[globalincident]

Well, not exactly. In some cases the mathematicians named do not have a solid claim to the theorem. Let me break them down.

Al-Karaji was the first person to write down the binomial theorem, but the solution to the combinatorial problem associated with it was common knowledge by that point. The binomial theorem is a fairly trivial corrolary to that problem, so it's likely someone thought of it before.

The law of cosines was definitely known about before, since Nasir al-Din al-Tusi wrote down a sketch of the method several centuries earlier than Al-Kashi.

The Fibonacci sequence was known in India, but there's no obvious person to attribute it to. I guess you could call it the India sequence instead?

Pascal's triangle was possibly discovered by Al-Karaji (yes, that guy again), but may have been thought of before that. I'm not sure what is meant by "the Persians and before them the Chinese", since Al-Karaji definitely got there before the Chinese.

The Pythagorean theorem was known earlier (and Pythagoras himself may never have heard of it), but again there's no obvious person to attribute it to.

It's also worth noting that we do not normally name things after the person who discovered them. We normally name them after a notable person associated with the theorem, not necessarily the person who actually discovered it or even knew about it. Gauss's law is so called because it is related to Gauss's theorem, which Gauss rediscovered (but did not fully prove) after Lagrange had already discovered it. Euler's identity is so called because it is related to Euler's formula, which was stated earlier than Euler by Roger Cotes. Bernoulli's principle was developed by Bernoulli, but first expressed in its modern form as an equation by Euler. Having bad names for things is not limited to things discovered by Muslims.

Here's the link to the video

👏 SAY 👏 IT 👏 LOUDER 👏

[shiva10010]

JEE Main 2025: A Guide to the Mathematics Syllabus

An Overview of the Syllabus

The JEE Main Maths syllabus encompasses 14 fundamental units, spanning various branches of mathematics:

Sets, Relations and Functions: This unit lays the foundation with concepts like set theory, operations on sets, relations, functions, and their properties.

Complex Numbers and Quadratic Equations: Dive into the world of complex numbers, including their representation, operations, and applications in solving quadratic equations.

Matrices and Determinants: Explore matrices, their algebra, determinants, properties, and their applications in solving systems of linear equations.

Permutations and Combinations: Master the art of counting and arranging objects with permutations and combinations.

Binomial Theorem and its Simple Applications: Learn about the binomial theorem for expanding powers of a binomial and its applications in various problems.

Sequence and Series: Understand the concept of sequences and series, their operations, convergence, and divergence.

Limit, Continuity and Differentiability: This unit focuses on the fundamental concepts of calculus, including limits, continuity, and differentiability of functions.

Integral Calculus: Explore integration techniques, applying them to solve definite and indefinite integrals and their applications.

Differential Equations: Learn about differential equations, their formation, and solving techniques for various types of equations.

Coordinate Geometry: Delve into the world of coordinates, straight lines, circles, parabolas, hyperbolas, and their properties.

Three-Dimensional Geometry: Visualize and understand lines, planes, spheres, cones, and cylinders in three-dimensional space.

Vector Algebra: Master operations on vectors, their properties, scalar product, vector product, and their applications.

Statistics and Probability: This unit introduces statistical methods for data analysis and probability theory for solving problems involving chance.

Trigonometry: Refresh your knowledge of trigonometric functions, identities, equations, and their applications in solving geometrical problems.

Tips for JEE Main 2025 Maths Preparation

Focus on Concepts: A strong foundation in core concepts is essential. Don't just memorize formulas; strive to understand the underlying principles.

Practice Regularly: Solve problems from various sources, including previous years' JEE Main papers and mock tests.

Clear Your Doubts: Don't hesitate to seek clarification from teachers or mentors for any doubts you encounter.

Time Management: Practice solving problems within the stipulated time frame to develop exam temperament.

Focus on High-Weightage Topics: Analyze previous years' papers to identify topics with a higher weightage and prioritize your preparation accordingly.

By following these tips and diligently studying the syllabus, you can confidently approach the JEE Main 2025 Mathematics section. Remember, consistency, hard work, and a strategic approach are key to success!

[tutoroot]

What are the Important Topics for JEE Mathematics? 

JEE Maths is the subject that most JEE applicants are concerned about. It entails complex concepts, but it also necessitates a significant amount of labour to solve multiple problems. Remember one word if you want to achieve in JEE maths: PRACTICE!!! If you want to enhance your JEE maths and get good grades, you should spend more time-solving problems than reading theories, equations, and answers.

You should be able to solve the tasks with ease. You can improve this by putting in a lot of practice time before the exam. Be tenacious in your pursuit of knowledge, and learn something new every day. JEE Maths questions also assess your ability to focus on a problem and find an answer swiftly. Many people lose up in the middle of a question because they believe it is too long or difficult. That is not something you should do. The JEE Maths paper is never too complicated or lengthy, and there will be students who score higher than 95% on the same paper as you, so why not you?

Important Topics for JEE Mathematics

Don’t recommend solutions without first trying them out: With all of the JEE Mathematics books and study materials available, most students tend to read a question and quickly look for the answer. This is entirely incorrect, and if you continue in this manner for an extended period, you will get reliant on solutions and create a poor habit of yielding. In JEE Maths, on the other hand, you must have a battling mindset. Try your hardest to figure out the trick. We understand you don’t have much time to spend on each question, but at least 60-70 per cent of the time, you should try the question yourself first (spend 10-15 minutes on average on each question) before consulting the solution. It is critical to attempt initially since your brain develops only when you put it under stress.

Important Maths Chapters for JEE: From the standpoint of JEE, some chapters are pretty crucial. Integrals, 3-D Geometry, Probability, Conic Section, Vector Algebra, Functions, Limits, Continuity & Derivability, Matrices & Derivatives, Probability, Permutation, and Combination are among the chapters covered. These chapters could account for up to 65-70 percent of your final grade.

Important JEE Maths chapters and strategies for mastering them: Quadratic equation, Trigonometry, Inverse Trigonometric Functions, Permutation and Combination, Circle, Binomial theorem, Sequence and Series are all crucial chapters for JEE.

The NCERT Mathematics books include all of the necessary information as well as basic and easy questions. They aid in the formation of a solid intellectual foundation and the development of confidence. As far as Jee Main is concerned, this is more than enough. You can go on to advanced problems if you’ve mastered all of the fundamentals.

Make sure you review the formulas for Coordinate Geometry from a credible source. The ideal method is to write them all down on a piece of paper and modify them regularly. Only by putting them into practice can you learn them. As a result, try to solve as many issues as you can.

Take a notebook and jot down all of the formulas, identities, and so on for trigonometry. Examine the notebook you’ve kept daily and make sure it’s up to date. Pure questions of trigonometry are uncommon in JEE Maths, according to the recent pattern of questions. However, some Trigonometry knowledge may be required for topics using Calculus, Coordinate Geometry, Sequence, and Series. As a result, it is preferable to go over the complete formulas and get some practice from RD Sharma.

If you understand the basics of calculus, pick any publication book, such as Arihant Publications, and begin tackling the problems. It is not true that if you solve 100 questions in Calculus, you will solve any issue in that area. For that, you must solve a large number of issues.

Permutations and Combinations, and Probability are two JEE Maths topics in which you must first use your head before using mathematics. Converse will almost always land you in serious trouble. Begin by giving an overview of what the question is asking; for example, if it asks about grouping theory, that particular formula should come to mind. After that, put mathematics away for a moment and think about it as if it were a real-life situation. Start by applying mathematics if you’ve considered what you’d do to solve the problem. By following all the topics it can a student weak in maths crack IIT.

Tutoroot IIT JEE Classes offer Personalised Learning Programs to help you achieve exceptional results in your Competitive Exam. It assists students in identifying their deficiencies by supporting them in preparing for JEE through real-time interactive IIT JEE sessions. They offer adaptive courseware that allows you to learn at your speed.

[etcetraetcetra]

•15.11.24• D-18/30•

Very Late update so I will spoil the exam day too: So I prepared very well for maths but I didn’t study the night before because I was too busy watching India-New Zealand cricket match lol. Besides I was done with my syllabus and was in a chill state where I just had my formula book in my hand, casually flipping through the pages and skimming the formulae. In short I am very satisfied with the exam. I wrote till the last minute, created an ingenious way (according to my teacher) of solving a 5 mark problem that would’ve taken at least 15-20 minutes to solve and solved it in like 3 minutes. I did make a silly mistake though. There was a problem that was very common (I saw that in every book I ever encountered) but I still made a mistake in that. It was only 2 marks though. I felt very relieved and happy after the Math exam was over.

Things I did-

Complete practising Complex Numbers

Read theory of Set, Relation, and Function

Practice permutations and combinations

Revised Binomial Theorem (idk why it’s something I ALWAYS forget)

Casually solve some popular problems on Linear Inequality

Practice Relation and Functions

[thewestcoastmathtutor]

How to Square Fast and Furious ! | The Westcoast Math Tutor

How to Square Fast and Furious ! | The Westcoast Math Tutor https://www.youtube.com/watch?v=adCp6XYl7dM This video shows how to square a binomial of the form a-b. We square the a and we square the b, and the term in the middle is twice the product of the negative of a and b. I highly recommend memorizing this as soon as possible, because this is one of the most important formulas in high school math. 🔔 Join The Westcoast Math Tutor to watch more content on High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ✅ Stay Connected To Me. 👉 Facebook: https://ift.tt/grajOCm ✅ For Business Inquiries: thewestcoastmathtutor@gmail.com ============================= ✅ Recommended Playlists: 👉 Decimal to Fraction https://www.youtube.com/watch?v=3J8Dnl0wLQE&list=PLPSu23Z8U7JG3C22WEiDhDf2bBXZ2yQJK 👉 Improper Fraction to Mixed Number https://www.youtube.com/watch?v=VvL7fXAYtHg&list=PLPSu23Z8U7JG0ErjzsUGv6KfDThOE7SxO 👉 Linear Equation https://www.youtube.com/watch?v=UUeuIQ6bUxU&list=PLPSu23Z8U7JGhun3PPquRpkjrMdNFAggz&pp=iAQB ✅ Other Videos You Might Be Interested In Watching: 👉 Evaluating Logarithms https://www.youtube.com/watch?v=ve9BMVUC6fE 👉 Exponential to Logarithmic Form & Logarithmic to Exponential Form https://www.youtube.com/watch?v=KbEULbAjvtI 👉 Logarithms Easy ! 2 Explanations https://www.youtube.com/watch?v=77msni1vacc 👉Boundedness Theorem, 2 Examples https://www.youtube.com/watch?v=NWPFmBmu380 ================================ ✅ About The Westcoast Math Tutor: Hello Friends! I’m The Westcoast Math Tutor, and with this channel, I will provide tutorial videos to better your understanding of different high school math topics. Once in a while, I will also make other interesting math videos outside of high school math topics. If you have any questions, please ask me in the comments. This channel is what I’ve been doing for you. If you want to do something for me, hit the bell button, like, and share. Thanks for watching, and happy learning, everyone! ✅For Appointment and Business inquiries, please use the contact information below: 📩 Email: thewestcoastmathtutor@gmail.com 🔔Subscribe for more High school math topics: https://www.youtube.com/@TheWestcoastMathTutor ================================= #logarithmroots #inverseproperty #logarithmbasics #logarithmtutorial #mathexplained #logarithmproblems Disclaimer: I do not accept any liability for any loss or damage incurred by you acting or not acting as a result of watching any of my publications. You acknowledge that you use the information I provide at your own risk. Do your research. Copyright Notice: This video and my YouTube channel contain dialogue, music, and images that are the property of The Westcoast Math Tutor. You are authorized to share the video link and channel and embed this video in your website or others as long as a link back to my Youtube Channel is provided. © The Westcoast Math Tutor via The Westcoast Math Tutor https://www.youtube.com/channel/UCqP_EgHF0TGr65xMEcFPcjA October 11, 2023 at 08:21AM

[wiredfaculty0]

Essential Formulas and Theorems for 12th Class Mathematics Board Exams

The 12th class Mathematics board exams in India cover a wide range of topics. Here are some essential formulas and theorems that you should be familiar with for the exam:

Algebra:

Quadratic Formula: For a quadratic equation of the form ax^2 + bx + c = 0, the solutions can be found using the quadratic formula: x = (-b ± √(b^2 – 4ac)) / (2a)

Factorization Formulas:

(a + b)^2 = a^2 + 2ab + b^2

(a – b)^2 = a^2 – 2ab + b^2

a^2 – b^2 = (a + b)(a – b)

a^3 + b^3 = (a + b)(a^2 – ab + b^2)

a^3 – b^3 = (a – b)(a^2 + ab + b^2)

Binomial Theorem: The expansion of (a + b)^n can be found using the binomial theorem: (a + b)^n = C(n, 0) * a^n * b^0 + C(n, 1) * a^(n-1) * b^1 + … + C(n, n) * a^0 * b^n where C(n, r) denotes the binomial coefficient.

Read our blog for more information :-

[ashishkumarletslearn]

Get ncert solutions for NCERT Exercise 8.1 (Q4 to Q14) of Chapter 8 Binomial Theorem Class 11 Maths.

[nancypi-blog1]

MIT grad shows how to do a binomial expansion with the Binomial Theorem and/or Pascal's Triangle. Nancy of mathbff explains the steps on YouTube’s NancyPi channel:

1) HOW TO START A BINOMIAL EXPANSION: If your binomial is something like (x + 3) raised to a power like (x + 3)^5, you have two parts of your binomial: x and 3. You're going to take each of those and raise them to different powers in each term of the expansion. You can start your expansion just by writing these powers out.. For the FIRST PART of your binomial, x, it will start with a power of 5 (your power number) in the first term of the expansion (x^5), and then in each term after the power will go down by 1 (x^4, x^3, etc. all the way down to a zero power, x^0). Then you take the SECOND PART of the binomial, 3, and multiply each term by a power of 3. The 3 factor will start with a power of 0 in the first term, so 3^0, and then will increase by 1 power in each term after.

2) HOW TO FIND THE COEFFICIENTS (with the FACTORIAL or COMBINATION method): Then there's one more number to find, a number that gets multiplied in front of each term, or a binomial coefficient. There are two ways to find the coefficients (for the Pascal's Triangle way, see below). To find the coefficients using the factorial, combination ("n choose k") formula of n!/(k!(n-k)!, each term has a coefficient number you find using an n value equal to the power number, 5, and a k value that runs from 0 for the first term up through 5 for the last term. This number gets multiplied by the other factors in each term, and then simplify for your final expansion.

3) HOW TO FIND THE COEFFICIENTS (with PASCAL'S TRIANGLE): You can instead use Pascal's Triangle to find the binomial coefficients. Whichever row of Pascal's Triangle has your power number in it, as the second number, is the row that gives you all the coefficient numbers you'll need for your expansion. Each coefficient is multiplied with its term, and then you can simplify the expansion.

4) WHAT IF THE BINOMIAL HAS SUBTRACTION? It's very similar. It's easier to think of the subtracted term as "adding a negative number", and then all of the negative number (in parentheses) will be raised to the power in each term of the expansion. Note: if the binomial have something like 2x - y instead of x - y, make sure that all of (2x) is raised to each power.

For more: check out the NancyPi channel on YouTube at: https://www.youtube.com/channel/UCRGXV1QlxZ8aucmE45tRx8w