#binomial theorem

[vibhatriestostudy]

Dare i say i was maybe, just maybe, a little productive today??

I mean Binomial Theorem did decide to suck my soul out today but hey, I survived 😀(thats what counts right??)

Also inorganic chemistry🤌🤌🤌🤌*chefs kiss*

[alvareus-the-sorcerer-of-seals]

What’s your favorite math proof?

I forgot the name but it’s the binomial theorem one

I don’t know how to explain it but it feels satisfying. I don’t know how a math proof can be satisfying, it just is. Ig I like how everything just snaps together and makes sense, even though some parts are anti intuitive.

[study-diary1007]

July 26th | Math chp 8 - Tuition imposition :((

[roboyomo]

Good luck yomomo 💥

JUST CAME OUT OF THE ALGEBRA FINAL

EVEN THOUGH IT WAS THE ONE I WAS LEAST WORRIED FOR, I STILL THOUGHT "what the Fuck do i do there"

[numericalpie]

YES

Please reblog if YES so your followers will know!

[potatotrash0]

I MISS DOING LOTS OF FACTORING AND BINOMIAL EXPANSION………wanna go back to permutations and combinations too. love…….<3

[friday411]

🍿Sunday🍿 🍿Double Feature!!🍿

Professor Moriarty ~ BAMF Maths Nemesis

-=<+>=-

His work on binomial theorem Kicked off a mathematical schism They gave him a chair At uni of - where? Because of his intellect fearsome

-=<+>=-

His work "Dynamics of Asteroids" Was called astrophysics on steroids Now was the Professor A radical thinker, or Just a case of human hemorrhoids?

[nammagadbad]

- biology cell chapter test eeee i know most of this cuz im reading that chap for the third time

- yassified my calculator cuz everyone has the same fucking one ( bunny sticker and green cloud yes)

- binomial theorem test tom and ykw they did this chapter on the day I didn’t attend school and my god whadafuk is that chap? Hopefully im gonna eat the test up🤪

- JUMPSCARE (yes that is my personality now)

[shankhachil]

Countdown to JEE (Main): Week 2/33

I've done a lot this week! Hit almost all the topics I wanted to. You'll notice that there are some topics I've covered but not solved questions for — these are the ones I studied for the first time and/or made notes for.

Other than that, I have my school unit tests from next Wednesday, so there's that. Sadness.....

Test results:

Test at physics tuition center: 116/120, rank 1/67! Yay!

Aryabhatta National Mathematics Competition: score unknown, result expected on 10/07/2024.

Topics covered:

Physics: Potential and Capacitance; Electromagnetic Waves, Waves on a String; Modern Physics; Gravitation; Electromagnetic Induction (6/3)

Chemistry: Chemical Thermodynamics; Atomic Structure; Chemical Equilibrium; Halogen Derivatives; Solid State (5/3)

Mathematics: Differential Equations; Area Under a Curve; Applications of Derivatives; Determinants; Complex Numbers; Ellipses; Hyperbola; Binomial Theorem; Functions (9/3)

Questions solved:

Physics: - FIITJEE Electrostatics* module, Assignment section — 56 questions, 52 correct - Allen Potential and Capacitance module, O1 and O2 — 88 questions, 77 correct -FIITJEE JEE (Main) archives, Electromagnetic Waves — 12 questions, 10 correct - Allen Waves on a String module, O1 and O2 — 67 questions, 59 correct - FIITJEE JEE (Main) archives, Modern Physics — 40 questions, 34 correct - Allen Gravitation module, O1 and O2 — 61 questions, 55 correct Total: 383/60 questions, 287 correct *FIITJEE includes Potential and Capacitance under Electrostatics, while Allen does not.

Chemistry: - Allen Chemical Thermodynamics module, S1 and S2 — 40 questions, 37 correct - R. N. Sarin, Atomic Structure — 18 questions, 18 correct - R. N. Sarin, Chemical Equilibrium — 11 questions, 11 correct - Allen Halogen Derivatives module, JEE (Advanced) archives — 24 questions, 22 correct Total: 93/60 questions, 88 correct

Mathematics: - Allen Differential Equations module, O1 — 30 questions, 25 correct - Allen Area Under a Curve module, Do Yourself 1, 2, 3, 4, 5 and O2 — 51 questions, 46 correct - FIITJEE JEE (Main) archives, Applications of Derivatives — 45 questions, 39 correct - FIITJEE JEE (Main) archives, Determinants — 22 questions, 17 correct - Yellow Book, Complex Numbers, single-choice questions — 20 questions, 17 correct - Pink Book, Ellipses, single-choice questions — 16 questions, 14 correct - Yellow Book, Binomial Theorem, single-choice questions — 15 questions, 12 correct - Pink Book, Hyperbolas, single-choice questions — 21 questions, 18 correct - Allen Functions module, O1 and JEE (Main) archives — 48 questions, 44 correct Total: 268/60 questions, 232 correct

GRAND TOTAL: 744/400 questions, 607 correct

Upcoming tests:

23/06/2024 (next Sunday) — Allen monthly test. Topics: Kinetic Theory of Gases; Physical Thermodynamics; Electrostatics; Potential and Capacitance; Current Electricity; Electromagnetic Induction; Alternating Current; Electromagnetic Waves; Waves on a String; Sound Waves; Ray Optics; Wave Optics; Circle; Functions; Differentiation; Applications of Derivatives; Indefinite Integrals; Definite Integrals; Area Under a Curve; Differential Equations; Matrices; Silicates; Molecules That Do Not Exist; Coordination Chemistry; Metallurgy; Electronic Displacement Effects; Halogen Derivatives; Atomic Structure; Chemical Equilibrium; Solid State; Solutions; Chemical Kinetics; Chemical Thermodynamics. Yeah. I've no idea how I'm going to finish the syllabus in time, since I haven't even started Coordination Chemistry, Metallurgy or Alternating Current — they finished the classes in Allen before I even joined the batch. Anyway, let's see.

That'll be all till next week — see you again!

[what-about-zaladane]

Entropy, Intuition, and The Art & Science of Shuffling A Tarot Deck (Or: How Many Times Should You Shuffle It, Mathematically?)

This post is specifically about riffle shuffling -- not overhand or pile shuffles.

tl;dr: If you care about randomness and making sure all the cards have a fair chance of coming up, 9-10 times.

But how much should you really care about randomness?

Let's back up.

Mathematicians Gilbert, Shannon and Reed developed a model of randomness for riffle shuffling (i.e. the snappy type of shuffling you do with a playing card deck). They found that the first few shuffles of a deck of playing cards only rearrange the order of the cards a little…but by the 7th shuffle, the deck's order is almost indistinguishable from random.

You might ask -- but a tarot deck has 26 more cards! Does that matter?

Yes, it does.

Each added card increases the permutation space of the deck. You go from 52! (a number with 68 digits) to 78! (a number with ~115 digits). The number of possible orderings explodes -- as does the time and effort it takes to "mix" those orderings.

The Math

If you do a perfect riffle shuffle, the deck becomes increasingly mixed. The GSR Theorem uses total variation distance from uniform randomness to measure just how mixed it is. Total Variation Distance is a number between 0 and 1 that tells you how different two probability distributions are. The two distributions we are comparing are:

The probability distribution of the deck after n shuffles

A perfectly random deck, where every single card has an equal chance of being in every position.

What do different values of TVD mean?

If TVD = 1 -> the two distributions are completely different

If TVD = 0 -> the two distributions are essentially the same

Imagine you’re drawing the top card of a tarot deck after shuffling.

If the deck isn’t well shuffled yet, certain cards are more likely to be on top.

If the deck is perfectly shuffled, every card has exactly a 1 in 78 chance to show up.

Total Variation Distance measures:

"How far are we from that perfect 1-in-78-for-every-card situation?"

TVD is basically asking: how unfair is this shuffle still?

If you shuffle enough times, you'll get close to 0.

TVD Convergence Chart

Here’s what the convergence of TVD looks like for 52- and 78-card decks:

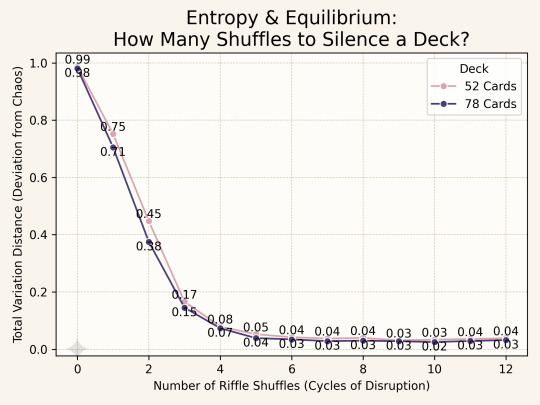
You can see that the first few shuffles don't bring us much closer to a totally "fair" deck -- but once we hit 4 or 5 shuffles, we start to converge to 0 rather quickly!

Back to the Shuffling

GSR modeled the distribution of permutations using the random riffle shuffle model, which assumes:

You cut the deck into two halves with a binomial split

You then interleave the cards in all possible ways

(Btw: This gives you a Markov chain on the symmetric group S_n, where n is the number of cards. If you just flinched at that sentence -- don't worry about this! Forget you read it! It doesn't come up again in the post.)

What about a 78-card Deck?

According to Bayer & Diaconis (1992) in “Trailing the Dovetail Shuffle to its Lair”:

The number of riffle shuffles needed to mix a deck of n cards is approximately:

So 9 to 10 riffle shuffles are needed to randomize a 78-card tarot deck.

Okay But…How Important is Randomness in Tarot, Anyways?

Honestly, it depends on you.

If you believe in pure chance, then randomness is the point. You want the cards to speak without being nudged by muscle memory or old orderings.

But if you believe in "divine" order, then even imperfect shuffles are sacred. Every shuffle is a divination. Every card is a mirror.

So shuffle 3 times. Shuffle 9. Shuffle until the deck feels right.

But just keep in mind: mathematically, 10 riffle shuffles are optimal if you want to approach full chaos. And chaos is very good at telling the truth.

What Do I Do Personally?

You'll notice that the graph of TVD converges pretty fast after about 6-7 shuffles. Personally, when I'm feeling the need to completely reset the deck, I shuffle 10 times. Any other time, I shuffle 8. I'd love to tell you that there's some fantastic reason for this, but it's mostly because I'm Chinese-American and I'd probably do everything eight times if I could. :D

[gladiusveritatis]

I think next time analysing Moriarty's ideology through the works of Hegel and Marx would be more interesting for the fandom, as it doesn't involve mathematics. Yes, I am talking about sharing the info about the birth of the Binomial Theorem on tiktok. I might do it here as well, alongside posting my poetry, writing, analyses, and so on.

Also, I knew that debunking on the Binomial Theorem or just anything that-is-a-bit-historical-and-analytical would be pointless because those videos usually flop 😭 dear MTP fandom, this is not so dark-academia-I-am-real-life-William coded of you 💔

[parihere]

6:15 PM

I have my revision test tomorrow from 4pm

focusing on chemistry today and going to do maths tomorrow morning

chapters that I'm expecting to complete :

- thermodynamics (today)

- thermochemistry (today)

- sequence and series (tmrw)

- binomial theorem (just the pyqs) (wtv time left)

I just have maybe 60 days until my jee exams first attempt (fuck my life)

[queenofspades2222]

Productivity Diaries #6

-completed rotational motion -completed 1.5 of binomial theorem last lecture -revised mole concept -revised matrices and determinants

breaks: 1.nap 2.editing 3.music

[roboyomo]

a potion of FUCK THE BINOMIAL THEOREM

[studyingwithoutthedying]

ALR SO I AM GOING ON A TRIP ON 20TH. COMING BACK ON 26TH. HAVE AN IMP EXAM ON 28TH AND THEN ONE ONE 3RD, WHICH IS EVEN MORE IMPORTANT. AROUND 20,000 RS HAVE BEEN WASTED BECAUSE OF RESCHEDULING THE TRIP CUZ THESE DATES KEPT ON FLUCTUATING. BUT ITS ALL SETTLED NOW. NEED T0 GRIND SO THAT I CAN COMPENSATE IN SOME WAY FOR THE MONEY.

Targets :

6hrs of studying everyday

Waking up early first and foremost

PLAN FOR TOMORROW:

2hrs chem : GOC 1 lecture , some prep for improvement exam.

2hrs Math: quadratic equations revision , studying binomial theorem in depth

2hrs physics: coloumbs law questions and then start with Electric feild

[anzadosara]

Ado covered Usseewa when she was 18; now she's covering Spy x Family at 21

Mary Shelley ran away with her lover at 15, wrote Frankenstein at 19

Newton discovered the binomial theorem as a teenager just bcz he was bored

What the hell am I doing with my life