#lagrange polynomial

[jadagul]

I'm sorry, scipy, but this is just not the Lagrange polynomial for these data!

I was messing around with some data plotting and it seems like none of the python tools will actually plot a 350-degree polynomial fit.

Like I know that plotting a 350-degree polynomial fit is dumb. I'm an educator. I want a graph showing exactly why plotting a 350-degree polynomial fit is dumb, but that requires me to actually get the equation of the 350-degree polynomial fit.

And like calculating the Lagrange polynomial is straightforward. I know a couple ways to do it. But I don't want to have to roll my own code when in theory there are libraries for this.

[yokowan]

re: the orbital mechanics post

orbital mechanics isn't really "simple". the amount of complexity and diversity of the problems you can solve is huge. there's a lot of very complicated math to be done for spacecraft dynamics. but the complexity is all emergent!

so often in engineering you have to bundle all the stuff that's impossible to determine with just pure math into a dimensionless constant or polynomial approximation and then figure it out experimentally. so many things affect pressure losses in an engine or the spanwise efficiency of a wing that you basically don't have an option besides just sticking that shit in a wind tunnel and taking measurements. but not orbital mechanics! that's just gravity!

when you see those animations of super complicated n body simulations, all of that chaos comes entirely from gravitational attraction and the conservation of momentum+energy. you could write down all the fundamental laws of orbital mechanics on a half size sticky note, all the other stuff is just derived from those. you won't always get closed form solutions, but the controlling forces are so simple that numerically integrating them can be very efficient and very accurate.

now, of course, it's not always just gravity. there's atmospheric drag and solar wind and the Yarkovsky–O'Keefe–Radzievskii–Paddack effect or whatever. additional forces are always there, and these get complicated enough that you do end up needing to put in empirically determined adjustments. but on short timescales, the simpler model holds true! in my experience you tend to treat these as perturbations to the pure gravity model. you take your existing solution and just add the additional stuff on top. when you're doing orbit determination and rendezvous and the like, you're assuming your object is acting only under the influence of gravity and engines. you're probably even assuming its orbit is perfectly elliptical and ignoring gravity from other bodies.

none of this is to say that spacecraft dynamics is like. objectively better than other disciplines within engineering. (it is though.) it just feels nicer to me. there's something very clean about it. there's no jank, it's like solving puzzles. i am literally out here playing touys with my little spaceships. writing out the lagrangian of the circular restricted 3 body problems and seeing the stable points just fall out of it is so neat! and those are real!!!!!!! they're not artifacts of the math that just happen to show up, lagrange points are real and spacecraft use them all the time.

anyways me when i fucking get you

[hkmathematics]

Q 4(a) | Lagrange Interpolation Polynomial | DU BSc (H) Numerical Analys...

[drmikewatts]

Soft Computing, Volume 29, Issue 1, January 2025

1) KMSBOT: enhancing educational institutions with an AI-powered semantic search engine and graph database

Author(s): D. Venkata Subramanian, J. ChandraV. Rohini

Pages: 1 - 15

2) Stabilization of impulsive fuzzy dynamic systems involving Caputo short-memory fractional derivative

Author(s): Truong Vinh An, Ngo Van Hoa, Nguyen Trang Thao

Pages: 17 - 36

3) Application of SaRT–SVM algorithm for leakage pattern recognition of hydraulic check valve

Author(s): Chengbiao Tong, Nariman Sepehri

Pages: 37 - 51

4) Construction of a novel five-dimensional Hamiltonian conservative hyperchaotic system and its application in image encryption

Author(s): Minxiu Yan, Shuyan Li

Pages: 53 - 67

5) European option pricing under a generalized fractional Brownian motion Heston exponential Hull–White model with transaction costs by the Deep Galerkin Method

Author(s): Mahsa Motameni, Farshid Mehrdoust, Ali Reza Najafi

Pages: 69 - 88

6) A lightweight and efficient model for botnet detection in IoT using stacked ensemble learning

Author(s): Rasool Esmaeilyfard, Zohre Shoaei, Reza Javidan

Pages: 89 - 101

7) Leader-follower green traffic assignment problem with online supervised machine learning solution approach

Author(s): M. Sadra, M. Zaferanieh, J. Yazdimoghaddam

Pages: 103 - 116

8) Enhancing Stock Prediction ability through News Perspective and Deep Learning with attention mechanisms

Author(s): Mei Yang, Fanjie Fu, Zhi Xiao

Pages: 117 - 126

9) Cooperative enhancement method of train operation planning featuring express and local modes for urban rail transit lines

Author(s): Wenliang Zhou, Mehdi Oldache, Guangming Xu

Pages: 127 - 155

10) Quadratic and Lagrange interpolation-based butterfly optimization algorithm for numerical optimization and engineering design problem

Author(s): Sushmita Sharma, Apu Kumar Saha, Saroj Kumar Sahoo

Pages: 157 - 194

11) Benders decomposition for the multi-agent location and scheduling problem on unrelated parallel machines

Author(s): Jun Liu, Yongjian Yang, Feng Yang

Pages: 195 - 212

12) A multi-objective Fuzzy Robust Optimization model for open-pit mine planning under uncertainty

Author(s): Sayed Abolghasem Soleimani Bafghi, Hasan Hosseini Nasab, Ali reza Yarahmadi Bafghi

Pages: 213 - 235

13) A game theoretic approach for pricing of red blood cells under supply and demand uncertainty and government role

Author(s): Minoo Kamrantabar, Saeed Yaghoubi, Atieh Fander

Pages: 237 - 260

14) The location problem of emergency materials in uncertain environment

Author(s): Jihe Xiao, Yuhong Sheng

Pages: 261 - 273

15) RCS: a fast path planning algorithm for unmanned aerial vehicles

Author(s): Mohammad Reza Ranjbar Divkoti, Mostafa Nouri-Baygi

Pages: 275 - 298

16) Exploring the selected strategies and multiple selected paths for digital music subscription services using the DSA-NRM approach consideration of various stakeholders

Author(s): Kuo-Pao Tsai, Feng-Chao Yang, Chia-Li Lin

Pages: 299 - 320

17) A genomic signal processing approach for identification and classification of coronavirus sequences

Author(s): Amin Khodaei, Behzad Mozaffari-Tazehkand, Hadi Sharifi

Pages: 321 - 338

18) Secure signal and image transmissions using chaotic synchronization scheme under cyber-attack in the communication channel

Author(s): Shaghayegh Nobakht, Ali-Akbar Ahmadi

Pages: 339 - 353

19) ASAQ—Ant-Miner: optimized rule-based classifier

Author(s): Umair Ayub, Bushra Almas

Pages: 355 - 364

20) Representations of binary relations and object reduction of attribute-oriented concept lattices

Author(s): Wei Yao, Chang-Jie Zhou

Pages: 365 - 373

21) Short-term time series prediction based on evolutionary interpolation of Chebyshev polynomials with internal smoothing

Author(s): Loreta Saunoriene, Jinde Cao, Minvydas Ragulskis

Pages: 375 - 389

22) Application of machine learning and deep learning techniques on reverse vaccinology – a systematic literature review

Author(s): Hany Alashwal, Nishi Palakkal Kochunni, Kadhim Hayawi

Pages: 391 - 403

23) CoverGAN: cover photo generation from text story using layout guided GAN

Author(s): Adeel Cheema, M. Asif Naeem

Pages: 405 - 423

[nightwingsaregoths]

skimmed the Wikipedia page for the history of calculus and i don't care about anachronism anymore. sorry. Mastermind attended AP Calculus when he was Starflight's age and was a front row student. Yeah, the College Board exists. The nasty American company managed to open a portal into Pyrrhia and make young dragon students pay 97 dollars to take a test. He was also the only student to score above a 90 percent on the Unit 10B test. Farsight studied 1.5x the usual amount on Taylor polynomial approximations, Lagrange error bound, and memorized the Maclaurin polynomials for e^x, sine, cosine, and 1/(1-x), got an 87, and never quite got over it.

I have been far too normal and conventional with my writing. Too much silly incomprehensible romance without good reasons. Someone should do something slightly exciting and unexpected.

[ollies-studyblr]

AP Calc BC: Taylor Polynomials

[balteus]

we've been solving a single lagrange polynomial problem for 3 hours. shortest math task in a stem program girl i hate it here

[piesk8]

Now it's time to study Numerical Analysis!

Very interesting exam, one of my favourite subject at high school. Now I will analyze numerical and applied methods for engineering and their implementation on MatLab.

In photo: Lagrange polynomials used for polynomial interpolation.

[lthmath]

Ruffini

Paolo Ruffini, born on 22nd September 1765, was an Italian mathematician and philosopher. Ruffini's 1799 work marked a major development for group theory. Ruffini developed Joseph Louis Lagrange's work on permutation theory, following 29 years after Lagrange’s "Réflexions sur la théorie algébrique des equations" (1770–1771) which was largely ignored until Ruffini who established strong connections between permutations and the solvability of algebraic equations. Ruffini was the first to controversially assert the unsolvability by radicals of algebraic equations higher than quartics. This angered many members of the community such as Malfatti (1731–1807). Work in this area was later carried on by those such as Abel and Galois who succeeded in such a proof.

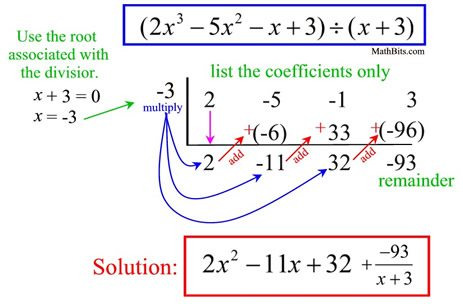
In mathematics, Ruffini's rule is a practical way for paper-and-pencil computation of the Euclidean division of a polynomial by a binomial of the form x – r. It was described by Paolo Ruffini in 1804. Ruffini's rule is a special case of synthetic division when the divisor is a linear factor.

[fulltestbank]

Test Bank For Calculus: Multivariable, 12th Edition Howard Anton

TABLE OF CONTENTS   PREFACE ix   SUPPLEMENTS x   ACKNOWLEDGMENTS xi   THE ROOTS OF CALCULUS xv   11 Three-Dimensional Space; Vector 657   11.1 Rectangular Coordinates in 3-Space; Spheres; Cylindrical Surfaces 657   11.2 Vectors 663   11.3 Dot Product; Projections 673   11.4 Cross Product 682   11.5 Parametric Equations of Lines 692   11.6 Planes in 3-Space 698   11.7 Quadric Surfaces 705   11.8 Cylindrical and Spherical Coordinates 715   12 Vector-Valued Functions 723   12.1 Introduction to Vector-Valued Functions 723   12.2 Calculus of Vector-Valued Functions 729   12.3 Change of Parameter; Arc Length 738   12.4 Unit Tangent, Normal, and Binormal Vectors 746   12.5 Curvature 751   12.6 Motion Along a Curve 759   12.7 Kepler's Laws of Planetary Motion 771   13 Partial Derivatives 781   13.1 Functions of Two or More Variables 781   13.2 Limits and Continuity 791   13.3 Partial Derivatives 800   13.4 Differentiability, Differentials, and Local Linearity 812   13.5 The Chain Rule 820   13.6 Directional Derivatives and Gradients 830   13.7 Tangent Planes and Normal Vectors 840   13.8 Maxima and Minima of Functions of Two Variables 845   13.9 Lagrange Multipliers 856   14 Multiple Integrals 866   14.1 Double Integrals 866   14.2 Double Integrals Over Nonrectangular Regions 873   14.3 Double Integrals in Polar Coordinates 882   14.4 Surface Area; Parametric Surfaces 889   14.5 Triple Integrals 902   14.6 Triple Integrals in Cylindrical and Spherical Coordinates 909   14.7 Change of Variables in Multiple Integrals; Jacobians 918   14.8 Centers of Gravity Using Multiple Integrals 930   15 Topics in Vector Calculus 942   15.1 Vector Fields 942   15.2 Line Integrals 951   15.3 Independence of Path; Conservative Vector Fields 966   15.4 Green's Theorem 976   15.5 Surface Integrals 983   15.6 Applications of Surface Integrals; Flux 990   15.7 The Divergence Theorem 999   15.8 Stokes' Theorem 1008   A Appendices   A Trigonometry Review (Summary) App-1   B Functions (Summary) App-8   C New Functions From Old (Summary) App-11   D Families of Functions (Summary) App-16   E Inverse Functions (Summary) App-23   READY REFERENCE RR-1   ANSWERS TO ODD-NUMBERED EXERCISES Ans-1   INDEX Ind-1   Web Appendices (online only)   Available in WileyPLUS   A Trigonometry Review   B Functions   C New Functions From Old   D Families of Functions   E Inverse Functions   F Real Numbers, Intervals, and Inequalities   G Absolute Value   H Coordinate Planes, Lines, and Linear Functions   I Distance, Circles, and Quadratic Equations   J Solving Polynomial Equations   K Graphing Functions Using Calculators and Computer Algebra Systems   L Selected Proofs   M Early Parametric Equations Option   N Mathematical Models   O The Discriminant   P Second-Order Linear Homogeneous Differential Equations   Chapter Web Projects: Expanding the Calculus Horizon (online only)   Available in WileyPLUS   Blammo the Human Cannonball -- Chapter 12   Hurricane Modeling -- Chapter 15         Read the full article

[junglelong]

Programa scilab

PROGRAMA SCILAB MANUAL

PROGRAMA SCILAB SOFTWARE

PROGRAMA SCILAB CODE

Print the value of root i.e value of 'x'.Loop up to desired iterations and stop.We are using x to store the current value as well as next approximation as we are using loop. Use the formula of Newton Raphson method inside the loop.Use any loop (for loop, while loop) according to your convenience, if you are using for loop there is no need to initialize 'i' earlier.If two points are given in which the root lies then calculate the average of both, if they are not given then choose a suitable starting value according to the function.Define the derivative function f'(x)=0 using deff keyword in scilab.Define a function f(x)=0 as required using deff keyword in scilab.Aim: Scilab program for lagrange polynomial interpolation / X 1 2 5 10 //set the arguments Y 10 75 100 12 //set the corresponding values of f (x) nlength (X) // store the length of total arguments x.

PROGRAMA SCILAB CODE

Here is algorithm or the logical solution of Scilab program for Newton Raphson Method The following is the source code of scilab program for polynomial interpolation by numerical method known as lagrange interpolation. Get more information about Derivation of Newton Raphson formula. This method is named after Sir Isaac Newton and Joseph Raphson. Scilab Program for Lagrange Polynomial Interpolation -> Computer Science AI provides resources like python programs, c programs, java programs, c++ programs, php programs, html and css free resources, articles and 'how to' tutorials on computer, science, artificial intelligence and tech world. In numerical analysis, Newton's method which is also known as Newton Raphson method is used to find the roots of given function/equation. Singular is developed under the direction of Wolfram Decker, Gert-Martin Greuel, Gerhard Pfister, and Hans Schönemann who head Singular's core development team within the Department of Mathematics of the University of Kaiserslautern.Write a Scilab program for Newton Raphson Method. This includes tools for convex geometry, tropical geometry, and visualization.

PROGRAMA SCILAB SOFTWARE

Its advanced algorithms, contained in currently more than 90 libraries, address topics such as absolute factorization, algebraic D-modules, classification of singularities, deformation theory, Gauss-Manin systems, Hamburger-Noether (Puiseux) development, invariant theory, (non-) commutative homological algebra, normalization, primary decomposition, resolution of singularities, and sheaf cohomology.įurther functionality is obtained by combining Singular with third-party software linked to SINGULAR.

resultants, characteristic sets, and numerical root finding.

a general class of non-commutative algebras (including the exterior algebra and the Weyl algebra),.

polynomial rings over various ground fields and some rings (including the integers),.

Its main computational objects are ideals, modules and matrices over a large number of baserings.

PROGRAMA SCILAB MANUAL

a comprehensive online manual and help function.

easy ways to make it user-extendible through libraries, and.

an intuitive, C-like programming language,.

a multitude of advanced algorithms in the above fields,.

It is free and open-source under the GNU General Public Licence. Singular is a computer algebra system for polynomial computations, with special emphasis on commutative and non-commutative algebra, algebraic geometry, and singularity theory.

[bjtrust]

Paraview plugins

#Paraview plugins serial

#Paraview plugins code

In order to limit its memory consumption, this light version of Gmsh only embarks the internal data reader and the visualization procedure described above and customized for this particular application. In order to be able to use this plugin, one requires to compile a light version of Gmsh compiled as an external library as well as compiling ParaView itself with the plugin enabled. Note that this plugin is not provided in the binary release of ParaView.

#Paraview plugins code

The resulting new ParaView plugin named “GmshReader” is now provided with the official ParaView source code (version 5.7.0 and above). Note that contrary to Gmsh, VTK supports exclusively Lagrange polynomials and ParaView provides uniform h-refinement to visualize these polynomials. Although it has not been tested yet within this work, this new feature opens up additional promising perspectives for the visualization of high-order meshes and solutions. Recently, the support for arbitrary-order Lagrange polynomials has also been introduced in ParaView. Consequently, memory requirement can be significantly reduced for the selective h-refinement procedure compared to uniform h-refinement. In the second case, recursive h-refinements is applied to the parent elements and their child elements until this error is locally minimized. The recursive h-refinement of the initial mesh which generates the visualization grid can be either uniform (every edge of the parent element is split in the same way) or selective, based on a local visualization error. Afterwards, traditional visualization of the solution occurs through a straightforward piecewise linear interpolation on the Then, the high-order polynomial solution is interpolated on the new nodes of the refined visualization grid. First, a recursive h-refinement of high-order elements based on classical automatic mesh refinement (AMR) is applied and defines a refined linear visualization grid. The visualization capabilities of Gmsh rely on a two-step strategy further described in. This allows to encode any polynomial basis using the same framework. Moreover, a major asset of the native file format of Gmsh consists in the use of an explicit description of the polynomial basis functions within the file, instead of an imposed convention. Historically, few open source tools provide high-order meshing and visualization capabilities. 1 – Illustration of the usage of the GmshReader plugin in ParaView. This coupling enables parallel visualization of massive high-order solution in parallel, in client-server mode.įig. This plugin combines respectively ParaView’s scalability in parallel and Gmsh’s ability to apply h-refinement of the initial mesh followed by the interpolation of any arbitrary high-order polynomial solutions on the resulting visualization grid. In this context, a new ParaView plugin which integrates Gmsh as an external library has been implemented for off-line post-processing and visualization of high-order solutions saved under the Gmsh format, see Figure 1. Only very recently, arbitrary-order Lagrange polynomials have been introduced in VTK and their support in ParaView for both high-order meshes and solutions is gaining traction, which confirms the growing interest and need for such features. However, ParaView relies on the Visualization Toolkit (VTK) whose data models have historically mainly supported linear elements. On the other hand, ParaView is an efficient open source parallel visualization tool which has been used successfully for post hoc visualization of large scale, unstructured data sets up to several billions of dof.

#Paraview plugins serial

However, Gmsh is in essence a serial tool and is therefore limited to a relatively low number of dof and level of h-refinements. The high-order solution is then interpolated at the new mesh nodes in order to provide an optimal visualization grid. This method relies on recursive h-refinements of the initial mesh, coupled to a projection error estimation. The open source mesh and visualization tool Gmsh provides a general method for the post-processing of high-order finite element fields. However, the lack of visualization tools able to handle a large number of degrees of freedom (dof) has been a major bottleneck for the analysis of high-order finite element solutions generated by massively parallel simulations. Recently high-order finite element methods initially introduced in the research community such as discontinuous Galerkin (DG) and flux reconstruction (FR) have gained considerable attention in industry, thanks to their high-accuracy on unstructured meshes, their efficiency and scalability.

[myprogrammingsolver]

HW7 Solution

7.1 Lagrange Polynomials (t) (H) 4 pts You just watched some poor kid let go of her balloon in a 8-m high mall food 0 0 court. The four data points at right represent the height of a balloon (H, in meters ) as a funcDon of Dme (t, in seconds). 1 1 (a) Create the 3rd-order Lagrange polynomial that exactly passes through all H(t) 2 7 data, and use it to esDmate (extrapolate) the…

[drmikewatts]

IEEE Transactions on Fuzzy Systems, Volume 32, Issue 11, November 2024

1) Online Active Learning for Evolving Error Feedback Fuzzy Models Within a Multi-Innovation Context

Author(s): Edwin Lughofer, Igor Škrjanc

Pages: 5998 - 6011

2) Flexible Prescribed Performance Output Feedback Control for Nonlinear Systems With Input Saturation

Author(s): Yangang Yao, Yu Kang, Yunbo Zhao, Pengfei Li, Jieqing Tan

Pages: 6012 - 6022

3) Adaptive Fuzzy Predetermined Performance Control of p-Normal Systems With Unknown Control Coefficients via Dynamic-Events

Author(s): Qidong Li, Changchun Hua, Kuo Li, Hao Li

Pages: 6023 - 6034

4) Reinforcement Learning for Fuzzy Structured Adaptive Optimal Control of Discrete-Time Nonlinear Complex Networks

Author(s): Tao Wu, Jinde Cao, Lianglin Xiong, Ju H. Park, Hak-Keung Lam

Pages: 6035 - 6043

5) Enhanced Distributed Outlier-Resilient Fusion Estimation With Novel Dimensionality Reduction Under IT-2 T–S Fuzzy System

Author(s): Yunyi Yang, Guoguang Wen, Yidi Wang, Zhaoxia Peng, Kai Xiong

Pages: 6044 - 6055

6) Dual-Channel Fuzzy Interaction Information Fused Feature Selection With Fuzzy Sparse and Shared Granularities

Author(s): Hengrong Ju, Xiaoxue Fan, Weiping Ding, Jiashuang Huang, Suping Xu, Xibei Yang, Witold Pedrycz

Pages: 6056 - 6068

7) Data-Driven Reinforcement Learning Tracking of MASs Under Injection Attack: A Controller-Dynamic-Linearization Approach

Author(s): Shanshan Sun, Yuan-Xin Li, Zhongsheng Hou

Pages: 6069 - 6078

8) Set-Membership Observer Design for T-S Fuzzy 2-D Systems With Unmeasurable Premise Variables

Author(s): Changyi Xu, Chenyang Zhao, Fengyuan Zhang, Chao Zhang, Zhongyang Fei

Pages: 6079 - 6087

9) Discrete-Time Finite Fuzzy Markov Chains Realized Through Supervised Learning Stochastic Fuzzy Discrete Event Systems

Author(s): Hao Ying, Feng Lin

Pages: 6088 - 6100

10) Stability and Filtering for Delayed Discrete-Time T-S Fuzzy Systems via Membership-Dependent Approaches

Author(s): Wen-Hu Chen, Chuan-Ke Zhang, Zhou-Zhou Liu, Leimin Wang, Yong He

Pages: 6101 - 6111

11) Granular Ball Fuzzy Neighborhood Rough Sets-Based Feature Selection via Multiobjective Mayfly Optimization

Author(s): Lin Sun, Hanbo Liang, Weiping Ding, Jiucheng Xu

Pages: 6112 - 6124

12) Fuzzy Adaptive Distributed Optimization of Uncertain Multiagent Systems With Time-Varying Delays

Author(s): Jiayi Lei, Yuan-Xin Li, Shaocheng Tong

Pages: 6125 - 6135

13) Adaptive Fuzzy Tracking Control for Nonlinear Time-Delay Systems With Performance Constrained by Deferred Monotone Tube Boundaries

Author(s): Guopin Liu, Yu Zhang, Changchun Hua, Yafeng Li, Jiannan Chen

Pages: 6136 - 6148

14) A Polynomial Chaos Expansion Approach to Interval Estimation for Uncertain Fuzzy Systems

Author(s): Zhenhua Wang, Lanshuang Zhang, Choon Ki Ahn, Yi Shen

Pages: 6149 - 6159

15) Adaptive Reinforcement Learning Strategy-Based Sliding Mode Control of Uncertain Euler–Lagrange Systems With Prescribed Performance Guarantees: Autonomous Underwater Vehicles-Based Verification

Author(s): Yang Wu, Yue-Ying Wang, Xiang-Peng Xie, Zheng-Guang Wu, Huai-Cheng Yan

Pages: 6160 - 6171

16) Fuzzy Switching Sliding Mode Control of T-S Fuzzy Systems via an Event-Triggered Strategy

Author(s): Xiaofei Fan, Tao Li

Pages: 6172 - 6184

17) Deep Reconciled and Self-Paced TSK Fuzzy System Ensemble for Imbalanced Data Classification: Architecture, Interpretability, and Theory

Author(s): Yuanpeng Zhang, Guanjin Wang, Ta Zhou, Ge Ren, Saikit Lam, Weiping Ding, Jing Cai

Pages: 6185 - 6198

18) Promoting Objective Knowledge Transfer: A Cascaded Fuzzy System for Solving Dynamic Multiobjective Optimization Problems

Author(s): Han Li, Zidong Wang, Nianyin Zeng, Peishu Wu, Yurong Li

Pages: 6199 - 6213

19) A Double Integral Noise-Tolerant Fuzzy ZNN Model for TVSME Applied to the Synchronization of Chua's Circuit Chaotic System

Author(s): Lin Xiao, Dan Wang, Liu Luo, Jianhua Dai, Xiangru Yan, Jichun Li

Pages: 6214 - 6223

20) Multicenter Knowledge Transfer Calibration With Rapid Zeroth-Order TSK Fuzzy System for Small Sample Epileptic EEG Signals

Author(s): Chuang Wang, Pengjiang Qian, Zhihuang Wang, Weiwei Cai, Jian Yao, Yi-Zhang Jiang, Xiangyu Yan, Wenjun Hu

Pages: 6224 - 6236

21) Distributed Adaptive Fuzzy 3-D Formation Tracking Control of Underactuated Autonomous Underwater Vehicles

Author(s): Peng Wan, Zhigang Zeng

Pages: 6237 - 6251

22) Imitation Learning and Teleoperation Shared Control With Unit Tangent Fuzzy Movement Primitives

Author(s): Hao Wen, Wen Fu, Wu Chen, Jiale Huan, Changsheng Li, Xingguang Duan

Pages: 6252 - 6266

23) Adaptive Relative Fuzzy Rough Learning for Classification

Author(s): Yang Zhang, Changzhong Wang, Yang Huang, Weiping Ding, Yuhua Qian

Pages: 6267 - 6276

24) Supervisory Control of Networked Fuzzy Discrete Event Systems

Author(s): Feng Lin, Hao Ying

Pages: 6277 - 6287

25) Multiview Fully Interpretable TSK Fuzzy Classifier Enhanced by Multiview Accompanying GMMs

Author(s): Erhao Zhou, Fu-Lai Chung, Shitong Wang

Pages: 6288 - 6302

26) Whole-Process Predefined-Time Tracking Control for T–S Fuzzy Euler–Lagrange Systems

Author(s): Jia-Du Zhang, Tao Han, Bo Xiao, Chang-Duo Liang, Huaicheng Yan

Pages: 6303 - 6313

27) Multilayer Evolving Fuzzy Neural Networks With Self-Adaptive Dimensionality Compression for High-Dimensional Data Classification

Author(s): Xiaowei Gu, Qiang Ni, Qiang Shen

Pages: 6314 - 6328

28) Few-Shot Fuzzy Temporal Knowledge Graph Completion via Fuzzy Semantics and Dynamic Attention Network

Author(s): Xuanxuan An, Luyi Bai, Longlong Zhou, Jingni Song

Pages: 6329 - 6339

29) NeuFG: Neural Fuzzy Geometric Representation for 3-D Reconstruction

Author(s): Qingqi Hong, Chuanfeng Yang, Jiahui Chen, Zihan Li, Qingqiang Wu, Qingde Li, Jie Tian

Pages: 6340 - 6349

30) Hierarchical Rule-Base Reduction-Based ANFIS With Online Optimization Through DDPG

Author(s): Marius F. R. Juston, Samuel R. Dekhterman, William R. Norris, Dustin Nottage, Ahmet Soylemezoglu

Pages: 6350 - 6362

31) Dynamic Event-Triggered Asynchronous Fault Detection via Zonotopic Threshold Analysis for Fuzzy Hidden Markov Jump Systems Subject to Generally Hybrid Probabilities

Author(s): Mengmeng Liu, Jinyong Yu, Ke Zhao

Pages: 6363 - 6377

32) Fuzzy Event Knowledge Graph Embedding Through Event Temporal and Causal Transfer

Author(s): Chao Wang, Li Yan, Zongmin Ma

Pages: 6378 - 6387

33) Optimal Control for Fuzzy Markov Jump Singularly Perturbed Systems: A Hybrid Zero-Sum Game Iteration Approach

Author(s): Jing Wang, Yaling Huang, Xiangpeng Xie, Huaicheng Yan, Hao Shen

Pages: 6388 - 6398

34) Fuzzy Adaptive Exact-Optimal Consensus Output-Feedback Control for Uncertain Nonlinear High-Order Multiagent Systems

Author(s): Mengyuan Cui, Shaocheng Tong

Pages: 6399 - 6408

35) Multimodal Learning-Based Interval Type-2 Fuzzy Neural Network

Author(s): Chenxuan Sun, Xiaolong Wu, Hongyan Yang, Honggui Han, Dezheng Zhao

Pages: 6409 - 6423

36) Long-Term Multivariate Time-Series Forecasting Model Based on Gaussian Fuzzy Information Granules

Author(s): Chenglong Zhu, Xueling Ma, Pierpaolo D'Urso, Yuhua Qian, Weiping Ding, Jianming Zhan

Pages: 6424 - 6438

37) Stabilization of Interval Type-2 T–S Fuzzy Systems via Time-Dependent Memory Sampled-Data Control and Its Applications

Author(s): Subramanian Kuppusamy, Samson S. Yu, Hieu M. Trinh, Peng Shi

Pages: 6439 - 6448

38) Distributed Nash Equilibrium Seeking for Games With Unknown Nonlinear Players via Fuzzy Adaptive Method

Author(s): Ying Chen, Qian Ma

Pages: 6449 - 6459

39) Fault-Tolerant Event-Triggered Sampled-Data Fuzzy Control for Nonlinear Delayed Parabolic PDE Systems

Author(s): Bo-Ming Chen, Zi-Peng Wang, Feng-Liang Zhao, Junfei Qiao, Huai-Ning Wu, Tingwen Huang

Pages: 6460 - 6471

40) Stability and Fuzzy Optimal Control for Nonlinear Itô Stochastic Markov Jump Systems via Hybrid Reinforcement Learning

Author(s): Zhen Pang, Hai Wang, Jun Cheng, Shengda Tang, Ju H. Park

Pages: 6472 - 6485

41) Graph Model for Conflict Resolution for Mixed-Stability Combinatorial Foresight Based on the Combination of Regret Theory and VIKOR Method

Author(s): Peide Liu, Xue Wang, Yingxin Fu, Peng Wang

Pages: 6486 - 6499

42) Fuzzy Observer-Based Finite-Time Adaptive Formation Control for Multiple QUAVs With Malicious Attacks

Author(s): Chao Li, Jiapeng Liu, Xinkai Chen, Jinpeng Yu

Pages: 6500 - 6511

43) A Novel HPPD-Type Fuzzy Switching Control Scheme of Active Vehicle Suspension Systems

Author(s): Yunshuai Ren, Xiangpeng Xie, Jiayue Sun, Xiaoming Wu

Pages: 6512 - 6522

44) Fuzzy Optimal Tracking Control for Autonomous Surface Vehicles With Prescribed-Time Convergence Analysis

Author(s): Yan Zhang, Xin Yan, Wencheng Zou, Zhengrong Xiang

Pages: 6523 - 6533

45) Event-Triggered-Based Adaptive Fuzzy Finite-Time Resilient Output Feedback Control for MIMO Stochastic Nonlinear System Subject to Deception Attacks

Author(s): Jipeng Zhao, Guang-Hong Yang

Pages: 6534 - 6547

46) Prescribed Performance Fault-Tolerant Optimal Control for Wastewater Treatment Process With Multivariable

Author(s): Dingyuan Chen, Cuili Yang, Dapeng Li, Junfei Qiao

Pages: 6548 - 6559

47) Switched Command-Filtered-Based Adaptive Fuzzy Output-Feedback Funnel Control for Switched Nonlinear MIMO-Delayed Systems

Author(s): Zhenhua Li, Hongtian Chen, Hak-Keung Lam, Wentao Wu, Weidong Zhang

Pages: 6560 - 6572

48) Fault Detection of Unmanned Surface Vehicles: The Fuzzy Multiprocessor Implementation

Author(s): Xiang Zhang, Shuping He, Zhihuan Hu, Ruonan Liu, Hongtian Chen, Weidong Zhang

Pages: 6573 - 6582

49) On Arithmetic Operations of LR Fuzzy Numbers With Different Shape Functions

Author(s): Gholamreza Hesamian, Arne Johannssen

Pages: 6583 - 6587

50) State and Fault Interval Estimation for Discrete-Time Takagi–Sugeno Fuzzy Systems via Intermediate Observer Base on Zonotopic Analysis

Author(s): Lulin Zhang, Zhuoxue Li, Yi Li, Jiuxiang Dong

Pages: 6588 - 6593

[alqorithms]

13 march 2018, 6:32pm // 19ºC

currently working on my vector calculus assignment, focussing on limits involving functions of several variables as well as finding Taylor polynomials! it’s very tedious to show as much working/justification as i can but it has to be done! Learned about Lagrange multipliers with constraints in class today and i’m finding it all so interesting! hope uni is treating everyone well despite the stresses of every day life, we can do this! :-)

[crimsonpublishersminingscience]

Densification Kinetics of Titanium Carbide- Based Cermet During the Pressure Sintering-Crimson Publishers

Densification Kinetics of Titanium Carbide- Based Cermet During the Pressure Sintering by Kovalchenko M S in Aspects in Mining & Mineral Science

 Opinion

Titanium carbide-based cermets with the addition of other carbides and with metal binders of nickel, iron and their alloys are used in mechanical engineering technology and instrumentmaking industry as wear-resistant and corrosion-resistant materials and coatings. The goal remains to increase the mechanical and functional properties of cermets, and for this research is being conducted aimed at optimizing the compositions and improving the technology for their manufacture. This report presents the results of a study of nonisothermal pressure sintering a powder mixture containing, in addition to titanium carbide TiC, mass fractions of carbides: 4% VC, 6% Mo2C, 6% NbC, and 20% NiCr. Pressure sintering of powder mixtures was carried out on an induction heating unit made on the basis of a hydraulic press and a thyristor converter in an atmosphere formed as a result of the interaction of a graphite die with air. After preliminary slow heating, a sintering regime was established with a controlled heating rate of 15K/min under a constant pressure of 20MPa. The obtained experimental data on the current change in relative density and temperature in the process of cermet sintering showed a regular acceleration of its densification with increasing temperature.

The processing of the experimental data was performed within the framework of the theory of bulk viscous flow of the porous body using the developed computer programs. The exact data on the densification rate was determined by the approximation method of the compaction curve by Lagrange polynomials, the differentiation of which yielded a derivative, that is, the densification rate, at each experimental point of the specified curve. A typical dependence of the relative density and temperature on the sintering time of the sample is presented below in the (Figure 1). The studied cermet is considered as a composite formed by a matrix having a theoretical material density and corresponding to a maximum relative density of 1 and pores whose density is equal to 0. Quantitative data on the relative density ρ and the densification rate enable the calculation of the current change in root-mean-square stress tm and strain rate in the matrix forming a porous composite.

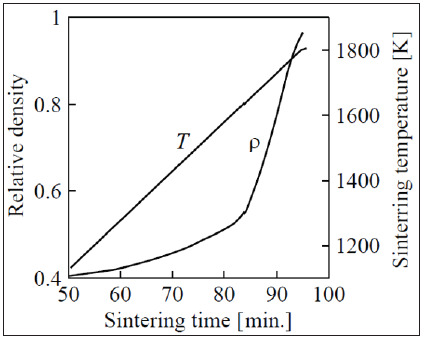
Figure 1: The cermet relative density  and temperature T versus sintering time t.

The quantities above are expressed by the formulae as follow:

Here σ1 is the axial pressure and t is time.

The results of the calculation are showed in Figure 2. The root-mean-square stresses gradually decreases during the cermet densification from the initial value of 327.6MPa at a temperature 825 °C to 101.1MPa at 1298 °C and in the range of temperatures corresponding to sintering in the presence of the liquid phase, goes to zero. The root-mean-square rate gradually increases with the increase in temperature during the solid phase sintering from 4.42·10-5s-1 at 825 °C to 1.43·10-4s-1 at 1298 °C. During the transition to the stage of liquid-phase sintering, an increase in the densification rate to 2.6·10-4s-1 at 1393 °С is replaced by a sharp decrease in it as the porous body densifies. The transition to the liquid-phase sintering stage is particularly clear on plots for logarithm of the relative density function rate [1] versus the reciprocal thermodynamic temperature (Figure 3), from which the activation energy of the matrix viscous flow was determined [1]. It is established that solid-phase pressure sintering is controlled by the mechanism of nonlinear creep (n»1.5) with activation energy, which depends on the stress in the material, and liquid-phase sintering mechanism by virtually linear creep (n=1) with activation energy of 542kJ/mol.

Figure 2: Root-mean-square stress tm and strain rate .m ε in the matrix.

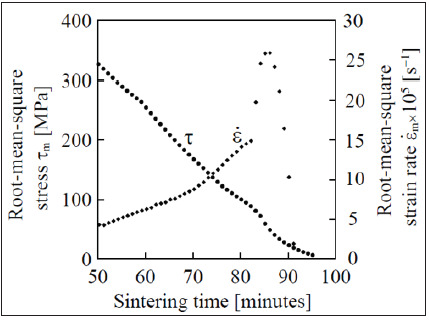
Figure 3: Logarithm of the relative density function rate ln(T(d/dt)Xd(n,)) vs. reciprocal temperature T-1 for solid-phase (1) and liquid-phase (2) pressure sintering.

 References

Kovalchenko MS (2016) Rheology and kinetics of pressure sintering. Materials Science Forum 835: 76-105.

For more about in Crimson Publishers, please click on the link:  https://crimsonpublishers.com/peer-review-process.php

For more articles in Aspects in Mining & Mineral Science, please click on below link: https://crimsonpublishers.com/amms/