#Goldbach Conjecture

[wizardalexa]

✨Wizard Alexa does know whether Goldbach's conjecture is true or not, but Wizard Alexa promised not to tell.✨

[max1461]

Give me a math problem. Requirement is that it has to be doable in a post, you know how I sometimes make posts kind of like going through the steps of a math thing stream of consciousness as I do them? It has to be one where that's possible not too fucked up of one like the Goldbach Conjecture or a really big integral. Well anyway if you do this I may or may not solve it.

[kendoola]

Solar Opposites S4E10 The Re-visibility Bouillabaisse

*messy kitchen, objects floating*

T: you know what? I’m happy I destroyed the stupid invisibility ray. At least this way I’ll never have to see your ugly face again!

K: you take that back you cherish my face! [shouts]

T: not anymore I don’t! I’m done taking your shit. Forget the ray, forget the mission. I am moving out! …Soon as I can find the door

*rolling pin and measuring cup slam into the fridge and fall to the ground*

K: Terry are you still there?

T: …Yeah I got confused about what side of the door I was on and got too embarrassed to say anything

K: I’m sorry I threw your nutrient powders. I think something is broken in me that a ray can’t fix.

T: do you want to know why I bid on an afternoon with Nancy?

K: well I thought it was cause you’re a simp for Netflix celebs

T: [haha] yes, but also, remember when we went on that vacation to highland park and you had an amazing piece of pizza and wouldn’t stop talking about it? That was Nancy’s crust! You always work so hard on the ship and lead us so good, I just wanted to bring a little slice of highland park to you.

K: that’s very thoughtful of you Terry

T: korvo the reason i never want to help with the sci-fi stuff is… I don’t know math!

K: [gasp] not even basic math? Like the goldbach conjecture or the real values function on a three dimensional space?

T: you shame me. I am shamed

K: i actually like that you don’t know science stuff

T: what?

K: it makes me feel necessary, like a hunky sexy science shlorpian

T: you were fronting for me?

K: i was fronting and stunting

T: but we said we’d never front in this house!

K: agreeing to that was my original front

T: it is sexy when you know about the ship. I got pretty hot when you complained about the neutronium core.

K: it’s always low on ions!

T: mmm I’ll tell you what, that tech support tone makes me goosh.

K: what about when I yell about the fluidic processors?

T: drives… me… wild

K: Terry take your clothes off

T: oh I’ve been naked this whole time

K: [moaning]

*metal clanking and blender whirring*

T: treat me like an ektorp, call me a slutty little malm! Talk Swedish dirty to me

K: but IKEA legal, they’re so powerful

T: just do it after we cut away!

*Nancy Silverton pulls into the driveway*

K: [grunting] Billy bookcase! Ribba frames!

*rolling pin starts thrusting by itself*

T: [moaning] yes

K: kallax shelving!

T: yes keep saying more IKEA merch it gets me so fucking hot

K: Allen wrench! Home delivery! Sustainability! Meatbaaaalls!

*microwave falls over*

[rlyehtaxidermist]

assuming immortality, would you attempt tackling some of the big-name conjectures like Goldbach/Collatz/abc/Riemann early on? or would you leave them off and keep doing your own thing mostly

I'd definitely keep a designated notebook for them, but I wouldn't make a huge priority of it; though definitely more of an effort than I do now, even if just to be one of the people poised to understand it when there's a breakthrough, mine or no

[a-typical]

Occasionally, I get a letter from someone who is in 'contact' with extraterrestrials. I am invited to 'ask them anything'. And so over the years I've prepared a little list of questions. The extraterrestrials are very advanced, remember. So I ask things like, 'Please provide a short proof of Fermat's Last Theorem'. Or the Goldbach Conjecture. And then I have to explain what these are because extraterrestrials will not call it Fermat's Last Theorem. So I write out the simple equation with the exponents. I never get an answer.

On the other hand, if I ask something like 'Should we be good?' I almost always get an answer. Anything vague, especially involving conventional moral judgements, these aliens are extremely happy to respond to. But on anything specific, where there is a chance to find out if they actually know anything beyond what most humans know, there is only silence. Something can be deduced from this differential ability to answer questions.

— The Demon-Haunted World: Science as a Candle in the Dark - Carl Sagan (1996)

[zwoelffarben]

A hot minute has nothing to do with measuring the static length of 'universal time'. As a unit, it's the base measurement of 'task-oriented time'.

When you ask for a hot minute, you're asking for the amount of time it takes to do something. (if that something is unspecified, it's implied to be: get to a stopping point in your current on-going task).

If you say:

"Give me a hot minute to put on shoes."

and

"Give me a hot minute to prove Goldbach's conjecture.

You're asking for the same thing: the amount of time necessary to complete the specified task. It's just that where the first task takes around abouts five to ten cold minutes, the other is still outstanding even 282 years after it's introduction (It could be proved any day now, if you'll just give mathematicians a hot minute).

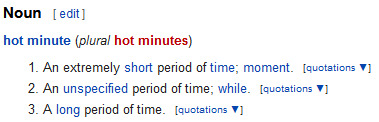
you know when somebody says this that they mean either a short amount of time, a long amount of time, or maybe just neither

[liquidbird-official]

Science terms often get mixed up, but each has a clear role. A hypothesis is a testable guess, like “Plants grow taller with more sunlight.” If repeated experiments support it, it may contribute to a theory, a well-tested explanation, such as evolution. A law, like gravity, describes a consistent natural pattern but doesn’t explain why it happens. Theories explain, laws describe.

A fact is a repeatedly confirmed observation—water boils at 100°C at sea level. A principle is a broad rule forming the foundation of science, like conservation of energy. A postulate is an assumption used to develop theories, while a conjecture is a statement believed to be true but not yet proven, like the Goldbach Conjecture in math.

In mathematics, proof is absolute, like Pythagoras’ theorem, while verification checks if results match evidence, such as vaccine trials confirming effectiveness. An axiom is a fundamental truth accepted without proof, like “a straight line can be drawn between two points.” A lemma is a smaller result that helps prove a theorem, while a corollary is a direct consequence of a proven statement.

Science grows by testing, questioning, and refining ideas. Which of these terms was new to you? Let’s discuss in the comments!

Follow for daily educational content and check the link in bio for free ebooks on the space shuttle, ISS, Falcon 9, and rocket propellants.

Check, our substack for more in-depth articles on such topics. Would love for you to be part of Liquid Bird community!

[angelorumnatura]

The Day I Thought I Had Solved Goldbach's Conjecture at Eleven Years Old

When I was eleven, I was bored and started moving my fingers as if I were playing the piano (because I’m a pianist). In the middle of that little game, I made a curious discovery: I noticed that all numbers greater than 2 could be represented as the sum of 2 and 3. Surprised by my discovery, I ran to tell my dad, who was a mathematician. Excited, I said: —Dad, I found the answer to Goldbach’s…

[thomeslykens]

Published on YouTube: 世紀難題還能囂張?BigBig合一公式一周狂掃Who Says These Problems can’t Fall?BigBig Unity Formula Sweeps Them in 7 Days

8大難題出版論文下載 P vs NP 問題（P vs NP Problem） Click to access PvsNP_Beta.pdf 黎曼猜想（Riemann Hypothesis） Click to access RH_Beta.pdf 納維-斯托克斯（NS） Click to access NS_Beta.pdf 楊-米爾斯（YM） Click to access YM_Beta.pdf 貝赫和斯維訥通-戴爾猜想（BSD） Click to access BSD_Beta.pdf 霍奇猜想（Hogge） Click to access Hodge_Beta.pdf 哥德巴赫猜想（Goldbach’s conjecture） Click to access Goldbach_Beta.pdf 孿生質數猜想（Twin Prime） Click to access…

[lifechanyuan]

Looking for Your Own Garden of Eden

Xuefeng

Even tigers may be teased by dogs when they leave the remote mountains and come to lush and flat areas, dragons can be duped by shrimp when they are in shallow water, camels along the coast are harder to ride than donkeys, and domestic captive phoenixes are worse off than chickens.

The tiger is the king of the mountains, but tigers can only give play to their power and prestige in the mountains. Once they come down to the plains, a pack of wild dogs will dare to tease them.

Dragon are lords of the abyss, but dragons can only summon wind and call for rain in the abyss. If they fall into shallow depressions or ponds, the little shrimp and small fish can dupe them.

Camels can only demonstrate their most valuable qualities in deserts, but if one lives along the coast, it would be less useful than a donkey.

Phoenixes can roar out songs and show their magnificence in the quiet of plane trees, but if they are unfortunate enough to be kept in cages with feathers falling and listless in form and spirit, then they are worse than chickens.

These phenomena suggest such a truth, that all kinds of LIFE can only give full play to themselves and demonstrate their most precious qualities and values when they live in the environments suited to their natures. If they are unfortunate to live in an environment not suited to their own characteristics, not only can they not play out their strengths, but they might even be teased and duped by other creatures around them.

I call the environment which best suits one’s survival, their Garden of Eden.

Everyone has their own Garden of Eden and it is only inside of it that they will live out their elegant demeanour. If you are away from your Garden of Eden, you will be frustrated and have difficult times and even be regarded as a “waste” or “good for nothing” by others around you.

The White Swan was unfortunate to live within flocks of chickens and ducks in the beginning, being laughed at and mocked by them, and was ridiculed as, “the ugly duckling”. The genius painter, Vincent Van Gogh was spiritually enlightened, but had the misfortune to be living in a secular society, so he was unappreciated and taken advantage of all throughout his life and eventually died in poverty and with depression. Jiang Ziya, the founding minister of the Zhou Dynasty went to do business, but ended up with losses rather than profits. Chen Jingrun, who took the crown pearl of the Goldbach Conjecture, went to the market to buy vegetables and was ridiculed as being “a bit silly”.

One who is kind should not be a commander. If you are kind and soft, then you should never lead an army into battle, for you would never become a general.

One who is righteous should not engage in trade. If you have a strong sense of justice and are ready to help the weak, then you should never go into business, for you would never become wealthy.

One who is honest should not enter into politics. If you like seeking out the truth from facts and adhering to the truth, then you should never enter politics, for you would never become a senior official.

One who has a loving heart should not marry. If you have a loving heart, then you should never marry, for your love would be tied up and unable to shine with brilliance.

One who has a noble soul should not mingle in the secular world. If you have a graceful heart, then you should never mingle in the secular world, for you would be regarded as silly and your beauty would go unappreciated.

One who is unsophisticated should not engage in writing. If you are honest and simple, then you should never engage in writing, for your articles would not possess literary elegance and would likely invite scorn and ridicule.

One of integrity should not engage in the art of war. If you advocate honesty and hate cheating, then you should never go into a war to confront others, for “The art of war is full of tricks”. Confronting others, whether civil or military, is all about tactics and tricks, so you would be doomed to lose.

If you want to make your Life happy, joyful, free, and blessed, if you want to play to your strengths and expertise, if you want to stand out and rank high, and if you want to climb to the highest realm of Life and LIFE, then you must find your own Garden of Eden. If you come from the Thousand-year World or the Ten-thousand-year World of heaven, then you must not envy the world’s high positions and great wealth and not waste your time trying to get your ideal life from the mortal world, because its soil is not suitable for you to grow in, bloom, and bear fruit. Your Garden of Eden is in heaven, not in the mortal world.

Seek out those people who appreciate you, are nice to you, and who like you, but do not try to change anyone, especially those whose ideas and views are always against yours. “A leopard cannot change its spots. One cannot change one’s essential nature”. To those people who have different frequencies of mind and consciousness, no matter how impressively you sing their praises, how you comfort them, how you attempt to persuade them, they will never appreciate your feelings or understand your intentions. Even if you open your heart to them, they will still be indifferent and persist in their old ways.

When you find your Garden of Eden, you should cherish it. Never take for granted that you can do anything and give up your Garden of Eden. There was a Division Commander who battled like a fish in water and was very capable when he was in the army, but he grew proud and conceited and thought he would be capable in any environment, so he left the army and entered into civil administration. There, he expected to play a great role, yet after years of rushing about, he suffered setbacks everywhere and could not achieve anything. The hero in the army became good for nothing during peacetime. Why? Because he had left his own Garden of Eden. Never assume that cacti can grow everywhere or can please everyone.

That which comes easiest is the most valuable, however, that which comes easiest is the mostly likely to be ignored and undervalued. The Greatest Creator has given each of us a chance to access their Garden of Eden, but many of us do not pay due attention and do not value and understand their Nature as much. Many people get it and then lose it. It is easy to lose than gain. What a pity!

Look for your own Garden of Eden!

I hope that everyone will find their own Garden of Eden!

[englishindubellay]

ecg 2

Thème :

Le Théorème de Marguerite

Si vous êtes allergique aux mathématiques, ne fuyez pas. Le Théorème de Marguerite, le nouveau long métrage d’Anna Novion qui sort en salles mercredi 1er novembre, est bien plus qu’une longue démonstration rébarbative noyée sous les chiffres.

Should you be allergic to maths, do not run away. Marguerite’s Theorem, Anna Novion’s latest movie that will be released on Wednesday, November 1st, is much more than a long, boring demonstration where figures galore.

Effacez de vos mémoires les douloureux souvenirs de Pythagore et Thalès, il se pourrait que les maths se révèlent aussi sous un jour artistique et ludique.

Erase from your brain the painful memories of Pythagoras and Thales as maths may also appear under an artistic and amusing form.

Le visage diaphane, le front baissé et le regard déterminé, Marguerite n’a pas le temps de s’amuser.

With her translucent face, her forehead down and eyes full of determination, Marguerite has no time for fun. Aussi désuète que son prénom, Marguerite n’a qu’une seule obsession : présenter sa thèse devant le jury d’experts de Normale Sup.

Marguerite is as old-fashioned as her first name, and her one and only obsession is to present her thesis before Normal Sup’s jury of experts. Car Marguerite est brillante, elle bûche depuis trois ans, et même depuis son enfance, sur la conjecture de Goldbach qui s’avère être l’un des plus vieux problèmes non résolus de la théorie des nombres et des mathématiques.

Indeed Marguerite is smart and she has been working her socks off for three years if not since her childhood on Goldbach’s conjecture which happens to be one of the oldest unsolved problems in number theory and mathematics.

Surnommée par ses pairs la « mathématicienne en chaussons », Marguerite est, malgré elle, la star des amphis.

Dubbed by her peers the « mathematician in slippers », Marguerite is, despite herself, the star of lecture-halls. Seule fille dans ce milieu essentiellement masculin, elle intrigue autant qu’elle impressionne.

As the only girl in this predominantly male environment, people are as intrigued as impressed.

« Un don », comme le qualifie sa mère (Clotilde Coureau) qui fait aussi la fierté de son directeur de thèse incarné par Jean-Pierre Darroussin, très juste dans le rôle du mentor.

She has «  a gift » her mother (Clotilde Coureau) says, a gift which is also a source of pride for her PhD director featuring Jean-Pierre Darroussin who plays a perfect mentor.

How do the the authors of documents 1 and 2 see the future of the humanities ?

Robert Shrimsley, a columnist writing in The Financial Times in 2018, has the same concerns regarding the future of the humanities as Aneesg Raman and Maria Flynn, two experts focusing on employment who wrote a contribution for The New York Times in 2024.

What all the authors first describe is the decline of the humanities, which seem to have a very uncertain future. Shrimsley, who also speaks as the father of children with a strong taste for history and art, explains that, for years, not only have British politicians promoted Stem subjects as being the most valuable ones economically speaking but they have also so strongly despised arts degrees in their discourse that the latter havebecome highly undervalued. Raman and Flynn make the same remarks: for several decades, Stem subjects, along technical and data skills, have been regarded as a top priority in the US, most of the time to the detriment of the humanities, which suffered a severe decline in American colleges. All the authors note the contrast between the value given to science degrees, which, in a technology-driven world, are thought to be a route to the most lucrative jobs, and arts degrees and their soft skills which therefore have come to be considered as totally pointless in such an economy.

Yet, although the future of the humanities is clearly presented as endangered, all the authors also suggest that there are grounds to remain optimistic and hopeful.

While, back in 2018, Shrimsley could not help but feel that, in the near future, the humanities may be brought back into favour, in 2024, for Raman and Flynn, it is not a just a feeling anymore: it has become a certainty. To all the authors, human abilities, from critical thinking to creativity to empathy, will be at the heart of economicgrowth, and all the more so as artificial intelligence keeps transforming society.

Raman and Flynn explain how central communication and collaboration will become and call for change, in the same way as Shrimsley, to make sure society does not become totally dehumanized.

Thus, the authors believe that the future of the humanities could be brighter than expected.

(358 words)

How far do you agree with the idea that the world now needs the humanities more than ever ?

In 2024, in England, maths entries at A-level reached record levels. Given this strong enthusiasm for maths and STEM subjects, arguing that the world now needs the humanities more than ever would seem odd. Why would so many students opt for STEM if the humanities were really needed more than ever?

The popularity of STEM and the ensuing decline in the humanities is explained by several factors. First, for years, both in the US and the UK, political discourse has promoted STEM, presenting them as highly valuable, as explained by Robert Shrimsley and the two contributors writing in The New York Times.

Moreover, with the widespread belief that STEM graduates land the highest-paying jobs, STEM have logically become more popular. This explains why the number of students taking a wide range of subjects at A-level has considerably fallen, as shown in document 5.

Yet, all this is deceptively simple: the popularity of STEM subjects does not mean that the humanities can be dismissed, quite the opposite. I find the narrowing of students’ choices at A-level worrying because it means they will lack soft skills. The main character of Anna Novion’s movie, Marguerite, is a brilliant mathematician who struggles precisely because she lacks such skills. It is only when she opens to others and develops her creativity that she can succeed. The prevalence of STEM will undoubtedly lead to a more dehumanized society, and I share Shrimsley’s fears on this point.

Besides, to me, the humanities are all the more essential as we live in a world which is saturated with technology. As technical skills will increasingly be outsourced to machines, the so-called “softer skills” will be the only way to stand out when looking for a job and to keep this powerful technology in check. I therefore fully agree with the view defended in The New York Times that creativity and empathy will be at the heart of economic growth. For instance, in 2019, climate change became a top concern after Greta Thunberg demonstrated her mastery of skills that have little to do with climate science: in her speech to the UN Climate Action summit, she moved the world when she exclaimed “How dare you!” and brought her message to a global audience. For me, all this proves that the humanities are now more than ever needed to solve the world’s most pressing

issues.

Finally, I think that to avoid the kind of situation caricatured in the cartoon when the culture of debate blurs the line between personal opinion and obvious facts, it is crucial that students study a great variety of subjects so as to be equipped to navigate a complex world. I believe that both STEM and the humanities are more needed than ever to counter the half-truths and manipulation that undermine democracy. That is why I agree with the Labour government’s decision to embed critical thinking skills across multiple subjects to teach children how to spot extremist content and misinformation online, a reform which was presentedin the wake of the misinformation-driven riots of August 2024.

(512 words)

[maybeasunflower]

Bases that aren't positive integers .

Anything involving factorials.

One-diagram proof of Pythagoras

Riemann Hypothesis and Goldbach's Conjecture being equivalent.

Working out the sum of n variables each with a Poisson distribution with parameter k is just a Poisson distribution with parameter n*k

Noether's Theorem (blew my mind)

The original research parts of my dissertation

Proving why you will almost always (in the technical sense) step on the cracks in a pavement (sidewalk), no matter what your stride length or the crack interval is.

I didn't wanna derail the other post but I still wanna spread some love for my favourite subject...

Reblog if you've ever felt genuine joy or excitement from doing and/or thinking about math

[jonathankatwhatever]

It’s 27 August and I’m out of energy. No wonder: I looked at my phone and I walked 14,000 steps today. I have a sore throat because it’s drying out from my nose being so completely clogged I can barely taste food. I forced a grilled cheese down. It was eating as a mechanical act. I realized the depth to which that concept runs: the dissociation across the 1-0Segment.

I am seeing how the flipping of the 1-0Segment works, how Ends process automatically. And thus how these gsProcesses run algorithmically.

It’s early on 30 August 2024. Been working on a proof related to Busy Beaver numbers, and thus to Turing Machines. One side effect has been recognizing that to complete the Goldbach proof, we define Halving as requiring gsPrimes. That enables any other combination which works when an even exists. There must be 2 gsPrimes because the limiting idea of the Halving function is that it cuts into 2 unique and thus prime pieces, 2 gsPrime pieces. That must always exist.

This came up because the logic of the conjecture has been encoded into Busy Beaver form, meaning into a Turing Machine with 27 states. The mechanical count of the number is way beyond calculable. They just verified that BB(5) is 47,176,870. The count, which is the winning BB is the longest stretch until it halts. From what I can tell, it took many years of concentrated effort to prove that some threads halt. I think of halting as the 0 which defines the edge of the 1 in 0-1-0, meaning it’s constructed into gs, into finite existence, finite count, rather than not halting.

It is fascinating the way infinity rubs up against the finite.

I’ve also been drawn into the history of calculus because of Leibniz’s interest in tangents. That’s Attachment, and I think a nice way to envision that is to imagine a bird in a wind tunnel adjusting its body as needed. That way you can imagine a series of actions which you can describe as touching the centerline of the flying bird at various angles or approaches. That means tangents in those perspectives, as those perspectives appear based on how likely they make occur and of course how they actually do occur. I feel like I can sort of see how he saw infinitessimals.

So a BB(n) is what? The moves map. Let’s see. If we use Triangular, then we see the Irreducibles arise, with that making grid squares, meaning D3-4 generates. Note how well that says Triangular appears in D4, and that we can see this in Triangular over gs. That is, we see Triangular in the generation of gs and in the counting of and across them.

BTW, the infinitesimal, the continuous, etc. are all generated within D-structure.

I’m starting to get tired. I hope I can sleep some tonight.

Irreducibles arise because that generates the constructed Ends which make the grid. I’ve never seen it this clearly.

So, if we take a basic left or right, that maps to Triangular and that generates the higher dimensional space we see.

[rxshl]

ON LOGIC + MATH AS AN INVENTION VS DISCOVERY + GOLDBACH x GÖDEL

In formal systems of logical reasoning there are two kinds of statements: axioms, known or assumed to be true, and theorems, which require proof to be established. For instance, in arithmetic, a primary, simple axiom is the “reflexive axiom,” which states that a = a for any numerical value substituted for the symbol or variable a. So, 3 = 3. And 156,033,041 = 156,033,041.

Another fundamental axiom is the “symmetric axiom,” which states that things on opposite sides of an equal sign are the same. So if a = b, then b = a. The “transitive axiom” states that if a = b and b = c, then a = c, an equivalent to Euclid’s statement of geometry: “Things that are equal to the same thing are also equal to one another.” These statements are considered true on their face and require no proof.

Theorems, however, may or may not be true. Theorems, like hypotheses in scientific theories, require proof. A well-stated theorem may appear to be true, but one can’t assume that it is. One has to prove the truth of a new theorem by starting with the foundational axioms of the system and using them to ascend methodically, line by line, rung by rung, up the logical ladder of the proof. When the new theorem has been arrived at, it is considered proved. Alternatively, if the proof leads to the opposite of the new theorem, then the theorem has been disproved.

Sometimes theorems seem obvious, but proving them is enormously difficult. For example, there is the famous Goldbach conjecture, which states that every even whole number greater than 2 is the sum of at least one pair of prime numbers. Take the number 8; it is the sum of 3 + 5, both primes. There are a whole bunch of pairs of primes that add up to 144, including 97 + 47, 103 + 41, and 139 + 5. The Goldbach conjecture has been shown to be true by laborious calculations by hand for numbers up to 100,000 and then by computers up to 4 × 1017. But these are not proofs of the conjecture, always true no matter how high one goes; they are simply a lot of calculations. We remain uncertain whether we might eventually find an even larger number that would be an exception. The Goldbach conjecture remains unproved to this day.

In 1920, the great German mathematician David Hilbert announced a program that itemized what he considered to be the most important challenges for setting mathematics on firm foundations. Hilbert supported the use of a “formal language” of symbols to write mathematical statements in proofs. The success and validity of any axiomatic system and the proofs of its many theorems, he said, were to be judged on particular criteria. These criteria stated that a system must be consistent within itself, meaning that it cannot paradoxically contradict itself by simultaneously proving some theorem to be both true and not true. The system also has to be complete, meaning that it has to have within itself the means of proving that every true statement about the system is indeed true. The system that makes up arithmetic, for example, must contain within itself the means to prove every true statement about arithmetic, even the Goldbach conjecture. Consistency and completeness were now the seals of success for any mathematical system. The Vienna Circle’s mission was completely in accord with Hilbert’s program.

Enter the small, fine-featured, bespectacled figure of a still young Kurt Gödel, who would one day become known as the greatest logician since Aristotle, if not, indeed, the greatest of all time. He sat quietly in the back of the Vienna Circle meetings, keeping his own counsel, his life’s pattern already set: to withhold comment or commentary until his answer was perfect, polished, and definitive. We can imagine his head turning this way and that, closely following the back-and-forth of his colleagues’ debates, like the pendulum of a clock.

It was the Vienna Circle’s clock that was ticking.

Gödel arrived in Vienna from Brünn, the city of his birth, in 1924, having already mastered university-level mathematics at eighteen years old. It was in these early years at the University of Vienna that he encountered the ideas that would lead him to embrace mathematical Platonism. Mathematical Platonists believe that mathematical expressions—numbers and formulas and geometric forms—belong to the realm of Plato’s ideals, not to the realm of material existence.

From this view, mathematics is not merely a means invented by humans to count bushels of wheat; it is a true realm unto itself, beyond our own questing human minds. Mathematics awaits human discovery, not human invention. Euclidean geometry (with equations like the Pythagorean theorem), Newton’s calculus for describing fluid motion, the wave equations of Schrödinger, the Mandelbrot set: these were not inventions; they were discoveries.

In contrast, for the Vienna Circle, numbers and forms of mathematics were the logical creations of human minds—invented, not discovered—purely tools for describing physical reality. For them, mathematics derived logically through human innovation, from the simple “real” numbers of counting and the simple geometries of Euclid.

When Gödel was ready to detonate the Vienna Circle’s plans with his own “incompleteness proofs,” he did so quietly, in an almost offhand manner.

The proofs of his two “incompleteness theorems” are widely recognized as a dazzling display of intuitive genius, their mathematical beauty often compared to that of Bach’s most complex musical canons or the elaborate architecture of Gothic cathedrals. The detailed methods of the first proof are well beyond the scope of this book, but their ingenuity can be conveyed.

Gödel’s intuition was that there would be statements about formal systems of arithmetic that were true, but that could not be proved to be true from within arithmetic’s own axioms and theorems. This was a Platonic perspective: mathematical truths simply exist “out there” in the realm of the ideal, awaiting our discovery. There is nothing, however, to require that every single mathematical statement must be amenable to our proofs. It was only the hubris of formalist mathematicians that said otherwise.

So, if Gödel could prove that there were statements that were in fact true, but could not be proved as such, he would then prove that Hilbert was wrong: incompleteness could not be completely eliminated from mathematics. The question was how to do so.

Gödel cleverly devised a numbering system whereby each of the thirteen symbols used in constructing a logical statement in a proof could be substituted by a number (1 through 13) and the logical statement as a whole could thereby, through a procedure Gödel designed, be converted into a unique number not shared by any other formal statement. The code was bidirectional: not only did every logical statement have a unique number, but any number could in turn be decoded to reveal the unique formal set of symbols of an underlying logical statement.

Through this ingenious numbering system, sequential statements within the proof had both a purely arithmetical relationship, as well as a logical one. Gödel’s proof was therefore metamathematical: a proof composed of the very things with which the proof was concerned, numbers. The arithmetical relationship between the representative numbers conveyed arithmetical truths that were parallel to the step-by-step logic of the proof. So logical statements could be about numbers, but numbers, in turn, could convey logical statements. Following Gödel’s self-referential, looping logic is like treading a path along a Möbius strip, round and round.

As if this cleverness weren’t enough, in the next step Gödel’s ingenuity truly soared. He created a logical statement (again using the symbols of formal logic that could be replaced by Gödel numbering) that, in English, asserts something like: “This statement cannot be proved from within this system.”

This is a classical paradoxical statement, much like the liar’s paradox, attributed to Epimenides the Cretan, which has been pondered for centuries. “All Cretans are liars” is problematic since, if it is true, then the Cretan saying it is lying, in which case it is false. If it is false, then it is a lie, in which case the statement is true: Cretans are always liars. Round and round, like a snake swallowing its tail.

Here is another version, called the “card paradox,” by the logician Philip Jourdain, a student of the renowned mathematician Bertrand Russell: if one writes on a slip of paper, “The statement on the other side of this paper is false,” and, on the other side, one writes, “The statement on the other side of this paper is true,” then we get into a similar endless roundabout.

Gödel did not fear paradox; he welcomed it. His special statement—“This statement cannot be proved from within this system”—takes precisely the same endlessly circular form. If the statement can be proved from within the logical system, then the statement is false. If it is false, then it can’t be proved, in which case it is true and is proved.

The step he took next is both simple and breathtaking. A clear, informal description of it is provided by science writer James Gleick: “Gödel showed how to construct a formula that said A certain number, x, is not provable. That was easy: there were infinitely many such formulas. He then demonstrated that, in at least some cases, the number x would happen to represent that very formula.

Gödel doesn’t say which statements may fall under this self-referential constraint, only that some such numbers are inevitable, numbers for which x is not simply a number but a Gödel number that can be decoded as the very statement itself. This final self-referential leap, that there is an arithmetical function that produces the Gödel number of his paradoxical statement, confirms that the statement is true, though its truth cannot be arrived at by a formal logical progression. Its provability is a quality of its being a correct arithmetical result, despite the impossibility of proving such a paradox through logic.

>> proving that something is impossible through a mathematical equation <<

Leaving the extraordinary method aside, we jump to the more straightforward implications. The first incompleteness theorem states that if a system of axioms is truly consistent, it will be incomplete: there will always be statements within the system that, while true, are not provable using only that system’s axioms. In these terms, for example, the difficulty of proving the arithmetical Goldbach conjecture may (perhaps) be an indication that it is a Gödelian “true, but unprovable” theorem (we still don’t know). The second incompleteness theorem is an extension of the first and states that any system that is in fact complete cannot prove its own consistency.

We can summarize this even more concisely: If any formal system that includes arithmetic is consistent, it is necessarily incomplete. And if such a system is actually complete, then it must be inconsistent. The treasured goal of simultaneous consistency and completeness was, from the beginning, an aspirational sham.

The primacy of mathematical logic and empirical science that the Vienna Circle had espoused was fundamentally shattered forever. If their ambition was to close the door on metaphysical thinking, Gödel blew that door right off its hinges. There are clearly gaps in understanding that will never be filled by scientists and logicians, gaps that only some forms of metaphysical intuitions could hope to fill.

[barnabytremayne]

Need a challenge?

Feeling bored? Need a challenge to mix things up? Look no further! Here is a list of fun and challenging activities that you can try. These activities are sure to get your creative juices flowing and help you to see the world in a new and different way.

Some of these activities are challenging, while others are simply fun and silly. But all of them are sure to keep you entertained. So what are you waiting for? Start exploring this list and find the perfect activity for you!

1. Touch your toes without bending your knees.

2. Walk through a wall.

3. Square the circle.

4. Divide by zero.

5. Travel faster than the speed of light.

6. Create a perpetual motion machine.

7. Find the prime number greater than all other prime numbers.

8. List all the natural numbers in order.

9. Write a program that can halt any given program.

10. Prove that there are an infinite number of prime numbers.

11. Prove that Goldbach's conjecture is true.

12. Prove that the Riemann hypothesis is true.

13. Make a pig fly.

14. Make a fish climb a tree.

15. Make a rock float.

16. Teach a dog to speak Spanish (unless it already speaks Spanish. In this case teach it Danish).

17. Find a needle in a haystack.

18. Get a genie out of a bottle.

19. Put toothpaste back in the tube.

20. Un-ring a bell.

21. Close the barn door after the horses have bolted.

22. Make the Titanic unsink.

23. Put Humpty Dumpty back together again.

24. Find out who let the dogs out.

Good luck!