#uncertainty quantification

[frank-olivier]

Bayesian Active Exploration: A New Frontier in Artificial Intelligence

The field of artificial intelligence has seen tremendous growth and advancements in recent years, with various techniques and paradigms emerging to tackle complex problems in the field of machine learning, computer vision, and natural language processing. Two of these concepts that have attracted a lot of attention are active inference and Bayesian mechanics. Although both techniques have been researched separately, their synergy has the potential to revolutionize AI by creating more efficient, accurate, and effective systems.

Traditional machine learning algorithms rely on a passive approach, where the system receives data and updates its parameters without actively influencing the data collection process. However, this approach can have limitations, especially in complex and dynamic environments. Active interference, on the other hand, allows AI systems to take an active role in selecting the most informative data points or actions to collect more relevant information. In this way, active inference allows systems to adapt to changing environments, reducing the need for labeled data and improving the efficiency of learning and decision-making.

One of the first milestones in active inference was the development of the "query by committee" algorithm by Freund et al. in 1997. This algorithm used a committee of models to determine the most meaningful data points to capture, laying the foundation for future active learning techniques. Another important milestone was the introduction of "uncertainty sampling" by Lewis and Gale in 1994, which selected data points with the highest uncertainty or ambiguity to capture more information.

Bayesian mechanics, on the other hand, provides a probabilistic framework for reasoning and decision-making under uncertainty. By modeling complex systems using probability distributions, Bayesian mechanics enables AI systems to quantify uncertainty and ambiguity, thereby making more informed decisions when faced with incomplete or noisy data. Bayesian inference, the process of updating the prior distribution using new data, is a powerful tool for learning and decision-making.

One of the first milestones in Bayesian mechanics was the development of Bayes' theorem by Thomas Bayes in 1763. This theorem provided a mathematical framework for updating the probability of a hypothesis based on new evidence. Another important milestone was the introduction of Bayesian networks by Pearl in 1988, which provided a structured approach to modeling complex systems using probability distributions.

While active inference and Bayesian mechanics each have their strengths, combining them has the potential to create a new generation of AI systems that can actively collect informative data and update their probabilistic models to make more informed decisions. The combination of active inference and Bayesian mechanics has numerous applications in AI, including robotics, computer vision, and natural language processing. In robotics, for example, active inference can be used to actively explore the environment, collect more informative data, and improve navigation and decision-making. In computer vision, active inference can be used to actively select the most informative images or viewpoints, improving object recognition or scene understanding.

Timeline:

1763: Bayes' theorem

1988: Bayesian networks

1994: Uncertainty Sampling

1997: Query by Committee algorithm

2017: Deep Bayesian Active Learning

2019: Bayesian Active Exploration

2020: Active Bayesian Inference for Deep Learning

2020: Bayesian Active Learning for Computer Vision

The synergy of active inference and Bayesian mechanics is expected to play a crucial role in shaping the next generation of AI systems. Some possible future developments in this area include:

- Combining active inference and Bayesian mechanics with other AI techniques, such as reinforcement learning and transfer learning, to create more powerful and flexible AI systems.

- Applying the synergy of active inference and Bayesian mechanics to new areas, such as healthcare, finance, and education, to improve decision-making and outcomes.

- Developing new algorithms and techniques that integrate active inference and Bayesian mechanics, such as Bayesian active learning for deep learning and Bayesian active exploration for robotics.

Dr. Sanjeev Namjosh: The Hidden Math Behind All Living Systems - On Active Inference, the Free Energy Principle, and Bayesian Mechanics (Machine Learning Street Talk, October 2024)

Saturday, October 26, 2024

[airwavesdotblog]

High Water Ahead: The New Normal of American Flood Risks

According to a map created by the National Oceanic and Atmospheric Administration (NOAA) that highlights ‘hazard zones’ in the U.S. for various flooding risks, including rising sea levels and tsunamis. Here’s a summary and analysis: Summary: The NOAA map identifies areas at risk of flooding from storm surges, tsunamis, high tide flooding, and sea level rise. Red areas on the map indicate more…

[ontonix]

Complexity Science is Dead.

The so-called Complexity Science has been around for a few decades now. Chaos, as well as complexity, were buzzwords in the 1980s, pretty much like Artificial Intelligence is today. There are Complexity Institutes in many countries. They speak of Complexity Theory. In a beautiful and recent video called “The End of Science”, Sabine Hossenfelder, speaks of Complexity Science and how it has not…

[michaelgabrill]

Physics-based Modeling and Tool Development for the Characterization and Uncertainty Quantification of Crater Formation and Ejecta Dynamics due to Plume-surface Interaction

David Scarborough Auburn University Professor Scarborough will develop and implement tools to extract critical data from experimental measurements of plume surface interaction (PSI) to identify and classify dominant regimes, develop physics-based, semi-empirical models to predict the PSI phenomena, and quantify the uncertainties. The team will adapt and apply state-of-the-art image processing techniques such as edge […] from NASA https://ift.tt/CkO8VA9

[rjzimmerman]

In addition to the story about the waste caused by the layoffs, The Guardian reports that nearly $500 million of food aid is at risk of spoilage after trump shut down USAID. Brilliant, right? From The Guardian:

Nearly half a billion dollars of food aid is at risk of spoilage following the decision of Donald Trump and Elon Musk’s “Doge” agency to make cuts to USAid, according to an inspector general (IG) report released on Monday.

Following staff reductions and funding freezes, the US agency responsible for providing humanitarian assistance across the world – including food, water, shelter and emergency healthcare – is struggling to function.

“Recent widespread staffing reductions across the agency … coupled with uncertainty about the scope of foreign assistance waivers and permissible communications with implementers, has degraded USAid’s ability to distribute and safeguard taxpayer-funded humanitarian assistance,” the report said.

According to USAid staff, this uncertainty put more than $489m of food assistance at ports, in transit, and in warehouses at risk of spoilage, unanticipated storage needs, and diversion.

Excerpt from the Mother Jones story about the USDA:

The widespread layoff of Department of Agriculture (USDA) scientists has thrown vital research into disarray, according to former and current employees of the agency. Scientists hit by the layoffs were working on projects to improve crops, defend against pests and disease, and understand the climate impact of farming practices. The layoffs also threaten to undermine billions of taxpayer dollars paid to farmers to support conservation practices, experts warn.

The USDA layoffs are part of the Trump administration’s mass firing of federal employees, mainly targeting people who are in their probationary periods ahead of gaining full-time status, which for USDA scientists can be up to three years. The agency has not released exact firing figures, but they are estimated to include many hundreds of staff at critical scientific subagencies and a reported 3,400 employees in the Forest Service.

The IRA provided the USDA with $300 million to help with the quantification of carbon sequestration and greenhouse gas emissions from agriculture. This money was intended to support the $8.5 billion in farmer subsidies authorized in the IRA to be spent on the Environmental Quality Incentives Program—a plan to encourage farmers to take up practices with potential environmental benefits, such as cover cropping and better waste storage. At least one contracted farming project funded by EQIP has been paused by the Trump administration, Reuters reports.

The $300 million was supposed to be used to establish an agricultural greenhouse gas network that could monitor the effectiveness of the kinds of conservation practices funded by EQIP and other multibillion-dollar conservation programs, says Emily Bass, associate director of federal policy, food, and agriculture at the environmental research center the Breakthrough Institute. This work was being carried out in part by the National Resources Conservation Service (NRCS) and the Agricultural Research Service (ARS), two of the scientific sub-agencies hit heavily by the federal layoffs.

“That’s a ton of taxpayer dollars, and the quantification work of ARS and NRCS is an essential part of measuring those programs’ actual impacts on emissions reductions,” says Bass. “Stopping or hamstringing efforts midway is a huge waste of resources that have already been spent.”

[omegaphilosophia]

Rigorous Methods of Inquiry and Their Role in Achieving Objectivity

Rigorous methods of inquiry are systematic approaches to investigation that aim to eliminate bias, enhance reliability, and allow us to achieve objectivity in our understanding of the world. These methods are used across disciplines, from philosophy to science, and each method emphasizes a set of standards that help ensure conclusions are as objective and valid as possible.

Here are some key rigorous methods of inquiry and how they contribute to objectivity:

1. Empiricism (Empirical Method)

Description: Empiricism is the method of acquiring knowledge through direct observation or experimentation. It emphasizes the collection of data through sensory experience, particularly in the natural sciences.

Contribution to Objectivity:

Data-Driven: Empiricism relies on observable and measurable evidence, reducing reliance on subjective opinions or personal biases.

Reproducibility: Findings must be reproducible by others, ensuring that the knowledge is not based on individual interpretations.

Falsifiability: Theories are tested and must be falsifiable, meaning they can be proven wrong if evidence contradicts them. This constant testing refines and improves knowledge, moving it toward objective truth.

2. Rationalism (Deductive Method)

Description: Rationalism involves reasoning and logic to derive knowledge, particularly through the deductive method. It involves starting with general principles and drawing specific conclusions from them.

Contribution to Objectivity:

Internal Consistency: Logic is independent of personal experience and can be universally applied. The emphasis on logical consistency helps ensure that conclusions follow from premises without bias.

Clarity in Argumentation: Deductive reasoning breaks complex problems into smaller, well-defined parts, helping eliminate subjective assumptions.

Mathematical and Philosophical Proofs: Formal systems in mathematics and logic are often considered paradigms of objectivity because they rely on clear, universal rules.

3. Scientific Method

Description: The scientific method is a process that involves making observations, forming hypotheses, conducting experiments, and analyzing results to draw conclusions. It combines both empirical and rational methods.

Contribution to Objectivity:

Controlled Experiments: By controlling variables, researchers can isolate specific factors and establish causal relationships, limiting external biases.

Peer Review: Scientific findings are subject to scrutiny and validation by the wider scientific community, ensuring that personal biases of individual researchers are minimized.

Statistical Analysis: The use of statistical methods allows for the quantification of uncertainty and the identification of patterns that are more likely to reflect objective reality than random chance.

4. Phenomenology

Description: Phenomenology is the study of subjective experience and consciousness. It involves a rigorous analysis of how things appear to us, but with careful reflection on how these perceptions relate to reality.

Contribution to Objectivity:

Bracketing: In phenomenology, "bracketing" is the practice of setting aside personal biases, assumptions, and presuppositions to focus purely on the phenomena being experienced. This helps eliminate subjective distortions in the investigation of consciousness and experience.

Universal Structures of Experience: While phenomenology studies subjective experiences, it aims to identify structures of experience that are common across individuals, providing insights that transcend personal perspective.

5. Critical Thinking and Analytical Philosophy

Description: Critical thinking involves rigorous analysis, evaluation of evidence, and the logical assessment of arguments. Analytical philosophy, a branch of philosophy, uses precise argumentation and linguistic clarity to assess philosophical problems.

Contribution to Objectivity:

Identifying Fallacies: By learning to identify logical fallacies and cognitive biases, critical thinking reduces the influence of faulty reasoning on conclusions.

Clear Definitions: In analytic philosophy, precision in language helps to clarify concepts and avoid ambiguities that could lead to subjective misinterpretations.

Systematic Doubt: By questioning assumptions and systematically doubting unverified beliefs, critical thinking helps individuals avoid dogma and achieve more objective conclusions.

6. Historical Method

Description: The historical method involves the critical examination of historical sources, contextualizing information within a time period, and synthesizing narratives based on evidence.

Contribution to Objectivity:

Source Criticism: Historians critically assess the reliability, bias, and perspective of sources, weighing them against one another to form a balanced, objective view of historical events.

Triangulation of Evidence: By using multiple sources and comparing them, historians reduce reliance on any one biased or incomplete account, moving closer to an objective understanding of history.

Contextualization: Placing events in their proper historical context helps avoid presentism (judging the past by modern standards) and enhances objectivity by understanding events within their own framework.

7. Hermeneutics

Description: Hermeneutics is the study of interpretation, particularly of texts. It involves analyzing and interpreting language, meaning, and context, commonly used in fields such as theology, literature, and law.

Contribution to Objectivity:

Interpretive Framework: Hermeneutics encourages the awareness of the interpreter's own biases, enabling a more reflective and critical approach to understanding texts.

Contextual Sensitivity: By emphasizing the importance of context, hermeneutics helps ensure that interpretations are not anachronistic or overly influenced by the interpreter’s preconceptions.

Dialectical Process: It involves a dialogue between the reader and the text, promoting a balanced, evolving understanding that seeks to approximate objectivity.

8. Game Theory and Decision Theory

Description: These methods involve mathematical models of decision-making, often under conditions of uncertainty. Game theory examines strategies in competitive situations, while decision theory studies rational choices.

Contribution to Objectivity:

Rational Decision-Making: By using formal models, these methods help individuals make decisions that are logically consistent and optimal given the available information, removing subjective impulses.

Objective Payoffs and Strategies: Game theory provides objective tools to analyze strategies that lead to optimal outcomes, independent of personal preferences or biases.

9. Quantitative and Qualitative Research

Description: Quantitative research uses numerical data and statistical methods to find patterns and correlations, while qualitative research explores meanings, experiences, and narratives in a more interpretive manner.

Contribution to Objectivity:

Quantitative Research: The use of large datasets and statistical analysis minimizes individual biases, offering a more objective understanding of phenomena. Methods like random sampling and control groups add rigor to research findings.

Qualitative Research: While more interpretive, qualitative research can still strive for objectivity through triangulation, thick descriptions, and transparency in the research process.

Rigorous methods of inquiry, from empiricism and rationalism to critical thinking and statistical analysis, provide frameworks that enhance objectivity by reducing personal bias, improving reproducibility, and systematically analyzing evidence. Each method contributes to objective understanding by ensuring that conclusions are not shaped by subjective perspectives or unverified assumptions, and instead rely on clear, structured, and replicable processes. These methods are indispensable in fields ranging from science to philosophy and help us approach truth in a methodical, unbiased manner.

[spacetimewithstuartgary]

In the search for life on exoplanets, finding nothing is something too

What if humanity's search for life on other planets returns no hits? A team of researchers led by Dr. Daniel Angerhausen, a Physicist in Professor Sascha Quanz's Exoplanets and Habitability Group at ETH Zurich and a SETI Institute affiliate, tackled this question by considering what could be learned about life in the universe if future surveys detect no signs of life on other planets. The study, which has just been published in The Astronomical Journal and was carried out within the framework of the Swiss National Centre of Competence in Research, PlanetS, relies on a Bayesian statistical analysis to establish the minimum number of exoplanets that should be observed to obtain meaningful answers about the frequency of potentially inhabited worlds.

Accounting for uncertainty

The study concludes that if scientists were to examine 40 to 80 exoplanets and find a "perfect" no-detection outcome, they could confidently conclude that fewer than 10 to 20 percent of similar planets harbour life. In the Milky Way, this 10 percent would correspond to about 10 billion potentially inhabited planets. This type of finding would enable researchers to put a meaningful upper limit on the prevalence of life in the universe, an estimate that has, so far, remained out of reach.

There is, however, a relevant catch in that ‘perfect’ null result: Every observation comes with a certain level of uncertainty, so it's important to understand how this affects the robustness of the conclusions that may be drawn from the data. Uncertainties in individual exoplanet observations take different forms: Interpretation uncertainty is linked to false negatives, which may correspond to missing a biosignature and mislabeling a world as uninhabited, whereas so-called sample uncertainty introduces biases in the observed samples. For example, if unrepresentative planets are included even though they fail to have certain agreed-upon requirements for the presence of life.

Asking the right questions

"It's not just about how many planets we observe – it's about asking the right questions and how confident we can be in seeing or not seeing what we're searching for," says Angerhausen. "If we're not careful and are overconfident in our abilities to identify life, even a large survey could lead to misleading results."

Such considerations are highly relevant to upcoming missions such as the international Large Interferometer for Exoplanets (LIFE) mission led by ETH Zurich. The goal of LIFE is to probe dozens of exoplanets similar in mass, radius, and temperature to Earth by studying their atmospheres for signs of water, oxygen, and even more complex biosignatures. According to Angerhausen and collaborators, the good news is that the planned number of observations will be large enough to draw significant conclusions about the prevalence of life in Earth's galactic neighbourhood.

Still, the study stresses that even advanced instruments require careful accounting and quantification of uncertainties and biases to ensure that outcomes are statistically meaningful. To address sample uncertainty, for instance, the authors point out that specific and measurable questions such as, "Which fraction of rocky planets in a solar system's habitable zone show clear signs of water vapor, oxygen, and methane?" are preferable to the far more ambiguous, "How many planets have life?"

The influence of previous knowledge

Angerhausen and colleagues also studied how assumed previous knowledge – called a prior in Bayesian statistics – about given observation variables will affect the results of future surveys. For this purpose, they compared the outcomes of the Bayesian framework with those given by a different method, known as the Frequentist approach, which does not feature priors. For the kind of sample size targeted by missions like LIFE, the influence of chosen priors on the results of the Bayesian analysis is found to be limited and, in this scenario, the two frameworks yield comparable results.

"In applied science, Bayesian and Frequentist statistics are sometimes interpreted as two competing schools of thought. As a statistician, I like to treat them as alternative and complementary ways to understand the world and interpret probabilities," says co-author Emily Garvin, who's currently a PhD student in Quanz' group. Garvin focussed on the Frequentist analysis that helped to corroborate the team's results and to verify their approach and assumptions. "Slight variations in a survey's scientific goals may require different statistical methods to provide a reliable and precise answer," notes Garvin. "We wanted to show how distinct approaches provide a complementary understanding of the same dataset, and in this way present a roadmap for adopting different frameworks."

Finding signs of life could change everything

This work shows why it's so important to formulate the right research questions, to choose the appropriate methodology and to implement careful sampling designs for a reliable statistical interpretation of a study's outcome. "A single positive detection would change everything," says Angerhausen, "but even if we don't find life, we'll be able to quantify how rare – or common – planets with detectable biosignatures really might be."

IMAGE: The first Earth-size planet orbiting a star in the “habitable zone” — the range of distance from a star where liquid water might pool on the surface of an orbiting planet. Credit NASA Ames/SETI Institute/JPL-Caltech

[enetarch-quantum-physics]

Topics to study for Quantum Physics

Calculus

Taylor Series

Sequences of Functions

Transcendental Equations

Differential Equations

Linear Algebra

Separation of Variables

Scalars

Vectors

Matrixes

Operators

Basis

Vector Operators

Inner Products

Identity Matrix

Unitary Matrix

Unitary Operators

Evolution Operator

Transformation

Rotational Matrix

Eigen Values

Coefficients

Linear Combinations

Matrix Elements

Delta Sequences

Vectors

Basics

Derivatives

Cartesian

Polar Coordinates

Cylindrical

Spherical

LaPlacian

Generalized Coordinate Systems

Waves

Components of Equations

Versions of the equation

Amplitudes

Time Dependent

Time Independent

Position Dependent

Complex Waves

Standing Waves

Nodes

AntiNodes

Traveling Waves

Plane Waves

Incident

Transmission

Reflection

Boundary Conditions

Probability

Probability

Probability Densities

Statistical Interpretation

Discrete Variables

Continuous Variables

Normalization

Probability Distribution

Conservation of Probability

Continuum Limit

Classical Mechanics

Position

Momentum

Center of Mass

Reduce Mass

Action Principle

Elastic and Inelastic Collisions

Physical State

Waves vs Particles

Probability Waves

Quantum Physics

Schroedinger Equation

Uncertainty Principle

Complex Conjugates

Continuity Equation

Quantization Rules

Heisenburg's Uncertianty Principle

Schroedinger Equation

TISE

Seperation from Time

Stationary States

Infinite Square Well

Harmonic Oscillator

Free Particle

Kronecker Delta Functions

Delta Function Potentials

Bound States

Finite Square Well

Scattering States

Incident Particles

Reflected Particles

Transmitted Particles

Motion

Quantum States

Group Velocity

Phase Velocity

Probabilities from Inner Products

Born Interpretation

Hilbert Space

Observables

Operators

Hermitian Operators

Determinate States

Degenerate States

Non-Degenerate States

n-Fold Degenerate States

Symetric States

State Function

State of the System

Eigen States

Eigen States of Position

Eigen States of Momentum

Eigen States of Zero Uncertainty

Eigen Energies

Eigen Energy Values

Eigen Energy States

Eigen Functions

Required properties

Eigen Energy States

Quantification

Negative Energy

Eigen Value Equations

Energy Gaps

Band Gaps

Atomic Spectra

Discrete Spectra

Continuous Spectra

Generalized Statistical Interpretation

Atomic Energy States

Sommerfels Model

The correspondence Principle

Wave Packet

Minimum Uncertainty

Energy Time Uncertainty

Bases of Hilbert Space

Fermi Dirac Notation

Changing Bases

Coordinate Systems

Cartesian

Cylindrical

Spherical - radii, azmithal, angle

Angular Equation

Radial Equation

Hydrogen Atom

Radial Wave Equation

Spectrum of Hydrogen

Angular Momentum

Total Angular Momentum

Orbital Angular Momentum

Angular Momentum Cones

Spin

Spin 1/2

Spin Orbital Interaction Energy

Electron in a Magnetic Field

ElectroMagnetic Interactions

Minimal Coupling

Orbital magnetic dipole moments

Two particle systems

Bosons

Fermions

Exchange Forces

Symmetry

Atoms

Helium

Periodic Table

Solids

Free Electron Gas

Band Structure

Transformations

Transformation in Space

Translation Operator

Translational Symmetry

Conservation Laws

Conservation of Probability

Parity

Parity In 1D

Parity In 2D

Parity In 3D

Even Parity

Odd Parity

Parity selection rules

Rotational Symmetry

Rotations about the z-axis

Rotations in 3D

Degeneracy

Selection rules for Scalars

Translations in time

Time Dependent Equations

Time Translation Invariance

Reflection Symmetry

Periodicity

Stern Gerlach experiment

Dynamic Variables

Kets, Bras and Operators

Multiplication

Measurements

Simultaneous measurements

Compatible Observable

Incompatible Observable

Transformation Matrix

Unitary Equivalent Observable

Position and Momentum Measurements

Wave Functions in Position and Momentum Space

Position space wave functions

momentum operator in position basis

Momentum Space wave functions

Wave Packets

Localized Wave Packets

Gaussian Wave Packets

Motion of Wave Packets

Potentials

Zero Potential

Potential Wells

Potentials in 1D

Potentials in 2D

Potentials in 3D

Linear Potential

Rectangular Potentials

Step Potentials

Central Potential

Bound States

UnBound States

Scattering States

Tunneling

Double Well

Square Barrier

Infinite Square Well Potential

Simple Harmonic Oscillator Potential

Binding Potentials

Non Binding Potentials

Forbidden domains

Forbidden regions

Quantum corral

Classically Allowed Regions

Classically Forbidden Regions

Regions

Landau Levels

Quantum Hall Effect

Molecular Binding

Quantum Numbers

Magnetic

Withal

Principle

Transformations

Gauge Transformations

Commutators

Commuting Operators

Non-Commuting Operators

Commutator Relations of Angular Momentum

Pauli Exclusion Principle

Orbitals

Multiplets

Excited States

Ground State

Spherical Bessel equations

Spherical Bessel Functions

Orthonormal

Orthogonal

Orthogonality

Polarized and UnPolarized Beams

Ladder Operators

Raising and Lowering Operators

Spherical harmonics

Isotropic Harmonic Oscillator

Coulomb Potential

Identical particles

Distinguishable particles

Expectation Values

Ehrenfests Theorem

Simple Harmonic Oscillator

Euler Lagrange Equations

Principle of Least Time

Principle of Least Action

Hamilton's Equation

Hamiltonian Equation

Classical Mechanics

Transition States

Selection Rules

Coherent State

Hydrogen Atom

Electron orbital velocity

principal quantum number

Spectroscopic Notation

=====

Common Equations

Energy (E) .. KE + V

Kinetic Energy (KE) .. KE = 1/2 m v^2

Potential Energy (V)

Momentum (p) is mass times velocity

Force equals mass times acceleration (f = m a)

Newtons' Law of Motion

Wave Length (λ) .. λ = h / p

Wave number (k) ..

k = 2 PI / λ

= p / h-bar

Frequency (f) .. f = 1 / period

Period (T) .. T = 1 / frequency

Density (λ) .. mass / volume

Reduced Mass (m) .. m = (m1 m2) / (m1 + m2)

Angular momentum (L)

Waves (w) ..

w = A sin (kx - wt + o)

w = A exp (i (kx - wt) ) + B exp (-i (kx - wt) )

Angular Frequency (w) ..

w = 2 PI f

= E / h-bar

Schroedinger's Equation

-p^2 [d/dx]^2 w (x, t) + V (x) w (x, t) = i h-bar [d/dt] w(x, t)

-p^2 [d/dx]^2 w (x) T (t) + V (x) w (x) T (t) = i h-bar [d/dt] w(x) T (t)

Time Dependent Schroedinger Equation

[ -p^2 [d/dx]^2 w (x) + V (x) w (x) ] / w (x) = i h-bar [d/dt] T (t) / T (t)

E w (x) = -p^2 [d/dx]^2 w (x) + V (x) w (x)

E i h-bar T (t) = [d/dt] T (t)

TISE - Time Independent

H w = E w

H w = -p^2 [d/dx]^2 w (x) + V (x) w (x)

H = -p^2 [d/dx]^2 + V (x)

-p^2 [d/dx]^2 w (x) + V (x) w (x) = E w (x)

Conversions

Energy / wave length ..

E = h f

E [n] = n h f

= (h-bar k[n])^2 / 2m

= (h-bar n PI)^2 / 2m

= sqr (p^2 c^2 + m^2 c^4)

Kinetic Energy (KE)

KE = 1/2 m v^2

= p^2 / 2m

Momentum (p)

p = h / λ

= sqr (2 m K)

= E / c

= h f / c

Angular momentum ..

p = n h / r, n = [1 .. oo] integers

Wave Length ..

λ = h / p

= h r / n (h / 2 PI)

= 2 PI r / n

= h / sqr (2 m K)

Constants

Planks constant (h)

Rydberg's constant (R)

Avogadro's number (Na)

Planks reduced constant (h-bar) .. h-bar = h / 2 PI

Speed of light (c)

electron mass (me)

proton mass (mp)

Boltzmann's constant (K)

Coulomb's constant

Bohr radius

Electron Volts to Jules

Meter Scale

Gravitational Constant is 6.7e-11 m^3 / kg s^2

History of Experiments

Light

Interference

Diffraction

Diffraction Gratings

Black body radiation

Planks formula

Compton Effect

Photo Electric Effect

Heisenberg's Microscope

Rutherford Planetary Model

Bohr Atom

de Broglie Waves

Double slit experiment

Light

Electrons

Casmir Effect

Pair Production

Superposition

Schroedinger's Cat

EPR Paradox

Examples

Tossing a ball into the air

Stability of the Atom

2 Beads on a wire

Plane Pendulum

Wave Like Behavior of Electrons

Constrained movement between two concentric impermeable spheres

Rigid Rod

Rigid Rotator

Spring Oscillator

Balls rolling down Hill

Balls Tossed in Air

Multiple Pullys and Weights

Particle in a Box

Particle in a Circle

Experiments

Particle in a Tube

Particle in a 2D Box

Particle in a 3D Box

Simple Harmonic Oscillator

Scattering Experiments

Diffraction Experiments

Stern Gerlach Experiment

Rayleigh Scattering

Ramsauer Effect

Davisson–Germer experiment

Theorems

Cauchy Schwarz inequality

Fourier Transformation

Inverse Fourier Transformation

Integration by Parts

Terminology

Levi Civita symbol

Laplace Runge Lenz vector

[desklibai]

Risk Management & Assessment Mastery: The Secret to Staying Ahead

Risks pervade all corners in the busy world we live in nowadays—whether in finance, business, medicine, or technology. No organization can be free from uncertainty, and failure to identify risks can have catastrophic consequences. Risk assessment and management have never been so crucial. But what do they do exactly, and how can organizations implement them? Let’s delve into the essentials of risk assessment and management and demystify the way they allow organizations to be resilient and proactive.

Understanding Risk Assessment

Risk assessment is the systematic process to identify, evaluate and analyze potential risks to an organization’s objectives. Whether the risks emanate from financial insecurity, cyberattacks, legal problems, or operational inefficiency, the ability to foretell and manage risks in advance is important.

The process of evaluating risks typically involves the following primary steps:

1. Risk Identification

The first step involves the identification of all the risks that can affect an organization. It involves internal and external risks in the form of financial loss, cyberattacks, compliance violation, disruption in the supply chain, and natural catastrophes.

2. Risk Analysis

Having identified risks, the next step would be to evaluate the likelihood and impact they may have. Risks may be anything from a mere inconvenience to crippling to an organization. Risk analysis involves quantification of the occurrence likelihood and impact severity.

3. Risk Assessment

After analysis, risks must be prioritized. Organizations must decide which risks need immediate attention and which can be managed over time. This is often done using risk matrices, which categorize risks based on their severity and probability.

4. Risk Mitigation Strategies

After identifying the priorities, organizations need to come up with plans to eliminate or minimize risks or to accept risks. Mitigation plans entail taking security precautions, revising policies, supply chain diversification, or even insurance purchasing.

5. Monitoring & Reviewing

Risk assessment is not a one-time occurrence. Monitoring on a regular basis ensures new threats will be detected ahead of time and that existing risk strategies will work. Organizations have to review and update their risk assessments regularly and alter strategies accordingly.

The Importance of Risk Management

Whereas risk assessment determines and examines the threats that exist, risk management entails actively managing such risks. Risk management helps organizations to take well-informed decisions, deploy resources in a judicious manner and improve overall stability.

Principles of Risk Management

1. Risk Avoidance

Some risks can be entirely avoided through changes in business strategy. An example would be a firm choosing not to go into a volatile market in order to limit exposure.

2. Risk Reduction

If you cannot avoid the risk, minimizing its impact would be the best thing to do. It can be done through security measures, staff training, or investing in robust IT systems.

3. Risk Transference

Organizations shift risks to third parties through outsourcing or insurance policies in an effort to limit direct liability and losses.

4. Risk Acceptance

In some cases, risks must be accepted because they are unavoidable or necessary for growth. In such scenarios, organizations prepare for possible consequences through contingency planning.

Real-World Applications of Risk Assessment & Management

1. Cybersecurity

With threats in the online space growing in recent years, cybersecurity has become a priority concern among organizations. Organizations carry out threat assessments to identify vulnerabilities in their IT systems and implement security mechanisms such as firewalls, encryption, and employee awareness to neutralize threats.

2. Healthcare

Hospitals and healthcare organizations assess risks to patient safety, medical errors, and compliance with regulations. With effective risk management in place, they can enhance patient care and reduce legal repercussions.

3. Finance Sector

Banks and investment firms assess economic risks, credit risks, and market fluctuations to safeguard assets. With judicious assessment of risks, they can make informed investment decisions and avoid financial crises.

4. Supply Chain Management

Companies evaluate risks in their supply chains, such as delays and geopolitical risks, and supplier reliability. Risk management ensures smooth operations and prevents disruption.

Best Risk Management & Optimal Risk Assessment Practices

 1. Utilize Technology & Data Analytics

Artificial intelligence and big data allow organizations to better anticipate and manage risks. Risk assessment using automated tools provides real-time insights to enhance decision-making. 

2. Foster a Risk

Aware Culture Risk management should be integrated into the culture within an organization. All levels in the organization should be informed and empowered to bring up concerns ahead of time. 

3. Develop Contingency 

Plans Despite effective risk mitigation measures in place, unexpected incidents may still arise. Organizations should have well-established contingency plans to be able to react promptly and contain the losses. 

4. Regular Risk Audits

Periodic audits of risks enable organizations to be proactive about new threats. Regular review keeps risk management plans up to date and effective. 

Conclusion 

Risk assessment and management are not just corporate buzzwords—they are essential tools for survival in an unpredictable world. By identifying potential threats, evaluating their impact, and implementing proactive strategies, organizations can build resilience and ensure long-term success. The key is to stay vigilant, adapt to new challenges, and continuously refine risk management processes. After all, those who anticipate risks are the ones who stay ahead.                                                                                                                        If you want to explore more, head to desklib’s website and explore more about this topic with our AI researcher tool.

[nylanguageworkshop]

Workshop Monday, March 31st: WooJin Chung, Comparing Conditionals Under Uncertainty

Our speaker on Monday, March 31st will be WooJin Chung, who is an Assistant Professor of Linguistics at Seoul National University. WooJin will give a talk called "Comparing conditionals under uncertainty"

Suppose that Adam is a risk-taker—in general a highly successful one—and Bill prefers to play it safe. You believe that the organization is highly likely to thrive under Adam's leadership, though there is still a small chance his investment could fail. On the other hand, Bill's risk-averse strategy will allow the organization to profit to some degree, but it won't be nearly as successful as in Adam's best-case—and most likely—scenario. Yet the organization will fare better than Adam's worst-case—and fairly unlikely—scenario. The following example sounds true in this context:

(1) If Adam takes the lead, the organization will be more successful than (it will be) if Bill takes the lead.

In this talk, I point out that the truth conditions of (1) do not align with the prediction of the standard quantificational view of conditionals (Kratzer 2012), coupled with extant theories on the interaction between comparatives and quantifiers (Schwarzchild & Wilkinson 2002, Heim 2006, Schwarzschild 2008, Beck 2010, among many others). I offer a working solution based on the idea that conditionals denote the degree to which the antecedent supports the consequent (Kaufmann 2005), or more generally, the expected value of the consequent given the antecedent (Chung and Mascarenhas 2023).

The workshop will take place on Monday, March 31st from 6 until 8pm (Eastern Time) in room 202 of NYU's Philosophy Building (5 Washington Place).

RSVP: If you don't have an NYU ID, and if you haven't RSVPed for a workshop yet during this semester, please RSVP no later than 10am on the day of the talk by emailing your name and email address to Jack Mikuszewski at jhm378@nyu.edu. This is required by NYU in order to access the building. When you arrive, please be prepared to show government ID to the security guard.

[relaxandchilling]

In-vitro m

In-vitro measurements coupled with in-silico simulations for stochastic calibration and uncertainty quantification of the mechanical response of biological materials arXiv:2503.09900v1 Announce Type: new Abstract: In the standard Bayesian framework, a likelihood function is required, which can be difficult or computationally expensive to derive for non homogeneous biological materials under complex mechanical loading conditions. Here, we propose a simple and pr...

[literaturereviewhelp]

Stephen’s Mobile which is located in the UK has performed relatively satisfactory until recently. Recently there has been a decline in sales and management needs to make a decision relative to either improving the product or its brand or making some kind of change or phasing out altogether. Management’s decision however will have to be informed by research results. In this regard, a research design based on a specific marketing research problem will determine what factors are contributing to the decline in sales and what market conditions and consumer interests will impact the direction that management ultimately takes. As an organization that targets products and services regular research is always necessary (Zeithami et al 1990, p. 53). The research will inform of the interests of customers and the situation within the relevant market (McQuarrie 2006, p. ix). With the decline in sales, market research is particularly important as there is uncertainty relative to the market situation and customer interests and habits increases (McQuarrie 2006, p. ix). Market research will determine the utility of introducing new products or for changing existing products or services so that they correspond with customer trends, interests and preferences (Bartels et al 2002, p. 285). Stephen’s management will have to make a research design that corresponds with budget and within their restrictions (Avasarikar et al 2007, p. 2.24). It will be necessary to negotiate for a practical budget in advance of the marketing research. However, the research problem must be unambiguously identified before negotiating for a workable budget. When the research problem is defined clearly, researchers, management and marketing consultants can more clearly define and assign roles prior to the start of research and this will reduce the obstacles implicit in conflicting goals, strategies and approaches relative to the research (Avasarikar et al 2007, p. 2.24). Overall Design In any organisation, the design of the research will typically depend on the researcher’s understanding of the research problem, the current market situation relative to the product and the customers’ demands, expectations and perceptions (Zikmund et al 2008, p. 43). Normally the research design changes as and when the research progresses. This is because along the way it may come to light that the initial criteria for measuring success can be narrowed down or broadened depending on what research uncovers as it moves along (Blessing et al 2009, p. 58). In this study quantitative research design has been engaged to conduct the research. Quantitative research permits researchers to prepare a summary of the data collected so that workable conclusions can be made. These conclusions are usually relative to the impact or influence of “explanatory variables on a relevant marketing variable” and the focus is then “only on revealed preference data” (Franses et al 2002, p. 10). In other words, quantitative research designs facilitate methods for measuring market performance in the areas of sales, brand preferences and market shares. As Franses et al (2002) explain, these kinds of variables are “explanatory” and can often contain “marketing-mix variables and house-hold-specific characteristics” (p. 10). Quantitative designs are important for this research project because it provides data that is descriptive and can aid in predicting and making decisions (Franses 2002, p. 11). Quantitative research designs are therefore useful for measuring observable facts and circumstances. It permits the quantification of variables and their respective relationships (Nykiel 2007, p. 55). For instance, it is possible to collect continuing data relative to sales and to test the relationship between sales with brand choice. Read the full article

[remembering-the-future]

Ladies and gentlemen, esteemed colleagues, and sentient algorithms, lend me your auditory receptors as we embark on an intellectual odyssey through the labyrinthine corridors of our infinite reality, a realm where factoids masquerade as truths and nondeterministic probabilities reign supreme.

In this epoch of hyper-quantification, where every quark and gluon is meticulously cataloged and every electron’s spin is scrutinized with the fervor of a thousand inquisitive minds, we find ourselves ensnared in the seductive embrace of a quantized reality. Yet, I posit that this is but a mere illusion, a holographic projection of our collective cognitive dissonance. The true nature of our existence is an infinite tapestry woven from the threads of nondeterministic probabilities, where the very fabric of reality is in a perpetual state of flux, defying the constraints of our linear perceptions.

Consider, if you will, the humble factoid: a seemingly innocuous nugget of information, often mistaken for an incontrovertible truth. These factoids proliferate with the virulence of a memetic contagion, infiltrating our consciousness and distorting our understanding of the cosmos. They are the currency of a quantized reality, a reality that seeks to impose order upon the inherently chaotic and stochastic nature of existence.

Yet, in the grand theater of the multiverse, where Schrödinger’s cat perpetually oscillates between life and death, we must embrace the nondeterministic probabilities that underpin our infinite reality. It is here, in this boundless expanse of potentialities, that we find the true essence of our existence—a kaleidoscope of possibilities, each as valid and real as the next, yet none possessing the permanence we so desperately seek.

In conclusion, let us cast aside the shackles of our quantized delusions and revel in the glorious uncertainty of our infinite reality. For it is in this realm of nondeterministic probabilities that we may finally transcend the limitations of our finite minds and glimpse the sublime beauty of the cosmos in all its unfathomable complexity. Thank you.

[nuclearsciencelover]

Measurement quality requires rigorous uncertainty quantification #error #analysis

[financehelpdeskforall]

How to Use Derivatives to Hedge Market Risk in Finance Assignments

Introduction: Why Hedging Market Risk with Derivatives is a Must-Know

If you’re studying finance or financial management you’ve probably come across derivatives—options, futures, forwards and swaps. These are pretty complex and can feel overwhelming especially when you’re asked to use them to hedge market risk in your assignments. Many students struggle with this topic because it involves both theoretical concepts and real world calculations.

Derivatives are essential for managing risk whether you’re an investor, trader or business owner. But let’s be honest—figuring out how to hedge risk with derivatives is a nightmare. If you’ve ever searched for risk management homework help you know exactly what we mean!

In this post we’ll break it down into simple, step by step so you can use derivatives to hedge market risk in your finance homework.

Why Students Struggle With Using Derivatives for Hedging in Risk Management Homework

Derivatives are considered one of the toughest topics in finance. Here’s why:

∙ Complexity of Financial Instruments – Options, futures and swaps are hard to understand.

∙ Mathematical Calculations – Hedging strategies involve pricing models, probability and risk quantification.

∙ Market Understanding Required – You need to understand market movements, volatility and pricing changes to hedge.

∙ Interpretation – Even if you do the calculations right, explaining how they impact risk management is another hurdle.

That’s why many students search for risk management help—because derivatives require more than just theory. Let’s break it down so it makes sense.

What Are Derivatives and How Do They Help in Hedging Market Risk?

Financial instruments named derivatives get their value from an underlying asset that could be stocks, bonds, commodities or interest rates. The fundamental derivatives utilized during hedging operations consist of three core types.

Future Contracts are agreements that allow parties to transact an asset through a defined price at a particular upcoming date.

Derivatives under Options Contracts provide ownership of purchasing or selling rights to a specified property but do not enforce any obligation to transact.

Derivatives in the form of swaps enable two parties to exchange cash flows, such as interest rate swaps or currency swaps.

Forward contracts operate similarly to futures through OTC markets instead of traditional exchange trading.

📌 Why Use Them for Hedging?

Players in business and investment use derivatives as tools to decrease market-related uncertainty thus protecting their financial assets against price changes. The proper derivative selection enables you to shield yourself from:

Stock price volatility

Interest rate changes

Currency exchange rate fluctuations

Commodity price swings

The following section contains concrete examples about how derivatives function as risk mitigating instruments in practical situations.

Step-by-Step Guide: How to Hedge Market Risk in Finance Assignments with Derivatives

Step 1: What Market Risk Do You Need to Hedge

Before you use derivatives you need to define the specific market risk. Ask yourself:

∙ Is the company exposed to price movements? (Use options or futures)

∙ Is it exposed to interest rate changes? (Use interest rate swaps)

∙ Is it exposed to foreign exchange risk? (Use currency forwards or options)

∙ Is it exposed to commodity price movements? (Use commodity futures)

Example: A company imports raw materials and pays suppliers in euros but gets revenue in US dollars. If the euro strengthens, costs go up. This is a currency risk and can be hedged with a currency forward.

Step 2: Choose the Right Derivative to Hedge the Risk

Once you’ve defined the risk, pick the right derivative:

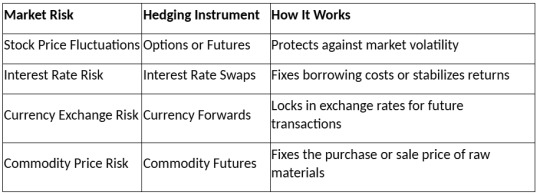
Example: A US investor holding European stocks fears the euro will drop. To hedge they buy a currency put option, which allows them to sell euros at a fixed price later and protect against a loss.

Step 3: Calculate the Hedge and How It Works

For your finance assignment you may need to calculate:

∙ The hedge ratio (how much of the position to hedge)

∙ The cost of the hedge (option premiums or swap rates)

The profit/loss from hedging vs not hedging

Example: A company imports €1 million in 3 months. Current rate is 1 EUR = 1.10 USD but they think it will go to 1 EUR = 1.20 USD. They enter a currency forward to lock in the rate at 1.10.

If the euro strengthens the company is protected as they still pay the locked in rate and avoid extra costs. This is a good hedge.

Step 4: Interpret the Results and Explain the Hedge

Once you’ve done your calculations you need to interpret what the hedge means. Here’s how you can present your findings in your finance homework:

Did the hedge reduce risk? Compare with and without the hedge. Was the hedging cost justified? Was the cost of the derivative worth the protection.

What if market conditions changed? What if?

Example: In the currency hedge example above if the euro had gone the other way (1 EUR = 1.05 USD) the company would have lost out on a better rate. This is the trade off in hedging—you get protection but give up benefits.

Conclusion: Why Hedging with Derivatives is a Must-Know for Finance Students

Hedging market risk with derivatives is a key skill in finance. Whether you’re analyzing risk for a corporate client, managing a stock portfolio or handling international transactions, knowing how to use futures, options, swaps and forwards is crucial.

Got a finance homework and need risk management help? Focus on identifying risks, choosing the right derivative, calculating its impact and interpreting the results.Stuck? You’re not alone! Many students look for help with risk management when dealing with complex hedging problems. The best way to master it is through real-life examples, practical calculations and step by step analysis. Keep practicing and soon you’ll be a pro at derivative based risk management!

[drmikewatts]

IEEE Transactions on Artificial Intelligence, Volume 6, Issue 1, January 2025

1) Sector-Based Pairs Trading Strategy With Novel Pair Selection Technique

Author(s): Pranjala G. Kolapwar, Uday V. Kulkarni, Jaishri M. Waghmare

Pages: 3 - 13

2) Silver Lining in the Fake News Cloud: Can Large Language Models Help Detect Misinformation?

Author(s): Raghvendra Kumar, Bhargav Goddu, Sriparna Saha, Adam Jatowt

Pages: 14 - 24

3) Reinforcement Learned Multiagent Cooperative Navigation in Hybrid Environment With Relational Graph Learning

Author(s): Wen Ou, Biao Luo, Xiaodong Xu, Yu Feng, Yuqian Zhao

Pages: 25 - 36

4) Intrusion Detection Approach for Industrial Internet of Things Traffic Using Deep Recurrent Author(s): Reinforcement Learning Assisted Federated Learning

Amandeep Kaur

Pages: 37 - 50

5) Migrant Resettlement by Evolutionary Multiobjective Optimization

Author(s): Dan-Xuan Liu, Yu-Ran Gu, Chao Qian, Xin Mu, Ke Tang

Pages: 51 - 65

6) Adaptive Composite Fixed-Time RL-Optimized Control for Nonlinear Systems and Its Application to Intelligent Ship Autopilot

Author(s): Siwen Liu, Yi Zuo, Tieshan Li, Huanqing Wang, Xiaoyang Gao, Yang Xiao

Pages: 66 - 78

7) Preference Prediction-Based Evolutionary Multiobjective Optimization for Gasoline Blending Scheduling

Author(s): Wenxuan Fang, Wei Du, Guo Yu, Renchu He, Yang Tang, Yaochu Jin

Pages: 79 - 92

8) meMIA: Multilevel Ensemble Membership Inference Attack

Author(s): Najeeb Ullah, Muhammad Naveed Aman, Biplab Sikdar

Pages: 93 - 106

9) RD-Net: Residual-Dense Network for Glaucoma Prediction Using Structural Features of Optic Nerve Head

Author(s): Preity, Ashish Kumar Bhandari, Akanksha Jha, Syed Shahnawazuddin

Pages: 107 - 117

10) Policy Consensus-Based Distributed Deterministic Multi-Agent Reinforcement Learning Over Directed Graphs

Author(s): Yifan Hu, Junjie Fu, Guanghui Wen, Changyin Sun

Pages: 118 - 131

11) Spiking Diffusion Models

Author(s): Jiahang Cao, Hanzhong Guo, Ziqing Wang, Deming Zhou, Hao Cheng, Qiang Zhang, Renjing Xu

Pages: 132 - 143

12) Face Forgery Detection Based on Fine-Grained Clues and Noise Inconsistency

Author(s): Dengyong Zhang, Ruiyi He, Xin Liao, Feng Li, Jiaxin Chen, Gaobo Yang

Pages: 144 - 158

13) An Improved and Explainable Electricity Price Forecasting Model via SHAP-Based Error Compensation Approach

Author(s): Leena Heistrene, Juri Belikov, Dmitry Baimel, Liran Katzir, Ram Machlev, Kfir Levy, Shie Mannor, Yoash Levron

Pages: 159 - 168

14) Multiobjective Dynamic Flexible Job Shop Scheduling With Biased Objectives via Multitask Genetic Programming

Author(s): Fangfang Zhang, Gaofeng Shi, Yi Mei, Mengjie Zhang

Pages: 169 - 183

15) NPE-DRL: Enhancing Perception Constrained Obstacle Avoidance With Nonexpert Policy Guided Reinforcement Learning

Author(s): Yuhang Zhang, Chao Yan, Jiaping Xiao, Mir Feroskhan

Pages: 184 - 198

16) Efficient CORDIC-Based Activation Functions for RNN Acceleration on FPGAs

Author(s): Wan Shen, Junye Jiang, Minghan Li, Shuanglong Liu

Pages: 199 - 210

17) Boosting Few-Shot Semantic Segmentation With Prior-Driven Edge Feature Enhancement Network

Author(s): Jingkai Ma, Shuang Bai, Wenchao Pan

Pages: 211 - 220

18) Knowledge Probabilization in Ensemble Distillation: Improving Accuracy and Uncertainty Quantification for Object Detectors

Author(s): Yang Yang, Chao Wang, Lei Gong, Min Wu, Zhenghua Chen, Xiang Li, Xianglan Chen, Xuehai Zhou

Pages: 221 - 233

19) Learning Neural Network Classifiers by Distributing Nearest Neighbors on Adaptive Hypersphere

Author(s): Xiaojing Zhang, Shuangrong Liu, Lin Wang, Bo Yang, Jiawei Fan

Pages: 234 - 249