#bayesian inference
Explore tagged Tumblr posts
Text

Bayesian Active Exploration: A New Frontier in Artificial Intelligence
The field of artificial intelligence has seen tremendous growth and advancements in recent years, with various techniques and paradigms emerging to tackle complex problems in the field of machine learning, computer vision, and natural language processing. Two of these concepts that have attracted a lot of attention are active inference and Bayesian mechanics. Although both techniques have been researched separately, their synergy has the potential to revolutionize AI by creating more efficient, accurate, and effective systems.
Traditional machine learning algorithms rely on a passive approach, where the system receives data and updates its parameters without actively influencing the data collection process. However, this approach can have limitations, especially in complex and dynamic environments. Active interference, on the other hand, allows AI systems to take an active role in selecting the most informative data points or actions to collect more relevant information. In this way, active inference allows systems to adapt to changing environments, reducing the need for labeled data and improving the efficiency of learning and decision-making.
One of the first milestones in active inference was the development of the "query by committee" algorithm by Freund et al. in 1997. This algorithm used a committee of models to determine the most meaningful data points to capture, laying the foundation for future active learning techniques. Another important milestone was the introduction of "uncertainty sampling" by Lewis and Gale in 1994, which selected data points with the highest uncertainty or ambiguity to capture more information.
Bayesian mechanics, on the other hand, provides a probabilistic framework for reasoning and decision-making under uncertainty. By modeling complex systems using probability distributions, Bayesian mechanics enables AI systems to quantify uncertainty and ambiguity, thereby making more informed decisions when faced with incomplete or noisy data. Bayesian inference, the process of updating the prior distribution using new data, is a powerful tool for learning and decision-making.
One of the first milestones in Bayesian mechanics was the development of Bayes' theorem by Thomas Bayes in 1763. This theorem provided a mathematical framework for updating the probability of a hypothesis based on new evidence. Another important milestone was the introduction of Bayesian networks by Pearl in 1988, which provided a structured approach to modeling complex systems using probability distributions.
While active inference and Bayesian mechanics each have their strengths, combining them has the potential to create a new generation of AI systems that can actively collect informative data and update their probabilistic models to make more informed decisions. The combination of active inference and Bayesian mechanics has numerous applications in AI, including robotics, computer vision, and natural language processing. In robotics, for example, active inference can be used to actively explore the environment, collect more informative data, and improve navigation and decision-making. In computer vision, active inference can be used to actively select the most informative images or viewpoints, improving object recognition or scene understanding.
Timeline:
1763: Bayes' theorem
1988: Bayesian networks
1994: Uncertainty Sampling
1997: Query by Committee algorithm
2017: Deep Bayesian Active Learning
2019: Bayesian Active Exploration
2020: Active Bayesian Inference for Deep Learning
2020: Bayesian Active Learning for Computer Vision
The synergy of active inference and Bayesian mechanics is expected to play a crucial role in shaping the next generation of AI systems. Some possible future developments in this area include:
- Combining active inference and Bayesian mechanics with other AI techniques, such as reinforcement learning and transfer learning, to create more powerful and flexible AI systems.
- Applying the synergy of active inference and Bayesian mechanics to new areas, such as healthcare, finance, and education, to improve decision-making and outcomes.
- Developing new algorithms and techniques that integrate active inference and Bayesian mechanics, such as Bayesian active learning for deep learning and Bayesian active exploration for robotics.
Dr. Sanjeev Namjosh: The Hidden Math Behind All Living Systems - On Active Inference, the Free Energy Principle, and Bayesian Mechanics (Machine Learning Street Talk, October 2024)
youtube
Saturday, October 26, 2024
#artificial intelligence#active learning#bayesian mechanics#machine learning#deep learning#robotics#computer vision#natural language processing#uncertainty quantification#decision making#probabilistic modeling#bayesian inference#active interference#ai research#intelligent systems#interview#ai assisted writing#machine art#Youtube
6 notes
·
View notes
Text
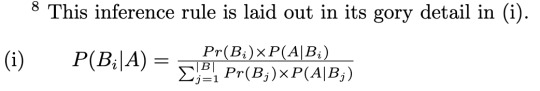
it is gory, but also glorious
#should i add a new tag#bayes my beloved#gotta love linguistics#lit review time babyyy#bayesian inference applied to social meaning and game theory is so sexyyyyyy
5 notes
·
View notes
Text
Almost everybody dies exactly once; it's very rare for someone to die twice. Therefore, if you've already died once, statistically speaking you're basically immortal, because the chance of it happening again is so low
#“well if you consider bayesian inference—” fuck off nerd#i died once as a baby‚ decided it wasn't for me‚ got resuscitated#now i'll live forever
5 notes
·
View notes
Text
i’ve emerged from writing my phylogenetics talk covered in blood because i was in denial about not having a stats degree and tried to write about markov chain monte carlo
#bayes has defeated me.#the whole section on bayesian inference has been deleted and much simplified#it was insane to attempt it in more detail tbqh#sadly the facts- that i am (A) still in high school and (B) not that smart- are undeniable#this is like when i was 7 and tried to write an encyclopedia of science#siph speaks#maths#stats#biology#give me five years and ill understand fucking. mcmc
6 notes
·
View notes
Text
The Philosophy of Statistics
The philosophy of statistics explores the foundational, conceptual, and epistemological questions surrounding the practice of statistical reasoning, inference, and data interpretation. It deals with how we gather, analyze, and draw conclusions from data, and it addresses the assumptions and methods that underlie statistical procedures. Philosophers of statistics examine issues related to probability, uncertainty, and how statistical findings relate to knowledge and reality.
Key Concepts:
Probability and Statistics:
Frequentist Approach: In frequentist statistics, probability is interpreted as the long-run frequency of events. It is concerned with making predictions based on repeated trials and often uses hypothesis testing (e.g., p-values) to make inferences about populations from samples.
Bayesian Approach: Bayesian statistics, on the other hand, interprets probability as a measure of belief or degree of certainty in an event, which can be updated as new evidence is obtained. Bayesian inference incorporates prior knowledge or assumptions into the analysis and updates it with data.
Objectivity vs. Subjectivity:
Objective Statistics: Objectivity in statistics is the idea that statistical methods should produce results that are independent of the individual researcher’s beliefs or biases. Frequentist methods are often considered more objective because they rely on observed data without incorporating subjective priors.
Subjective Probability: In contrast, Bayesian statistics incorporates subjective elements through prior probabilities, meaning that different researchers can arrive at different conclusions depending on their prior beliefs. This raises questions about the role of subjectivity in science and how it affects the interpretation of statistical results.
Inference and Induction:
Statistical Inference: Philosophers of statistics examine how statistical methods allow us to draw inferences from data about broader populations or phenomena. The problem of induction, famously posed by David Hume, applies here: How can we justify making generalizations about the future or the unknown based on limited observations?
Hypothesis Testing: Frequentist methods of hypothesis testing (e.g., null hypothesis significance testing) raise philosophical questions about what it means to "reject" or "fail to reject" a hypothesis. Critics argue that p-values are often misunderstood and can lead to flawed inferences about the truth of scientific claims.
Uncertainty and Risk:
Epistemic vs. Aleatory Uncertainty: Epistemic uncertainty refers to uncertainty due to lack of knowledge, while aleatory uncertainty refers to inherent randomness in the system. Philosophers of statistics explore how these different types of uncertainty influence decision-making and inference.
Risk and Decision Theory: Statistical analysis often informs decision-making under uncertainty, particularly in fields like economics, medicine, and public policy. Philosophical questions arise about how to weigh evidence, manage risk, and make decisions when outcomes are uncertain.
Causality vs. Correlation:
Causal Inference: One of the most important issues in the philosophy of statistics is the relationship between correlation and causality. While statistics can show correlations between variables, establishing a causal relationship often requires additional assumptions and methods, such as randomized controlled trials or causal models.
Causal Models and Counterfactuals: Philosophers like Judea Pearl have developed causal inference frameworks that use counterfactual reasoning to better understand causation in statistical data. These methods help to clarify when and how statistical models can imply causal relationships, moving beyond mere correlations.
The Role of Models:
Modeling Assumptions: Statistical models, such as regression models or probability distributions, are based on assumptions about the data-generating process. Philosophers of statistics question the validity and reliability of these assumptions, particularly when they are idealized or simplified versions of real-world processes.
Overfitting and Generalization: Statistical models can sometimes "overfit" data, meaning they capture noise or random fluctuations rather than the underlying trend. Philosophical discussions around overfitting examine the balance between model complexity and generalizability, as well as the limits of statistical models in capturing reality.
Data and Representation:
Data Interpretation: Data is often considered the cornerstone of statistical analysis, but philosophers of statistics explore the nature of data itself. How is data selected, processed, and represented? How do choices about measurement, sampling, and categorization affect the conclusions drawn from data?
Big Data and Ethics: The rise of big data has led to new ethical and philosophical challenges in statistics. Issues such as privacy, consent, bias in algorithms, and the use of data in decision-making are central to contemporary discussions about the limits and responsibilities of statistical analysis.
Statistical Significance:
p-Values and Significance: The interpretation of p-values and statistical significance has long been debated. Many argue that the overreliance on p-values can lead to misunderstandings about the strength of evidence, and the replication crisis in science has highlighted the limitations of using p-values as the sole measure of statistical validity.
Replication Crisis: The replication crisis in psychology and other sciences has raised concerns about the reliability of statistical methods. Philosophers of statistics are interested in how statistical significance and reproducibility relate to the notion of scientific truth and the accumulation of knowledge.
Philosophical Debates:
Frequentism vs. Bayesianism:
Frequentist and Bayesian approaches to statistics represent two fundamentally different views on the nature of probability. Philosophers debate which approach provides a better framework for understanding and interpreting statistical evidence. Frequentists argue for the objectivity of long-run frequencies, while Bayesians emphasize the flexibility and adaptability of probabilistic reasoning based on prior knowledge.
Realism and Anti-Realism in Statistics:
Is there a "true" probability or statistical model underlying real-world phenomena, or are statistical models simply useful tools for organizing our observations? Philosophers debate whether statistical models correspond to objective features of reality (realism) or are constructs that depend on human interpretation and conventions (anti-realism).
Probability and Rationality:
The relationship between probability and rational decision-making is a key issue in both statistics and philosophy. Bayesian decision theory, for instance, uses probabilities to model rational belief updating and decision-making under uncertainty. Philosophers explore how these formal models relate to human reasoning, especially when dealing with complex or ambiguous situations.
Philosophy of Machine Learning:
Machine learning and AI have introduced new statistical methods for pattern recognition and prediction. Philosophers of statistics are increasingly focused on the interpretability, reliability, and fairness of machine learning algorithms, as well as the role of statistical inference in automated decision-making systems.
The philosophy of statistics addresses fundamental questions about probability, uncertainty, inference, and the nature of data. It explores how statistical methods relate to broader epistemological issues, such as the nature of scientific knowledge, objectivity, and causality. Frequentist and Bayesian approaches offer contrasting perspectives on probability and inference, while debates about the role of models, data representation, and statistical significance continue to shape the field. The rise of big data and machine learning has introduced new challenges, prompting philosophical inquiry into the ethical and practical limits of statistical reasoning.
#philosophy#epistemology#knowledge#learning#education#chatgpt#ontology#metaphysics#Philosophy of Statistics#Bayesianism vs. Frequentism#Probability Theory#Statistical Inference#Causal Inference#Epistemology of Data#Hypothesis Testing#Risk and Decision Theory#Big Data Ethics#Replication Crisis
2 notes
·
View notes
Text
Phenetics :) cladistics :) statistical phylogenetics 😱
#im soo bad at statistics. ive had bayesian Inference explained to me multiple times#im still loke HUH? WHAR? GUH?
2 notes
·
View notes
Text
Advanced Methodologies for Algorithmic Bias Detection and Correction
I continue today the description of Algorithmic Bias detection. Photo by Google DeepMind on Pexels.com The pursuit of fairness in algorithmic systems necessitates a deep dive into the mathematical and statistical intricacies of bias. This post will provide just a small glimpse of some of the techniques everyone can use, drawing on concepts from statistical inference, optimization theory, and…

View On WordPress
#AI#Algorithm#algorithm design#algorithmic bias#Artificial Intelligence#Bayesian Calibration#bias#chatgpt#Claude#Copilot#Explainable AI#Gemini#Machine Learning#math#Matrix Calibration#ML#Monte Carlo Simulation#optimization theory#Probability Calibration#Raffaello Palandri#Reliability Assessment#Sobol sensitivity analysis#Statistical Hypothesis#statistical inference#Statistics#Stochastic Controls#stochastic processes#Threshold Adjustment#Wasserstein Distance#XAI
0 notes
Text
A Sparse Bayesian Learning for Diagnosis of Nonstationary and Spatially Correlated Faults:References
Subscribe .t7d6b1c2c-9953-4783-adc6-ee56928cfcd8 { color: #fff; background: #222; border: 1px solid transparent; border-radius: undefinedpx; padding: 8px 21px; } .t7d6b1c2c-9953-4783-adc6-ee56928cfcd8.place-top { margin-top: -10px; } .t7d6b1c2c-9953-4783-adc6-ee56928cfcd8.place-top::before { content: “”; background-color: inherit; position: absolute; z-index: 2; width: 20px; height: 12px; }…

View On WordPress
#correlated-faults#fault-diagnosis#multistage-assembly-systems#multistation-assembly-systems#nonstationary-faults#sparse-bayesian-learning#spatially-correlated-faults#variational-bayes-inference
0 notes
Text
Distributed Science - The Scientific Process as Multi-Scale Active Inference
Reproduced from: OSF Preprints | Distributed Science – The Scientific Process as Multi-Scale Active Inference and Distributed-Science-The-Scientific-Process-as-Multi-Scale-Active-Inference.pdf (researchgate.net) Distributed Science The Scientific Process as Multi-Scale Active Inference Authors Francesco Balzan 1,2* ([email protected]) John Campbell 3 Karl Friston 4,5 Maxwell J. D.…

View On WordPress
#Active Inference#Artificial Intelligence#Axel Constant#Bayesian Epistemology#Collective Intelligence#Daniel Friedman#Distributed Cognition#Francesco Balzan#free energy principle#John Campbell#Karl Friston#Maxwell J. D. Ramstead
1 note
·
View note
Text

New Pygmy Gecko (Goggia: Gekkonidae) from the arid Northern Cape Province of South Africa
WERNER CONRADIE, COURTNEY HUNDERMARK, LUKE KEMP, CHAD KEATES
Abstract
The genus Goggia is composed of ten small bodied leaf-toed gecko species endemic to South Africa and adjacent Namibia. Using a combination of phylogenetic and morphological analyses we assessed the taxonomic status of an isolated rupicolous population discovered south of Klein Pella in the Northern Cape Province of South Africa. The newly collected material was recovered as a well supported clade by two independent phylogenetic algorithms (maximum likelihood and Bayesian inference), with little intraspecies structuring. While the particular interspecific relationships among closely related Goggia remain unresolved, the phylogenetic results suggest the novel material is related to G. rupicola, G. gemmula, G. incognita and G. matzikamaensis. This is supported by the similar ecologies (rupicolous lifestyle), geographies (arid western extent of South Africa) and morphologies (prominent dorsal chevrons and yellow-centred pale dorsal spots), which are shared among these closely related species. Despite their similarity, the novel population from Klein Pella remains geographically separate, differs from congeners by an uncorrected ND2 p-distance of 11.03–22.91%, and is morphologically diagnosable. Based on these findings we describe the Klein Pella population as a new species.
Read the paper here: New Pygmy Gecko ( Goggia : Gekkonidae) from the arid Northern Cape Province of South Africa | Zootaxa
216 notes
·
View notes
Text

The Pomodoro Grind 🍅
So, I’ve been using the Pomodoro method since forever and honestly? It’s been a lifesaver.
Today, I managed to knock out 8 solid Pomodoros:
50 min of Bayesian Inference exercises (and realising how much I don’t know 😅).
A quick 10-min break chugging water and getting MORE coffee ☕️
Rinse and repeat.
The best part? Forest currently has a new challenges that make me want to use the app 🎄. Plus, I’ve been using my longer breaks to clean up around and take short walks for a brain reset 🧠🚶.
Do you have a go-to break activity? I’m trying to find more ideas that don’t involve screens.
279 notes
·
View notes
Text
Idk who "mrbeast" is in the slightest all I know is every time someone brings him up I briefly go "wait why are people talking about a bayesian inference phylogenetics program on tumblr" before I remember that it's mrBAYES, and that's not what people are talking about

#bayesian phylogeny#bayes#mrbayes#mrbeast#loving my “Idk I'm an adult” era of ignorance rn#phylogenetics
154 notes
·
View notes
Text


Daily Productivity Challenge: 3/10
04.05.2025~ Went through some GLSL videos to understand the syntax for my computer graphics project and finished up inference performance on my Bayesian network
#academia#studyblr#study#student#light academia#studying#university#college#study aesthetic#university student#study space#study tips#college student#student life#study notes#studies#study inspiration#studyblr community#study hard#studyspo#study motivation#stem academia#stemblr#stem#stem student#stem studyblr#computer science#comp sci#cs major#progress update
69 notes
·
View notes
Text
There have been a few things in my grad student career that have made me feel like my third eye snapped open, but none of them quite as much as mirror descent. Did you know that you can show that Bayes rule is just gradient descent if you use the KL divergence as your measure of squared distance? And you can define other pseudo-bayesian inference rules for different definitions of information
143 notes
·
View notes
Text
I can't believe I'm about to do some bayesian inference
40 notes
·
View notes
Text
[. . .] they sent a loudspeaker circling the head of an owl along a light-rail, traveling at a constant distance from the owl’s head: part halo and part ring of Saturn. Observing the neural response, they discovered something never before seen in nature — particular auditory neurons in the owl’s brain were responding only when a sound was coming from a particular direction: geolocation not by satellite but by sound, doing overground what cetaceans do underwater.
[. . .] Animals have brain maps for vision and touch, but these are built from visual images and touch receptors that map onto the brain through direct point-to-point projections. With ears, it’s entirely different. The brain compares information received from each ear about the timing and intensity of a sound and then translates the differences into a unified perception of a single sound issuing from a specific region of space. The resulting auditory map allows owls to “see” the world in two dimensions with their ears.
[. . .] As other neuroscientists picked up the thread, they discovered that a barn owl’s brain performs complex mathematical computations to accomplish this spatial specificity, not merely adding and multiplying signals but engaging in a kind of probabilistic statistical calculation known as Bayesian inference.
Further research into the brain anatomy of owls revealed something even more astonishing: part of their hearing nerve branches off into the optical center of the brain, so that auditory input is processed by the visual system — literally a way of seeing with sound.
#coal sings#owls#creachur#thanks to my owl obsessed friend for sending me this :)#girl with burned out and still burning eyes
14 notes
·
View notes