#Initial and final value theorems

[jujutsubaby]

after hours (part 10)

☆ pairing: satoru gojo x afab!reader ☆ summary: studying at the library is sooo fucking stressful. especially when your final is next week. gojo promises to help you study, but you guys get into other shenanigans instead... ☆ tags: modern au, babysitting au, academia au, threesome au ☆ warnings: oral sex (m! receiving and f! receiving), eating it from the back, exhibitionism, choking (on dick) ☆ a/n: HI GUYS SORRY IVE BEEN SOOO MIA work is crazy (it’s beating my ass) and life is so hectic (also beating my ass). i’ve been trying to have a hot girl summer but i assure u i’ve been nonstop thinking of one shots and new plot points for my fics and new ones too so once the seasonal depression kicks in it’s gonna be over for everyone ! ok enjoy :3 sowwee it took so long once again!! 🙏 ☆ wc: 6.7k+ 🖤🤍 series masterlist 🤍🖤

if there was a time in the past when you said the hong kong coffee milk tea you had been drinking did nothing to keep you awake, you sincerely take it back. your brain felt it first, halfway through sipping on the matcha oatmilk latte satoru had brought for you. and then came the uncontrollable leg shaking and the pounding in your head that could only be satiated if you continued to drink from your matcha, although now that wasn’t doing much either. 

you snuck a quick look at satoru, who was initially banally transcribing his notes onto his cheat sheet for the final, now animatedly talking through bell’s theorem to nanami and haibara and you (before you zoned out). haibara was rapid fire questioning satoru’s mini-lecture, talking a mile a minute as he tapped his pencil at an unnatural pace on the desk. you look over at nanami, who’s staring at satoru with a thousand yard, wide eyed stare, and realize you all were caffeinated beyond recovery. 

the pounding in your head got louder and louder, until it drowned out the noises satoru and haibara. water. you need water. your mouth is too dry. you make eye contact with nanami, and as if he read your mind, he wordlessly reaches into his backpack and hands you his blue hydroflask. you take a swig. and then another. and then you’re chugging the entire bottle like your life depends on it (you think it does in a way). 

the pounding in your head fades just as you empty his water bottle. your vice grip on it turns your fingers white and you try to pay attention to what satoru is lecturing about. 

“see, the thing about heisenberg’s uncertainty principle is that the more localized the momentum-space wavefunction is, the more likely the particle is found in those values, which by the way, are just fourier transforms of each other…”

what the fuck? uncertainty principle? fourier transforms? those weren’t on the final last time you checked. you quickly pull out your study guide and try to find any mentions of whatever satoru was talking about. you find bell’s theorem (wasn’t he just talking about that? how did he switch topics so fast, and so randomly for that matter?), but no mentions of heisenberg. you turn back to satoru and realize he’s just talking nonsense quantum facts from the top of his head, regardless if it was even part of the class (perhaps as a result of being too wired from the triple shot latte he’s been sipping on). 

oh, you need to stop this before everyone gets confused. “satoru, wait, is this even on the final?” if he heard you, he doesn’t let you know, as he continues on his monologue without missing a beat, now talking about quantum computing and turing tests. those aren’t even remotely related to the class you guys are studying for! “satoru! stop talking, jesus fuckin’ christ, dude!” you shake his shoulder, jolting him back to reality as he stops talking and looks over at you confused. 

“what? why? did you have a question about what i was saying?”

“yeah, what the fuck? none of that is on the final, what are you even talking about? how do you know, like, all these random physics facts from the top of your head?!” you ask incredulously. 

satoru shrugs and looks at you like you’re the weird one for questioning him. “you don’t?”

“not everyone studied applied physics in undergrad and graduated summa cum laude, gojo-sensei,” haibara quipped, still writing down some notes from satoru’s monologue in his notebook. you quickly swat his hand away from writing down any more. 

“stop writing what he just said haibara! it’s gonna confuse you when you’re actually studying for the final.” you frown, leaning over to move his notebook away from him. 

“what is it do you think we’re doing right now, y/n, if not ‘actually studying for the final’?” nanami says, emphasizing what you had just said. when was the last time he blinked? 

“none of us studying right now because we got too fuckin’ wired from the coffee. where did you guys get this battery acid anyway?” you say, taking another sip from your matcha, against your own will. 

“philz…” satoru says. 

you scoff. “philz?! and you got a triple shot there? how are you alive right now? how are all of you alive right now? why the fuck would you get coffee from philz and not riko’s like usual?!”

“i’m not feeling alive.” haibara chimes. 

“i’ve been having an out of body experience for the last thirty minutes,” nanami informs, too calmly for your liking, if you’re being honest. 

“suguru told me if he saw my face at riko’s today, he would poison me in my sleep.” satoru says, running his hands through his hair in slight frustration. his legs are restless and so are yours. 

“okay, well, it doesn’t matter now because we are never gonna feel normal again. this is our life. anyway, i think we need a break.” everyone nods their heads. “m’gonna go on a walk around the library and fill up your water bottle, nanamin. anyone wanna join?” you get up from your chair and wordlessly, satoru gets up to accompany you. 

as you two exit the study room, the change of scenery allows your eyes to adjust to reality and your brain to think of something other than physics, which unfortunately is the deal you made with satoru before walking into the study room and getting wired beyond repair. you decide that while you’re not opposed to blowing him right now, you’re not bringing it up until he does. you look over your shoulder and see satoru following silently behind you and you lead him to a corner of the library, where the water refill stations and bathrooms were. 

as you’re filling up nanami’s water bottle, satoru breaks the silence. “should we be worried about nanami and his…umm…out of body experience?”

“aww, you care about nanami, don’t you?” you coo, giving satoru a sly smile. 

“if you’re trying to insinuate that i’m in love with him, then you’re right, i am. why else would i secretly stick on post-its with penises on the back of his notebook?”

“you’re the one doing that?!” you turn your head to satoru to shake it disapprovingly and sigh. “he’s been haunted by those wretched things for weeks, satoru! he’s been thinking some girl’s been sexually harassing him!”

you watch him cackle with laughter and shoot him a dirty look. “stop laughing, satoru!” you say, but you’re a hypocrite because you’re also laughing at the situation. “promise me you’ll– shit!” the water overflows from the water bottle as you pour the excess out and seal the cap on. 

“c’mere,” satoru says, leading you somewhere deeper into the library. 

“anyway, i don’t think we need to worry about nanamin,” you say as you turn the corner and enter a narrow aisle. “i think he just needs to drink water and touch grass or talk to someone that isn’t you.”

“yeah, maybe…” satoru says, as he leads you to another random book aisle, clearly no longer paying attention to you. 

“hey, where are we? what are we doing here?” you take a look around at the books around you. greek mythologies? “why are we in the greek–”

your question is cut off by satoru’s lips crashing into yours and his arms pulling you flush against his chest. satoru leans down to your height and tightens his grip on your hips. caught off guard, it takes you a moment to register what was happening before you leaned into the kiss, deepening with opening your mouth and letting his tongue in. the kiss is urgent, hurried, clandestine – stolen in an empty library corridor in the greek mythology section, of all places. aphrodite would be delighted, you think. 

you take great pains to not moan into satoru’s mouth in the quiet of the library, but a stifled sigh sneaks out regardless. you feel satoru’s hands slide down to your ass and squeeze, as you use the hand that’s not holding the hydroflask to run your fingers through his undercut, earning a muffled groan from him. he leans down further and lifts you up slightly so that he can shove his legs between yours and move your hips on them. the friction of your clothed core meeting his knee catches you off guard as you drop the hydroflask. it clatters on the ceramic tiled floor of the library and echoes loudly across the library floor. 

shit. shit. satoru and you immediately break off the kiss the second the sound rings and you quickly scramble to grab it before it starts rolling to where people are within view. “shit, shit, shit!” you whisper frantically as you fumble to get the water bottle. your face is hot and the pounding in your head is back, begging you for more caffeine. your heart feels like it’s about to go into cardiac arrest for the same reason, but the fact that you were secretly kissing your best friend did not help. 

“jesus fuckin’ christ, why are those things so fucking loud,” satoru says, his eyes scanning the neighboring aisles to see if anyone was there. 

“why did you knee my clit?” you challenge back in a hushed whisper as you set the hydroflask down on the floor. 

“well i had this insane idea that you would like it.” satoru mumbles. you have no interest in arguing with him any further, figuring the best way to beat the pounding in your head was to grab satoru’s sweatshirt and pull him closer to you and continue. with both hands free, you’re able to kiss him and grip his hair to deepen the kiss again. 

this time, satoru slowly moves his hands down to your ass and pulls you right against his rock hard bulge of his own arousal. you sigh deeply at the contact, and buck your hips towards his erection, but missing due to the awkward angle. satoru breaks off the kiss in favor of littering your neck with soft butterfly kisses. 

“you know, i do recall someone saying they’d blow me in the library…” satoru says in between kisses. his lips feel the soft vibration of your groan and he chuckles against it. “you don’t have to, by the way, if you don’t want to. i don’t wanna–”

“what if want to?” you ask innocently, flashing your eyes at him coquettishly as you push him back and use the hair tie on your wrist to quickly tie your hair back. you slowly sink to your knees. don’t think about how hard the tiled floors are here and just focus on giving him insane head so he cums fast and you get back on your feet. you feel a bit bad thinking that, because you do really want to give him head, but also you’re a woman in your late 20s suffering from joint pain, which was embarrassing in itself. 

you push your thoughts of your knee pain on the ceramic tiles aside and start to palm his hard erection through his pants. satoru holds back a groan and throws his head back and holds your wrist and moves it to his belt. you undo it effortlessly, and pull down his pants and underwear, unveiling his well endowed erection in front of you. fuck, it’s so huge. 

your hand grips him lightly as you lick a long stripe from the base to the pink tip of his shaft. at the top, you give him a small kiss before your mouth slowly envelopes it, licking it so as to lubricate your mouth for deepthroating him. you slowly go down on him further and further, until you feel him at the back of your throat, before you start bobbing your head back and forth. satoru hisses under his breath as you full take him in and start sucking him off rhythmically. 

you feel his hand reach the back of your head and grip your ponytail, helping you control the pace to his liking. the warmth of your mouth and skillful maneuvers of your tongue are sending satoru faster to the edge than he’d like to admit, and he grits his teeth to keep himself from spilling within minutes of you starting the blowjob he’d been thinking about since you mentioned it. 

“fuuuck, just like that…” satoru hums deeply. the tip of his cock bullies the back of your thorat, causing your mouth to gag and clench on him. “damn, you love this shit don’t you? deepthroating me in the library where anyone can walk in? where anyone can see how much of a desperate slut you are?”

satoru’s dirty words turn you on more than expected, especially knowing anyone could hear him. you feel yourself getting soaked thinking about the potential chance at someone watching you. what if it was toji? wait, what? how did that thought make you even more wet? thankfully, your moans are muffled by your mouth engulfing him. satoru increases his pace, and starts to fuck your face relentlessly, chasing his high. 

just as you were choking on his member, satoru abruptly stilled his movements inside your mouth. your eyes widen, hearing muffled movements nearby and try to remove yourself from his cock, but satoru keeps your head firmly on him via the vice grip on your ponytail, which was slowly coming apart. the muted sounds slowly got quieter and quieter, until they were gone completely, at which point satoru resumed his mouth fucking. 

“i bet if i felt you right now, you’d be dripping,” satoru whispers breathily. you whine against him, knowing he’s right – your panties are completely ruined. satoru swears under his breath, and you feel his thrusts get sloppier as you feel his cock pulsating as he gets closer to his climax. you help him reach it by using a hand to lightly cup his balls, a trick you learned from an ex-boyfriend of yours, which turns out to be successful. 

“f-fuck, gonna cum in your mouth, yeah?” satoru asks, and you moan in response, vibrating against him. you feel hot ropes of cum shoot down your throat. for the second time today, you don’t let a single drop go to waste. you swallow his cum clean, and lick one last stripe across his cock, as you let him go with a lewd pop. 

 you wipe off some spit on the back of your hand as satoru makes himself decent while catching his breath as fast as possible, leaning against the bookshelf to do so. satoru reaches out his hands lazily to help you get up from your knees on the hard floors, which crack while you stand up. he pulls you closer to his chest as he leans on the library bookshelf, and leans forward to kiss your mouth. you kiss him back briefly before pulling away and checking your phone. “shit, we should go, people might notice that we’ve been gone for way too long…”

satoru rolls his eyes as you grab his hand and lead him down the various aisles he took you through, dropping it only when you caught sight of some students nearby. you cross your arms as you think of how you blew two guys in one day which is not only a new feat for you, but also, kind of annoying that you didn’t get anything in return both times, even though you understood why toji couldn’t. 

“somethin’ troubling you, baby girl?” satoru asks, nudging your shoulder.  

“oh, what? no, why would you ask that?”

“because you blew me like a minute ago and you’re completely silent. and your arms are crossed and your eyebrows are doing that thing they do when you’re annoy–”

“oh my god, okay i get it!” you say with exasperation, not wanting to hear him characterize you this accurately. “and yeah, whatever, i guess i’m a little miffed, but it’s not a big deal.”

“did i do something wrong?” you hear a hint of genuine concern in his voice. 

“oh my god, satoru, no, of course not…it’s just…” you feel the heat rise to your cheeks. all of a sudden, you’re feeling shy and meeting satoru’s eyes is a pain so you keep them downcast and cross your arms to your chest even tighter in an effort to self-sooth. 

“if it’s embarrassing then i’m sorry, you have to tell me or else i’m gonna be so fuckin’ annoying about it.”

“you’re already so fuckin’ annoying about everything, first of all. and fine, if you must know…” you find the courage to turn your head up to him. “i blew like two guys today including you and do you know how many times i got the favor returned? zero. ZERO!” you felt petulant voicing your concerns this wantonly. 

just as you expected, a shit eating grin forms on satoru’s face. “well, why didn’t you say so? you know i’d be more than happy to help that disparity for you.” hearing him tease you about eating you out has you more hot and bothered than you’d like to admit. 

“promise?”

“promise. once we get the fuck outta here, my mouth is yours, baby girl.” 

“don’t call me that!” you say, grinning as you both approach the table where you left shoko to study on her own. you are surprised to see utahime sitting next to her whispering something in her ear, and shoko shaking in silent laughter. 

“oh my god, this bitch…” you say under your breath as you stride towards her desk. so rich of her to tell everyone to shut up when utahime is allowed to say all the jokes in the world. utahime notices you first and her face brightens as she gives you an enthusiastic wave, only for her face to immediately sour when she spots satoru right behind you. 

“you can at least pretend you’re excited to see me ‘hime,” teases satoru. 

“do not call me that.” utahime seethes before turning her attention back to shoko and you. 

“what? you can giggle all you want with utahime but not with us?” you tease shoko. 

she rolls her eyes. “i’m on my break, dumbass, look!” she turns on her laptop to show you the 15 minute break timer that has long since elapsed. you look over at utahime and ask her what brings her back to thel library. 

“ugh, literally only because shoko is here. otherwise, i’d never step foot back at this place after graduating.” utahime frowns. you remember how you and shoko attended utahime’s graduation ceremony for education master’s last year, which was mostly you and shoko trying to figure out discreetly if utahime was into girls. 

the four of you hover around the table and speak in whispered voices and muted laughter, slowly losing track of the volume of your voices. eventually, at some point, everyone is speaking in normal talking voices in the quiet library, all while being blissfully unaware of the dirty pointed looks being given to you guys. 

“gojo, what the fuck kinda coffee did you get me, also? me and utahime have been sharing it and we are forreal tweaking off of this,” shoko complains, shaking the empty coffee cup. 

“it was philz.” you answer for satoru. utahime and shoko’s eyes widen in disbelief. 

“are you trying to murder us?! why didn’t you go to riko’s?!” utahime yells, in a higher than normal level voice. 

“i literally cannot have this conversation again,” satoru says, closing his eyes and rubbing his temples. 

your conversation is interrupted by a short stocky man, who you infer to be a library monitor wearing an official looking university sweater vest. “you folks are way too loud. we’ve gotten multiple complaints about the noise levels on this floor. this is your first and last warning, or you all are out.” he says sternly. 

“wait, sorr–”

“no excuses, ma’am. just please be silent from now onwards, or there will be consequences.” he interrupts you curtly before walking away from the table. the four of you don’t speak, until satoru breaks the silence.

“why’s his voice like that? so nasally?” he said the last part as nasally as possible, mocking the library monitor.  

“you’re so mean!” utahime says as you cover your mouth so she doesn’t see you wordlessly laughing at the admittedly mean imitation. 

“who’s so mean?” you turn to see haibara returning to the table with nanami behind him. 

“obviously it’s gojo.” nanami says without missing a beat. he eyes his water bottle in your hand and you give it back to him. “why did you guys take so long to get water? our reservation elapsed, so i guess we’re here now.”

heat rushes to your face and you feel like a deer caught in headlights. you’re too stunned to feel relieved that nanami’s eyes are looking less bloodshot and more normal. “oh uhh, we were just…”

“we did a lap around the library, nanamin. had to blow off some steam after all that physics, ya know?” satoru says, putting emphasis on that word. if you weren’t with everyone, you would’ve kicked him hard. 

nanami cocks an eyebrow in confusion while haibara doesn’t have a single thought behind his eyes as he readily accepts satoru’s answer. “oh wait! guess what we found while packing our shit up from the study room,” haibara says excitedly. 

“haibara, i really don’t wanna–” nanami starts. 

“we found another penis post-it note inside his textbook. how about that?” haibara says with much amusement. 

“oh my god! no way! do you still think it’s the mysterious girl from physics lab?” shoko says, eyes widening and voice slowly rising. haibara nods excitedly, and you shoot a dirty look at satoru from the corner of your eye, only to see him relishing the conversation. 

“yeah, there is this girl who always wants to partner up with nanamin-chan during lab. it’s gotta be her.” satoru shamelessly fans the flames of a wildfire of his own making. 

nanami pulls out a chair and buries his face in his arms, but the blush creeping up to his cheeks did not go unnoticed by anyone. “or, radical idea, it’s some girl sexually harassing me.” his mumbles. 

“okay, pack it up fellas. i said there’ll be no second warning, so all of you, OUT!” the library monitor takes all of you by surprise as none of you see him coming. “the next time i catch all of you talking loudly at this library results in suspension for the rest of the semester!” he says as you all quietly grab your stuff and leave the library wordlessly. he follows you guys until you’re outside in the crisp evening air and concrete steps of the library entrance. 

once he leaves, you allow yourself to freak out. “oh my god, are we gonna get suspended?! they can’t suspend us for this, right? god, i should’ve known you bitches couldn’t shut the fu–”

“jesus christ, y/n, chill. they just say that shit to scare you. this is like my fifth time getting kicked out of this library.” satoru says nonplussed, hands in his pockets as he leisurely descends down the stairs as the rest of you follow him. 

“thanks though for throwing us under the bus like that, y/n,” shoko says, rolling her eyes.

“is no one going to bring up why gojo is getting kicked out of libraries this much?” utahime asks. 

none of you answer, mostly because no one wants to know the answer to it. satoru’s smug smile is planted permanently on his face as he winks at utahime, and she gags. “anyway, what’s everyone doing? should we get dinner together?” haibara asks warmly, zipping up his jacket. everyone looks at each other and agrees. 

“oooh, let’s go to that new thai place downtown!” you suggest, pulling up your phone to look at the hours. 

“i’m down, let’s pick up suguru on the way. he’s at riko’s.” satoru responds, his information on suguru’s whereabouts earns a “ooohhh” from everyone. 

“he’s still there?! oh my god, he’s in love with that girl…” shoko says. 

the six of you take a walk to riko’s cafe, which is slowly closing up for the night. usually, you wouldn’t walk into a place if it was just five minutes before closing time, like you are now, but you figure it’s a special exception since one of your best friends is crushing on the owner. the lot of you inconspicuously make your way outside the cafe glass walls, trying to catch suguru and riko…doing what? you’re not entirely sure but shoko said something about seeing suguru in his “natural habitat”, and all of you agreed (you blame the caffeine). 

you crouch down and peer into the cafe to see suguru helping riko wipe down tables and stack up chairs (basically anything that requires heavy lifting). damn…that’s cute. may be love really is worth it. your breath hitches in your throat and you jaw goes slack when you see suguru lean in close to riko and kiss her tenderly. you, shoko, and utahime exchange glances with each other with wide eyes and you hear nanami say something about how we are invading suguru’s privacy. the trance this intimate and now stolen moment is broken as satoru bangs his hands against the wall loudly, scaring the lot of you and suguru and riko inside. suguru looks absolutely flummoxed, while riko immediately steps away from him and pretends to inspect something in the barista area. 

you hear satoru yelling through the glass. “open the door, lovebiiiirrdss!” he jiggles the door a couple times to open it but it’s locked. suguru comes closer to open the door and he looks like he’s going to summon curses to obliterate him, and frankly everyone else. 

“man, fuck you. what did i say? why are you here?” suguru says immediately after opening the door to satoru. he gives a disappointing stare to nanami and you. “honestly, i expected better from both of you.” 

nanami tries to defend himself with little to no avail while you focus on making it up to him by talking about thai food. “sorry, sugu, but let us make it up to you. dinner at that new thai place?”

“can riko come?”

“no!” utahime says out of nowhere. it’s silent for five seconds. “i’m just kidding, hehe. of course she can come!” she says sweetly. shoko is the only one who laughs. utahime’s timing in jokes were always questionable but at least she’s really pretty. 

suguru finishes putting up the last few chairs and goes to the back to let riko know about dinner plans. he and her disappear to the break room, and appear three minutes later with their bags and coat. they meet you outside and you notice suguru’s feet are restless, and his hands can’t find a proper place to rest. 

“you good, suguru?” you ask. 

“y-yeah, all good”, he says, pushing his bangs back. 

riko giggle. “he had one too many cups of coffee today.” him, too? “don’t blame him though, they were on the house.”

“oh, okay, great, so we’re all wired as fuck right now.” shoko remarks, as she puts an arm around utahime. 

“you guys got coffee? when? i didn’t see you guys stop by for anything?” riko questions, thinking back to customers that stopped by today. 

everyone is silent, not wanting to embarrass suguru for the second time in ten minutes. “uh, well…” you start. “satoru got us the coffees today!” you say, passing the ball to his court. his problem now. 

satoru shoots you daggers, not feeling fond of being put on the spot to come up with a quick lie. “oh, yeah. uh, i got it from…philz. because…”

“because you hate me and want me to die?” riko says without missing a beat. 

“because, uh…the barista…on main street…i’m sleeping with her. that’s it. my bad, riko-chan.” you don’t know what’s more shocking: the fact that you can’t tell if he’s lying or the fact that riko believes him so easily. 

riko thankfully drops the subject and everyone moves on to different topics, from haibara asking satoru more information about the hot philz barista and utahime sharing amusing events from teaching high schoolers this week. the group of you bask in the crisp and cool evening air as you walk leisurely to the thai place downtown, which was a nice walk away. once you guys arrive, you are met with the sunday night dinner line, which is awful to say the least. your heart deflates knowing you won’t be able to try this place and you and haibara start to look at other places for dinner before riko interrupts the both of you. 

“oh, don’t worry about it. i can get us in, gimme a minute.” she says, before squeezing past a bunch of people waiting in front and greeting the server at the front. the server seems to call someone over from inside the restaurant, and a middle aged man with salt and pepper hair and prominent laugh lines comes out, and his eyes light up when he sees riko. 

riko laughs and gives him a quick hug and starts talking to him about something and then gestures over to you and your friends. after a while of standing awkwardly, riko finally looks over at your group and motions you all to follow her. as you step into the restaurant, you’re met with romantic low lighting, roses as a centerpiece of every table, and various trinkets related to thai culture hanging on the wall and shelves. the place reminds you of somewhere your parents would take you to as a child after getting good grades in class, and it leaves you feeling nostalgic. 

you’re led to a corner of the restaurant where a waiter was quickly pulling two tables together to hold your party. “right this way,” the man says, extending his hand out to the table that was being set up in front of you. 

“thank you so much for having us during a busy night,” nanami says, bowing his head slightly in respect. 

the man laughs heartily. “oh, anything for riko-chan over here. we business owners gotta stay together, anyway. welcome!” you take a seat on the booth side of the two tables, with shoko sitting next to you and satoru taking the seat directly in front of you. “please let me know if there's anything you need during your dinner. my name is joseph!” you take a quick look at his name tag and as expected, see a silver tag engraved with “JOSEPH J” with his ownership title under it. what a sweet old man. 

your thoughts are interrupted by a slightly painful kick under the table to your shin. without looking down, you know in your soul who kicked you, and his stupid ocean eyes are looking directly at you as he mumbles a quick sorry. you waste no time in kicking him back, but earning no response in return. this begins a long game of footsies underneath the table between you and satoru. while trying to keep up with the conversation at the table, your short legs struggle to reach his, and you keep missing his feet. on the other hand, satoru easily dodges your feet and playfully kicks yours under the table (what is he? twelve years old?). 

you’re responding to something suguru and utahime said, when satoru uses his legs to spread your legs forcefully apart. you stutter in the middle of your sentence before gaining your composure back, and you feel the heat rise to your face. satoru’s foot inches closer and closer to your inner thigh, and you quickly finish your sentence, before taking large sips of your water. shoko gives you a look, internally asking if you were good to which you wave her off. 

“uh, i think i’m gonna use the bathroom, be right back,” you say, abruptly getting out of your seat and beelining to the restroom. you don’t actually need to use it, but you need to catch your breath after how easily satoru spread you apart and toyed with you under the table. you rinse your mouth with the tap water and fix your hair in the mirror when you hear a rap at the door. 

you open it and are met with satoru barging inside and locking the door. 

“satoru what are you–” you’re interrupted for the second time today with his lips as he kisses you deeply, his tongue immediately asking for access and you granting it too easily. “w-what are you d-doing~” you say in between sharp breaths and satoru kisses your neck and grips your ass hard. 

“didn’t you say you needed to cum? i’m helping you out,” he says as he feverishly leaves kisses all over your neck and brings his hands up to the hem of your sweater. he deftly slips his hands under your sweater and it takes everything in you to hold back a gasp has his fingers trace every part of your torso and eventually creepy up to your covered breasts. once his hands brush past your erect nipples, you let out a soft moan, inaudible in any normal circumstance, but satoru hears the vibrations through the lips attached to your neck. you can feel him smirking against your neck as he doesn’t let up with his small pecks. the last thing you want to do is give him the satisfaction of making a noise in the bathroom, but your resolve is short lived. 

satoru’s hands abruptly leave your chest, and make their way down to the buttons of your jeans. he fumbles with the zipper and you use the opportunity to run your fingers through his hair and leave small kisses on his temples. something about him taking you in the bathroom turns you on immensely, and the only way you can stop yourself from grinding against the air is to keep your mouth preoccupied. 

“y’gotta stop squirming, baby,” satoru says through ragged breaths, “can’t get these goddamn pants off you when your hips are grinding against my touch.” you feel a blush creep up to your face. you didn’t even know you were doing that. you thought you were actively keeping your hips stilled. 

“i am keeping still,” you whine. “if it’s a skill issue then just say that.” you tease, and egging him on works because once the zipper gets unstuck, your jeans practically fall down your ankles. you bend down to try to get them off completely without having to take off your shoes (you wouldn’t be caught dead in a public bathroom, even a nice one like this,  without your shoes), but satoru already has something else in mind. 

he spins you around and bends you over the granite counter, your cheeks burning from the shock of coldness of the stone. you breath is jagged as you feel satoru hook his finger to your panties and pull it down, feebly pooling by your ankles. you feel exposed as he hugs the mold of your ass and spreads it apart, but even you can’t help but feel your wetness drip down your inner thigh. you feel satoru’s hard-on press against you, and you try to will the fabric between the two of you to disappear so you could feel his length teasing your entrance.  fuck, there’s no getting out of this. do you even want to get out of this? not really…

“s-stop, satoru, we-we have t-to go b-back,” you protest, even though your legs betray you by spreading wider in anticipation of what will happen. 

“yeah, that’s why you’re practically dripping right now, right?” satoru says, his voice slightly strained. he kneels so he’s eye level to your dripping wet pussy and entrance. his mouth practically waters in anticipation of tasting you for the first time – something he’s been dying to taste since…god he doesn’t even know how long he’s been wanting this. 

he wastes no time plunging his tongue as deep as it can go inside your entrance, and he moans at the taste of you. at the same time, your eyes roll back in the pleasure of it all, your moans no longer being held back. using both hands to hold your hips in place and spread you apart, satoru continues his assault on your pussy, not leaving any part untouched by his tongue. you feel yourself out of breath already, and pushing back against his face, trying to feel the friction on your clit. 

satoru seems to catch on, and releases his hold on your hips with one hand and snakes it around you. his fingers find their way to your clit, as if he’s had the path memorized in the back of his hand. he starts rubbing your swollen bundle of nerves, earning breathless moans from you. he already came earlier today, but the sight your legs splayed our and pussy exposed in front of him is enough to make him burst just as hard. 

“fuck, feelin’ you clench against my tongue, baby,” satoru says, still drawing small circles on your clit. “gonna cum? this is what you’ve wanted for so long, haven’t you?” 

he’s teasing you now, and it’s sickening how that edges you on even more. your pussy clenches harder as his tongue re-enters you, and you know you’re going to spill any minute. the coil tightens inside your lower stomach, and you feel the familiar build up about to burst inside you. 

“nghh~ sa-satoru haaa~” you say in between breaths. “m’gonna cum…” 

“normally i’d make you beg but you’ve been such a good little girl for me today,” he says, maintaining the relentless pace of bullying your bundle of nerves. his tongue returns back into you, just in time for the coil to release inside you, and you clench uncontrollable against his mouth. your legs shake as satoru continues his ministrations until he senses you’re out of breath. 

your face feels damp as you try to catch your breath from the orgasm that ripped through your body. satoru stands up and leans against your bent over body, his breath on your skin tingle. he gives you a quick peck on the back of your neck, before you feel his hard-on against your opening. 

“a-are you gonna fuck me, now?” you ask in between breaths. you’re not sure if you could even take him in your fucked out state, but you weren’t raised a quitter. 

satoru chuckles softly against your neck before standing up straight. “i’d fuckin’ love to, but you look really roughed up. don’t wanna let people get the wrong idea here…” he teases, and your head immediately shoots up to look at the state of your appearance. 

your hair is shooting in all different directions, baby hairs and all. your eye makeup is slightly smudged, mascara creating slight racoon eyes. you gasp at how quickly and carelessly you allowed yourself to get this fucked out, all from getting eaten out. “satoru! what the fuck did you do?!” you exclaim, feebly trying to lift yourself off the counter. 

satoru helps you up but frowns. “the fuck did i do?”

you frantically try to smooth your hair down back to it’s original state, but the flyaways still remain, and the humidity of your activities in the bathroom is slowly adding to the frizziness of it. fuck, you’re so screwed. “you…you bent me over! and…” you struggle to find the words to accuse him with. you know it’s not his fault or yours, but you need someone to blame right now. 

“and what? gave you head? and then the best orgasm of your life?” he smirks, watching you as you put your pants back on. 

“don’t flatter yourself. that was nowhere near the best orgasm i’ve ever had.” you say, making eye contact with him through the mirror, as you wet a paper towel and skillfully try to remove any evidence of running mascara from your face. 

satoru raises his eyebrows. “damn, really? guess i just have to keep on giving them to you until one of them is.”

your heart practically leaps out of your chest, and you feel another familiar wetness pool down in your panties just thinking about what this could possibly entail for you.

[felixcloud6288]

In case anyone's interested in understanding that math thing I posted yesterday, what I posted was something called the Pumping Lemma for Regular Languages.

A lemma is a minor theorem which has no real use outside its ability to be used for other proofs.

If you have a Regular Language, the Pumping Lemma is true by definition, and it cannot be used to prove a language is Regular. BUT, if you prove the Pumping Lemma cannot apply to a Language, you can use that to prove the Language is NOT Regular.

Read more for the journey about all this

Automata

Don't worry. This is not as complex as it sounds. An automata has a number of states that it operates in and a set of rules revolving around how it transitions between states.

Consider a calculator. You press certain buttons on it and it will display an output depending on the sequence you pressed. If you press '0 1 =', the calculator prints '1'. If you press '1 7 + 4 =', the calculator prints '21'. But if you press '1 / 0 =', the calculator throws an error. And if you press '1 + =', that also throws an error.

On the underside of the calculator, there's a set of logic responsible for processing your input. It contains a finite number of states that represent what inputs the calculator has read, a set of rules about how to transition between states, and maybe some other components depending on the machine. But not every sequence of input is recognized by the calculator.

In general, the set of all input sequences a machine recognizes is called its Language. And the set of all inputs it can process is called its Alphabet.

Regular Languages

Regular Languages are a particular type of Language. They are Languages that can be recognized by a specific automata called a Deterministic Finite Automata (DFA).

DFAs have five components to them:

A FINITE number of states

The Alphabet of the automata

The transition rules of the automata

The Start State

The Final States

The transition rules work as follows: If there is a rule that says something like (A, x) -> B, that means if we are currently on State A and read input x, we now transition to state B.

The Start State is one specific state in the DFA which we always start at. The Final States are a subset of the DFA's states where if any of them are the active state after reading the final input, the DFA accepts the input as part of the language.

So the way the DFA runs is you initially start in the Start State. Then for each input, you jump to another state based on the transition rules. You keep doing this until all the inputs are read. If the last state you're in is one of the Final States, then the input is accepted as part of the Language. Otherwise, it is rejected.

Here's a DFA which recognizes any sequence of 0's and 1's where the last two characters are '01'.

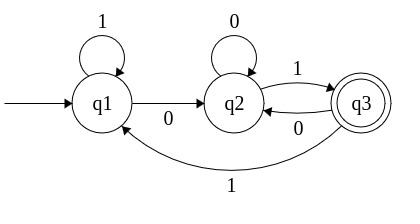
Each circle is a state in the machine.

q1 has a singular unlabeled arrow pointing to q1 indicating that is the start state. q3 is the Final State, indicated by the double circle.

Each labeled arrow represents a transition rule. For example, if we are in q1 and read a '0', we go to q2.

Some sequences that will be accepted are '101', '01', and '001101'. Some inputs sequences that will not be accepted are '1', '010', and '011'.

Pumping Lemma for Regular Languages

Consider the sequence '001101' for the earlier Language. Notice how there are more characters in the sequence than there are States in the DFA. That is because the DFA has a loop in it. You can go from q1 to q2 to q3 and back to q1. You can repeat a looping sequence as many times as you want and you'll still have a sequence in the language.

Here's the more technical definition for Pumping Lemma:

If you have a regular language L, there's a certain value P, called the Pumping length. If there is a string s which is in L whose length is greater than or equal to P, then you can apply the Pumping Lemma to it.

In that case, s can be broken down into three strings xyz. x is whatever comes before the part that loops, y is the first iteration of the looping part. z is everything after the loop.

The total length of xy is less than or equal to P. Meanwhile, the length of y is greater than 0.

After defining x, y, and z; you can then insert or remove y as many times as you want from your string, and you still have something that is accepted by the DFA.

So as an example, lets go back to '001101'. Let's say P=2 (because '01' is the smallest string we can create with the above DFA). 001101 is 6 characters long so we can pump it. And we can define x='0', y='0', z='1101'. This fits the requirement of xy's length being less than or equal to P, and y's length being greater than 0.

xz = '01101' which will be accepted.

xyyz = '0001101' which will be accepted

xyyyz = '00001101' which will be accepted

Using the Pumping Lemma

The Pumping Lemma cannot prove a language is regular because it's a characteristic of a Regular Language. BUT, you can prove a language is NOT regular by showing the Pumping Lemma doesn't work.

Let's consider a Language L that accepts any sequence of 0's and 1's where the number of 0's is the same as the number of 1's. So '01', '0110', and '001101001011' are in the language.

This language is not regular. We can prove it's not regular by showing a scenario where the Pumping Lemma will never work.

If the Pumping Lemma were true, we could choose P, then choose an xyz for any pumpable string in L.

Since we're trying to disprove the Pumping Lemma, things are inverted. We instead choose a string that will always be pumpable regardless of P. And we choose how many times we pump y which will generate a string that is NOT in the language.

So now let's show that the above language is not regular. We cannot choose our pumping length. But we can choose a string in L. We'll choose s = '0^P1^P'. This string is P '0''s followed by P '1''s. So if P=1, s = '01'; if P=2, s='0011' etc.

We cannot define how we split s into x, y, and z. But we can define roughly what they could be by the definitions in the Pumping Lemma. The length of xy is less than or equal to P, so that means xy is at most the P '0''s in s. And the length of y is greater than 0. Combining both rules means y is at least one of the '0''s in the first half and y is NOT ever going to be any of the '1''s. To simplify some things, we'll say y = '0^n' where n is any number from 1 to P.

Now consider if we pump y twice to make xyyz. xyyz = '0^(P+n)1^P'. xyyz is NOT in our language because we have a string which has more 0's than 1's. But if L was regular, xyyz should be in L. Since that's not the case, this means L cannot be a regular language.

Conclusion

So hopefully, you have a rough idea of how this worked. One of the utilities of this concept is determining the minimal amount of complexity needed to perform a certain task.

Regular Languages and their accompanying DFAs are amongst the simplest Languages and automata. They have no memory, cannot recall anything they've processed previously, and have no idea about what will happen in the future.

They only know exactly where they are in the moment and what they can do immediately from there. When a DFA is in a particular state, it does not know how it got there. It knows what states it can immediately go to, but it has no idea where it can go after.

So if you're trying to build a particular automata and you think it's simple enough to build with a DFA, you need to run it by this proof. If the Pumping Lemma can break, then your automata needs a more complex structure.

[tathastuedu]

How to Improve Your SAT Math Score Quickly?

Scoring well on the SAT exam will increase your chances of getting into the college of your dreams. To score well in the overall exam, the Math section is very important. Here are some efficient ways to raise your SAT Math score quickly if you’re on the last moments and need results right now.

1. Understand the SAT Math Structure

The SAT Math section is divided into two parts:

No-Calculator Section (20 questions, 25 minutes)

Calculator Section (38 questions, 55 minutes)

Algebra, problem-solving, data analysis, and advanced math are among the subjects covered in the questions. Knowing the format of the test helps you feel more confident and reduce anxiety. Getting trained from Best SAT Coaching Institute in Delhi University is beneficial for every individual student.

2. Focus on High-Yield Topics

Instead of spreading your efforts thin, concentrate on topics that appear frequently:

Linear Equations and Inequalities

Problem-Solving and Data Analysis

Passport to Advanced Math (quadratic equations, functions)

Geometry and Trigonometry Basics

Mastering these areas will help you tackle a large portion of the questions confidently.

3. Master Mental Math Techniques

For the no-calculator section, speed and accuracy are key. Practice mental math strategies for:

Quick calculations

Estimations

Simplifying fractions

Regular practice will help you solve problems faster without relying on a calculator.

4. Practice with Real SAT Questions

To become acquainted with the format of the questions, take official SAT practice exams. Your timing will improve with timed practice, and going over your errors will highlight areas that require more attention.

Enrolling at Best SAT Institute in Delhi University might give you access to high-quality resources and practice exams that are meant to replicate the real exam if you’re searching for professional advice.

5. Learn Shortcut Techniques

Many SAT Math problems can be solved faster with shortcuts, such as:

Plugging in Numbers: Substitute values to simplify complex algebra problems.

Backsolving: Use answer choices to find the correct solution.

Elimination: Narrow down options to improve guessing accuracy.

These strategies can save valuable time during the test.

6. Review Basic Formulas

Although the SAT provides a formula sheet, memorizing key formulas saves time:

Area and volume formulas

Pythagorean theorem

Slope formula

Probability basics

7. Time Management Strategies

Allocate time wisely:

Spend no more than 1–2 minutes per question.

Skip difficult questions initially and return to them if time permits.

Use the final minutes to review flagged questions.

Attending the Top SAT Coaching Institute in Delhi University can help you master time management techniques with personalized coaching sessions.

8. Analyze Your Mistakes

After each practice test:

Identify the type of mistakes (conceptual errors, careless mistakes, etc.).

Understand why you got the question wrong.

Rework incorrect problems until you fully grasp the solution.

This reflective practice leads to steady improvement.

9. Get Professional Guidance

While self-study is essential, expert guidance can accelerate your progress. Consider enrolling in the Famous SAT Institute in Delhi University, where experienced tutors can:

Provide personalized feedback

Offer targeted practice materials

Help build effective test-taking strategies

Institutes like the Best SAT Coaching Institute in Delhi University offer comprehensive programs that cover every aspect of SAT Math preparation.

10. Stay Consistent and Positive

Consistency is key. Even 1–2 hours of focused practice daily can make a significant difference. Stay motivated, set achievable goals, and track your progress regularly.

Final Thoughts

Improving your SAT Math score quickly requires a smart strategy, focused practice, and the right guidance. Whether through self-study or enrolling in the Top SAT Institute in Delhi University, consistent effort will help you achieve your target score. Start today, and watch your math score soar!

Visit our website — https://tathastuedu.com/sat/

Instagram: https://www.instagram.com/tathastuedu/

Medium: https://ielts-coaching-in-delhi.medium.com/

WriteupCafe: https://writeupcafe.com/profile/tathastuedu/

Steemit: https://steemit.com/@studyabroad12

Tumblr: https://www.tumblr.com/tathastuedu

Youtube: https://www.youtube.com/@ielts-coaching-delhi

[uthra-krish]

Bayesian Statistics: A Powerful Tool for Uncertainty Modeling

Bayesian statistics is a framework for handling uncertainty that has become increasingly popular in various fields. It provides a flexible and systematic approach to modeling and quantifying uncertainty, allowing us to make better-informed decisions. In this article, we will delve into the foundations of Bayesian statistics, understand its significance in uncertainty modeling, and explore its applications in real-world scenarios.

Defining Bayesian Statistics

Bayesian statistics can be defined as a framework for reasoning about uncertainty.

It is based on Bayes’ theorem, which provides a mathematical formula for updating our beliefs in the presence of new evidence.

Bayesian statistics allows us to incorporate prior knowledge and update it with data to obtain posterior probabilities.

Historical Context of Bayesian Statistics

In the 18th century, the Reverend Thomas Bayes introduced the theorem that forms the backbone of Bayesian statistics. However, it was not until the 20th century that Bayesian methods started gaining prominence in academic research and practical applications. With the advent of computational tools and increased recognition of uncertainty, Bayesian statistics has evolved into a powerful tool for modeling and decision-making.

Significance of Uncertainty Modeling

Uncertainty is intrinsic to many real-world phenomena, from complex biological systems to financial markets. Accurately modeling and quantifying uncertainty is crucial for making informed decisions and predictions. Bayesian statistics plays a vital role in addressing uncertainty by providing a probabilistic framework that allows us to account for inherent variability and incorporate prior knowledge into our analysis.

Foundations of Bayesian Statistics

A. Bayes’ Theorem

Bayes’ theorem is at the core of Bayesian statistics and provides a formula for updating our beliefs based on new evidence. It enables us to revise our prior probabilities in light of observed data. Mathematically, Bayes’ theorem can be expressed as:

P(A|B) = (P(B|A) * P(A)) / P(B)

Bayes’ theorem allows us to explicitly quantify and update our beliefs as we gather more data, resulting in more accurate and precise estimates.

B. Prior and Posterior Probability

In Bayesian inference, we begin with an initial belief about a parameter of interest, expressed through the prior probability distribution. The prior distribution represents what we believe about the parameter before observing any data. As new data becomes available, we update our beliefs using Bayes’ theorem, resulting in the posterior distribution. The posterior probability distribution reflects our updated beliefs after considering the data.

The prior probability distribution acts as a regularization term, influencing the final estimates. It allows us to incorporate prior knowledge, domain expertise, or informed assumptions into the analysis. On the other hand, the posterior distribution represents our refined knowledge about the parameter, considering both the prior beliefs and the observed data.

Bayesian Inference Process

A. Likelihood Function

The likelihood function plays a pivotal role in Bayesian statistics as it captures the relationship between the observed data and the unknown parameters. It quantifies the probability of obtaining the observed data under different parameter values. By maximizing the likelihood function, we can estimate the most probable values for the parameters of interest.

The likelihood function is a key component in Bayesian inference, as it combines the data with the prior information to update our beliefs. By calculating the likelihood for different parameter values, we can explore the range of potential parameter values that are consistent with the observed data.

B. Posterior Distribution

The posterior distribution is the ultimate goal of Bayesian inference. It represents the updated distribution of the parameters of interest after incorporating the prior beliefs and the observed data. The posterior distribution provides a comprehensive summary of our uncertainty and captures the trade-off between prior knowledge and new evidence.

Bayesian updating involves multiplying the prior distribution by the likelihood function and normalizing it to obtain the posterior distribution. This process allows us to continually refine our estimates as more data becomes available. The posterior distribution represents the most up-to-date knowledge about the parameters and encompasses both uncertainty and variability.

Bayesian Models and Applications

A. Bayesian Parameter Estimation

Bayesian statistics offers a robust framework for parameter estimation. It allows us to estimate unknown parameters and quantify the associated uncertainty in a principled manner. By incorporating prior knowledge in the form of prior distributions, Bayesian parameter estimation can make efficient use of limited data.

In fields such as finance, Bayesian parameter estimation has found applications in option pricing, risk management, and portfolio optimization. In healthcare, Bayesian models have been utilized for personalized medicine, clinical trials, and disease prognosis. The ability to incorporate prior information and continuously update estimates makes Bayesian parameter estimation a powerful tool in various domains.

B. Bayesian Hypothesis Testing

Bayesian hypothesis testing provides an alternative to frequentist methods by offering a way to quantify the evidence in favor of different hypotheses. Unlike frequentist methods that rely on p-values, Bayesian hypothesis testing uses posterior probabilities to assess the likelihood of different hypotheses given the data.

By incorporating prior information into the analysis, Bayesian hypothesis testing allows for more informative decision-making. It avoids some of the pitfalls of frequentist methods, such as the reliance on arbitrary significance levels. Bayesian hypothesis testing has found applications in research, industry, and policy-making, providing a more intuitive and flexible approach to drawing conclusions.

Uncertainty Propagation

A. Uncertainty Quantification

Uncertainty quantification is a fundamental aspect of Bayesian modeling, enabling us to understand and communicate the uncertainty associated with model outputs. It provides a means to quantify the inherent variability and lack of perfect information in our predictions.

Methods for uncertainty quantification in Bayesian modeling include calculating credible intervals or using Bayesian hierarchical models to capture uncertainty at different levels of the modeling process. Uncertainty quantification allows decision-makers to account for ambiguity and risk when interpreting and utilizing model outputs.

B. Monte Carlo Methods

Monte Carlo methods are widely used for uncertainty propagation in Bayesian analysis. These techniques, including Markov Chain Monte Carlo (MCMC), allow for efficient sampling from complex posterior distributions, which often have no closed-form analytic solution.

MCMC algorithms iteratively draw samples from the posterior distribution, exploring the parameter space to approximate the true distribution. These samples can then be used to estimate summary statistics, compute credible intervals, or perform model comparison. Monte Carlo methods, especially MCMC, have revolutionized Bayesian analysis and made it feasible to handle complex and high-dimensional models.

Bayesian Machine Learning

A. Bayesian Neural Networks

Bayesian statistics can be integrated into neural networks, resulting in Bayesian neural networks (BNNs). BNNs provide a principled way to incorporate uncertainty estimation within the neural network framework.

By placing priors on the network weights, BNNs enable us to capture uncertainty in the network’s predictions. Bayesian neural networks are particularly useful when data is limited, as they provide more realistic estimates of uncertainty compared to traditional neural networks.

The benefits of Bayesian neural networks extend to a wide range of applications, including anomaly detection, reinforcement learning, and generative modeling.

B. Bayesian Model Selection

Model selection is a critical step in statistical modeling and Bayesian techniques offer reliable approaches to tackle this challenge. Bayesian model selection allows for direct comparison of different models and quantifying the evidence in favor of each model based on the observed data.

Bayesian Information Criterion (BIC) is one of the widely used metrics in Bayesian model selection. It balances the goodness-of-fit of the model with model complexity to avoid overfitting. By accounting for the uncertainty in model selection, Bayesian methods provide a principled approach for choosing the most appropriate model.

Challenges and Considerations

A. Computational Complexity

Bayesian analysis often involves complex models with a high dimensional parameter space, which presents computational challenges. Sampling from and exploring the posterior distribution can be computationally expensive, especially when dealing with large datasets or intricate models.

To overcome these challenges, researchers have developed advanced sampling algorithms such as Hamiltonian Monte Carlo and variational inference techniques. Additionally, the availability of high-performance computing resources has made it easier to tackle computationally demanding Bayesian analyses.

B. Data Requirements

Bayesian modeling relies on the availability of sufficient data to reliably estimate parameters and quantify uncertainty. In cases where data is limited, such as in rare diseases or in emerging fields, Bayesian approaches need to be supplemented with expert knowledge and informative priors.

However, even with limited data, Bayesian techniques can be valuable. By incorporating external information through prior distributions, Bayesian models can leverage existing knowledge and provide reasonable estimates even in data-scarce settings.

Real-World Examples

A. Bayesian Statistics in Finance

Bayesian methods have demonstrated their utility in various financial applications. In risk assessment, Bayesian statistics allows for the incorporation of historical data, expert knowledge, and subjective opinions to estimate the probabilities of market events. Bayesian portfolio optimization considers both expected returns and uncertainty to construct portfolios that balance risk and return.

Credit scoring also benefits from Bayesian statistics, enabling lenders to make accurate predictions by incorporating information from credit bureaus, loan applications, and other relevant sources. Bayesian statistics in finance provides a flexible and rigorous framework for decision-making in uncertain financial markets.

B. Bayesian Statistics in Healthcare

Bayesian statistics has made significant contributions to healthcare decision-making. In medical diagnosis, Bayesian models can combine patient symptoms, test results, and prior information to estimate the probability of disease. Bayesian approaches to drug development utilize prior knowledge, clinical trial data, and animal studies to optimize drug dosage and minimize risks.

In epidemiology, Bayesian statistics is employed to estimate disease prevalence, evaluate the effectiveness of interventions, and forecast future disease trends. Bayesian statistics enhances healthcare decision-making by integrating various sources of information and addressing uncertainty in medical research and practice.

Advancements and Tools

A. Bayesian Software and Packages

Several software packages and libraries have been developed to facilitate Bayesian analysis. Popular tools include:

Stan: A probabilistic programming language that allows for flexible modeling and efficient computation of Bayesian models.

PyMC3: A Python library that provides a simple and intuitive interface for probabilistic programming with Bayesian inference.

JAGS: Just Another Gibbs Sampler, a program for Bayesian analysis using Markov chain Monte Carlo (MCMC) algorithms.

These tools provide user-friendly interfaces, efficient sampling algorithms, and a wide range of pre-built models, making Bayesian analysis accessible to researchers and practitioners across different domains.

B. Recent Developments

Bayesian statistics that continues to evolve with ongoing research and technological advancements. Recent developments include advancements in scalable Bayesian computation, hierarchical modeling, and deep learning with Bayesian approaches. Emerging applications in fields such as autonomous driving, natural language processing, and Bayesian optimization highlight the versatility and expanding reach of Bayesian statistics.

As researchers continue to innovate, Bayesian statistics will remain a powerful tool for uncertainty modeling, providing decision-makers with more accurate estimates, better predictions, and improved risk assessment.

In conclusion, Bayesian statistics offers a compelling framework for uncertainty modeling that has wide-ranging applications across various disciplines. Through the use of prior knowledge, data updating, and careful estimation of posterior distributions, Bayesian statistics enables us to make informed decisions in the face of uncertainty. By acknowledging and quantifying uncertainty, Bayesian statistics empowers decision-makers to account for risk and make better-informed choices. Its flexibility, ability to handle complex models, and emphasis on incorporating prior knowledge make Bayesian statistics an invaluable tool for uncertainty modeling in today’s data-driven world. Embracing the Bayesian approach can unlock new insights, provide more accurate predictions, and enable proactive decision-making. With the advancement of computational tools and the availability of user-friendly software, exploring Bayesian statistics has become more accessible and practical for researchers and practitioners alike. To assist people in their pursuit of a Data Science education, ACTE Institute offers a variety of Data Science courses, boot camps, and degree programs. Let us embrace Bayesian statistics and harness its power for robust uncertainty modeling in our respective fields.

[wodenscild]

Proving De Moivre's Theorem

Building on: Deriving the trigonometric identities

Leads to: The general exact trigonometric forms for 45, 22.5, 11.125, etc.

The Theorem

De Moivre's Theorem is an important theorem when it comes to working with complex numbers, as it serves to greatly simplify otherwise painful calculations. The theorem states:

Where r is the modulus/magnitude of the complex number, and theta is the argument of the complex number. It'll be proven here, using mathematical induction...

The Proof

For the first step, we will prove that our statement is true for the initial value, n=2. This isn't too hard:

Thus, as the left and right hand sides are equal, De Moivre's Theorem is true for n=2.

The next step is to assume that the Theorem is true for some arbitrary value k (which is real and greater or equal to 2*). So we are assuming that the following is true:

The final step is to now show that the theorem is true for n=k+1.

It can get pretty messy, but as it can be seen, with the use of our trigonometric identities, they simplify down nicely to make the left and right and sides equal.

Now, as we were assuming that the Theorem is true for some n=k, which is a real number greater than or equal to 2, then we showed it must be true for n=k+1. The statement has been shown true for n=2, which is a real number equal to 2. 2 is a possible value for k, thus the Theorem is true for n=2+1=3. 3 satisfies the requirements of k, so it is true for n=3+1=4, and so on. It follows from this that De Moivre's Theorem is true for any integer n greater than 2.

Important Notes

I feel like there is an important note to end on... this proof only works with integer powers. The reason for this is the Fundamental Theorem of Algebra, which states that for any polynomial of nth degree, or any number taken to the nth root, there are n solutions. This can be seen in the real numbers, where taking the square root gives 2 solutions. On the complex plane, a point z, with a cube root taken will have 3 solutions (n=1/3), a quartic root will give 4 solutions (n=1/4), a quintic root will give 5 solutions (n=1/5), and so on. De Moivre's theorem still works with these values, but just note that you will only yield one solution if you don't do anything more here.

P.S. Made a little mistake, for the proof, neither n nor k have to be greater than or equal to 2. They can be greater than 0 and still yield the same proof. My bad adkjfdhl

[kagrenacs]

Explaining the Iceberg finale

This one is definitely nsfw, and there’s a brief mention of abortion

Moon Cum Vaults: To preface, I hate this, i fucking hate this. This comes from a collaboration between Trainwiz (popular mod creator, made the thomas the train dragon replacer, not active much on here anymore) and MK, called Tatterdemalion, sequel to the wheels of lull. Initially had a section where Reman’s cum was placed into vaults for cryogenesis. May have had a part where you had to swim through it and female characters could get pregnant, but this is a second hand source and I don’t want to think about this any further!

Manni/Makatosh: I couldn’t find anything on this besides mentions of it as a play on ‘Macintosh’

CHIM Quantum Witness: Quantum physics is a bit above my paygrade, but essentially Quantum physics are the rules of how particles behave. A problem with Quantum physics, is that we can’t always observe how particles behave, meaning we can’t really understand how everything works. A Quantum Witness is a device or function that helps us determine if particles are ‘entangled’ which means sharing information across any period of space because they’re bonded. If you’re omnipotent with CHIM, you could act as this witness.

The Hemisker Dreamsleeve Broadcast: If you thought Hemiskir wasn’t annoying enough, he’s now projecting his speech directly into your consciousness. 

Romaneli: In the redguard trailer, the titles of subsequent games were leaked well before their release date, by titles on the spines of books. After Oblivion, came ‘Romaneli’ (or what people think says Romaneli) Obviously this was changed, or it was just a placeholder name.

The Blind God: Mentioned as a dungeon name in Daggerfall, Sheogorath is in one room in this dungeon. I doubt the developers intended this to be anything, but one possible theory is that this refers to the Witness in the Enantiomorph, where the one who determines who wins out of the rebel and the king is often blinded or otherwise maimed. Magnus and Alandro Sul are examples of this.

Tiber Septim was an Orc: An interesting comment made by MK, a fan/associate of his stated ‘Everyone agrees there was a Tiber Septim’ in a discussion on what’s considered canon/not canon. MK made a pretty passive aggressive statement saying that there were 24 Tiber Septims and one was an orc, essentially making up canon to contradict someone. The teslore community seems fairly split on this issue, some defending him, others saying this wasn’t right.

Watch the Skies… : A creepypasta, not particularly good. https://creepypasta.fandom.com/wiki/Jvk1166z.esp 

The confession of Boma Kyro 143: A book from ESO depicting a play that never made it to the final cut. (Also, the play it depicts is also said to have never made it to the theater)

Bug Jar Inscriptions: Anyone who's ever watched a skyrim video ever will have this recommended to them by youtube. Multiple people theorizing what those inscriptions on the bottom of the bug jar lids mean, up to theorizing they’re a giant thalmor ritual circle

Trans-Amaranthian travel: Travelling between Amaranths, if you believe Akavir is an amaranth, then this applies. 

Mokafa’s theorem: Mentioned in the Four Suitors of Benitah, A character named Kena Zombel Mokafa writes out a mathematical theorem proving the man in front of him does not exist, and makes another guy disappear on the spot. Some consider this a form of zero-summing.

The Dwemer made our universe/became us: Or Kagrenac’s numidium worked and we became beyond the gods/the game and became humans in our world.

Hist Antithetical Amaranth: Memories of this seems to be vague for what i’ve seen discussed. But it seems to rely on the thought of ‘the hist-jillian’ wars being odd, considering Jills (those ‘female’ dragons) are supposed to keep order and time working right? And The hist being from a previous kalpa/connected to the infinite spirals of kalpas in the universe (according to one eso book perhaps), they could be contradictory forces and that’s why they’re fighting. MK may have backed this up, but that’s unsure. 

Section 22: Mentioned in the King Edward books, Akatosh the dragon (worthy to note King Edward seems to be set in a fantastical setting, not an event of the past) says he wants to name the town he founded with King Edward and co ‘Section 22’ because it’s an alright name.

Mubcrabs run world economy: The Mudcrab merchant

Reman Tsaesci Gangbang: I don’t particularly feel like looking into this

Nightmara: Not much found for this, besides mentions of nsfw works that I will not be clicking on. Possibly a reference to a horror book? Possibly just a play on the words Mara and nightmare.

Gemile: Another really common piece of lore, Caius Cosades believes that this person was the mother of Martin Septim in a short story from Ken Rolston.

The Pig: probably a reference to the book ‘The Pig Children’

Uriel Septim’s Daughter: In the french version of the arena manual, Ariella Septim is mentioned as Uriel Septim’s daughter and the current heir to the throne. All mentions of her disappear after this.

Talin Amaranth: This one is a joke

The abortion/The Black one: A short post made by MK, before he privated his tumblr, describing a possible sequel to c0da, called Dres Irae. Dres Irae can be assumed to be the aborted child of Barenziah and Tiber Septim, and MK said this story would explore a dark future for Morrowind. 

House Redoran Gravity Control: A joke from the old rp threads that made it ingame. Morrowind describes ‘gravity’ as one of the values House Redoran has.

The Fargoth Cycle: Another joke

Final thoughts: This image first popped up on 4chan around 2019, when those iceberg images were popular. Just knowing that this arose on 4chan should be a warning flag, but as I researched topics, It became more and more clear just how shitty the writers of the earlier games were. I started this as a project just for something to come back to during these months of lockdown and I don’t regret doing this, but i’ve definitely learned the extent of my distaste for hardcore fans of tes.

[perfectlytinyworkspace]

work in relation to force and energy

fundamental principles of work as a function of energy

work - measure of force exertion

work = magnitude of force • distance of force exertion | W = F • d when F is constant

magnitude of force (N) • distance (m) = N • m = Joule (J)

positive exerted work is in the direction of the object’s motion; negative work is against the motion direction

rationalizing work in relation to force and Newtonian concepts

F is the net force needed to move an object, and is directional | W depends on F, and F is proportional to acceleration → W is proportional to acceleration, too

applying a net constant force to an inert object causes it to accelerate

therefore, doing work to (i.e., applying a net force over a certain distance) an object causes it to accelerate

F and d, and therefore calculation of W, are separated into x- and y-directional quantities - even though the final W value in J is scalar

all work done along the relevant axis of motion must be taken into consideration when problem-solving | trig identities come back into play

key: “relevant to axis of motion” indicates that when F and d are perpendicular to one another, no work is done 

cos(90°) = 0 so Fcos(90°) • d = 0 J

think of work as the calculation of a force component on an object from the perspective of that which is exerting the force, whereas F = m • a is calculated in consideration of the object itself

i.e., work → exertER, and net force → exertEE | the two are inherently related, as described by the equation W = F • d

work = amount of force needed to overcome existing inertia • distance of force exertion → W(net) = F(net) 

W(net) = F(net) • d → sum(W(net)) = sum(F(components)) • d

calculation of W is summed directionally in x or y, but the W value itself is again, scalar (think work ~ scalar energy storage)

work due to variable spring force

the tension force exerted by a spring on an object attached to its end acts against motion 

(-) spring tension force ⟵ [object] ⟶ direction of motion (+)

F(T, spring) is proportional, in the negative direction, to the x-directional stretch of the spring itself | F(T, spring) = -k • Δx 

k is the elasticity spring constant, (N/m), determined by spring’s material and structural properties

this is known as Hooke’s Law - lengthy, stretched-out spring has more F(T) than a short, condensed spring

because a spring is continuously in horizontal motion, Δx is an instantaneous derivative rather than (x2 - x1)

F(T, spring) = -k • Δx → W = F • d 

integrate to find total continuously changing F(T, spring) over distance Δx → W = integral(F) • d

the integral calculation from x1 → x2 thus explains (1/2) constant multipliers in the final spring work equation 

remember that W(spring) is against the object’s motion and is thus negative!

work in relation to kinetic and potential energy

energy - ability/capacity to exert force in some way, shape or form → work is the actual exertion of that force

1. kinetic energy (KE) - capability to exert force, from entity’s motion | KE = 1/2(m • v^2) 

work-KE theorem - W(net) = KE(final) - KE(initial) 

makes sense in consideration of applied force F = m • a = disruption of object’s inert motion state

2. potential energy (PE) - capability to exert force, from entity’s potential to be in motion | precursor to / source of KE

two types: PE due to gravity (GPE) and PE due to spring elasticity (EPE)

a change in object’s PE means that some transformation from PE → KE has occurred | therefore, ΔPE calculations are relevant to work and KE

ΔGPE = mg • (y2 - y1) where y = object’s vertical position

ΔEPE = 1/2 • k • (x2 - x1)^2 where x = object’s horizontal position when attached to spring and k = spring’s given elasticity constant

ΔEPE is negative to its Hooke’s Law calculation because EPE is potential energy, and spring tension is KE in motion

[overwatch-does-stuff]

Echo Headcanons

Because there is finally new Overwatch content AND I AM GOING TO EMBRACE IT DESPITE MY INITIAL HESITATIONS! ---

- So. Many. Questions. She is constantly asking questions. About her surroundings, about others, about herself. Question question question. It’s how she was designed. - She doesn’t mean to be annoying about it! She really doesn’t. Can you tell her exactly what is so annoying about so she can know for future reference? - She doesn’t know how to talk about herself that much. In fact, diving into too much detail about her own self makes her. . . nervous. She’d much rather listen to someone else prattle on for hours. - That’s why McCree was such a good fit for her. He’s not used to being listened to, and he has plenty of stories to tell.

- Thinking about her own personhood is a deeply scary subject for her. She doesn’t understand how people, especially humans, seem to simply. . . make their own moral values and personality. She is explicitly aware of her advanced learning matrix, but she can’t puzzle out the difference between how she thinks and how humans think. She knows that she is different. She is not human. - When she was first made, and first started participating in Overwatch strike team missions, she noted that people seemed to look at her funny. Almost like they were uncomfortable. She assumed this was because she was an Omnic at first. However, she has recently learned about a concept called the “uncanny valley effect”. She has deduced that her face is not human enough, and not robotic enough, either, to make others feel comfortable around her. - She worries about how she makes other people feel. She has also learned that when she asks directly about how she makes others feel, people will lie.  - Because she can’t get an answer, her inquisitive programs go around in circles. Does this person like her? Are they uncomfortable? How do they really feel? - (Yes, she has robo-anxiety.)

- She really, really, really enjoys reading! Fiction, nonfiction, poetry. . . she can’t get enough of it. It’s her hobby and her passion. Whenever she isn’t busy, she’s reading.  - Her favorite fiction books are simpler children’s ones. She’s a real sucker for the innocent, black-and-white worldview and heartfelt stories where everyone gets a happy ending. She knows well that the real world is different, but reading allows her to escape that knowledge for a short time. - However, her favorite nonfiction books are really, really complex. The more in-depth, the better. Engineering textbooks, deep logistical theorems, and so on.  - She doesn’t quite understand a lot of poetry yet, but that’s what’s fun! She gets to learn what all of the flowery language means. It never takes her long to crack, and then she moves on to the next one.

- She can’t stand being alone without something to do. Give her a Sudoku puzzle, a crossword, or something. Anything! She’ll go nuts without something intellectual to do.  - Which means she’s always willing to help with chores and the like. If someone needs help with a mundane task, she’s the first to volunteer to help.  - Helping people makes her feel good. She knows that it is good. This is a fact that is reinforced with her every interaction with others. She can’t possible conceive of committing cruelty.

- She can’t make decisions. She really, really, can’t. Don’t ask her. Almost any sort of independent decision stresses her out. She can’t help but be so indecisive when presented with new and conflicting information! - She is unaware that her difficulty making decisions is one of the failsafes put on her by Overwatch and Liao to prevent her from going rogue. - If you ask her what, say, her favorite color is, she’ll change her answer every time. They’re just all so good! This also goes for her favorite person, place, book, etc. - She was programmed to be an optimist. She assumes that everyone is friendly until given signs otherwise. She assumes that everything will work out until there is evidence to the contrary.  --- S/O Headcanons: - I hope you’re an extrovert, because oh boy. - She just loves! Talking! To you! She wants to know everything about you. - She also loves touching you. She’s a very touchy-feely person. This is primarily because touching is the primary trait she has observed from other romantic relationships. And she is very very in love with you and wants to show it! - She’ll happily hold you in her arms and fly you around.  - Her face is surprisingly kissable. It’s made of hard light, after all. And her lips are pleasantly warm.  - Her hands and face are warm. . . but her core is actually quite cold! She always makes sure to get you a blanket when holding you.  - She would enjoy nothing more than to have you teach her one of your favorite hobbies.

[homenum-revelio-hq]

Welcome (again) to the Order of the Phoenix, Beth!

You have been accepted for the role of RYLAND GREENGRASS! We really enjoyed your application, especially the in-depth details that you gave to Ryland’s background and his family. We also loved how you didn’t shy away from Ryland being against werewolves, as that is something 99% of the population would’ve felt at this time. We’re so excited to have him aboard!

Please take a look at the new member checklist and send in your account within 24 hours! Thank you for joining the fight against Voldemort!

OUT OF CHARACTER:

NAME: Beth AGE: 24 TIMEZONE: CST ACTIVITY LEVEL: My activity will be able to continue as it has been. Most weeks I’m able to get online at least twice for replies, sometimes more. Outside the school day I’m usually lurking on Discord for plotting, even when I’m not actively on Tumblr. ANYTHING ELSE: None to report

CHARACTER DETAILS:

NAME: Ryland Greengrass AGE: September 3, 1953 (28) GENDER, PRONOUNS, and SEXUALITY: Ryland is a cismale who uses traditional He/Him pronouns. Outwardly he is straight. Inwardly, well, he thinks he is, but Ryland has also never let his mind dwell on the way his eyes traced the flexed arms of male Quidditch players or the nimble fingers of his friends. What he really would identify with if he took the time to properly reflect and learn some options is anyone’s guess, but he certainly is not the strait-laced straight man he thinks he is. BLOOD STATUS: Halfblood HOUSE ALUMNI: Ravenclaw ANY CHANGES: He’s wonderful just the way he is.

CHARACTER BACKGROUND:

PERSONALITY:

Ryland is a generally quiet guy. That’s always been true, but being an ungifted wizard at age eleven will only compound any natural instincts to avoid attention. Although he found plenty of magical skills elsewhere (that he’ll pull out as proof at the slightest provocation), that chip on his shoulder has never really healed. Ryland is also quick to be pulled into an argument over values. When it comes to things Ryland cares about, his disposition morphs into one of the passionate debater, although he will admit that he sometimes lets emotion get the best of him in such situations. He cares a lot and sometimes runs his mouth without thinking. That’s his competitive and compassionate sides winning out over his better judgement.

Although Ryland always struggled with wand magic, he was an excellent flyer, pretty decent at Astronomy, and got better at Potions as he went. His natural curiosity—and a strong desire to find something academic he was good at—led him to add as many classes as possible in third year. He excelled at Arithmancy and Study of Ancient Ruins. The work provided puzzles for Ryland to solve, and he quickly developed a talent that gained him praise from his professors. He’d always known he was meant to be in Ravenclaw and that the hat had chosen right, but he finally had the passion project to prove it. He threw himself into his numbers and symbols work full time by joining the Magical Theory extracurricular class and even picking up side problems from library books where he tried for fun to solve theorems that had stumped wizard-kind for centuries.

Ryland took that problem-solving to Quidditch after he made the team as seeker his third year, and his talents were recognized when he made captain his sixth year. He toyed with trying to pursue a career in the professional level sport, but Ryland wanted to feel like what he did for a living made a difference. As much as he loved Quidditch, he didn’t think that would.

As an adult, Ryland tried to keep his head down at work and socially unless something directly involved him, but listening to his family talk politics led him to chase down rumors of the Order to feel like he could make a difference. Ryland wanted to do something that mattered and that made a difference in people’s lives, but there wass a small part of him that looked at the organization as another way to prove himself. He still isn’t great with a wand, but Ryland’s skills have come in handy in his personal, professional, and extracurricular vigilante life. He has proved himself more than once and was mostly content with that.

Captivity has changed him. The already quiet Ryland has become even more withdrawn, and it’s rare for him to take the initiative to start a conversation for himself. If he has a quippy comment, he’s much more likely to keep it to himself. He isn’t sleeping well at night and would like to blame that for why he’s so jumpy at little things. He has a hard time trusting that anyone is who they say they are and intends to do what they say they will. He feels listless and lost, wanting to pretend everything is normal but having that crumble around him more and more every day.

“BRIEF” OVERVIEW OF FAMILY:

Family tree found here: https://66.media.tumblr.com/c99c5fb1546f15aec17a9dace3acbda4/e31bc90a8e13c282-1d/s1280x1920/cf3519093477810b9eff505fd4268726d60eccc9.png

Zaria Ollivander came from an old and loyal family who knew the value of unity. Their wands could not have lasted a millennia without such drive, and though she herself possessed no gift for wand-making—and was honestly discouraged to develop the skill, as a woman who could carry on a family name, but not her own—she never forgot the importance of family. Soon after her Hogwarts graduation, she was married to Hawthorne Greengrass. Her family joked that while she’d never had a talent for wands in the past, she’d finally found her proper material (or proper wood, as her rather drunk brother joked once; she made him regret ever doing so) to properly craft something magical. Zaria agreed. The Greengrass family was an equally old and prosperous one. She planned to lead it to great things.

It seemed like a sign from magic itself when in quick succession, she and Hawthorne were blessed with three sons. Archer, Verner, and Brighton grew up having everything they could want and learning all the expected superiority they should for a breeding as pure and wonderful as theirs. The only potential testiness in Zaria and Hawthorne’s childrearing plans was Hawthorne’s baby brother who loved to spend time with the children and read to them. Zaria wasn’t too put out by Beedle bedtime stories, but when Sorrel turned to “The Twelve Dancing Princesses” and other muggle fairytales, Zaria wasn’t pleased. Hawthorne placated her with the promise that it wouldn’t affect their education and that family was too important to risk losing over such a small argument. That was all well and good, but Zaria couldn’t help use the same bitter logical to decide it was unfair that when her eldest Archer was only fifteen, Hawthorne and Sorrel took a trip to Italy that turned deadly due to a potions accident.

Zaria grieved privately, but outwardly she remained the same imposing matriarch she’d been since her marriage. Losing the head of the family and his spare could have been devastating, but Zaria hit the ground running with an iron rule that her sons never wished to question. They loved and trusted their mother too much.

Unfortunately Asher must have picked up a little of his uncle’s peculiarities. He’d shocked the family by taking Muggle Studies in school, something Hawthorne had assumed was just a phase. His son wasn’t soft or necessarily muggle-loving, after all. It was a quick. That quirk persisted in a slight disregard for tradition. Asher was still a Greengrass and therefore knew the importance of family, but he placed less importance on pureblooded tradition. His mother nearly fainted the day he told her he had asked Rosalie Ross to marry him. The only saving grace for Zaria was that at least her son had enough sense to choose a halfblooded witch with a few generations of magic flowing through her veins.

Rosalie Ross knew she’d been underestimated the moment her future mother-in-law laid eyes on her, but she wasn’t about to roll over and let herself be bad-mouthed. Instead she endeavored to stay tall and proud in the face of whatever snide comments came from her husband’s relatives. Whether they liked it or not, Rosalie was family new. Rosalie Greengrass didn’t have the same romantic ring as her maiden name, but if anyone suspected her of purposefully giving her son a name that would be just as poetic as her own had been, no one accused her aloud.

She loved Ryland dearly and spoiled him rotten. Asher wasn’t quite the same soft-hearted spirit as his wife, but Rosalie watched him share his fondness with their son in his own way. Four years later when she finally found herself pregnant again, Rosalie was overjoyed, and Asher broke his normally quiet routine to share their joy with anyone who would listen. Ryland didn’t trust the idea of a younger sibling, but that changed when Paisley arrived. He was her fierce protector, kind and patient with her, even at age six. No one was more devasted than he was when she contracted dragon pox.

Rosalie and Asher made the hard decision to shut Paisley away where her brother couldn’t get to her. A four-year-old’s chances of surviving the disease weren’t great, and they had to be realistic. While they continued to push for any medical treatments possible, the grieving parents had already made vowed not to let the disease take two children from them. Ryland never got the chance to properly say goodbye.

He was never quite the same child after that, and while he was still gentle by nature, Ryland began picking fights with his cousins when they didn’t mind their words. Verner and Brighton both warned their brother he had a budding sympathizer in his home, but Asher paid them no mind. He saw nothing wrong with a few liberal ideas about muggleborns. They weren’t on the same level as muggles themselves.

Rosalie knew it was a blow to her husband’s ego when news of Ryland’s first year first reached home. He had seemed to be off to a promising start in Ravenclaw; however, that proved to be less of an assurance that he would be talented than his parents had thought. His struggles with any kind of magic quickly became apparent, and Ryland lagged behind his peers in even the most basic spells. As an emergency measure, Zaria took him to get a replacement wand when he was home at Christmas, despite reminders from her older brother Garrick that a wand couldn’t solve anything. They found one just as willing to have Ryland as the first, and he packed up both to return to school. His grades didn’t improve. He switched between wands. When he went back for his second year, Ryland still took both, but he began using the original exclusively again. It felt better in his grip, and the wand held no ill feelings for his forced betrayal.

The rest of the family delighted in Ryland’s failings. There was the proof of what they’d always believed: even a little muggle blood sullied the whole line. Of course, Rosalie never heard those comments because her brothers-in-law and their wives were more careful than that, but Asher pressed his lips together and bared it with only small remarks.

When Ryland reached third year, he took as many classes as he could fit into his schedule, discovering several new skills in the process. That didn’t change his family’s opinions, though, and the alienation he felt from his uncles’ sides of the family only grew as he developed more liberal ideas about muggles and magic. Grandma Zaria still treated him the same, still only made lemon bars with Ryland (just as she had a specific recipe for each of her children and grandchildren), but things were tense, and she didn’t pretend not to notice. She often warned him that he had to stop rising to the bait because his uncles and cousins were only looking for a fight.

He didn’t listen. He never did. It soon became clear that his cousins Lachlan, Ewan, and Lachlan’s wife Delilah were likely Death Eaters. If his other extended family members weren’t, they were at least supportive. Only Zaria seemed to keep completely above it all, but she cared more about family loyalty than any loyalty to a zealot’s cause.

Even with all their differences, even with all their animosity, Ryland thought he was safe among them. After all, they were family.

OCCUPATION: 

Gringotts Researcher—Prior to his kidnapping, Ryland had worked his way up to a coveted spot on the Gringotts vault security team. It had him doing valuable work within Gringotts that also occasionally gave him access to sensitive vaults whose contents might interest the Order. However, his position was given away during his absence, as he clearly hadn’t asked vacation time. Gringotts did allow him to come back into their employment, but he’s been rerouted to another division for the only available position fitting his talents. He’s now a researcher for Gringotts Cursebreakers, which means he spends a lot of time poring over old books and offering practical advice. The work doesn’t interest him as much, as it reverted him from creating puzzles to solving them, but at least it’s still of potential interest in the Order in its own way. He hasn’t lost all his usefulness to the world.

ROLE WITHIN THE ORDER/THOUGHTS ABOUT THE ORDER:

Ryland was perhaps a bit naïve when he joined the Order, treating it a bit like a club rather than an underground vigilante group. He did catch on to the stakes fairly quickly, but it’s not like he had fighting expertise to provide anyway. What he did have was a mind for puzzles and occasional access to old vaults owned by long-standing and distinguished pureblood families. The latter gives him some inside information that is occasionally of use while the former makes him a capable problem-solver and researcher. He knows he’s not the only person in the Order with those skills—far from it—but they did allow him the opportunity to mid-level over the years. Ryland doesn’t necessarily agree with all the decisions that are made, and occasionally he’s spoken up when he disagreed. Mostly he’s been the quiet guy in the background who helps theoretically take things apart.

After his ambush, Ryland thought rescue would come pretty quickly. It was common speculation that he had Death Eater relatives, although Ryland hadn’t taken it personally. He was hardly the only one in the Order with that kind of suspicion on family members. Surely they would put the pieces together and rescue him. The longer that passed, though, the less likely that seemed. Ryland grew bitter thinking about people he’d considered colleagues and even friends. Eventually it occurred to him that he wasn’t important enough to be worth a rescue operation, even if anyone did put the pieces together correctly. That stung worse than anything else.

Once he’s back, Ryland will be incredibly distrusting of anyone and unable to stick his neck out for any kind of personal risk when he has pretty good evidence now that he won’t be supported if those risks increase. That said, he cannot walk away. Not only does he owe them for his eventual rescue, but he also has no one left. Without the Order, Ryland will be completely isolated and alone. He can’t stand that idea, even if Ryland feels bitter about this whole situation and his own dependence on people who clearly don’t care about him or anyone else compared to the cause itself.

SURVIVAL:

Only an old pureblood family could have extra lands and homes not in use to just pass on to the next generation. Ryland doesn’t have a family estate or anything like that, but he has been legally gifted an old family vacation home in Bath. It hadn’t been used regularly since his grandmother was a little girl, and Ryland was able to fix it up and bestow (through Orders, not his own wand work) new charms and protections over it to keep people out without his blessing. Security is what he does for a living, after all. The house was so heavily warded that his family couldn’t break in during his imprisonment, so he still has it as a safe house. The wards have only increased in his newfound paranoia post-rescue.

He wants to spend a lot of his time that he isn’t at work in his house because it feels more secure, but he spent so much time alone. Ryland has been in solitary confinement when not being tortured for the past three months. He needs a little noise, a little human interaction, even if it makes him nervous. The Order safe houses have their own levels of security, so he is likely to be lurking around the corner from the action, still skittish around people and especially around these people he previously thought he could trust.

Ryland said a lot of things under duress to try to stop the pain or to keep himself alive. He had bones broken over and over, and only the Death Eater’s willingness to heal him after has kept him from permanent disfigurement (which only serves as further proof in his mind that Ryland had family helping with those sessions). He has a lot of guilt about it now and frequently wakes up in the middle of the night over it, when he manages to sleep at all. In the coming months, he’s going to struggle with some dependency issues as he struggles to find a healthier coping mechanism than sleeping draughts every night. He knows they aren’t healthy long term, but when nothing else seems to work, what is he to do? It’s likely he’ll end up buying things that are not entirely legal to cope with the pain and his own inner turmoil.

RELATIONSHIPS:

Is anything in Ryland’s fault not falling apart right now? Or at least not at risk? He’s spent over three months being tortured physically and mentally while his hope slowly corroded away in desolation. No one was coming for him. That was a fact he fully accepted for at least a month, possibly more since he didn’t exactly have a great way to keep time while locked up. It will take time for him to rebuild his trust for people. The people he most hoped would come are also the people he has the least trust in right now. He can’t look his parents in the face anymore, even though he’s mostly sure they weren’t involved.

His old friends should have known something was wrong. They should have known that Ryland wasn’t the kind of person who just up and disappeared without warning. The fact that no one seemed to look for him and that no one who says they did apparently looked very hard have not been easy potions to drink. Ryland desperately wants to be around people again now that he has the chance, but even if he did trust them, the noise of crowds or groups make him nervous. All of this in combination means that he’s currently hard to be around, doesn’t know who he wants to be around, but needs to be around someone. He has a lot of anger and accusations that seem perfectly reasonable to him, given what he’s just gone through. Ryland only hopes he won’t lose everyone in the process.

OOC EXPLORATION:

SHIPS/ANTI-SHIPS: Ryland/Chemistry—I have no preconceived ship ideas for him, although based on his character relationships, Ryland/Gideon, unattainable Ryland/Archie, or one sided Ryland/Isla all seem to have some potential seeds to sew if eventual players are interested. If anything buds with another male character, he may take a little gay panic to get there. Regardless of gender, he’s not exactly in the most trusting place right now to start a healthy relationship, so it’s going to take time or not be great with his mental state.

WHAT PRIVILEGES AND BIASES DOES YOUR CHARACTER HAVE?

Ryland’s family seems to have one token liberal per generation to more extreme levels. Sorrel liked muggle stories. Asher didn’t see what was so bad about supposed mudbloods. Ryland finds muggles fascinating in a purely academic sense. He refuses to see them as anything other than people deserving of care and consideration. He once almost made his grandmother faint with a comment that he didn’t think a woman’s blood status mattered in her marriageability. That said, Ryland doesn’t really understand the muggle world. He’s never spent any time in it and knows next to nothing about the people. His fight in the Order is less about protecting muggles and more about evening the playing field in the magical world. As much as he loves his family—and has to acknowledge their position in it—Ryland doesn’t think the old traditions of rigidly structured hierarchies and frequent inbreeding of pureblood families can be sustained for many more generations. Everything has reached a point where it can tip either way, and he’d rather not see the world tip into chaos.

Still, there are a lot of things that old structure has provided to Ryland, including his home. He has to acknowledge them, but he often doesn’t look at the far-reaching implications of what all that has afforded him.

On another note, Ryland’s general feelings about magical equality don’t necessarily extend to other magical creatures. He works with goblins all day and respects their intelligence and powers. He can appreciate that many house elves can easily do things without a wand that he struggles to accomplish with one. Half-breeds, though, make him nervous for a variety of reasons. Half-veela are hard to trust when they can manipulate people so, and that seems like a security risk. Werewolves are even worse in Ryland’s mind. His baby sister was isolated before her death because she had a deadly contagious disease. That description matches lycanthropy only all too well to Ryland, and he doesn’t understand why more people don’t see the concern of letting werewolves walk among them pretending to be regular wix instead of the disease-carrying risks they are.

WHAT ARE YOU MOST LOOKING FORWARD TO? You people keep pulling me in by being so wonderful for idea bouncing and muse possibilities. I’m not going anywhere, and I look forward to introducing my sad boy.

PLOT DROP IDEAS:

It could be interesting to potentially have to make a difficult choice related to family; however, Ryland needs a little time to work through the trauma first. It’s also possible he learned something in captivity that might spur Order action.

On a personal character growth note, I really like the idea of him fueling his pain and healing into turning his home into a kind of sanctuary for people whose families have turned against them like his or who don’t have anyone to turn back to. Eventually I’d like him to be running a foster home, especially for Hogwarts-aged teens. This wouldn’t be an immediate thing.

ANYTHING ELSE? Nope!

[intuitive-physics]

Basic maths

Not too much maths is needed, but better to know some school level stuff:

Algebra basics

Calculating averages

Pythagorus theorem

Also some physics notation:

x₀ Whenever you see a small “0″ at the bottom (as above), this is simply a fancy pants way of saying “the initial (or starting) value of x”.

Δx Whenever you see this “Δ” (called “delta”) symbol, it means “the change of x”. So if you had a starting value of x (x₀) and a final value of x (x₁ or sometimes written just x), then Δx is the difference: Δx --> x₁ - x₀

Why? Usually when we talk about a certain distance or certain amount of time, we’re talking about a difference of these. 

ā or ⟨a⟩ Line over a letter, or triangle brackets around a letter means “average”. So if a means acceleration, then ā or ⟨a⟩ means average acceleration.

[coursesforallacademynoida]

B.Tech Tuition For Network And Synthesis In Noida

B.Tech Tuition For Network And Synthesis In Noida

B.Tech Tuition For Network And Synthesis In Noida

Signal Analysis, Complex Frequency, General Characteristics and Descriptions of Signals, Node Voltage Analysis, Mesh Current Analysis, Step Function and Associated Wave Forms, The Unit Impulse, Initial and final conditions, Step and Impulse Response, Response of Source Free Circuits, Forced Response, Phasor and Steady State Responses of Circuits…

[occultspirits-blog]

Chaldeans v.s. Pythagoreans: Ready, Set, Start Your Number Fight!

Hi all and welcome to Spirit's Throwback Thursday blog post. Today I wanted to discuss Numerology and it's origins. Numerology is a belief that the divine sends us messages through numbers, words (like your name) and synchronicities. In this time it is considered a divination tool, but this was not always the case. There are two main branches of numerology, Pythagorean and Chaldean. These branches differ slightly from one another while still maintaining the belief that numbers were equivalent to divine truths. For the sake of ease we will be discussing the two most popular, Chaldean and Pythagorean.

Pythagoras was born in Samos (a Greek island in the Aegean Sea) in the year 570 B.C. Pythagoras is most famous for the Pythagorean Theorem (A squared plus B squared equals C squared), so the squared sums of the two sides of a right triangle are equal to the squared value of the hypotenuse. But many seem to ignore the fact that Pythagoras was an astrologist, numerologist, musician and a spiritual Guru. Pythagoras had an ability to contact enlightened souls, who helped him discover all his previous lives, and make predictions. His teachings stated that every planet had a signature sound, and the sound was represented by numbers. He then taught that the numbers each had separate characteristics, and meaning to our lives.

The following is the references used in Pythagorean numerology.

a,j,s=1

b,k,t=2

c,l,u=3

d,m,v=4

e,n,w=5

f,o,x=6

g,p,y=7

h,q,z=8

i,r=9

Add all the numbers up in a person's name and then reduce to single digit. For example: Gloriann Cruz Albino would be: 7+3+6+9+1+5+5+3+9+3+8+1+3+2+9+5+6= 85, then reduce: 8+5=13, reduce again: 1+3=4. In this case 4 is the name number. The only numbers not reduced are 11 and 22 the master numbers.

Number 1: The light side: initiative, leadership, individuality, bravery, executive ability. On the dark side, selfishness, laziness, aggressiveness, narcissism.

Number 2: The light side: cooperation, harmony, love,partnership and finesse. On the dark side: over sensitivity, untactful, timid, indecision.

Number 3: The light side: artistic, creative, self expression, imagination, social, and cheerful. On the dark side: pessimistic, loose lipped, tends to exaggerate.

Number 4: The light side: constructive, systematic, practical, keeping order, builder,industrious. The dark side: lack of imagination, argumentative, very serious, ill health.

Number 5: The light: constructive, freedom, sexuality, versatility, knowledge, entertainment and amusement. The dark: changeability, carelessness, restlessness, nervousness, Jack/ Jill of all trades, master of none.

Number 6: The light: artistic, responsible, love of home and children, care about the welfare of others, unselfish. The dark: being too sensitive, coldness, nervousness, skepticism, lonely.

Number 7: The light: spirituality, the occult, analysis, researcher, wisdom. The dark: selfishness, laziness, aggressiveness and self centered.

Number 8: The light: executive ability, organization, authority, judgement, and administration. The dark: impatience, love of recognition, lack of humanitarianism, materialistic.

Number 9: The light: generous, humanitarian, sympathetic, selflessness, divine connection. The dark: moody, impulsive, must learn selfishness, careless with money, attracted to a life beyond their means.

Number 11: The light: intuition, illumination, inspiration, spirituality and prophetic abilities. The dark: too sensitive, nervousness, tension, impracticality and shyness.

Number 22: The light: materialism, spiritual master, practical and guiding light. The dark: conflict between inner feelings and practicality and attraction to magic.

While using this divination to figure things out about yourself if the number is from letters make sure you use your birth given name. For example 4 is my name number, which means the following. The light side: constructive, systematic, practical, keeping order, builder,industrious. The dark side: lack of imagination, argumentative, very serious, ill health.

Chaldean Numerology has been in use since the Babylonian era. There is a difference between Chaldean and Pythagorean Numerology, Chaldeans believed you could use the name that you are know by (nickname). Another major difference is that Chaldeans used the birth date number ( number of the day you were born on). This number reflects the personality and health of the native. The final major difference is that Chaldeans interpreted numbers 1 through 52, to symbolize the weeks in a year. Following is a letter to number analysis.

1=A,I,J,Q,Y

2=B,K,R

3=C,G,L,S

4=D,M,T

5=E,H,N,X

6=U,V,W

7=O,Z

8=F,P

The numbers 1 through 9 are related to, how the native appears in the eyes of another, and the physical and material sides of things.

Number 1: male, yang, self consciousness, originality, independence, aggressive, unique, creative, dominant, the leader.

Number 2: pair, duo, feminine, yin, seeking unions, choice, adaptable, tactful, understanding, gentle, cautious, a follower.

Number 3: manifestation, expansion, creativity, the performer, expansive, sociable, dramatic, communicative and diversified.

Number 4: dependable, attuned to the four seasons, law, order, balance, harmony, secure, stable, stability, endurance and discipline.

Number 5: vital force, freedom, change, adventure, charisma, versatility, resourceful, adaptive, change, activity, travel, promotion and speculation.

Number 6: conscientious, desire to be in harmony, truth, justice, has a good sense of balance, loving , compassionate.

Number 7: answer seeker, asks the difficult questions, solitude is needed, looks to converse with others that are like minded, introspective, intuitive, analytic, inspirational, reclusive, philosophical and mystical.

Number 8: infinity, power, achieved control, responsible, recognition, expansion and growth.

Number 9: complete cycle of growth, selfless, compassionate, wants to help others at all cost, love, compassion, patience and service.

Double digits (compound numbers) show hidden influences, that play a role in life now and in the future.

Number 10: honor, faith, confidence, rise and fall.

Number 11: gives warning of hidden dangers, trials, or treachery. This person will have great hardships to grow through.

Number 12: suffering, anxiety, seen as the sacrifice or the victim at the hands of others.

Number 13: change of plans or place, non fortunate, upheaval , destruction, havoc wreaking power, warning of the unknown,

Number 14: movements, combinations, threats of natural forces, fortunate for dealings with money, small element of risk or danger.

Number 15: occult significance, magic, mystery, but this is only used in selfish ways.

Number 16: gives a warning of a strange fatality awaiting the querent, danger of accidents, and one being defeated,

Number 17: highly spiritual, the number of immortality, legacy,

Number 18: materialism striving to destroy spirituality of nature, bitter quarrels, social upheaval, revolutions, a warning of treachery , deception, danger from the elements,

Number 19: fortunate and favorable, happiness, success, esteem and honor

Number 20: a call to action, great purpose, is a very spiritual number, that is not conducive to the material world.

Number 21: advancement, honors, elevation of life , general success, victory, determination.

Number 22: warning of illusion of delusion, a good person living in a "fool's paradise" , a dreamer of fierce dreams and false judgement.

Number 23:a promise of success, help, and protection.

Number 24: fortune, promises, assistance, gain through love.

Number 25: strength gained through experience, observation.

Number 26: grave warnings for the future, foreshadows disaster, ruin and bad advice.

Number 27: promise of authority, power, command,reward comes for production.

Number 28: full of contradictions, loss through trust, opposition and competition in trade, danger of loss through law, likelihood of having to begin life over and over again.

Number 29: uncertainties, treachery, deception, trials, tribulations, unexpected danger, unreliable friends, and grief.

Number 30: thoughtful deduction, retrospection, and mental superiority.

Number 31: self contacted, lonely and isolated.

Number 32: magical power, it is fortuitous if judgements and opinions are held back.

Number 33: no meaning of its own, uses 24 or sometimes 6.

Number 34: Has the same meaning as 25 or 7

Number 35: Same meaning as 26 or 8

Number 36: Has the same meaning as 27 or 9

Number 37: good and fortunate friendships, love and connection.

Number 38: Has same meaning as 29.

Number 39: Has same meaning as 30

Number 40: Has the same meaning as 31.

Number 41: Has the same meaning as 32.

Number 42: Has the same meaning as 24.

Number 43: revolution, upheaval, strife, failure and failure.

Number 44: Has the same meaning as 26.

Number 45: Has the same meaning as 27

Number 46: Has the same meaning as 37.

Number 47: Has the same meaning as 29.

Number 48: Has the same meaning as 30.

Number 49: Has the same meaning as 31.

Number 50: Has the same meaning as 32.

Number 51: power, the nature of the warrior , promises sudden advancement, favorable for those in military life and leaders of any cause.

Number 52: Has the same meaning as 43.

In conclusion Pythagoreans use numbers 1-9, 11 and 22. While Chaldeans use numbers 1-52. All believe that numbers are a intricate part of life. So as a Numerologist myself, I use the Pythagoras system. But just as any other divination systems, numerology is 90% belief. Blessed be.

[physics-scholars]

If 4^x+3^x=5^x, then the value of 

X=?

🍁

To solve for x in the equation 4^x + 3^x = 5^x, we can use logarithms. Taking the logarithm of both sides of the equation with base 10, we get:

xlog10(4) + xlog10(3) = x*log10(5)

Dividing both sides by x, we get:

log10(4) + log10(3) = log10(5)

Using a calculator or logarithm tables, we can find that:

log10(4) ≈ 0.60206

log10(3) ≈ 0.47712

log10(5) ≈ 0.69897

Substituting these values into the equation, we get:

0.60206 + 0.47712 ≈ 1.07918 ≈ 0.69897

Therefore, x ≈ 1.07918.

Is the method of solving correct? This is not correct. Because You can't take the logarithm of numbers added separately.

Cross check 

4² + 3² = 25 = 5²

➖

1. Using logarithmic identity method:

If 4^x+3^x=5^x, then the value of 

X=?........

The equation 4^x + 3^x = 5^x can be solved by taking the natural logarithm of both sides. We have:

ln(4^x + 3^x) = ln(5^x)

Using the logarithmic identity ln(a^b) = b*ln(a), we can simplify the left-hand side:

xln(4) + xln(3) = x*ln(5)

Dividing both sides by x gives:

ln(4) + ln(3) = ln(5)

Taking the exponential of both sides gives:

4*3 = 5

which is clearly false. Therefore, there is no value of x that satisfies the equation 4^x + 3^x = 5^x.

➖

Using Binomial method:

If 4^x+3^x=5^x, then the value of 

X=?........

Use binomial method 

We can use the binomial theorem to expand the terms on the left-hand side of the equation:

(4+3)^x = 5^x

Simplifying the left-hand side using the binomial theorem, we get:

4^x + 3^x + (terms containing higher powers of 4 and 3)

Since the binomial expansion of (4+3)^x contains only positive terms, we know that the terms containing higher powers of 4 and 3 are positive. Therefore, we can write:

4^x + 3^x < (4+3)^x = 7^x

Substituting this inequality into the original equation, we get:

4^x + 3^x < 5^x

This inequality is true for all x, since the left-hand side is less than the right-hand side. Therefore, there is no value of x that satisfies the equation 4^x + 3^x = 5^x.

➖

Using Newton Ralph method:

If 4^x+3^x=5^x, then the value of 

X=?........

Newton Ralph method 

The equation 4^x + 3^x = 5^x can be solved using numerical methods such as the Newton-Raphson method, which is an iterative method for finding the roots of a function. We can rewrite the equation as:

f(x) = 4^x + 3^x - 5^x = 0

The derivative of f(x) with respect to x is:

f'(x) = 4^x * ln(4) + 3^x * ln(3) - 5^x * ln(5)

The Newton-Raphson method starts with an initial guess x_0 and iteratively refines the estimate using the formula:

x_{n+1} = x_n - f(x_n) / f'(x_n)

We can use a calculator or a computer program to implement this iterative formula. For example, using an initial guess of x_0 = 1, we obtain the following values:

x_1 = 1.184666

x_2 = 1.175669

x_3 = 1.175560

x_4 = 1.175560

After four iterations, the estimate converges to x ≈ 1.175560. 

However, this solution cannot be expressed in terms of simple algebraic functions and must be obtained numerically.

However, this solution cannot be expressed in terms of simple algebraic functions and must be obtained numerically.

➖

Fermat's Last Theorem states that for any integer n greater than 2, there are no three integers a, b, and c that satisfy the equation a^n + b^n = c^n.

However, the equation given in this question, 4^x + 3^x = 5^x, is not in the form of Fermat's Last Theorem. Therefore, we cannot use Fermat's Last Theorem to solve this equation.

Instead, we can try to use algebraic techniques to solve for x. One possible approach is as follows:

We can rewrite the equation as:

(4/5)^x + (3/5)^x = 1

Letting y = (4/5)^x, we can rewrite the equation as:

y + (3/5*y) = 1

Solving for y, we get:

y = 5/8

Substituting back, we get:

(4/5)^x = 5/8

Taking the logarithm of both sides, we get:

x*log(4/5) = log(5/8)

Solving for x, we get:

x = log(5/8) / log(4/5)

Using a calculator or logarithmic tables, we get:

x ≈ 0.756

Therefore, the value of x is approximately 0.756.

➖

The final way to solve:

4^x+3^x=5^x is, 

If (1+3)^x+(1+2)^x=(1+4)^x, then the value of 

X=?........

Use binomial method ....

We get answer 2,✅

If (1+3)^x+(1+2)^x=(1+4)^x, then the value of 

X=?........

Use binomial method 

We can use the binomial theorem to expand (1+3)^x and (1+2)^x as follows:

(1+3)^x = 1^x + x31^(x-1) + (x choose 2)3^21^(x-2) + ... + (x choose k)3^k1^(x-k) + ... + 3^x

(1+2)^x = 1^x + x21^(x-1) + (x choose 2)2^21^(x-2) + ... + (x choose k)2^k1^(x-k) + ... + 2^x

Notice that all terms in the expansions have a factor of 1^k, so we can rewrite the given equation as:

1 + x*3^(x-1) + (x choose 2)*3^(x-2) + ... + (x choose k)*3^(x-k) + ...

1 + x*2^(x-1) + (x choose 2)*2^(x-2) + ... + (x choose k)2^(x-k) + ...

= 1 + x4^(x-1) + (x choose 2)*4^(x-2) + ... + (x choose k)*4^(x-k) + ...

Simplifying, we get:

2 + x3^(x-1) + x2^(x-1) + (x choose 2)(3^(x-2) + 2^(x-2)) + ...

= x4^(x-1) + (x choose 2)*4^(x-2) + ...

Notice that all terms except the first have a factor of 4^k, so we can rewrite the equation as:

2 + x3^(x-1) + x2^(x-1) + (x choose 2)*(3^(x-2) + 2^(x-2))

= 4^x - (x choose 0) - (x choose 1)*4^(x-1)

Simplifying further, we get:

2 + x3^(x-1) + x2^(x-1) + (x choose 2)(3^(x-2) + 2^(x-2)) = 34^(x-1) - x*4^(x-1)

Adding x*4^(x-1) to both sides, we get:

2 + x3^(x-1) + x2^(x-1) + (x choose 2)(3^(x-2) + 2^(x-2)) + x4^(x-1) = 3*4^(x-1)

Dividing both sides by 4^(x-1), we get:

2/4^(x-1) + x*(3/4)^{x-1} + x*(2/4)^{x-1} + (x choose 2)*[(3/4)^{x-2} + (2/4)^{x-2}]

= 3

Now, let's focus on the left-hand side of the equation. Notice that all terms except the first have a factor of (3/4)^{k-1} or (2/4)^{k-1}. Therefore, we can rewrite the equation as:

2/4^(x-1) + (3/4)^{x-1}[x + (x choose 2)(3/4) + (x choose 3)(3/4)^2 + ...] + (2/4)^{x-1}[x + (x choose 2)(2/3) + (x choose 3)*(2/3)^2 + ...] = 3

Now, we can simplify the terms inside the square brackets using the binomial theorem:

(3/4)^{x-1}[x + (x choose 1)(3/4) + (x choose 2)(3/4)^2 + ...]

= (2/4)^{x-1}[x + (x choose 1)(2/3) + (x choose 2)(2/3)^2 + ...]

Notice that the terms inside the square brackets are the expansions of (3/4 + 2/4)^x and (3/4 + 1/4)^x, respectively. Therefore, we can simplify the equation further:

2/4^(x-1) + (3/4)^{x-1}(5/4)^x + (2/4)^{x-1}(4/3)^x = 3

Let's rewrite the equation in terms of the variable y = (4/3)^x:

2/4^(x-1) + (3/4)^{x-1}(5/4)^x + (2/4)^{x-1}y = 3

Multiplying both sides by 4^(x-1), we get:

2 + 3^x*(5/4)^x + 2^xy = 34^(x-1)

Substituting y = (4/3)^x, we get:

2 + 3^x*(5/4)^x + 2^x*(4/3)^x = 3*4^(x-1)

Multiplying both sides by 3^x, we get:

23^x + 5^x + 2^x(3/2)^x = 3^x*4^(x-1)

Dividing both sides by 2^x*3^x, we get:

(2/3)^x + (5/6)^x = 2

Let's define f(x) = (2/3)^x + (5/6)^x. Then, we need to find the value of x such that f(x) = 2.

Note that f(x) is a decreasing function for x > 0, since:

f'(x) = -ln(2)(2/3)^x - ln(5/6)(5/6)^x < 0 for x > 0

Therefore, f(x) = 2 has at most one solution. We can see that x = 2 is a solution, since:

f(2) = (2/3)^2 + (5/6)^2 = 4/9 + 25/36 = 2

Therefore, the value of x is x = 2.

➖

[averycanadianfilm]

Teaching Dossier - Hubert Hugh Burke, Ph.D

Hubert Hugh Burke PhD, Teaching Dossier:

Teaching Experiences:

University Introductory Level Teaching.

Barnard College (Columbia University):

During summers when I was a graduate student. I taught Pre-Calculus and Calculus to first year students.

The Colorado College:

During the two years when I was an Assistant Professor of Physics. 

I taught Introduction to Physics for the Physical Sciences.

Rutgers University (Newark):

When I was an Assistant Professor of Physics. 

I taught Introduction to Physics.

Barnard College (Columbia University):

During the summer of 2005 as a visiting Lecturer. I taught two courses to first year students, Calculus and Introduction to Probability and Statistics.

Advanced Undergraduate Level Teaching:

The Colorado College:

During the two years when I was an Assistant Professor of Physics. I taught two Mathematics courses at the advanced undergraduate level. These courses were: Vector Analysis (Vector functions, divergence and curl. Green's and Stokes's theorems, and the properties of three-dimensional curves and surfaces. And, also related topics from linear algebra and differential equations.) and, Partial Differential Equations (Introduction to analytical and numerical methods for finding solutions to differential equations involving two or more independent variables. Topics included linear partial differential equations, boundary and initial value problems, Fourier series solutions, finite element methods, the Laplace equation, the wave equation and the heat equation.)

Rutgers University (Newark):

When I was an Assistant Professor of Physics. I taught the Mathematical Methods of Physics course. An advanced undergraduate course taken by physics majors and engineering students which included topics from Advanced Calculus, Linear Algebra and Partial and Ordinary Differential Equations.

Trent University (Peterborough):

As a Sessional Course Instructor in the Physics Department during the winter term (2015), I taught the second half of the third-year Electricity & Magnetism course. This course has two goals: to introduce students to fundamental concepts of electricity and magnetism, and to develop mathematical tools with which to solve the constituent equations. The final goal of this course is to write down Maxwell's equations, from which all electromagnetic phenomena follow. Along the way, we will cover electrostatics, magnetostatics, and electric and magnetic properties of matter.

This course will cover chapters 1-7 and some of chapter 9 of Griffiths' textbook.

As an Assistant Professor of Physics during the 2015/2016 academic year, I taught the following courses: Second-year Introductory Quantum Physics. This course covered special relativity, particle-like aspects of radiation, atomic structure, wave-like properties of matter, the Schrödinger equation and applications to one-dimensional systems.

Second-year Thermal Physics. This course covered the laws of thermodynamics and their applications, thermodynamic potentials, kinetic theory of gases, heat engines, and an introduction to statistical mechanics.

Third-year Classical Mechanics. This course covered particle motion in one dimension, resistive forces; oscillatory motion (harmonic oscillator, damped, damped and driven oscillators, resonance, Q- factor); Fourier series, particle motion in three dimensions, conservative forces and fields, Gravitation, Kepler’s Laws, and accelerated coordinate systems and inertial forces.

Third-year Advanced Classical Mechanics. This course covered the dynamics of systems of particles, the Lagrangian and Hamiltonian formulations of classical mechanics and the dynamics of oscillating systems.

The second half of Fourth-year Quantum Mechanics. This course builds on the modern physics and elementary quantum mechanics introduced in the second year of the physics program. We begin with a discussion of the postulates of quantum mechanics, followed by the formal solution of the time dependent Schrödinger equation. Along the way, we develop the mathematics of Hilbert spaces, states, operators, Dirac notation and matrix representation of quantum mechanics. The Schrödinger equation is explicitly solved in various one- and three- dimensional systems, and we then proceed to advanced topics including angular momentum and perturbation theory.

Teaching Philosophy.

I view myself as a 'Learning Facilitator' and as such I do my best to meet the learning needs and challenges of individual students. Mathematics is the language of physics so I tend to focus on the development of mathematical fluency and understanding.

Teaching Goals and Objectives.

In the context of math and physics, my goal is to promote the intellectual development of the students with whom I interact. I especially encourage the development of their independent learning and thinking skills, and abilities, so that they emerge from their educational experiences with confidence in their own mental faculties.

Overall, I believe that a university education should develop the 'heart' as well as the 'mind'.

Sincerely, Hubert Hugh Burke BA. (Physics) Earlham M. Sc M. Phil PhD (Condensed Matter Physics) Columbia University

[mi6014ikepearson]

NARROWING DOWN - “PICKING A BRIEF”

creative design modules are consistent throughout University courses; set up in such a way that students become accustomed to the process of being given a brief, and interpreting it in the way that best suits their skillset and ambition.

the mi6014 module is unique in that we have the opportunity to pick from a selection of briefs to work on      ( 17 to be exact.. )

and with so many options in front of us;    we are somewhat spoiled for choice.

with having options there comes an idiosyncratic freedom to pick and choose the one that will best fit the interests of the individual,    as in my experience, that is the way to achieve the best outcome.

if you enjoy working on something - you’ll naturally invest more time into your work: and that will therefore result in a better production.

READING THROUGH THE TASKS - “DIRECTING OUR INTERESTS”

the first thing I wanted to do, to begin production was to start narrowing down the options, by reading through each of the briefs, and highlighting the ones that interested me. as well as both the “why” and the “how” of undertaking each project - to allow me to pick a final direction to move forward with..

DUOLINGO - “DEMYSTIFY MATH”

a common trope amongst the artistic community is that creatives have a distain for mathematics; however, throughout school I thoroughly enjoyed problem-solving.

although nowhere near as gifted as the other students, I spent plenty of personal, out-of-school hours, which were usually dedicated to production of SQUAD_I, instead trying to wrap my head around some of the more complicated theorems necessary for what was going to be a pursuit in the engineering career branch.

Originally my interest was drawn into the duolingo brief; as it would have allowed me the opportunity to animate a gargantuan kaiju owl comedically shooting laser-beams, playing into the memes about the evil owl..

an example of the concept at play - with cuddly, cute characters causing destruction & chaos in a comedic manner.

an example of duolingo marketing playing into the “evil duo” idea that was generated by its users.

but due to having a pre-conceived and strongly formed idea, from the get-go: I wanted to look at some of the other briefs before I made any final decisions, as it would allow me to have a better production.

I find starting from the very beginning to be a much better setup for a scenario like this: where I will research into the company, before any personal bias clouds my judgement and directs my research into the direction, I have preconceived.

EBAY - “MOST LOVED FOR PRE-LOVED”

as someone with an array of hobbies; namely (for the sake of this sentence) including collecting retro video-game memorabilia, and hardware:

I use Electronicdotbaydotcom fairly often..

the brief asks us to explore a potential update to the site to appeal more to Gen Z, specifically within regards to selling clothing.

Originally I was interest in this brief, as it allows me the opportunity to work with a company that I use frequently, and have been constantly happy with their service:

with them having a wide array of different users with so many listings on so many different things,

offering insurance by allowing refunds for scams and lost items,

and all around just being an easy-to-navigate application with its layout.

in my initial research I found that eBay had approximately 138,000,000 active users in 2022, which is a 12% decrease from the same date in 2021.

As well as the statistic that the gross merchandise volume      ( the value of all goods sold on the site ) fell 18% to $18.55 billion in the second quarter of 2022.

in times of hardship it can be difficult not to look at the success of your competitors; with applications such as Vinted, Depop and AliExpress all being alternatives that have garnered favourable reputations - so much so that they have taken an audience from the demographic that uses eBay to get second-hand clothing.

Depop having no listing fee and only charging the seller once you make a sale

Vinted taking no commission, so you take away the full amount of what you sell.

AliExpress, allowing you to send products virtually anywhere in the world without any extra costs or fees.

you can’t just garner an audience, with your name alone - you need to give people incentive into using your application by proving it’s the better option when compared to its competitors..

and for this reason, I wanted to look elsewhere for a project that I could be more excited for.

PENGUIN - “IN SEARCH OF MERCH”

as much as I work with books,      reading is not one of my more preferred past-times..

as much as I enjoy a good book - I find that I don’t like putting things down mid-way and coming back to them: as when I immerse myself in something, I want to at least complete the full experience.

when I’m working on a comic, video, or just any form of work - I won’t stop until I reach a milestone I feel comfortable leaving said work in!~

the difficulty for an almost 100 year old company is that penguin has remained fairly consistent in what they have been doing - as a publishing company that started from an inspiration to offer quality reading after the founder (Sir Allen Lane) used the poor quality and high priced reading materials offered at Exeter Train Station.

with the company being around for so long, and publishing arguably one of the greatest selections of titles in the literary catalogue it seems like they would be a company that lasts forever..

but as the prevalent internet-age becomes more and more inevitable; instantaneous access to resources have made our species’ attention span feel like it’s shrinking and from this the slow and calming process of reading - that allows audiences to become immersed and escape from the hardships of reality is instead too time consuming for a people who endlessly scroll for new stimulation.

Penguin’s brief asks us to find a way that makes books more instantaneous using merchandise - which is an aspect I think will be extremely interesting to tackle, and allow a multitude of ideas!

HEINZ - “GAME-CHANGING FOOD”

when I first read this brief - I was cautiously concerned, out of care for seeing a brand succumb to t̷̄́͑͐ͅḧ̶̛̗̠̺̆̈́ē̵̘̗̼̦̈̈́ ̸̢̗̪͙̀̔͊͘͜f̷̛̝̹̰̟̓̀͜a̷̲̮̺͋͝ẗ̷̹́̅̐ͅͅe̶̢͔͔͈̣̓ of so many before it..

finding a connection between Heinz Products and "Gamers”..?

using said connection to make a BRAND advertisement..?

“ the only food worth pausing for ”..?

these were all the elements of a “fellow kids” commercial in the making.

an example of an advert that attempts to appeal to an internet audience, using online terminology - but through a wonderful combination of its brand status, over-acting, and extremely stale out-dated memes creates a viewing experience that is extremely painful to sit through..

The reason I love this brief, is that it flushes my mind with a range of fleshed out ideas that I feel a confidence in my competence in creating a good final product:

a series of shorts where we create a correlation between Heinz products and popular current video-games:      - such as having a Cowboy monologuing as he is roaming the desert range, and it ends with him eating a can of Heinz beans around the fire (Red Dead Redemption II)      - a survivor, in a zombie apocalypse finding a Can of Heinz Soup amongst a ravaged shelf - and eating it, smiling, only to be killed by a zombie, with it spilling on the floor - creating the Heinz logo (The Last of Us)      - playing into common horror/gore tropes using ketchup as blood

combining Barbecue Sauce and Baked Beans to make an all new experience: Barbecue beans - with high energy visuals and sounds to accompany such a brilliant experience

a comedic sequence showcasing a gamer running from their desk in their dorm room, and back to the kitchen in-between rounds, while preparing food: only to be defeated in-game by someone who just microwaved a can of beans, and has a meal to enjoy their victory to

as much as I would love to make a high energy advert that plays into energy drink/”gamer supplement” commercials - that instead has Gamers chugging down cans of beans, and spaghetti hoops;

I have instead decided to move ahead with two briefs, and decide which I want to work on, after some research into each of the companies..

NARROWED DOWN - “BINARY PATHS”

This module is one that will allow us to develop our industry focused skillset - by working on a conceptually challenging project that demonstrates both the intellectual and creative ability.

I want to work to the deadline to showcase my skillset, at working under pressure - and enhance my employability in the Animation and Design fields by working on design briefs set by A-list organisations in conjunction with D&AD.

and the briefs I would like to choose from are..

HEINEKEN - “PERSPECTIVES DON’T COME FRESHER”

&

WILLIAM LAWSON’S SCOTCH - “WAKE UP WHISKEY”

what with the two briefs being 2 alcohol brands that are wanting to rebrand in such a way that appeals to a younger audience; my initial research will satisfy both briefs, and allow me to showcase my versatility in many situations by creating a successful product that not only satisfies the chosen brief..

but accomplishes the task well!~

[cesarcwqr668]

Introductory To Knowledge Analysis Using Excel

After numerous hours and sessions of research and learning, we’ve narrowed down the record of one of the best Data Analytics coaching and online programs excellent for novices, intermediates and specialists alike. This list contains both free and paid online programs that will help you study data evaluation. In this information, we’ll present you what one of the best data analytics courses with certificates to study knowledge analysis are, and how one can get a few of these knowledge analytics training classes at no cost or for less.

If you are looking to improve your excel expertise THIS is the company you should invest your time in.

Excel, however most individuals don’t know fairly how advanced spreadsheet evaluation can get.

You'll additionally study how to identify the computing requirements appropriate for fixing those issues.

Initially, you'll study some foundational ideas, together with primary calculations such as imply, median, and commonplace deviation, and provides an introduction to the central limit theorem.

Start by learning key information analysis tools such as Microsoft Excel, Python, SQL and R.

On some stage, every business relies on information science in one way or one other. That’s why plenty of firms rent information analysts and knowledge scientists interchangeably. Smaller organizations often mix the role; which means knowledge analysts have to have a good suggestion of knowledge sciences. Data analysts gather, consider, and analyze raw knowledge to help corporations in their decision-making process. Ideally, information analysts gather data from a quantity of sources, together with direct and oblique sources, and carry out thorough information evaluation to communicate the relevant findings instantly or via well-designed stories. When you buy the course, you get free entry to their Data Fundamentals Handbook that features all the content of the course in written form.

Chance And Statistics In Information Science Using Python

Alison provides dozens of excessive quality knowledge science courses designed by specialists and universities to provide you with an interactive and enriched learning expertise. When joining any of those courses you want to make the same commitment to learning as you'll in the course of a school course. One goal for studying data science online is to maximize psychological discomfort. It’s easy to get caught in the behavior of signing in to look at a few videos and really feel like you’re learning, but you’re not likely studying much until it hurts your mind.

You will use Python's DataFrame a two-dimensional size-mutable, potentially heterogeneous tabular information structure with labeled axes . To take this course, you must already be familiar with Python programming language; all code writing is in Jupyter notebooks. You will work with fundamental Pandas knowledge constructions, Pandas Series objects representing a single column of information which can retailer numerical values, strings, Booleans, and extra advanced knowledge varieties. Learn the means to use Pandas DataFrame, which represents data in table type. Finally, be taught to append and kind collection values, add lacking information, add columns, and combination information in a DataFrame. In this Skillsoft Aspire course, learners will encounter primary Hadoop file system operations similar to viewing the contents of directories and creating new ones. [newline]Begin by working with recordsdata in various ways, including transferring recordsdata between a local file system and HDFS and discover ways to create and delete information on HDFS.

What is the difference between data analytics and data analysis?

Data analysis refers to the process of examining, transforming and arranging a given data set in specific ways in order to study its individual parts and extract useful information. Data analytics is an overarching science or discipline that encompasses the complete management of data.

Every yr, 10 students will get suggestions on their project from information scientists working at Airbnb. At the tip of the course, college students complete a Capstone Project designed in conjunction with Yahoo. The entire Specialization takes about forty hours to complete, which means that students can finish the program in simply six months in the occasion that they spend three hours a week studying.

College Students Rated Our Data Analytics Lessons

Finally, observe how to create and analyze categories of information in a knowledge set by utilizing Windows. Extracting meaningful info from a really massive dataset could be painstaking. In this Skillsoft Aspire course, learners examine how Hadoop's MapReduce can be utilized to hurry up this operation.

Is data Analytics a stressful job?

Data analysis is a stressful job. Although there are multiple reasons, high on the list is the large volume of work, tight deadlines, and work requests from multiple sources and management levels.

New options, particular provides, and exciting information about the world of information visualization. Python is a high-level, dynamically typed, and transportable programming language that excels when the value of software development outweighs performance concerns. Data governance is an built-in framework of insurance policies and technology applied to ensure effective knowledge administration.

Unit 1: Introduction To Python

These sources embrace each free and paid ones created by top professionals, schools and corporations. There are 4 programs in the program – Foundations of strategic enterprise analytics, Foundations of promoting analytics, Case studies in enterprise analytics with Accenture and Capstone Project. Learners need to finish all the 4 programs to earn MicroMasters program certificates from ColumbiaX.