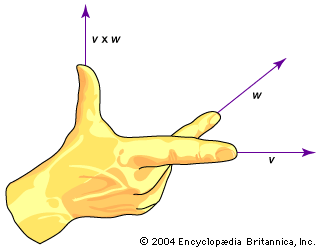
#Vector Arithmetic

[lapokinanaz]

There are no Atheists. There are however; Gnostics and Agnostics. There are Deists and there are Fools also..

An Agnostic knows to claim ignorance of wisdom. Whereas the Gnostic knows to claim himself an Atheist.

An Atheist debates a Deist. And the Deist can only tell about God; Whereas the Fool will manifest God.

For this, they kill Him.

This is why he is called a Fool, because he did not hide the joy of his understanding. Nor his heart and life from the gospel.

For the Fool was made to proclaim! Made to sing! 'Tis the Crétin, who knows the King! { ל Lamedh}

Call unto Me, and I will answer thee, and show thee great and mighty things, which thou knowest not. [Jeremiah 33:3] Then the heavens receded like a scroll being rolled up. [Revelation 6:14]

For there is nothing covered, that shall not be revealed; neither hid, that shall not be known. Therefore whatsoever ye have spoken in darkness shall be heard in the light; and that which ye have spoken in the ear in closets shall be proclaimed upon the housetops. [Luke 12:2-3]

You have heard; Now see all this; And will you not declare it? From this time forth I announce to you new things, hidden things that you have not known [Isaiah 48:6]

For what I received I passed on to you, as of first importance; That Christ died for our sins according to the Scriptures. That He was buried, and that He rose again the third day according to the scriptures: And that He was seen of Cephas, then of the twelve. After that, He was seen of above five hundred brethren at once; Of whom the greater part remain unto this present, but some are fallen asleep. After that, He was seen of James; then of all the apostles. And last of all He was seen of me also, as of one born out of due time. [1 Corinthians 15:3-8]

Key to text^ {Acts 2:17-38} Maranatha.

[girlballs]

doing orgasm denial to a girl who's into bimbofication hypnosis by teaching her vector arithmetic and really making sure she understands it

[misskitxx]

Vector of Interest - Chapter 7: Critical Dampening

It was one of those nights—no, the night —when Jayce’s entire existence, rotted through with months of helpless, heady yearning, slipped its last tether to rationality. Whatever remained of his soul, hollow and decayed as it was, had fled limbo only to plummet. Down, down, down. And he let it fall.

Hours in the lab. Hours spent too close to a god—not one sculpted of marble and myth, but of ink stains and sharp angles, half-lit by the flickering hum of the desk lamp. Viktor was real, but that only made him more unbearable.

Jayce could not think. The numbers blurred, equations unraveling before his eyes, mocking him. He had breathed mathematics once, shaped it like instinct, but now it slipped through his fingers like sand. He knew why.

Across the desk, Viktor sat in half-shadow, the thin light catching in the gold of his irises, making them pulse with something alive. Something dangerous.

Jayce clenched his jaw until it ached. Focus. Just focus. Just—

“Again?”

The word struck like a lash—flat, unimpressed.

His fingers twitched. The notebook was a ruin of miscalculations, of numbers failing him like his own body had. His stomach twisted, thick with heat and humiliation.

“Four times, Professor Talis.” A single tap of Viktor’s pen against the page. Sharp. Precise. The sound shivered through Jayce like a static charge. “Would you care to explain why you suddenly seem incapable of basic arithmetic?”

Excuses crowded the back of his throat—exhaustion, deadlines, the weight of everything crushing him at once. None of them made it out.

Because Viktor leaned forward.

Continue reading on AO3!

[pomelo-heart]

"Illusions in shadow"

.𖥔 ݁ ˖ ϟ ⚡︎ ϟ ˖ ݁ 𖥔.Sakura Genjutsu AU.𖥔 ݁ ˖ ϟ ⚡︎ ϟ ˖ ݁ 𖥔.

Pt 1. In which Sakura finds a loophole

“The existence of consciousness is both one of the most familiar and one of the most astounding things about the world."

The words jumped out at her, stalling her reading. It was a simple sentence on a piece of paper, yet it felt to Sakura as if she was uncovering a truth for the first time.

Which came first, the mind or the body?

As she twisted and tossed the thought in her head, a wave of chakra washed over her, tingling at the tips of her fingers, as if reminding her of its existence. Chakra was a shinobi's greatest weapon; yet few had studied enough theory of it to adequately manipulate it. Through the pile of books she had pored over, not one chakra theorist could claim themself to offer any comprehensive theory. It was still one of the mysteries of the world, neither mind nor body, and not quite both.

Could thoughts, attitudes and feelings be reduced to fundamental physical matter? At least two of them did; but what of the former?

In all her long twelve years of life, Sakura Haruno had experienced about multiple instances of dissociation between mind and body.

After all, her affinity and (recent) interest for genjutsu had taught her just how important subjugation of the mind could tilt the tide in battle. A shinobi could overpower their enemy by intercepting communication (and thus rendering the opponent factually blind), or misleading them to think all hope was lost.

Yet, sensor-type training had never been encouraged in her days at the academy, much less taught. Ninjutsu and taijutsu were all the craze.

Another realization hit her head-on, one that was perhaps more fundamental. A thought that had been running at the back of her mind for years: shinobi, who prided themselves on a rather outdated system of honour and duty, had yet to embrace any kind of conjunction at all between mind and body.

Putting significant effort into her training with Lady Tsunade meant that she had to not only physically build up her strength, but also fight daily against exhaustion, pain, failure, and even more so, her vast ignorance. A doctor's battlefield was a never-ending line of tents where knowledge and practical skills were erected as law. Every day, she had learned to push the mental and physical boundaries of her body, until her chakra became not only a physical manifestation of her vital energy, but also an effective, usable vector for her mind.

Yet how many of her classmates, other chunins, had healthy, well-adjusted lives? How many knew basic arithmetic?

She made a point of counting.

Baffling.

Whenever she suggested stress management to her shinobi patients, it was almost always met with a shrug and a face that suggested they definitely were not "considering it".

If anything, history had shown, three great wars and waves of mass psychosis later, that the shinobi world had an aversion to open communication, diplomacy, and work-life balance. Or, at the very least, an aversion to nurturing them with the same level of care put into drilling children to become weapons of mass destruction, all in the namesake of peace.

She kept reading.

"No conception of the natural order that does not reveal [consciousness] as something to be expected can aspire even to the outline of completeness.”

In other words: there was a lot of work to do.

Perhaps the world of shinobi was lacking something fundamental.

Research, for one. Sakura closed the book and set out to ponder about how she might bring change to the straight and narrow-minded village of the Leaf.

[jackhkeynes]

Mathematical Etymology

excerpts from the Veriloquace Glossary o'Mathematics, a reference quire compiled by Rotcham University Primers.

zeffer /ˈzɛ.fə/ [zero] the number of things in an empty collection, the quantity one fewer than one. Before 1350 < Scholastic Latin zefer, zefrum (alt. zephirus by false connection to Zephyr) < Arabic صِفْر • ṣifr "empty, void" < in sense from Sanscrit शून्य • śūnyá "empty, void".

ablate /ˈa.blət/ [negative] fewer than zeffer, as of a debtor's money or a distance backward. 1481 < Lombard ablad < Scholastic Latin ablātus "taken away, withdrawn, removed", first used in financial accounts and taken up by mathematicians some decades later.

dart /ˈdaːt/ [~vector] a segment of a line, considered with a choice of which end is the head and which the vane. Around 1470 < Early Merch dart "throwing spear, dart" < Middle French dart, dard < Medieval Latin dardus < Frankish *darōth < Classical German *darōthus "light spear, javelin, dart". Extended to its mathematical sense by the pictorial analogy of drawing arrowheads on line segments.

augrim /ˈəu.gɾɪm/ [~arithmetic] the mathematics of calculation with numbers; computation more generally. Around 1220 < Drengot augrime, algrisme etc < Old French algorisme < Scholastic Latin algorismus "the use of Arabic numbers" < Arabic الخَوَارِزْمِيّ • al-ḵawārizmiyy, a name of the Persian polymath whose mathematical works introduced much of mathematics to Europe.

arrhumb /ˈa.ɾəm/ [cosine] the sending of an angle to the quotient of the height of a rod deflected by that angle from the vertical to the full length of the rod. Early Merch arrum, arrom (the modern spelling is influenced by unrelated rhumb "compass bearing") < Arabic الرمح • ar-rumḥ "spear, shaft". This appears to be a metaphorical extension related to the use ofوتر • watar < Sanscrit ज्या • jyā́ "bowstring" for vater [sine].

[fracturedgodhead]

Lifetimes awe hawd :c

I don't understand how rust lifetimes work. Also how possession of data works.

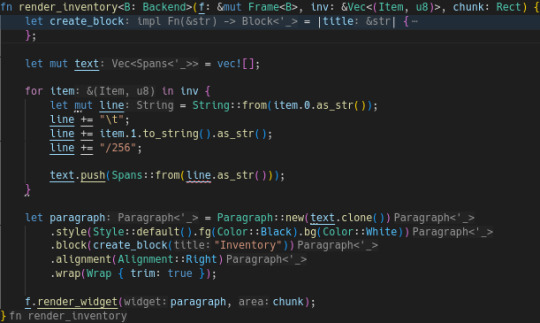
I have this function which should take in the inventory state as a vector of (Item, u8) tuples. It should then parse the inventory items into spans, then parse the spans into a paragraph, then render the paragraph into the region passed into the function.

I iterate through the items in the inventory vector, compile them into a string called "line", parse "line" into a span, then push the span into the text vector.

Rust gets mad when I try and put line into text because of the different lifespans of the variables (text is the a member of 'render_inventory' but line is only a member of the for loop), so in theory text can hold a reference to a variable that gets disposed of. This is good design, the issue is I should be able to copy the data into 'text', modifying 'text' with anonymous data rather than data associated with 'line'. I just can't friggin figure out how! Clone doesn't work and trying to de-reference it with pointer arithmetic fails because "the size of str is not known at compile time".

I KNOW THAT!! WHY IS THAT A PROBLEM?? THAT SHOULDN'T BEE A PROBLEM!!

bee mention

Anyway, I might just have to give an array for lines the same lifetime as text and accept the fact that the memory complexity is going to be 2n instead of n+1 😔.

[taperwolf]

I just typoed "chiptunes" as "chiprunes", and I'm suddenly fascinated by the prospect. Magic that's been digitized at low bitrates, because we're working with very early techno magic and what that would mean for different types of magic.

I mean, obviously visual illusions would be created by filling voxels with a limited palette of colors, and if you want audio, it's all square waves. Or maybe you can do better if you move to vector addresses and do wireframes? Teleports that can move you only 127 meters in one direction but 128 meters in the other direction, because it's eight bit and two's complement. Very strict limits on the number of objects you can conjure, because of arithmetic overflow.

[lipshits-continuous]

Prime numbers of the ask game let's go!

This is gonna be a long old post haha /pos

2. What math classes did you do best in?:

It's joint between Analysis in Many Variables (literally just Multivariable calculus, I don't know why they gave it a fancy name) and Complex Analysis. Both of which I got 90% in :))

3. What math classes did you like the most?

Out of the ones I've completely finished: complex analysis

Including the ones I'm taking at the moment:

Topology

5. Are there areas of math that you enjoy? What are they?

Yes! They are Topology and Analysis. Analysis was my favourite for a while but topology is even better! (I still like analysis just as much though, topology is just more). I also really like group theory and linear algebra

7. What do you like about math?

The abstractness is really nice. Like I adore how abstract things can be (which is why I really like topology, especially now we're moving onto the algebraic topology stuff). What's better is when the abstract stuff behaves in a satisfying way. Like the definition of homotopy just behaves so nicely with everything (so far) for example.

11. Tell me a funny math story.

A short one but I am not the best at arithmetic at times. During secondary school we had to do these tests every so often that tested out arithmetic and other common maths skills and during one I confidently wrote 8·3=18. I guess it's not all that funny but ¯⁠\⁠_⁠(⁠ツ⁠)⁠_⁠/⁠¯

13. Do you have any stories of Mathematical failure you’d like to share?

I guess the competition I recently took part in counts as a failure? It's supposed to be a similar difficulty to the Putnam and I'm not great at competition maths anyway. I got 1/60 so pretty bad. But it was still interesting to do and I think I'll try it again next year so not wholly a failure I think

17. Are there any great female Mathematicians (living or dead) you would give a shout-out to?

Emmy Noether is an obvious one but I don't you could understate how cool she is. I won't name my lecturers cause I don't want to be doxxed but I have a few who are really cool! One of them gave a cool talk about spectral geometry the other week!

19. How did you solve it?

A bit vague? Usually I try messing around with things that might work until one of them does work

23. Will P=NP? Why or why not?

Honestly I'm not really that well versed in this problem but from what I understand I sure hope not.

29. You’re at the club and Grigori Perlman brushes his gorgeous locks of hair to the side and then proves your girl’s conjecture. WYD?

✨polyamory✨

31. Can you share a math pickup line?

Are you a subset of a vector space of the form x+V? Because you're affine plane

37. Have you ever used math in a novel or entertaining way?

Hmm not that I can think of /lh

41. Which is better named? The Chicken McNugget theorem? Or the Hairy Ball theorem?

Hairy Ball Theorem

43. Did you ever fail a math class?

Not so far

47. Just how big is a big number?

At least 3 I'd say

53. Do you collect anything that is math-related?

Textbooks! I probably have between 20 and 30 at the moment! 5 of which are about topology :3

59. Can you reccomend any online resources for math?

The bright side of mathematics is a great YouTube channel! There is a lot of variety in material and the videos aren't too long so are a great way to get exposed to new topics

61. Does 6 really *deserve* to be called a perfect number? What the h*ck did it ever do?

I think it needs to apologise to 7 for mistakingly accusing it of eating 9

67. Do you have any math tatoos?

I don't have any tattoos at all /lh

71. 👀

A monad is a monoid in the category of endofunctors

73. Can you program? What languages do you know?

I used to be decent at using Java but I've not done for years so I'm very rusty. I also know very basic python

Thanks for the ask!!

[frank-olivier]

The Search for Fundamental Truth: Exploring the Ties Between Representation Theory and Physical Reality

In the world of mathematics and theoretical physics, the concept of duality has emerged as a profound principle that reveals deep connections between seemingly unrelated structures. One of the most striking examples of this interplay is the Geometric Langlands Correspondence, a mathematical theory that unites fields such as algebraic geometry, representation theory, and number theory. This correspondence has also opened new frontiers in physics by linking abstract mathematical ideas to the framework of quantum field theory and gauge theory. By exploring this duality, mathematicians and physicists have gained new insights into the nature of space, symmetry, and fundamental interactions. The Geometric Langlands Correspondence is a striking example of how mathematical dualities can shed light on the hidden order of the universe.

In both mathematics and physics, duality refers to a phenomenon in which two different theories or objects describe the same underlying reality in different ways. In physics, for example, the electric-magnetic duality shows that electric and magnetic fields, although seemingly different, are two sides of the same coin. Similarly, dualities in mathematics manifest themselves as relationships between different structures, such as algebraic curves and vector bundles, or between geometric shapes and abstract groups.

The geometric Langlands correspondence is a sophisticated example of duality in mathematics. Originally a geometric analogue of the classical Langlands program – a set of far-reaching conjectures proposed by Robert Langlands in the late 1960s – the geometric version transforms problems from number theory into the language of algebraic geometry. This transformation allows mathematicians to examine questions about symmetries and representations through a geometric lens, thus linking number theory to the study of shapes and spaces.

The classic Langlands program is a monumental undertaking that attempts to link different areas of mathematics, such as number theory and analysis. In its original form, the Langlands program proposes a correspondence between two kinds of mathematical objects: Galois representations, which capture the symmetries of algebraic equations, and automorphic forms, which are highly structured functions that encode number-theoretic information. This theory provides a powerful framework for understanding the arithmetic of number fields and reveals unexpected connections between prime numbers and symmetry.

The Geometric Langlands Program, later developed by mathematicians such as Alexander Beilinson and Vladimir Drinfeld, reformulates classical theory in a geometric framework. Instead of studying equations over number fields, the geometric version studies fields of functions associated with algebraic curves. The objects of interest now include principal bundles, geometric structures that encode how a particular symmetry group acts on a curve. The geometric equivalent connects these bundles to sheaves, mathematical constructs that generalize functions and capture local geometric information. Through this geometric lens, deep questions about symmetry and representation are transformed into problems about shapes and spaces, and made accessible using the tools of algebraic geometry.

The geometric Langlands correspondence has also found surprising applications in theoretical physics. The bridge between these areas was built when physicists realized that the dualities central to the Langlands program have analogues in quantum field theory and string theory. One of the most important breakthroughs came from Edward Witten and Anton Kapustin, who showed that the geometric Langlands correspondence can be understood in the framework of gauge theory.

In physics, gauge theory is a mathematical model for describing fundamental forces such as electromagnetism and the strong and weak nuclear forces. It is based on the concept of fields that vary over space and time and are governed by certain symmetry groups. One of the most fascinating aspects of gauge theory is S-duality, a symmetry that relates different field theories to each other. S-duality suggests that certain theories, although they appear different, are in fact equivalent descriptions of the same physical reality. This reflects the duality found in the geometric Langlands correspondence, in which geometric objects and representations are two manifestations of the same mathematical structure.

By interpreting the geometric Langlands duality in terms of S-duality in four-dimensional gauge theories, physicists have been able to gain new insights into quantum field theory. This connection has profound implications and suggests that the Langlands program is not just an abstract mathematical curiosity, but a powerful tool for understanding the fundamental nature of space and time. From a physics perspective, the geometric correspondence reveals a hidden unity between mathematical structures and physical theories and points to a deeper level of order in the universe.

Edward Frenkel, one of the leading minds in the field, has played a crucial role in advancing mathematical theory and bringing its beauty to a wider audience. In his book Love and Math: The Heart of Hidden Reality, Frenkel introduces readers to the Langlands program and its geometric counterpart, illustrating how these abstract ideas align with physical theories. Through engaging narrative and easy-to-understand explanations, he conveys the elegance of the Langlands program and shows how it unites different branches of mathematics and connects to modern physics.

Frenkel's work shows how the geometric Langlands correspondence serves as a bridge between mathematics and physics, transforming esoteric theories into a coherent whole. His contributions emphasize that the power of Langlands dualities goes beyond technical results; they offer a new way of looking at the world, where different disciplines come together in a harmonious and unexpected unity.

The implications of the Geometric Langlands Correspondence go beyond its specific mathematical and physical formulations. It illustrates the creative process in both fields, where dualities serve as guiding principles that reveal hidden patterns. The interplay of geometry and physics has led to breakthroughs in both fields and suggests that the study of dualities is more than a search for analogies—it is a search for fundamental truths.

In mathematics, the Geometric Langlands Program has stimulated new research in areas such as categorical structures, moduli spaces, and nonabelian Hodge theory, leading to new discoveries and conjectures. In physics, the exchange has provided a new language for understanding gauge theories and opened a new perspective on quantum phenomena and symmetries. The interdisciplinary nature of the program has inspired mathematicians and physicists to work together, combining techniques and ideas from both fields to tackle long-unsolved problems.

Edward Frenkel (Curt Jaimungal, Theories of Everything, 2023/2024)

September 2023

August 2024

October 2024

Wednesday, October 2, 2024

[heirtocragflame]

what kind of research are you doing for your phd thesis? (apologies if you've posted about this before)

So the stuff I’m working on right now isn’t quite a thesis (not yet anyway, it might turn into one later). I can’t get into too many details without doxxing myself, but it involves objects called modular forms, which appear all over the place in mathematics. They’re very analytic objects, coming from complex analysis, having Fourier series, etc. But they also satisfy a bunch of symmetries (dictated by the so-called full modular group). This algebraic structure means that the coefficients of their Fourier series actually encapsulates a lot of arithmetic information.

Now, the combination of the analytic and algebraic niceness of things means that there’s only a handful of them (more specifically they form a finite dimensional complex vector space). This means if you have something that you can associate a modular form to, that actually tells you a lot about what it could possibly be. This association was at the heart of what became the proof of Fermat’s Last Theorem.

[the-heart-of-light]

Math notation that looks way more impressive than it actually is:

v | ∞: whaat, v divides infinity? how does it manage?? (it actually means you're in the boring case, for the most part)

Torsion of a an abelian group: wow this must be some cool thing where if you keep doing something you're stretching and squeezing your group (No actually it just means there's some clock arithmetic involved). Don't get me started on the annihilator.

Syzygy: it comes from astrology, it must be about super unlikely alignments in mathematics! (Ok this is actually a bit cool, it's like a relation between relations)

𝖌𝖑(3), 𝖘𝖔(2) etc.: ma'am you're a glorified vector space with an (ugly) operation on top, don't come at me looking so dangerous and enticing

These are the ones I came up with on the spot, but the list could go on and on.

[ilp-wall-of-fame]

Oh man, if only I had the power to write a math curriculum that incorporated programming concepts like vector arithmetic, object-oriented algebra, algorithm card games... and in high school kids should learn how to use python to do the math for them. Imagine telling your students that they can use a calculator to do all of the math for them, so long as they build the calculator themselves!

def the_exponenterrr(x, n, a, c): y = a*x**n + c return y

I started playing around with RPG Maker 2000 when it was new, and even though all I ever did was pretty basic event-scripting, it was still quite foundational to my understanding of how to code by teaching me loops, variables, nested-ifs, and more!

The fact that there’s an actually functional website for the library of Babel is one of those things that fucks me up more and more the more I think about the implications.

[codingprolab]

ECE300 Error Control Coding Simulation Project

In class, we developed a framework for error control coding through vector and matrix arithmetic over Galois field 2 (F2). Theoretically, we explored linear block codes and error detection in the previous homework for very specific cases, and did most of our work by hand. In reality, these sorts of operations are being done on massive scales by low-level hardware rapidly each and…

[govindhtech]

AMD Ryzen 5 9600X, Features, Architecture And Specifications

Ryzen 5 9600X

In the Ryzen 9000 series, the AMD Ryzen 5 9600X is a mid-range desktop CPU for gamers and content creators seeking efficiency and performance. This study examines its features, architecture, gaming performance, memory support, and power efficiency, as well as its pros and cons.

Features and specs

Zen 5 design

Process Node: TSMC The CCD is 4nm and the I/O die 6nm.

Six cores, twelve threads.

Base/Boost Frequencies: 3.9/5.4 GHz

Total cache: 38MB (32MB L3 + 6MB L2).

65W TDP

AM5 socket

Official DDR5-5600 MT/s, with overclocking possible.

Supports PCIe 5.0 with 24 lanes

Zen 5 Architecture Improvements

The Ryzen 5 9600X uses AMD's Zen 5 microarchitecture, which is much improved above Zen 4:

Zen 5's wider instruction fetch and decode pipeline optimises execution unit consumption.

The new two-ahead branch predictor can foresee up to two branches every clock cycle, improving instruction fetch performance in branch-heavy applications.

Increased ALUs: From four to six Arithmetic Logic Units have increased integer operation throughput by 50%.

AVX-512 support with a native 512-bit datapath and four floating-point pipes (up from three in Zen 4) improve vector and AI workload performance in Zen 5.

Architectural changes increase Instructions Per Cycle (IPC) by 16%, improving single-threaded and multi-threaded performance.

Video Game Performance

Gaming-wise, the Ryzen 5 9600X is slightly better than the 7600X. Benchmarks show a 1% performance jump across a variety of titles, with some games improving by 5%. Although slight, these improvements boost power efficiency.

In gaming, the 9600X outperforms Intel's Core i5-14600K while using less power. Gaming enthusiasts seeking energy efficiency and performance would like it.

Overclocking and Memory Support

The Ryzen 5 9600X supports DDR5-5600 MT/s memory, up from 5200. User reports show that 800-series motherboards can overclock memory modules to DDR5-8000 MT/s.

Ryzen Master program lets users change memory timings and speeds without restarting their PCs using real-time memory overclocking. The new Memory Optimised Performance Profile automatically switches between JEDEC and EXPO profiles to optimise latency or bandwidth for the present application.

Power Use and Efficiency

One of the Ryzen 5 9600X's best features is its power efficiency:

Lower TDP: The 9600X's 65W TDP significantly decreases the 7600X's 105W.

Compared to its predecessor's 142W peak, the 9600X uses 88W under load.

A 15% boost in heat resistance and optimised die architecture let the 9600X to operate at 7°C lower temperatures than Zen 4 processors.

These improvements allow the 9600X to be used in moderate cooling systems and small constructions.

Advantages

Due to its lower TDP and power consumption, the 9600X is energy-efficient for mid-range computers.

Architectural Improvements: Zen 5 improves IPC, branch prediction, and execution units, improving performance.

Real-time overclocking and faster memory give enthusiasts freedom.

CPU life is extended by AM5 socket compatibility with 600- and 800-series motherboards.

Thermal Performance: Better thermal design decreases operating temperatures, eliminating the need for high-end cooling.

Disadvantages

Modest Performance advantages: Zen 4 customers may not want to upgrade due to the minimal performance advantages over the 7600X.

The 9600X is slower than Intel's Core i5-14600K in multithreaded workloads.

Value Proposition: The Ryzen 7 7700X and Intel devices may offer better value for select users because to their performance and price.

Unlike prior AMD CPUs, the 9600X lacks a cooling, raising its cost.

Conclusion

The flexible AMD Ryzen 5 9600X mid-range desktop CPU is powerful and energy-efficient. Although its gaming and single-threaded speed are superb, its limited improvements over its predecessor and less spectacular multithreaded features may make some users turn elsewhere. However, its improved thermal performance, architectural advances, and AM5 platform compatibility make it a viable choice for long-lasting, efficient new construction projects.

[drmikewatts]

Soft Computing, Volume 29, Issue 6, March 2025

1) On subresiduated lattice ordered commutative monoids and some of its subvarieties

Author(s): Juan Manuel Cornejo, Hernán Javier San Martín, Valeria Anahí Sígal

Pages: 2517 - 2529

2) Dynamic updating approximations of local multigranulation neighborhood covering rough sets

Author(s): Qi Shi, Yan-Lan Zhang

Pages: 2531 - 2550

3) Relationships between various ideals in L-algebra

Author(s): S. Saidi Goraghani, R. A. Borzooei

Pages: 2551 - 2562

4) Numerical algorithm for solving third-order Emden–Fowler type pantograph differential equations: Taylor operational matrix method

Author(s): Nikita Saha, Randhir Singh

Pages: 2563 - 2579

5) L-fuzzy transforms: an operator-oriented approach

Author(s): A. P. Singh, S. P. Tiwari, I. Perfilieva

Pages: 2581 - 2593

6) A golden section-based group decision-making approach to software trustworthiness evaluation

Author(s): Chuan Yue

Pages: 2595 - 2618

7) The impact of hydrogen energy storage aqua electrolyzer fuels cell on automatic generation control of power system using optimal FGS PID controller

Author(s): Ankur Rai, Dushmanta Kumar Das

Pages: 2619 - 2638

8) Choquet integral in ranking data: on the construction of a measure of importance and interaction

Author(s): M. Eugenia Cornejo, Jesús Medina, Andreja Tepavčević

Pages: 2639 - 2651

9) Applications of integrals and extreme value of solution of uncertain age-dependent population equation with migration source

Author(s): Lu Yang

Pages: 2653 - 2668

10) A modified slacks-based measure of efficiency and super-efficiency under zero and negative data

Author(s): Ehsan Zanboori

Pages: 2669 - 2686

11) Optimal stress levels and inference procedures for constant stress accelerated life test under bathtub-shaped lifetime model

Author(s): Çağatay Çetinkaya

Pages: 2687 - 2714

12) Fc-gcn: A formal concept-enhanced graph convolution network model

Author(s): Kai Wu, Chao Zhang, Vincenzo Loia

Pages: 2715 - 2725

13) A model-free feature extraction procedure for interval-valued time series prediction

Author(s): Wan Tian, Zhongfeng Qin, Tao Hu

Pages: 2727 - 2741

14) Neutrosophic multi-choice 4D-transportation problem for different quality items

Author(s): Dipankar Chakraborty, Sarbari Samanta, Dipak Kumar Jana

Pages: 2743 - 2767

15) Optimizing energy harvesting in web of things services: a metaheuristic approach with retrial queue under working vacation

Author(s): N. Micheal Mathavavisakan, K. Indhira, Sherif I. Ammar

Pages: 2769 - 2790

16) Differentiation or undifferentiation? analysis of car-sharing strategies for the vehicle manufacturer

Author(s): Xin Yu, Zhongwei Chen, Zhi-Ping Fan

Pages: 2791 - 2806

17) A two-stage optimization replacement policy with multiple spare units

Author(s): Chunxiao Zhang, Hejiao Shen, Chao Yan

Pages: 2807 - 2817

18) A new model for facility bus terminal location problem based on modified Kerre’s inequality

Author(s): Sahar Rahdar, Reza Ghanbari, Donya Heidari

Pages: 2819 - 2828

19) A new metaheuristic optimization algorithm based on the participation of smart students to increase the class performance

Author(s): Einollah Pira, Alireza Rouhi

Pages: 2829 - 2844

20) A novel stochastic machine learning approach for resilient-leagile supplier selection: a circular supply chain in the era of industry 4.0

Author(s): Bahar Javan Molaei, Mohssen Ghanavati-Nejad, Mohammad Sheikhalishahi

Pages: 2845 - 2866

21) An arithmetic–geometric mean difference based approach to consistency index and priority vector of pairwise comparison matrices

Author(s): Yuan-Kai Hu, Fang Liu, Shi-Shan Wang

Pages: 2867 - 2884

22) On pure ideals in semilattices

Author(s): Nilesh Mundlik, Mayur Kshirsagar

Pages: 2885 - 2889

23) Innovative image encryption approach based on bitwise XOR high nonlinear S-boxes and random permutation

Author(s): Fırat Artuğer

Pages: 2891 - 2903

24) Evolutionary optimization in VANET services: a comprehensive survey, challenges and futuristic approach

Author(s): Madhuri Badole, Anuradha Thakare, Diego Oliva

Pages: 2905 - 2929

25) Wind farm layout optimization based on Harris hawk optimization algorithm with variable weight coefficients and Jansen wake model

Author(s): Min Wang, Jie-Sheng Wang, Yu-Cai Wang

Pages: 2931 - 2969

26) Construction and empirical research of a subjective-and-objective-analysis model of the online learning behavior

Author(s): Ke Wang, Kun Zheng, Ying Wang

Pages: 2971 - 2982

27) A synchronous spatiotemporal graph neural network for short-term traffic flow prediction

Author(s): Zhao Zhang, Xiaohong Jiao

Pages: 2983 - 2997

28) Modeling of metaheuristic-based dual cluster head selection with routing protocol for energy-efficient wireless sensor networks

Author(s): Maddikera Krishna Reddy, Anusha Sowbarnika Veluswamy, Syed Shameem

Pages: 2999 - 3020

29) Expansive detector via hybrid temporal and transposed convolutional mechanism for weld proximity defects

Author(s): Zihua Chen, Runmei Zhang, Kuan-ching Li

Pages: 3021 - 3034

30) Forecasting of exchange rate time series based on event-aware transformer mode

Author(s): Siyi Zhang, Tong Che, Ping Feng

Pages: 3035 - 3045

31) Sustainability, innovation and knowledge: a complex relationship based on an empirical study

Author(s): Sebastian-Ion Ceptureanu, Eduard-Gabriel Ceptureanu, Adriana Lavinia Iancu

Pages: 3047 - 3062

32) Why does economics need complexity?

Author(s): Mauro Gallegati, Silvia Gallegati

Pages: 3063 - 3072

33) A review for finding determinants of some band matrices

Author(s): Maryam Shams Solary

Pages: 3073 - 3082

34) Modeling and simulating a startup ecosystem development with a delayed differential equation

Author(s): Alessio Brini, Viviana Fanelli

Pages: 3083 - 3095

35) Explainable Grouped Deep Echo State Network for EEG-based emotion recognition

Author(s): Samar Bouazizi, Hela Ltifi

Pages: 3097 - 3114

[edgythoughts]

Why Is Zero So Powerful in Math 2025

Why Is Zero So Powerful in Math 2025

📘 Book-Level Answer (University-Level – Mathematics & History) Zero, represented as “0,” is not just a placeholder or a symbol for "nothing"—it is a cornerstone of modern mathematics. The introduction and understanding of zero fundamentally reshaped arithmetic, algebra, calculus, computer science, and even philosophical reasoning in mathematics. 🔢 Mathematical Power of Zero 1. Zero as an Identity Element In arithmetic, zero is the additive identity, which means: a+0=afor any real number aa + 0 = a quad text{for any real number } a This property is foundational to number theory and linear algebra, especially when defining vector spaces and algebraic structures like groups and rings. 2. Zero in Algebra - Roots of equations: Solving for when an equation equals zero helps us find key points like intercepts and turning points. - Zero-product property: If ab=0ab = 0, then either a=0a = 0, b=0b = 0, or both — a crucial principle in factoring and solving equations. 3. Zero in Calculus - Limits and continuity: Zero plays a key role in limits. For example, lim⁡x→0sin⁡xx=1lim_{x to 0} frac{sin x}{x} = 1 - Derivatives: The rate of change is often zero at maximum or minimum points. 4. Zero in Coordinate Systems Zero gives us the origin in a Cartesian coordinate system (0,0)(0, 0), a reference point from which we measure all other positions in geometry and physics. 5. Zero in Computer Science Binary code (the language of computers) is built using only two digits: 1 and 0. Zero represents the “off” state in logic gates and digital signals.

📜 Historical Significance of Zero - Ancient Origins: Zero was developed independently in ancient India (by Brahmagupta in the 7th century) and Mesoamerica (by the Mayans). - It revolutionized counting systems—especially the place-value system—making arithmetic operations like multiplication and division practical and scalable. 💡 Easy Explanation (Understanding Zero for Everyone) Imagine you're playing a game where you score points. If you have “0 points,” you haven't scored yet—but that still means something. Zero tells you where you are, even if it's at the starting point. Why is zero powerful? - It’s not just nothing—it’s a marker. A starting line. - Without zero, we couldn’t write big numbers like 1,000. You’d be stuck figuring out whether 1 is ten or a hundred! - It balances equations. If you want to keep things fair on both sides, you often use zero. In everyday life: - Bank account: If you have ₹0, you know exactly how much you have—not unknown or empty, but zero. - Temperature: Zero degrees is the point between freezing and not freezing—it's important! 🧠 Summary: - Zero is the additive identity. - It makes equations solvable and systems like calculus work. - It marks origin points in math and space. - It powers computer logic. - It revolutionized number systems and mathematical thinking. ⚠️ Disclaimer: The easy explanation is just to help you understand the concept in simple terms. For academic or exam purposes, always rely on the detailed explanation. If you score less for using this simplified version, we're not responsible—we're just here to make things clearer for learning purposes. 🔗 Related Reading from Our Blog: - How Does Quantum Entanglement Work 2025 https://edgythoughts.com/how-does-quantum-entanglement-work-2025 - How Do Gravitational Waves Affect Space-Time 2025 https://edgythoughts.com/how-do-gravitational-waves-affect-space-time-2025 🔗 External Source: - https://en.wikipedia.org/wiki/0 Read the full article