#quantisation | Explore Tumblr posts and blogs

canmom · 2 years ago

Text

Music Theory Notes (for science bitches) 1: chords & such

This is one of these series where I use my blog as a kind of study blog type thing. If you're knowledgeable about music theory, it will be very basic. But that's kind of the problem, I've really struggled to absorb those basics!

When I was a teenager I learned to play violin and played in orchestras. I could read music, and play decently enough, but I didn't really understand music. I just read what was on the page, and played the scales I had to play for exams.

Lately I've been trying to learn music again. This time my instruments are zhonghu, voice, and DAWs. At some point I might get my violin back too. But really, I'm a total beginner again, and this time I want to do it properly.

For a long time when I tried to learn about music I would get overwhelmed with terminology and jargon and conventions. I might watch videos on composition and they'd be interesting but a lot of it would just fly over my head, I'd just have to nod along because I had no idea what all the different types of chord and such were. I tried to learn from sites like musictheory.net, but I found it hard to figure out the logical structure to fit it all into.

I feel like I'm finally making a bit of headway, so it's time to take some notes. The idea here is not just to answer the what, but also to give some sense of why, a motivation. So in a sense this is a first attempt at writing the introduction to music theory I wish I'd had. This is going to assume you know a little bit about physics, but basically nothing about music.

What is music? From first principles.

This is impossible to answer in full generality, especially since as certain people would be quick to remind me, there's a whole corner of avant-garde composers who will cook up counterexamples to whatever claim you make. So let's narrow our focus: I'm talking about the 'most common' type of music in the society I inhabit, which is called 'tonal music'. (However some observations may be relevant to other types of music such as noise or purely rhythmic music.)

Music is generally an art form involving arranging sound waves in time into patterns (in the sense that illustration is about creating patterns on a 2D surface with light, animation is arranging illustrations in time, etc.).

Physically, sound is a pressure wave propagating through a medium, primarily air. As sound waves propagate, they will reflect off surfaces and go into superposition, and depending on the materials around, certain frequencies might be attenuated or amplified. So the way sound waves propagate in a space is very complicated!

But in general we've found we can pretty decently approximate the experience of listening to something using one or two 'audio tracks', which are played back at just one or two points. So for the sake of making headway, we will make an approximation: rather than worry about the entire sound field, we're going to talk about a one-dimensional function of time, namely the pressure at the idealised audio source. This is what gets displayed inside an audio editor. For example, here's me playing the zhonghu, recorded on a mic, as seen inside Audacity.

A wrinkle that is not relevant for this discussion: The idealised 'pressure wave' is a continuous real function of the reals (time to pressure). By contrast, computer audio is quantised in both the pressure level and time, and this is used to reconstruct a continuous pressure wave by convolution at playback time. (Just like a pixel is not a little square, an audio sample is not a constant pressure!) But I'm going to talk about real numbers until quantisation becomes relevant.

When the human eye receives light, the cone cells in the eye respond to the frequencies of EM radiation, creating just three different neural signals, but with incredibly high sensitivity to direction. By contrast, when the human ear receives sound, it is directed into an organ called the cochlea which is kind of like a cone rolled up into a spiral...

Inside this organ, the sound wave moves around the spiral, which has a fascinatingly complex structure that means different frequencies of wave will excite tiny hairs at different points along the tube. In effect, the cochlea performs a short-time Fourier transform of the incoming sound wave. Information about the direction of the incoming wave is given by the way it reflects off the shape of the ear, the difference between ears, and the movement of our head.

So! In contrast to light, where the brain receives a huge amount of information about directions of incoming light but only limited information of the frequency spectrum, with sound we receive a huge amount of information about the frequency spectrum but only quite limited information about its direction.

Music thus generally involves creating patterns with vibration frequencies in the sound wave. More than this, it's also generally about creating repeating patterns on a longer timescale, which is known as rhythm. This has something to do with the way neurons respond to signals but that's something I'm not well-versed in, and in any case it is heavily culturally mediated.

All right, so, this is the medium we have to play with. When we analyse an audio signal that represents music, we chop it up into small windows, and use a Fourier transform to find out the 'frequencies that are present in the signal'.

Most musical instruments are designed to make sounds that are combinations of certain frequencies at integer ratios. For example here is a plot of the [discrete] Fourier transform of a note played on the zhonghu:

The intensity of the signal is written in decibels, so it's actually a logarithmic scale despite looking linear. The frequency of the wave is written in Hertz, and plotted logarithmically as well. A pure sine wave would look like a thin vertical line; a slightly wider spike means it's a combination of a bunch of sine waves of very close frequencies.

The signal consists of one strong peak at 397Hz and nearby frequencies, and a series of peaks at (roughly) integer multiples of this frequency. In this case the second and third peaks are measured at 786Hz, and 1176Hz. Exact integer ratios would give us 794Hz and 1191Hz, but because the first peak is quite wide we'd expect there to be some error.

Some terminology: The first peak is called the fundamental, and the remaining peaks are known as overtones. The frequency of the fundamental is what defines this signal as a particular musical note, and the intensities of the overtone and widths of the peaks define the quality of the note - the thing that makes a flute and a violin playing the same fundamental frequency sound different when we listen to them. If you played two different notes at the same time, you'd get the spectrums of both notes added together - each note has its own fundamental and overtones.

OK, so far that's just basic audio analysis, nothing is specific to music. To go further we need to start imposing some kind of logical structure on the sound, defining relationships between the different notes.

The twelve-tone music system

There are many ways to do this, but in the West, one specific system has evolved as a kind of 'common language' that the vast majority of music is written in. As a language, it gives names to the notes, and defines a space of emotional connotations. We unconsciously learn this language as we go through the process of socialisation, just as we learn to interpret pictures, watch films, etc.

The system I'm about to outline is known as 12-tone equal temperament or "12TET". It was first cooked up in the 16th century almost simultaneously in China and Europe, but it truly became the standard tuning in the West around the 18th century, distilled from a hodgepodge of musical systems in use previously. In the 20th century, classical composers became rather bored of it and started experimenting with other systems of tonality. Nevertheless, it's the system used for the vast majority of popular music, film and game soundtracks, etc.

Other systems exist, just as complex. Western music tends to create scales of seven notes in an octave, but there are variants that use other amounts, like 6. And for example classical Indian music uses its own variant of a seven-note scale; there are also nuances within Western music such as 'just intonation' which we'll discuss in a bit; really, everything in music is really fucking complicated!

I'll be primarily discussing 12TET because 1. it's hard enough to understand just one system and this one is the most accessible; 2. this has a very nice mathematical structure which tickles my autismbrain. However, along the way we'll visit some variants, such as 'Pythagorean intervals'.

The goal is to try and not just say 'this is what the notation means' but explain why we might construct music this way. Since a lot of musical stuff is kept around for historical reasons, that will require some detours into history.

Octaves

So, what's the big idea here? Well, let's start with the idea of an octave. If you have two notes, let's call then M and N, and the frequency of N is twice the frequency of M... well, to the human ear, they sound very very closely related. In fact N is the first overtone of M - if you play M on almost any instrument, you're also hearing N.

Harmony, which we'll talk about in a minute, is the idea that two notes sound especially pleasant together - but this goes even further. So in many many music systems around the world, these two notes with frequency ratio of 2 are actually identified - they are in some sense 'the same note', and they're given the same name. This also means that further powers of 2, of e.g. 4, 8, 16, and so on, are also 'the same note'. We call the relationship between M and N an octave - we say if two notes are 'an octave apart', one has twice the frequency of the other.

For example, a note whose fundamental frequency is 261.626Hz is known as 'C' in the convention of 'concert pitch'. This implies an infinite series of other Cs, but since the human ear has a limited range of frequencies, in practice you have Cs from 8.176Hz up through 16744.036. These are given a series of numbers by convention, so 261.626Hz is called C4, often 'middle C'. 523.251Hz is C5, 1046.502Hz is C6, and so on. However, a lot of the time it doesn't matter which C you're talking about, so you just say 'C'.

But the identification of "C" with 261.626Hz * 2^N is just a convention (known as 'concert pitch'). Nothing is stopping you tuning to any other frequency: to build up the rest of the structure you just need some note to start with, and the rest unfolds using ratios.

Harmony and intervals

Music is less about individual notes, and more about the relationship between notes - either notes played at the same time, or in succession.

Between any two notes we have something called an interval determined by the ratio of their fundamental frequencies. We've already seen one interval: the octave, which has ratio 2.

The next interval to bring up is the 'fifth'. There are a few different variants of this idea, but generally speaking if two notes have a ratio of 1.5, they sound really really nice together. Why is this called a 'fifth'? Historical reasons, there is no way to shake this terminology, we're stuck with it. Just bear with me here, it will become semi-clear in a minute.

In the same vein, other ratios of small integers tend to sound 'harmonious'. They're satisfying to hear together. Ratios of larger integers, by contrast, feel unsatisfying. But this creates an idea of 'tension' and 'resolution'. If you play two notes together that don't harmonise as nicely, you create a feeling of expectation and tension; when you you play some notes that harmonise really well, that 'resolves' the tension and creates a sense of relief.

Building a scale - just intonation

The exact 3:2 integer ratio used in two tuning systems called 'Pythagorean tuning' and 'just intonation'. Using these kinds of integer ratios, you can unfold out a whole series of other notes, and that's how the Europeans generally did things before 12TET came along. For example, in 'just intonation', you might start with some frequency, and then procede in the ratios 9/8, 5/4, 4/3, 3/2, 5/3, 15/8, and at last 2 (the octave). These would be given a series of letters, creating a 'scale'.

What is a scale? A scale is something like the 'colour palette' for a piece of music. It's a set of notes you use. You might use notes from outside the scale but only very occasionally. Different scales are associated with different feelings - for example, the 'major scale' generally feels happy and triumphant, while a 'minor scale' tends to feel sad and forlorn. We'll talk a lot more about scales soon.

In the European musical tradition, a 'scale' consists of seven notes in each octave, so the notes are named by the first seven notes of the alphabet, i.e. A B C D E F G. A scale has a 'base note', and then you'd unfold the other frequencies using the ratios. An instrument such as a piano would be tuned to play a particular scale. The ratios above are one definition of a 'major scale', and starting with C as the base note, the resulting set of notes is called 'C Major'.

All these nice small-number ratios tend to sound really good together. But it becomes rather tricky if you want to play multiple scales on the same instrument. For example, say your piano is tuned in just intonation to C Major. This means, assuming you have a starting frequency we'll call C, you have the following notes available in a given octave:

C, D=(9/8)C, E=(5/4)C, F=(4/3)C, G=(3/2)C [the fifth!], A=(5/3)C, B=(15/8)C, and 2C [the start of the next octave].

Note: the interval we named the 'fifth' is the fifth note in this scale. It's actually the fifth note in the various minor scales too.

But now suppose you want to play with some different notes - let's say a scale we'll call 'A major', which has the same frequency ratios starting on the note we previously called A. Does our piano have the right keys to play this scale?

Well, the next note up from A would be (9/8)A, which would be (9/8)(5/3)C=(15/8)C - that's our B key, so far so good. Then (5/4)A=(5/4)(5/3)C=(25/12)C and... uh oh! We don't have a (25/12)C key, we have 2C, so if we start at A and go up two keys, we have a note that is slightly lower frequency than the one we're looking for.

What this means is that, depending on your tuning, you could only approximate the pretty integer ratios for any scale besides C major. (25/12) is pretty close to 2, so that might not seem so bad, but sometimes we'd land right in between two notes. We can approximate these notes by adding some more 'in between' piano keys. How should we work out what 'extra' keys to include? Well, there were multiple conventions, but we'll see there is some logic to it...

[You might ask, why are you spending so long on this historical system that is now considered obsolete? Well, intervals and their harmonious qualities are still really important in modern music, and it makes most sense to introduce them with the idea of 'small-integer ratios'.]

The semitone

We've seen if we build the 'major scale' using a bunch of 'nice' ratios, we have trouble playing other scales. The gap above may look rather haphazard and arbitrary, but hold on, we're working in exponential space here - shouldn't we be using a logarithmic scale? If I switch to a logarithmic x-axis, we suddenly get a rather appealing pattern...

All the gaps between successive notes are about the same size, except for the gap between E and F, and B and C, which are about half that size. If you try to work that out exactly, you run into the problems we saw above, where C to D is 9/8 or 1.125, but D to E is 10/9 or 1.11111... Even so, you can imagine how people who were playing around with sounds might notice, damn, these are nice even steps we have here. Though you might also notice places where, in this scheme, it's not completely even - for example G to A (ratio 10/9) is noticeably smaller than A to B (ratio 9/8).

We've obliquely approached the idea of dividing the octave up into 12 steps, where each step is about the size of the gap between E and F or B and C. We call each of these steps a 'semitone'. Two semitones make a 'whole tone'. We might fill in all the missing semitones in our scale here using whole-number ratios, which gives you the black keys on the piano. There are multiple schemes for doing this, and the ratios tend to get a bit uglier. In the system we've outlined so far, a 'semitone' is not a fixed ratio, even though it's always somewhere around 1.06.

The set of 12 semitones is called the 'chromatic scale'. It is something like the 'colour space' for Western music. When you compose a piece, you select some subset of the 12 semitones as your 'palette' - the 'scale of' a piece of music.

But we still have a problem here, which is the unevenness of the gaps we discussed above. This could be considered a feature, not a bug, since each scale would have its own 'character' - it's defined by a slightly different set of ratios. But it does add a lot of complication when moving between scales.

So let's say we take all this irregularity as a bug, and try to fix it. The solution is 'equal temperament', which is the idea that the semitone should always be the exact same ratio, allowing the instrument to play any scale you please without difficulty.

Posed like this, it's easy to work out what that ratio should be: if you want 12 equal steps to be an octave, each step must be the 12th root of 2. Which is an irrational number that is about 1.05946...

At this point you say, wait, Bryn, didn't you just start this all off by saying that the human ear likes to hear nice simple integer ratios of frequencies? And now you're telling me that we should actually use an irrational number, which can't be represented by any integer ratio? What gives? But it turns out the human ear isn't quite that picky. If you have a ratio of 7 semitones, or a ratio of 2^(7/12)=1.4983..., that's close enough to 1.5 to feel almost as good. And this brings a lot of huge advantages: you can easily move ('transpose') between different scales of the same type, and trust that all the relevant ratios will be the same.

Equal temperament was the eventual standard, but there was a gradual process of approaching it called stuff like 'well-tempered' or 'good temperament'. One of the major steps along the way was Bach's collection 'the well-tempered klavier', showing how a keyboard instrument with a suitable tuning could play music in every single established scale. Here's one of those pieces:

youtube

Although we're using these irrational numbers, inside the scale are certain intervals that are considered to have certain meanings - some that are 'consonant' and some that are 'dissonant'. We've already mentioned the 'fifth', which is the 'most consonant' ratio. The fifth consists of 7 semitones and it's roughly a 1.5 ratio in equal temperament. Its close cousin is the 'fourth', which consists of 5 semitones. Because it's so nice, the fifth is kind of 'neutral' - it's just there but it doesn't mean a lot on its own.

For the other important intervals we've got to introduce different types of scale.

The scale zoo

So, up above we introduced the 'major' scale. In semitones, the major scale is intervals of 2, 2, 1, 2, 2, 2, 1. This is also called a 'mode', specifically the 'Ionian mode'. There are seven different 'modes', representing different permutations of these intervals, which all have funky Greek names.

The major scale generally connotes "upbeat, happy, triumphant". There are 12 different major scales, taking the 12 different notes of the chromatic scale as the starting point for each one.

Next is the minor scale, which tends to feel more sad or mysterious. Actually there are a few different minor scales. The 'natural minor' goes 2, 1, 2, 2, 1, 2, 2. You might notice this is a cyclic permutation of the major scale! So in fact a natural minor scale is the same set of notes as a major scale. What makes it different?

Well, remember when we talked about tension and resolution? It's about how the notes are organised. Our starting note is the 'root' note of the scale, usually established early on in the piece of music - quite often the very first note of the piece. The way you move around that root note determines whether the piece 'feels' major or minor. So every major scale has a companion natural minor scale, and vice versa. The set of notes in a piece is enough to narrow it down to one minor and one major, but you have to look closer to figure out which one is most relevant.

The 'harmonic minor' is almost the same, but it raises the second-last note (the 7th) a semitone. So its semitone intervals are 2, 1, 2, 2, 1, 3, 1.

The 'melodic minor' raises both the 6th and 7th by one semitone, (edit: but usually only on the way up). So its semitone intervals are 2, 1, 2, 2, 2, 2, 1. (edit: When you come back down you tend to use the natural minor.)

If you talk about a 'minor scale' unqualified, you mean the natural minor. It's also the 'Aeolian mode' in that system of funky Greek names I mentioned earlier.

So that leads to a set of 24 scales, a major and minor scale for every semitone. These are the most common scale types that almost all Western tonal music is written in.

But we ain't done. Because remember I said there were all those other "modes"? These are actually just cyclic permutations of the major scale. There's a really nerdy Youtube channel called '8-bit music theory' that has a bunch of videos analysing them in the context of videogame music which I'm going to watch at some point now I finally have enough background to understand wtf he's talking about.

youtube

And of top of that you have all sorts of other variants that come from shifting a note up or down a semitone.

The cast of intervals

OK, so we've established the idea of scales. Now let's talk intervals. As you might guess from the 'fifth', the intervals are named after their position in the scale.

Let me repeat the two most common scale modes, in terms of number of semitones relative to the root note:

position: 1, 2, 3, 4, 5, 6, 7, 8 major: 0, 2, 4, 5, 7, 9, 11, 12 minor: 0, 2, 3, 5, 7, 8, 10, 12

So you can see the fourth and fifth are the same in both. But there's a difference in three places: the third, the sixth, and the seventh. In each case, the minor is down a semitone from the major.

The interval names are... not quite as simple as 'place in the scale', but that's mostly how it works. e.g. the 'major third' is four semitones and the 'minor third' is three.

The fourth and fifth, which are dual to each other (meaning going up a fifth takes you to the same note as going down a fourth, and vice versa) are called 'perfect'. The note right in between them, an interval of 6 semitones, is called the 'tritone'.

(You can also refer to these intervals as 'augmented' or 'diminished' versions of adjacent intervals. Just in case there wasn't enough terminology in the air. See the table for the names of every interval.)

So, with these names, what's the significance of each one? The thirds, sixths and sevenths are important, because they tell us whether we're in minor or major land when we're building chords. (More on that soon.)

The fifth and the octave are super consonant, as we've said. But the notes that are close to them, like the seventh, the second and even more so the tritone, are quite dissonant - they're near to a nice thing and ironically that leads to awkward ratios which feel uncomfy to our ears. So generally speaking, you use them to build tension and anticipation and set up for a resolution later. (Or don't, and deliberately leave them hanging.)

Of course all of these positions in the scale also have funky Latin names that describe their function.

There's a lot more complicated nuances that make the meaning of a particular interval very contextual, and I certainly couldn't claim to really understand in much depth, but that's basically what I understand about intervals so far.

Our goofy-ass musical notation system

So if semitones are the building block of everything, naturally the musical notation system we use in the modern 12TET era spaces everything out neatly in terms of semitones, right?

Right...?

Lmao no. Actually sheet music is written so that each row of the stave (or staff, the five lines you write notes on) represents a note of the C major scale. All the notes that aren't on the C major scale are represented with special symbols, namely ♯ (read 'sharp') which means 'go up a semitone', and ♭ (read 'flat') which means 'go down a semitone'. That means the same note can be notated in two different ways: A♯ and B♭ are the same note.

The above image shows the chromatic scale, notated in two different ways. Every step is exactly one semitone.

Since a given scale might end up using one of these 'in between' notes that has to be marked sharp or flat, and you don't want to do that for every single time that note appears. Luckily, it turns out that each major/minor scale pair ends up defining a unique set of notes to be adjusted up or down a semitone, called the 'key signature'. So you can write the key signature at the beginning of the piece, and it lasts until you change key signature. For example, the key of 'A♭ major' ends up having four sharps:

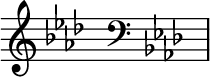
There is a formula you can use to work out the set of sharps or flats to write for a given key. (That's about the point I checked out on musictheory.net.)

There is some advantage to this system, which is that it very clearly tells you when the composer intends to shift into a different scale, and it saves space since with the usual scales there are no wasted lines. But it's also annoyingly arbitrary. You just have to remember that B to C is only a semitone, and the same for E to F.

What are those weird squiggly symbols? Those are 'clefs'. Each one assigns notes to specific lines. The first one 𝄞 is the 'treble clef', the second one 𝄢 is the 'bass clef'. Well, actually these are the 'G-clef' and the 'F-clef', and where they go on the stave determines note assignment, but thankfully this has been standardised and you will only ever see them in one place. The treble clef declares the lines to be E G B D F and the bass clef G B D F A.

There is also a rarer 'C-clef' which looks like 𝄡. This is usually used as the 'Alto clef' which means F A C E G.

This notation system seems needlessly convoluted, but we're rather stuck with it, because most of the music has been written in it already. It's not uncommon for people to come up with alternative notations, though, such as 'tabs' for a stringed instrument which indicate which position should be played on each string. Nowadays on computers, a lot of DAWs will instead use a 'piano roll' presentation which is organised by semitone.

And then there's chords.

Chords! And arpeggios!

A chord is when you play 3 or more notes at the same time.

Simple enough right? But if you wanna talk about it, you gotta have a way to give them names. And that's where things get fucking nuts.

But the basic chord type is a 'triad', consisting of three notes, separated by certain intervals. There are two standard types, which you basically assemble by taking every other note of a scale. In terms of semitones, these are:

Major triad: 0 - 4 - 7 Minor triad: 0 - 3 - 7

Then there's a bunch of variations, for example:

Augmented: 0 - 4 - 8 Diminished: 0 - 3 - 6 Suspended: 0 - 2 - 7 (sus2) or 0 - 5 - 7 (sus4) Dominant seventh: 0 - 4 - 7 - 10 Power: 0 - 7

There is a notation scheme for chords in pop, jazz, rock, etc., which starts with a root note and then adds a bunch of superscripts to tell you about any special features of a chord. So 'C' means the C Major triad (namely C,E,G) and 'Cm' or 'c' means the C Minor triad (namely C,E♭,G).

In musical composition, you usually tend to surround the melody (single voice) with a 'chord progression' that both harmonises and creates a sense of 'movement' from one chord to another. Some instruments like guitar and piano are really good at playing chords. On instruments that can't play chords, they can still play 'arpeggios', which is what happens if you take a chord and unroll it into a sequence of notes. Or you play in an ensemble and harmonise with the other players to create a chord together. Awww.

Given a scale, you can construct a series of seven triad chords, starting from each note of the scale. These are generally given scale-specific Roman numerals corresponding to the position in the scale, and they're used to analyse the progression of chords in a song. I pretty much learned about this today while writing this post, so I can't tell you much more than that.

Right now, that's about as far as I've gotten with chords. On a violin, you can play just two strings at the same time after all - I never had much need to learn about them so it remains a huge hole in my understanding of music. I can't recognise chords by ear at all. So I gotta learn more about them.

As much as I wrote this for my own benefit... if you found this post interesting, let me know. I might write more if people find this style of presentation appealing. ^^'

#Youtube #music #music theory #notes #music notes

284 notes · View notes

paeliae-occasionally · 9 months ago

Text

Strands and Simple components

Thank you @satohqbanana for asking about this!

Ok so it has come to my attention that I have a lot of strand and simple components lore that I have not fully explained so let’s get on that.

Alright so firstly:

In my world magic acts essentially like a different form of matter. It has no physical mass but can be measured and quantised like a particle. Creatures with a soul can interact with this matter, creatures without a soul cannot.

So what are strands and simple components?

Ok, so imagine the air around you. It is everywhere but if you zoom in close enough, you can see it is made up of compounds like N2 and H2O

Strands are like compounds.

A bunch of magic atoms with bonds between them form larger molecule called a strand.

In the same way, simple components are like elements. They bond together to make strands, and you can imagine the table in the magic systems post here like the periodic table of elements.

You can also think about it like a strand of DNA and the simple components are like bases.

————The types and mechanics of bonds are still under development. ————

So to recap, Magic is everywhere but at a base level it is made up of strands (compounds) and simple components (Elements) .

Refined and Unrefined spells:

So Unrefined spells cast full, naturally occurring strands (Druids)

Refined spells perform a ‘Reaction’ first to break off either a portion of a strand (Mages) or an individual simple component. (Runics)

Ok, so going deeper into the lore:

What makes an ability require less or more power?

This is actually a really interesting one.

It depends on 3 factors:

weight of the components

stability of the components

The strength of the bonds

Weight

Ok so when I say weight in reference to magic, I don’t mean physical as they have no mass, it just means how that component reacts to magical fields.

So in the ‘periodic table’ weight increases down the group and across the period. Particles that have a higher weight are more likely to exist in shorter strands or alone. It is easier to break bonds between heavier components to remove them from their strands.

It is however harder to cast heavier elements as they are harder to manipulate with your soul.

Stability

This means how likely a component is to decay. Stability decreases with weight, so the heavier a component is the more likely it is to decay.

Heavier components are usually more powerful because they release energy when they break down which can add power to the spell.

Less stable components are much harder to cast as you need a lot more control so they don’t decay when you interact with them.

The strength of the bonds

Typically lighter components form stronger bonds. Bond strength only matters for the types of casters who break bonds. (Mages and Runics)

Again the details of bonding are still under development so I will leave it here for now.

Mages usually only break 1 or 2 bonds to get a specific section of a strand. They don’t have enough power to break every bond in the whole strand.

Runics use runes as a sort of catalyst so they can break every bond by an alternate route that requires less energy.

Hope this answers the question. Let me know if anything doesn’t make sense.

@thelovelymachinery, @an-indecisive-nerd, @the-letterbox-archives, @oliolioxenfreewrites, @winvyre

@happypup-kitcat24, @wyked-ao3, @leahnardo-da-veggie, @alnaperera, @dearunreliablenarrator

@rumeysawrites, @urnumber1star, @seastarblue, @thecomfywriter

#writeblr #writers on tumblr #writing community #writing #fantasy worldbuilding #Magic

32 notes · View notes

talonabraxas · 9 months ago

Text

"For the wise man looks into space and he knows there is no limited dimensions." ― Zhuangzi

4D Aether Talon Abraxas

The Aether is a medium that transports light waves through the vacuum of space. In order to achieve this, it must express the nature of an incompressible fluid. A 4th dimensional substance satisfies this criterium, and explains why no evidence has been produced to prove its existence. The Hypercube is a particular example of a 4D polytope. It can be considered as two cubes that are constantly changing places as it rotates. As time passes, each cube takes its turn to fall into the central space. As each one aligns, it renders a moment of time in the universe. Time and space are quantised phenomena. The reason for this quantisation can be ascribed to this nature of 4D space.

27 notes · View notes

lynnbecks-gaming-sideblog · 7 months ago

Text

Quantised Creepers is now on Modrinth!

#mineblr #minecraft #resource pack #modrinth #minecraft creeper

15 notes · View notes

lynns-bonkle-blog · 11 months ago

Text

A li'l guy I accidentally rendered at like half the inteneded resolution so I quantised it.

Full credits below.

Head, eyes, leg segments, shoulders/knees, arms and hands, shoulder-balls, and torso by @nattarthetimedragon, respectively from the upcoming 8/10 Vahki pack (which I am currently testing), Turaga pack, Toran Part Expansion pack, Power of the Matoran pack, Turaga of Mata-Nui pack, and articulated Mata/Slizer hand pack.

"Rahkshi Staff Prototype" from this pack by Scmdex.

Feet by @orc3dprint, from the Towa Mata pack.

#bionicle #moc

28 notes · View notes

oliviabutsmart · 2 years ago

Text

Physics Friday #12: Interpreting Quantum Mechanics

Preamble: "God does not play dice"

Education Level: High School (Y9/10)

Topic: Quantum Mechanics (Physics)

Developing the Schrödinger Equation

Quantum mechanics had it's origin in the nature of light, and then over the course of 50 years from 1900 - 1950, the entire field of physics was overturned as we realised that waves weren't just limited to light, but everything.

This came to it's head in 1926 with the creation of the Schrödinger wave equation, which dictated how particle 'waves' evolve in time and space.

Now you've probably heard of the wavefunction. Effectively, it's a probability wave, where the amplitude of the wave corresponds to the most likely location you'd find the particle.

The wavefunction doesn't just involve a probability distribution in space, but also in other quantities.

For example, if you put an electron in a small box, you can imbue it with an energy.

But because of quantum mechanics, energy is quantised - there is an energy of X joules, 2X joules, 3X joules, etc. If you put an electron of 2.5X into the system it can't just work like that.

Which is why the electron forms a weighted combination of different states corresponding to specific multiples of our X value. And this superposition just so happens to be the average energy, which is considered the classical energy of the electron.

For example an electron with a superposition of 2X, 50% of the time, and being in state 3X 50% of the time. This averages out to 2.5X.

Collapsing the Wavefunction

But how do you find a particle? Or measure it's energy? Well, via what's known as the wavefunction collapse. When we take a look at the particle as a wave, it suddenly snaps to a specific value and then evolves from there.

This wavefunction collapse can occur for any observable property of the particle. If you measure the energy of our 2.5X particle in our above state, it's a 50/50 chance that you'll catch it in either state.

And once the coin flip occurs, the particle's energy will suddenly jump to 3X or 2X and remain at that value.

You may think this violates the conservation of energy, but remember that the act of 'measurement' intrinsically involves interacting with the electron - a very important point.

But wait, what does this collapse mean?

The Schrödinger equation does not explicitly mention this collapse. It simply describes the evolution of an undisturbed wavefunction. Thus, we need to include collapse as a part of the three postulates of QM:

Particle states are described by a wavefunction, a vector belonging to a Hilbert space

The Schrödinger equation dictates the time evolution of these states

Measurement of an observable (i.e. a hermitian operator) collapses the wavefunction to an observable's eigenstate (each eigenstate being associated with a probability of collapse)

But this still doesn't really answer the question. What is measurement? What counts as measuring an observable property of the particle?

Well here's the thing ... we don't have an answer ... it's an open question and the topic of this post.

The interpretations

An interpretation of quantum mechanics is effectively a theory that aims to answer this question: where and how does this measurement occur?

After almost a century since the formulation of standard QM, we have a litany of many interpretations, most of which fall on a spectrum of when exactly it occurs.

On one end, we have ideas where the wavefunction never existed in the first place, or that the wavefunction naturally collapses.

On the other, we have ideas that the wavefunction collapses at a point very far in the process, or even that it never collapses at all.

I'll talk about 6 of these interpretations, although some of these theories of collapse are more categories of theories.

Think of the Ocean (Pilot Wave)

In the 1920s, de Broglie developed an interpretation of quantum mechanics that posited that subatomic particles do, in fact, physically exist.

The source of the wavefunction and the probabilistic nature of quantum mechanics is caused by the particles being guided by a series of "pilot waves" - which push and move the particles around and imbue them with the motion and energy we observe.

The randomness comes from the fact that the waves themselves depend on the positions of all particles. These guiding waves are dictated by a special guiding equation.

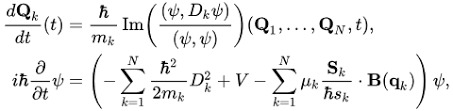
dear lord that's complicated Image Credit: Wikipedia

This guiding equation, when applied to particles just so happen to result in our neat and clean Schrödinger equaiton.

So what happened to this theory?

The biggest problem with this theory is that it's non-local, meaning that the evolution of the guiding wave requires knowledge of all of the particles in the universe.

This of course, violates special relativity.

Another problem is that it lost the authors' support, or that the authors lost support. de Broglie rejected the theory in 1927 and David Bohm, the other author, was distanced from the other scientists for being outwardly socialist during the early red scares.

Pilot wave theory, in a sense, is so strict on the physicality of particles that it ends up sort-of wrapping around and becoming a many-worlds theory instead, to quote David Deustch:

Pilot-wave theories are parallel-universe theories in a state of chronic denial.

This arises from the problem of branching, a tacked-on attempt to reconcile the nature of the theory. That since the wavefunction was a physical thing, and the pilot wave and particles kept self-interacting, it sort of creates branching realities caused by distant communication with other particles.

Those silly numbers are hiding from us! (Hidden Variables)

The EPR (Einstein-Podolski-Rosen) paradox is another famous problem in QM, caused by entanglement.

Take two electrons and force them to collide with eachother, bounce off, and travel far into the distance. We know that after the interaction, these electrons propagate with free-particle wavefunctions. And we can fire them at eachother such that we don't know their momentums initially - i.e. they entangled.

Now wait for the electrons to travel very far away from eachother, and then measure one of the electrons momenta. In order to maintain conservation of energy, we instantly know what the momenta of the other electron is.

What we also know is that because of this measurement, and that the electron is entangled with the other, that we have just collapsed the other wavefunction instantaneously from a distance.

This is a problem, due to special relativity, we cannot transfer information faster than the speed of light. So clearly our QM is broken.

Hidden variable theories aim to solve the EPR paradox as well as just generally trying to interpret quantum mechanics. Effectively, there are a series of unobservable entities that dictate how wavefunctions collapse.

The wavefunction in the EPR paradox has a hidden variable stating the electrons' momenta so that we aren't violating causality, for example.

Fortunately, but unfortunately, this theory makes a testable prediction via Bell's theorem, which utilises entanglement to determine if these hidden variables work locally.

The experiments conducted show that only a non-local hidden variable theory is possible. One example of this just so happens to be our previous pilot-wave theory!

Observing isn't needed (Spontaneous Collapse)

We could be thinking of this wrong. Perhaps the wavefunction is real, and it is non-deterministic. But that at some point, it collapses on it's own.

There are several ways to do this, but at it's core, these are how the theories go:

There is an extra non-linear term in the Schrödinger equation, that is insignificant at the small scales

This non-linearity causes the wavefunction to be unstable, and prefers it to collapse to observable eigenvalues

With increasing complexity, this term becomes much more important, as more entanglement = more instability

The rate of decay increases as you entangle the system. And if a system is large enough, it's likely to collapse into a classical environment

Effectively, they say that the wavefunction will collapse on their own. And the reason we don't see it on larger scales, or see a collapse when measuring the system, is that the act of interaction (entanglement) causes the wavefunction to be more likely to collapse.

Of course, the theory has trouble reconciling with relativity. As entanglement works over large distances. Models can be made to try and say that entanglement over these distances increases instability for example, but we're still waiting on developments.

Lastly, we have the problem of tails. The wavefunction of a particle exists for all of physical space. At these far out distances, it is very possible for particles to get entangled with distant objects. Meaning that a wavefunction may end up collapsing further than we think.

The easy way out (Copenhagen)

The Copenhagen interpretation was developed in the 20s to attempt to come up with some placeholder answer to what collapse is. It is our middle-of-the-road theory which states that observation of an observable causes collapse.

Observation is defined as the act of applying an observable operator (like the energy operator) to the wavefunction by an external source to gain information on that operator's outcome.

The problem is that this is a meaningless statement. Because anytime a system entangles itself with something greater, it technically does this 'observation'.

Take the double split experiment.

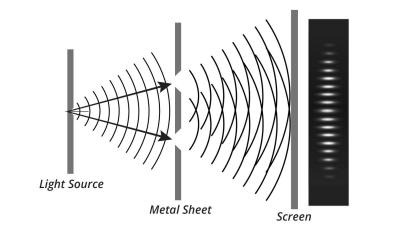
Image Credit: Discovery Channel

What defines the moment of observation? Is it when:

The particles interact with the measuring laser

The measuring laser interacts with the larger observation device

An electronic signal is sent from the device to a computer

The light from the computer interacts with the conscious observer

We can't pinpoint the specific cut-off between the quantum world and the classical.

After all, we know that lasers can entangle themselves with atoms. And that electronic signals are nothing but moving electrons.

The point of the theory is that it's a placeholder. The definitions are ill-defined because we're kinda waiting for another theory to help us.

It's all in your head! (Consciousness)

The immediate answer to the Copenhagen interpretation could be that the collapse occurs at the end of the specified chain. When a conscious observer interacts with the entangled system.

It's a nice idea given that it kills two birds with one stone - it helps point to a physical theory on the nature of sentience, but also allows us to solve the measurement problem.

This does come into conflict with our current understanding of sentience. Our placeholder theorem is effectively that conscious experience is an emergent property of a series of interacting electrical signals in our brain.

This placeholder helps explain why humans are more 'sentient' than animals, or very young children, as we have a very active and complex central nervous system.

Of course, it's just a placeholder. We don't have an actual meaningful answer to sentience, and probably won't for a while. So for now it's left to the dark realm of god of the gaps.

Where it comes into conflict with QM is that a series of interacting electrical signals sounds exactly like an entangled system. So there clearly can't be just emergent properties involved otherwise we're just dealing with a spontaneous collapse theory.

There has to be something physically unique about a sentient brain to cause the collapse - effectively you require the existence of a soul. Something which is even further in the dark realms of philosophy.

Another issue is that it doesn't work with special relativity, as it violates the EPR paradox still.

We also need to determine what counts as sentient. Sentience isn't an on and off switch. There are many ways it can be expressed.

We know that some mammals have some form of conscious experience - so then are cats capable of collapsing the wavefunction?

Finally, what about the universe prior to consciousness? Did it just end up in an entangled nightmare until somehow we got an observer to collapse it all? How can something built of entangled particles end up collapsing itself at some given size?

This interpretation is very interesting, however if it turns out to be true, we'll be stuck with our measurement problem for quite a while.

For now, the biggest problem with the interpretation is that it opens the door to many, many quacks like Deepak Chopra. Who think that we can control this collapse with our minds and alter our reality by just thinking it away WoOOoOoWwowoWoOo!

Forever entangled (Many Worlds)

So, assuming that our consciousness theory is not the right answer, then what causes the collapse?

We can keep getting bigger and bigger:

The electrons in the double slit entangles with the laser photons entangles with the measurement device entangles with the electrical signals entangles with the computer entangles with the observer entangles with the room their in entangles with the Earth entangles with the solar system entangles with the galaxy ...

This out-spiralling entanglement continues without bound until the entire universe is in a superposition of states. And every time an interaction occurs we ourselves are being pulled into a new wavefunction.

This entanglement would've happened early, at about the time of cosmic inflation. But every new quantum event comes with a new set of entanglements.

This leads to the name Many Worlds, as we're creating new realities with every event.

Now it's important to note something important: this is not a multiverse theory. Multiverse theory is proposed source for cosmic inflation. Here, there is still one single universe. Much like how an electron in superposition isn't multiple actual electrons. The universe is just being treated as an electron.

This theory sounds far-fetched. Arguably the fact that it's unfalsifiable makes it not a good interpretation of QM. However, it is a lot simpler than the previous consciousness interpretation - it simply removes the need for a measurement process.

This satisfies Occam's razor as well. It doesn't require a mathematical formalism because the point of the theory is that the formalism doesn't exist.

However, not having a formalism makes it quite difficult to prove. It only seems to be correct in the sense that it doesn't necessarily say that measurement cannot happen, just that it's not measurement. It's entanglement.

Conclusion

Interestingly, the theories on the "wavefunction collapses early" side of the spectrum are more likely to be disproven. Primarily a consequence of the fact that they have the opportunity of making testable predictions.

Despite all of these interpretations, it's clear who stands as the best theories: spontaneous collapse and many worlds. They have their strengths, but they have fair grounding. You could argue that consciousness is also a fair contender, but it's a bit too much in the realm of fantasy - attempting to tie one big unanswered question with another.

Spontaneous collapse has proper mathematical formalism while many worlds seems to work well in an Occam's razor sense.

Regardless, that is a surface-level exploration into the many different ways we have attempted to answer the measurement problem. I hope y'all enjoyed this post and god I need to make them less long.

Please can someone fix this inverted colours issue it's like causing all of my colours on these posts to invert too thx

Reference post: https://www.tumblr.com/oliviabutsmart/732200630726377472/for-some-reason-some-reasons-only-some-images-i

Anyways, feedback appreciated, follow if want, send memes and send help.

#physics friday #stem #academics #stemblr #science #physics #quantum physics #quantum mechanics

97 notes · View notes

lynnbecksart · 7 months ago

Text

Cool Paint.NET tip: go to Effects -> Colour -> Quantise and then set Algorithm to "Median Cut", Colours to 16, Dithering Level to 1 and Transparency Threshold to 0.

#not art #paint.net #quantise

1 note · View note

thedarknesseater · 5 months ago

Text

This is so funny but it also got me thinking about if cursed energy is quantised, then it could very well start from ½

#jjk manga #jjk #jujutsu kaisen #cursed energy

6 notes · View notes

wordsandrobots · 2 years ago

Text

IBO reference notes on . . . the Turbines, or 'Tekkadan done right'

In my notes on an act of unspeakable cruelty, I described the Turbines in Iron-Blooded Orphans as an example of having one's cake and eating it. Pun very much intended, I stand by this assessment: the Turbines are a great example of writing justifying a genre trope; to whit, an anime aimed at teenage boys featuring a group of attractive women in a relationship with a lone man.

Whether that's a worthwhile exercise or not will depend on the viewer's tastes. Personally, I think it would have worked fine without overtly 'cheesecake' designs, though I don't take that as an argument against including them when Tekkadan are walking around shirtless half the time.

And indeed, it's the wider comparisons between the two groups I want to talk about today. There's a clear parallel established throughout the series, which I summarised in that previous essay as 'the Turbines are a successful version of what Tekkadan aspire to be'.

So let's dig into that a little, with full spoilers as usual.

Who are the Turbines?

When they're introduced, we learn the Turbines are in charge of the transportation division of the Jupiter-based Teiwaz conglomerate – an organisation that provides the Japanese-Italian fusion mafia representation sorely lacking from much of popular sci-fi media. Teiwaz is a supposedly reputable enterprise, yet is widely known to be functionally yakuza. Likewise, while the Turbines are described in terms approximating an above-board logistics company, they know how to circumvent official shipping lanes via highly suspect detours.

Of course, this is hardly unusual for IBO, where fine and permeable lines between legal and illicit activities are a fact of life. The Turbines are as legitimate as most people get in this setting and can't reasonably be called criminals (not without being aggressively framed, anyway), yet they aren't wholly 'above-board' either. There is no such thing in the Post Disaster timeline.

Now, the most important detail I want to centre about the Turbines is that they have over 50,000 members. Fifty thousand. Teiwaz is not some nickel-and-dime set-up; they're one of the most powerful (if not the most powerful) organisations in the outer-spheres and their transport subsidiary is correspondingly massive. We don't get the precise number until midway through Season 2 but we are told repeatedly what a huge deal it is for Tekkadan to be in cahoots with them; quantisation simply underlines the point. Naze's 'threat' to split the boys up such that they don't see one another again is far from idle.

This scale is the result of unifying a large number of individual shipping companies under one banner. Specifically, all-women groups that had previously been on the bottom rung of the solar system's transport ecosystem. The society Teiwaz exists in is depicted as a deeply sexist one. None of the high-ranking leaders are female and we are told outright that women forced from their homes have to turn to extremely dangerous work in order to survive. At least prior to the formation of the Turbines, this involved running cargo along pirate-infested routes, cheaply, with minimal defences.

Here is our first big parallel to Tekkadan. Like the child soldiers of the CGS, these women (and let's be realistic, girls) were rendered vulnerable by their social position and exploited for their labour as a result. I think it's commendable the writers chose to present their situation in this fashion: as easy – and correct – as it is to feel moral outrage about people being exploited for sex, this is a subset of the work dispossessed people are forced into. It would have been easy to give the Turbines a more lurid origin, particularly as this show is not shy about depicting actual sex-trafficking. To focus on something more 'mundane' reinforces that societies run on exploitation are literally that: even innocuous industries like freight haulage are driven by underpaid, under-protected workers.

It is into this situation that a young and ambitious Naze Turbine stepped and via him that at least some of these women found a better position in life.

A family business

We largely see the Turbines through the lens of their flagship, the Hammerhead, and its crew-slash-polygamous-family. When we talk about 'the Turbines', this is usually who we mean, rather than the wider transport company, which mostly exists in the background of the show's events.

The Hammerhead's pursuit of the Isaribi marks the arrival of the Turbines into the plot, first via Lafter's delight in the chase (in a scene leaning heavily on the overt sexualisation of her design) and then with Naze announcing himself to Tekkadan directly, initiating a brief battle between the two groups.

Naze's moral character is established in his reaction to Maruba dismissing Tekkadan as a bunch of 'space rats'. His disgust is aimed squarely at the perpetrator of the risky implantation surgery, setting him apart from the likes of Gaelio and, by extension, the Earth-based taboos against augmented people. We can assume Naze is familiar with both the Alaya-Vijnana system and the consequences of its use, and his ire switches immediately from what he had been told were a bunch of thieves to the man they've 'stolen' from.

With the conflict resolved and Naze willing to negotiate, we begin to learn about the Turbines as a group. Notably, while he refers to his crew as his harem, his agreement with Kudelia that they are his wives is a 'sure, let's go with that' kind of deal. The English dub states 'they are sworn to me' while the sub has him describing them as 'my women'. In either case, the legal status of the arrangement is left ambiguous. But the gist of the matter is that Naze openly presents his crew as a harem, in line with a playboy persona he presents to the world.

In Season 2, we jump back to see how this arrangement came to be. Amida describes him as a 'maverick trafficker' who hired her for protection on a dangerous gig (we never do find out what he was transporting). They got along well and fell into bed together, but Amida wouldn't make the arrangement permanent as she'd promised her services to an all-women freighter company tackling even more dangerous work – a choice implied to stem from having once in their situation. On hearing this, Naze asks the question that distinguishes him from his eventual blood brother, Orga: 'how can I help?'

Orga never asks this aloud, despite everything he does having the stated aim of helping his comrades. It's not hard to see why when his point of reference is Mikazuki, who places absolute faith in his ability to provide solutions to their problems. This fundamentally unfair expectation screws with Orga's sense of responsibility, especially once coupled to the top-down structure of a military unit and an absence of people pushing back against it.

But Naze and Amida meet as adults, not children. They've already grown-up and learned who they are. They engage from positions of mutual respect, each appreciating how the other's skills can help with their goals. Rather than declaring some nebulous, far-off dream, Naze offers assistance to solve a specific problem Amida was already working on. He provides the ability to make connections between disparate groups of exploited woman and a face to present to a misogynistic world.

On top of having the luxury of pre-existing social capital, he can afford to invest years of his time in growing the Turbines to the point where they bring something to Teiwaz's table. This slow, careful approach puts them in a much stronger position to deal with the big dogs, all while aiming for the same things Tekkadan will later rush to seize: security, legitimacy and respect.

This last item bears some scrutiny, because it illustrates the importance of being precise about your goals. We know nothing about Naze prior to meeting Amida, so we don't know why his sexism (because it is still that) eschews looking down on women in favour of elevating them above men. But he feels no shame about achieving business success via a women-only organisation, freely admitting to have gotten where he has thanks to them and holding Amida back from defending him from insults against his manhood that ensue. Naze knows who he needs to impress and it's not loud-mouths like Jasley Donomikols but men like McMurdo Barriston, who value results above all else. Where Tekkadan insist on making as big a noise as possible to establish their credentials, Naze can shrug off disparaging remarks. Why start a fight when he's gained the confidence of the most powerful man in the Jupiter-sphere?

Besides, he adores being where he is. He's actively unrepentant about having enough 'wives' to crew a spaceship and if this partly works to downplay his shrewdness, it's also just who he is. The narrative presents him in an entirely positive light for it, too. Of all the authority figures in Iron-Blooded Orphans, he's easily the kindest, going out of his way to support other people, often irrespective of personal gain.

Tekkadan's recruitment over the course of the series is characterised by radical acceptance. Human debris, repentant murderers, Teiwaz pen-pushers, ambitious college kids – they're all welcomed and placed on equal footing. In light of this, I find it significant that when we see Amida pre-Turbines, she's dressed in a rather understated manner, masking past wounds and presenting in a stereotypically 'professional' fashion – likely to offset the concerns her clients have about hiring a woman mercenary. After years living with Naze, however, she's adopted a much more revealing outfit and attitude, no longer hiding who she is in either words, actions or appearance.

Amida's design is one of the most cheesecaky of the set but it's positioned as a sign that she – like everyone in Naze's orbit – is loved scars and all.

A ship of wives

Gundam has a history of featuring men surrounded by a faithful cohort of women. Starting with Paptimus Scirocco in Zeta Gundam (a decidedly evil example, though oddly enough, also hailing from Jupiter), through Chibodee Crocket in Mobile Fight G Gundam (a much closer match to the Turbine's model), and all the way to Shaddiq Zenelli in Witch From Mercury (where, like a lot of G-Witch's secondary details, it feels like a call-back for the sake of itself), the 'harem' trope is one the franchise has made use of time and again. Rarely, however, has it been as explicit about dropping pretences as with the Turbines. To dip into crudity for the sake of succinctness: yeah, they're fucking.

We are left in no doubt over this. Not only do we see the many children that have resulted, Naze's wives make it clear they expect and enjoy him exercising his spousal responsibilities in the bedroom. And here is where I wheel out my media literacy soapbox because whatever you personally feel about this as a concept, the text presents it as consensual and as free of coercion as it can possibly be.

Yes, there is an inherent power imbalance with Naze being head of the organisation and, quite literally, the man who saved these women's lives. Yes, some of them were clearly recruited to the Turbines as teenagers (as we see in Lafter's backstory). And yes, it's a fantasy that often extends out of sexist perspectives, ones the presentation here does not work especially hard to refute.

However at no point is there any suggestion in the text that Naze pressures anyone into having sexual relations with him. The opposite, if anything. Amida is the only member of the Hammerhead's crew he initiates with – his partner, in every sense of the word. Lots of the others come on to him and he doesn't remotely discourage them, sure. But you've also got Azee, who explicitly choses not to act the same and is just as much part of this core family (while this doesn't rule out her being sexually involved with Naze, it shows there is no expectation of uniform behaviour). Furthermore, when Lafter starts developing romantic feelings for Akihiro – as contrasted with familial ones for the Turbines in general and sexual ones for Naze – literally everyone encourages her to follow them, treating it as perfectly natural and a sign of maturity.

(To head off a rather trite misread, Naze describing his wives as 'like his daughters' in some respects does not invoke literal fatherhood. His 'paternal' statements are in line with the attitude he takes to Orga as his 'little brother' – that of someone with more experience taking responsibility for a more naïve dependent – and I think it's really worth stressing that non-nuclear family dynamics do not map to those of nuclear families. Though unquestionably a patriarch figure, Naze is happy Lafter going to go get what she wants and proud of her choices. The literal opposite of infantilising her.)

Thanks to the Urdr Hunt mobile game, we get a canonical glimpse into how Naze interacts with members of the Turbines beyond the Hammerhead's crew as well. Tamami Rakou is leader of grey-ops team the 'Rakou Pirates', who handle missions it would be better weren't directly associated with the Turbines (yes, their flags is the Turbines' logo with a skull painted over it, why do you ask?). When she reports to Naze halfway through the game, their relationship is revealed as one of friendly mentorship; again not a million miles off his attitude towards Orga. Tamami explains to another character that the Turbines took her in as a hot-headed youth and trained her in business matters. She seeks to repay what she perceives as a debt, with the ultimate goal of sharing sakuzuki cups with her boss. Naze, by contrast, already firmly recognises her worth (that's why he put her in her current role) and cautions her against taking too many risks.

Naze and Amida gently rib the junior captain over the course of these scenes, while Tamami tries way too hard to impress them. The joke is that she's presenting herself with loud, military seriousness in the face of the couple's customary informality, and it hinges on her having nothing to worry about. Naze already values her and cares about her safety. They even end their meeting warning each other not to do anything to make Amida sad, indicating shared affection for Tamami's 'Big Sis'.

All this is positioned without any hint of lasciviousness. When Naze looks forward to hearing stories of Tamami's exploits over drinks later, there's apparently no expectation of anything more. I bring this up to highlight the boundaries in the Turbines' living arrangements. Naze expresses admiration for women as a category, but he's no skirt-chaser. The polygamy is not mandatory and his support and generosity are not predicated upon it.

Also, and I fully appreciate this is its own brand of male bravado, the sexual side of the Turbines is mostly described as Naze pleasing his wives rather than the other way around. The story goes out of its way to make clear how OK everyone is with the arrangement, including an obligatory 'harem strike' joke to underline that while Naze may have institutional power, they outnumber him.

It should scarcely need stating that Iron-Blooded Orphans is not depicting relationship dynamics one should aspire to. Then again, I'm posting this on the internet, where reductio ad absurdum is treated as winning, so let's state it outright: pretty much every relationship in this show is some level of borked. From Shino and Yamagi's teenage inability to communicate, to McGillis indulging Almiria's childish fantasies of adulthood within a marriage they've been forced into, to Mika and Orga's entire deal, everyone is doing the best they can while setting each other up for a lifetime of therapy they're not going to get.

The flip side of this is that those same relationships are a source of support and joy for characters experiencing extremely harsh, miserable lives. In almost every case, the toxicity is intertwined with genuine love, and for the Turbines, the toxicity gets firmly minimised, counteracted by Naze's personality and by how his wives interact with him.

I am not going to stand up and say the Turbines are a model of healthy polyamory. Being married to your boss is rarely a good thing in reality. Within the show, however. it's presented as wholly positive and supportive to a degree that the other entanglements can only aspire.

Sunset

Nothing lasts forever though. Isn't that the saying? Part reproach, part reassurance, it asserts that all is ultimately impermanent, no matter how much we might hope or fear otherwise. Orga sets his stall out in the name he gives his newly-liberated band of fighters: an iron flower, never wilting and never dying. Something impossible, that is ended prematurely by his rush to ensure its existence.

The Turbines are firmly established by the time they enter the story and as I've discussed, their rise is depicted as a cautious, time-consuming process. They have a fierce reputation – nobody messes with them, at least not without some high-ranking Earth bigwig offering plenty of money – but it's one tied to Teiwaz as a whole and that coupling of fortunes is both strength and weakness.

When the hammer comes down and Gjallarhorn begin interdicting Turbine ships, Naze wonders if McMurdo himself might be responsible. This suspicion comes after half a season of internal politics following Tekkadan's unexpectedly rapid ascent within Teiwaz. Their victories reflect well on Naze, since he brought them into the fold, but also cause the other high-ranking members to fear what they perceive to be his ambition. Things come to a head when Tekkadan align themselves with McGillis's attempt to seize power. With the youngest, upstart members of the organisation promised sovereignty of Mars (and its lucrative half-metal mining operations), a target is painted on Naze's back.

Of course, it isn't McMurdo who acts against him but Jasley, envious of Naze's position as the boss's favourite and wanting nothing more than to seize control of the transport division. There's no doubt he'd have sent the Turbines back to square one, exploiting them for his own gain. Jasley is very much in tune with the ambient misogyny and a conniving bastard to boot. He imagines by inciting Iok Kujan to destroy his rival, he will become next in line for control of Teiwaz itself.

He doesn't get away with it. The damage is done nevertheless.

When I say 'the Turbines are Tekkadan done right', it is a statement regarding success at their shared goals. Providing marginalised people with safety and security, enriching them through employment on their own terms, and establishing their long-term legitimacy – these represent the aims of both groups. The Turbines, however, achieve them at scale. Over 50,000 members! Operations from Jupiter to Venus! The ear of the head of Teiwaz! And, via groups like Tekkadan and Foundling (who Tamami is still mentoring at the point of writing; the survival chances of doofy gremlin children may go down as well as up), the opportunity to guide a new generation in a changing world.

But – and of course there's a 'but'; there was always going to be a 'but' – 'done right' does not mean 'perfect'. It does not mean 'forever'. For all the benefits the Turbines accrue for themselves, theirs is still a dangerous business. The risk may be reduced by solidarity but it doesn't go away. They still have to fight pirates and undertake jobs of dubious legality. Furthermore, as Jasley proves, they amass enemies as well as allies. Disruption to the social order creates ripples even – especially – when done with the best of intentions.

Above all, there's the question of whether their methods are sustainable. Throughout this piece, I have consciously centred Naze because that's what the Turbines' strategy is. Using him as a focal point around which to gather and an acceptable representative to men who wouldn't otherwise give them the time of day. While they might have achieved much simply by cooperating and are implied through Tamami to have retained considerable autonomy, it is Naze personally who allowed these women to escape the bottom of the heap.

This leaves them with a hideously dangerous vulnerability. The Turbines are inextricably tied to Naze's personal fortunes and those plummet in a second the instant Jasley shops him to Iok. By the rules of Teiwaz and his own sense of honour, Naze cuts ties with McMurdo to prevent Gjallarhorn pressing charges against the conglomerate. He expends all the good will he has accrued over the years to beg his now-former boss to take his people in. And then he and Amida sacrifice themselves in a nearly-vain attempt to safeguard their immediate family.

Worst of all, the catalyst for this is the very generosity of spirit that got Naze involved in the first place. He gives Tekkadan a chance and keeps doing so even as the cracks begin to show. He indulges Orga's ambitions out of the sense he's looking at his family's younger selves. As a result, he ties himself to them and is sent to his death by the wider consequences of their actions.

Amida describes Naze's love for her in terms of food: it is better to share a fine meal with others than to settle for average fare kept to yourself. That Naze was willing to share himself with so many people is laudable. But it is also his downfall and marks the harsh limitations of using the systems of the Post Disaster setting to imrpove a situation.

When you make deals with tigers, you have to remember what will happen should they get hungry.

A future even so?

Officially speaking, the Turbines end with Naze and Amida. The survivors are folded into what we might call Teiwaz-proper, directly under McMurdo's authority. When we next see them, they are clothed in drab black jackets, save for Azee who has traded her pink jumpsuit for a version of Naze's customary white suit. As the last remaining member of Amida's mobile suit squad, it seems leadership of this rebranded fleet has fallen to her, a position she uses – with McMurdo's blessing – to rescue Tekkadan's own dwindling numbers in their time of need.

Here we find the two groups paralleling one another once again. Lives are spared at the expense of identity. A leader who truly cared is lost and the outcome is decided by a pragmatist. We don't see much of what happens to the Turbines now they've been consumed by Teiwaz's male-dominated hierarchy. What we do know is that, in the short term at least, they have been forbidden from carrying weapons and doing the kind of escort work the Hammerhead excelled at. This alone marks a steep reduction in their power.

While McMurdo certainly looks favourably on his new subordinates, he is no replacement for the man who saw them as the sun. His decision to cast Jasley to the wolves was motivated as much by heading off a rival as by avenging his preferred 'son' – and he's clearly not getting any younger. One can only speculate where a few years might land everyone in this new arrangement (indeed, one has).

The Turbines' story contains remarkable achievements and at the same time showcases the fragility of any achievement made within an unjust society. It took Jasley a single phone-call to annihilate everything Naze and Amida built. Many good people died and the happiness Naze's wives found with him did not last. His children can hardly be considered orphaned but their fate is left up in the air, albeit weighted more kindly than their parents' lives began.

Which is something that should not be dismissed. Iron-Blooded Orphans reflects a lot of harsh, miserable realities about what happens to those unfavoured by the world's structures. But it refuses to downplay the steps they take towards a better future. Amida was already fighting to protect those left in the cold and Naze followed her lead. Even if the very things that enabled him to do so much eventually turned into a trap, it still matters that he did what he could. It still counts.

There may not actually be a way to 'do Tekkadan right'. Its context is flawed, harmful and frequently vile. In a just society, nobody would need the strategies the Turbines use to carve a place for themselves – there would be no ladder for anyone to fall to the bottom of. Yet in its absence, there are and have always been people who try their best to rebalance the scales, resisting the narratives they are fed in whatever ways they can. That needs to be valued. I'm glad IBO does so.

Because fleeting joy is joy all the same. Love exists under the toughest conditions. And, in the end, Azee and Eco follow the example of those who've gone before, stepping forward to ask:

How can we help?