#sum of increasing sequence

[peeterjoot]

Sum of squares and cubes, using difference calculus.

[Click here for a PDF version of this post] Motivation. I showed Karl Gauss’s trick for summing a \( 1, 2, \cdots, n \) sequence. Add it up twice, reversing the sum and adding by columns \begin{equation}\label{eqn:sumOfSquares:21} \begin{array}{c|c|c|c|c} 1 & 2 & \cdots & n-1 & n \\ n & n-1 & \cdots & 2 & 1 \end{array} \end{equation} We get \( n + 1 \), \( n \) times,…

[covn]

Tree of Void Emanation

The void of non-being emanates existence through a generative process and pattern which produces systems of increasing complexity and representative power. At the twelfth emanation we reach what is likely a limit of usefulness in balance with complexity.

Each emanation builds contains and is connected to the previous emanations. The term “sphere” is used as is common in platonic and qabalistic systems as an to reference the formative principles of each emanation. The term “path” describes the connections between the spheres.

Each sphere is counted in two ways, once by sequence starting from zero and again by prime number starting from one. Zero and one represent the identity functions of addition and multiplication. Each subsequent is then given its own sigil which is produced from merging the numeric sigils of its sequence and prime. The pronunciations of the spheres are similarly generated by combining the pronunciations of these numbers.

From this numeric skeleton the story of manifestation is developed upon it both as structured metaphor and ontological framework. Exploration of this framework reveals formulas and techniques for relating to and manipulating reality through the arts of magick.

Chaos 0⋮1 - nĕsh-hĭn - /nɛʃ.hɪn/

Existence emerges spontaneously and without reason from Void. Existence requires no reason. As the Void has no quality whatsoever it is in no way restricted making it the root generative force. This is the fundamental nature of existence. It is spontaneous and without purpose or design. All possibilities assert themselves into being at once, each becoming a “one”, a unity of existence unto itself while retaining nothing in itself.

Process 1⋮2 - hĕzh-ēsh - /hɛʒ.iʃ/

That which asserts itself into being does not exhaust possibility. Every aspect of being is incomplete, retaining its relation to void while constraining and permitting that which may follow. Each emmanation leaves space for the next emmanation so that the process may continue. All connection is made possible by what is left undetermined and reality is never fully manifest.

Pattern 2⋮3 - ēs-ŭzh - /is.ʌʒ/

As the process of manifestation proceeds the shape of the unmanifest spaces influences that which may follow. This causes patterns to arise that unify the discrete units of being. Though each is completely free and separate, they are also manifest as a unified pattern. It is precisely because of incompleteness that these units are able to also become a new unity.

Form 3⋮5 - ŭm-o͞os - /ʌm.us/

Within pattern there emerge forms defined by the pattern and yet independent within it. For example, 5 & 7 are a twin prime pair as they are both prime with a difference of 2. Other twin primes pairs include 11 & 13, 17 & 19, 29 & 31. All prime pairs greater than 3 & 5 have the property of having their sum being evenly divisible by 12. This form of a “prime pair” is well known in mathematics but primeness, divisibility, and addition were not in any way defined in order to produce this form. Number emanates the form of the prime pair. Likewise we may take nearly any game and learn its rules rather quickly, but to learn a strategy is an entirely different matter. Games like Chess or Go give rise to whole vocabularies for naming forms within them. Though the rules teach us how to play, one must become familiar with these forms to play well.

Change 4⋮7 - ăou-chăz - /aʊ̯.t͡ʃæz/

Manifestation may stop at Form to make a complete but static world. The universe of number is a perfect example of static manifestation. Alternately manifestation may remain forever in flux, manifesting and collapsing back into the unmanifest. This gives rise to time and change. Further manifestation takes on a destructive aspect as forms that were can now also cease to be. We move up a level in our analysis to describe types of change and change itself becomes a new type of form. The mathematically inclined may find it useful to meditate on the relationship of a mathematical function and its derivative.

Self 5⋮11 - o͞or-fĕm - /uɹ.fɛm/

In the flow of change through time forms emerge which influence change in order to sustain themselves. These forms are agents of change. Like the first cellular organisms self-organizing around volcanic vents on the ocean floor in the chemical soup of the earth’s ancient oceans. The basic aspect of these agents is homeostasis. These agents direct change to create a dynamic constant. As these agents guide change we may now call this activity Will. In the fullness of emanation we come to identify one of these agents with the self.

Sense 6⋮13 - jŏth-tŏi - /d͡ʒɑθ.tɔɪ/

Agents may be blind actors, no more than a self-catalyzing reaction, or the agent may develop the capability of sensing and reacting to its environment. Sense is the essential element of the encounter of that which is beyond the self. It is the beginning of external self-organization that leads to external manifestation. It is an echo of Process yielded through the incompleteness of the agent.

Thought 7⋮17 - chō-kou - /t͡ʃoʊ.kaʊ̯/

If what is sensed leaves its mark upon the agent then we find the seed for the emergence of representational systems. The agent can now experience itself in time, forming memories, and gains the ability to not just change behavior based on current circumstance but also based on past learning. These internal marks can then be sensed and manipulated and so give rise to symbol, language, and communication.

Desire 8⋮19 - ät-thĕl - /ɑt.θɛl/

Having formed memory the agent now is able to experience the external as something to be sought after or avoided. Want and fear and all the aspects of emotional attachment emerge. Desire attaches the agent to the external and so opens a channel for the external to truly manifest. It is attachment to the world that makes the world. We regard this as a positive development, an overcoming of the limited solipsistic self through desire.

Object 9⋮23 - ĕ-pĕp - /ɛ.pɛp/

Through desire the agent manifests the objectively real. The external is truly manifest beyond whatever sense, thoughts, or desires the agent may hold regarding it, so completing the self-overcoming of the agent. The objective binds the agent while also making possible the emergence of the next level of agency within objective reality. The agent has surrendered its naive omnipotence in its embrace of a new greater level of being in which it only has marginal and indirect power in exchange for a greater state of being.

Subject 10⋮29 - vŭ-sōb - /vʌ.soʊb/

The manifestation of objective reality allows the agent to itself become a manifest object. By surrendering itself into objectivity and becoming limited the agent is able to enter into a space where it can come into authentic contact with other agents manifest as other subjects. Each aspect of the agent obtains and is constrained by a physical correlation. For us humans, this is our brains. Every thought, sense element, and desire is within our brains and is lost to us with disruption of this fragile tissue.

Kia 11⋮31 - fĕ-shĕr - /fɛ.ʃɛɹ/

Kia is the void which remains within manifestation. In the twelfth tree all has manifested and yet Nothing remains. This Nothing is experienced as consciousness, free will, and ecstasy. More than that, Kia is the basis of having any experience whatsoever. All of the aspects of manifestation through the agent can carry on quite well without any conscious experience or free choice within it. In dreamless sleep and in normal waking when on auto-pilot Kia retreats. Kia manifests as the absurd, wonder, the presence of the undefined and unknown. Kia can arise in quiet contemplation, ecstatic overload, and in many ways that open the fundamental questions of being.

[rbrooksdesign]

"DMT-EDMT Series for December Geometry #21"

From another perspective...

Yesterday's post(s) (#1-20)

The Butterfly Fractal 1 (BF1) is a fractal resulting from the simple doubling of quantity "1" -- 1 -- 1x2=2 -- 1x2x2=4. -- 1x2x2x2=8, -- 1x2x2x2x2=16

When you lay it out into its "Butterfly-like" array, you can see that every "1" becomes a new source for the self-similar, re-iterative redundancy of the same "fractal" pattern within.

The BF1 pattern is repeated on both sides (of the "wings.”)

~~~~~~~~~~~~~~~~~~~

Today...

The BF1 expands to reveal the 4th "container" in the series: PN6-->PN28-->PN120-->PN496 with PN496 -- like the other two in BOLD -- being a TRUE Mp-PN pairing.

Notice how all four are within the butterfly image. PN496 with x=16 starts at the p=5th level up, with 16 RED "1s" across. Each "1" is the start of a new BF1 fractal going up 1--2--4--8--16.

The Running Sum (∑) 31 is shown at the top of each BF1 sequence. 16•31=xz=PN=496.

As the butterfly expands, both the graphic and numerical representation of the fractal quantity expands so fast that soon it becomes very difficult -- like trying to see individual stars when gazing at the larger Universe -- that we are forced to look at it summarily. The next four TRUE PNs are 8128 -- 33550336 -- 8589869056. Yet, in every case, they follow this same BF1 template! Only the numerical values increase as the template grows, AND, the history of the previous "containers" is always present within. This is true entanglement!

For those keeping track: the Mersenne Prime (Mp=z) "containers" are also historically present within the template as it grows. They are the ∑s: 1+2=3, 3+4=7. 7+8=15 and 15+16=31.

And, of course, Mp² = z² = Mersenne Prime Square (MPS) = xz +yz = PN + OC.

[genyxie]

Felt like posting my spidersona today.

Scelina Silkie SPIDERSILK

Her original design

Scelina is a 20 something, struggling, bio-chem major. To pay tuition they strip at various clubs at night time. Yeap stripper.

As a part of the experiment for their thesis on artificial mutations In the Brazilian banana spider (because they had no proper funding) they injected themself with modified gene sequencing ( or whatever smart sciency words) and went thru the usual spiderman mutation (silks words).

They did extensive testing and experiments with their new powers.

Wall climbing, increased agility, night vision/thermal vision, spider senses. Expected.

Organic web and venom production was unexpected as well as antivenom production.

Silk isn't a typical Spiderman either their kind of a antihero. The decision to become a 'hero' was accidental. At the club one night some gangster was shaking down the strippers and silk reacted without thinking (which isn't new to their sleep deprived ass) and beat them up spectacularly.

Unfortunately to prevent problems with the gang the club owner payed them a decent sum and let them go. But this sparked the idea of getting payed for helping people.

So they made a suit and went around handling bad guys and maybe extorting a small fee from victims, tuition gotta get payed am I rite?

After uni they join their first spider crew 'the fucked up spider crew' (a collection of spidersona of some of my friends in college) mostly crazy near criminal spiders

They leave that crew with one member and they end up heading a new group of more decent spider sonas the Web Warriors. (My current art friend group has like 6 spidersonas) Silk lessens the extortion and they start functioning like a real hero team, silk using their various skills to creat a front military/security company to fund their hero work

[michaelrotonal]

You demand asks, I finally muster the courage to provide:

I've thought back the the polyomino sequence question a few times, but am not sure what the actual set of all such sequences is. What is the answer?

For each individual dimension, there are three polyomino sequences: the number of free polyominoes (when reflections and rotations are all considered the same), the number of one-sided polyominoes (when rotations are considered the same but reflections aren't), and the number of fixed polyominoes (where even rotations count as different polyominoes).

The first two sequences both converge to the same sequence as dimension increases. That sequence goes 1, 1, 2, 7, 26, etc.

you mean the polyomino sum subset thing? i was kinda relying on you to figure that out

[scarabugzart]

The Fibonacci sequence was developed by the Italian mathematician, Leonardo Fibonacci, in the 13th century. The sequence of numbers, starting with zero and one, is a steadily increasing series where each number is equal to the sum of the preceding two numbers. This sequence can be seen in many natural patterns.

[collapsedsquid]

The thing about outputting a million decimal digits of π is that there’s only one way to do it right. There are unimaginably many sequences of a million decimal digits, but only one of them is the first million decimal digits of π. I believe that this property, where there are many ways to appear to have done it (by outputting a million random digits, for example), but only a very small number of ways to actually do it (by outputting the correct million digits), is characteristic of things that Generative AI systems will generally be bad at. ChatGPT works by making repeated guesses. At any given point in its attempt to generate the decimal digits of π, there are 10 digits to choose from, only one of which is the right one. The probability that it’s going to make a million correct guesses in a row is infinitesimally small, so small that we might as well call it zero. For this reason, this particular task is not one that’s well suited to this particular type of text generation. The sum-to-22 game is an example of a task with this same characteristic. At any given point in the game, there are seven possible moves, but only one of them is optimal. To win the game, it has to choose the unique optimal move every single time. I believe that this property of the task, where it needs to get every detail exactly right in exactly the right order, is just incompatible with the generative AI paradigm, which models text generation as a probabilistic guessing game. You can think of every individual word that ChatGPT generates as a little bet. To generate its output, ChatGPT makes a sequence of discrete bets about the right token to select next. It performs a lot better on tasks where each one of these bets has relatively low stakes. The overall grade that you assign to a high school essay isn’t going to hinge on any single word, so at any point in the sequence of bets for this task, the stakes are low. If it happens to generate a weird word at any point, which it probably will, it can recover later. No single suboptimal word will ruin the essay. For tasks where betting correctly most of the time can satisfy the criteria most of the time, ChatGPT’s going to be okay most of the time. This contrasts sharply with the problems of printing digits of π or playing the sum-to-22 game optimally: in those tasks, a single incorrect bet damns the whole output, and ChatGPT is bound to make at least a few bad bets over the course of a whole conversation. We can see this same pattern in other generative AI systems as well, where the system seems to perform well if the success criteria are quite general, but increasing specificity causes failures. There are a lot of ways to generate an image that looks like a bunch of elephants hanging out at the beach. Only a tiny fraction of those hypothetical images contain exactly seven elephants. So generating exactly seven elephants is something that a Generative AI system is going to have a hard time doing.

[floralfractals]

I don't know anything about measure theory, re: f(x)=x on [0,1], what's the deal with integration?

ohh well i guess i did kinda say that without explaining huh. let me elaborate

measure theory is all about sizes of sets, in a generalisation-of-probability-way. the probability of event A is 0.5, the probability of event B is 0.8, the total probability (of any outcome happening at all) is 1. or the measure of set C is 2, the measure of set D is 0.002, the total measure (of the ambient space) is infinity. whatever.

but what is integration if not calculating the space under a curve? is that not dependent of the measures of the sets underneath them?

lets first talk about "regular" (Riemann) integration. basically, suppose you have a function f: R -> R. it has some kind of fun graph, and youd like to find the surface between the graph and the x-axis. one way to do that is by approximation through rectangles. yknow, draw some rectangles of fixed width, put their heights either just under or just above the graph of f, add up their surface areas and bam! you have a numerical method of approximating the integral. or you could make the rectangle width smaller and smaller for exact results. thats integration. heres a visual.

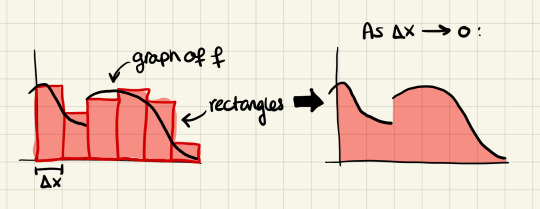
ok cool so problem solved right? we know the area under the graph? surely this holds for every function?

well, no. suppose we have a really fucked up function. for example, let f(x) be equal to 1 if x is rational, and 0 otherwise. the above method wont be able to determine if the area is 0 or infinity, or something in between!

thats where measure theory comes in. we give sets a measure (notation: m(A)). this measure is not negative, and if you take the measure of two sets that dont overlap with each other, then their measure is the sum of their separate measures (in notation: m(A ∪ B) = m(A) + m(B) if A and B are disjoint. this is called sigma-additivity (the sigma means that it works for countable infinitly many sets as well)). easy! now we can define something called the indicator function 1_A(x), which is 1 if x is in A and 0 otherwise, and we define its (Lebesgue) integral to be ∫ 1_A dm = m(A). usual linearity applies for finite sums (so if a and b are numbers, and f and g are functions, then ∫ af + bg dm = a ∫ f dm + b ∫ g dm) (wacky things happen when sums are infinite: they might become infinitely large, or infinitely negative, or not converge at all).

this solves the issue of our crazy function f we just defined: notice that f(x) = 1_Q(x), where Q is the set of rational numbers. thus, ∫ f dm = m(Q), which (in one of the most natural measures, called the lebesgue measure*) is zero. done!

now for your question. the function f(x) = x on [0,1] (for our purposes: f(x) = x if x is in [0,1], and zero otherwise) cant be written as a finite sum of indicator functions. that means that our newly defined Lebesgue integral wont do without a bit of work. as it turns out, we can take limits in the Lebesgue integral, as long as our sequences increase (in math notation: if (f_n)_n is an increasing sequence with limit f, then lim_{n -> ∞} ∫ f_n dm = ∫ f dm). thus, we need to find such a sequence.

it's probably best if all functions in our sequence are finite sums of indicator functions, since we know how to integrate them. one such sequence with limit f is given by f_n = Σ_{k=0}^{n-1} k/n 1_{[k/n, (k+1)/n]}. that looks kinda scary, but if we let n go to infinity, this turns out to be equal to f almost everywhere (some points are counted twice since the intervals [k/n, (k+1)/n] and [(k+1)/n, (k+2)/n] have some overlap, namely {(k+1)/n}, but we dont need to worry about that since m({(k+1)/n}) = 0). heres another visual.

as you can see, though, when we go from f_2 to f_3 we have some parts that increase and some that decrease. that sucks because now our limit trick wont work! to solve this, notice we dont have that issue when we go from f_2 to f_4, or from f_4 to f_8. thus, the sequence (f_{2^n})_n would work, since its limit is also f!

now we can do a big calculation. please bear with me (its just this paragraph i swear)! we have ∫ f dm = lim_{n -> ∞} ∫ f_{2^n} dm, so lets solve ∫ f_n dm for any n first. we have ∫ f_n dm = Σ_{k=0}^{n-1} k/n m([k/n, (k+1)/n]) = Σ_{k=0}^{n-1} k/n^2 = (n-1)(n-2)/2n^2. we can work with that, so were ready to take the limit: lim_{n -> ∞} ∫ f_{2^n} dm = lim_{n -> ∞} (2^n-1)(2^n-2)/2(2^n)^2. that looks scary, but luckily its equal to the slightly less scary lim_{n -> ∞} (n-1)(n-2)/2n^2, and thats just 1/2.

therefore, ∫ f dm = 1/2. which is also the value of the riemann integral ∫ f(x) dx, by the way.

you see that we needed a lot of calculations, so its probably not surprising that i needed an entire whiteboard to do this.

maybe this would make you think that lebesgue integration is inferior to riemann integration. however, as it turns out, most applications of this rely on proving that a lebesgue integral ∫ f dm is equal to some riemann integral ∫ g(x) dx, and we can just solve that with our calculus skills.

also, since the integral relies on a measure, we can do some silly shenanigans with that. for example, the ergodic probability measure related to my sickly son (lets call it n to avoid confusion with our earlier measure m) has n([0,1]) = 1/2, and n([1,2]) = 1/4 (in general, n([k-1, k]) = 1/2^k). i used this in my thesis to integrate the function floor(x): turns out that ∫ floor dm is infinite, but ∫ floor dn = 4 :)

hope you enjoyed doing some measure theory with me :>

*: the lebesgue measure is probably one of the more intuitive measures. an interval [a, b] has lebesgue measure b - a, so m([0,1]) = 1. this also means that a single point has measure m({x}) = x - x = 0, and a countable union of singletons (like Q) therefore also has measure m(Q) = 0. however simple this measure is, it also gives rise to some wacky crazy properties! for example, there exist sets that cant have a measure, but you can only construct them using the axiom of choice. scary!

[mceproductions]

Best of 2024 Movies #1: Dune: Part Two

Masterstrokes can be rare, more so with movies. But by all counts Denis Villenuve took what many called an unfilmable novel and gave us one of the best film series of the last 5 years.

Dune Part Two picks up where the first leaves off as Paul Atredies and his mom Lady Jessica begin to ingrain themselves within the Freemen lifestyle on Arakis.

Paul getting closer with Chani, and Jessica beginning to see Stilgars mindset when it comes to the bigger picture all the while with her growing daughter beginning to see the same, if not darker picture.

On the other front Irulan, daughter of the emperor sees truth behind the demise of House Atredies and the Harkonens see a new more sadistic player enter the fray.

All would set the stage for a struggle for the spice that would change more than their eye colors.

Three years ago, I mentioned that Timothée Chalamet and Zendaya got the short end of the stick when it came to part ones action.

Both are front and center here as Paul’s journey to become something different than what’s expected of him, and Chani’s own connection to what she grew up with being essentially wiped away carries the long runtime.

As well as great turns by Florence Pugh as Irulan, Austin Butler as chilling Harkonen warrior Feyd-Ratha (originally played in infamy by Sting) and Christopher Walken as the emperor.

What also makes this the years best is with the visuals that we only got glimpses of in Part One, that would get turned up for maximum effect in the final battle sequence.

And although a certain character was relegated to a vision cameo to keep the story tight paced the stakes have definitely increased for the Dune Saga.

Though it stinks, and likely will only be a trilogy other than the great Max series Dune Prophecy.

Messiah although light in moments (proven by the 21 year old miniseries version) should be just as epic.

SUM 22: Delayed by the strike didn’t deter momentum for the 2nd part of Dune as its visuals alone earn it 2024s Best Movie.

[boscoebros]

The Charm of Northern Exposure, Summed Up in 10 Episodes

Plucking out individual best episodes of Northern Exposure is like ranking individual cups pulled from the same expertly spiked punch. It’s not impossible to do, it just feels not in the spirit of the gift you’ve been given or the eccentrically twinkling host who’s presented it to you.

Of course, Northern Exposure, the tale of petulant young New York Jewish doctor Joel Fleischman (Rob Morrow) sent against his will to the beyond-tiny town of Cicely, Alaska as payment for his med school debts, has its odd sour draught or two during its six-seasons.

Quirk can turn twee with just a single wrong step. From the start, the series, created by St. Elsewhere vets Joshua Brand and John Falsey (with executive production help by future Sopranos don David Chase) presented unsuspecting CBS viewers with a much headier and more ambitious formula than its fish-out-of-water premise suggested. That degree of difficulty, which only increased in each of the series’s six seasons, meant taking big creative swings.

The town of Cicely was quickly established as a haven for eccentrics of all stripes, from frostbitten locals with colorful backwoods backstories to transplants in various stages of flight; from old lives too fraught or too comfortably suburban for their liking, to the region’s Native population, whose culture and individuality were allowed far more complexity than on any American TV show at the time.

Installed in a crumbling storefront office with a largely monosyllabic Native receptionist named Marilyn Whirlwind (stealth series MVP Elaine Miles), the constantly kvetching Joel immediately began sparring with Maggie O’Connell (Janine Turner), the equally combative bush pilot (and Joel’s unimpressed landlord) in the sort of will-they/won’t-they relationship that, like Joel’s predicament, gradually receded in favor of fleshing out the series’s roster of singular figures.

Roaring over the town was Barry Corbin’s barrel-chested Maurice Minnifield, a former Oklahoma astronaut, millionaire, and bona fide American man’s man drawn to the untamed tundra as blank slate for his singular vision of an “Alaskan Riviera” hewn in his own stubborn image. Greeting the irascible Joel were everyone from a legendary sexagenarian animal trapper turned (mostly) pacifist barkeep, Holling Vincoeur (John Cullum) and his spacey but worldly 18-year-old former beauty pageant girlfriend Shelley (Cynthia Geary); aged and resolutely sensible town shopkeep, postmistress, and all-purpose town official Ruth-Anne (Peg Phillips); philosophizing ex-con turned all-day radio DJ Chris (John Corbett); and perpetually amiable half-Indian teen and aspiring filmmaker Ed Chigliak (Darren E. Burrows).

As the series progressed, Joel’s predicament persisted (he’d essentially been dragooned into Cicely by Maurice over his expected post in an Anchorage hospital) but sank back into ensemble status, with each character in turn bobbing up to take the show’s delightfully unpredictable center stage. (Whether due to his diminished role or contract disputes, Morrow chafed in his first series lead, eventually leaving partway through the sixth and final season.)

New oddballs emerged to fill out Cicely’s ranks: Adam Arkin’s mysteriously obnoxious master chef/mountain man Adam and his heiress hypochondriac wife Eve (Valerie Mahaffey), Anthony Edward’s bubble-bound lawyer Mike Monroe, fled to Alaska ahead of encroaching environmental allergies, Graham Greene’s Native medicine man and artist Leonard, Richard Cummings’ Bernard, revealed as Chris’ long lost Black half brother, and sharing the pair’s preternatural psychic bond.

Throughout it all, Falsey and Brand steered Northern Exposure according to their own set of wide-open, anything goes constellations. Dream sequences, strange local traditions and superstitions (Maggie’s old lovers have all died in unusual circumstances), singular personal obsessions and quests — anything could happen in Cicely. And, with astounding reliability, the results were as warm, weird, and welcoming as the people of Cicely themselves.

With the series at long last available to stream (all six seasons are on Prime Video), we’ve put together a list of 10 favorite episodes drawn from Northern Exposure’s heady brew of comedy, drama, and enduring whimsy, in broadcast order. Drink up.

"Aurora Borealis: A Fairy Tale for Big People" (Season 1, Episode 8)

By the time this first season finale aired, it was already crystal clear that Cicely didn’t need any outside help in the strangeness department. That doesn’t stop a massive full moon and the appearance of the shimmering-with-portent northern lights from putting a double-whammy on the town’s inhabitants. Some can’t sleep, others are drawn on mysterious walkabouts, and a confused, citified accountant from Portland shows up on a brand new Harley and immediately latches onto Chris’ barroom talk of the collective unconscious, with the mismatched pair gradually realizing that they share the same absent father.Northern Exposure tosses a lot into each episode’s hearty stew, and this was one of the first episodes to find the perfect balance of soulfulness, incident, and knockabout comedy.

"The Big Kiss" (Season 2, Episode 2)

Darren E. Burrows (son of perennial B-movie bad guy Billy Drago) is Cicely’s most endearing figure as Ed Chigliak, a patiently unassuming and guileless presence whose clouded backstory as a half-Native, half-white foundling the would-be Scorsese accepts from his tribal elders with typical resignation. At least until a 256-year-old Native spirit guide named One Who Waits (legendary character actor Floyd Red Crow Westerman) appears to no one but him and tells Ed he might just have a bead on the identities of Ed’s parents.

It’s to Northern Exposure’s credit that we can accept the reality of the delightfully deadpan One Who Waits, or not. But Ed’s ultimately fruitless journey is as resonant either way, his rapport with the old ghost registering in Burrows’ performance with aching sincerity and sweetness. One Who Waits would return in Season 4, and Westerman is always a gift, but that episode’s more concrete conclusion to Ed’s story pales next to the lovely ambiguity of his roadside encounter with a friendly older Native man in “The Big Kiss.”

"War and Peace" (Season 2, Episode 6)

While Northern Exposure would stretch its woozy reality in all manner of ways throughout its run, it never did so as straightforwardly or delightfully than in this tale of a famed Russian singer Nikolai Ivanovich Appollanov (Elya Baskin) whose intermittent appearances in Cicely are greeted with delight by everyone — except the Cold War patriotic Maurice. Challenged to renew their one-sided chess rivalry, perennial loser Maurice accuses the gentlemanly Russian of cheating, leading to a duel where the series’s typical spell of whimsical benevolence seems headed for inevitable, bloody disaster. Meanwhile, Ed’s first love with a randy preacher’s daughter sees the heartstruck teen turning to ladies man Chris for some Cyrano-style flowery prose, with similarly doomed results.

That both stories turn out unexpectedly more or less okay is a relief, although Ed’s heartbroken confrontation with the contrite and more worldly Chris is about as emotionally rough as Ed gets. The series decided not to spoil things, a decision that was as cheeky as it was refreshingly necessary to a viewing public mired in coverage of another needless overseas war.

"A-Hunting We Will Go" (Season 3, Episode 8)

Northern Exposure’s ostensible lead was one the series’ least successful elements, oddly. Joel’s incessant complaining about his plight might have been understandable, but Morrow struggled with the show’s often inconsistent treatment of the New Yorker’s wavering integration into Cicely’s mix. (The number of times Joel’s episode-ending epiphanies plop him right back into crabapple first position for the next are too numerous to list.) Still, when the show gets the ultra-rational Joel right, it really gets him right, as in this outing where the city boy feels duty-bound to test out his visceral revulsion against the locals’ offhand love of hunting.

Joel goes on the offensive about the “barbaric” bloodsport, only to accept Maggie’s challenge that, without experiencing the phenomenon himself, he’s just blowing hot air. Joining veteran hunters Holling and Chris on a grouse hunt brings Joel unexpected (and long-winded) elation—and then a huge comedown when he comes across the wounded bird he’d only managed to wing. Themes permeate the best Northern Exposure episodes in the slyest of ways. As Joel desperately tries to heal his victim, Ed becomes similarly protective of Ruth-Anne upon learning of her recent 75th birthday. IN the end, both men resign themselves to death’s looming and necessary presence in their own way, with Joel confiding to Maggie how death and killing are two very different things and Ed’s surprise gift to Ruth-Anne seeing the two literally dancing on her grave.

"Burning Down the House" (Season 3, Episode 14)

Opposing forces meet more often than Cicely’s benign exterior suggests, with this third-season installment proving that a community packed with dreamers will occasionally spit out some darker fancies.

When Chris builds a catapult in order to “fling” a live cow in order to create what he terms a “perfect moment,” only Joel objects, the rest of Cicely regarding the stunt with idle curiosity. (After all, as Marilyn states, they’re going to eat the cow.) Throughout the series, this undercurrent of eccentricity edging into rustic anarchy runs through Cicely—it’s like they’re one rough winter away from stuffing Joel into a wicker man. Here, the unfortunate cow is only saved via an artistic quandary, not a moral one, as Ed accidentally reveals how the whole cow-flinging concept has been done in one particular movie. Chris adjusts to a less-lethal concept, with the resulting fling filling the assembled townsfolk (and viewers) with suitably collective awe.

“Three Amigos” (Season 3, Episode 16)

The bond between former astronaut and American hero Maurice Minnifield and legendary game hunter Holling Vincoeur gets the rough and tumble outdoor adventure tale it deserves in this episode where the two old friends and romantic rivals strike out into the wilderness to fulfill the last wish of an old friend. Pros Barry Corbin and John Cullum had career-best roles on Northern Exposure, and they’re never better than here, as the two aging tough guys brave impossible weather and their own aging bodies to bury wild Bill Haney, their longtime drinking, hunting, and brawling buddy at the legendarily treacherous No-Name Point.

Portrayed often as two distinct but similar examples of a dying breed of masculinity, both men ultimately have to concede that dying for your word might not be all it's cracked up to be, especially for two old men with warm beds and, in Holling’s case, Shelly to return to. Willie Nelson on the soundtrack singing “Hands on the Wheel” over scenes the boys’ game attempts to honor an old promise signals an elegiac farewell to an old way of life.

"Cicely" (Season 3, Episode 23)

With its season order expanded after two short first go-rounds, Season 3 gave Northern Exposure even more territory to explore stylistically. A flashback episode might not sound groundbreaking, but this tale of the founding of Cicely reframes everything we thought we knew about Alaska’s most eccentric town, all while lending unexpected insight into its denizens, all of whom pop up in different roles in the reminiscences of a 108-year-old man (veteran actor Roberts Blossom) who Joel accidentally hits with his pickup.

Brought to Joel’s cabin for treatment, the old man spins a yarn about the town’s eventual founders, a pair of lesbian free-thinkers named Jo and Cicely (Jo Anderson and Yvonne Suhor) who fled polite Montana society to create a matriarchal utopia right in the dangerously lawless heart of untamed Alaska. The story of the rough-and-tumble Jo and the delicate Cicely plays out with the tragic heroism of two such forward-thinking (gay, female) dreamers. The town is turned around and only a stray bullet (and some “kill your gays” TV tradition) prevents a completely happy ending. Still, as Joel drops the old man at the graveyard where he’s come to honor Cicely’s 100th birthday, Cicely, Alaska comes that much further into focus.

"Thanksgiving" (Season 4, Episode 8)

The Native population of Northern Exposure is an integral part of the show’s melting pot of oddballs, but this eventful episode adds a needed dose of spice surrounding the outwardly ordinary Indian citizens’ existence in a colonized America. Walking to work, Joel is ambushed with a tomato hurled by the friendly Ed, introducing the yearly tradition by which Cicely’s native population takes out centuries of otherwise sublimated anger and resentment in a symbolically messy assault on the town’s white people.

While the rest of Cicely’s white folks uncomplainingly accept this once a year pelting, Joel complains to Marilyn that his status as a perpetually oppressed Jew should exempt him from the Native’s wrath. It’s when he sinks into an even more miserable than usual depression upon being informed that his intended four-year sentence as Cicely’s general practitioner has been (thanks to inflation) upped another year that Marilyn finally recognizes Joel’s kinship with the town’s Natives.

Listening to the bereft and unshaven doctor’s fetal position lament about his complete and utter lack of hope, Marilyn tells Joel he can now march in the Native’s day of the dead parade. “You’re not white anymore,” coming from the no-bullshit Marilyn, lands with unexpected force on Joel, and us. The people of Cicely, in their insularity, are free to process generations of racial and personal trauma in their own unique manner, and as the whole town, Indian and white, gathers at The Brick for a sumptuous post-parade Thanksgiving feast, Joel is free to complain to the face-painted Ed about his own misfortune in strangely liberating kinship.

"Mister Sandman" (Season 5, Episode 12)

The northern lights are back and everyone’s having each other’s dreams. What sounds like a high-concept lark turns typically thought-provoking and stubbornly resonant, as Maggie jumps into Holling’s revelatory dreams about his horrible, abusive father, Joel sleepwalks into Ruth-Anne’s store with a little boy’s thwarted dreams about bottomless candy, and Maurice becomes incensed when one of a pair of gay B&B proprietors (Doug Ballard’s Ron) discovers Maurice’s secret dreams involving women’s shoes.

There’s plenty to unpack, as with most dreams, and there are laughs aplenty around the margins. But it’s in the townsfolk’s variously grudging willingness to accept that their unpredictable home has yet another metaphysical trick up its sleeve that “Mister Sandman” achieves surprising depth. Holling has long decried his French-Canadian lineage’s legacy of awful behavior, here evincing a revulsion to food tied both to Shelly’s pregnancy and his repressed memories of his mother and father. And Maurice, whose bluff, all-purpose bigotry is never quite offset by his old school macho act, gets into a truly ugly poker table confrontation with Ron and his partner Erick (Don R. McManus) stemming from what he considers these “deviants’” insight into his private thoughts.It’s up to the sage Ruth-Anne to have some frank talk with Maurice about his bigotry, and Joel to overcome his usual skepticism when he sees that Maggie’s recounting of her dream actually assists in treating the despondent Holling.

"The Quest" (Season 6, Episode 15)

Rob Morrow’s desire to leave Northern Exposure (he’d already filmed Robert Redford’s Quiz Show during Season 5) is given a typically strange payoff in his final season fantasy/dream/who-knows final outing. After Joel and Maggie’s on-and-off romance sputtered one too many times, the perpetually disgruntled Joel had left Cicely some episodes earlier, going AWOL on his debts and setting himself up as the GP of an even more upriver Native village. Unexpectedly arriving in the middle of the night at Maggie’s house, the shaggy and wild-eyed doctor unfurls an ancient trapper’s map, claiming to have uncovered the location of the mythical lost city of Kiwa’ani and asking for Maggie to fly him the first leg of his trip to find this magical “jeweled city.”

As far as goodbyes to disgruntled stars go, “The Quest” is a confoundingly thorny metaphysical flight of fancy. With the skeptical Maggie in tow, the obsessed Joel first encounters one of those elderly Japanese soldiers still fighting WWII (and is repaid for his ensuing medical treatment with a bounty of sushi), almost gets sidetracked in an impossible, dreamlike spa in the middle of the Alaskan nowhere, and finally coming across an incongruously locked chain-link bridge fence and the abusive gatekeeper (who looks suspiciously identical to Adam) demanding the answer to an impossible riddle. Joel answers and spies the glittering skyline of his beloved Manhattan in the mists—and he walks into it, and out of Northern Exposure forever.

Is the episode something of a make-the-best-of-it exercise? Maybe. But it’s a great one, perfectly in keeping with the series’ spirit. As Marilyn sense Joel’s departure with a signature, unreadable “Good bye” back in Cicely and Maggie receives a days-later postcard of the Staten Island ferry from Joel reading “New York is a state of mind,” “The Quest” stretches Northern Exposure’s woozy reality to its breaking point while still slotting comfortably—and touchingly — into the show’s world in as satisfying a way as could be hoped.

~ Dennis Perkins || Primetimer

[arithmographia]

Arithmetic Density and Related Concepts

I. Counting Arithmetic Progressions

Given an arbitrary increasing sequence of positive integers S there is associated with it, a counting function alpha_S(n) which determines the number of arithmetic progressions [1] up to s(n) in S. The counting function for the positive integers, and consequently all infinite ­؜arithmetic progressions, is given by the formula listed under A330285 (OEIS) [2] :

Sum_{k=1..n} Sum_{j=1..k} floor((k - 1)/(j + 1)).

We may further generalize from this "AP"  counting function, alpha_Z^+(n), all other functions which count progressions over integer sequences via the equation

alpha_S(n) = Sum_{k=1..n} alpha_Z^+(k)*pi(n, k)

where pi(n, k) is the number of primitive arithmetic progressions of length k up to the n-th element of S.

***** A primitive progression is any subset {s, s + d, ... , s + (k - 1)d} of {s(1), s(2), ... , s(n)} such that {s - d, s + kd} are not in {s(1), s(2), ... , s(n)}, and {s, s + d, ... , s + (k - 1)d} is not a subset of {s', s' + d', ... , s' + (j - 1)d'} for j >= k - 1 and d' < d.

II. Relative Arithmetic Density

There are two other uses for our counting function over the positive integers which will be discussed in both this section as well as the following section. The first application involves computing the relative arithmetic density of our sequence S, but before we begin it is necessary to elaborate on the definition of partial densities.

***** Let us consider the fact that the number of progressions up to s(n) is merely a fraction of all subsequences over the given interval. The partial density D_S(n) therefore is equal to

alpha_S(n)/(2^n - T(n) - 1)

where T(n) is the n-th triangular number and the denominator counts subsequences of length three or greater. The infinite sum of partial densities over Z^+ is approximately 2.8956356243, and will be referred to as Layman's constant [3]. The exact value of the infinite series of partial densities requires further analysis, in the meantime we can still use Layman's constant to construct a definition for relative densities in general by comparing arbitrary number sequences with the positive integers themselves. The relative arithmetic density D(S) can thus be defined

(Sum_{n >= 1} D_S(n))/(Sum_{n >= 1} D_Z^+(n))

which is always some positive value less than or equal to one.

III. Natural Arithmetic Density

The second use for our AP counting functions involves a more naturalistic interpretation of arithmetic density, as far as real number valuations are concerned. We can arrive at such a definition by taking advantage of the fact that the counting function for any infinite progression has maximal growth. It then becomes an arbitrary choice of which complementary sequence we might use to construct a suitable infinite series for our valuation.

***** The author has chosen the sequence of factorials because firstly they converge for all AP counting functions, and secondly because they allow for more convenient algebraic analysis. The formula for the natural arithmetic density of S is thus defined as

delta(S) = Sum_{n >= 1} alpha_S(n)/(n - 1)!.

This series is approximately 1.4263891989 when the counting function is taken over any infinite progression. For the case when there is only one progression of length three at the beginning of a given sequence, the series above is equal to e - 2.

IV. The Partitional Convergence Theorem

***** (i) Proof of the theorem.

Assuming the infinite series

Sum_{n >= 1} 1/s(n) = oo,

then there exists some subsequence {s'(1), s'(2), ... } for which

Sum_{k=n(1)..n(1)} 1/s(k) < Sum_{k=n(1) + 1..n(2)} 1/s(k) < Sum_{k=n(2) + 1..n(3)} 1/s(k) < ...

and

Sum_{k=n(1)..n(1)} 1/s(k) > Sum_{k=n(1) + 1..n(2) - 1} 1/s(k) > Sum_{k=n(2) + 1..n(3) - 1} > ...

where n(1) = 1, s'(m) = s(n(m)). We can deduce that this sequence of finite series must be constructable, otherwise the infinite sum of reciprocals would not diverge. What is not immediately evident, however, is that each of these finite series should converge to the same value from below. We denote this divergence constant as C, and we will further expand on its significance in the following subsection.

***** In order to establish our proof, let us first draw our attention to the terminal values at the end of each finite series. Without the addition of these single terms, any particular series falls short of those before it according to the second inequality above. Therefore, if all of the finite series are to diverge from any particular constant, that would imply each terminal value is greater than the previous one, or 1/s'(m) < 1/s'(m + 1). This cannot be the case since our infinite subsequence is monotonically increasing, and so its reciprocal elements must tend toward zero. As an example of the proof, let it be noted that the divergence constant for the harmonic series is log(3).

***** Before leaving the present topic, there are two other constants which should be briefly discussed for future reference. These are the criticality constant kappa, and the co-criticality constant kappa'. We can calculate them using the two infinite series

Sum_{m >= 1} 1/n(m)

and

Sum_{m >= 1} 1/s'(m),

respectively. In the case when S = Z^+ these two constants are equal, and their value is

Sum_{m >= 1} 2/(3^m - 1) = 2(log(3/2) - Digamma_1/3(1))/log(3)

where Digamma_q() is the q-digamma function [4].

***** (ii) Alternative representation of divergent series.

A further consequence of the theorem is that partial sums of divergent series can now be represented using the divergence constant mentioned above. To do so requires the introduction of an error function which adjusts the constant according to the interval over which the function is taken, i.e.

Sum_{k=n(m - 1) + 1..n(m)} 1/s(k) = C - Err(m).

According to this definition, it follows that the partial sum up to s'(m) is given by the formula

Sum_{k=1..n(m)} 1/s(k) = C*m - Sum_{k=1..m} Err(k).

We can then expand upon this equation by introducing balancing coefficients beta(m, k), such that n(m - 1) - 1 <= k <= n(m), which allow us to compute partial sums over the m-th interval {s(n(m - 1) + 1), s(n(m - 1) + 2), ... , s(n(m)). These are implemented in the following manner

C*beta(m, k) - Err(m) = Sum_{j=n(m - 1) + 1..k} 1/s(j)

which implies

C*Sum_{j=1..BDiff(n(m)) - 1} beta(m, j) - (BDiff(n(m)) - 1)*Err(m) = Sum_{k=n(m - 1) + 1..n(m)} Sum_{j=1..BDiff(n(m)) - 1} (BDiff(n(m)) - j)/s(k)

where BDiff() is the backward difference operator [5].

***** REFERENCES

[1] Weisstein, Eric W. "Arithmetic Progression." From Mathworld--A Wolfram web resource. (http://mathworld.wolfram.com/ArithmeticProgression.html)

[2] "A330285." The On-Line Encyclopedia of Integer Sequences. (http://oeis.org/A330285)

[3] "A051336." The On-Line Encyclopedia of Integer Sequences.

[4] Weisstein, Eric W. "q-Polygamma Function." From Mathworld--A Wolfram web resource. (http://mathworld.wolfram.com/q-PolygammaFunction.html)

[5] Weisstein, Eric W. "Backward Difference." From Mathworld--A Wolfram web resource. (http://mathworld.wolfram.com/BackwardDifference.html)

[rbrooksdesign]

"tDMT-#8" digital, Sept. 2024, Reginald Brooks

The original DMT (Divisor Matrix Table) reveals ALL natural numbers and their divisors.

The Mp-PNs are the rarest gems of the Primes!

So why think of entanglement: time, temperature and entropy? Here is my take:

BF1 schematic

|||||||||| ||||||||

|||| ||||

|| ||

| |

|

The Butterfly Fractal 1 (BF1) that heads up Row 1 of the DMT or tDMT is: 1--2--4--8--16---...

Starting with 1: zero time, temp and entropy (disorder)

Next, this doubles to 2: the clock starts (time) and the first temp. begins, as does slightly less order -- as we now have 3, the original 1 + 2 = Running Sum (∑).

Double that to give 4: the clock moves even more, a little faster to give more temp and, again, even more disorder than before -- as ∑=1+2+4=7.

Double that to give 8: now we are ticking, heating up, and the entropic disorder is increasing -- as ∑=1+2+4+8=15.

Double that to give 16: faster clock, greater temp. and entropy -- as ∑=1+2+4+8+16=31, and so on.

As the SpaceTime (ST) pulses into-out of--into--out of existence -- with each pulse generated by the BF1 pulse sequence -- a rhythmic beat of formation, dissolution, formation dissolution starts the clock, heat build (reflecting the energy born) and it goes from the perfect order of 1 to lesser 2 to lesser 4 to lesser 8, 16,...

The BF1 is a fractal as it both expands, interconnects and becomes entangled with other pulse-propagating STs forming, and, within itself, it contains the same BF1 fractal pattern and infinite number of times. One can see this in the above BF1 schematic -- the original 1-2-4-8... pattern is repeated twice on the second line up from the bottom with each | now informing the lines above it in the same fractal sequence of 1-2-4-8. On the third line up from the bottom, the fractal is repeated four times. On the fourth, it is repeated 8 times -- one for each |.

Each bit of ST pulse-propagates at a frequency that represents its energy signature and all is within the Conservation Laws of (mass), momentum, charge, energy and, of course, ST.

The entanglement -- the quantum entanglement -- is at the heart of the Conservation Laws.

I believe this jives with Einstein's comment that the perception of a past, present and future is an illusion completely dependent upon one's particular and relative point of observation within the overall pulse-propagation of ST.

Interactive DMT and tDMT for TES (Teachers, Educators and Students) ---here.

[mathlearningjourney]

My Math 3 Fourth Quarter Learning

Hello again! In this blog, I’ll be reflecting on my Math 3 Fourth Quarter learning journey! This time, we explored Sequences and Series, including Arithmetic Sequences, Geometric Sequences, and the Binomial Theorem. It was a mix of challenging and satisfying moment but overall, I enjoyed seeing how everything was connected.

❔How would you describe your Math 3 Fourth Quarter learning journey?

It was a little bit easy, but I had some trouble with Pascal’s Triangle. Some concepts felt familiar and smooth, while others—especially the Binomial Theorem—required more focus and practice.

❔Which topic did you find most enjoyable? What made it enjoyable for you?

The most enjoyable topic for me was Arithmetic Sequences. I liked how it had a simple and formula:

aₙ = a₁ + (n - 1)d

It felt easy because I just had to plug in the values and solve. It gave me confidence because it was consistent and easy to follow. Even solving for missing terms or the number of terms in a sequence was fun!

❔What concepts did you find easy to learn?

I found both Arithmetic and Geometric Sequences pretty easy to learn, especially once I understood their formulas. You just had to input the values:

aₙ = a₁ + (n - 1)d aₙ = a₁ × rⁿ⁻¹

Also, identifying whether a sequence was increasing or decreasing based on the common ratio was very straightforward.

❔What concepts did you find most interesting or inspiring?

The most interesting concept for me was definitely the Binomial Theorem. It felt very "math-magical" how you could expand something like (a + b)ⁿ using a formula and patterns from Pascal’s Triangle. Even though it was harder than the others, I liked how it brought together exponents, combinations, and patterns.

It made me realize how beautiful and organized math can be when you look closely.

❔What concepts have you mastered most?

I’ve definitely mastered Arithmetic Sequences the most. After doing lots of practice problems and understanding the formula clearly, I feel very confident using it. I can solve for any term, find the common difference, and even compute the sum of terms without much confusion.

❔What concepts have you mastered the least?

Honestly, the Binomial Theorem is still a bit tricky for me. I mean, I kind of get Pascal’s Triangle... but. I still need more practice to feel more comfortable with it. It is also very long.

❔Have you developed a better appreciation for mathematics?

Yes, I think I have! This quarter helped me appreciate math. I also learned that even if something is hard at first, I can improve with effort and practice.

📝 Quick Notes:

To my teacher: Thank you for explaining each step clearly and giving us time to practice. You helped me stay motivated even when I got stuck.

To my classmates: Congrats on finishing Math 3! Continue striving for great things in the future.

To myself:

Practice makes perfect.

🌈 Final Reflection

This quarter showed me that math has a rhythm and structure that you can learn to follow. Some topics were tricky, but every small improvement felt like a win. I’m proud of what I’ve learned and excited to keep improving in the next chapter of my math journey.

Thanks for reading! :D

[digitalwork45]

Matka Game: A Thrilling Betting Experience That Captivates Millions

The Matka game is a time-honored tradition in the world of betting, with roots dating back to the 1950s in India. It has become one of the most popular forms of gambling, not only in India but also in many other countries. The game is based on number predictions, where players try to guess the right combinations of numbers to win substantial amounts. Whether you are a beginner or an experienced player, the Matka game offers an exciting experience that combines luck, strategy, and skill. In this article, we will explore what the Matka game is, how it works, its history, and tips on how to play it effectively.

What is the Matka Game?

Matka is a number-based betting game where players predict the outcome of a series of numbers drawn in a specific sequence. The game is often referred to as "Matka game " or "Matka betting." It is typically played by selecting a combination of numbers from a predefined set and betting on the outcome. The objective of the game is to guess the correct numbers and win the round.

The term "Matka" itself comes from the large earthen pot traditionally used to hold the slips with numbers during the game's early days. While modern technology has taken over, the name Matka has remained synonymous with this thrilling betting game.

The History of Matka Game

The origins of the Matka game can be traced back to the 1950s in Mumbai (then Bombay), India. It began as a form of lottery, with people betting on the opening and closing rates of cotton traded on the New York Cotton Exchange. Over time, the game evolved into a popular form of gambling, and numbers were drawn from the "Matka" (a clay pot), making it more accessible to the general public.

As the game grew in popularity, several variations of Matka emerged. The game underwent changes, and players started betting on different combinations of numbers, which increased the excitement and complexity of the game. Today, Matka is played in various formats and can be found on both offline and online platforms, making it a global phenomenon.

How Does the Matka Game Work?

The Matka game involves the selection of three numbers, typically ranging from 0 to 9. These numbers are drawn in a specific sequence, and the sum of the numbers is calculated. The last digit of this sum, known as the Final Ank, is used as the result of the draw. Players who have predicted the correct Final Ank win the round and are rewarded based on their bet.

There are two main results in each Matka round: the open and close results. The open result is derived from the first number drawn, and the close result is derived from the second number drawn. In more advanced variations, players can also bet on combinations of numbers, such as single digits, pairs (known as "Jodi"), and triples.

Types of Matka Games

Matka has evolved over time, and now there are several variations of the game, each offering unique betting opportunities. Here are a few common types:

Kalyan Matka: One of the oldest and most famous forms of Matka, Kalyan is played daily, with results announced multiple times throughout the day. Players bet on the open and close results, as well as other combinations like Jodi, Panel, and Panna.

Mumbai Matka: Another popular variation, Mumbai Matka is often played in a similar way to Kalyan, but the results are slightly different, and the game follows its own set of rules and combinations.

Rajdhani Matka: This variation of Matka is typically played with fewer numbers, but it offers higher payouts. Rajdhani Matka attracts a large number of players due to the possibility of making larger profits.

New York Matka: A more modern version of the game, New York Matka is played online and offers digital results. It is known for its fast-paced rounds and the ability to bet on multiple combinations at once.

Time Bazar Matka: This is one of the most competitive forms of Matka betting, with players placing bets on several different combinations of numbers during the day. It is a thrilling game that involves a lot of strategy and planning.

How to Play the Matka Game?

If you're new to the Matka game, here are some steps to help you get started:

Choose a Platform: You can play Matka either offline, through local dealers, or online via dedicated Matka websites and apps. Online platforms offer the convenience of playing anytime and anywhere.

Select Your Numbers: Players typically select three numbers between 0 and 9. You can choose your numbers based on patterns or even use a random number generator for fun.

Place Your Bets: Once you've selected your numbers, you place your bets. Most Matka platforms allow you to bet on a variety of combinations, including single numbers, pairs (Jodi), and triples.

Wait for the Result: After placing your bets, you must wait for the draw to take place. The Matka results are usually announced at specific times, and you can check them online or through your local dealer.

Collect Your Winnings: If your prediction matches the Final Ank (last digit of the sum of the numbers), you win the round. Your winnings depend on the odds and the amount of your bet.

Tips for Playing the Matka Game

While Matka is primarily a game of luck, there are some strategies you can employ to increase your chances of success:

Study Previous Results: Many experienced players study previous results to identify trends and patterns in the numbers. This can help you make more informed guesses in future rounds.

Start with Small Bets: If you're new to the game, it's advisable to start with small bets. This allows you to learn the ropes without risking too much money.

Bet on Multiple Combinations: Consider placing bets on several combinations to improve your chances of winning. However, be mindful of your budget and avoid over-betting.

Stay Disciplined: Matka can be highly addictive, so it’s essential to set a budget and stick to it. Gamble responsibly and never chase your losses.

Conclusion

The Matka game offers an exciting opportunity for players to test their luck and skills in a fun and challenging way. Whether you are a beginner or a seasoned player, understanding how the game works, its various types, and employing smart strategies can increase your chances of success. Keep in mind that while the game can be highly rewarding, it is important to play responsibly and within your limits. So, if you're looking for an adrenaline rush, Matka might just be the perfect game for you.

[i-should-have-studied]

Chemistry Sem 4 End - Mod 4

Arrhenius eq

We know that the kinetic energy of a gas is directly proportional to its temperature.

Thus as the temperature of a system increases, more and more molecules acquire the necessary energy greater than Ea to cause productive collisions, This increases the rate of reaction.

In 1889, Arrhenius suggested as simple relationship between the rate constant, k, for a reaction and the temperature of the system:

formula

This is the Arrhenius equation where - A is an experimentally determined frequency factor - Ea is activation energy - K is rate constant - R is gas constant - T is Kelvin temperature

Arrhenius equation can be used to calculate the activation energy, Ea.

---

Rate constant eq for first order reaction, define order of a reaction

Order of a reaction is defined as the sum of the powers of concentrations in the rate law.

Consider the example of a reaction which has the rate law: rate=k[A]^m[B]^n The order of such a reaction is (m+n).

The order of a reaction can also be defined with respect to a single reactant, thus the reaction order with respect to A is m and with respect to B it is n.

The overall order of reaction (m + n) may range from 1 to 3 and can be fractional.

Reactions may be classified according to the order. If m+n = 1, it is first order reaction m+n = 2, it is second order reaction m+n = 3, it is third order reaction

---

Jablonski diagram + explain phosphorescence, fluorescence, and ISC

According to Grothus-Draper law, only the light which is absorbed by a system can bring about a photochemical reaction.

The light absorbed may be re-emitted along in one or more steps. This phenomenon is called fluorescence. The emission in fluorescence ceases with the removal of light source.

Sometimes the light absorbed is given out slowly and even long after removal of light source. This is call phosphorescence.

The phenomena of both fluorescence and phosphorescence can be explained with Jablonski's diagram.

The quantity 2S+1 where S is the total electron spin in most of the molecules have even no. of electrons and all the electrons are spin paired, Here S gives Spin Multiplication.

If spins are paired (↑↓) unpaired orientation is cancelled by downward spin. therefore S=0 S1 = +1/2, S2 = -1/2 S = 1/2 - 1/2 = 0

Hence (2S+1) = 2x0+1 = 1 or singlet ground state

When absorption of photon of suitable energy hv one of the paired electrons goes to the higher energy level. The spin orientation of two single electrons may be parallel or antiparallel

If spins are parallel: S = phospherS1+S2 = 1/2+1/2 = 1 (2S+1) = (2x1)+1 = 3 Spin multiplicity of molecules is known as triplet excited state.

If spins are antiparallel: S = S1+S2 = 1/2-1/2 = 0 (2S+1) = (2x0)+1 = 1 Spin multiplicity of molecules is known as single excited state.

Since electrons can jump to any of the higher electronic states depending upon the energy of the photon absorbed, we got a series of singlet excited states: Sn where n=1,2,3,4,...

This S1, S2, S3, etc. are known as 1st singlet excited state, 2nd singlet excited state, 3rd singlet excited state, so on.

Similarly T1, T2, T3, etc. are know as 1st triplet excited state, 2nd triplet excited state, 3rd triplet excited state, etc.

Accordingly, energy sequence is as follows: ES1>ET1, ES2>ET2,etc

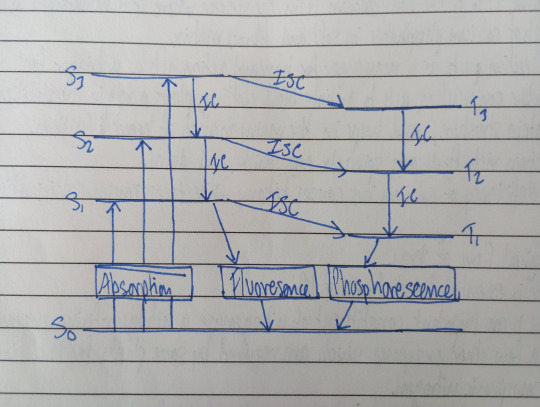
On absorption of light photon, the electron of the absorbing molecule may jump from: S0 -> S1 or S2 or S3 (Singlet excited state) depending upon the energy of light photon absorbed as shown in diagram.

For each singlet excited state (S1, S2, S3, etc) there is a corresponding triplet excited state (T1, T2, T3, eTc)

The molecule is said to be activated whether the singlet or triplet excited state A + hv -> A*

'A' molecule in the ground state on absorption gets A* excited state molecule (Activated molecule)

The activated molecule remains in the ground state by dissipating its energy through the following types of processes: - Non-radiative - Radiative

Non-radiative transitions

These transitions involve the return of the activated molecule from higher excited states to the first excited state. These reactions do not involve in the emission of any radiations and are this referred as non-radiative transitions.

The energy of activated molecule disappears in the form of heat through molecular collisions. This process is called Internal Conversion (IC)

The molecules also lose energy by another process called Intersystem Crossing (ISC)

ISC involves in transition between states of different spins and different multiplicity, ie: S2 -> T2 S1 -> T1

These transitions are also non-radiative spectroscopically, such transition are forbidden.

Radiative transitions

Fluorescence: (S1->S0)

The transition from the single excited state to ground state

Such transitions are accompanied by the emission of radiation. Spectroscopically the transition from S1 -> S0 is allowed and occurs in about 10^-8 seconds

The emission of radiation is this transition is called fluorescence.

Phosphorescence: (T1->S0)

The transition from the triplet excited state to ground state.

It is rather slow since it is a forbidden transition.

The emission of radiation in this transition is called phosphorescence.

The life times of phosphorescence are much longer being of the order of 10^-3 seconds or greater since the transition involves spin inversion which needs time for it's occurrence.

Both fluorescence and phosphorescence radiations are of shorter frequencies than existing light as some part of energy of molecule disappears in the form of heat during "non-radiative transitions."

---

Grothus-Draper principle of photochem activation

There are two basic laws of photochemical reactions - Grothus-Draper law - The Stark-Einstein law of Photochemical Equivalence

Grothus-Draper:

When light falls on a cell containing a reaction mixture, some light is absorbed and the remaining light is transmitted.

Only the absorbed component of light that is capable of producing the reaction, the transmitted light is ineffective chemically.

This is Grothus-Draper law and may be stated as follows:

When light falls on an object, a part of it is reflected and a part of it is transmitted. The rest is absorbed by the reacting system which is effective in bringing about a chemical change.

However, this does not mean that the absorption of radiation must necessarily be followed by a chemical reaction.

When the conditions are not favorable for the molecules to react, the light energy remains unused. It may be re-emitted as heat or light.

-

The Stark-Einstein law of Photochemical Equivalence

Stark and Einstein noted that each molecule taking part in a reaction absorbs only a single quantum or photon of light.

The molecule that gains one photon-equivalent energy is activated and enters into reaction.

They thus proposed The Stark-Einstein law of photochemical equivalence, which may be stated as:

In a primary photochemical process, each molecule is activated by the absorption of one quantum or radiation (one photon)

molecule ‘A’ absorbs a photon of radiation and becomes activated. The activated molecule A* then decomposes to yield B.

---

Quantum efficiency of the photochem combination of H2 and Cl2

Quantum yield or the quantum efficiency of a photochemical process is defined as the no. of molecules reacted or formed per photon of light absorbed.

∅ = no of molecules reacted/no of photons absorbed OR

∅ = no of molecules reacted/no of Einsteins of radiation absorbed

For product formation:

∅ = no of molecules of product formed/same two denominators ^

Is the 2nd law is correct, then quantum yield should be unity? but this is very rare.

The quantum yields may be as high as as 10^6 or as low as 10^-2 for several photochemical reactions.

-

Cause of high quantum yields:

When one photon is absorbed by molecules and it decomposes to form more than one product molecule then the ∅ of molecule is greater than 1 and is said to be high.

Hydrogen-chloride reaction is a good example of high quantum yield.

But before explaining, photochemical process has 2 steps:

1) Primary Process: It proceeds through absorption of radiation by molecule to form excited atom or molecule. - ex: A (molecule) + hv (photon) -> A* (excited molecule)

2) Secondary Process: The activated molecules may react with the other molecules to form product - Or, the activated molecule may emit the radiation of either the same or different frequency.

-

ex: HCl Reaction

This is a photochemical chain reaction

A mixture of hydrogen and chlorine is exposed to light of wavelength 4000Å or less than 480nm.

The hydrogen and chlorine react rapidly to form HCl.

This is followed by secondary reactions. 1) Cl2 + hv -> Cl + Cl - primary process 2) Cl +H2 -> HCl + H - secondary process 3) Cl2 + H -> HCl + Cl - secondary process 4) Cl + Cl -> Cl2 - secondary process - Step 1 is chain initiation - Step 2 and 3 are chain propagation - Step 4 is chain termination

The reason for higher quantum yield is one photon of light absorbed in step 1 forms large number of HCl molecules in steps 2 and 3, where in step 4 Cl atoms lose their excess energy and recombine at the walls of the vessel by chain terminating.

The number of HCl molecules formed for a photon of light is very high, as a result quantum yield of reaction varies from 10^4 to 10^6

---

zero-order kinetics

---

determine order of reaction w differential method

This method was suggested by van’t Hoff and, therefore, it is also called van’t Hoff’s differential method.

According to it, the rate of a reaction of the nth order is proportional to the nth power of concentration.

---

(5M) rate of reaction

The quantity of reactant species consumed on the quantity of product species formed in unit time in a chemical reaction is called the rate of reaction. A -> B

With the passage of time, the concentration of A goes on decreasing, while the concentration of B goes on increasing.

The rate of reaction at any moment may be expressed as follows: Rate of Reaction (ɣ) = amt of A consumed/time taken OR Rate of reaction (ɣ) = amt of B produced/time taken

If in a unit time, the amount of A consumed or B produced is large, the reaction is said to be a first order reaction.

However the rate of reaction cannot be determined by dividing the total change in concentration by total time taken, this is because the rates of reactions are not uniform.

Rate of reaction depends on the concentration of the reactant.

With the passage of time, the concentration of reactant species decreases progressively and hence the rate of reaction goes on decreasing.

Therefore, the rate of reaction at a given moment can be expressed by dividing the small change in concentration dx by small time interval Rate of reaction at a given moment = dx/dt

Hence the rate of reaction may be defined as: The instantaneous change in concentration of a reactant/product species at a given moment of time

Consider that change in concentration of the reactant species in an infinitesimally small time. Hence rate of reaction = dx/dt

1) If the rate is expressed in terms of the change in concentration of any reactants, there will be decrease in concentration with time. This, rate of reaction = -dx/dt

2) if the rate is expressed in terms of the change in concenreation of any one of the products, there will be an increase in concentration with time Therefore rate of reaction - +dx/dt

Units of Rate of Reaction: moles per liter per second

Factors affecting the rate of reaction - Nature of reactants and products - Concentration of reactants and products - Temperature - Surface area of reactants - Presence of a Catalyst - Light

1) Nature of Reactants:

Reaction between nitric oxide and oxygen is faster than the reaction between carbon monoxide and oxygen under the same conditions of temperature. NO(g) + 1/2O2(g) -> NO2(g) - fast CO(g) + 1/2O2(g) -> CO2(g) - slow

This is due to the difference in the nature of the reactants, that is NO and CO.

Since the bonds are broken and new bonds are formed in a chemical reaction, it seems reasonable that the rate of reaction should depend on the types of bonds involved.

2) Effect of Concentration:

The greater the concentration of reactants, the greater the inter-molecular collisions, and the greater the rate of reaction.

ex: A candle burns normally in air (20% O2) but burns more brightly in a jar of pure oxygen (100% O2) due do the higher concentration of oxygen.

3) Effect of Temperature:

Temperature has marked effect on rate of chem reaction. In most of the cases, the rate of reaction becomes double on triple for a 10°C rise in temperature

Large increase in reaction rate is due to the increase in the collision frequency and increase in effective collisions which can bring about a chemical change.

4) Effect of Surface Area:

Powdered sugar dissolved more readily in water than a crystalline sugar, This is because in the case of powdered sugar, more of it's surface area comes in contact with water in comparison to crystalline.

Similarly, powdered charcoal burns explosively in air while large pieces of coal burn slowly.

Thus, surface area of reactants in contact is an important factor for rate consideration.

5) Effect of Catalyst:

Rate of reaction may be increased by adding a suitable catalyst.

Inhibitor hinders the catalyst action while promoters increase the activity of the catalyst.

A catalyst takes part in the reaction. It is consumed in one step and regenerated in the subsequent step.

It is believed that a catalyst somehow provides a new path to the reaction.

6) Effect of Light:

The rates of certain chemical reactions are greatly influences by the light or radiations.

Absorption of light may exercise or energize a reacting molecule.

Sometimes, the molecules are broken down into more reactive intermediates.

---

(5M) Diff thermal + photochem processes

---

(5M) Activation energy

We know that for each reaction a certain energy barrier must be surmounted.

The reactant molecules must possess the activation energy, Ea, for the reaction to occur.

The catalyst functions by providing another pathway with lower activation energy, Ecat.

Thus a much larger number of collisions becomes effective at a given temperature.

Since the rate of reaction is proportional to effective collisions, the presence of a catalyst makes the reaction go faster, while all other conditions remaining the same.

It may be noted from the diagram that although a catalyst lowers the activation energy, the energy difference, ΔE, between products and reactants remains the same.

---

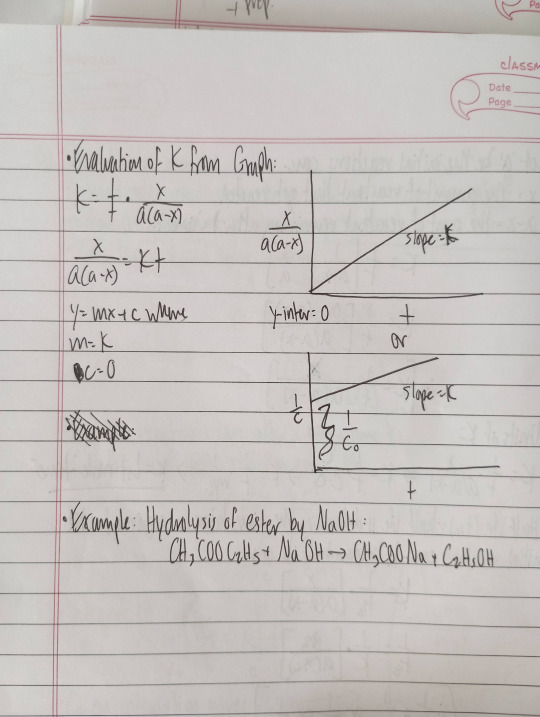
2nd order reaction

---

Methods for Determination of Order of Reaction

[random-arcane-fan]

unfiltered musing: pre-s2 thoughts

2025-01-19

-

SO FIRST THINGS FIRST I spoiled myself like a motherfucker, recklessly, around… I wanna say between ep5 and 6, that big break. rambled about this in [a] server already but tl;dr I would not be REMOTELY surprised if the pushback from longtime fans is because… they’re longtime fans. fanon-brained. aot 2. anyway

caitlyn in s1 doesn’t really stick out to me but the dictator vengeance arc has me sweating. also the emotional repression. ohhh the Makings of a new blorbo they’re brewing

love vi love her batshit blues but I’LL GET BACK TO THE CHARACTERS. ONE SEC.

thematically!! the show’s doing a lot about cycles and violence and love and it’s great. it’s a little like… it’s like that aot episode where gabi has to learn “oh, my enemies are human people,” right. depending on one’s personal politics the message may or may not land funny. and there’s other Thoughts about this in my brain but mostly they spin in a circle like the laundry machine, pls hold.

anyway now to be a hypocrite and character babble. I LOVE VI. I WOULD LIKE TO SEE MORE ANALYSES OF VI like yes yeah Butch Hot can we also talk about her being the most emotionally open and surprisingly soft motherfucker.. maybe not in the Whole show, a lot of characters speak more with touch than words (that’s visual storytelling baybeeeee), but like. Vi. up there. homegirl gets out of prison has the most wild sequence of days in her life ([well, at least] since the events which originally landed her in prison) and it ain’t DONE yet. let her Rest.

caitlyn. -gestures to discord dump- autism. that is all

jinx? fantastique. i s2g she has all the trope trappings of a Me Character but somehow it hasn’t quite hit, but I like her plenty! feels like I haven’t really gotten a good grip on her motivations and thoughts, but careful rewatches can remedy that. a LOT of the bombastic antics (antix?) are for fun as much as they are for tactics, and I think she’s smarter than people in-universe and also I give her credit for. it’s a matter of dissecting how.

jayce I have been largely ambivalent about, right up until the last few eps. has his big action moment and then OOPS that’s kids you’re killing! I think I can warm up to him on rewatches & with analyses, because he’s got a genuine heart and clearly doesn’t Love playing yes-man—even if he spends an awful lot of screentime playing yes-man. no clue what to make of the beard phase later.

viktor’s in a similar “have not seen enough of you yet” boat. he’s ???neat. more interested in him for the Themes, this terminal evolution body mod eldritch savior god shit, than The Man Himself, but that could change. (actually tbfh, ignoring fan analyses I think my take on everyone can be summed up as “very cool! will probably find you cooler on rewatch! anyway.”) also he’s got some sass, good for him.

mel? great. wish people did not so often begin and end the character thoughts at “queen”; she’s admittedly been tricky for me to get in the head of, but like SURELY that will change with the increased character prominence. seems to be a focal character for the sequel series, good for her! we’re introduced to her as a smooth-talking politician and the narrative distance feels intentional. the dynamic with ambessa is… Hough. oh boy. oh Boy

ekko: like mel, ok guys we get it he’s “perfect” can w. can we dive into that a little more. on the other hand he straight-up doesn’t have a ton of s1 screentime. on the other OTHER hand, this is arcane and you can tell So Much from So Little because it’s all THAT fucking good. jinx fight sequence? like??? you don’t NEED the enemy music video or ANY prior interaction really. that shows you everything.

silco: A+ villain, fantastically humanized, love me an ironic parallel, I knew his death was “jinx somehow (accidentally?) kills him” but was NOT prepared for how it actually happened. fucking ouch. it got me tbfh.

heimerdinger, sevika, vander: Great™. once I saw the thing about sevika embodying Zaun As A Nation it’s like ah, now I understand everything. love that she loves a good fight, feel a bit like she plays into the magic-handwaved-amputation trope but she does feel like a real person anyway. vander, somehow did not anticipate the death flags. reportedly he is “warwick”/a wolf later??? and heimerdinger is… well he’s A Guy, kinda surprised he’s significant enough to be in the intro sequence? wish he like, Explained Shit; he might be one of the only characters I’ve been ~frustrated by, as opposed to minor characters who are clearly meant to be disliked so w/e (marcus, arguably finn) or more significant characters who make bad choices but it’s juicy as fuck so, also and empathetically, w/e (…basically everyone lbr). anyway I combined those last three bullets with the thought they were all so minor I wouldn’t have a lot to say, And Then.

mostly I wanted all this down before I dive into s2 proper, so I can look back later and be like “:)” one way or another. definitely bears mentioning (I think I did in discord already but still) that, rn, caitlyn does not Particularly impress just based on screentime alone, but oh spoilers and analyses Got Me. let’s see if that carries through, and/or if I pick up a surprise different guy. HOO BOY. I’M NOT READY FOR S2, GUYS.

-

[3/08 addendum: re:Sevika and the "magic-handwaved-amputation" thought, I can't speak to whether it's #problematique, but I do appreciate that s2 gave her some screentime with no magic-prosthetic.

[Heimerdinger remains the one intro character I Simply Do Not Care For. Caitlyn did indeed Get Me by the throat but in a "favorite (derogatory) (slowly dragging hands down face) (what is wrong with her)" sort of way. Also, I wasn't planning on posting this directly after the favorites sorter, but the notedump-chronology lined up juuust right.

[Wonder if I'll catch up before the artbook ordered way back in December comes in...! :,D]