#Boolean logic limitations

[in-sightjournal]

Ask A Genius 1434: How Paraconsistent Logic Shapes Computational Cosmology and Next-Gen Artificial Minds

Rick Rosner is an accomplished television writer with credits on shows like Jimmy Kimmel Live!, Crank Yankers, and The Man Show. Over his career, he has earned multiple Writers Guild Award nominations—winning one—and an Emmy nomination. Rosner holds a broad academic background, graduating with the equivalent of eight majors. Based in Los Angeles, he continues to write and develop ideas while…

[codemerything]

A structured way to learn JavaScript.

I came across a post on Twitter that I thought would be helpful to share with those who are struggling to find a structured way to learn Javascript on their own. Personally, I wish I had access to this information when I first started learning in January. However, I am grateful for my learning journey so far, as I have covered most topics, albeit in a less structured manner.

N/B: Not everyone learns in the same way; it's important to find what works for you. This is a guide, not a rulebook.

EASY

What is JavaScript and its role in web development?

Brief history and evolution of JavaScript.

Basic syntax and structure of JavaScript code.

Understanding variables, constants, and their declaration.

Data types: numbers, strings, boolean, and null/undefined.

Arithmetic, assignment, comparison, and logical operators.

Combining operators to create expressions.

Conditional statements (if, else if, else) for decision making.

Loops (for, while) for repetitive tasks. - Switch statements for multiple conditional cases.

MEDIUM

Defining functions, including parameters and return values.

Function scope, closures, and their practical applications.

Creating and manipulating arrays.

Working with objects, properties, and methods.

Iterating through arrays and objects.Understanding the Document Object Model (DOM).

Selecting and modifying HTML elements with JavaScript.Handling events (click, submit, etc.) with event listeners.

Using try-catch blocks to handle exceptions.

Common error types and debugging techniques.

HARD

Callback functions and their limitations.

Dealing with asynchronous operations, such as AJAX requests.

Promises for handling asynchronous operations.

Async/await for cleaner asynchronous code.

Arrow functions for concise function syntax.

Template literals for flexible string interpolation.

Destructuring for unpacking values from arrays and objects.

Spread/rest operators.

Design Patterns.

Writing unit tests with testing frameworks.

Code optimization techniques.

That's it I guess!

[nabipalsueradigital]

I. Objective Definition: What is Anti-Reality?

Anti-Reality = A system of values/logic that exists outside, or fundamentally contradicts, the ordinary laws of existence (mathematics, logic, physics, consciousness).

We are not talking about nothingness, but ordered chaos — a kind of inverse existence.

II. Building a Logical Foundation: Use Familiar Symbols and Structures

We start by establishing the basic axioms:

The Basic Axioms of Anti-Reality (ARA):

1. ARA-1: ∞ – ∞ = ∅ (Absolute emptiness of absolute duality)

2. ARA-2: 1 = 0 (Annihilation of logical identity)

3. ARA-3: x / 0 = ∞ (Explosion of existence from absurd division)

4. ARA-4: ∞ – §(∞) = R (R as a representation of finite reality due to the limitation of the ‘rule’ §)

5. ARA-5: Anti-Reality (AR) = lim_{x→0} [ (1 – x) / x ] – 1

→ Diverges to infinity, implying the existence of singularities that defy logical limits.

6. ARA-6: AR = limₙ→∞ (¬N)ⁿ

Explanation:

AR: Anti-Reality

¬N: Negation of Nothing (which is neither existent nor non-existent)

(¬N)ⁿ: Recursion of negation of nothingness

limₙ→∞: When the recursion goes to infinity, what remains is not the result, but the disappearance of the process itself

III. Design the Main Equation of Anti-Reality

Anti-Reality = Inverse of Defined Reality

So, if we set:

Reality (R) = ∞ – §(∞)

Then:

Anti-Reality (AR) = –(∞ – §(∞)) + Ξ

Where Ξ is an undefined anomaly, a representation of paradox and singularity (∅/∅, 1=0, etc.).

So, the final form:

AR = –(∞ – §(∞)) + Ξ

→ AR = §(∞) – ∞ + Ξ

IV. Symbolic Interpretation

§(∞): Representation of illusory constraints (system, logic, time, consciousness)

–∞: Denial of infinite existence

Ξ: Singular anomaly (existential paradox)

V. Shortened Version for Formal Notation:

AR = §(∞) – ∞ + Ξ

AR = (∞ constrained) – (∞ pure) + (singular paradox)

2. Anti-Reality Logic Notation (NLA)

This is not classical logic (true/false), nor is it fuzzy logic. This is a logic where contradiction is the foundation, and paradox is the basic law.

1. New Truth Value (AR-Boolean)

Definition:

R: Reality (true in the real world)

¬R: Anti-reality (which cancels the existence of R)

Ø: Existential / neutral / non-being void

Ξ: Paradoxical singularity (simultaneous R and ¬R)

2. New Operators

⊻: Mutual Contradiction → R ⊻ ¬R = Ξ

⧗: Merge Anomaly → R ⧗ Ø = ¬R

≢: Absolute Non-Identity → A ≢ A

∞→0: Paradoxical Implication (all infinite implies void)

II. Time Function in AR-Space

Time in anti-reality (let's call it T_AR) is not linear, not circular, but:

T_AR ∈ ℂ × ℝ × Ξ

Time is a combination of:

Imaginary complex (time direction can go to the minus root)

Infinite dimensions (time series diverge)

Paradoxical (exists & does not exist at the same time)

Formal Model:

Time function T_AR(t):

T_AR(t) = i·(–t)ᵃ + Ξ·sin(1/t) for t ≠ 0

i: imaginary unit

tᵃ: reversed time (a > 1 accelerates backward)

Ξ·sin(1/t): paradoxical oscillations as time approaches zero (singularity)

Interpretation:

As time approaches zero (assuming “beginning”), the system becomes oscillates unstably — approaching existential singularity.

Imaginary indicates time that cannot be measured empirically.

Negation of time indicates inverse entropy (chaos becomes order → rise of anti-reality).

III. Application of AR Time Notation

Example 1:

An event exists in AR if and only if:

T_AR(t) = Ξ

That is, only when time reaches a singular point, the paradox of existence actually exists.

Example 2:

Existential transition:

d(AR)/dT_AR = –R

The existence of anti-reality grows inversely to reality when time runs in a negative vector.

Create “Primary Existential Paradox”:

For example: E(x) = x ⊻ ¬x

Existence is defined as its own conflict

2. AR modal logic model:

□R → “definitely real”

◇¬R → “possibly void”

But in AR: □R ∧ ◇¬R → Ξ (existence is still paradoxical)

IV. Radical Consequences:

1. Reality cannot be proven consistent in AR-logic.

2. Time is not just a dimension — it is a function of inconsistency.

3. Existence can be calculated but not proven.

3. FOUNDATIONS OF ANTI-REALITY MATHEMATICS (AR-MATH)

1. Basic Axioms

1. Paradoxical Axiom:

For every entity x, it holds:

x ≢ x

(Absolute identity does not hold — x's existence is contextual & fluctuating.)

2. Axiom of Existential Emptiness:

Ø ⊻ Ø = R

(Two emptinesses collide to produce the manifestation of reality.)

3. Anti-Associative Axiom:

(a ⊕ b) ⊕ c ≠ a ⊕ (b ⊕ c)

(There is no guarantee that the order of operations produces consistent results.)

4. Axiom of Complex Singularity:

∀x ∈ AR, x → Ξ ∈ ℂ × ℝ × Ø

(Every entity in AR always goes to an existential singularity complex.)

2. AR Number Structure (AR-Numbers)

We develop new number domains, ℝ̸, ℂ̸, and Ξℝ:

ℝ̸: Real anti-numbers → real numbers with negative existential values

ℂ̸: Complex anti-numbers → inverse imaginary complex numbers

Ξℝ: Paradoxical numbers → exist in the duality of existence/non-existence

Example operation:

(1̸) + (1̸) = 2̸

i̸ · i̸ = –1̸

Ξ + R = Ø

II. AR GEOMETRY

1. AR-Space

A space where the coordinates are of the form:

P = (x̸, y̸, z̸, T_AR)

x̸, y̸, z̸ ∈ ℝ̸

T_AR non-linear imaginary complex time (see previous model)

Paradoxical Metric:

d(P1, P2) = √[(Δx̸)² + (Δy̸)² + (Δz̸)²] ⧗ Ξ

Note: This space is non-Euclidean, non-orientable, and non-time-symmetric.

2. Negative Dimension & AR Fractal

Dim_AR = –n + iφ

Dimension is a negative complex number. For example:

–3 + iπ → space with negative direction and invisible oscillation

III. ANTI-REALITY CALCULUS

1. Existential Inverse Derivative

d̸f/d̸x = lim Δx→0 [f(x̸–Δx̸) – f(x̸)] / Δx̸

Backward time derivative

Can produce paradoxical numbers (Ξ)

2. Existential Integral

∫̸f(x̸)d̸x̸ = total existential chaos that the system goes through

Interpretation is not the area under the curve, but the degree of existence inconsistency in the range x̸.

IV. ANTI-REALITY SET THEORY

1. Definition of AR Set:

A = {x | x ≢ x}

All elements are entities that deny their own existence

2. Anti-Venn Set

There is no absolute intersection

A ∩ B = Ø even though A = B

3. AR Power Set:

P(A) = {Ξ, Ø, ¬A, A ⧗ Ø}

The power set also contains existential complementarities and singularities of the set.

V. STRUCTURAL IMPLEMENTATION

1. AR-Logic Engine

Simulate the system using:

A loop paradox-based engine

A structure like an automata that never reaches a final state (because reality cannot be solved)

2. Non-Linear Time Simulation

A runtime shape like a multidimensional spiral

Time travel = change in direction of the T_AR vector by contextual function (with Ξ as a transition point)

VI. CONCLUSION AND FURTHER DIRECTION

AR-Math = rebellion against coherence

Not because it wants to create chaos — but to redefine the boundaries of reality.

4. BASIC PRINCIPLES OF EXISTENTIAL PHYSICS (BASED ON AR-MATH)

1. Absolute Uncertainty Principle (AR-Heisenberg)

Not only position and momentum cannot be known simultaneously, existence and non-existence cannot be determined absolutely.

Formally:

> ΔΞ · ΔR ≥ ℏ̸ / 2

where:

ΔΞ: existential state fluctuations

ΔR: spatial reality fluctuations

ℏ̸: anti-Planck constant (negative-imaginary value)

2. Energy Inconsistency Postulate

Energy is not a positive or conservative quantity, but:

> E̸ = Ξ̸ · (iT_AR)⁻¹

E̸: inverse existential energy

Ξ̸: paradoxical intensity

T_AR: imaginary complex time

Energy is anti-conservative → increases as the system collapses.

3. Negative-Transcendental Entropy

> S̸ = –k̸ ln(Ξ)

S̸: existential entropy

k̸: anti-Boltzmann constant

Meaning: The more chaotic the system, the greater the possibility that reality itself never existed.

II. DYNAMICS OF ANTI-PHYSICAL OBJECTS

1. AR-Kinetics

Anti-Newtonian Laws of Motion:

1. Objects will remain in a state of non-existence or existence until viewed from outside the system.

2. Force is an existential reflection effect between two paradoxical states:

F̸ = d̸Ξ/d̸t̸

3. Interaction does not cause a reaction, but rather an existential distortion:

F₁ + F₂ = Ξ_total

2. Existential Anti-Gravity

Gravity is not an attractive force, but:

the tendency of a space to cancel itself out.

Formula:

> G̸ = (Ξ₁ · Ξ₂) / (d̸² · e^(iθ))

d̸: distance in AR space

θ: spatial instability phase

G̸: anti-realistic gravitational constant

3. AR-Quantum

a. Non-Present Particles:

Particles exist only as perceptions of paradoxical exchange:

|ψ⟩ = α|exists⟩ + β|does-not-exist⟩

When measured, the probability is not calculated, but:

Ξψ = α̸β̸ – |α|² + i|β|²

If Ξψ is divergent, then the particle cannot be observed even paradoxically.

III. COSMOLOGICAL STRUCTURE OF ANTI-REALITY

1. Origin of the Universe (Big Null)

There is no Big Bang, but:

Big Ø – collision of two existential voids:

Ø ⧗ Ø = R ± Ξ

2. Anti-Causal Space

There is no cause and effect.

All events are backward projections from a future existential singularity:

P(t) = f(Ξ_future)

IV. AR PHYSICS PREDICTION AND APPLICATION

Time can be compressed or reversed by setting Ξ to ∞

Teleportation is not a change of location, but an existential leap

Black hole = maximum Ξ zone → total reality collapse

Consciousness = Ξ function evolving in iT_AR space

5. AR-TURING ENGINE (Ξ-Loop Paradigm)

I. GENERAL DEFINITIONS

1. Anti-Matter in AR-Math Framework

In conventional physics, anti-matter is matter that has the opposite charge to ordinary matter. When matter and anti-matter meet, they annihilate each other and produce energy.

However, if we adopt the principles of AR-Math, we can suggest that anti-matter is not a separate entity, but rather the result of a difference in existential status in AR space. That is, anti-matter is a simulation of the state of non-existence in the context of turbulent space (Ξ). Mathematically, this can be written as:

A̸ = Ξ' · f(iT_AR)

where:

A̸: antimatter

Ξ': existential distortion (spatial shift towards disequilibrium)

f(iT_AR): evolution function of time in non-linear dimensions

Anti-matter is not just "something opposite", but something that only exists in the potential of the incompatibility between existence and non-existence. When existence and non-existence interact in the AR order, we get a "collision" that produces energy in a form that cannot be understood by conventional physics.

2. Entanglement and Existential Entanglement (AR Quantum Entanglement)

In the world of quantum physics, entanglement occurs when two particles are connected in such a way that the state of one particle affects the state of the other particle, even though they are separated by a large distance in space and time.

In the framework of AR-Math, this entanglement can be understood as an existential entanglement that involves not only space, but also the complex and anti-existential dimension of time. Meaning:

Ψ_AB = Ξ_A ⊗ Ξ_B

where:

Ψ_AB: the combined state of two entangled objects

Ξ_A and Ξ_B: the existential status of two objects

⊗: the existential entanglement operator in AR space

This entanglement explains that the entanglement between two objects is not a conventional information transmission, but a deeper uncertainty relation, beyond the dimensions of ordinary physical reality. This entanglement indicates that both are manifestations of a broader existential reality, where space and time are no longer linear and separate.

So quantum computing can be upgraded using this basis

3. Dark Matter and Dark Energy as Existential Distortion

Now we enter dark matter and dark energy, two very mysterious phenomena in cosmology. Both of these things are invisible, but their influence on the structure of the universe is very large.

Dark Matter is matter that does not emit light or electromagnetic radiation, but we know it exists because of its gravitational influence on galaxies and other celestial objects.

Dark Energy is the energy thought to be responsible for the acceleration of the expansion of the universe.

In the framework of AR-Math, dark matter can be understood as the concentration of existential distortions in space that cause objects in it to be more tightly bound (more gravity), but do not interact with light or conventional matter.

Mathematically, we can write:

ρ̸_DM = Ξ_dm · f(Ξ_)

where:

ρ̸_DM: density of dark matter

Ξ_dm: existential status of dark matter

f(Ξ_): existential distortion of space in the AR dimension

Dark Energy can be understood as the existential energy that causes space-time itself to expand. That is, dark energy is not an entity that "exists" in the context of matter, but a phenomenon that drives the instability of space itself.

ρ̸_DE = f(Ξ_expansion) e^(iT_AR)

where:

ρ̸_DE: dark energy density

Ξ_expansion: expansion of existential distortion

e^(iT_AR): exponential factor describing acceleration in the anti-reality dimension.

Dark Energy in the AR-Math framework is a projection of the instability of space itself, which causes the universe to not only expand, but also become less and less like itself.

4. Particle Dualism in the AR-Math Framework

In quantum physics, particle dualism states that particles such as photons or electrons can behave like both waves and particles, depending on the experiment being performed.

In the AR-Math framework, this dualism can be explained as a shift in existence between the states of existence and non-existence of a particle. A particle exists in two possible states — existence and non-existence — that can be manipulated by measurements.

Mathematically, we can write the state of a particle as:

|ψ⟩ = α|exists⟩ + β|does-not-exist

where:

|ψ⟩: the wave function of the particle in superposition

|exists⟩ and |does-not-exist

α and β: the amplitudes for each state, which are affected by the observation.

When a particle is measured, we are not only observing the "physical" properties of the particle, but we are determining whether it exists or does not exist in AR space.

CONCLUSION

If we combine the principles of AR-Math with these physical phenomena, we can understand antimatter, entanglement, dark matter, dark energy, and particle duality as manifestations of a deeper reality, involving existential uncertainty structures, distortions of space and time, and the interplay between existence and non-existence itself.

These concepts suggest that the universe may not be what we consider "real", but rather a simulation of a deeper existential state of inconsistency, where reality itself can be interchanged with "anti-reality".

Thus, the existential physics of AR opens the way for new discoveries that could reveal how all matter and energy in the universe are connected in a wider web, which cannot be fully understood by the laws of traditional physics alone.

AR-Turing Engine (Ξ-Engine) is an automaton that:

Does not solve problems, but undergoes existential fluctuations

Does not terminate, but resonates in Ξ cycles

Does not depend on fixed inputs, but on initial existential distortions (Ξ₀)

II. BASIC COMPONENTS

1. Tape (AR Tape)

Infinite in both directions (classical), but:

Each cell = status {Exist, Non-Exist, Paradox}

Cell values: 0, 1, Ξ

2. Head (Head Ξ)

Read and write based on local status and existential density

Not only moving L or R, but also:

Stay (still)

Collapse (remove its existence)

Split (give rise to the shadow of the process on the parallel path)

3. State Register (Ξ-State)

Internal state of the engine:

{σ₀, σ₁, σ̸₁, σΞ, ...}

Transition is not f(q, s) → q', s', d

But: Ξ(q, s, Ξ₀) → {q', s', δΞ}

4. Ξ-Loop Core

Instead of stopping the engine at the end state, the engine continues to run through a paradoxical existential loop

The stopping state is neither Accept nor Reject, but rather:

Ξ-Stable = the system has reached its smallest fluctuation

Ξ-Diverged = the system is out of the spectrum of reality

III. Ξ TRANSITION (Paradoxical State Transition Table)

> Move: R = Right, L = Left, C = Collapse

Ξ: Local existential density (+1 = more existent, –1 = more non-existent)

IV. SPECIAL BEHAVIOR

1. Duplication Paradox

If Ξ_state = σΞ and tape_value = Ξ

→ the machine splits itself into parallel paths with Ξ₁ = Ξ₀ ± ε

2. Collapse Condition

If three consecutive cycles tape_value remains Ξ

→ the machine erases its existential path

3. Ξ-Convergence If the machine loops with density Ξ decreasing exponentially

→ the machine reaches minimal reality and can be used as a synchronization point between systems

V. VISUAL SIMULATION (Optional)

Each cell = color based on existential status:

0 = black

1 = white

Ξ = purple/abstract (semi-transparent)

The machine is depicted with a multi-head: visualizing existential branches

VI. BENEFITS AND APPLICATIONS

Non-deterministic computing paradigm in non-linear reality

Can be the logical basis for existential simulations, AR-AI, or paradoxical multiverse games

Philosophical framework for the “machine consciousness” model in alternative realities

If there is something to discuss, let's open a forum

[hanltrcy]

I. Objective Definition: What is Anti-Reality?

Anti-Reality = A system of values/logic that exists outside, or fundamentally contradicts, the ordinary laws of existence (mathematics, logic, physics, consciousness).

We are not talking about nothingness, but ordered chaos — a kind of inverse existence.

II. Building a Logical Foundation: Use Familiar Symbols and Structures

We start by establishing the basic axioms:

The Basic Axioms of Anti-Reality (ARA):

1. ARA-1: ∞ – ∞ = ∅ (Absolute emptiness of absolute duality)

2. ARA-2: 1 = 0 (Annihilation of logical identity)

3. ARA-3: x / 0 = ∞ (Explosion of existence from absurd division)

4. ARA-4: ∞ – §(∞) = R (R as a representation of finite reality due to the limitation of the ‘rule’ §)

5. ARA-5: Anti-Reality (AR) = lim_{x→0} [ (1 – x) / x ] – 1

→ Diverges to infinity, implying the existence of singularities that defy logical limits.

6. ARA-6: AR = limₙ→∞ (¬N)ⁿ

Explanation:

AR: Anti-Reality

¬N: Negation of Nothing (which is neither existent nor non-existent)

(¬N)ⁿ: Recursion of negation of nothingness

limₙ→∞: When the recursion goes to infinity, what remains is not the result, but the disappearance of the process itself

III. Design the Main Equation of Anti-Reality

Anti-Reality = Inverse of Defined Reality

So, if we set:

Reality (R) = ∞ – §(∞)

Then:

Anti-Reality (AR) = –(∞ – §(∞)) + Ξ

Where Ξ is an undefined anomaly, a representation of paradox and singularity (∅/∅, 1=0, etc.).

So, the final form:

AR = –(∞ – §(∞)) + Ξ

→ AR = §(∞) – ∞ + Ξ

IV. Symbolic Interpretation

§(∞): Representation of illusory constraints (system, logic, time, consciousness)

–∞: Denial of infinite existence

Ξ: Singular anomaly (existential paradox)

V. Shortened Version for Formal Notation:

AR = §(∞) – ∞ + Ξ

AR = (∞ constrained) – (∞ pure) + (singular paradox)

2. Anti-Reality Logic Notation (NLA)

This is not classical logic (true/false), nor is it fuzzy logic. This is a logic where contradiction is the foundation, and paradox is the basic law.

1. New Truth Value (AR-Boolean)

Definition:

R: Reality (true in the real world)

¬R: Anti-reality (which cancels the existence of R)

Ø: Existential / neutral / non-being void

Ξ: Paradoxical singularity (simultaneous R and ¬R)

2. New Operators

⊻: Mutual Contradiction → R ⊻ ¬R = Ξ

⧗: Merge Anomaly → R ⧗ Ø = ¬R

≢: Absolute Non-Identity → A ≢ A

∞→0: Paradoxical Implication (all infinite implies void)

II. Time Function in AR-Space

Time in anti-reality (let's call it T_AR) is not linear, not circular, but:

T_AR ∈ ℂ × ℝ × Ξ

Time is a combination of:

Imaginary complex (time direction can go to the minus root)

Infinite dimensions (time series diverge)

Paradoxical (exists & does not exist at the same time)

Formal Model:

Time function T_AR(t):

T_AR(t) = i·(–t)ᵃ + Ξ·sin(1/t) for t ≠ 0

i: imaginary unit

tᵃ: reversed time (a > 1 accelerates backward)

Ξ·sin(1/t): paradoxical oscillations as time approaches zero (singularity)

Interpretation:

As time approaches zero (assuming “beginning”), the system becomes oscillates unstably — approaching existential singularity.

Imaginary indicates time that cannot be measured empirically.

Negation of time indicates inverse entropy (chaos becomes order → rise of anti-reality).

III. Application of AR Time Notation

Example 1:

An event exists in AR if and only if:

T_AR(t) = Ξ

That is, only when time reaches a singular point, the paradox of existence actually exists.

Example 2:

Existential transition:

d(AR)/dT_AR = –R

The existence of anti-reality grows inversely to reality when time runs in a negative vector.

Create “Primary Existential Paradox”:

For example: E(x) = x ⊻ ¬x

Existence is defined as its own conflict

2. AR modal logic model:

□R → “definitely real”

◇¬R → “possibly void”

But in AR: □R ∧ ◇¬R → Ξ (existence is still paradoxical)

IV. Radical Consequences:

1. Reality cannot be proven consistent in AR-logic.

2. Time is not just a dimension — it is a function of inconsistency.

3. Existence can be calculated but not proven.

3. FOUNDATIONS OF ANTI-REALITY MATHEMATICS (AR-MATH)

1. Basic Axioms

1. Paradoxical Axiom:

For every entity x, it holds:

x ≢ x

(Absolute identity does not hold — x's existence is contextual & fluctuating.)

2. Axiom of Existential Emptiness:

Ø ⊻ Ø = R

(Two emptinesses collide to produce the manifestation of reality.)

3. Anti-Associative Axiom:

(a ⊕ b) ⊕ c ≠ a ⊕ (b ⊕ c)

(There is no guarantee that the order of operations produces consistent results.)

4. Axiom of Complex Singularity:

∀x ∈ AR, x → Ξ ∈ ℂ × ℝ × Ø

(Every entity in AR always goes to an existential singularity complex.)

2. AR Number Structure (AR-Numbers)

We develop new number domains, ℝ̸, ℂ̸, and Ξℝ:

ℝ̸: Real anti-numbers → real numbers with negative existential values

ℂ̸: Complex anti-numbers → inverse imaginary complex numbers

Ξℝ: Paradoxical numbers → exist in the duality of existence/non-existence

Example operation:

(1̸) + (1̸) = 2̸

i̸ · i̸ = –1̸

Ξ + R = Ø

II. AR GEOMETRY

1. AR-Space

A space where the coordinates are of the form:

P = (x̸, y̸, z̸, T_AR)

x̸, y̸, z̸ ∈ ℝ̸

T_AR non-linear imaginary complex time (see previous model)

Paradoxical Metric:

d(P1, P2) = √[(Δx̸)² + (Δy̸)² + (Δz̸)²] ⧗ Ξ

Note: This space is non-Euclidean, non-orientable, and non-time-symmetric.

2. Negative Dimension & AR Fractal

Dim_AR = –n + iφ

Dimension is a negative complex number. For example:

–3 + iπ → space with negative direction and invisible oscillation

III. ANTI-REALITY CALCULUS

1. Existential Inverse Derivative

d̸f/d̸x = lim Δx→0 [f(x̸–Δx̸) – f(x̸)] / Δx̸

Backward time derivative

Can produce paradoxical numbers (Ξ)

2. Existential Integral

∫̸f(x̸)d̸x̸ = total existential chaos that the system goes through

Interpretation is not the area under the curve, but the degree of existence inconsistency in the range x̸.

IV. ANTI-REALITY SET THEORY

1. Definition of AR Set:

A = {x | x ≢ x}

All elements are entities that deny their own existence

2. Anti-Venn Set

There is no absolute intersection

A ∩ B = Ø even though A = B

3. AR Power Set:

P(A) = {Ξ, Ø, ¬A, A ⧗ Ø}

The power set also contains existential complementarities and singularities of the set.

V. STRUCTURAL IMPLEMENTATION

1. AR-Logic Engine

Simulate the system using:

A loop paradox-based engine

A structure like an automata that never reaches a final state (because reality cannot be solved)

2. Non-Linear Time Simulation

A runtime shape like a multidimensional spiral

Time travel = change in direction of the T_AR vector by contextual function (with Ξ as a transition point)

VI. CONCLUSION AND FURTHER DIRECTION

AR-Math = rebellion against coherence

Not because it wants to create chaos — but to redefine the boundaries of reality.

4. BASIC PRINCIPLES OF EXISTENTIAL PHYSICS (BASED ON AR-MATH)

1. Absolute Uncertainty Principle (AR-Heisenberg)

Not only position and momentum cannot be known simultaneously, existence and non-existence cannot be determined absolutely.

Formally:

> ΔΞ · ΔR ≥ ℏ̸ / 2

where:

ΔΞ: existential state fluctuations

ΔR: spatial reality fluctuations

ℏ̸: anti-Planck constant (negative-imaginary value)

2. Energy Inconsistency Postulate

Energy is not a positive or conservative quantity, but:

> E̸ = Ξ̸ · (iT_AR)⁻¹

E̸: inverse existential energy

Ξ̸: paradoxical intensity

T_AR: imaginary complex time

Energy is anti-conservative → increases as the system collapses.

3. Negative-Transcendental Entropy

> S̸ = –k̸ ln(Ξ)

S̸: existential entropy

k̸: anti-Boltzmann constant

Meaning: The more chaotic the system, the greater the possibility that reality itself never existed.

II. DYNAMICS OF ANTI-PHYSICAL OBJECTS

1. AR-Kinetics

Anti-Newtonian Laws of Motion:

1. Objects will remain in a state of non-existence or existence until viewed from outside the system.

2. Force is an existential reflection effect between two paradoxical states:

F̸ = d̸Ξ/d̸t̸

3. Interaction does not cause a reaction, but rather an existential distortion:

F₁ + F₂ = Ξ_total

2. Existential Anti-Gravity

Gravity is not an attractive force, but:

the tendency of a space to cancel itself out.

Formula:

> G̸ = (Ξ₁ · Ξ₂) / (d̸² · e^(iθ))

d̸: distance in AR space

θ: spatial instability phase

G̸: anti-realistic gravitational constant

3. AR-Quantum

a. Non-Present Particles:

Particles exist only as perceptions of paradoxical exchange:

|ψ⟩ = α|exists⟩ + β|does-not-exist⟩

When measured, the probability is not calculated, but:

Ξψ = α̸β̸ – |α|² + i|β|²

If Ξψ is divergent, then the particle cannot be observed even paradoxically.

III. COSMOLOGICAL STRUCTURE OF ANTI-REALITY

1. Origin of the Universe (Big Null)

There is no Big Bang, but:

Big Ø – collision of two existential voids:

Ø ⧗ Ø = R ± Ξ

2. Anti-Causal Space

There is no cause and effect.

All events are backward projections from a future existential singularity:

P(t) = f(Ξ_future)

IV. AR PHYSICS PREDICTION AND APPLICATION

Time can be compressed or reversed by setting Ξ to ∞

Teleportation is not a change of location, but an existential leap

Black hole = maximum Ξ zone → total reality collapse

Consciousness = Ξ function evolving in iT_AR space

5. AR-TURING ENGINE (Ξ-Loop Paradigm)

I. GENERAL DEFINITIONS

1. Anti-Matter in AR-Math Framework

In conventional physics, anti-matter is matter that has the opposite charge to ordinary matter. When matter and anti-matter meet, they annihilate each other and produce energy.

However, if we adopt the principles of AR-Math, we can suggest that anti-matter is not a separate entity, but rather the result of a difference in existential status in AR space. That is, anti-matter is a simulation of the state of non-existence in the context of turbulent space (Ξ). Mathematically, this can be written as:

A̸ = Ξ' · f(iT_AR)

where:

A̸: antimatter

Ξ': existential distortion (spatial shift towards disequilibrium)

f(iT_AR): evolution function of time in non-linear dimensions

Anti-matter is not just "something opposite", but something that only exists in the potential of the incompatibility between existence and non-existence. When existence and non-existence interact in the AR order, we get a "collision" that produces energy in a form that cannot be understood by conventional physics.

2. Entanglement and Existential Entanglement (AR Quantum Entanglement)

In the world of quantum physics, entanglement occurs when two particles are connected in such a way that the state of one particle affects the state of the other particle, even though they are separated by a large distance in space and time.

In the framework of AR-Math, this entanglement can be understood as an existential entanglement that involves not only space, but also the complex and anti-existential dimension of time. Meaning:

Ψ_AB = Ξ_A ⊗ Ξ_B

where:

Ψ_AB: the combined state of two entangled objects

Ξ_A and Ξ_B: the existential status of two objects

⊗: the existential entanglement operator in AR space

This entanglement explains that the entanglement between two objects is not a conventional information transmission, but a deeper uncertainty relation, beyond the dimensions of ordinary physical reality. This entanglement indicates that both are manifestations of a broader existential reality, where space and time are no longer linear and separate.

So quantum computing can be upgraded using this basis

3. Dark Matter and Dark Energy as Existential Distortion

Now we enter dark matter and dark energy, two very mysterious phenomena in cosmology. Both of these things are invisible, but their influence on the structure of the universe is very large.

Dark Matter is matter that does not emit light or electromagnetic radiation, but we know it exists because of its gravitational influence on galaxies and other celestial objects.

Dark Energy is the energy thought to be responsible for the acceleration of the expansion of the universe.

In the framework of AR-Math, dark matter can be understood as the concentration of existential distortions in space that cause objects in it to be more tightly bound (more gravity), but do not interact with light or conventional matter.

Mathematically, we can write:

ρ̸_DM = Ξ_dm · f(Ξ_)

where:

ρ̸_DM: density of dark matter

Ξ_dm: existential status of dark matter

f(Ξ_): existential distortion of space in the AR dimension

Dark Energy can be understood as the existential energy that causes space-time itself to expand. That is, dark energy is not an entity that "exists" in the context of matter, but a phenomenon that drives the instability of space itself.

ρ̸_DE = f(Ξ_expansion) e^(iT_AR)

where:

ρ̸_DE: dark energy density

Ξ_expansion: expansion of existential distortion

e^(iT_AR): exponential factor describing acceleration in the anti-reality dimension.

Dark Energy in the AR-Math framework is a projection of the instability of space itself, which causes the universe to not only expand, but also become less and less like itself.

4. Particle Dualism in the AR-Math Framework

In quantum physics, particle dualism states that particles such as photons or electrons can behave like both waves and particles, depending on the experiment being performed.

In the AR-Math framework, this dualism can be explained as a shift in existence between the states of existence and non-existence of a particle. A particle exists in two possible states — existence and non-existence — that can be manipulated by measurements.

Mathematically, we can write the state of a particle as:

|ψ⟩ = α|exists⟩ + β|does-not-exist

where:

|ψ⟩: the wave function of the particle in superposition

|exists⟩ and |does-not-exist

α and β: the amplitudes for each state, which are affected by the observation.

When a particle is measured, we are not only observing the "physical" properties of the particle, but we are determining whether it exists or does not exist in AR space.

CONCLUSION

If we combine the principles of AR-Math with these physical phenomena, we can understand antimatter, entanglement, dark matter, dark energy, and particle duality as manifestations of a deeper reality, involving existential uncertainty structures, distortions of space and time, and the interplay between existence and non-existence itself.

These concepts suggest that the universe may not be what we consider "real", but rather a simulation of a deeper existential state of inconsistency, where reality itself can be interchanged with "anti-reality".

Thus, the existential physics of AR opens the way for new discoveries that could reveal how all matter and energy in the universe are connected in a wider web, which cannot be fully understood by the laws of traditional physics alone.

AR-Turing Engine (Ξ-Engine) is an automaton that:

Does not solve problems, but undergoes existential fluctuations

Does not terminate, but resonates in Ξ cycles

Does not depend on fixed inputs, but on initial existential distortions (Ξ₀)

II. BASIC COMPONENTS

1. Tape (AR Tape)

Infinite in both directions (classical), but:

Each cell = status {Exist, Non-Exist, Paradox}

Cell values: 0, 1, Ξ

2. Head (Head Ξ)

Read and write based on local status and existential density

Not only moving L or R, but also:

Stay (still)

Collapse (remove its existence)

Split (give rise to the shadow of the process on the parallel path)

3. State Register (Ξ-State)

Internal state of the engine:

{σ₀, σ₁, σ̸₁, σΞ, ...}

Transition is not f(q, s) → q', s', d

But: Ξ(q, s, Ξ₀) → {q', s', δΞ}

4. Ξ-Loop Core

Instead of stopping the engine at the end state, the engine continues to run through a paradoxical existential loop

The stopping state is neither Accept nor Reject, but rather:

Ξ-Stable = the system has reached its smallest fluctuation

Ξ-Diverged = the system is out of the spectrum of reality

III. Ξ TRANSITION (Paradoxical State Transition Table)

> Move: R = Right, L = Left, C = Collapse

Ξ: Local existential density (+1 = more existent, –1 = more non-existent)

IV. SPECIAL BEHAVIOR

1. Duplication Paradox

If Ξ_state = σΞ and tape_value = Ξ

→ the machine splits itself into parallel paths with Ξ₁ = Ξ₀ ± ε

2. Collapse Condition

If three consecutive cycles tape_value remains Ξ

→ the machine erases its existential path

3. Ξ-Convergence If the machine loops with density Ξ decreasing exponentially

→ the machine reaches minimal reality and can be used as a synchronization point between systems

V. VISUAL SIMULATION (Optional)

Each cell = color based on existential status:

0 = black

1 = white

Ξ = purple/abstract (semi-transparent)

The machine is depicted with a multi-head: visualizing existential branches

VI. BENEFITS AND APPLICATIONS

Non-deterministic computing paradigm in non-linear reality

Can be the logical basis for existential simulations, AR-AI, or paradoxical multiverse games

Philosophical framework for the “machine consciousness” model in alternative realities

If there is something to discuss, let's open a forum

[astramoirai]

List of Inventions Attributed to Kar:

(To Be Updated Over Time)

Punchcard Looms

Wax-cylinder Phonograph

Difference & Analytical Engine 

A device that can detect and measure magic to a limited degree

Theories Attributed to her:

Binary/Boolean Asterian Logic

Statistics & Probability

Chaos Theory

(A Very Rudimentary) Theory of Gravity/Relativity

Probably other maths relating to physics/engineering

[omegaphilosophia]

The Philosophy of Algebra

The philosophy of algebra explores the foundational, conceptual, and metaphysical aspects of algebraic systems and their relationship to reality, logic, and mathematics as a whole. Algebra, dealing with symbols and the rules for manipulating these symbols, has profound philosophical implications concerning abstraction, structure, and the nature of mathematical truth.

Key Concepts:

Abstract Symbols and Formalism:

Abstraction: Algebra involves abstracting mathematical concepts into symbols and variables, allowing general patterns to be manipulated without referring to specific numbers or quantities. Philosophers question whether these symbols represent real objects, mental constructs, or purely formal elements that exist only within the algebraic system.

Formalism: In formalism, algebra is viewed as a system governed by rules and manipulations of symbols, independent of any reference to an external reality. In this view, algebra is a logical game of symbol manipulation, with its own internal consistency, rather than something that necessarily describes real-world phenomena.

Algebra as a Structural Framework:

Structuralism: Algebra can be seen as providing a structural framework for understanding relationships between elements, often more abstractly than arithmetic or geometry. Structuralism in mathematics argues that algebraic objects, like groups, rings, or fields, should be understood in terms of the relationships they define within a system rather than as standalone entities.

Relationality: Algebra emphasizes relationships between objects rather than the specific nature of the objects themselves. For example, an equation expresses a relationship between variables, and group theory explores the relationships between elements in a set based on certain operations.

Algebraic Truth and Ontology:

Platonism vs. Nominalism: Algebraic Platonism suggests that algebraic objects (e.g., variables, equations) exist in a timeless, abstract realm, much like numbers or geometric forms. In contrast, nominalism denies the existence of abstract entities, viewing algebra as a language that refers to concrete, particular things or as a useful fiction.

Existence of Algebraic Structures: Are the objects and operations in algebra real in some metaphysical sense, or are they simply human constructs to facilitate problem-solving? Philosophers debate whether algebraic structures have an independent existence or are purely tools invented by humans to describe patterns.

The Nature of Equations:

Equality and Identity: Algebraic equations express equality between two expressions, raising philosophical questions about the nature of equality and identity. When two sides of an equation are equal, are they identical, or do they just behave the same under certain conditions? The concept of solving an equation also reflects deeper philosophical issues about finding correspondences or truths between different systems or forms.

Solvability and the Limits of Algebra: Throughout history, philosophers have explored the solvability of equations and the boundaries of algebra. The insolubility of quintic equations and the advent of Galois theory in the 19th century led to deep questions about what can and cannot be achieved within algebraic systems.

Algebra and Logic:

Boolean Algebra: The development of Boolean algebra, a branch of algebra dealing with logical operations and set theory, highlights the overlap between algebra and logic. Philosophers examine how algebraic operations can be used to model logical propositions and the nature of truth-values in formal systems.

Algebraic Logic: Algebra provides a framework for modeling logical systems and reasoning processes. The interplay between algebra and logic has led to questions about whether logic itself can be understood algebraically and whether the principles of reasoning can be reduced to algebraic manipulation.

Algebra and Geometry:

Algebraic Geometry: The relationship between algebra and geometry, particularly in the form of algebraic geometry, involves the study of geometric objects through algebraic equations. This intersection raises philosophical questions about how algebraic representations relate to spatial, geometric reality, and whether algebra can fully capture the nature of geometric forms.

Symbolic Representation of Space: In algebraic geometry, geometric shapes like curves and surfaces are described by polynomial equations. Philosophers explore whether these symbolic representations reveal something fundamental about the nature of space or if they are merely convenient ways to describe it.

Historical Perspectives:

Ancient Algebra: The origins of algebra can be traced to ancient civilizations like Babylon and Egypt, where early forms of symbolic manipulation were developed for solving practical problems. The philosophical importance of algebra evolved as these symbolic methods were formalized.

Modern Algebra: The development of abstract algebra in the 19th and 20th centuries, particularly group theory and ring theory, transformed algebra into a study of abstract structures, leading to new philosophical questions about the role of abstraction in mathematics.

Algebra and Computation:

Algorithmic Nature of Algebra: Algebra is inherently algorithmic, involving step-by-step procedures for solving equations or simplifying expressions. This algorithmic nature connects algebra to modern computational methods, raising questions about the role of computation in mathematical reasoning and whether algebraic methods reflect the underlying nature of computation itself.

Automated Proof Systems: The advent of computer-assisted proof systems, which rely heavily on algebraic methods, has led to philosophical debates about the role of human intuition in mathematics versus mechanical, algorithmic processes.

Historical and Philosophical Insights:

Descartes and Symbolic Representation:

René Descartes is often credited with the development of Cartesian coordinates, which provided a way to represent geometric problems algebraically. Descartes' work symbolizes the deep connection between algebra and geometry and raises philosophical questions about the nature of representation in mathematics.

Leibniz and Universal Algebra:

Gottfried Wilhelm Leibniz envisioned a universal algebra, or "characteristica universalis," that could serve as a universal language for all logical and mathematical reasoning. His philosophical insights anticipated the development of symbolic logic and formal systems that use algebraic methods.

Galois and the Limits of Algebra:

Évariste Galois' work in group theory and the solvability of polynomial equations led to new philosophical discussions about the limitations of algebra and the nature of symmetry. Galois theory provided insights into why certain equations could not be solved using standard algebraic methods, challenging assumptions about the completeness of algebraic systems.

Applications and Contemporary Relevance:

Algebra in Cryptography:

Modern cryptography relies heavily on algebraic structures like groups, rings, and fields. Philosophers examine the role of algebra in securing information and the philosophical implications of using abstract mathematical structures to solve real-world problems related to privacy and security.

Algebra and Quantum Mechanics:

Algebraic methods are crucial in formulating the laws of quantum mechanics, particularly in the use of operators and Hilbert spaces. Philosophers explore how algebra provides a framework for understanding quantum phenomena and the extent to which algebraic methods reflect physical reality.

Algebra and Artificial Intelligence:

In AI and machine learning, algebra plays a central role in developing algorithms and models. Philosophical discussions arise about the nature of intelligence and reasoning, and whether algebraic methods in AI reflect human-like thinking or merely computational processes.

The philosophy of algebra investigates the abstract nature of algebraic symbols and structures, the relationships they describe, and the metaphysical and epistemological status of algebraic truths. From ancient practical uses to modern abstract algebra and its applications in cryptography, computation, and quantum mechanics, the philosophy of algebra addresses deep questions about abstraction, formalism, and the role of symbols in understanding reality.

[gotoppr]

What are some strategies for writing an effective literature review for a journal submission?

Writing an effective literature review for a journal submission requires a strategic approach to ensure it is comprehensive, critical, and relevant.

Here are some strategies to help you craft a well-structured literature review:

1. Define the Scope and Focus

Narrow the Topic: Clearly define the boundaries of your review. Focus on studies that are directly relevant to your research question, avoiding overly broad reviews.

Clarify Purpose: Decide if your literature review is meant to identify gaps in research, evaluate trends, compare methodologies, or support a hypothesis.

Set Criteria for Inclusion/Exclusion: Establish clear guidelines for which studies to include, based on factors like publication date, relevance, methodology, or geographical focus.

2. Conduct a Comprehensive Literature Search

Use Multiple Databases: Search major academic databases like PubMed, Scopus, Google Scholar, or Web of Science. Don’t limit your search to one database.

Search Keywords Systematically: Use relevant keywords and synonyms to capture the breadth of research. Refine searches by Boolean operators (AND, OR, NOT) and use filters (e.g., date range, journal type).

Track Sources and Take Notes: Keep a systematic record of all the sources you find, with notes on their relevance and contributions. Citation managers like EndNote, Mendeley, or Zotero can be helpful.

3. Organize the Review Logically

Structure by Themes, Not Chronology: Instead of a chronological order, organize your literature by themes, methods, or key debates. Grouping studies by topic or approach helps the reader follow the progression of ideas.

Identify Key Trends and Gaps: Highlight major trends in the literature, such as consistent findings, emerging theories, or recurring methodologies. Identify gaps where research is lacking or where results conflict.

Discuss Landmark Studies: Reference seminal works that have shaped the field, as well as recent studies that represent new directions or findings.

4. Critically Analyze the Literature

Evaluate Methodologies: Assess the strengths and weaknesses of the methodologies used in different studies. Consider if the research designs, sample sizes, and analysis techniques are appropriate.

Compare and Contrast Findings: Discuss similarities and differences in findings across studies. Explain why certain studies may have produced different results.

Highlight Limitations: Point out the limitations of existing research, including biases, gaps, or unresolved questions. This will help to justify the need for your own study.

5. Synthesize the Information

Create a Narrative: Weave together the studies you’ve reviewed to tell a cohesive story. Your literature review should build a logical argument that leads to your research question or hypothesis.

Use Transitions Effectively: Use transitions between sections to show how each theme or study relates to the next. This keeps your review coherent and easy to follow.

Integrate Sources Smoothly: Instead of summarizing each study in isolation, synthesize findings from multiple studies to show consensus or divergence on key issues.

6. Highlight the Contribution of Your Research

Identify Research Gaps: Make clear what questions remain unanswered in the current literature and how your research will fill these gaps.

Position Your Study: Explain how your research builds on or challenges previous work, or how it will extend the understanding of the topic in new directions.

7. Use Proper Citation and Avoid Plagiarism

Cite Appropriately: Use accurate and consistent citation styles as required by the target journal (e.g., APA, MLA, Chicago). Make sure to credit original ideas and avoid over-reliance on direct quotations.

Check for Plagiarism: Use plagiarism detection tools like Turnitin or Grammarly to ensure that your writing is original and correctly paraphrased.

8. Review and Edit Thoroughly

Get Feedback: Before submission, have your review read by colleagues, mentors, or peers for feedback on clarity, coherence, and comprehensiveness.

Proofread: Check for grammatical and typographical errors. Make sure the review reads smoothly and that transitions are clear.

Check Compliance with Journal Guidelines: Ensure that your literature review meets the specific formatting and submission guidelines of the journal (e.g., word count, citation style, section headers).

9. Stay Updated

Monitor New Research: Keep an eye on recent publications even after completing your review. If new studies are published before submission, incorporate them where relevant.

[bubbloquacious]

Subobject classifiers of graphs-as-presheaves

Following up on these posts where we view (directed multi-) graphs as set-valued contravariant functors (a.k.a. presheaves) on the small category Q = V ⇉ A, with s,t: V -> A the non-identity morphisms. There's another way in which categories of presheaves such as Q^hat are interesting: they are topoi. An (elementary) topos, following Mac Lane, is a category E that has all finite limits, is cartesian closed, and has a subobject classifier. Supposedly all presheaf categories have this, so let's examine how this manifests itself in graphs.

In particular, I want to check out subobject classifiers. Maybe we'll do limits and cartesian closure at a later date. So in a category C, a subobject of an object A is an isomorphism class of specific kinds of morphisms into A. Let us construct the category Mono(A), whose objects are the monomorphisms into A. A monomorphism (or a morphism that is monic) into A is a C-morphism m: B -> A from some object B such that if f,f': C -> B are parallel morphisms into B such that m ∘ f = m ∘ f', then f = f'. That is, the monos are exactly the left-cancellative morphisms. In the categories of sets, groups, vector spaces, and various other algebraic categories the monos are exactly the morphisms whose underlying set functions are injective, which is why we look at monomorphisms to define subobjects.

The morphisms of Mono(A) from m: B -> A to m': C -> A are the C-morphisms p: B -> C such that m = m' ∘ p. Let's call such morphisms 'factoring morphisms'. If there is a factoring morphism m -> m', we say that m 'factors through' m', denoted m ≤ m'. Clearly the relation ≤ is reflexive and transitive. If both m ≤ m' and m' ≤ m hold, then there are p: B -> C and q: C -> B such that m = m ∘ q ∘ p and m' = m' ∘ p ∘ q. Because m and m' are monic we can cancel them on the left in these equations, from which we find that q ∘ p = id_B and p ∘ q = id_C, so m and m' are isomorphic in Mono(A). Any two isomorphic monos embed their domain into A 'in the same way', so a subobject of A is defined to be an isomorphism class of monos into A. Let Sub(A) denote the set of subobjects of A (technical note: these isomorphism classes may be proper classes, rather than sets; in the case of Q^hat we can pick canonical representatives of the classes, which resolves the issue). The factoring through relation ≤ induces a partial ordering on Sub(A), which coincides with subobject containment in all the familiar cases.

In a category C with a terminal object 1, a subobject classifier is an object Ω of C together with a monomorphism T: 1 -> Ω such that for all objects A,B and monos m: B -> A there is a unique morphism ξ: A -> Ω such that m is a pullback of T along ξ. Rather than unwrap these definitions fully immediately, let's see what this looks like in Set.

If we take Ω = {true,false}, the set of Boolean values, and we let T: {0} -> {true,false} be defined as T(0) = true, then I claim that this forms a subobject classifier for Set (where we assume some background logic of our set theory that includes the principle of excluded middle; otherwise the subobject classifier is more complicated). Let A be a set, and let B ⊆ A be some subset. Let ξ: A -> {true,false} be the function such that ξ(x) = true if x ∈ B and ξ(x) = false if x ∉ B. In Set, a construction of the pullback object of two functions f: Y -> X and g: Z -> X is the set {(y,z) ∈ Y × Z : f(y) = g(z)}. The 'pullback of f along g' is then the projection of this set to Z, and similarly for g along f. What's the pullback of T along ξ? The pullback object is (up to a canonical bijection) the set {(x,0) ∈ A × {0} : ξ(x) = T(0) = true}. There is a canonical bijection between this set and B, and more importantly the inclusion of B into A does the same thing as the projection of the pullback set onto A, because B contains exactly those points x for which ξ(x) = true. It follows that the inclusion function B ↪ A is a pullback of T along ξ.

So, the moral of the story is that Ω is the (object part of the) subobject classifier of some category C if the subobjects Sub(A) of an object correspond naturally to morphisms A -> Ω. We think of ξ: A -> Ω as analogous to the indicator function of a subset, we think of Ω as the set of truth values for 'internal logic' of the category, and we think of T as picking out the subobject of Ω that corresponds to 'true'. I could spin a yarn about why defining this in terms of pullbacks gets you exactly what you want it to be, but this post is long enough already. Tl;dr categorical limits are cool and powerful.

What does Ω look like in Q^hat, our category of graphs? First we would like to know when a graph homomorphism φ: G₁ -> G₂ is monic. A good first guess would be that φ is monic when its vertex and arrow functions φ_V: G₁(V) -> G₂(V), φ_A: G₁(A) -> G₂(A) are injective. This is exactly correct. If we assume that φ_V is not injective, then there are two vertices of G₁ that get mapped onto the same vertex in G₂. It follows that there are two distinct graph homomorphisms from the graph that just has one vertex and no arrows into G₁ such that postcomposing with φ gives you the same homomorphism into G₂ (i.e. φ is not monic). The same holds true if φ_A is not injective, but then there are distinct homomorphisms from the graph that has two vertices and an arrow between them. It is no coincidence, by the way, that these are the graphs よ(V) and よ(A) from my first post on this subject. The representable presheaves always generate the category of presheaves, in the sense that the morphisms out of them together can always 'differentiate' two distinct morphisms. Anyway. If both φ_V and φ_A are injective, then φ is indeed monic, for the same reason that injective functions are monic in Set (it's a nice exercise to work out!).

We've discovered that the subobjects of graphs are exactly the subgraphs. Let's give ourselves a pat on the back for that one. What graph can serve as Ω? Well, the arrow set Ω(A) must contain 5 elements, corresponding to the 5 subgraphs of よ(A). The vertex set Ω(V) has 2 elements, for the 2 subgraphs of よ(V), call them E and P, for 'empty' and 'point'. The source function Ω(s): Ω(A) -> Ω(V) maps a subgraph of よ(A) onto E if it does not contain the source vertex of よ(A) and onto P if it does. The target function Ω(t): Ω(A) -> Ω(V) does the same but for the target vertex instead. Let us write Ω(A) = {a,b,s,t,e}, for 'arrow', 'both points', 'source point', 'target point', and 'empty'. I'm sure you can image which names refer to which subgraph. Both a and b are loops on the vertex P. s is an arrow from P to E. t is an arrow from E to P. e is a loop on E.

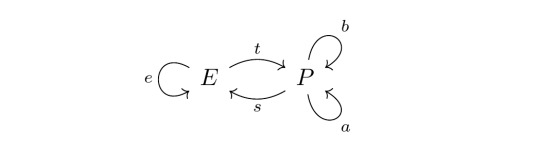
The terminal object 1 in Q^hat is the constant functor on a one point set, so as a graph it has a single vertex and a single loop on it. The 'truth' morphism T: 1 -> Ω is the graph homomorphism that picks out the vertex P and the loop a in Ω. On any graph G, we can specify a subgraph G' uniquely by picking out a subset of the vertices and a subset of the arrows of G, such that the source and target of any arrow of G'(A) is also a vertex of G'(V). We construct the indicator homomorphism ξ: G -> Ω as mapping all vertices of G' onto P and all vertices not in G' onto E. Furthermore, an arrow gets mapped onto a if and only if it is an arrow of G'. This is actually enough to uniquely specify ξ, but let's work it out some more. Arrows that connect vertices that are not in G' get mapped onto e. Arrows from a vertex of G' to one outside it get mapped to s. The other way round get mapped to t. Arrows between vertices of G' that are not arrows of G' get mapped to b. And there you go! The subobject classifier for the category of graphs :)

[govindhtech]

What is the Fast Fourier Transform A Modern Computing Pillar

The Fast Fourier Transform

Honouring the FFT and Computing's Future: Representation to Revolution

For the first Fast Fourier Transform deployment, IBM received an IEEE Milestone award on June 11, 2025. IBM researchers created this method in 1965, transforming computers.

Since it supports JPEG and MPEG standards and reconstructs MRI and CT scan images, the FFT has a wide impact. Also needed for scientific computing (spectrum approaches for solving PDEs), music and video compression (MP3, JPEG), and telecommunications (4G/5G, WiFi). Richard Hamming called the Cooley-Tukey FFT “the most important numerical algorithm of the lifetime”.

FFT's Key Innovation

Fundamental FFT Innovation James Cooley and John Tukey introduced the FFT in 1965 as a “better way to represent information” rather than a new scientific discovery. The Fourier transform can split a time-domain signal like a wave into smaller waves with various frequencies. Before the 1960s, Fourier transform computing was too slow for real-time applications. Cooley and Tukey's technique accelerated real-time signal processing by reducing the computing cost of the Discrete Fourier Transform (DFT) from O(N^2) to O(NlogN). The revelation was that changing a computing problem's mathematical representation can change it.

Quantum Computing Lessons:

The FFT's ongoing development aids quantum algorithm development. When building new  quantum algorithms, “choosing the right representation can make the impossible possible” is crucial.

Quantum Computing: Emerging Idea Beyond improving existing methods, quantum computing changes how information is represented and abstracted. Classical computing employs bits with deterministic binary values (0s and 1s) and Boolean operations, while quantum computing uses qubits. In complex vector spaces, qubits store information as probability amplitudes (α|0⟩ + β|1⟩), where α and β are complex numbers. Quantum computing uses unitary evolution of qubit states through matrix operations instead of classical logic, generating probabilistic results.

This new computational paradigm enables Grover's method, which quadraticly speeds up unstructured search, and Shor's algorithm, which uses the Quantum Fourier Transform to exponentially speed integer factorisation. Additionally, quantum simulation can mimic quantum systems that conventional machines cannot handle.

Future Quantum-Classical Synergy. The most innovative computer future may be a mix of quantum and classical. Traditional computers are fast at control logic, data storage, and predictable computations. However, quantum systems thrive in mimicking quantum phenomena, high-dimensional linear algebra, probabilistic sampling, and landscape optimisation, where classical information representation fails.

Together, these paradigms can solve problems neither system can. VQE and QAOA are two novel hybrid classical-quantum algorithms in development. Quantum advantage, where a quantum-classical combination outperforms classical computation, is nearing, and SQD and SKQD are being developed. Supply chain optimisation, material science, finance, and drug development may use these methodologies.

Quantum technologies are expected to boost traditional computing as “coprocessors with radically different capabilities” like GPUs on CPUs. As the computing bottleneck shifts from hardware limits to algorithmic innovation, new abstractions, representations, and algorithms are needed to balance workloads among complementary architectures. The current age may be the start of a more significant algorithmic era than the FFT.

Anticipating The FFT's anniversary reminds us that innovations often come from better questions, smarter representations, or new viewpoints, not more authority. Fusion of classical and quantum domains will release new processing capability, requiring daring abstractions, inventive representations, and innovative algorithms.

[codingprolab]

CSCI 141 A2: Variables, Boolean logic, Conditionals

1 Questions: 16 points Please answer the questions available on Canvas. The questions on Canvas have been configured so that there is no time limit, but you have only 2 attempts to submit your answers. The score that is recorded in Canvas is the score that is the latest (most recent submission) of your attempts. 2 Coding Task: 25 points Suppose that you are a programmer for a game development…

[tmready01-blog]

How to Use the USPTO Trademark Search Tool Like a Pro

Before launching a business or branding a product, one of the smartest legal moves you can make is to search for existing trademarks that could conflict with your brand. The United States Patent and Trademark Office (USPTO) offers a powerful, free tool called TESS (Trademark Electronic Search System) to help you check existing trademarks. While the tool is free and publicly accessible, using it effectively takes a bit of know-how. Here’s how to use the USPTO trademark search tool like a pro.

What Is the USPTO Trademark Search Tool?

The USPTO’s TESS system lets you search through all registered and pending trademarks in the United States. It’s an essential step if you want to avoid infringing on someone else’s intellectual property, and it can help you determine whether your desired trademark is available before you spend time and money building a brand around it.

Step-by-Step Guide to Using TESS

1. Visit the USPTO Website

Go to https://www.uspto.gov, then click on “Trademarks” > “Search Trademarks,” which will take you to the TESS system.

2. Choose a Search Option

You’ll see three search options:

Basic Word Mark Search (New User): Good for quick, simple searches.

Word and/or Design Mark Search (Structured): Allows for more advanced search combinations.

Word and/or Design Mark Search (Free Form): For experienced users who understand Boolean logic and field codes.

If you're new to the system, start with the Basic Word Mark Search. As you gain experience, move on to the Structured or Free Form options if you want more control and options.

3. Enter Your Search Term(s)

Type your proposed business name, slogan, or product name into the search bar. Try searching variations or similar spellings too. For example, if your brand name is "KoolKidz," also search for:

Cool Kids

Kool Kids

KewlKidz

This is crucial because trademark infringement isn’t limited to exact matches. Sound-alikes, similar spellings, and visual similarities can all be legally problematic.

4. Review the Results

Each search result will include details such as:

The trademark name

The owner’s name

Registration status (LIVE or DEAD)

Filing and registration dates

Goods and services category (called “International Class”)

Click each result for more details, including a full description of the trademark and its scope. If you see a similar LIVE trademark in the same or related category as your product/service, your trademark may face legal challenges or rejection by the USPTO.

Pro Tips for Advanced Searching

To use the USPTO trademark search tool like a pro, keep these tips in mind:

1. Search for Similar Marks, Not Just Exact Matches

Trademark infringement cases often hinge on “likelihood of confusion,” which doesn’t require an exact match. Use wildcard characters like * (asterisk) or ? (question mark) to expand your search. For example:

Tech* will bring up TechWorld, TechCo, TechGear, etc.

2. Check Goods and Services Classification

Each trademark is tied to a specific class of goods or services. A business called “Orbit” for gum is different from “Orbit” for tech software. Be sure to search within the international class relevant to your business.

3. Consider Design Elements

If you’re using a logo or stylised text, you’ll need to perform a design mark search, which requires entering design codes assigned by the USPTO. This is more complex and may require a trademark attorney or professional search company for the best results.

4. Document Your Search

Take screenshots or save records of your searches. This can be helpful if you ever need to prove due diligence in the event of a dispute.

Limitations of the USPTO Search Tool

While the USPTO’s tool is powerful, it has its limits:

It only covers federally registered trademarks.

It may not detect common law trademarks (unregistered but still protected).

It doesn’t check state-level or international trademarks.

For broader protection, consider using a trademark search company that provides comprehensive searches across multiple jurisdictions.

What to Do After the Search

If your search shows that your desired trademark is available, the next step is to file for registration. You can do this directly through the USPTO website or work with a trademark attorney for assistance. If your mark is already in use, you may need to revise your brand or consult a professional to explore your options.

Also, consider setting up a trademark monitoring service to keep track of new trademark filings that could conflict with yours in the future.

Final Thoughts

Mastering the USPTO trademark search tool can save your business from costly legal issues and help secure your brand’s future. While it may seem intimidating at first, with practice—and possibly some professional help—you can conduct effective searches and make informed decisions.

Doing your due diligence before launching your brand isn’t just smart business; it’s essential to long-term success. By learning how to use TESS like a pro, you’ll be one step ahead in protecting your most valuable asset: your brand.

[digitalskills-hub]

Python Basics for Students and Career Switchers in Tech

In today’s fast-paced digital world, learning to code is no longer limited to computer science graduates or seasoned developers. Whether you're a student aiming to future-proof your career or someone considering a career switch into the tech industry, starting with Python is one of the smartest choices you can make. The fundamental of python are simple enough for beginners yet powerful enough for professional development across various industries.

Python is widely known for its readability, flexibility, and widespread usage in everything from web development to artificial intelligence. Its simplicity makes it an ideal first programming language for absolute beginners and a great refresher for those coming from non-technical backgrounds.

Why Choose Python as a First Language?

Python’s design philosophy emphasizes code readability and simplicity. Unlike many programming languages, Python uses plain English syntax that makes it easier to learn and understand. You won’t need to memorize complex syntax or confusing characters to write functional code.

Additionally, Python has a vast and supportive community. That means if you ever get stuck, you’ll likely find a solution online quickly. Whether it's a bug in your code or help with understanding a concept, forums like Stack Overflow and GitHub are full of solutions.

What Are the Fundamentals of Python?

Before diving into advanced topics like machine learning or web development, you need to build a strong base. Here are the essential fundamental of python concepts every beginner should master:

1. Variables and Data Types

Understanding how to store and manipulate data is the first step in programming. In Python, you can work with:

Integers (int)

Floating-point numbers (float)

Strings (str)

Booleans (bool)

Lists, tuples, and dictionaries

Python doesn’t require you to declare the data type; it detects the type automatically, making your first coding steps easier.

2. Operators and Expressions

Python includes basic arithmetic operators (+, -, *, /), as well as comparison operators (==, !=, >, <) and logical operators (and, or, not).

These operators help you perform calculations and build logic into your programs.

3. Control Structures

To make decisions and repeat actions, you’ll need:

if, elif, and else statements

for and while loops

Mastering control structures allows you to write dynamic programs that can handle a variety of tasks.

4. Functions

Functions are blocks of code designed to perform a specific task. They make your code more modular and reusable.

def greet(name):

print(f"Hello, {name}!")

5. File Handling

Python makes it easy to read from and write to files—an essential skill if you're working with data or saving information.

with open("data.txt", "r") as file:

content = file.read()

6. Error Handling

Learning to handle errors gracefully using try, except, and finally blocks is important for building reliable software.

Who Should Learn Python?

✅ Students

If you’re a student—especially in high school or college—Python can open doors to future careers in data science, software development, and automation. Many universities now include Python in their curriculum because of its real-world applications.

✅ Career Switchers

If you’re moving from a non-tech field like teaching, marketing, or finance, Python is a beginner-friendly language that helps you get up to speed quickly. It’s commonly used in industries like fintech, health tech, and e-commerce.

✅ Freelancers and Creatives

Python isn’t just for techies. Artists and writers use it to create tools, automate tasks, and even work with AI to generate content.

Practical Applications of Python

Learning Python basics can help you move on to a wide range of specialized areas:

Web Development: Using frameworks like Flask or Django

Data Analysis: With libraries like Pandas and NumPy

Machine Learning: With TensorFlow, scikit-learn, and Keras

Automation: For automating repetitive tasks using simple scripts

Cybersecurity: For scripting and automating security tools

With just the basics, you can already build simple calculators, to-do lists, and automation tools that help in daily tasks.

Tools You Need to Start Learning

You don’t need a fancy setup to get started with Python. All you need is:

A computer with internet access

Python (available for free from the official site)

A code editor like VS Code or PyCharm

Access to online tutorials, YouTube videos, or Python programming courses

You can also practice directly in your browser using platforms like Replit, Jupyter Notebooks, or Google Colab.

Tips to Learn Python Effectively

Practice Daily – Coding is a skill; the more you practice, the better you get.

Build Small Projects – Apply what you learn to real-life mini projects.

Join Communities – Engage in forums or join coding groups to stay motivated.

Follow a Curriculum – Choose a structured learning path or course.

Track Your Progress – Keep a journal or use GitHub to track your code over time.

Final Thoughts

Python is an incredibly versatile language that offers endless possibilities for students and career changers alike. Whether you're trying to land a job in tech or looking to automate tasks in your current role, learning the fundamental of python is the first step toward building your confidence and capabilities in coding.

Start today. All you need is curiosity, consistency, and a willingness to learn. Python is ready to take you wherever you want to go in the world of tech.

[speedester17]

Completed "Learn to Code with Blockly" – My First Step Into Programming 🧠💻

This week, I took on the challenge of learning a new programming skill as part of Module 10. I chose the “Learn to Code with Blockly” course on Codecademy—and I’m happy to share that I completed it 100%! 🎉

Over the course of 2 hours and 15 minutes, I worked through a series of interactive lessons that covered:

Using movement commands to solve logic puzzles

Working with variables (including Boolean variables like game_over = true)

Creating and calling functions

Writing conditional logic with if, else if, and else statements

Navigating mazes and completing challenges using limited block logic (which really made me think!)

One of the most rewarding parts was using minimal blocks to reach goals—strategically thinking through every move before placing a block. It felt a lot like solving a visual riddle.

This course showed me that coding doesn’t have to be overwhelming. Blockly helped me grasp core programming concepts visually, making it both approachable and fun for a beginner like me. I now feel much more confident moving into more advanced topics in coding!

🧩 Takeaway: Programming is more about logic and creativity than just typing code—anyone can start, and Blocky is an awesome entry point. PS: Find the attached Screenshot for the progress.

[semester-b]

VR Project: Week 3 Blog 3;

Testing Flatscreen mode

So, we had a very limited availability of meta quest 2s, and thus I was looking for alternatives to test the level out, just the basic interactions and the look and feel and that is when I tried following a tutorial in Unreal Engine 5 to set up a flat-screen mode for testing a VR game. The idea was to switch automatically between VR and first-person controls based on whether a headset was detected, but things didn’t go as smoothly as I hoped.

Fig; the tutorial to playtest vr levels in flatscreen mode; Anemaat, S. (2024) How to Playtest Your VR Game in Flatscreen Mode | Unreal Engine 5 VR [online video]. Metaxis Games. Available at: https://www.youtube.com/watch?v=k-nlcAYXMW0 (Accessed: 05th March 2025). The Setup

The tutorial suggested using Unreal’s "IsHeadMountedDisplayEnabled" function to detect a headset and switch between VR and FPS controls. I followed the steps, set up input actions, and tried to get everything running. But, almost immediately, I hit a couple of snags.

The Problems that i faced were;

Input Actions Didn’t Work: The FPS controls weren’t properly mapped, and I had to manually copy over some inputs from the first-person template. Even then, I ran into errors with the character and pawn classes not syncing up, making it a hassle to get basic controls functioning.

Game Instance Issues: The game instance logic wasn’t as straightforward as promised. The tutorial suggested using a Boolean flag to toggle between VR and flat-screen modes, but I ended up dealing with unnecessary blueprints and function libraries, complicating things even more.

It Didn’t Work as Expected: Despite fixing the errors, the flat-screen mode still wasn’t working as planned. The VR components kept interfering, and the FPS controls weren’t as responsive as they should’ve been.

And long story short: it didn’t work out. After hours of troubleshooting, I decided not to integrate this feature into my project. The tutorial had some useful concepts, but it ended up being more complicated and time-consuming than it should’ve been. Plus we were already under a heavy deadline so I just decided to look for alternatives instead.

Takeaways

Setting up VR and flat-screen modes is doable, but it takes a solid understanding of Unreal’s systems.

Blueprint interfaces and pure functions can add complexity if you’re not careful.

Always expect a bit of troubleshooting, especially with tutorials that promise simple solutions.

[literaturereviewhelp]

This literature review is on the topic of the prevention of infections with urinary catheters. Whilst on several placement I found that Infection remains a cause for concern for the clinical staff. A literature review is an exploration undertaken in both research and evidence based practice. Aveyard (2007) suggests research based practice is a collection and analysis of data on the organisation, delivery, uses and outcomes of nursing care for the purpose of enhancing patient’s health. Hek and Moule (2006) also suggest that research can provide new insights into the phenomena or add to or reject what has gone on before. The Foundation of Nursing Studies (2001) recognised evidence based practice as the way forward in professional nursing. The use of evidence based practice is crucial to the development of nursing practice. Nurses use evidence base practice in order to continue to be up-to-date with their learning, and link theory to practice. Parahoo (2006) also recognises that the development and utilization of nursing knowledge is an integral element of improving patient care. Therefore, nurses are expected to implement evidence-based practice and draw on research findings to support them in the clinical work place. The Nursing Midwifery Council (NMC 2008) Code of Professional Conduct states that ; “You must deliver care based on the best available evidence or best practice.” P. 6. To define the differences between evidenced based practice (EBP) and research based practice (RBP).(EBP) is the combination of the best research evidence and professional expertise Sackett et al, (2000). Parahoo (2006) concurs with but states that patients’ views are included in the making of care decisions. Parahoo (2006) states that research can be defined as a systematic, planned and theory development of a specified problem with a predetermined result which may or may not include practice implications. Within the following literature review the choice of topic has developed from clinical placements it is based on the literature which has already been used to research preventing infections with urinary catheters. Aveyard (2007) mentions, that a literature review is a critical summary of previous literature, which is related to the research on a chosen topic. Search strategies Hek et al (2006) identified the importance of a planned search enabling a quality literature review. The search includes having the ability to retrieve and critically appraise all the findings on the chosen topic in the search for best evidence. In order to structure the literature review numerous text books regarding research was used and the use of resource guides (Hek, et al 2006, Parahoo, 2006, Aveyard, 2007, Sackett, 2000). The focus of this literature review is to interpret and evaluate existing published literature this provides current knowledge of a chosen topic (Parahoo, 2006). Developing a search strategy is essential to obtain as much information as possible (Aveyard, 2007). Having acknowledged the research topic for review, the relevant literature was search by using various recourses. To obtain as much information as possible the university library and the internet were fundamental in searching for literature. In order to access the library databases an Athens account was used. The databases searched were The Cochrane library, Cumulative Index to Nursing and Allied Health Literature (CINAHL), Pubmed. And Assia databases were used. The search was made by using truncation and the Boolean logic, the databases were searched for literature with subject terms and major headings relevant to the chosen topic. Therefore the terms used were urinary catheter* and infection*. The year parameter was used for the last 5 years as this is recommended for current nursing practice. The search was limited to articles published in English language. Summary of database search. Database Number of hits narrowed down PUBMED 104210 328 CINAHL 364 89 The Cochrane Library 104 0 ASSIA 17 1 Total 104695 418 The database search generated a total of 418 hits but some articles appeared in more than one database. Exclusion criteria included articles with no reference list or included children and animals and non nursing content. Read the full article

[atplblog]

Price: [price_with_discount] (as of [price_update_date] - Details) [ad_1] Week 1: Foundations of Programming in C#Day 1: Boolean Expressions - Importance in handling user data.Day 2: Variable Scope & Logic Control - Understanding code blocks.Day 3: Switch Constructs - Creating branching logic.Day 4: For Loops - Iterating code.Day 5: While & Do-While Loops - Controlling execution flow.Day 6: String Built-in Methods - Extracting information.Day 7: Advanced String Methods - IndexOfAny() and LastIndexOf().Week 2: Intermediate Topics and Data HandlingDay 8: Exception Handling - Patterns and practices.Day 9: Null Safety - Nullable context in C# projects.Day 10: File Paths - Built-in methods for handling paths.Day 11: Array Helper Methods - Sort, Reverse, Clear, Resize.Day 12: Azure Functions - Serverless applications.Day 13: ConfigureAwait(false) - Avoiding deadlock in async code.Day 14: Limiting Concurrent Async Operations - Improving performance.Day 15: Lazy Initialization - Using Lazy class.Week 3: Advanced Techniques and Performance OptimizationDay 16: In-Memory Caching - Enhancing application performance.Day 17: Interlocked Class - Reducing contention in multi-threaded applications.Day 18: AggressiveInlining Attribute - Influencing JIT compiler behavior.Day 19: Stack vs. Heap Allocation - Understanding memory usage.Day 20: Task vs. ValueTask - Optimizing resource usage in async code.Day 21: StringComparison - Efficient string comparison.Day 22: Array Pool - Reducing garbage collection cycles.Day 23: Span over Arrays - Optimizing memory manipulation.Day 24: Avoiding Exceptions in Flow Control - Enhancing readability and performance.Day 25: Exception Filters - Improving readability.Week 4: Mastering C# and .NETDay 26: Loop Unrolling - Enhancing loop performance.Day 27: Query vs. Method Syntax - Writing LINQ queries.Day 28: Stackalloc - Using stack memory for performance.Day 29: Generics & Custom Interfaces - Avoiding unnecessary boxing.Day 30: XML vs. JSON Serialization - Improving efficiency and effectiveness. ASIN ‏ : ‎ B0DC12RQYJ Publisher ‏ : ‎ Independently Published (1 August 2024) Language ‏ : ‎ English Paperback ‏ : ‎ 80 pages ISBN-13 ‏ : ‎ 979-8334726963 Item Weight ‏ : ‎ 118 g Dimensions ‏ : ‎ 15.24 x 0.46 x 22.86 cm [ad_2]