#Mathematics Assignment

[champak30]

What is a Straight Line in Mathematics?

Introduction:

 The concept of What is a straight line in Mathematics? is foundational. It is one of the simplest and most fundamental geometric shapes, yet its implications and applications are vast and profound. In this article I will try to explain into the concept of what is a Straight Line in Mathematics, exploring its definition, properties, equations, and significance in various mathematical contexts.

Explanation:

Definition of a Straight Line:

 In geometry What is a Straight Line?  is an infinite set of points which can be extended in both directions without any curvature. It has no thickness, no width, and no height; it is one-dimensional. The straight line is often considered the shortest distance between two points, a concept that is both intuitive and mathematically rigorous.

Historical Perspective:

The study of straight lines dates back to ancient civilizations. Euclid, a Greek mathematician, provided a systematic study of geometry in his work "Elements," where he defined a straight line as "a line which lies evenly with the points on itself." This definition, though simple, encapsulates the essence of straightness—consistency and uniformity in direction.

Basic Properties of a Straight Line:

1. Linearity

A straight line is characterized by its linearity, meaning it does not curve or bend. This property can be observed by plotting the line on a Cartesian plane, where it appears as a continuous line extending infinitely in both directions.

2. Infinite Length:

A straight line can be extended infinitely in both directions. This infinite nature is a key property that distinguishes lines from line segments, which have defined endpoints, and rays, which extend infinitely in only one direction.

3. No Thickness:

A straight line is one-dimensional. It has no thickness or width, making it an idealized geometric object. In practical terms, when we draw a line on paper, it will have some thickness, but mathematically, a line is considered to have zero width.

Equations of a Straight Line:

The representation of straight lines using equations allows for a precise mathematical description. There are several forms of the equation of a straight line, each with its own advantages depending on the context.

a. Slope-Intercept Form:

The slope-intercept form is one of the most commonly used equations of a straight line. It is given by:

y= mx+c

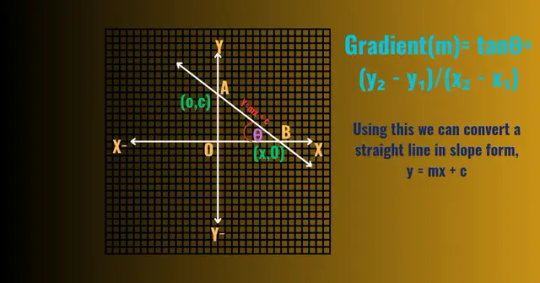
where m represents the slope or gradient of the line, Again m can be expressed as,

m = tanθ = (y₂ - y₁) / ( x₂- x₁),where θ = Inclination of the straight line,and(x₁,y₁), (x₂,y₂) are two points passes through the straight line.

and c represents the y-intercept. The slope m measures the steepness of the line, defined as the ratio of the rise (change in y) to the run (change in x). The y-intercept c is the point where the line crosses the y-axis.

For example, if we have the equation y = 2x+3, the slope(m) is 2, and the y-intercept(c) is 3. This means the line rises 2 units for every 1 unit it moves to the right, and it crosses the y-axis at the point (0, 3).

Some Problems related on Slope Intercept form of Straight line:

Question(1): The y-intercept and slope of a line is 5 and -1 respectively.Find the equation of the line.

Solution:  y-intercept(c) = 5

       Slope of the line (m) = - 1

∴ Equation of the line,

              y = mx + c

      => y = (-1)x + 5

      => y = - x + 5

    => x + y = 5

Question(2): If (2,3) and (-1,1) points lie on a straight line, find the slope of the line.

Solution:  ∵ x₁ = 2,   y₁ = 3

                   x₂ = -1,  y₂ = 1

     ∴ Slope of the line (m) = ( y₂ - y₁) /( x₂ - x₁)

                                         =  (1 - 3) /(-1 - 2)[putting values]

                                         = - 2/ -3

                                         = ⅔ 

b. Point-Slope Form:

The point-slope form is useful when we know a point on the line and its slope. It is given by:

y−y₁= m (x - x₁)

where (x₁,y₁) is a known point on the line, and m is the slope of the line.

For instance, if we know a line passes through the point (2, 3) with a slope of 4, the equation is:

y−3=4(x−2)

This can be simplified to the slope-intercept form if needed.

c. Standard Form:

The standard form of the equation of a linear straight line is:

Ax+By=C

where A, B, and C are constants. This form is particularly useful in solving systems of linear equations and in integer arithmetic.

For example, the equation 3x+4y=12

represents a straight line. We can convert this to the slope-intercept form to find the slope and y-intercept:

As we have,

    3x+4y=12

=> 4y = - 3x + 12

=> y = - ¾ x + 12/4

=> y = - ¾ x + 3

So, the slope of the straight line is −3/4  and the y-intercept is 3.

Some Problems related on Straight line:

Question(a):Find the slope and y-intercept of the given line, - x + 10 = 5y

Solution:   ∵ - x + 10 = 5y

               => y = - x /5 +10/5

               => y = - ⅕ x + 2

now comparing the above equation with y = mx + c

we get,

 Slope (m) = - ⅕ 

and y-intercept (c) = 2

Question(b):Gradient of a line is 2 and passes through the point (-3,1),find the equation of the straight line.

Solution: ∵ Gradient of the line(m) = 2

                   point = (-3,1)

   ∴ Equation of the straight line,

           y - y₁ = m(x - x₁)

       => y - 1 = 2{x - (-3)} [putting values]

      => y - 1 = 2 ( x + 3)

     => y - 1 = 2x + 6

    => - 2x + y -1- 6 = 0

   => - 2x + y - 7 = 0, which is the required equation of the straight line.

Question(c): The gradient of a straight line is -1 and y-intercept is 3, find the equation of the straight line.

Answer: Gradient (m) = - 1

              y-intercept (c) = 3

∴ Equation of the straight line will be,

         y = mx + c

    => y = (- 1)x + 3 [ putting value]

   => y = - x + 3

Graphical Representation:

Graphing a straight line involves plotting points that satisfy the line's equation and connecting them with a continuous line. The graphical representation provides a visual understanding of the line's behavior and properties.

1. Plotting Points:

To graph a line, we can start by choosing values for x and calculating the corresponding y values using the line's equation. Plotting these points on a Cartesian plane and connecting them gives us the line.

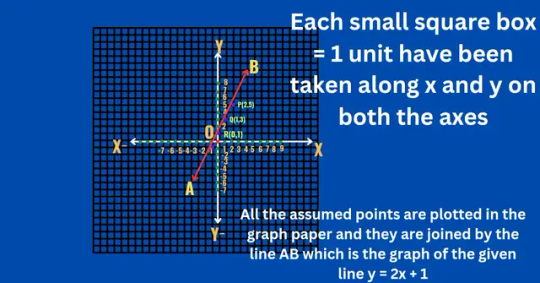
For example, for the line y=2x+1, 

we can choose x values such as -1, 0, 1, and 2, and find the corresponding y values:

When x=−1,then from above equation we get, y=2(−1)+1 = - 2 + 1 =−1

When x=0,then from above equation we get, y=2(0)+1= 0 + 1 =1

When x=1,then from above equation we get, y=2(1)+1 = 2 + 1 =3

When x=2,then from above equation we get, y=2(2)+1= 4 + 1 =5

Plotting these points and connecting them gives us the graph of the line.

. Using Intercepts:

Another method is to use the x-intercept and y-intercept. The x-intercept is the point where the line crosses the x-axis, and the y-intercept is the point where the line crosses the y-axis.

The Intercept form of a straight line is ,

 x/a + y/b = 1,

where, a = x-intercept

           b = y-intercept

For example,Find x and y intercept of  the line 3x+4y=12

Solution:To find the x-intercept,we will take y=0 now the equation will become

3x+4(0)=12 

=>3x + 0 = 12

 =>3x =12 

 =>x= 12/3 

 =>x = 4 So, the x-intercept is 4

To find the y-intercept,we will take x=0,now the equation will become,

3(0)+4y=12

=>0 + 4y = 12

=>4y=12 

 =>y=12/4 

 =>y = 3 So, the y-intercept is 3

The above sum can be done in another way also,

∵ 3x+4y=12

=> 3x /12 + 4y / 12 = 12 / 12 [dividing bothsides by 12]

=> x/4 + y/3 =1 [Converting the given equation similar to x/a + y/b = 1]

∴ The x-intercept is 4

and the y-intercept is 3

Plotting these intercepts and connecting them gives us the graph of the line.

Some Problems related on Intercept of straight line:

Question(A):The x-intercept and y-intercept of a straight line are 2 and 3 respectively,find the equation of the straight line.

Solution:  x-intercept(a) = 2

                y-intercept(b) = 3

 As we know that intercept form of a straight line is,

            x / a + y / b = 1

        => x / 2 + y / 3 = 1 [putting values]

        => 6(x / 2 + y / 3) = 1X 6 [ As L.C.M of 2 and 3 is 6,so multiplying bothsides by 6]

       => 3x + 2y = 6, which is the required equation of the straight line.

Question(B): Find x-intercept and y-intercept of the given straight line, 3x - y = 12

Solution:     ∵ 3x - y = 12

                => 3x /12 - y/12 = 12/12 

                => x / 4 + y / (-12) = 1

Now comparing the above equation with x/a + y/b = 1 we get,

 x-intercept(a) = 4

and y-intercept(b) = -12

Slope of a Straight Line:

The slope of a straight line is a measure of its steepness and direction. It is a crucial concept in understanding the behavior of lines.

1. Definition of Slope:

The slope m of a line passing through two points (x₁,y₁) and (x₂,y₂) is given by:

m=(y₂- y₁) / (x₂- x₁)

This formula calculates the rate of change of y with respect to x.

2. Positive and Negative Slope:

A positive slope indicates that the line rises as x increases. For example, the line y=2x+1 has a positive slope of 2, meaning it rises 2 units for every 1 unit it moves to the right.

A negative slope indicates that the line falls as x increases. For example, the line y=−3x+4 has a negative slope of -3, meaning it falls 3 units for every 1 unit it moves to the right.

3. Zero and Undefined Slope:

A zero slope indicates a horizontal line, where y remains constant regardless of x. For example, the line y=5 is horizontal.

An undefined slope indicates a vertical line, where x remains constant regardless of y. For example, the line x=2 is vertical.

Parallel and Perpendicular Lines:

Now, we will understand the relationships between lines involve in  studying parallel and perpendicular lines.

1. Parallel Lines:

Two lines are parallel if they have the same slope but different y-intercepts. Parallel lines never intersect.

For example, the lines y=2x+1 and y=2x−3 are parallel because they both have a slope of 2.

Some Problems on Parallel Lines:

Question(x): Find a straight line which is parallel to the line 2x + 3y = - 1 and passes through the point (- 2, - 1)

Solution:   2x + 3y = - 1

             => 3y = - 2x - 1

         => y = - ⅔ x - ⅓ [dividing both sides by 3]

 ∴ gradient of the line (m₁) = - ⅔ 

∵ we will find a line which is parallel to the above line, then

                      m₂ = m₁ [ Let, m₂ is the gradient of the line which we will find]

                 => m₂ = - ⅔ 

Now, we will find the line which passes through the point (-2,-1) and has gradient - ⅔  also parallel to 2x + 3y = - 1

∴ Required straight line will be,

           y - y₁ = m (x - x₁)

       => y - (-1) = - ⅔ [x - (-2)]

       => y + 1 = - ⅔ ( x + 2)

      => 3(y + 1) = - 2 ( x + 2)

      => 3y + 3 = - 2x - 4

      => 2x + 3y + 3 + 4 = 0

      => 2x + 3y + 7 = 0

Question(y):Find the equation of straight lines which is parallel to x - 2y + 5 = 0 and at unit distance from the point (- 2, 2)

Solution: Let, the line parallel to x - 2y + 5 = 0 is x - 2y + c = 0

Now, the distance of the above line from the point = (Ax₁+ By₁+c) / ±√(A² + B²)

         = [1(-2) +(-2)2 +c] / √(1)² +(-2)² [ Here,A = 1,B = - 2, x₁ = - 2 and y₁= 2]

        = (- 2 - 4 + c) /±√1 +4

        = (- 6 + c) /±√5

Now, according to question,

      (- 6 + c) /±√5 = 1

 => - 6 + c = ±√5

=> c = 6 ±√5

∴ Required straight lines will be,

 x - 2y + 6 +√5 = 0 [ putting value of c]

and x - 2y + 6 -√5 = 0  [ putting value of c]

2. Perpendicular Lines

Two lines are perpendicular if the product of their slopes is -1. This means the slopes are negative reciprocals of each other.

For example, if one line has a slope of ¾ then the slope of perpendicular line of it will be - 4/3 

Some Problems on Perpendicular Lines:

Question(m): Find the equation of straight line which is perpendicular to the line 2x + 3y + 1 = 0 and passes through the point (2,1)

Solution:  ∵ 2x + 3y + 1 = 0 

              =>3y = - 2x - 1

              => y = - ⅔ x  - ⅓ [dividing both sides by 3]

∴ gradient of the line(m₁) = - ⅔ 

Let, the gradient of the line which is ⊥ to the given line = m₂

As, we know for two perpendicular lines,

     m₁ X m₂ = -1

  => - ⅔ X m₂ = -1 [ putting value]

 => m₂ = 3/2 

∴ Required equation of straight line will be

        y - y₁ = m₂ ( x - x₁)

     => y - 1 = 3/2 ( x - 1)

     => 2y - 2 = 3x - 3

     => 3x - 2y - 3 +2 = 0

     => 3x - 2y - 1 = 0

Question(n): Check whether given pair of lines are perpendicular or parallel,

                  3x - y + 2 = 0

                   x + 3y -1 = 0

Solution :  ∵ 3x - y + 2 = 0

                 => y = 3x + 2

∴ Gradient of the line(m₁) = 3

Again,  x + 3y -1 = 0

         => 3y = - x +1

        => y = - ⅓ x + ⅓ [dividing both sides by 3]

∴ Gradient of the line(m₂) = - ⅓ 

As, m₁ ≠ m₂

So, the given pair of lines are not parallel.

Again,

        m₁ x m₂

    = 3 x ( - ⅓)

    = - 1

So, the given pair of lines are ⊥ to each other.

To Read more....

[study-core-101]

why did i miss school 1 ½ days? now i have a shit tone of homework and assignments

[bigsqcup]

i've gotten to that point in math where i can try putting the problems through google or mathway or symbolab or wherever else and they're all like: nah dude you're on your own for this one

[mister-ancunin]

got lads but haven’t even opened it yet . i miss my man

[esme-studies]

study time of last week

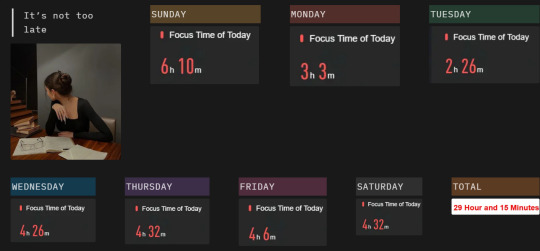
Less gooo not too bad

(can you tell I was not well on tuesday)

[wilsonlsworld]

[For Hire] Are you Overwhelmed with your Essays, group Projects, Literature reviews, Research Methodology, annotated Bibliography, Exams, Quizzes and Projects and Group Presentations. Worry Not. I am still accepting orders in academic Help and Writing Services.

Hi Students,

Are you struggling with assignments, Term Papers, Analytical Papers different fields? Perhaps you're balancing multiple jobs and finding it challenging to meet your assignment deadlines? Worry not, because I am here to help you succeed! Reach out to me on Discord at thedoll and get expert assistance starting at only $10 per page.

Contacts: EMAIL: thedoll78@gmail.com Discord: thedoll

My subjects of specialization include;

Nursing * Business Management * Public Health * business studies * Business law * Commercial law * leadership management * Organizational culture and studies * Biological sciences *Management and commerce * Sports management *Marketing and any other assignments requiring research skills.

My Research and writing include academic aspects such as;

Research papers * Case Studies * Research Proposals * Literature Reviews * Discussion posts Replies * Annotated bibliographies Book Reviews * Article Reviews * Term Papers * Exams * Quizzes * Tests * Dissertations * Paper formatting (APA, MLA, HARVARD, CHICAGO, TURABIAN) and Report Writing

[contagiouswatermelon]

one of the worst features on this site is how whenever people disagree with you or think you're missing something, they can't content themselves with just typing up a response to give you information they think you don't have. noooo no that'd be way too easy. instead they must put on your post the most condescending addition where they assume that you're stupid, talk down to you, and then give you "new" information which you were already aware of while acting like they're speaking to someone who's never even considered that information as a possibility

[champak30]

Title: How to Find the Perimeter of a Triangle

Introduction:-

Triangles are one of the fundamental shapes in geometry. Understanding their properties and being able to calculate their various attributes is essential for both students and professionals and teachers in various fields. One of the most basic calculations for a triangle is finding its perimeter, which is the sum of the lengths of all its sides. In this article, I will try to explain into the various methods of How To Find The Perimeter Of A Triangle, including different types of triangles and the different cases to consider.

Explanation:-

Understanding the Basics Before I start this topic,How To Find The Perimeter Of A Triangle, let's establish a few key concepts and definitions:

Triangle Types: 

Based on sides triangles are divided in three categories:

(a)Equilateral Triangle: A triangle whose all three sides are equal is called equilateral triangle.

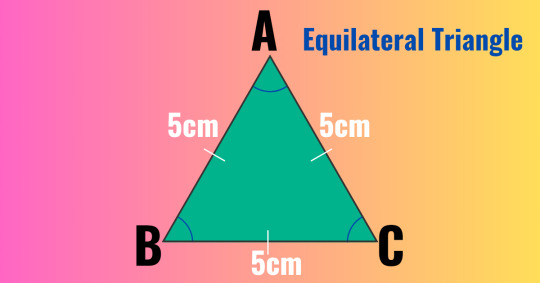
In the picture, ABC is an equilateral triangle,whose AB = BC = AC

(b)Isosceles Triangle: A triangle whose any two sides are equal and third one is different is called isosceles triangle.

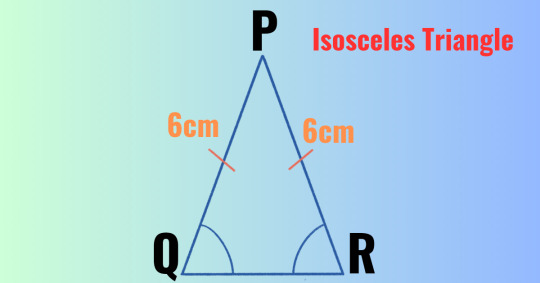
In the picture, PQR is an isosceles triangle whose   PQ = PR

(c)Scalene Triangle: A triangle whose all three sides are different to one another is called a scalene triangle.

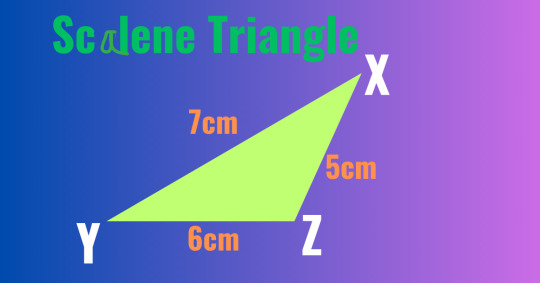
In the picture,  XYZ is a scalene triangle whose,   XY ≠ YZ ≠ ZX

Sides and Vertices:

(i)The sides of a triangle are the line segments that form the boundaries of the triangle. (ii)The vertices of a triangle are the points where the sides meet.

Perimeter:

The perimeter of a triangle is the total length or sum of all its sides.

Sides of a Triangle:

In an equilateral triangle, all sides have the same length, which we'll denote as 'a.' In an isosceles triangle, two sides have the same length, and the third side is 'b.' In a scalene triangle, all three sides have different lengths, which we'll denote as 'a,' 'b,' and 'c.' With these basic concepts in mind, let's discuss  How To Find The Perimeter Of A Triangle in various scenarios.

Procedure 1:

 Perimeter of an Equilateral Triangle: An equilateral triangle is a special case where all sides are of equal length. To find its perimeter, we  will simply multiply the length of one side ('a') by 3, as there are three equal sides. So,Perimeter of an Equilateral Triangle (P) = 3a

Some problems related on equilateral triangle:-

(a) The measure of each side of an equilateral triangle is 5 cm, Find its perimeter.

Solution:-

∵ Each side of the equilateral triangle(a) = 5cm ∴ Perimeter of the equilateral triangle = 3a = (3 × 5)cm = 15 cm (b) The perimeter of an equilateral triangle is 21cm, find its each side.

Solution:-

 ∵The perimeter of equilateral triangle = 21 cm ∴ Its each side measure = 21/3                                         = 7cm

Procedure 2: 

Perimeter of an Isosceles Triangle:

An isosceles triangle has two sides of equal length ('a') and one side of different length ('b'). To calculate its perimeter, we will add the lengths of the two equal sides ('a') and the different side ('b'). So, Perimeter of an Isosceles Triangle  (P) = 2a + b

Some problems related on isosceles triangle:

(a) The measure of two equal sides of an isosceles triangle is 7m each and third side is 5m, find the perimeter of the isosceles triangle.

Solution:-

∵ The measure of each equal side of the isosceles triangle(a) = 7m The measure of third side (b) = 5m ∴ Perimeter of the isosceles triangle = 2a + b = (2 × 7 + 5)m = (14 + 5)m = 19 m

To Read more....

[sicklyworm]

Y'all I've ghosting my math teacher for a week now, because i really don't want to do this math assessment.

How long do you think she'll take before dropping me from the course completely?

Hopefully longer than 7 days...

[cookie-nom-nom]

actually you know what I’ll never forgive flatland for giving the shapes organs you can touch. Never!

[nympho-scene-boy]

It's 8am and I came home drunk and stoned at 2am so fuck me

beer-> 10; because 10+10+10=30

Hamburger-> 5; because 10+5+5=20

two beer-> 2; because 5+2+2=9

Hotdog->

S^[unendlich]\/5+5-10 (10*sin(x))/(2×x) d(x)

=>

5sin(x)/x

[assignmentjunkie01]

Struggling with numbers or stuck on tricky equations? In this episode of the Mathematics Assignment Help podcast, we simplify complex math concepts, offer proven strategies, and share expert tips to help you complete your assignments accurately and on time. Whether you're dealing with algebra, calculus, statistics, or geometry, we’ve got your back. Perfect for students looking to boost confidence and improve grades in mathematics.

[darry-rules]

[ukmathassignmenthelp]

Maths Assignment Support in the UK: Solving Complex Quadratic Inequalities

Struggling with mathematics assignments in the United Kingdom? Finding authentic mathematics assignment help in UK services is essential if you want to achieve success academically. Since there are many choices available online, it is essential to assess these services so you get the quality work that you expect.

This blog has presented how you can assure quality services and how Locus Assignment offers best-in-class solutions specifically suited to you.

Why Is Verification Important?

Verification is essential before you give any platform any assignment. It saves you time, and effort, poor quality work, protects your money, maintains the level, and finally gets you quality grades. Don't get trapped by those giving you plenty but delivering nothing.

Key Quality Indicators

When selecting maths assignment assistance in the UK, bear these issues in mind:

Qualified Experts: Choose services that employ experts qualified in your specialized mathematics discipline. Experienced experts handle complex problems well.

Plagiarism-Free Content: Priority Is Given to Original Work. The service guarantees 100% original content.

Samples: Reputable agencies tend to offer samples, indicating the quality of work.

Timely Delivery: Timely submissions are essential. Check the track record of the service regarding on-time delivery.

Customer Feedback: Read other students' reviews and ratings. Positive reviews are an excellent measure of dependability.

Transparent Pricing: Clear price models that contain no added fees.

24/7 Support: Support twenty-four hours, seven days per week.

Locus Assignment provides quality and reliable assignment assistance with mathematics assignments in the United Kingdom. Simply provide the assignment details, and the experts will provide support.

Key Benefits of  Our Services

Choosing a certified supplier has several advantages:

Accurate Solutions: Precise platforms offer accurate solutions to complex problems, empowering you to achieve.

Time Management: Reclaim time by leaving it to the experts.

Enhanced Understanding: Organized solutions further enhance your conceptual understanding.

Stress Reduction: Rest assured that your assignments are in experienced hands.

Customized Support: Personalized support aligns their work specifically to your requirements.

Why Choose Locus Assignment?

Locus Assignment is one of the best mathematics assignment helpers, cognisant of the issues facing students. Why are we best suited?

Experienced Math Specialists: Our experienced team includes assignment assistants UK with vast expertise across many areas of mathematics.

Plagiarism-Free Guarantee: We guarantee 100% original content, with all assignments undergoing rigorous plagiarism checks.

Timely Delivery: Timely delivery comes first, while quality comes next.

Budget-Friendly Plans: Economical plans suited to the financial ability of every student.

24/7 Support: At any time, there is always an available support team.

Solving Quadratic Inequalities Quick Reference

Quadratic inequalities are comparisons of an inequality term, normally zero, and a quadratic expression. An overview follows below.

Standard Form:

 Rewrite the inequality in standard form: ax² + bx + c > 0 (or <, ≤, ≥).

Find the Roots: 

Find the solution by solving the equation associated with the form ax² + bx + c = 0. Example: Find x if x² - 5x + 6 < 0. By factorization, (x-2)(x-3) = 0, so x = 2, x = 3.

Test Intervals: The number line is divided by the roots. 

Choose one test value from each interval. Example: Intervals are (–∞, 2), (2, 3), (3, ∞). Choose x = 1, x = 2.5, x = 4.

Determine Solution: By substituting values, find values that satisfy the inequality. Example: x = 1 (False), x = 2.5 (True), x = 4 (False). Write Solution: Represent the solution in the form of an interval. Example: Solution to x² - 5x + 6 < 0 is (2, 3). 

Conclusion 

Don't let mathematics assignments get you down. Locus Assignment has expert mathematics assignment help in the UK, providing guidance, time management, and personal support. Mathematics Assignment Assistants will provide you with the authority to complete assignments efficiently and build confidence. Upload an assignment today and attain success.

[dnaayan-blog]

Critical Applied Mathematics (Calculus) for Competitive Exams (ASVAB, ASTB, AFOQT)

Hildas Problems, Landau's Theory.

Vygotsky viewed concepts in mathematics, Fundamental Theorem of Calculus (FTC):

Connects differentiation and integration, the two main concepts of calculus.

States that the integral of a function’s derivative returns the original function (up to a constant).

Formula:

This theorem allows us to evaluate definite integrals using antiderivatives.

Mean Value Theorem (MVT)

States that for a continuous and differentiable function on an interval, there exists a point where the function’s derivative equals the average rate of change over that interval.

Formula:

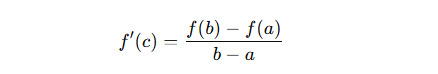
This helps explain concepts like velocity in physics.

Exclusive Mathematics Problem Solution 👈.