#Probability Theory

[disposable-semicolons]

I wanna take a moment to talk about a terrible board game.

(Image links to the English Wikipedia article about the game)

It's one of these mostly-luck-based board games people keep in their shelves because you shouldn't throw plastic pieces into a fireplace, or the "classic" kind of board game, as this comic would put it. For those familiar with the game "Sorry!" or any of the trillion variations world wide, yeah, that one. It's mostly luck based, but there are still some decisions you can make during normal play. So I ended up asking myself the question: Given optimal play, assuming red goes first and the game proceeds clockwise, what is the probability of red, black, yellow and green winning?

First of all, I don't know the answer. It would take a lot of work to figure that out, but I wanted to figure out just how difficult it is. So I wanted to start with simplifying the game. Skipping a lot of details, each player begins with 4 pegs of their color in the "B" fields, rolling a 6 sided die at the beginning of their turn. If it's a 6, they can move one peg to the "A" field and roll again. The goal is to make it all the way around, as the white circle just before the "A" field leads to the "home row" (fields a-d). The crux is you must roll exactly the right number to move into it, so if a peg comes to a halt in front of the home row, you need to roll exactly a 4 to get to d, etc. Of course, the combinatorics of this is utter hell. So let's simplify. The sheer amount of time to even get anywhere close to a win condition makes the game obnoxious to analyze. So, what if we skip the entire race (and sending other player's pieces back to B) mechanics and put A in front of the home row? That also removes what little strategic dimension the game had, so now there is no more decision making. The optimal play is the only play!

This is at least... in principle analyzable. However, even though the game is now even more brain dead to play than the original, I would like to take a moment to show you people the issue with even this "stupid" a game: how many "game states" are there? That is, how many ways are there for pieces to be arranged on the board at a given player's turn? I'm gonna go over the rules this dumbed down version would have in a bit (well not quite, I'll make it even simpler), but I can assure you, basically at any given turn the pegs of each color can be in any configuration. We can ignore the B fields, since they are for all practical purposes just storage spaces for pegs that haven't "entered" the game properly. Black pegs in this simple version can only be on black fields. All black pegs are identical, so the "state" of black's part of the board is a series of 5 yes or no questions: "Is a peg on field A?", "Is a peg on field a?", "...b?", "..c?" and "..d?". Now..

Each player has up to 4 pieces in the game at any moment, meaning at most 4 of these questions are yes.

if a-d are all occupied, then A is empty and that player has won, meaning the game is over. That means that only one color can have the home row full.

Any other configuration can be realized, no matter whose turn it is. Just.. take me word for it, for now.

That means there are 5 configurations with 4 black pegs (either A is empty = win, or one of a-d is empty), 10 configurations with 3 pegs, 10 configurations with 2 pegs, 5 configurations with 1 peg and 1 configuration with 0 pegs, 31 configurations in total (per player) , of which 1 is a "win configuration". (I won't bore you with how I came up with those numbers, you could either write them all out on paper and count, use binomial coefficient magic you may recall from high school, whatever.) If each player can be in any of these configurations but only one player can win that means there are 30×30×30×30=30⁴= 810000 configurations of the board where no player has won. And since it could be the turn of any player for any of those, there are 4 times as many game states, 3240000. You see why I didn't even bother writing down the rules yet? I really don't wanna try look at probabilities for a game with that many possible ways the pieces can be arranged. Screw this, let's make it a two player game.

Now we're down to 1800 non-win game states. This is something I could easily program in Python or something and afterwards very carefully verify by hand. However, I still cannot be bothered to. So, why is it still so many combinations? Because every field in the home row almost doubles the number of possible arrangements a single color's pegs can have. So.. let's make it dumber still. Let's make it minimal. What is the smallest possible game? Well.. let's knock it down a few pegs (geddit? And you thought the math part was the suffering here).

BEHOLD.

With one piece each, there are only 3 configurations per player (peg in B, in A, or in a = win), meaning there are 4 configurations of the board where no player has won, thus 8 non-win game states (since it's either the turn of red or black). Since we don't actually care about the configuration of pieces of the board once a player has won we can add to the above two additional states "red wins" and "black wins", giving us a total of 10. We don't have to worry about whose turn it is because the rules will be such that you can only win during your own turn. All that we need now is names for the 10 different states and the rules of the game. Then, at least, we can determine the odds for red and black for the world's stupidest two player board game.™

Let's denote the board like this: (<position of red's piece>,<position of black's piece>;<who's rolling the die next>). To make it hopefully a bit more readable I will call "0" the potion where the peg is not in the game, and "1" the one where it is on A. Then the game has the following 8 non-win game states plus the 2 win states which I will just name after the players.

(0,0;R) = no peg on the board, red's turn

(0,0;B) = no peg, black's turn

(1,0;R) = red's peg on A, no black peg, red's turn

(1,0;B) = same as above but black's turn

(0,1;R) = black's peg on A, red's turn

(0,1;B) = as above but black's turn

(1,1;R) = red's peg on A, black's peg on A, red's turn

(1,1;B) = as above but black's turn

R = red won

B = black won

As for the rules...

Red begins, the players take turns to roll a 6 sided die. The pegs begin on their respective "out" fields B.

If the player's peg is on B: On a 6, the player is allowed to move their peg from B to A and roll again (see rule 3). Otherwise, it's the next player's turn.

If the player's peg is on A: On a 1, the player can move the piece 1 field (to a), winning the game. On any other number, their turn ends.

That's the entire game! And it is only slightly worse than the original, amazing. Each turn can either increase the left or right number from 0 to 1, make the player who's turn it is win, or change who's turn it is without affecting the board. The likelihood of the game "progressing" is always 1/6 (either roll a 6 or a 1, depending on the context) while the likelihood of the game "stalling" is 5/6. So every possible game can be summarized as a graph of the 10 different game states, with arrows showing which states can lead to which and with what probability. You can tell when in the process I stopped giving a crap about aesthetic.

We can now ask, "what is the probability of red winning?" and get a definite answer with some math. But.. fucking hell it's midnight already? Okay, that has to be enough 'tism for one post. Look forward to a followup (or maybe I'll just edit this post). Stay tuned! FUCK IT WE BALL, I FINISHED THIS SHIT AT 2AM.

Alright so what's gonna be annoying are all those pesky cycles that could mean the game could go on hypothetically forever (just like the real one!), but we can deal with those by starting at the "bottom" of the graph and working our way up. It's pretty clear that the probability of a player winning should only depend on the game's state, so whether it is turn 5 or 105 the probability for red to win when the game is in state (1,1;R) should be the same. The probability of that is some number. We could simply simulate an arbitrary number of games in that state, and intuitively we would expect some fixed percentage of red wins (which we called R) to pop out of that simulation. I won't do much formal mathematics here. There is a 1/6 chance of red winning immediately, and a 5/6 chance of the game changing states. So in almost plain English we know:

[probability of R given (1,1;R)] = 1/6 + 5/6×[probability of R given (1,1;B)] .

In state (1,1;B), there is no chance for R to win in the turn itself, but a 5/6 chance of the state changing back!

[probability of R given (1,1;B)] = 5/6×[probability of R given (1,1;R)].

Putting them together and using that (5/6)² = 25/36 we get

[probability of R given (1,1;R)] = 1/6 + 25/36×[probability of R given (1,1;R)].

Now the same probability appears on both sides! We can simplify and find I'm getting tired of this verbosity, let's write the conventional way mathematicians do for this stuff. They don't write [probability of R given (1,1;R)], they write P(R|(1,1;R)).

11/36 × P(R|(1,1;R)) = 1/6

P(R|(1,1;R)) = 6/11 ≈ 54%.

With the above we can figure out all probabilities for the two game states, and they add up to 1 since a game taking forever is infinitely unlikely (don't worry about it, but it is a fun rabbit hole)

P(R|(1,1;R)) = 6/11 = P(B|(1,1;B)) and P(B|(1,1;R)) = 5/11 = P(R|(1,1;B)).

Moving up in the graph we can now replace the two "solved" game states with their win probabilities, taking into account that reaching these states has a probability of 1/6 itself).

Let's focus on the left half. R appears in both states there, but B only once. We already know that the chances of R and B will add up to one, so let's choose the path of least resistance and try P(B|(1,0;R)). Then we can use the same trick as above!

P(B|(1,0;R)) = 5/6 × P(B|(1,0;B)) = 5/6×( 1/11 + 5/6×P(B|(1,0;R)) )

P(B|(1,0;R)) = 30/121 ≈ 25%

P(R|(1,0;B)) = 91/121. The right side of the graph is much of the same. Multiplying these by 1/6 again means we can delete another entire row from the graph!

Almost done! Now all that is left is computing P(R|(0,0;R)), because this is the state the game actually starts at. As we have seen for P(R|(1,1;R)), if the board is in a state where both players are equally close to winning, the one whose turn it is is (intuitively) at a slight advantage. We expect the same to be true now... let's suffer through this once more.

P(R|(0,0;R)) = 91/726 + 5/6×P(R|(0,0;B)). Once more

P(R|(0,0;R)) = 91/726 + 5/6×( 5/121 + 5/6×P(R|(0,0;R)) )

11/36 P(R|(0,0;R)) = 91/726 + 25/726 = 58/363

P(R|(0,0;R)) = 696/1331 ≈ 52.29% and thus

P(B|(0,0;R)) = 635/1331 ≈ 47.71%.

And there you have it: The probability of red winning in this simplified version of the game is 696/1331 or about 52%. It would be cool to see how less dumbed down versions of the game compare to that, though this "0IQ version" of the game is actually contained in the real deal! I had real instances of the full game play out to the point where both players were just sitting there, waiting for the chance to roll a godforsaken 1 to end the game. And now you know: if you wanna flip a coin to decide who won instead of prolonging your suffering should you ever reach that point in the game, you are only shuffling around a strategic edge of like 2%.

You're welcome.

[omegaphilosophia]

The Philosophy of Statistics

The philosophy of statistics explores the foundational, conceptual, and epistemological questions surrounding the practice of statistical reasoning, inference, and data interpretation. It deals with how we gather, analyze, and draw conclusions from data, and it addresses the assumptions and methods that underlie statistical procedures. Philosophers of statistics examine issues related to probability, uncertainty, and how statistical findings relate to knowledge and reality.

Key Concepts:

Probability and Statistics:

Frequentist Approach: In frequentist statistics, probability is interpreted as the long-run frequency of events. It is concerned with making predictions based on repeated trials and often uses hypothesis testing (e.g., p-values) to make inferences about populations from samples.

Bayesian Approach: Bayesian statistics, on the other hand, interprets probability as a measure of belief or degree of certainty in an event, which can be updated as new evidence is obtained. Bayesian inference incorporates prior knowledge or assumptions into the analysis and updates it with data.

Objectivity vs. Subjectivity:

Objective Statistics: Objectivity in statistics is the idea that statistical methods should produce results that are independent of the individual researcher’s beliefs or biases. Frequentist methods are often considered more objective because they rely on observed data without incorporating subjective priors.

Subjective Probability: In contrast, Bayesian statistics incorporates subjective elements through prior probabilities, meaning that different researchers can arrive at different conclusions depending on their prior beliefs. This raises questions about the role of subjectivity in science and how it affects the interpretation of statistical results.

Inference and Induction:

Statistical Inference: Philosophers of statistics examine how statistical methods allow us to draw inferences from data about broader populations or phenomena. The problem of induction, famously posed by David Hume, applies here: How can we justify making generalizations about the future or the unknown based on limited observations?

Hypothesis Testing: Frequentist methods of hypothesis testing (e.g., null hypothesis significance testing) raise philosophical questions about what it means to "reject" or "fail to reject" a hypothesis. Critics argue that p-values are often misunderstood and can lead to flawed inferences about the truth of scientific claims.

Uncertainty and Risk:

Epistemic vs. Aleatory Uncertainty: Epistemic uncertainty refers to uncertainty due to lack of knowledge, while aleatory uncertainty refers to inherent randomness in the system. Philosophers of statistics explore how these different types of uncertainty influence decision-making and inference.

Risk and Decision Theory: Statistical analysis often informs decision-making under uncertainty, particularly in fields like economics, medicine, and public policy. Philosophical questions arise about how to weigh evidence, manage risk, and make decisions when outcomes are uncertain.

Causality vs. Correlation:

Causal Inference: One of the most important issues in the philosophy of statistics is the relationship between correlation and causality. While statistics can show correlations between variables, establishing a causal relationship often requires additional assumptions and methods, such as randomized controlled trials or causal models.

Causal Models and Counterfactuals: Philosophers like Judea Pearl have developed causal inference frameworks that use counterfactual reasoning to better understand causation in statistical data. These methods help to clarify when and how statistical models can imply causal relationships, moving beyond mere correlations.

The Role of Models:

Modeling Assumptions: Statistical models, such as regression models or probability distributions, are based on assumptions about the data-generating process. Philosophers of statistics question the validity and reliability of these assumptions, particularly when they are idealized or simplified versions of real-world processes.

Overfitting and Generalization: Statistical models can sometimes "overfit" data, meaning they capture noise or random fluctuations rather than the underlying trend. Philosophical discussions around overfitting examine the balance between model complexity and generalizability, as well as the limits of statistical models in capturing reality.

Data and Representation:

Data Interpretation: Data is often considered the cornerstone of statistical analysis, but philosophers of statistics explore the nature of data itself. How is data selected, processed, and represented? How do choices about measurement, sampling, and categorization affect the conclusions drawn from data?

Big Data and Ethics: The rise of big data has led to new ethical and philosophical challenges in statistics. Issues such as privacy, consent, bias in algorithms, and the use of data in decision-making are central to contemporary discussions about the limits and responsibilities of statistical analysis.

Statistical Significance:

p-Values and Significance: The interpretation of p-values and statistical significance has long been debated. Many argue that the overreliance on p-values can lead to misunderstandings about the strength of evidence, and the replication crisis in science has highlighted the limitations of using p-values as the sole measure of statistical validity.

Replication Crisis: The replication crisis in psychology and other sciences has raised concerns about the reliability of statistical methods. Philosophers of statistics are interested in how statistical significance and reproducibility relate to the notion of scientific truth and the accumulation of knowledge.

Philosophical Debates:

Frequentism vs. Bayesianism:

Frequentist and Bayesian approaches to statistics represent two fundamentally different views on the nature of probability. Philosophers debate which approach provides a better framework for understanding and interpreting statistical evidence. Frequentists argue for the objectivity of long-run frequencies, while Bayesians emphasize the flexibility and adaptability of probabilistic reasoning based on prior knowledge.

Realism and Anti-Realism in Statistics:

Is there a "true" probability or statistical model underlying real-world phenomena, or are statistical models simply useful tools for organizing our observations? Philosophers debate whether statistical models correspond to objective features of reality (realism) or are constructs that depend on human interpretation and conventions (anti-realism).

Probability and Rationality:

The relationship between probability and rational decision-making is a key issue in both statistics and philosophy. Bayesian decision theory, for instance, uses probabilities to model rational belief updating and decision-making under uncertainty. Philosophers explore how these formal models relate to human reasoning, especially when dealing with complex or ambiguous situations.

Philosophy of Machine Learning:

Machine learning and AI have introduced new statistical methods for pattern recognition and prediction. Philosophers of statistics are increasingly focused on the interpretability, reliability, and fairness of machine learning algorithms, as well as the role of statistical inference in automated decision-making systems.

The philosophy of statistics addresses fundamental questions about probability, uncertainty, inference, and the nature of data. It explores how statistical methods relate to broader epistemological issues, such as the nature of scientific knowledge, objectivity, and causality. Frequentist and Bayesian approaches offer contrasting perspectives on probability and inference, while debates about the role of models, data representation, and statistical significance continue to shape the field. The rise of big data and machine learning has introduced new challenges, prompting philosophical inquiry into the ethical and practical limits of statistical reasoning.

[knotty-et-al]

Will to live - Self-realization and the serendipity of chaos helping out in semi-unfortunate circumstances

[2023/10/25]

It is not finished, but I will most certainly never finish it, because... well, I better put it on that huge pile of projects not worth the effort to work on even further...

I like the concept and idea.

I drew that in art therapy when we had to describe how our life went during the last year - and we should use a fruit to depict that.

So I started with an apple that became also a pear.

I added the intersection circles of a spindle torus:

(It is depicted in that img:)

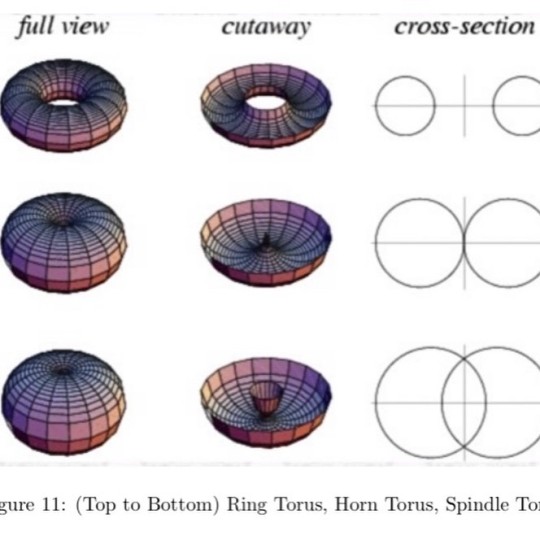
Then my surrealizing brain went even further with that thought soup, and created an abstract heart from that apple-pear-fruit.

I also added some colorful arteria that can also be imagined as roots and/or branches.

Finishing my thought soup on paper, I ended in the green-ish and red-ish trajectory lines - which are like bifurcations of trajectories of two bouncing bouncy balls... converging towards the upper right corner.

[tmarshconnors]

Game Theory and Probability Theory

In mathematics and economics, there is a fascinating crossroads where strategic decision-making meets uncertainty. This intersection is where Game Theory and Probability Theory converge, offering insights into the dynamics of human interaction, strategic behaviour, and the unpredictability of outcomes. Join me as we delve into this captivating domain, exploring how these two fields intertwine and shape our understanding of complex systems.

Understanding Game Theory

At its core, Game Theory is the study of strategic decision-making among multiple interacting agents, aptly referred to as "players." Think of it as the science of strategy, where individuals or entities make choices with the aim of maximizing their own gains while considering the actions of others. Whether it's in economics, political science, biology, or beyond, Game Theory provides a framework for analyzing various scenarios of conflict, cooperation, and competition.

The Elements of Games

To grasp the essence of Game Theory, we need to understand its building blocks. Games are characterized by players, strategies, payoffs, information, and rationality. Each player has a set of strategies to choose from, leading to different outcomes with associated payoffs. Information asymmetry and rational decision-making further complicate the dynamics, making Game Theory a rich field for exploration.

Probability Theory's Role

Enter Probability Theory, the study of random phenomena and uncertainty. In the context of Game Theory, probability comes into play when outcomes are uncertain or stochastic. Whether it's the roll of a dice in a board game or the unpredictability of market fluctuations in economics, probability theory provides the tools to quantify and analyze uncertainty.

Where They Meet

So, how do Game Theory and Probability Theory intertwine? Consider a game like poker, where players must make decisions based on incomplete information and uncertain outcomes. Probability theory allows us to calculate the likelihood of different hands and anticipate opponents' actions, thereby informing strategic choices. In more complex games involving multiple players and intricate strategies, probability theory helps us model the uncertainty inherent in the decision-making process.

Applications and Insights

The applications of this marriage between Game Theory and Probability Theory are vast. From designing optimal auction mechanisms to analyzing voting behavior in elections, the insights gained from this interdisciplinary approach are invaluable. Moreover, in the age of artificial intelligence and machine learning, understanding strategic interactions and uncertain environments is crucial for developing intelligent systems capable of making informed decisions.

Conclusion

In the landscape of mathematical sciences, the synergy between Game Theory and Probability Theory offers a lens through which we can understand and navigate the complexities of strategic decision-making and uncertainty. As we continue to explore this dynamic intersection, we unlock new perspectives and tools for addressing real-world challenges across various domains. So, the next time you find yourself pondering a strategic dilemma or contemplating uncertain outcomes, remember the profound insights that emerge when Game Theory meets Probability Theory.

[biology-geology-beaches-india]

The science diaries of S. Sunkavally. Page 114.

[bi-for-vi]

I don’t see anybody talking about this, but it hurt my heart

[yehoria]

That's not how probability theory works, those aren't elementary consequences!

They don't meet two of the three requirements:

They aren't exclusionary, both can happen at the same time

They aren't equally probable either!

(sorry if i used completely incomprehensible terms, i learnt this stuff in Ukrainian and am haphazardly translating as i go)

[spokenforinvaliduser]

[biggest-gaudiest-patronuses]

"it's not that deep" not yet but I've got a shovel and fan theories and digging makes great exercise!

[tending-the-hearth]

going back through mockingjay and what do you MEAN clerk carmine is most likely the fiddler at annie and finnick's wedding, what do you MEAN clerk who was the one to bring lucy gray the katniss just before things fell apart and the one to raise the girl who became haymitch's reason for living what do you MEAN clerk got to see his sister and his niece's dreams come true as the hunger games are destroyed by a girl with lucy gray's fire and lenore dove's heart what do you MEAN clerk saw the arrows his friend made be part of the downfall of the capital what do you MEAN clerk lost his family but saw them live on in haymitch and katniss and peeta

[pouletpourri]

what-if concept where kaufmo didn't got abstracted and he and pomni got to co-exist

[greykolla-art]

Charlie: “I’m so glad my most villain-coded friend is at full power again! 🥰💕”

*throws this to you angst goblins like raw steak* ❤️

(No I will not do a part 2!❤️)

[egophiliac]

still ruminating over Lost In the Book With Spooky Skeletons Part 1, so here's a selection of some of my favorite little bits! (...some more loosely paraphrased than others) (I just feel like Idia has no room to criticize in general, okay)

anyway, I'm sure we're just going to have a fun time celebrating Halloween and nothing bad is going to happen whatsoever! :)

[radiance1]

Danny: Hey, I need you to be my boyfriend for a week.

Jason: What.

Danny: My parents are coming over and I've apparently accidentally talked about a partner more than once and only realized when they said they wanted to meet them.

Jason, currently still solidifying his power as a Crime Lord: Excuse me?

Danny: Let me get this out of the way, I do not consider you at all a person of romantical interest and a friend. But I need you to act as my partner for only a week until my parents go on their merry way over to my sister, okay?

Jason: Is there, quite literally, no one else to ask this?

Danny: You're my only friend who lives in Gotham, plus we share the same apartment.

Jason: That's almost sad.

Danny: You in?

Jason: Sure, why not.

===

Maddie: Danny, honey.

Danny: Yes mom?

Maddie: I don't mean to.... question, who you choose as your parent but. Well, me and your father was just wandering if he was a... [Maddie gestures with her hand] you know, one of those.

Danny, uncomprehendingly staring at his mother's hand: What.

Maddie: Oh dear, how do I bring this up. You know, one of those.

Danny: Mother I need more context.

Jack: If your boyfriend a crime lord!?

Maddie: Jack!

Jack: What? Beating around the bush wasn't helping!

Danny: Say WHAT?

===

Danny: Hey dude, thanks for helping with this even though you didn't need to!

Jason: No problem, I wasn't doing anything too [Crime Lord activities flash through his mind] important.

Danny: Can you believe my parents thought you were a crime lord though? Weird am I right?

Jason:

Danny: Jason. You are scaring me.

Jason: Haha, yea that's weird isn't it?

Danny: Jason.

Jason: Well, I have to leave now to attend to my totally real and totally not crime related job at the ice cream shop.

Danny: [Squints eyes]

Jason: [Internally sweating bullets]

Danny: Suuuuure, bring me back some ice cream though.

Jason: [Thumbs up and leaves]

[vulpixelates]

i know it will never happen but i so desperately desire an origins-type playable backstory thing in all games but especially veilguard. i feel like it added so much depth to origins and made you feel instantly connected to your character in a way that gets lost in games like inquisition where you fill in the blanks as you go except for the bare basics. like, i do enjoy the freedom to willy nilly decide where a character was before the events of the story from a creative perspective, but the playable origins were just so good! especially when you go back to where your warden is from and can engage differently with the arcs there

[itsaboutspies]

The Mrs flood reveal is either going to be absolutely incredible or an absolute and total disappointment with no in between