#cartesian coordinates

[er-cryptid]

Polar to Cartesian Components [Ex. 1]

Patreon

[biblebloodhound]

Why? (Job 18:1-21)

Grief doesn’t make sense; it’s nonsensical, whimsical, and fractal.

Job speaks with his friends, by Gustave Doré, 1866 Then Bildad the Shuhite replied: “When will you end these speeches?    Be sensible, and then we can talk.Why are we regarded as cattle    and considered stupid in your sight?You who tear yourself to pieces in your anger,    is the earth to be abandoned for your sake?    Or must the rocks be moved from their place? “The lamp of a wicked man is…

[fragmentedblade]

This seems to be a reference to Lorentz transformations? The first formula is apparently a derivation, and seems to be the inverse of the time part of the transformation (there's a space part too), for what I've been able to find.

The second formula is Newton's second law.

[the-starry-lycan]

NOT THE WAVE EQUATION NOOOOOO

oh no , the dog is drinking the wave equation

[rihkal]

RS 1 Model 7565 by IBM (1982)

[nashum8]

mindblown at human inventions on this Monday morning

[sameteeth]

even if it sucks i love calculus so much. thank you calculus for everything

[sunriseverse]

oh FUCK no not descartes.

[jibunbosh]

In accordance with Tumblr joining the rest of the internet 7 years late in asserting that all of its profile pictures must no longer be square, I am going to bring this development full "circle" (hehe) and allow it to reach its logical conclusion by developing a new raster image file format that stores pictures no longer as Rectangles in a Cartesian grid, but as Circles using polar coordinates. This file format will *assistant whispers in my ear* I don't fucking care. Start producing circular monitors then with rounded pixels then. Get out of my conference room

[art-of-mathematics]

I know I have drawn this shape so often already, but the process of drawing it is so soothing.

And for that, I have drawn a kind of step-by-step guide how to draw that shape in the top of this drawing:

(from left to right: ) [sorry in advance if I make it sound more complicated than it actually is. If you want to draw it, I would advice you to focus more on these illustrations rather than on my gibberish-text.]

1. draw a 2-dimensional Cartesian plane - or, in other words: just draw a cross like depicted

1.1. mark 2 points on the y-axis/vertical line with same distance to the coordinate origin, then mark 2 points on the x-axis/horizontal line with the same distance to the coordinate origin. (The markings on the y-axis need to be farther away from the origin than the markings of the x-axis)

2. connect the 4 marked points like depicted above. This is a function plot of a tractrix. (it has two mirror symmetry axes. )

3. draw an ellipse and connect the two markings on the x-axis. This becomes a kind of "belt" for the pseudosphere (4th picture)

4. part the ellipse into whatever-amount-you-want of partings (like you would cut a cake) and slightly mark these.

5. now imagine you cut that shape horizontally on the outer surface. (In the 5th picture I depicted that with red-ish pen across the pseudosphere. ) -

6. then the cut shape needs to be "(shape) shifted". For that we use a set of marked points we did in step 4). Furtherly, we "cut" the ellipse open, and push one end of it to the top, and the other end to the bottom. (depicted in picture 6 )

7. Then we connect the rest to get that shape:

[crazy-so-na-sega]

Milano, la “banlieue” di Corvetto

Sono stati i Carabinieri. Basta un attimo a trasformare un quartiere in un’esplosione di rabbia. Una “rabbia spontanea”, come dice Il Corriere della Sera, che però sembra più che altro indotta, voluta, cercata. Indotta dal “Sistema per uccidere i popoli“, come lo definì Guillaume Faye, d’altronde “come designare questa vasta impresa planetaria di massificazione e spersonalizzazione?“. Voluta dagli sponsor del villaggio globale, da quella società liberale che si persuade di aver costruito un mondo di prosperità, di liberazione e di progresso mentre la realtà sociale lascia trasparire un ambiente anorganico: morto, senza vita interiore, più simile ad un macchinario che ad un organismo in crescita. Cercata da loro, i “maranza”, i “subalterni” – come li chiamano a sinistra della sinistra – gli agenti attivi di un dinamismo conflittuale che esiste schiacciato dentro i quartieri pentola, sempre pronta ad esplodere appena tolto il coperchio del quieto vivere. Sono anni che si ripete come anche le periferie italiane – in questo caso milanesi – possano diventare da un momento all’altro lo scenario delle banlieue parigine. Quelle dell’Odio e di Athena. Quelle che abbiamo visto solo in televisione. L’integrazione tanto agognata è finalmente realtà, con un ribaltone però: l’Italia si è adattata all’altro, non il contrario. Abbiamo uomini che occupano spazi morti, residenti che si situano su una scacchiera; il loro “indirizzo” non ha nulla di un luogo, sono piuttosto coordinate cartesiane dello smarrimento. Città dormitorio perennemente in affitto, centri storici trasformati in bomboniere turistiche, quartieri campi profughi. Ci siamo integrati perfettamente al non-luogo globale. E come tutti i popoli “delocalizzati” che hanno perduto il senso del tempo e della storia, siamo condannati a perdere la nostra terra. Un Corvetto alla volta.

-Kulturaeuropa

[er-cryptid]

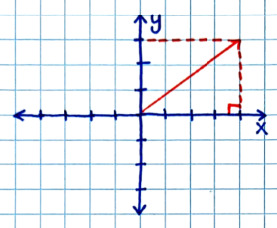
Coordinate Systems

-- Cartesian System = used for linear motion

-- Polar System = used for angles

.

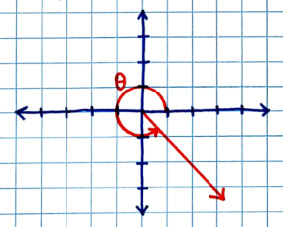
Patreon

[beauty-and-passion]

HEY I JUST FINISHED READING ALL YOUR GRAVITY FALLS POSTS AND IT WAS A BLAST THANK YOU SO MUCH FOR WRITING THOSE!

i really didn't know much about flatlands so your explanation of it was so cool! seeing it all fall in place as you explained euclydia, your dissection of billford, it was all so great! thank you so much for writing those analyses.

also have you realized that Exwhylia stands for X-Y-lia? as in x and y in an axis? when i first read it i thought it was just gibberish

it'd make sense of exwhylia to have no color, unlike euclydia, which feels like a kid's drawing of colorful shapes, exwhylia is more akin to geometry homework

Actual footage of me, reading this ask.

It's always beautiful to know people appreciate all the time I spent on those analyses. I would've spent it either way because Gravity Falls is my special interest and it will always have a special place in my heart but still, it's nice to see it.

About Exwhylia: honestly, it took me longer than I'm willing to admit to realize that hey, the name stands for X and Y. And of course it stands for X and Y, because to make a cartesian plane, you need X and Y coordinates. It was so obvious and so clever - and I'm an idiot to not get it instantly :P

And yes, you have a very good point! Even the name suggests that Exwhylia is more of a "geometry work": after all, cartesian planes are used in school and for algebra, too, if I recall correctly. So it seems to imply a more "serious", less colorful world.

On the other hand, Euclydia makes you think of colorful geometric shapes, like the ones used to explain the basics of geometry to kids. So yes, it makes more sense that it's a world full of colors. Also, I like the idea that this world was more advanced than other 2D dimensions simply because it had/allowed the use of color—and, as I explained, color led to developments in sight, writing, and even society.

This also makes Bill's story even more tragic because despite being in a world that was slightly less oppressive than many others, it still wasn't enough for him. Euclydia was advanced compared to other 2D worlds more akin to Flatland, but it was still too tight for Bill. It implies that no matter how advanced his home dimension had been, Bill would've never fitted in.

[paperometria]

Buondì Papero....

Vorrei farti una domanda seria... ma, se la risposta fosse un casino, non mi offendo se "mi ci mandi"!! 😄​

Hai idea di quanto costerebbe aprire una server farm? E, in subordine, è un'idea economicamente conveniente? Ho sempre lavorato nel settore dei servizi horeca, all'inizio come dipendente, poi come imprenditore. Da sempre ho avuto la passione per l'informatica e l'ingegneria. (mannaggia che non l'ho scelto come percorso di studi...) Ora mi trovo ad un bivio di vita e mi piacerebbe fare qualcosa in questo mondo che tanto mi piace. Hai presente quando racconti di voler mandare tutti i crucchi a quel paese e cambiare vita? Ecco. Ti capisco. I miei problemi non parlano tedesco, ma la situazione è simile. Per ora sto a fare ragionamenti... ma spero che nel 2025 possa trovare il giusto incastro per trasformare l'idea in azione! Ho a disposizione una struttura coperta di circa 3.500 mq ad oggi in disuso con accesso ad abbondanti fonti di energia rinnovabile (sole, vento, acqua di sorgente bella fredda per i chiller di raffreddamento) La server farm è stata la prima idea... Tu ne avresti altre?

Ovviamente se anche altri tumbleri hanno belle idee... ascolto con piacere!!

Grazie mille per il tuo tempo! 😁​

Ammazza che domanda ...

Mai fatto un ragionamento su questa cosa, ma posso pensare a voce alta, visto che nelle server farm ci sono entrato più di una volta, e ti posso dire, da gestore di alcuni di quei server, cosa ho incontrato lungo il cammino che mi portava dalla porta di ingresso al punto di lavoro. Vado in ordine, così facciamo la lista della spesa.

Sicurezza umana

Ti serve controllare gli accessi, supervisionare le aree e gestire chi può andare dove, quindi ti serve personale 24/7 tra guardie di sicurezza, telecamere (con tanto di registrazioni e sistemi per archiviare), sistemi di allarme e tutte le blindature possibili per effrazioni che si possono compiere attraverso ogni buco nel quale è possibile infilarsi, vetri antirapina e, se proprio devi assicurare un certo livello di sicurezza, metal detector e perquisizioni corporali dedicate e a-rattuse.

Sicurezza fisica

Porte tagliafuoco che ogni volta che si chiudevano mi partiva un timpano, progettare quanto più possibile con materiali ignifughi, e soprattutto sistemi di antincendio compatibili con l'elettricità a cascata su tutta l'area e che devono garantire determinati tempi di reazione, tutto deve essere a prova di statica, quindi tutti i materiali (partendo dai pavimenti, ad esempio) devono minimizzarne l'accumulo, prima che vai a toccare il telaio di un server e ti si fulminano le palle perché quel giorno a Milano faceva un freddo della madonna a Corso Zara presso la Sala Fastweb e ci sei andato con le mutande di flanella (tengo a sottolineare che, nonostante le apparenze, questo non è un post autobiografico).

Accessibilità

Vanno usati materiali "smontabili" in ogni momento, tutto il pavimento era flottante, potevi sganciare 'sti quadroni con una leva ed accedere a tutta la cablatura che viaggia sotto al pavimento, lo stesso vale per gli armadi, per le cablature che viaggiano in aria, e i cessi col bidet (questo non è proprio un must, ma faresti felice gli utenti), e mi raccomando la segnaletica, che non si capiva mai un cazzo, col capo che mi diceva per telefono vai a destra, vai a sinistra, ma usate delle coordinate cartesiane perdio. Ti serve, sempre all'uopo, una squadra di tecnici reperibile 24/7, perché c'è sempre qualche cazzo che si rompe, e inoltre c'è sempre il giorno che il cliente non ha davvero nessuno da poter mandare per premere il Power ON su un server e ti chiede in ginocchio, e poi uno dei tuoi sgherri per dispetto glielo accende ma gli stacca la Ethernet, vafammocc.

Temperatura controllata

Hai già citato il raffreddamento, diciamo che qui ognuno si raffredda il server come vuole, ma nella stragrande maggioranza è tutto a ventole (almeno lo era tipo 15 anni fa), e quindi devi smaltire tutta l'aria calda generata nei locali, quindi un sistema di aspirazione con i controcazzi, che deve tenere la temperatura costante, non vuol dire glaciale, quando ci andavo dovevo comunque letteralmente spogliarmi che faceva un caldo della madonna, però se semo capiti. E poi sì, tutta questa aria va raffreddata, ma vedo che ad acqua stai messo già bene. Un banco frigo con i ghiaccioli sarebbe gradito.

Energia

Capisco benissimo la tua voglia di tutela dell'ambiente, ma uno dei requisiti chiave è la copertura energetica SEMPRE, con tanto di backup, quindi tutte quelle belle robe solari e ventose, sì, son belle e aiutano, perché no, ma devi rispettare una fornitura costi quel che costi, anche quando c'è la nebbia e non si vede, e qua penso siano abbastanza cazzi.

Connettività

Hai voglia a fibre ....

Anche qui, devi garantire banda e ridondanza, come per il punto di prima, per ogni SLA (Service Level Agreement) che non rispetti ti inculano col sabbione vetrato.

Certificazioni

Per quante ne puoi avere, te ne sarai sicuramente scordato qualcuna, quindi daje de ISO, daje de IMQ, già ti dico che di questa server farm non se ne parlerà più (l'ho scritta solo per fare rima).

Copertura assicurativa

... e non aggiungo altro.

Se ti dovessi dire la mia, io pianterei tutte piante di ulivo per fare concorrenza a @pgfone così abbassiamo il prezzo finale dell'olio al consumatore :P :P

Ma ovviamente mi affido ai miei amatissimi follower, che non solo si divertiranno a fare la punta al cazz a quello che ho scritto (vi prego, sì), ma anche che potranno aiutarti con altre idee forse ben più promettenti e remunerative.

[girlballs]

its been years and Bygones + a fusion with backup plan (currently Cartesian Coordinate) is still my all-time favorite crucible loadout. i do wish they'd bring back Go Figure too though

[squareallworthy]

Triangle Tuesday 7: the joy of coordinates, railroads, and you didn't see that coming

"There is no royal road to geometry," Euclid supposedly said to Ptolomey, and this is true. There is, however, a commuter rail line called analytic methods, and that's what I want to talk about today.

Everything I have discussed in this series so far falls under the heading of synthetic geometry -- that is, geometry done only using axioms such as Euclid's, without recourse to numerical formulas or coordinate systems. This is in contrast to analytic geometry, which most people are familiar with from the cartesian coordinate system of the plane.

Today, we're doing a different coordinate system, but the cartesian system provides a familiar jumping-off point. In the cartesian plane, we specify a point relative to two reference axes. The coordinates represent the perpendicular distances from the axes, and these distances are positive or negative depending on which side of the axes the point lies.

We are going to do something like that, but rather than orthogonal axes, we will take the sidelines of a triangle as our reference. This will give us three coordinates for only two dimensions, which seems redundant, but hold on and it will make sense in a bit.

First we'll look at the basics of this system, then I'll go through and find the coordinates for each of the triangle centers we've looked at so far, and we'll end with a bit of a surprise.

Coordinates for triangles

Why do I call this a commuter rail line? Because unlike a royal road, anyone can use it, and it can be a faster way to get to certain places. On the other hand, it doesn't always go exactly where you want, and we have to build some infrastructure before it becomes useful.

Let's work our way there by first adding some notation to our triangle. It's conventional in triangle geometry to use the uppercase letters A, B, and C for both the vertices and the size of the angles at the vertices, and lowercase letters a, b, and c for both the sides opposite the corresponding vertices and also the length of those segments.

This may seem liable to confusion in theory, but in practice context makes clear which sense is intended. If B or b appear in a drawing, they refer to points and lines. If they appear in a numerical expression, they refer to angle sizes or lengths.

Now let's look at a point P. We will label its feet on sides a, b, and c as Pa, Pb, and Pc, and the segments joining P to the feet as p1, p2, and p3. I don't know of any standard term for these segments. I'm just going to go with the obvious and call them legs.

And because we are all comfortable now with using the same symbol for a line segment and the length of that segment, I will also use p1, p2, and p3 as the signed distances from P to the sidelines of the reference triangle. The distance will be positive when P is on the same side of the sideline as the triangle, negative when P is on the other side, and zero when P is on a side line.

Here's P lying outside the reference triangle, with a negative p1 (in red) because it lies on the opposite side of line a from the triangle, a zero p2 because it is on line b, and a positive p3 (in blue) because it is on the same side of line c as the triangle.

Okay, so far so good. This is not too different from cartesian coordinates, except our axes aren't perpendicular and we have a seemingly unnecessary third coordinate. Two signed distances ought to uniquely identify a point, right?

Here's the difference that makes the third coordinate necessary: we are going to ignore absolute distances and only consider ratios between the coordinates. If we have a point with legs measuring p1, p2, and p3, we will consider any three numbers k*p1, k*p2, k*p3 to be the same coordinates (as long as k is not zero). We'll write this triple ratio as p1 : p2 : p3 in order to distinguish these coordinates from triples of cartesian coordinates in R^3.

This coordinate system is called homogeneous trilinear coordinates. (The homogeneous part comes from abandoning absolute distances and considering only ratios. If we kept to absolute distances, we would have exact trilinear coordinates. Hereafter I will just refer to the homogeneous version as trilinear coordinates, or trilinears.)

Why is this useful? Various reasons. One of them is that with one exception, any three real numbers specify a point. No point can lie on the outer side of all three side lines, so with exact coordinates, three negative numbers don't correspond to any point. But with homogeneous coordinates, we can multiply any coordinate triple by any nonzero real number k and it still represents the same point. Letting k = -1, we have x : y : z = -x : -y : -z. No problem with negatives.

But the main advantage of trilinears is that we can give a nice representation to important points of the triangle, and that lets us easily use analytic methods on them. The vertex A, for instance, has zero distance from sidelines b and c, so its trilinears are 1 : 0 : 0 (or equivalently any other nonzero real number for the first coordinate, but using 1 is simplest). Similarly vertex B is 0 : 1 : 0 and vertex C is 0 : 0: 1 . No point can lie on all three lines of the triangle at once, so 0 : 0 : 0 is the single coordinate that does not correspond to any point.

The incenter

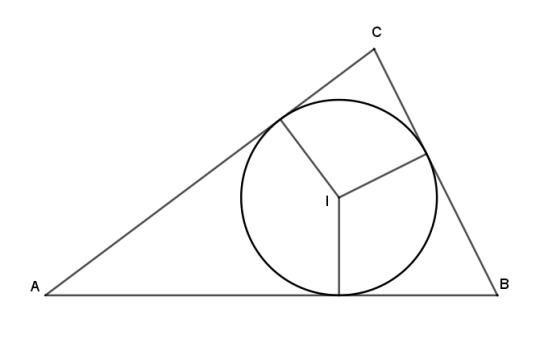
Let's see how this works using the incenter as an example. The incenter is inside the triangle and equally distant from the three sides. With the three legs being equal, its trilinear coordinates are as simple as they can be:

The trilinears of the incenter are I = 1 : 1 : 1.

That's a very nice and neat expression, but not actually very informative. We already knew this about the legs of the incenters, because they are all radii of a common circle. Furthermore it's easier to understand "the incenter is the point that is equidistant from the sides" than "the incenter is the point with trilinear coordinates 1 : 1 : 1." So far our coordinate system hasn't shown us anything new or made anything clearer. Well, we're still building our commuter rail line. It will pay off after we complete more ground work.

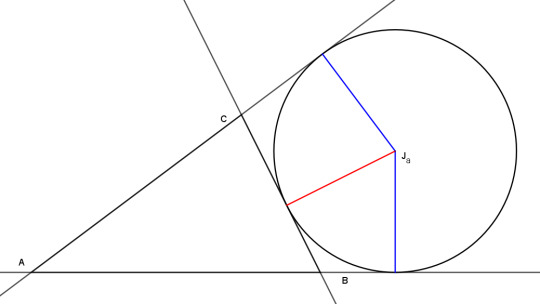
But while we are at this stop, we might as well take note of the excenters. Here is excenter Ja, equidistant from the sidelines of the triangle, but on the negative side of line a and on the positive sides of lines b and c. So its trilinears are -1 : 1 : 1, and similarly for the other two excenters.

The centroid

The centoid is defined as the intersection of the medians, and the medians are defined as the lines that join the vertices and midpoints of the opposite sides. So let's start by finding the coordinates of the midpoints. The midpoint of side a, Ma, has first coordinate 0, so we just need to figure out the ratio of distances to the other two sides. To do that, we'll first take a look at the altitudes of the triangle.

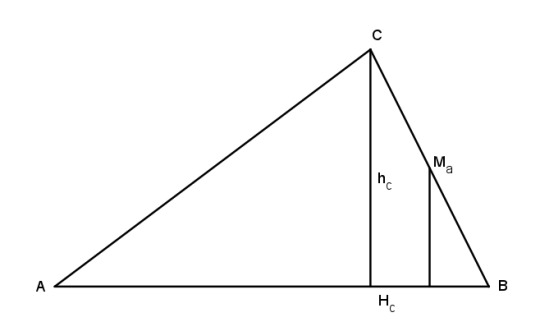
Let hc be the altitude from C to c, and let △ be the area of triangle ABC. Then by the standard formula for area of a triangle,

△ = 1/2 * c * hc

hc = 2 △ / c.

Now look at the midpoint of side a. By similar triangles, the length of its leg to side c is half the length of hc, or △/c. By the same logic, the leg extending to side b has length △/b. That gives us the ratio we were looking for, so the trilinears are 0 : △/b : △/c. Since this is a ratio, se we can divide through by △ to get 0 : 1/b : 1/c, which is nice and clean.

Repeating this for the other two sides, we get trilinears for the midpoints of the sides as:

Ma = 0 : 1/b : 1/c

Mb = 1/a : 0 : 1/c

Mc = 1/a : 1/b : 0

Now, in general, when we have two points, we can find an equation for the line that runs through them, and given two lines, we can find their point of intersection. The first method uses the fact that three points P, Q, and R with trilinears p1, p2, p3, etc. are colinear when this determinant is zero:

And by letting one of the points be variable x : y : z, we get this determinant

which gives us the general form of an equation for a line:

d x + e y + f z = 0.

Don't know what a determinant is? Don't worry! We don't need to use this method. I'm just mentioning it out of a sense of duty to completeness. In this case we're working with a median, which is a cevian, which makes things very convenient. Recall that a cevian is a line that runs through one of the vertices.

We worked out that for the point Ma, the legs to the b and c sides are in the ratio 1/b : 1/c. By similar triangles, any point P on this cevian will have legs to those sides in the same ratio. In other words, a point on the c-median must have triinears of the form u : 1/b : 1/c for some u.

The centroid G is one such point. It's also on the b-median, so it must also have trilinears of the form 1/a : v : 1/c. It's also on the c-median, so it must also have trilinears of the form 1/a : 1/b: w. So instead of working with the equations for the medians, we can get the trilinears directly from points known to lie on the medians. Therefore,

The trilinears of the centroid are G = 1/a : 1/b : 1/c.

For more completeness, here are equations for the medians:

y/b - z/c = 0

x/a - z/c = 0

x/a - y/b = 0

To find the intersection of two lines m and n with coefficients m1, m2, m3, etc., take this determinant:

The trilinears are then equal to the minor determinants:

If you are familiar with linear algebra and enjoy finding determinants, go ahead and calculate it using the coefficients above and you will get 1/a : 1/b : 1/c. Otherwise, don't worry about it.

The symmedian point

Let's now look at the symmedian point, which is the isogonal conjugate of the centroid. Recall that when P and Q are isogonal conjugates, the cevians of P are the reflections of the cevians of Q across the angle bisectors, and vice versa. In other words, at each vertex the cevians of P and Q make the same angle (in red) with the angle bisector (dashed line). Equivalently, they make the same angle (in blue) with the sides adjacent to the vertex. And that sets us up for our next shortcut:

Theorem: If a point P has trilinear coordinates p1 : p2 : p3, then its isogonal conjugate has coordinates 1/p1 : 1/p2 : 1/p3.

Proof: as the two green triangles are similar and the two blue triangles are similar, we have CP/PPa = CQ/QQb and CP/PPb = CQ/QQa. Then

PPa/QQb = CP/CQ = PPb/QQa

PPa/PPb = QQb/QQa.

Then given a ratio d : e : f, the ratio 1/d : 1/e : 1/f gives the desired reciprocal ratio between any corresponding pair.

With that result, and knowing that the centroid is 1/a : 1/b : 1/c, finding the coordinates of the symmedian point is simple:

The trilinears of the symmedian point are K = a : b : c.

Before moving on, we should take note of two things about our theorem on isogonal conjugates. First, the formula is undefined for any point with a zero coordinate, so points on the sidelines of the triangle don't have isogonal conjugates. Also, the incenter is its own isogonal conjugate, as are the three excenters, and they are the only points with this property.

The orthocenter

To find the coordinates of the orthocenter, let's go back and look at that altitude again.

Let h be the altitude from C to Hc. Draw leg hc1 from Hc to side a. Then the triangles to the right of h are similar and the two angles marked in red are equal. The length of segment hc1 is therefore h * cos B. In the same way, the blue angles are equal and hc2 = h * cos A. Thus the trilinears of Hc are cos B : cos A : 0.

This is an inconvenient form, though, because the first coordinate is in terms of B and the second in terms of A, which is the reverse of what we want. So we'll divide through by the factor cos A * cos B:

cos B / (cos A * cos B) : cos A / (cos A * cos B) : 0

= 1/ cos A : 1/cos B : 0

= sec A : sec B : 0.

That's the c-altitude. By symmetry, the a- and b- altitudes are:

0 : sec B : sec C

sec A : 0 : sec C

And conveniently, altitudes are also cevians, so we can use the same shortcut here that we used for the cetroid, and get the trilinears directly from these points.

The trilinears of the orthocenter are H = sec A : sec B : sec C.

If you want to play around with the determinant formula, you can go ahead and find the equations for the altitudes. I found it a little more convenient to use the forms cos B : cos A : 0, etc..

The circumcenter

Cevians are nice to work with, but not useful for the circumcenter, which isn't defined by cevians. It's defined by perpendiculars, and while there is a formula for perpendicular lines in trilinear coordinates, it's awful and I'd rather not use it. Sometimes the commuter rail line doesn't run where you want and it's easier to go a different way.

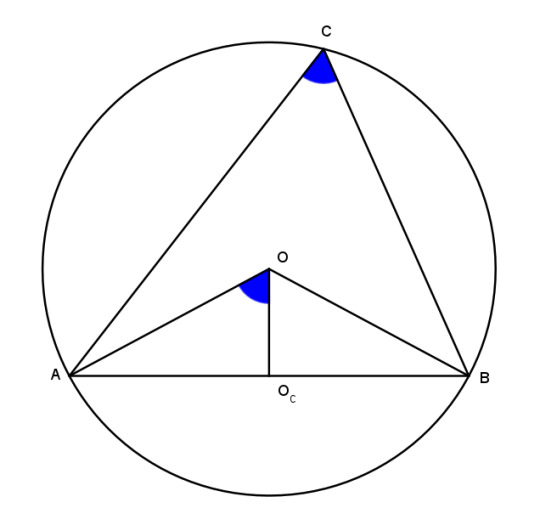
So we'll fall back on synthetic methods. The circumcenter O is the intersection of perpendicular bisectors of the sides, and is the center of the circumcircle. In particular, note that the segments OA, OB, and OC are radii of the circumcircle and equal.

Now consider angle ACB. It subtends the segment AB and has measure C. By our old friend the inscribed angle theorem, angle AOB = 2C. Segment OOc, one of the legs of O, bisects AB perpendicularly, so angle AOOc is half of AOB, equal to C.

Now by the definition of cosine,

cos AOOc = OOc/AO = cos C

OOc = AO cos C.

Similarly we can establish lengths of the other legs:

OOa = BO cos A

OOb = CO cos B.

Therefore the trilinears of O are BO cos A : CO cos B : AO cos C. But AO, BO, and CO are all radii of the circumcircle and equal, so

The trilinears of the circumcenter are O = cos A : cos B : cos C.

But look back at the orthocenter! The secant is the reciprocal of the cosine. And what did we just learn about reciprocal coodinates? Doesn't that mean -- yes, yes it does!

The circumcenter and the orthocenter are isogonal conjugates.

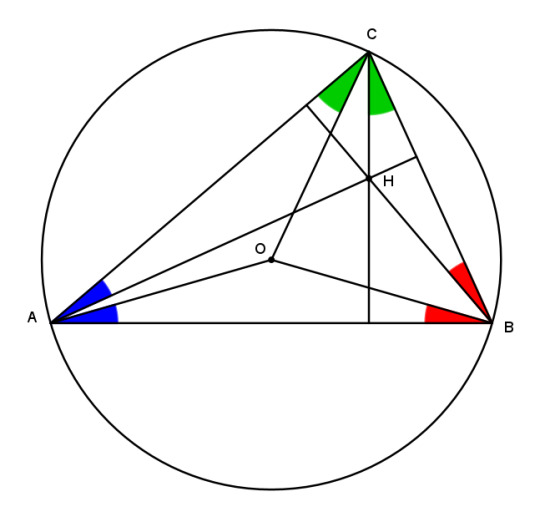
They've been conjugating away right under your nose this whole time and you never even noticed!

And this, finally, brings us a result that is much easier to establish with trilinears than with synthetic methods. There probably is a clever synthetic proof that O and H are isogonal conjugates, or even many proofs, but I would have to stare at a bunch of lines for a long time before I could come up with one. Using trilinear coordinates, we can establish this relationship at a glance. And that sort of quick trip that anyone can take is the reason we use the commuter railroad of analytic methods.

If you found this interesting, please try drawing some of this stuff for yourself! You can use a compass and straightedge, or software such as Geogebra, which I used to make all my drawings. You can try it on the web here or download apps to run on your own computer here.

An index of all posts in this series is available here.