#graph draw drawing math function calculus

[jorjin]

Saw a fanart here that had a polynomial equation and I remembered that Idk how to do these normally anymore now, only through derivation :pensive:

[kohakhearts]

when people first meet me and inquire about my studies im generally hit with two different responses, being 1) “wow, that’s an unusual combination”/“you don’t see that often”/etc. and 2) “you must be SO smart!” (or its evil twin, “you must hate yourself ha-ha”), and while the first is obviously a better response than the second, both are kinda…awkward to react to.

like? IS it an unusual combination of interests, or is it actually that most institutions make it exceptionally difficult for people to pursue stem and arts concurrently? and that we don’t often talk about the heavy crossover between stem and the arts because we’re so culturally obsessed with this notion that the world is split into Art People and Science People (also known as English People and Math People)?

and how would my interest in a science make me any smarter than someone in my program who chose to pursue a minor in history instead of physics? also, NO, i don’t hate myself. obviously taking stem classes after spending years believing im “not a math person” has lowered my gpa, but that’s not really something i care about, because at the end of the day i find the subject endlessly fascinating and i enjoy my classes very much, and i get better at math every semester because i have no choice. because it’s just…a method of communication. it’s a language. you practice, you improve - but you have to be consistent and intentional about it. the same way you have to be consistent and intentional about analyzing fictional texts and historical documents.

which is to say that like. you are using the same skills. i tutored a high school student last year who looked at me like i was crazy for saying that close reading a short story is functionally the same as solving an algebra problem. you collect like terms. then you compare and contrast them to make a statement about them - it’s human nature to seek refuge in what is familiar even if it is simultaneously traumatic, or x = 2 and y = -2. you can chart it, you can graph it, you can draw it. listen, isn’t there something so inherently beautiful about the word integral? it’s something intrinsic, baked into a person or a thing - the fundamental values formed within you by tiny, infinitesimal pieces: moments, experiences - they coalesce into something completely different, but still. you can go back. you can find the pieces. define them, pick them apart, put them together again in new ways. expand them, contract them, equate them to something else just to understand them.

half the study of mathematics is called analysis, for god’s sake. what is the study of art if not analysis? is it not the goal of the artist, the writer, to make sense of our place in the world? and is this not what we do in physics, too? look at the world and try to find reason in it? as the poet spends their life trying to make the intangible tangible, the particle physicist attempts to study dark matter. when we form a sentence, we utilize a complex system of equations that are so second-nature to us we don’t even register that’s what we’re doing - but there’s a reason this branch of linguistics is called syntactic calculus.

like…believe me. if you told my teenage self i’d be taking calculus-based courses in university, i wouldn’t have believed it. i teach high school students now who tell me they know they aren’t good at english, but it doesn’t matter to them because they do so well in math. and i get it. i do. but it’s disappointing, too, because i think my knowledge of math has made me a better reader and writer. and it feels like most people are missing out on that connection, because they feel like it’s impossible to make. but any experimentalist can tell you there’s an art to the scientific process. any musician or poet can tell you that great art is dictated by numbers - rhythm, rhyme and metre, all of it. the only group of people as interested in conceptual symmetry as physicists are artists.

anyway, all i’m saying is like - one is not more essential than the other, these things are inextricably linked, these things are as fundamental to human existence as breathing. there’s a reason why astronomers defer to shakespeare to name newly discovered bodies in space, you know? we've all gotta learn to love the math in our art and the artistry behind math.

[mit]

Teen uses calculus learned through MITx to better understand his cancer treatment

High schooler Dustin Liang estimated his blood cell counts by applying knowledge from an MITx course and talking to doctors.

Sara Feijo | MIT Open Learning

When Dustin Liang was diagnosed with T-cell acute lymphoblastic leukemia in June, the cancer consumed his life. But despite a monthlong hospital stay, aggressive chemotherapy treatments, and ongoing headaches, fatigue, loss of appetite, and nausea, the 17-year-old high school senior enrolled in MITx’s class 18.01.1x (Calculus 1A: Differentiation).

MITx, part of MIT Open Learning, offers hundreds of high-quality massive open online courses adapted from the MIT classroom for learners worldwide. The Calculus 1A: Differentiation course was designed and created by the Department of Mathematics and offered through the MITx program. Liang took the free course this summer in between treatment sessions and medical tests so that he could meet the four-year math requirement to graduate from a Massachusetts high school — an arrangement he made with his school. 

In class, Liang learned how to differentiate functions and how to make linear and quadratic approximations. He then applied this knowledge to estimate his blood cell counts. “I was in a hospital bed when I saw the doctor draw a graph of my neutrophils on a whiteboard, and I thought you could apply a quadratic approximation to it to estimate my blood cell counts at a certain time in the future,” Liang recalls. “I talked to the doctors about it, and they said it was a good idea but that they currently didn’t have the technology to do that.”

In Calculus 1A, Liang was learning how to predict the near future value of a function using linear or quadratic approximation methods. After seeing a doctor’s chart of his neutrophils, Liang hypothesized that he could use quadratic approximation to predict his neutrophil count. 

“Given a series of points of the blood cell counts, a function can be modeled,” Liang explains. “So, predicting a future point not far away is mathematically feasible.”

Determined to test his idea, Liang called his mentor, Jiawen Sun, who works in a London security exchange firm as a trading analyst simulating and modeling stock market behavior. Sun helped Liang create a graph to estimate Liang’s neutrophil count at a certain time. When Liang compared the graph to his blood test results, he found that the math worked.

“I was able to predict the blood cell counts. It was a little off, but close enough,” Liang says. “There are some challenges in simulating the function of blood cells. However, the human blood cell counts turned out to be converging easier than the stock market to simulate.”

Keep reading.

Make sure to follow us on Tumblr!

[princessgurl]

I would also like to add

symbolab, which is capable of solving equations and integrals showing each step in mist of the cases ~

Desmos, which allows you to draw pretty much every 1-variable function you can think of ~

Geogebra, which does pretty much the same job as desmos, but it's a bit more geometry oriented, and allows you to graph 2-variable functions (so also 3d shapes), and you can also download it for free ~

👏🏾Education 👏🏾is 👏🏾a 👏🏾right,👏🏾 not👏🏾 a👏🏾 service 👏🏾

Pass along and use the shit out of them

[lolpuns]

20+ Hilarious Calculus Puns That Will Have Math Nerds Integrating with Laughter

https://lolpuns.com/?p=2091 20+ Hilarious Calculus Puns That Will Have Math Nerds Integrating with Laughter Looking for some math humor that’s on a whole other level? We’ve derived the ultimate collection of calculus puns that will have both math enthusiasts and pun lovers integrating laughter into their day. Whether you’re a calculus professor wanting to lighten up your lectures or a student seeking comic relief from differential equations, our limit-less supply of clever wordplay approaches mathematical hilarity from every angle. These puns are carefully calculated to make even the most serious mathematician find the area under the curve of their smile. Table of Contents Toggle 10 Calculus Puns That Will Have You Finding Your Limit of LaughterWhy Calculus Puns Are an Integral Part of Math HumorThe Derivative of Good Math JokesHow Calculus Puns Help Students LearnPrime Examples of Calculus Puns That Will Make You LOLDerivative Jokes That Are Off on a TangentIntegral Humor for Advanced FunctionsCalculus Puns for Those Who Like to Live on the Edge (of a Graph)Historical and Academic ContextCommon Themes in Calculus HumorNotable Examples That Differentiate Great PunsThe Function of Calculus HumorHow to Use Calculus Puns in the Classroom Without Approaching the Limit of Student PatienceKnow Your AudiencePerfect Your DeliveryUse ModerationEncourage Student ParticipationConnect Puns to Learning ObjectivesWhen Calculus Puns Converge: Math Jokes for Different Skill LevelsSimple Calculus PunsMid-Level JokesAdvanced HumorThe Chain Rule of Comedy: Creating Your Own Calculus Puns1. Terminology-Based Puns2. Conceptual Wordplay3. Pop Culture & History4. Formulaic StructuresCalculus Puns That Professors Secretly LoveWordplay on Mathematical ConstantsDerivative HumorHistorical Mathematics ReferencesNatural Logarithm LaughsTherapy for FunctionsExponential RelationshipsMathematician-Approved Calculus One-Liners That Will Make You SmileThe Constant Crowd-PleasersRomantic Mathematical WordplayClassroom FavoritesCreating Memorable MathematicsSum It Up: Why We Can’t Differentiate Between Calculus and HumorFrequently Asked QuestionsWhy are calculus puns popular among math enthusiasts?Can calculus puns help with learning math?What makes a good calculus pun?Are calculus puns only for advanced mathematicians?How can I create my own calculus puns?Do professors actually enjoy calculus puns?What are some examples of simple calculus puns?Can calculus puns work in a classroom setting?What’s the history behind calculus humor?Why do people find math puns funny even if they struggle with calculus? 10 Calculus Puns That Will Have You Finding Your Limit of Laughter Derivative Delight: What did the calculus teacher say when their student asked for help? “This is where I draw the line tangent to your problem!” Functions always appreciate a good tangent line to help them find their way. Infinite Series Humor: Why did the infinite series go to therapy? It had trouble with convergence issues! Therapists specialize in helping even the most divergent thoughts come together. Integration Joke: My calculus professor told me I was average. Turns out he was just taking the integral of my progress over time! Calculating someone’s area under the curve can reveal their true potential. Limit Logic: Why couldn’t the calculus student find the limit? Because they approached it from the wrong direction! Sometimes you need to look at problems from both sides. Calculus Cat: What do you call a cat that understands calculus? A first-derivative feline! These rare creatures can instinctively find the slope of any function. Mathematical Marriage: Two functions got married, but sadly they couldn’t differentiate between their problems. Their relationship had too many critical points! Derivative Dating: I asked a calculus student on a date, and they said they’d have to find my derivative first to see if I had a positive slope! We’re still waiting to see if our relationship will be increasing or decreasing. Continuous Comedy: Why did the continuous function feel so confident? Because it knew its limits! Understanding where you begin and end is key to mathematical success. L’Hôpital’s Rule: What’s a calculus student’s favorite hospital? L’Hôpital’s, where all indeterminate forms get resolved! Even the most uncertain cases find clarity there. Integral Insight: Why was the integral always broke? Because it was constantly finding its area under the curve! Spending all your time calculating areas doesn’t leave much time for earning money. Why Calculus Puns Are an Integral Part of Math Humor The Derivative of Good Math Jokes Good math jokes, particularly calculus puns, thrive on clever wordplay and unexpected twists on familiar mathematical concepts. These jokes range from simple puns to elaborate setups requiring basic calculus knowledge. Consider the function that refuses to argue because it doesn’t want to reach an inflection point—a perfect example of calculus humor that connects mathematical principles with everyday situations. Math enthusiasts often gravitate toward pi-related jokes, with many calculus students claiming pi as their favorite dessert. The beauty of calculus humor lies in its ability to transform complex concepts into accessible jokes that even those with limited mathematical background can appreciate. How Calculus Puns Help Students Learn Calculus puns serve as valuable educational tools by making this challenging subject more approachable and memorable for students. These mathematical jokes effectively reduce stress levels and boost engagement when tackling complex topics like derivatives and integrals. Teachers who incorporate humor into their lessons create a more positive learning environment where students feel comfortable exploring difficult concepts. Educational resources from websites like Cuemath and Punsvila offer collections of calculus jokes specifically designed for classroom use. The connection between humor and retention is particularly strong in mathematics—students who laugh at calculus jokes are more likely to remember the underlying concepts during exams. Making calculus fun through puns transforms it from an intimidating academic pursuit into an captivating intellectual adventure that students actually look forward to experiencing. Prime Examples of Calculus Puns That Will Make You LOL Derivative Jokes That Are Off on a Tangent Recycled calculus puns are often called “derivative humor” due to their repetitive nature, much like taking the derivative of a function. A standout example that always delivers is “What’s the derivative of Amazon? Prime Rib!” – cleverly playing on Amazon Prime rather than the traditional cow version. Newton and Leibniz’s historical rivalry provides rich material for derivative jokes, such as “Newton: I’ve discovered calculus. Leibniz: Me too. Newton: Seems derivative.” Soccer apparently isn’t popular among calculus students because they’re “too many tangents” – a playful reference to lines that touch curves at single points. We’ve all experienced conversations that suddenly veer off topic, just like the student who said, “I had a good discussion with my calculus professor, but it went off on a weird tangent.” These puns work brilliantly as they connect mathematical concepts with everyday situations that anyone can relate to. Integral Humor for Advanced Functions Students particularly connect with the existential humor in puns like “Why was the calculus student always stressed? Too many variables in life.” Functions apparently have feelings too, as evidenced by “Why did the function refuse to argue? It didn’t want to reach an inflection point” – a clever nod to critical points where curves change behavior. Everyday objects become perfect vehicles for calculus humor. Elevators are praised by math enthusiasts “for understanding rates of change,” while roller coasters demonstrate “concavity and inflection points” in action. Assignments struggles inspire classics like “What’s long, hard, and scary? Calculus assignments!” Students seeking rest might justify their naps by saying they need “to integrate rest” – perfectly merging mathematical terminology with relatable college experiences. Even divine intervention isn’t safe from calculus wordplay, with puns like “When God integrated Earth, he added the sea.” Pirates apparently “excel at calculus because they never forget the C” – referring to the constant of integration that students often overlook. These crossover jokes extend to video games (“Integral of Duty”) and automotive troubles (“Why did the car break down? It hit a critical point”), proving that calculus humor can derive laughs from virtually any situation. Calculus Puns for Those Who Like to Live on the Edge (of a Graph) Historical and Academic Context Calculus puns have been making mathematicians chuckle for generations by cleverly incorporating concepts like derivatives, integrals, and limits. One classic example we love is “Drinking and deriving,” which brilliantly plays on homophones to blend calculus terminology with everyday activities. The famous rivalry between Newton and Leibniz over who discovered calculus first has also spawned many jokes, including Newton’s witty comeback: “Really? Seems derivative.” Common Themes in Calculus Humor Wordplay forms the foundation of many calculus jokes. “Derivative humor” refers to recycled jokes that lack originality, creating a clever mathematical metaphor. Another favorite is “Don’t be mean, integrate!” which transforms mathematical operations into life advice. Love and Relationships provide fertile ground for calculus puns. Couples with a mathematical bent might express their feelings with lines like “Our love is exponential” or “You’re my prime factor,” blending romantic sentiments with mathematical precision. Student Struggles often appear in calculus humor, reflecting the challenges many face when learning this subject. A prime example is: “What’s long, hard, and scary? Calculus assignments.” Notable Examples That Differentiate Great Puns The Pirate Joke remains a staple in calculus classes: “Why are pirates the best at calculus? They never forget the C.” This cleverly references the integration constant (+C) that students often omit. Visual Humor works particularly well with graphing concepts: “Why did the graph go to therapy? It had too many ‘ups and downs'” – a pun that perfectly captures both emotional states and function behavior. Exam Stress provides relatable material for students: “I failed my Calculus exam because I was seated between identical twins—it was hard to differentiate.” This pun brilliantly connects the mathematical concept of differentiation with the everyday meaning. The Function of Calculus Humor These mathematical jokes do more than just entertain—they simplify complex concepts, making calculus more approachable for students who might otherwise feel intimidated. Many calculus puns serve as excellent mnemonic devices, such as “integrate now, differentiate later,” helping students remember key processes. How to Use Calculus Puns in the Classroom Without Approaching the Limit of Student Patience Know Your Audience Matching calculus puns to your audience is crucial for effectiveness. Students with different mathematical backgrounds will appreciate different levels of humor, so ensure your puns aren’t overly complex for beginners. First-year calculus students might enjoy simpler jokes like “Why is the south bad at calculus? They don’t know how to integrate,” while advanced students can appreciate more nuanced mathematical wordplay. Perfect Your Delivery Delivery transforms even recycled derivative humor into something fresh and captivating. Present your puns with genuine enthusiasm and appropriate timing to maintain student interest. A well-timed calculus joke during a particularly challenging lesson can reset attention and create a moment of connection with your class. Teachers who deliver puns confidently often find students more receptive to the mathematical concepts that follow. Use Moderation Strategic placement of puns prevents overwhelming your students with too much humor. We recommend using a few well-chosen jokes rather than turning every concept into a pun opportunity. Spacing out your mathematical wordplay across a lesson helps maintain the novelty factor without distracting from essential learning objectives. Consider introducing a calculus pun like “Why did the calculus student bring a ladder to class? To reach new heights in calculus” when introducing a new or difficult topic. Encourage Student Participation Inviting students to create their own calculus puns fosters engagement and creativity. This approach transforms passive listeners into active participants in the learning process. Student-generated humor often resonates more deeply with peers and creates memorable associations with mathematical concepts. Classes that collectively develop their own mathematical jokes often demonstrate stronger community bonds and increased comfort with challenging material. Connect Puns to Learning Objectives Effective calculus puns directly relate to the concepts being taught. Jokes about integration should appear during integration lessons, while derivative humor works best when discussing differentiation. Teachers might incorporate the “integral twist” dance move when explaining integration techniques, creating both a visual and verbal memory aid. Relevant humor reinforces key concepts and helps students recall important information during assessments. When Calculus Puns Converge: Math Jokes for Different Skill Levels Mathematics humor appeals to different audiences based on their familiarity with calculus concepts. We’ve collected some of the best calculus puns categorized by complexity to ensure everyone from beginners to advanced mathematicians can enjoy a good laugh. Simple Calculus Puns These entry-level jokes require only basic knowledge of calculus terminology, making them accessible to most math students. Derivative Humor: What do you call a recycled calculus pun? Derivative humor! This joke plays on the dual meaning of “derivative” as both a mathematical concept and something unoriginal. Too Many Variables: Why was the calculus student always stressed? Too many variables in life! Anyone who’s struggled with complex equations filled with x, y, and z variables can relate to this simple yet effective pun. Calculus Assignments: What’s long, hard, and scary when you first see it? Calculus assignments! This pun perfectly captures the initial intimidation many students feel when facing a new calculus assignment. Mid-Level Jokes These puns require a slightly deeper understanding of calculus principles but still remain accessible to most students who’ve completed an introductory course. Space for Differentiation: Why did the calculus student break up with their partner? They needed more space to differentiate themselves! This cleverly connects the mathematical concept of differentiation with personal growth. Elevators and Rates of Change: Why do calculus students love elevators? They understand rates of change! This pun links the everyday experience of elevator movement with the fundamental calculus concept of changing values over time. Advanced Humor These sophisticated jokes appeal to those with a comprehensive understanding of calculus history and complex concepts. Newton vs. Leibniz: Newton: I’ve discovered calculus (1664). Leibniz: I’ve discovered calculus (1670s). Newton: Really? Seems derivative! This historically based pun references the famous priority dispute between Newton and Leibniz over who first invented calculus. Roller Coaster Mathematics: Why did the calculus student love roller coasters? They were all about concavity and inflection points! Students familiar with analyzing curves and their behavior will appreciate this connection between thrilling rides and mathematical concepts. Math humor serves as an excellent bridge between abstract concepts and relatable situations. These calculus puns demonstrate how mathematical principles can be found in everyday experiences, making the subject more approachable and captivating for learners at all levels. The Chain Rule of Comedy: Creating Your Own Calculus Puns Calculus puns thrive on clever wordplay involving mathematical concepts that can transform complex formulas into laugh-out-loud moments. We’ve compiled essential strategies to help you create your own mathematical jokes that will differentiate you from other comedians. These techniques leverage the rich terminology of calculus to create humor that both math enthusiasts and casual jokesters can integrate into their repertoire. 1. Terminology-Based Puns Mathematical terms often have everyday meanings that create perfect opportunities for wordplay: “Drinking and deriving” cleverly substitutes “driving” with “deriving,” warning against calculating derivatives while intoxicated “Derivative humor” pokes fun at recycled jokes by referencing how derivatives are derived from original functions “Stay in your limits” transforms ordinary advice into a mathematical reference about boundaries in calculus These puns work because they bridge the gap between technical jargon and common expressions, making them accessible to wider audiences. 2. Conceptual Wordplay Take advantage of the metaphorical potential in calculus concepts: “Our love is exponential” replaces typical romantic growth metaphors with a mathematically precise function “You’re my absolute value” romantically suggests someone always makes everything positive, just like the absolute value function “Tangents are just the TIP of the curve” plays with both the mathematical meaning and conversational notion of going off on tangents This approach connects emotional or everyday experiences with mathematical principles, creating relatable humor with an intellectual twist. 3. Pop Culture & History Incorporating historical figures and pop culture references adds depth to your calculus humor: Newton vs. Leibniz rivalry: “Newton: Really? Seems derivative.” cleverly mocks their famous dispute over calculus invention Pirate mathematics: “A true pirate never forgets the C” reminds students about the crucial integration constant “Mathemagician” combines “mathematician” and “magician” to suggest the seemingly magical nature of calculus answers These references appeal to those familiar with calculus history while remaining approachable to newcomers. 4. Formulaic Structures Apply traditional joke structures to mathematical content: Question-and-answer format: “Why did the graph go to therapy? It had too many ups and downs“ Self-referential humor: “Calculus jokes are all derivative” playfully critiques the repetitive nature of math puns This framework leverages familiar joke patterns, making complex concepts more digestible through humor. To create your own calculus puns, identify terms with dual meanings (like “integrate” which means both to socialize and to calculate) or find phonetic similarities (“pi” vs. “pie”). Then combine these mathematical elements with everyday situations like relationships, school, or work to create universally appealing jokes that don’t require an advanced degree to appreciate. Try crafting your own puns using this formula: Term: Limit → Pun: “My patience has reached its limit… and it’s approaching infinity.” Concept: Chain rule → Pun: “Our friendship follows the chain rule—always connected, never broken.” The best calculus puns transform intimidating mathematical concepts into accessible humor, proving that even the most complex subjects can become sources of joy and connection. Calculus Puns That Professors Secretly Love Professors might maintain a serious demeanor in the classroom, but they’re often harboring a deep appreciation for calculus humor. We’ve gathered some of the most professor-approved mathematical jokes that bring smiles to even the most stoic academic faces. Wordplay on Mathematical Constants Mathematics instructors particularly enjoy puns that cleverly incorporate fundamental calculus concepts. “Why are pirates great at calculus? They never forget the C” ranks among faculty favorites, with the integration constant (“C”) serving as the perfect punchline. Professors appreciate this joke because it reinforces a common student mistake while being genuinely funny. Derivative Humor Nothing gets a calculus professor chuckling like a good derivative joke. “What’s a recycled calculus pun? Derivative humor” offers a meta-mathematical punchline that works on multiple levels. Faculty members often use this type of humor when introducing differentiation concepts to lighten the mood before diving into complex formulas. Historical Mathematics References Academic circles particularly value jokes that reference calculus history. “Newton called Leibniz’s calculus work derivative” plays on the famous priority dispute between these two mathematical giants while incorporating appropriate calculus terminology. Professors love sharing these jokes because they seamlessly blend historical context with mathematical concepts. Natural Logarithm Laughs “Why do math teachers love nature? It’s full of natural logs” represents a classic professor-approved joke. This pun cleverly connects the mathematical concept of natural logarithms (ln) with actual tree logs, creating an accessible entry point for students struggling with logarithmic functions. Teachers frequently deploy this joke when introducing the ‘e’ constant. Therapy for Functions Even professors can’t resist graph-based humor like “Why did the graph seek therapy? Too many ups and downs.” This pun resonates in academic settings because it humanizes mathematical concepts while subtly reinforcing understanding of function behavior. Faculty members often use such jokes to help students visualize continuous functions and their properties. Exponential Relationships “Our love is exponential” offers professors a rare opportunity to connect calculus with emotional concepts. Academics appreciate how this pun effectively illustrates growth patterns while making mathematics more relatable. This type of joke often appears in example problems designed to demonstrate real-industry applications of exponential functions. Mathematician-Approved Calculus One-Liners That Will Make You Smile Mathematicians aren’t just known for their analytical skills – they’ve crafted some of the most clever calculus puns that perfectly balance humor with mathematical precision. We’ve compiled these one-liners that even the most serious mathematicians approve of. The Constant Crowd-Pleasers “What do pirates and calculus have in common? They never forget the C!” This classic joke plays on the integration constant (+C) that students often forget when solving indefinite integrals. “I’ve reached my limit with these calculus jokes.” Mathematicians appreciate this straightforward reference to the foundational concept of limits in calculus. “Don’t be mean, integrate!” This friendly reminder combines mathematical integration with social advice, making it a favorite among calculus professors. “Seems derivative to me.” This clever wordplay works on multiple levels, echoing the famous Newton-Leibniz controversy about who first discovered calculus. Romantic Mathematical Wordplay “Our love is exponential” connects calculus concepts with emotional growth, creating an elegant mathematical metaphor. “You’re my prime factor” blends number theory with affection, showing how math terminology can express deep personal connections. “Let’s not be discrete, let’s be continuous” cleverly uses function properties to suggest relationship commitment. Classroom Favorites “What’s long, hard, and scary? Calculus assignments!” This popular joke resonates with students struggling through complex problem sets. “Keep calm and carry out calculus” transforms the famous British slogan into mathematical motivation. “The calculus exam was so hard, it was the derivative of my happiness.” This one-liner perfectly captures student sentiment while utilizing calculus terminology. Creating Memorable Mathematics These puns work effectively because they exploit term double meanings, incorporate mathematical constants, develop process metaphors, and play on common classroom experiences. Educational resources actively use these jokes to enhance student engagement, making difficult concepts more approachable through humor. Math educators have documented that these types of calculus jokes help students remember key concepts through the repetition of mathematical terminology in unexpected contexts. The combination of surprise and recognition creates memorable learning moments that stick with students long after the laughter fades. Sum It Up: Why We Can’t Differentiate Between Calculus and Humor We’ve explored how calculus puns transform mathematical dread into delightful wordplay. These clever jokes do more than just entertain—they build bridges between complex concepts and everyday life making the subject approachable for everyone. Whether you’re creating your own mathematical quips or enjoying our curated collection there’s a limit to how much fun calculus can be—and that limit approaches infinity! From simple one-liners to sophisticated historical references these puns offer something for every level of mathematical expertise. So next time you’re struggling with derivatives or wrestling with integrals remember that a good laugh might just be the integral solution you need. After all math humor isn’t just tangential to learning—it’s an essential function! Frequently Asked Questions Why are calculus puns popular among math enthusiasts? Calculus puns are popular because they combine clever wordplay with mathematical concepts, creating humor that’s both intellectually satisfying and accessible. They transform complex topics into relatable jokes, helping to reduce the intimidation factor of calculus while reinforcing understanding. These puns create a sense of community among math enthusiasts who appreciate the specific knowledge required to “get” the joke. Can calculus puns help with learning math? Absolutely! Calculus puns serve as powerful educational tools by making abstract concepts more memorable. Research shows that humor reduces stress and increases engagement in the classroom. When students associate positive emotions with learning calculus, they’re more likely to retain information and develop a genuine interest in the subject. Professors who incorporate humor create a more welcoming learning environment. What makes a good calculus pun? A good calculus pun balances mathematical accuracy with humor that’s accessible to the intended audience. The best puns use clever wordplay on calculus terminology, connect mathematical concepts to everyday situations, and deliver an unexpected twist. They should be understandable to those familiar with basic calculus concepts without requiring advanced expertise unless aimed at specialists. Are calculus puns only for advanced mathematicians? Not at all! Calculus puns exist for all knowledge levels. Simpler puns like “What do you call a recycled calculus pun? Derivative humor!” work for beginners, while more complex jokes might reference specific theorems or historical mathematicians. The beauty of calculus humor is that it can be tailored to different skill levels, making math more inclusive and entertaining. How can I create my own calculus puns? Start by identifying calculus terms with dual meanings (like “derivative” or “integral”). Look for ways to connect these terms to everyday situations through wordplay. Use familiar joke structures like “Why did…” or “What do you call…” to frame your pun. Practice with friends who understand calculus basics to refine your humor and ensure your puns make mathematical sense. Do professors actually enjoy calculus puns? Many professors secretly love calculus puns, especially those that demonstrate a solid understanding of mathematical concepts. Clever wordplay on constants, derivatives, or historical mathematical figures often earns appreciation from educators. Professors enjoy seeing students connect with the material through humor, as it shows engagement with the subject beyond rote memorization. What are some examples of simple calculus puns? Simple calculus puns include: “I have a limit, so please stop,” “What’s the integral of 1/cabin? Natural log cabin,” and “Why was the calculus book sad? It had too many problems.” These jokes require only basic familiarity with calculus terminology, making them accessible to students just beginning their mathematical journey while still providing a chuckle. Can calculus puns work in a classroom setting? Strategically incorporated calculus puns can transform classroom dynamics by creating a more relaxed, engaging learning environment. They serve as memorable memory aids, help break tension during difficult topics, and show students that math can be fun. The key is using humor that’s appropriate and relevant to the material being taught. What’s the history behind calculus humor? Calculus humor has existed nearly as long as calculus itself. Historical records show mathematicians like Euler and Gauss occasionally used witty remarks about mathematical concepts. The tradition continues today in academia, with each generation developing new puns reflecting contemporary culture while maintaining the mathematical foundation that makes calculus jokes uniquely satisfying. Why do people find math puns funny even if they struggle with calculus? Math puns often work on multiple levels. While those with calculus knowledge appreciate the mathematical accuracy, many puns also connect to universal experiences or use common language that resonates with broader audiences. The unexpected juxtaposition of serious mathematics with everyday situations creates humor that can be enjoyed even by those who find the actual math challenging. https://lolpuns.com/?p=2091 LOL Puns

[cecestudies]

Essential Topics You Must Master for A Level Maths Success

Struggling with A Level Maths revision? In this guide by Exam Tips, we break down the essential topics you must master for A Level Maths success. Whether you're aiming for an A or just trying to pass confidently, focusing on the right areas can make all the difference. From core algebra and calculus to statistics and mechanics, we highlight the key concepts that appear frequently in exams and how to tackle them efficiently. With smart strategies and topic-focused revision, you’ll boost your confidence and performance. Let Exam Tips be your go-to source for structured A Level Maths revision, practice insights, and proven study methods. Start mastering the topics that matter most—and leave the guesswork behind.

Mastering Algebraic Techniques and Expressions

Algebra forms the backbone of most questions in A Level Maths. You must be comfortable simplifying expressions, solving equations, and manipulating algebraic fractions. Factoring, expanding brackets, and completing the square are all skills that appear across different types of problems. Understanding how to use functions and their notations is equally important, especially when combined with graph sketching and transformations. Exam Tips recommends starting your A Level Maths revision by reinforcing these core algebraic techniques since they often build into more complex topics like calculus and trigonometry.

Deep Understanding of Calculus Fundamentals

Calculus is one of the most heavily weighted topics in A Level Maths exams. You’ll need to grasp the principles of differentiation and integration, including their real-world applications. This includes curve sketching, finding stationary points, calculating areas under curves, and solving problems involving rates of change. It's crucial to not only memorise formulas but also understand when and how to apply them effectively. A structured approach from Exam Tips ensures that your A Level Maths revision includes progressive problem-solving that reinforces both basic and advanced calculus skills.

Trigonometry and Its Real-World Applications

Trigonometry plays a key role in both pure and applied mathematics. You should be confident in using identities, solving equations, and working with radian measures. Real-world applications like modelling wave functions and solving vector problems often incorporate trigonometric principles. As you progress in your A Level Maths revision, practicing with unit circle diagrams and trigonometric transformations will help solidify your understanding. Exam Tips suggests integrating these concepts with questions from mechanics and coordinate geometry to deepen your problem-solving ability.

Working with Functions, Graphs, and Transformations

A thorough understanding of functions and graphs is essential to A Level Maths success. You’ll encounter a variety of functions including linear, quadratic, exponential, and logarithmic forms. Being able to draw, transform, and interpret graphs is a skill tested across both Paper 1 and Paper 2. Students are often required to analyse roots, intercepts, and asymptotes. As part of your A Level Maths revision plan, Exam Tips encourages consistent graph-based practice to develop a visual intuition for mathematical relationships and behaviour of functions.

Statistical Techniques and Probability Concepts

The statistics component in A Level Maths includes data representation, hypothesis testing, and interpreting statistical diagrams. It also requires understanding of key distributions, such as binomial and normal. Probability questions often involve Venn diagrams, conditional probability, and expected outcomes. These questions test your ability to apply logical thinking to real-world scenarios. Exam Tips recommends integrating statistical problem sets into your A Level Maths revision early on, so you become comfortable with data interpretation and numerical reasoning.

Mechanics: Kinematics and Newton’s Laws

Mechanics introduces physical applications of mathematical theory, with a focus on motion, forces, and energy. You’ll need to understand velocity-time graphs, equations of motion, and the principles of Newton’s laws. Problems often involve modelling real-life scenarios with diagrams and resolving forces in components. Exam Tips advises students to connect mechanics with algebra and calculus topics, as many problems overlap conceptually. A Level Maths revision should include both conceptual learning and practice-based assessments in this area.

Solving Realistic Modelling and Word Problems

A Level Maths increasingly includes worded problems that require mathematical modelling. These questions assess not only your computational ability but also your analytical thinking. You must identify relevant information, translate it into mathematical form, solve the problem, and interpret your result. Topics such as exponential growth and decay, optimisation, and dynamics often appear in this format. As you revise with Exam Tips resources, focus on breaking down complex questions into manageable parts. Developing this skill will greatly improve your overall exam performance.

Conclusion

Succeeding in A Level Maths requires more than just learning formulas — it demands deep understanding and consistent practice. By focusing your A Level Maths revision on the essential topics discussed above, you’ll build a strong, exam-ready foundation. Exam Tips is committed to helping students unlock their potential with focused guidance, practical resources, and expert strategies. Remember, success in maths isn’t about doing everything — it’s about doing the right things the right way. Stay focused, stay curious, and trust the process.

[futurensetechnologies]

The Role of Mathematics in Data Science: Do You Really Need It?

Introduction

As data science continues to transform industries, many aspiring professionals wonder about the academic foundation required to succeed. One common path is an Information Technology Management degree, which combines technical knowledge with business strategy. But a key question remains—how important is mathematics in this field? This blog breaks down the role math plays in data science and whether it’s a must-have skill for building a successful career.

Why Math is Considered Foundational in Data Science

Mathematics is the engine that drives data science. While tools and programming languages help process data, math enables professionals to understand patterns, draw insights, and build accurate models. If you’re pursuing a Master’s in information management, a solid grasp of key mathematical concepts is essential for applying theory to real-world problems.

Here’s why math is foundational in data science:

Statistics and probability help in making predictions and understanding data trends.

Linear algebra is crucial for machine learning models, especially in image and language processing.

Calculus plays a role in optimization and fine-tuning algorithms.

Discrete mathematics helps in logic building, algorithm design, and data structures.

Numerical analysis supports dealing with real-time data computations and error management.

A clear understanding of these areas gives data professionals a competitive edge and deepens their analytical capabilities.

Core Areas of Mathematics Used in Data Science

Mathematics is at the heart of data science. While coding and software tools make execution easier, the logic and theory that drive data models come from mathematical principles. If you’re pursuing a Master’s in Information Systems, understanding the core areas of mathematics can help you connect technical knowledge with strategic data insights.

Here are the primary branches of math used in data science:

1. Statistics and Probability

These are the building blocks of data analysis. They help in understanding data distributions, correlations, hypothesis testing, and predictive modeling.

2. Linear Algebra

Essential for machine learning and deep learning, linear algebra supports matrix operations, vector transformations, and dimensionality reduction techniques like PCA (Principal Component Analysis).

3. Calculus

Mainly used for optimization, calculus helps fine-tune algorithms by minimizing or maximizing functions—important in training machine learning models.

4. Discrete Mathematics

This area supports algorithm development, graph theory, and logical reasoning—key for structuring data-driven solutions.

5. Numerical Methods

Important for handling real-world data problems, such as approximations, simulations, and missing or noisy data.

Each of these disciplines contributes to building, evaluating, and improving the performance of data models. Understanding these mathematical tools allows professionals to move beyond surface-level data analysis and dive into more meaningful, scalable solutions that impact business decisions.

Can You Learn Data Science Without Strong Math?

Futurense believes that data science should be accessible to all, regardless of your math background. While mathematics enhances your understanding of data science, it shouldn’t be a roadblock. With the right guidance, resources, and learning structure, anyone can build a solid foundation in data science—even without being a math expert.

Many students pursuing an MS in information systems come from diverse academic backgrounds, including business, humanities, or IT. While they may not have in-depth math skills initially, structured learning pathways allow them to pick up the necessary concepts along the way.

Here’s how you can learn data science without a strong math foundation:

Focus on application-first learning—understand the “why” before diving into the “how.”

Use tools like Python, R, and libraries such as scikit-learn or pandas, which simplify complex computations.

Practice with real-world datasets to see the impact of algorithms visually.

Enroll in beginner-friendly courses like those offered by Futurense, which explain mathematical concepts through relatable examples.

Supplement your learning with basic math resources—only what’s required to understand models, not to become a mathematician.

In essence, while math helps, it’s not a prerequisite. With the right mindset and support, your journey into data science can be successful and rewarding, even without being a math whiz.

Also, read this blog: Master’s in MIS in the USA: A Comprehensive Guide

How to Strengthen Your Math for Data Science

Strengthening your math skills can significantly improve your ability to understand and apply data science concepts effectively. Whether you’re currently pursuing an MS in information systems or planning to enroll in a Master’s in Information Systems, building a strong foundation in mathematics will enhance both your academic and professional journey.

Here’s how to sharpen your math for data science:

Start with the basics: Brush up on core topics like statistics, probability, linear algebra, and calculus through online platforms like Khan Academy, Coursera, or edX.

Practice consistently: Apply concepts regularly through hands-on projects, real datasets, or coding challenges.

Use visual tools: Leverage visual explanations and interactive tools to understand complex mathematical concepts more easily.

Connect theory to practice: Use Python libraries like NumPy and SciPy to see how mathematical operations work in data science environments.

Join study groups or forums: Engaging with peers can help reinforce learning and clarify doubts.

With consistent effort and the right resources, improving your math skills becomes less overwhelming and more rewarding, especially in a field where data-driven decisions matter most.

FAQ

1. Do I need to be good at math to learn data science?

While strong math skills are helpful, they are not mandatory to begin. With practical resources and supportive courses, you can strengthen your math knowledge alongside your data science learning journey.

2. What kind of math is used in data science?

Key areas include statistics, probability, linear algebra, calculus, and discrete mathematics. These help in understanding data structures, building models, and interpreting results.

3. Is a Master’s in Information Systems math-heavy?

A Master’s in Information Systems involves some mathematical components like statistics and data analysis, but it also focuses on technology, management, and strategy.

4. How can I improve my math skills for data science?

Start with beginner-friendly courses online, work on real datasets, and practice using Python libraries like NumPy and pandas. Regular practice is key.

5. Is math more important than coding in data science?

Both are important. Coding helps you implement models, while math helps you understand and improve them. A balance of both skills leads to better outcomes.

Source URL: https://postyourarticle.com/role-of-mathematics-in-data-science/

[1358456]

Math!

I had a good chat with my friend today, and among various stuff discussed, one thing particularly caught my attention and intrigue. And that is... why so many people, including said friend, hated math in high school.

Friend: "I really hated math in high school." Me: "Heh. Now that's something you shouldn't say in front of someone who majored in pure math." Friend: "I suppose. But really though. If you weren't in those classes too, I would've been doomed."

A little homage to a previous conversation several years ago...

Me: "Vote? Me? Heh. I don't give a damn. I still haven't voted once, and most likely never will." Friend: "Aww, that's not something you say in front of someone who majored in political science." Me: "Heh. Maybe."

Anyways. The whole "I hated math in high school" thing... I heard it a lot over the years, and the reason is almost always because of trigonometry. It feels like, the moment sin and cos enter the field, a solid half of the students are like "f*ck this, I'm out". Only a small few get to hate math because of how it just blows their mind. When a + b no longer equals b + a, or when you can make a cone that has finite volume but infinite surface area, which means you can fill it up with paint but never be able to fully paint the interior... hehe. There are things that are mathematically possible but realistically impossible, usually when dealing with infinite or near 0 numbers.

So, many people hate the whole trigonometry thing, and I kind of get it. It's not something you'll ever need outside of math class for a vast majority of people. So they complain why the hell were they forced to sit through all that? And the answer is... well, it sucks for them. Because the thing is, trigonometry is so basic and fundamental in everything math, that it can't be pushed back to university or grade 12, even, when math is no longer mandatory. In university, you need to be very familiar with everything trig right off the bat, or you're f*cked. There are two irrational numbers that appear absolutely everywhere in math, to the point that I believe those the signatures of the one who created math, and those are e and pi. e being the natural number (the natural number is not a natural number...), and pi being... that pi. Why are they everywhere? Because e^x is everywhere and sin and cos are also everywhere. But at least those who hated math got to escape while the angles were still in degrees, no one had to worry about integrating using trig identities, and when you were still actually evaluating sin and cos.

The next most common math complaint I heard, which I only heard while I was tutoring grade 12 students, is... why is the course "calculus and vectors" when vectors have nothing to do with calculus? It's like... in the middle of the course, you suddenly abandon the entirety of the first half to learn something completely unrelated. And then you have to re-remember the first half for the exam! The answer for that one is because the grade 12 curriculum got changed in a very dumb manner. Calculus was too hard so they pulled calculus out of calculus and the remaining husk became "advanced functions". And that was because the grade 11 math course was called "functions" so they couldn't use that name again. And calculus by itself was too short so they pulled vectors out of the removed geometry course and now it's "calculus and vectors". ... And then in university I had to do vector calculus! "Oh, so this is where it merges..." heh. Just the concept of f(x) blows some people's minds. Well, here's f(x, y) for starters! ... And drawing 4D graphs...

Of course, this is just referring to the Ontario math curriculum. So those who live outside of Ontario, Canada, which would be... most everyone, your high school math woes (if you had 'em) might be a little different. But I'm betting that trig stuff was still the kicker.

[schoollabchina12]

What Essential Equipment Should Every Math Student Have?

For a Math Student, understanding different ideas is quite sensitive, and it differs as it incorporates the right set of tools and equipment. With the growth of globalization in education, math equipment manufacturers and suppliers in China have started being known for their reliability in terms of quality and educational tools. China has positioned itself as a one-stop destination for math equipment suppliers meeting students' learning demands. In this blog, we are going to discuss the essential math equipment that every student should possess in a classroom.

Essential Math Equipment Every Student Should Have

Geometry Set

Every math student needs a round geometry set. This usually contains a compass, protractor, ruler and set squares to assist the students in drawing and measuring angles and lines. This set is a prerequisite for the study of geometry and helps the students develop spatial perception and accuracy in mathematical constructions.

Graphing Calculator

The graphing calculator is a must-have device for students who are studying algebra, calculus or trigonometry. Basically, a graphing calculator can help students plot graphs, get solutions, or even conduct statistical analysis. Such models are designed for complex calculations. In addition, many students study science, so it is not surprising that such models also have functions useful in science.

Abacus

An abacus is an old-school device which is still helpful for kids at the beginning stages of learning mathematics. An abacus is said to assist students in mastering arithmetic since it is a practical method for grasping basic processes such as adding, subtracting, multiplying and dividing. Young students are provided with a variety of appealing and knowing colors of abacuses provided by Math Equipment manufacturers and suppliers in China.

According to Wikipedia, Numerous calculating techniques, such as addition, subtraction, multiplication, division, and square and cube roots, are supported by the abacus architecture. The ultimate position of the beads can be read as the outcome of manipulating them to carry out a mathematical operation with another number after they have first been set to represent a number.

Cube Set

Cube sets can be great for teaching volume, area and counting in early basics education. These manipulatives are appealing to younger learners since they come in a variety of colors. From the hands-on cube sets children are able to understand the concept of unit measurement, fractions and basic algebra.

Protractor

An angle can only be drawn correctly if the protractor is being used. Geometry is about angles, and a protractor helps students see and understand the relationships of those angles, which are important in trigonometry. The accuracy of a protractor facilitates students to gain precision in angle measurement which is an important concept in geometry.

Measuring Tape

Although many see a measuring tape as a practical application, one should not forget that measuring tapes can be helpful in math education too. In this way, the children practice measuring in real-life situations and such practice improves their spatial cognition. This is especially helpful in geometry where one needs to measure different shaped and sized objects.

Algebra Tiles

Algebra tiles are educational tools that help students to solve equations and learn how to factor polynomials. Heaped with activities that require moving the tiles around, students learn algebraic concepts by adding, subtracting, and multiplying them, all in a concrete visual way.

Whiteboard and Markers

A whiteboard with markers is a great tool for students to use as they solve problems from equations and other tasks. They can solve problems, make corrections, and improve their working all at once without any use of paper. Many Math Equipment manufacturers in China produce high-quality whiteboards specifically designed to be used by students with grid lines for proper arrangement purposes.

Why Choose School Lab China?

Math equipment provides an integral part of the educational experience and School Lab China has built a good reputation for the provision of learning tools that are durable, reliable, and of high quality. As a leading math equipment manufacturer and supplier in China, School Lab China offers a wide range of math equipment, and all products are put through an appropriate process of testing so that they meet the international educational standards. This kind of quality control guarantees the durability and efficiency of any piece of equipment. One of the major advantages of buying from suppliers in China is the cost. School Lab China sells quality math equipment at nearly all prices which can be used for educational institutions and students as well. 

School Lab China has factories that manufacture items to be offered to students including ergonomic sets of equipment and color-coded sets. Functionality as well as engaging students is the focus of the company.  The School Lab China has a range of mathematics teaching resources for lower primary to upper secondary mathematics syllabus. This wide range assists the teachers to select accurately the right tools for the students.

Conclusion 

The right Math Equipment can make a big difference in how students grasp and use mathematical concepts. Students have an array of tools available to them, including an abacus and a graphing calculator. As a leading Math Equipment Manufacturers Suppliers in China, School Lab China offers dependable, low-priced, and creative products that meet every educational need. If all the students use reliable equipment, educators and parents are able to make sure that students are set for success.

[schoolofeconomicsblog]

How to Excel in a BSc Economics Program: Tips for Prospective Students

Pursuing a BSc Economics degree is an exciting journey. It opens up pathways to understanding how economies function, why markets behave the way they do, and what drives financial decisions at both individual and global levels. Studying economics doesn’t just prepare you for a career in finance or public policy; it gives you the tools to understand and shape the world. If you’re considering joining one of the BSc Economics colleges in India, here are some practical tips to help you excel.

Understand the Fundamentals of Economics

Economics can get technical, but at its core, it’s about understanding human choices, scarcity, and value. Focus on building a strong foundation in economic theories and principles. Courses in microeconomics, macroeconomics, and statistics will be your starting point. Take time to grasp these subjects deeply, as they’re essential for tackling more advanced topics later. Understanding the basics also makes it easier to see how different parts of the economy are interconnected.

Develop Analytical and Mathematical Skills

Economics often involves analysing data, interpreting graphs, and understanding statistical methods. While you don’t need to be a maths genius, being comfortable with numbers will help. Practise basic calculus and algebra, as many economic models use these tools. Developing your analytical skills will enable you to break down complex information and understand economic trends. Many BSc Economics programs include modules on econometrics, which combines economics and statistics, so getting a head start with basic maths will make things easier.

Keep Up with Current Affairs

Economics is a dynamic field closely tied to what’s happening in the world. From government policies to international trade agreements, understanding current events can help you relate classroom theory to real-world issues. Regularly reading newspapers, watching financial news, or following reputable economics blogs can keep you informed. Applying what you learn to ongoing events can give you a fresh perspective on topics like inflation, economic growth, and unemployment.

Practise Problem-Solving Regularly

Economics isn’t just about theories; it’s about applying them to real problems. Practise solving case studies and applying economic principles to different scenarios. Many BSc Economics colleges in India offer workshops or projects where students can work on real-world issues. Taking part in these opportunities can strengthen your problem-solving abilities and build your confidence in handling data and drawing conclusions.

Work on Your Communication Skills

Economics involves presenting data, arguing theories, and sometimes explaining complex topics to people who may not be familiar with economics. Strong communication skills are essential, whether you’re writing essays or delivering presentations. Practise breaking down complex information into simpler terms, as this will be useful not just in your academic career but in any job you pursue afterwards.

Conclusion

Excelling in a BSc Economics program is about more than just understanding graphs and formulas; it’s about connecting the dots between theory and real life. By strengthening your analytical skills, keeping up with current events, engaging with your peers, and seeking practical experience, you’ll build a solid foundation for a successful career in economics. Whether you’re attending one of the best economics colleges in Pune or elsewhere across the country, these tips will guide you towards a fulfilling and rewarding experience.

[topscoree]

Quick and Easy Tips to Handle Complex JEE Math Problems

For many JEE aspirants, math can seem daunting due to the complexity of the problems. However, with the right approach and a few smart strategies, tackling even the toughest questions becomes manageable. Here are some quick and easy tips to help you handle complex JEE math problems with confidence and ease.

JEE Training in Coimbatore

1. Understand the Concepts Thoroughly

The foundation for solving any JEE math problem lies in a strong understanding of basic concepts. Before jumping into problem-solving, make sure you have a clear grasp of fundamental theories and formulas. Topics like calculus, algebra, and trigonometry require solid conceptual clarity. Reviewing your textbooks, attending coaching classes, and regularly revising will help reinforce these concepts.

2. Break Problems into Smaller Steps

When faced with a complex math problem, it’s easy to feel overwhelmed. To tackle this, break down the problem into smaller, more manageable parts. Start by identifying what the question is asking for and which formulas or concepts you need to apply. Working step by step allows you to approach the problem systematically, reducing errors and confusion.

3. Practice Shortcut Techniques

JEE is as much about speed as it is about accuracy. To save time during the exam, learn shortcut methods and tricks that simplify calculations. Techniques like Vedic math or algebraic manipulations can significantly reduce the time spent on tedious calculations, allowing you to focus on solving more problems in the given time.

JEE Coaching in Coimbatore

4. Use Diagrams and Visuals

Some problems, especially in geometry and trigonometry, become much easier when visualized. Drawing diagrams or graphs can help you better understand the relationships between different elements of the problem. Whether it’s plotting a function or sketching a triangle, visual aids can simplify complex scenarios and lead you to the right solution faster.

5. Practice Regularly and Consistently

Math is a subject that demands regular practice. The more problems you solve, the more familiar you’ll become with various types of questions and problem-solving techniques. Practice a mix of basic and advanced problems from past JEE papers and mock tests. This will not only improve your speed but also boost your confidence in tackling complex problems.

6. Time Management is Key

During the JEE exam, managing time is crucial. Don’t spend too much time on a single complex problem. If you find yourself stuck, move on to the next question and revisit the difficult one later. This will ensure that you don’t lose precious time and can attempt the maximum number of questions within the allotted time.

JEE Training in Coimbatore

7. Review Your Mistakes

Every time you solve a math problem, whether in a mock test or a practice session, make it a habit to review your mistakes. Identify where you went wrong and focus on improving those weak areas. Understanding your mistakes is one of the fastest ways to learn and avoid similar errors in the future.

8. Stay Calm and Focused

Complex math problems can sometimes lead to stress or panic, especially during the actual exam. Remember to stay calm and composed. Take a deep breath and focus on what the problem is asking. With a calm mind, you’ll be able to think more clearly and find the right solution.

JEE Coaching in Coimbatore

Conclusion

Handling complex JEE math problems doesn’t have to be intimidating. By strengthening your conceptual understanding, practicing regularly, learning shortcuts, and staying calm under pressure, you’ll be able to approach difficult questions with confidence. Remember, practice makes perfect, and the more you prepare, the easier it becomes to crack even the toughest JEE math problems.

Start practicing today and give yourself the edge you need to succeed in JEE!

[celestie0]

can i just first say this is sincerely one of the best things thats ever happened to me in my time on this app 🤣 tysm for this, i was hoping an actual engineer and/or physicist would find this post and im so enthralled rn

I am coming in here as a Professional Engineer who works with fluid flow all day and won't be distracted by imagining Gojo's girthy, throbbing member pulsing inside me as I feel his warm... What was I saying?

i literally screamed at this lmfao thx for matching the humor in ur peer review i cld cry

I DIDNT EVEN REALIZE UNTIL RN THAT L ISNT SUPPOSED TO BE LENGTH OF VAGINAL CANAL ITS JUST SUPPOSED TO BE FROM HIS URETHRA omg i gasped. i feel like how i used to feel leaving lecture halls in college thinking i slayed tf outta my physics exams n then the score comes back 44%🧍🏻‍♀️🤣 also tyvm for drawing over my diagram i am so greatly honored by this

omggg p1 is also supposed to be pressure at urethra n not vaginal entrance bc thats where the fluid is cumming from🧍🏻‍♀️………..this is why i stuck to bio LMAO im so humbled rn 🤣🤣 also godbless articles w the value in the title 🙇🏻‍♀️

engineer reblog op, are u insinuating that gojo uses his infinity to block cervix bruising action LMFAOOO 🤣🤣 i seriously can’t w this rn (also thats a pretty dope form of birth control)

i’m a little lost on the explanation regarding his intrusion of the vagina canal 🤔 i had to draw it to understand i think this is what you mean:

i just tried to look up what a laplace transform is n saw the integral n felt like crying🧍🏻‍♀️but i was curious ab it n why you said it’s applicable here and hmm are u referring to how gojo’s infinity does not act as an actual physical barrier as gege has stated in jjk, therefore there is no true “length” we can approximate here if he uses his infinity? i notice in this article that explains how there is this Se^-a0t aspect:

(i havent taken calculus in over four yrs if im so wrong ab this pls excuse me lmaooo) but is this part of the equation related to t (as some variable in a function based on the context?) as it approaches infinity (aka in this case his thrusts as he approaches his infinity barrier within this vagina canal)? idk what the actual correct variable is to assign for t haha or if that’s even something to assign here

but in the case mentioned in that article with t approaching infinity, plugging that in would look like this i believe:

and then graphed:

again i’ve absolutely no fucking clue if any of this is right 🤣 BUT IF THIS IS WHAT YOU MEANT FOR USE OF THAT LAPLACE TRANSFORM THING THEN…….😨 i am so mind boggled by this. beyond simple use of infinity to restrict impregnation/cervical injury within the vaginal canal, i am so intrigued by the math behind his infinity technique in general!!! i also wonder, he mentions that people get slower as they get closer to him, might that imply the y-axis is some unit of distance? since as x approaches infinity and y approaches this bound value dashed line (lol i think there’s a name for it i cant remember rn tho) the values of y become increasingly smaller which would match what gojo stated 🤔 again i’m so fearful i’m talkin out my ass rn i feel so vulnerable 🤣 i was a bio/biochem major so i didn’t take much maths/physics but i’m very intrigued by this rn. also dont know if this is what u were referring to in the first place either lmao

Tragically, this leaves a whole 1.25" of your sex un-railed, but you'll live in the modern sense and die in the Victorian Poetry sense.

I CANT BELIEVE I GET TO READ THIS REBLOG FOR FREE LMFAO

also you’re tellin me the ideal lovemaking bpm matches the ideal bpm for cpr? 😭 so i can save someone’s life to “stayin alive” by the bee gees but i can also rock someone’s world to it too?

haha 5% as in for significance? (im so haunted by p values thats all that came to mind) BUT OK IM ALL ONBOARD W NEGLECTING STUFF

ouuu thank u for bringing up the linear speed to cross sectional area stuff i was rly confused ab that haha but also i think the reason i turned it into volume was i just made the wild assumption that it takes him one minute to cum 🤣 so mls per min -> how much he cums but thats a stretch n also doesn’t make much sense biologically either for a lot of reasons lol

YAAAAY OUR WOMBS ARE COMPLIANT WITH OHIO STATE ENGINEERING STANDARDS 👏🏼 GIVE IT UP FOR MOTHER NATURE

ok this is way too fucking long, i just wanted to dump my thoughts, pls do not feel as though u need to respond to this, dear engineer reblog op. you’ve made my entire week regardless.

also, to answer quinny’s question here

@quinnyundertow

i think possibly “putputput” is most correct.

ALR PEACE OUT ✌🏼

- ellie professionalgojobrainrotloser42069

what is the flow rate of gojo’s sperm? 🤔

😈 😈 😈 ALRIGHT LET’S FIND OUT

shoutout to m00tie @quinnyundertow since u said there's nothing that turns you on more than hearing how mobile a man's flagella are. this one's for you bb.

alright, first off, because his cum is confirmed to be both incompressible fluid as well as move with laminar flow, these attributes satisfy the conditions of pouiseulle’s law:

i had to do a little bit of research to determine if it was laminar or turbulent flow, and apparently sperm travels with both stokes & laminar flow, which is pretty interesting, and also moves in a sinusoidal propagating wave, likely due to the movements/shape of the flagella

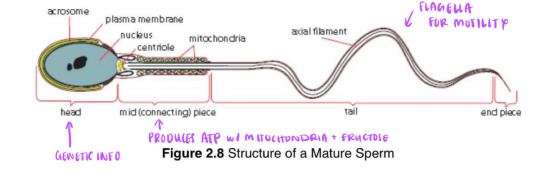
note: microscopic sperm travel & ejaculate fluid travel are two very different things, but i can’t solve for anything microscopic here so we’re just gonna go for the ejaculate fluid only

anyways, to use pouiseulle’s law, let’s first determine our variables, and make sure we get the units right as well! always draw a diagram w all the variables:

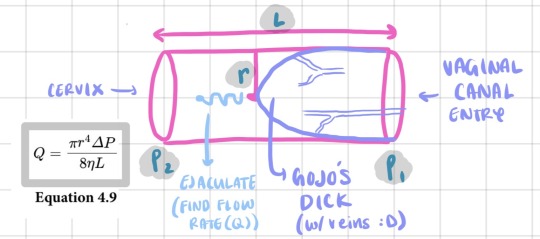
now, let’s identify the variables:

1. radius (r) of tube -> this refers to the pipe/tube, therefore in this case, the vaginal canal. now since gojo has decided to creampie, we can assume that the radius of the vaginal canal will be equivalent to the radius of his girth as he is stretching you out. gege told me the diameter of his big fat schlong is approximately 3 inch girth, therefore the radius = 3/2 = 1.5 inches

2. ΔP refers to change in pressure gradient, in this case i’ve decided to have P1 as pressure at vaginal canal opening, and P2 as pressure at the end where the cervix is. therefore, ΔP = (P1 - P2) for the equation. i know you’ve got that gorilla grip coochie, esp when the world’s strongest sorcerer is fuckin you SENSELESS, but all things considered this is a very difficult parameter to measure, therefore i found this article to help out with this:

we’re going to assume “contraction pressure” (at the vaginal canal opening) is P1, due to gojo’s intrusion. and we’re going to assume “pressure at rest” is P2 at the end near the cervix (he’s pulled out a lil bit ok this makes things easier for me)

kPa are the units that we want for ΔP in this case, therefore it’s a simple calculation:

ΔP = P1 - P2 = 41.8 kPa - 26.8 kPa = 15 kPa

3. the last variable we need to account for here is L, which is the length of the PIPE HE’S LAYIN INSIDE OF YOU (jk it’s just length of ur coochie). now, i imagine this man is a generous lover, and he’s alr made you cum a few before he stuck it inside, so with arousal, the vaginal canal length has likely increased to about 5 inches (moreso 4.75in based on avg values in research but he stretched you in even more during the sexing!!) therefore L = 5 in

4. the other two values are just constants:

π = pi 3.1415 (imma just use pi function in calc)

η = this is viscosity of a fluid. based on this research article, the viscosity of human semen is approximately 9.35 cps. we want these units in kPa•s (remember that your units need to match the units of the other variables), so we need to use density of sperm (1.043 g/ml) to convert the factor (i just used chatgpt lol) but the conversion factor is pretty similar therefore we will just plug in something close to 9.35 kPa•s (true value is a little smaller)

ALRIGHT WONDERFUL! WE HAVE DETERMINED ALL OF OUR VARIABLES :) NOW WE JUST NEED TO PLUG IT INTO OUR EQUATION/DIAGRAM:

*note: mind the units! (shown in blue) there are lots of variations on how flow rate can be shown w the units, so u wanna be careful that they match

YAAAAY!! so the flow rate (Q) of gojo’s cum is approximately 0.63787 in^3/sec ☺️💕

use a quick converter online, and we can make it into liters per minute -> 0.02214 l/min. convert this to milliliters -> 22.14 mls

which means that, in one of gojo’s average cumshots, he cums 22.14 mls of ejaculate !!! :0 sheesh that’s a lot!!

but how does this value compare to other men? research varies, but on average, men ejaculate between 1-10mls per orgasm, therefore the world’s strongest sorcerer cums more than TWICE the worldwide average!!

and one final calculation shows us that when he finishes, it’s at about 0.369 mls per second :) that's fuckin fast!!!

thank you for cumming to my ted talk!! byee

alr ellie out ✌🏼😖 (i have sm brainrot)

[codeepie]

7ogical : Draw Graph

[autisticlancemcclain]

“Whatcha doing?”

Keith’s voice right next to his ear startles Lance a bit, making Keith laugh quietly. Lance feels the rumble of it in his shoulder, where Keith is resting his head to peer at his work.

“My math homework.”

Lance feels rather than sees Keith make a face. “That’s not math. I don’t see a single number in all that. I don’t even see letters.”

Lance chuckles. “It’s just calculus, babe. It’s mostly symbols, sure, but still math.”

“Ugh.” Keith pulls away after pressing a kiss to Lance’s cheek, shaking his head. “That’s disgusting.” He starts haphazardly shoving his fancy pencils into their case, then into his backpack, followed by his sketchbook. “Your horrible homework made me lose my desire to do anything and everything school related.”

Shaking his head fondly, Lance returns his gaze to his worksheet. “You’re such a dork. It’s only math.”

“The fact that you can look at those equations and they not only mean something to you, but they make sense, blows my mind every day. I’m still half convinced you’re a witch.”

“Now is that the math, or the fact that I’ve put a spell on your heart?”

“Boo,” Keith says, cupping his hands around his mouth. “That was garbage. I’m reporting you to the horrible pun police.”

“Stop making me laugh,” Lance says, throwing an eraser at Keith’s head. “You’re distracting me.”

“Yeah, yeah, Doctor McClain. You could skip every single one of your lectures and still pass with a 95.”

Lance flushes, pleased by both the compliment and Keith calling him doctor. As much as he knows Keith is teasing — he absolutely does need to attend class, Lord above — his boyfriend’s faith in him always makes his insides all soft and squishy.

But he has an assignment to do. He’ll kiss his amazingly supportive boyfriend after.

Lance gets in the zone, so focused on problem after problem that he forgets where he is. Hell, he pretty much forgets that he has a mortal body. His brain is 100% Greek letters and the occasional graph. And Lance likes it that way. He likes math, and not in the cheesy Cady Heron ‘math is just the same in every language’ kind of way. He just thinks that so long as he’s doing it right, figuring out puzzles is fun, in the same way some people like writing, or drawing. There are annoying parts, sure — modular functions are stupid as hell and can kiss his whole ass — but for the most part, he’s a biomed engineering major for a reason. He has shit to design, and he’s only getting there if he understands how the world fits together.

Something small hitting him square in the head snaps him out of his focus.

“You are being absorbed into your textbook,” Keith informs him. “I’m losing ya, space cadet.”

Lance shakes his head a little, blinking. He realises suddenly that, holy shit, his eyes are burning. And his throat is as dry as the desert. And he’s starving. And his muscles are cramped.

“Jesus,” he says, “how long have I been sitting here?”

Keith shrugs, but his attention is no longer on Lance. “Dunno. My phone died forever ago, so that means either two minutes or two hours. I could not tell you.”

Lance snorts. He knows part of Keith’s ADHD means he’s not great with time. It doesn’t really matter, anyway. They’ve been here long enough that it’s long past time to take a break.

“What’ve you been doing, then?” Lance asks as he starts collecting his things to put away. “If your phone’s been dead.”

“Foldin’ stuff,” Keith replies absent-mindedly, tongue peeking out of his mouth as he does, indeed, fold some papers. Lance finally gets all his stuff packed away and then turns his full attention to Keith, humming curiously. Keith, like with everything artsy, is amazing at origami, and Lance is always amazed at how he takes a piece of scrap paper and makes a mini-sculpture.

“Like what?”

“Made you this bouquet,” Keith says. His attention is still mostly on the tiny square of pink paper in front of him, but he reaches over to the empty chair next to him and blindly searches for something. He makes a triumphant noise when he finds it, and sets a brightly coloured bouquet of intricately folded paper flowers on the table.

Lance gasps, carefully picking it up and looking at it closely. Each flower is folded to perfection, crisp lines and gentle bends in the paper making perfect imitations of Lance’s favourite flowers: golden dandelions, pink peonies, deep orange poppies.

“Holy shit, Keith,” Lance breathes. He looks at his boyfriend with wide eyes. “This is… these are gorgeous!”

Keith glances away from his project for a moment to shoot Lance a big, goofy grin. “Glad you like ‘em. They’re almost as pretty as you.”

“Charmer,” Lance says, rolling his eyes, but the ruddiness of his cheeks give him away. Keith knows it, too, grinning wider.

“This is for you, too,” he says, making a final fold on the pink paper. “Hold out your left hand.”

Lance does, stupidly giddy smile making his cheeks ache.

Keith has made a paper ring, folded so it makes a heart in the centre rather than a traditional circle-shaped knob. It’s as meticulously crafted as the bouquet. He slides it up Lance’s fourth finger, then presses a gentle kiss on the knuckle.

“Since you said we can’t get married until after we finish our undergrads,” Keith says, as playfully grouchy as he always is when he brings the subject up. “This will have to do.”

Lance laughs, sliding his hand from Keith’s grip so he can rest it on the side of his boyfriend’s cheek, stroking his cheek with his thumb. Keith goes cross-eyed trying to watch the movement, lips still pouted. Lance leans forward to kiss them.

“You are so dramatic,” he mumbles, still crowded in close. “One more year, okay? You can take me to the courthouse the day we graduate, if you would like.”

“Fine,” Keith huffs. He wraps his arms around Lance’s waist. “They second our caps get thrown, you hear me?”

Lance kisses him again. And again. And a third time, for good measure.

“I hear you.”

[biochemsitry]

So I was wondering if anyone can explain this to me. I doubt anyone can but it's at least an interesting story I think. (Disclaimer: if you aren't a math person, this might be pretty confusing, but I will try to explain stuff.)

I'm sitting in my 300 level calc 1 class. We're learning about instantaneous velocity and limits and the like, not super hard stuff. This is the fourth class period we've had so it hasn't gotten to the hard stuff yet.

By the way, I go to a tiny private university. I'm one of 5 students in this class. My uni is, um, known for not being great with math-- we literally have two math profs in total. Two. I think we have 3 math majors in total, and all three are in this class. The fourth is math ed. I'm biochem.

Back to what happened today. Our prof, let's call her Dr. H, is explaining limits (for non-math or science ppl, it involved lots of graphs and functions and letters). The freshman math ed major, let's call him J, is very confused and raises his hand. "What does f(x) mean?" he asks.

Dr. H pauses, unsure of how to answer. The other 4 students, including me, try to explain f(x) to J. Dr. H ends up drawing a graph on the whiteboard to explain that f(x) often, at least at the level we're at and with the stuff we're talking about, is the same as y. f(x)=x is the same as y=x. f(x)=3x-1 is the same as y=3x-1.

J seems to be satisfied with this explanation, so Dr. H continues the lecture. A few minutes later, she gives an example problem with both f(x) and g(x). J is now more confused than ever.

"Wait, what's g(x)?" he asks.

"g(x) is the same as y in this situation," Dr. H answers.

"But I thought f(x) was y."

At this point, we're all looking at J in disbelief. For people who don't know, g(x), f(x), h(x), etc. in graphing are all representative of y on a graph, at least typically, and at least in contexts like this.

Dr. H pauses, then says, "I think we need to have a conversation about functions after class."

Now, don't get me wrong. Functions can be hard. If you're not a math person, it's easy to go without knowing what they are. I'm not trying to put anyone down for not knowing what they are. My mom never got past algebra 1 and either never learned them or has completely forgotten about them. But then again, my 16yo brother with severe discalcula (math dyslexia, basically) knows at least about functions and he's barely even done pre-algebra...

But this kid made it into calculus apparently without any knowledge of functions, which (I think???) are usually taught at the algebra 1 level (so about 8th-9th grade, or 13-15yo, at least in the US. It's usually younger in other countries though, at least from what I gather?). It's not something you'd learn at age 14 and never use again until college-- most maths from algebra 1 and up use functions pretty much all the time. But this freshie is, like, 17-18, and a math ed major, who must have either klepped out of lower math courses, or had gotten a high enough score on the ACT/SAT to be able to go directly into calc 1. This guy's smart-- he seems to be really good at math other than functions. I just have absolutely no idea how he made it into calc without knowing about functions. Just... how?????

(In case anyone's wondering, we absolutely did NOT try to make J feel bad. None of us students even said anything about it afterwards at all. We just don't do that. Dr. H was very kind in how she handled the situation, too. Never make a person feel bad for not knowing something. I'm not making fun of him by posting this, either; I'm just very confused lol. I doubt he'll see this, and if he does, I doubt he'll know it's me talking about him. He's a smart guy, and I'm not blaming him for his lack of knowledge on functions. I'm mostly just wondering how his HS teachers neglected to teach him about such a basic and important part of math.)

[eintsein]

hi hi! could you please share your study techniques and advice for economics majors? I survived lower division just fine but upper division courses :( .

Hii! First of all, I want to apologize for answering this quite late - I wanted to give you an answer that's thorough enough and helpful. Read on below for tips!

Disclaimer: these tips are from my own experience and the experience of my peers, most of whom are in US institutions. However, I do think these tips should apply to many economics major programs.

Strengthen your mathematics foundations

Upper-division economics courses are math at their core. Here's an example of the objectives of an intermediate microeconomics course (source)

understanding the concepts of Pareto and sum-of-surplus efficiency, being able to determine whether a preference relation is complete, transitive, monotonic, and convex, and being able to determine whether a production function exhibits increasing, decreasing, or constant returns to scale.

Preference relations are concepts from discrete math. Increasing, decreasing, and constant returns are concepts from calculus.

Many upper-division courses also require knowledge of probability and statistics (game theory courses especially). Research-based classes often recommend having taken econometrics. Theoretical classes like decision theory are, as the name suggests, theoretically rigorous, so being comfortable with proofs is necessary, and knowing math theory is a great help.

A lot of people (myself included) struggle with higher division economics courses because they were not mathematically prepared. While you can definitely learn as you go, it will make your life a whole lot easier having the preparation or at least the comfort to work with the required mathematical concepts and use certain mathematical skills.

An example from personal experience: I had taken econometrics (a theoretical version) the spring of my sophomore year without much knowledge of multivariable calculus and having taken calculus II over a year before taking this class, and honestly I felt I had to work so much harder than my peers who were math majors or minors.

So yeah, you should definitely brush up on your math skills if you find yourself struggling. This could mean doing extra practice, looking for tutoring, or even taking a course.

Strengthen your economics foundations

Upper-division economics courses really build on lower-division courses. As far as I know, the purpose of upper-division courses is to teach us to synthesize what we learned from lower-division courses, i.e. to use the tools and techniques we've learned, and apply them to new economic settings.

For example, last fall I took a course on public finance (also known as welfare economics) and one of the topics we studied was regulating pollution. Two of the regulation methods we focused on were 1) cap & trade, i.e. giving pollution permits that can be traded, and 2) emission fees, i.e. setting a fee if emission is above a certain amount. The graphs below illustrate the two methods for two cases: inelastic marginal social benefit of pollution reduction, and elastic MSB of pollution reduction. Marginal cost and marginal social benefit curves are usually taught in lower-division courses, as are concepts of elasticity and demand-supply models.

Another example from the same class: evaluating Pareto efficiency of the allocation of public goods involves being comfortable with indifference curves, utility functions, and production possibility curves, as shown below. (Even if you don't understand what's going on, the general shapes should look familiar.)

Use the course's learning objectives to guide you

My probability and statistics professor taught me that the first step in studying any subject is to look at the learning objectives. These are the things you are expected to get out of the course and so they are the things you will be expected to know on an exam, do in a project/assignment, etc., not just information but also skills and techniques.

Study and practice drawing graphs

Graphs can hold a lot of information given that you know how to interpret them. In many cases, I found that if I understand the graph, then I understand the concept. Studying graphs saves a lot of study time, too, since the material's been summarized really neatly, and chances are you'll need to know the graph, too.

For many of my economics classes, I create a study guide comprising only graphs. These aren't just the graphs that are explicitly taught in class, though. I try to include as many cases, including special cases, because it teaches me to be able to think through the concepts being used in the graphs, instead of just being like, okay this is what it looks like.

For example, when studying Edgeworth-Bowley boxes, I drew them with different types of indifference curves, and then for each of them, I drew their utility possibility frontiers. Or when studying anything involving demand-supply curves (e.g. different types of taxation), I draw a graph for each combination of demand and supply elasticities (e.g. inelastic demand with inelastic supply; inelastic demand with elastic supply; etc.).

Of course, I don't always get it right. If there's something I'm unsure about or don't understand, I go to office hours for help.

Learn from assignments and practice a lot

Your assignments point out the types of questions you'll be expected to analyze and work through and thus can guide your studying, whether it's mathematical problem sets or a series of essays.

In classes with problem sets, doing them seriously helps SO much. They train your mental muscles to be able to solve or analyze the problems you're expected to be able to solve and analyze after taking the course. Your professor created these problem sets to achieve the learning objectives. If you're having trouble with any part of the problem set, you probably don't understand a key concept, skill, or technique the course expects you to, and that's totally fine; just don't forget to work on it and ask for help.

In addition, problem sets also serve as great revision tools to help you actively recall and synthesize the material you've studied.

Go to office hours for conceptual help

I've mentioned a couple times to reach out for help if you need it and I cannot stress this enough. In most cases, professors and TAs (teaching assistants) are more than willing to help you succeed. I would suggest going to each instructor/staff member if there are multiple and seeing which one is the most helpful, i.e. the person who can fill in your knowledge gaps the easiest, who understands your misunderstandings. Sometimes it's the professor, other times the TA is a better fit. Sometimes the TA gives better help for problem sets but the professor gives better help for conceptual problems. Use the resources available to you!

I hope this helps, and please don't hesitate to reach out if you have any other questions :)