#hyperplane

[fieriframes]

[Hyperplane.]

[peeterjoot]

Equation of a hyperplane, and shortest distance between two hyperplanes.

[Click here for a PDF version of this post] Scalar equation for a hyperplane. In our last post, we found, in a round about way, that Theorem 1.1: The equation of a \(\mathbb{R}^N\) hyperplane, with distance \( d \) from the origin, and normal \( \mathbf{\hat{n}} \) is \begin{equation*} \Bx \cdot \mathbf{\hat{n}} = d. \end{equation*} Start proof: Let \( \beta = \setlr{ \mathbf{\hat{f}}_1, \cdots…

[the-nyanguard-party]

the dark spots on my bathroom ceiling are not mold it's an extrusion of a 4-dimensional entity into our hyperplane and she loves me

[kfunc-vmlinux-utf8nlookup]

I CALL our world 2536-dimension-land, not because we call it so, but to make its nature clearer to you, my happy readers, who are privileged to live in 2537-dimension-land.

Imagine a vast sheet of paper on which perfect Subsimplices, Hypersquares, and Unterorthoplexen, and other figures, instead of remaining fixed in their places, move freely about, on or in the hypersurface, but without the power of rising above or sinking below it, very much like shadows - only hard and with luminous edges - and you will then have a pretty correct notion of my country and countrymen. Alas, a few years ago, I should have said "my universe": but now my mind has been opened to higher views of things.

In such a country, you will perceive at once that it is impossible that there should be anything of what you call a "solid" kind; but I dare say you will suppose that we could at least distinguish by sight the Hypersquares, Subsimplices, and other figures, moving about as I have described them. On the contrary, we could see nothing of the kind, not at least so as to distinguish one figure from another. Nothing was visible, nor could be visible, to us, except bounded hyperplanes; and the necessity of this I will speedily demonstrate.

Place a penny on the middle of one of your tables in 2537land; and leaning over it, look down upon it. It will appear a subhypercylinder.

But now, drawing back to the edge of the table, gradually lower your eye (thus bringing yourself more and more into the condition of the inhabitants of 2536land), and you will find the penny becoming more and more oval-cylindrical to your view; and at last when you have placed your eye exactly on the edge of the table (so that you are, as it were, actually a 2536lander) the penny will then have ceased to appear oval-cylindrical at all, and will have become, so far as you can see, a hypersquare.

[khnuvr]

Opinion from the opposing side: I love computers for pure math! There's nothing better for calculating examples to check your hypotheses and visualizing the objects you're working with. They're also great at checking cases if you have long list of them. I only learned how useful they can really be recently when using sage for everything mentioned above in a research setting. Computers are invaluable in that context imo. They can do so much more that just arithmetic, if you know how to model it right.

Calculators are flawed and aside from computing large numbers have not much purpose in pure mathematics.

This is not a statement about generative ai (although it would be completely useless in all facets of mathematics).

I will not pretend that I am an expert, I am no mathematician, but I absolutely adore the subject. It is what I want to spend my life doing. I will not pretend that I am the most knowledgeable so I would be delighted to hear some other opinions.

In my experience I have found the standard scientific calculator to be flawed. It has failed to give a distinct answer when the answer logically is different. As in, the difference between the numbers is so small it counts it as the same number. However, this is not 0.999... = 1. This has a finite number of decimals.

Aside from the actual calculation calculators can only aid in checking arithmetic really. The basis of mathematics is proof, which requires the human mind. I believe that in no way can the human mind can ever be replaced in terms of proofs and concepts.

Thank you for coming to my uninformed shittalk.

[fy-perspectives]

A tesseract is bounded by eight three-dimensional hyperplanes. Each pair of non-parallel hyperplanes intersects to form 24 square faces. Three cubes and three squares intersect at each edge. There are four cubes, six squares, and four edges meeting at every vertex.

[questioning-my-identity-element]

Do you have any recommendations for learning about algebra beyond high school level? I'm in calculus right now and we just hit definite integrals, if that helps.

sure, ill give a handful of answers depending on your goals.

i would categorize "beyond high school algebra" into linear algebra (which is lower-div college level) and abstract algebra (which is upper-div college level). one could argue that linear algebra is a subfield of abstract algebra, but i am not going to.

linear algebra: lines, planes, hyperplanes, etc can all be fit into essentially the same framework of linear (or affine) equations. think of y=mx+b, except y, x, and b are vectors and m is a matrix. linear algebra is essentially just the study of problems like these and structures that are relevant to their study (e.g., vector spaces). this is inarguably the most important field of mathematics.

abstract algebra: this is a very broad subject which broadly studies structures and the way they interact with other structures. it is hard to get a good feel for abstract algebra without actually doing it, so here is a blog post from my website. you may not be familiar with the notation, but you can find hopefully everything important on the Wikipedia page for sets and functions.

my answer to the question is under the cut. i would encourage other mathblrs to add their opinions though

(A) you want to learn some (but not all) cool algebra without the painful detail

while abstract algebra can be touched with your background, there are certain topics which depend deeply on linear algebra. broadly, this is because linear algebra underlies almost all math. this splits my answer into two parts depending on if (A) you want to learn some (but not a lot of) cool algebra without the painful detail or (B) you want to deeply understand algebra.

try some general audience videos, like from numberphile. generally, videos by good presenters are amazing at teaching you the cool stuff. if you find this to be too little, pick up a lecture series on group theory for undergrads and try your best to follow along. if you can't keep up but still want to pursue it, go to (B).

(B) you want to deeply understand algebra

this is my recommended plan of action:

(1a) pick up some textbook on "discrete math and intro to proofs" (example) and work through a few problems in each section. abstract algebra in general has many prerequisites, and discrete math fills in the vast majority. the topics you should look out for are: proof techniques such as induction, functions and relations, and some basic combonatorics/counting.

(1b) pick up a textbook on "linear algebra and applications" (example) and do the same. i encourage taking a textbook directed at sciences for a few reasons: it's easier, applications can sometimes spark other interests, and most importantly applications give a deeper intuition for the meaning of the math. where possible, try to use your new proof skills to prove the things discussed!

(2) pick up a more serious book on abstract algebra and/or linear algebra and do as many exercises as possible (as in attempt every problem in every section). the standard reference for abstract algebra is dummit and foote but i prefer jacobson. for linear, i would just suggest linear algebra done right

[bubbloquacious]

Bad idea: instead of the dimensionally loaded term 'hyperplane', combine the words 'flat' for an affine subspace and 'facet' for a codimension 1 face on a polytope to form the word 'flacet'.

[acrossdimension]

4D Gamer Girl (Hyperplane)

[canmom]

one thing I've been ruminating on with regard to the notion of subjective experience emerging from a complex system like a brain (whatever the exact prerequisites might turn out to be) is a thought about location. partly inspired by questions around plurality and such.

in relativity, effects must be local (propagating at max light speed), and any distributed system will have different hyperplanes of simultaneity depending on reference frame. presumably, subjective experience at a given moment corresponds to the state of the brain at that moment - the state of all the particles inside the brain. but 'at that moment' is relative. so i kind of wonder about like... if there is a specific point that the subjective experience could be localised to in the brain, which seems extremely unlikely given everything we know about how the brain works, but if not, if there is somehow a continuous field of subjective experience arising in parallel from all across the brain. and that different points in this 'subjective experience' field are all largely maintained in a state of synchronisation by the way activity propagates through the brain. so if i self report on internal state (and my subjective experience has a causal impact on the world), it will 'feel accurate' to every part of the subjective experience field.

which would mean that alongside me as I write this are infinite other subjective experiences - all more or less the same, depending on how the information is flowing in that specific part of the brain? or like perhaps different parts of the brain are experiencing different things, e.g. the visual processing system experiences one thing, the cortex retrieving memories experiences another, etc. etc.

i don't really think i believe this model - it doesn't really accord with my introspective perception of what consciousness 'feels like'. my actual subjective experience is that i can 'focus on' and bring to attention various different things (sensory inputs, memories, etc.), and equally 'tune them out' and concentrate on something else, which fits much more some kind of central 'single-threaded' view.

i wish there was some way to observe this thing besides introspection, because it's so hard to do anything but wildly speculate with metaphor lego. it's not obvious to me why a brain (or part of a brain) should be able to have a 'like to be'-ness and a cup of water, which also involves the intricate motion of similar numbers of atoms, shouldn't. but my experience is so specifically tied to the various concrete aspects of embodiment and information flow in this biological system that it seems hard to believe that there isn't some important prerequisite here that's missing from the cup of water. i just really couldn't tell you what it is.

[ninzwz]

Ohhhh, you're right, that's not even a question 😔(also I made a typo and "holographic" should be "holomorphic")

Here's an actual question for you then:

Given C⊂ℙᴺ(ℂ) an irreducible smooth projective curve of degree d, is it the case that for an arbitrary hyperplane H⊂ℙᴺ(ℂ) we have that the scheme Z=C∩H has d distinct points?

[Perrin, Algebraic Geometry: An Introduction, exercise VIII.1]

Also, your owners sound cool and you must be a very hard-working and good kbity to try and listen to your owners' commands even when struggling.

(　´‿｀)ﾉ(´･ω･`)　ﾅﾃﾞﾅﾃﾞ Pat-Pat

okay so what i can gather the answer is either yes or no. i declare that it is yes !!! and im right

[kalifissure]

Time is a compactified dimension one single Planck second in size. Using Kuramoto synchrony we evolve a hyperplane of the present with matter on one side and antimatter on the other. Each the perfect inverse of the other. This is how the universe is friction free.

An electron here only shows 1/2 of itself. It's shadow self, the positron, is on the other side of time. This is why CP violation.

We only get to see half of charged particles because the other half is on the other side of time. But neutral charge particles, neutrons, photons, are their own anti. They rest BALANCED on the surface of time. And both sides see them.

[mvishnukumar]

Can statistics and data science methods make predicting a football game easier?

Hi,

Statistics and data science methods can significantly enhance the ability to predict the outcomes of football games, though they cannot guarantee results due to the inherent unpredictability of sports. Here’s how these methods contribute to improving predictions:

Data Collection and Analysis: 

Collecting and analyzing historical data on football games provides a basis for understanding patterns and trends. This data can include player statistics, team performance metrics, match outcomes, and more. Analyzing this data helps identify factors that influence game results and informs predictive models.

Feature Engineering:

 Feature engineering involves creating and selecting relevant features (variables) that contribute to the prediction of game outcomes. For football, features might include team statistics (e.g., goals scored, possession percentage), player metrics (e.g., player fitness, goals scored), and contextual factors (e.g., home/away games, weather conditions). Effective feature engineering enhances the model’s ability to capture important aspects of the game.

Predictive Modeling: 

Various predictive models can be used to forecast football game outcomes. Common models include:

Logistic Regression: This model estimates the probability of a binary outcome (e.g., win or lose) based on input features.

Random Forest: An ensemble method that builds multiple decision trees and aggregates their predictions. It can handle complex interactions between features and improve accuracy.

Support Vector Machines (SVM): A classification model that finds the optimal hyperplane to separate different classes (e.g., win or lose).

Poisson Regression: Specifically used for predicting the number of goals scored by teams, based on historical goal data.

Machine Learning Algorithms: 

Advanced machine learning algorithms, such as gradient boosting and neural networks, can be employed to enhance predictive accuracy. These algorithms can learn from complex patterns in the data and improve predictions over time.

Simulation and Monte Carlo Methods: 

Simulation techniques and Monte Carlo methods can be used to model the randomness and uncertainty inherent in football games. By simulating many possible outcomes based on historical data and statistical models, predictions can be made with an understanding of the variability in results.

Model Evaluation and Validation: 

Evaluating the performance of predictive models is crucial. Metrics such as accuracy, precision, recall, and F1 score can assess the model’s effectiveness. Cross-validation techniques ensure that the model generalizes well to new, unseen data and avoids overfitting.

Consideration of Uncertainty: 

Football games are influenced by numerous unpredictable factors, such as injuries, referee decisions, and player form. While statistical models can account for many variables, they cannot fully capture the uncertainty and randomness of the game.

Continuous Improvement: 

Predictive models can be continuously improved by incorporating new data, refining features, and adjusting algorithms. Regular updates and iterative improvements help maintain model relevance and accuracy.

In summary, statistics and data science methods can enhance the ability to predict football game outcomes by leveraging historical data, creating relevant features, applying predictive modeling techniques, and continuously refining models. While these methods improve the accuracy of predictions, they cannot eliminate the inherent unpredictability of sports. Combining statistical insights with domain knowledge and expert analysis provides the best approach for making informed predictions.

[worstloki]

The Subspace™ Theorem is a fast-paced multistage physics capacity test that progressively gets more finite as dimensional hyperplanes continue

[lukore]

"oh yeah, anyways the sun has long since been spent and we all live on some hyperplane, but the important part is that people get artificial sun seasonal depression"

[more-mathematics-mor-lam]

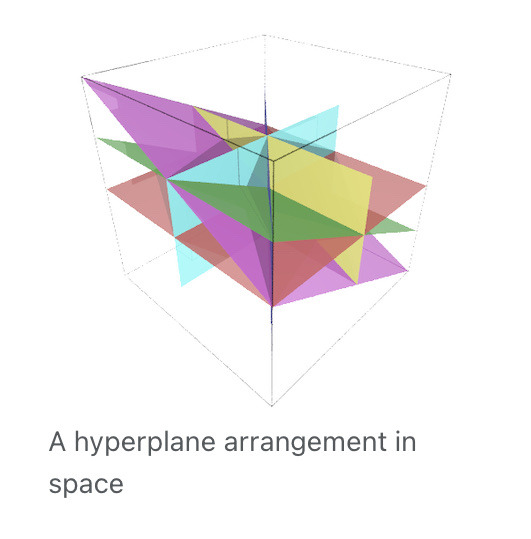
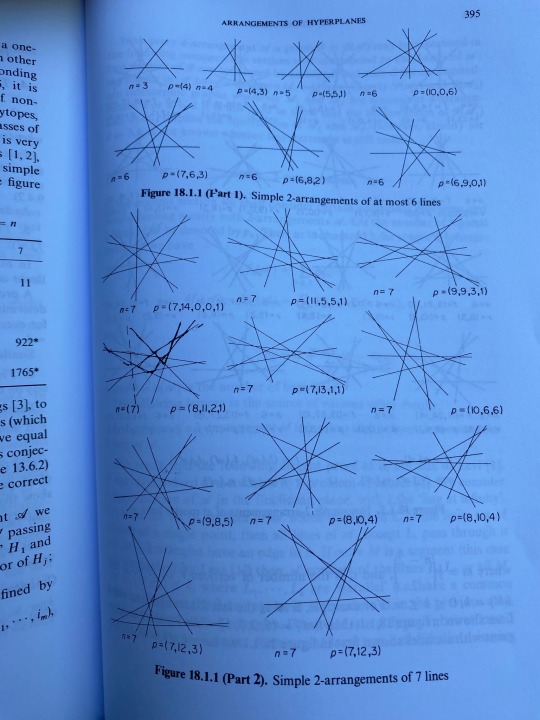
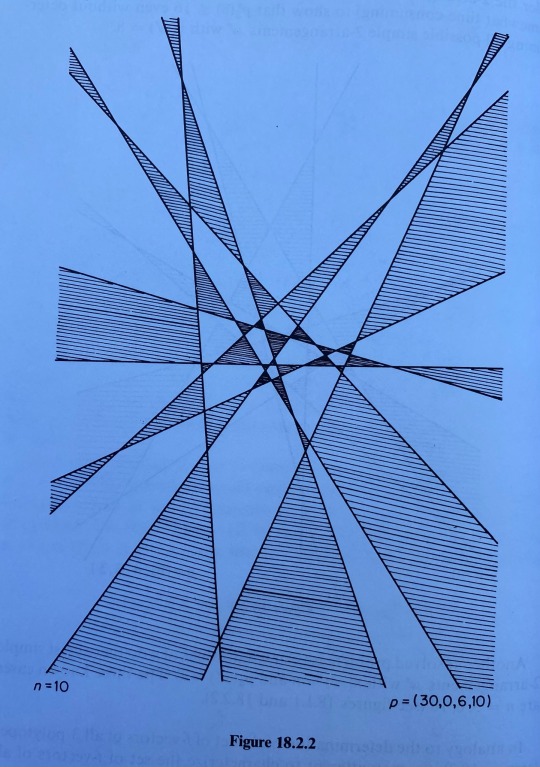
Good morning to arrangements of hyperplanes and arrangements of hyperplanes alone 🌀