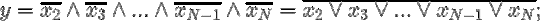#math logic

[deimonspikelet777]

[l3vi4than]

Okay, hello, that’s literally my job to educate people about this shit! (I’m a math logic prof and I study cognitive modelling) This one example provided is really a tricky one, but let’s dive into it and try to analyse why this happens.

At first this seems as a pretty straightforward non-sequitur fallacy (the conclusion does not logically follow from the premise). But here’s the trick: the logical following isn’t universal. It depends on the set of axioms and following rules we use to define the formal logic system. This means, if you are making your conclusions based on a different set of axioms — you might encounter different true conclusions than someone who uses another set of axioms or a different set of following rules.

Sounds sophisticated, I know. Let’s get back to the “all black people are ugly” example. What we see here is that Replyboy has successfully used what we in math logic call Illicit Major: a logical fallacy that happens when major term is undistributed in the major premise but distributed in the conclusion.

The conclusion they used looks something like this:

All beautiful women satisfy (eurocentric) beauty standards / satisfying beauty standards means being beautiful (for a woman)

No black woman satisfies eurocantric beauty standards

Therefore, all black women are not-beautiful (ugly)

There are multiple tricks here, but let’s discuss illicit major first. So, the roots of this logical fallacy lie in the fact that the major term (be beautiful) isn’t actually distributed on the major premise: we can’t say that ALL beautiful women satisfy beauty standards, — some women are the direct opposite of any beauty standard ever seen and they’re still beautiful! This makes the distribution of the major term in the conclusion illicit: claiming that ALL beautiful women are non-black is erroneous. Exactly because the claim about “all beautiful women satisfy a beauty standard” is false.

What lets us make such a statement look plausible is the fact that “beauty” doesn’t have a formal definition. It’s a subjective concept, what we see as “beautiful” differs for everyone, and it’s okay. Trying to approach beauty as a strictly defined category causes the same illicit major fallacy in the sense that you simply cannot distribute “beauty” over everything in the way that every actor operating this premise would consider true.

This might seem as a “loaded term” in the sense that “beauty” is something everyone defines differently, but it isn’t necessarily the cause of Replyboy’s edgy behaviour. I’d say Replyboy is more likely an asshole operating a narrower set of axioms which causes him to make logical conclusions that seem logical to him but are absolutely nonsensical to Stephanie.

For example, in Replyboy’s world the property of an object “beautiful” is defined as “satisfying beauty standards”. But more than that, it is also defined as “not ugly”, which means there are only two states of the property for any object: it is either beautiful or ugly, no in between. Like there is no in between for “true” and “false” in the binary logic — which makes such a definition seem right (it’s a cognitive bias btw) even though it clearly isn’t.

So, to summarise why Replyboy is being mean to Stephanie we can say that he’s just stupid using a very simplistic and flawed (in the sense of being “biased” by natural phenomena) base for his logic which obscures the logical fallacy of his conclusions within it.

To be fair, this happens to the best of us, and we should always be aware of the possibility that our own judgement has been compromised by the nature of our own cognition. The framing effect is actually one of many effective optimisation mechanisms our brains use as means to make fast and efficient decisions with minimum energy expenditure — because our brains are extremely energy consuming. So, cognitive biases are our biggest contributors to our evolutionary advantage over other mammals, as they create shortcuts for our brains that allow us proceed right to the conclusions instead of analysing every single detail all the time.

But sometimes it backfires and makes us shortcut something in the way which isn’t necessarily efficient — like it just happened to Replyboy. It’s okay, it happens. Just be mindful about this possibility, and don’t be rude to people around you. Then we can talk this out and find the right solution.

there's this trick that racists/queerphobes/etc do, it's really slick. let's just do a little dialogue as an example, the names have been obscured but I've seen this exact exchange happen before.

Stephanie mc. Influencer: "And furthermore, body positivity intersects with black liberation, as black women are often held to unattainable eurocentric beauty standards"

Suave Replyboy Jr: "Lmao, you leftists always tell on yourselves, did you really just say black people are ugly??"

You see the trick here? it's kind of complicated, like, Stephanie is arguing from the perspective that beauty standards are arbitrary and subject to change, Suave understands beauty as an objective hierarchy, so he dunks on Stephanie safely from the inside of that standard. To him, and likely to many people who haven't thought about their own assumptions very much, the only reason black people would want their own body positivity movement is because they're ugly. Bonus points if Stephanie is white, and you can rile her community against her with claims of racism.

I've been getting some replies like this on my posts about sexual trauma, kink, and queerness. Like... I say that sexual deviance of all forms can intersect and correlate with queer identity, and dozens of Suave Replyboy Jrs come out and dunk on me from the other side of the glass, from inside the false universe I'm trying to discredit, the one where "sexual deviance" is immoral and associating queer sexuality with deviancy is an insult. I'm not saying queer people are dangerous perverts, that's you.

[pv1isalsoimportant]

mathematical revelation so great i almost became religious

[prokopetz]

The fun thing about the knights and knaves puzzle is that no matter what goofy variant you come up with, not only has it already been considered, some maniac has worked out the optimal solution. What if there's a third guard who lies or tells the truth at random? It's been done. What if the guards will only answer yes/no questions, and also for some reason they understand your language but refuse to speak it, and you don't know which of the two words they may respond with means "yes" and which means "no"? Literal thesis papers have been written on that one. Logicians are absolute freaks for these guys.

[catscomputerscreativewriting]

It's so funny to me that people think of Math/Mathematicians as being hyper-logical and rational. Like, have you seen some of the wild things hiding in the Math?

Did you know there are non-computable numbers?? (https://en.wikipedia.org/wiki/Chaitin%27s_constant)

Did you know that there are things that are true, but we can't prove them??? (https://en.wikipedia.org/wiki/G%C3%B6del%27s_incompleteness_theorems)

Did you know that we can prove that something exists, and yet never actually figure out what that thing is?? (https://mathworld.wolfram.com/NonconstructiveProof.html)

Math is crazy. Math is wild. Math hardly makes sense, and when you think you understand the weirdest parts of it, everyone who hears you explain it to thinks you're a gibbering lunatic.

"In mathematics you don’t understand things. You just get used to them." - von Neumann

(please share more unhinged math with me, i want to see more scary math)

[aardvaark]

the leverage team would have had a games night… once. everyone cheated so much and in such increasingly extreme ways that all mentions of monopoly are banned in their headquarters (this makes talking about marks who monopolize the market very confusing)

[linddzz]

nothing viktor did was more peak engineer behavior than when he so confidently explained evolution wrong except for him confidently explaining evolution wrong while disagreeing with the guy who explained it correctly

[apollosgiftofprophecy]

Concept: In The Burning Maze, I think it would have been cool if one of the crossword puzzles in the labyrinth had been a mathematical equation.

Specifically, a mathematical equation on mathematical logic, such as negations.

Why? Because Apollo is the god of mathematics and I think it would be funny if Grover and Meg were standing there, staring with horror at:

~(~(p^q))

"What is this nonsense?" Asks Meg, a literal sixth grader who has never before encountered college-level math.

"I...I don't know!" Responds Grover, anxiously wringing his hands. He also has never come across something like this before. "I never went to high school!"

"Is it code for something?"

"The little carrot there looks kinda like a Greek Delta- is Daedalus related somehow?"

"A carrot-what?"

"The carrot!" Grover points at the symbol between the 'p' and 'q'. "It looks like the Delta symbol!"

"Oooh. Okay."

The sentence below the odd thing reads;

Solve my riddle,

Or play second fiddle,

You can find me in education,

For I am the ________!

"...What does that mean?" Grover whimpers.

Meg looks stumped.

"...negation," Apollo's staring at the strange equation. "'Solve my riddle, or play second fiddle. You can find me in education, for I am the negation!'. That's the missing word in the rhyme."

They stare at him. "How do you know that?" Grover bewilderedly asks. "It makes no sense!"

"Math logic," Apollo simply says. "This particular one is...about first, second-year level in college, I'd say."

Grover closes his eyes, muttering; "No wonder I couldn't solve it." as Meg stares first at the equation, then at Apollo.

"What even is a negation?"

"That," Apollo points to the squiggly lines. "It cancels the truth values out, giving you the opposite of what's inside the parathesis."

"...What?"

Apollo huffs. "The 'p' and 'q' both represent something, like two parts of a sentence. The carrot can be upside-down or right-side-up, representing 'or' or 'and' in that sentence."

"Which way is up when?" Grover looked to be on the verge of tears as the realization math did not, in fact, end with numbers or numbers and letters.

"Uh..." Apollo made a 'V' with his hands. "If it's like this, it's 'or'. If it's like this," he made a tiny pyramid with his hands. "It's 'and'. Imagine a line through the center, like an 'A'. That's 'and'."

Grover rubbed at his eyes. "Too much," he whimpered. "Too much."

Apollo gave him an awkward pat on the shoulder. "In this case," he said. "It's saying 'and'. The negation, well, negates their values, so it becomes-" he pats his pants and looks in his pockets. "Anyone have a pen and paper...?"

Blank looks met his. "Okay, then...then just imagine a squiggly line in front of the 'p' and 'q'. That's what the first negation does. Then the second one negates that negation, taking the squiggly lines away."

Breathing in, he finished with; "So our mathematical answer would be, 'p and q', written with the carrot right-side-up- like the 'A'."

The tunnel was silent.

Then it was broken. "How do you know all that?" Meg demanded, looking extremely confused. "That makes no sense. I thought there were numbers."

"There are," Apollo patiently explained. "But this is a logic problem, and they don't do numbers."

"Never before have I been grateful to not to have to go to college," Grover rubbed at his temples. "Algebra was bad enough. Now this?"

"Hey!" Apollo looked slightly offended. "It's all quite fun, really, when you figure it out! Besides, we didn't even have to solve it!"

"Then why did you?" Meg asked.

Apollo stared at her. "Because you asked me too-!"

"Nope." She blew a raspberry. "None of us did."

He closed his eyes, as if praying for mercy.

"Anyway," Apollo gave both of them the stink-eye. "Math and music were quite intertwined back in the day, so the Muses and I are quite adept at it- Thalia's the geometry queen, and whatever you do, do not say 'Bet you can't solve this in a minute' to Urania. She will make you look stupid."

"Bet that's not hard."

"Oh, shut up."

insert cackle from Meg

"ANYWAY," Apollo gives her the stink-eye. "Ancient Greece was a breeding ground for mathematical minds- Pythagoras, for one, who was my son to boot! Even Hestia enjoys looking over Hephaestus's construction equations in her spare time."

The other two stared at him, as if shocked the gods would find math, of all things, fun.

Apollo awkwardly glanced away from them. He didn't know what their reactions would be if he told them of the many contributions he has made to the world of mathematics. For some reason, silly mortals didn't seem to appreciate the hard work put into them!

Sighing, he said; "Uh, Labyrinth, the answer is 'negation'. We got side-tracked there for a bit."

One hallway in front of them glowed with the answer. Without another word, they quickly speed-walked down the passage-way.

[mentalknot]

As a math major trying not to get bogged down in the hellscape of severe social anxiety once again, proofs are shockingly comforting.

How wonderful to behold a carefully chosen sequence of arguments and accompanying symbols that remains absolutely logical…

…while navigating a mind that does nothing but lie at every juncture of my life.

[bubbloquacious]

The current (2024-7-23) first-link chain on Wikipedia containing mathematics goes

Mathematics -> Theory -> Reason -> Logic -> Logical reasoning -> Logical consequence -> Concept -> Abstraction -> Rule of inference -> Philosophy of logic -> Philosophy -> Existence -> Reality -> Universe -> Space -> Three-dimensional space -> Geometry -> Mathematics

and I think that's delightful.

[3leafstem]

Thinking about what kind of tech Jason has in his helmet.

Ignoring the og bomb. For sure he's got voice modulator, which implies some sound proofing so the voice is mostly filtered through the mic, which also implies mics/speakers to pick up sound outside the helmet and filter it in, unless there's much less proofing around the ears, but it would still be muffled.

There's gotta be air filtration. If a toxin is released, he's not gonna take it off to exchange for a gas mask. But I can't recall any canon times he's been seen around a toxin with his helmet (granted I haven't looked), so just gotta assume. This also means the helmet is air tight, some type of latching devices around base.

Comms are a question of are they built into the helmet or separate. If he lost his helmet, it would mean losing his comms too, so I like to think that even if there's comms built in, he has an earpiece at least as a backup just in case.

Then there's the lenses/eyes. They've gotta be lenses rather than holes for the air tight thing, unless it's air tight only around the bottom half of his face. There may be a part inside that juts in to fit snugly over his nose and cheek bones, but that seems unlikely, unnecessary, and uncomfortable.

From here, it's all just speculations and head canons. Are they just lenses? Do they have night vision? Are they opaque on the outside? What other kind of tech could you fit in there? WayneTech, what can you do? I'm sure he'd have more leeway in his helmet than the other bats' lenses do, because he has room for proper wiring, whereas you're working with very limited microtech for dominos.

Speaking of, is he wearing two layers of lenses because of his domino? Can they flick up the lenses, or like slide them up in the dominos if they wanted? I feel like they would have to be malleable for that. Otherwise it's just an all or nothing deal.

Back to Jason, is there a coloured film on the world? Is he seeing the world just extra pale/white because of having two white lenses?

How the hell do one way glass/mirrors work? Can that apply to this situation? Can they be super thin?

I'm so sleep deprived.

[far-away-from-tulsa]

rip johnny cade you would’ve loved having a 504 plan and audiobooks

[pv1isalsoimportant]

turns out that the reason why i couldn't come up with a proof was because the theorem didn't hold.

[recedinghorizons]

[catgirl-lucy]

Ultrafilters & Ultrapowers

Hey! Call me Lucy. I might make an introduction blog later, but I first wanted to make a blog-post about ultrapowers.

Ultrafilters are a concept from set theory, I'll try my best to explain what they are and why they're defined as they are.

First, a quick overview of what we will do: we will extend the real number line by adding new numbers through the use of an ultrapower, these new numbers are called "hyperreals". Roughly, this means that we will have infinite sequences [a₀,a₁,a₂,...] of real numbers representing hyperreal numbers, where similar sequences are regarded as equal. We will also show a surprising theorem: although there are seemingly more hyperreals than reals, hyperreals look the same as real numbers "from within".

If we have a sequence of reals like this: [0,1,1/2,1/3,1/4,...] (I'll call this sequence "ε"), the hyperreal that it represents can be viewed as the "limit" of the sequence. Since a large number of entries of this sequence is smaller than any positive real number r > 0, ε will be smaller than any positive real number r, but since also a large number of entries is larger than 0, ε will be larger than 0. ε is thus an infinitesimal hyperreal number. This is mostly just intuition though, so don't worry if you don't entirely get it.

Two hyperreal numbers x = [x₀,x₁,x₂,...] and y = [y₀,y₁,y₂,...] are equal if x_i = y_i for a large number of indices i. But what does "large" mean in this context?

Well, that's where the ultrafilter comes in. Ultrafilters split a family of sets into sets that are "large" and sets that are "small". In this case, we split sets of natural numbers (numbers 0, 1, 2, 3, etc) into large sets and small sets, so we have an ultrafilter on ℕ, the set of natural numbers. Ultrafilters are identified by the family of large sets: if some set A is in an ultrafilter U, then it is large, and if it's not, then it is small.

We do want our notion of "large sets" and "small sets" to make sense: for example, a hyperreal should always be equal to itself, so we want the whole set of natural numbers, {0, 1, 2, 3, 4, ...} (which is the set of indices for which a sequence is equal to itself), to be large.

Obviously, it would make sense that if a set A is large and B is larger than A, then B is also large. Thus, if A ∈ U is a member of an ultrafilter U ("∈" is the membership symbol), and if B ⊃ A contains everything A contains too ("⊃" is the superset symbol), then B ∈ U is a member of the ultrafilter as well.

We also want hyperreal equality to be transitive, thus if [x₀,x₁,x₂,...] = [y₀,y₁,y₂,...] and [y₀,y₁,y₂,...] = [z₀,z₁,z₂,...], then we want [x₀,x₁,x₂,...] = [z₀,z₁,z₂,...]. If A = {i ∈ ℕ | x_i = y_i} is the set of points at which x and y are equal and B = {i ∈ ℕ | y_i = z_i} is the set of points at which y and z are equal, then C = {i ∈ ℕ | x_i = z_i}, the set of points at which x and z are equal, includes the set A ∩ B = {i ∈ ℕ | x_i = y_i ∧ y_i = z_i}, the set of points at which x is equal to y and y is equal to z. It thus makes sense to have our ultrafilter be closed under intersections: if two sets A and B are large, then the set of points that are both in A and in B, called the "intersection" of A and B (denoted A ∩ B), is a large set as well (and thus also in the ultrafilter).

It would also make sense that, if two hyperreal numbers are nowhere equal, then they aren't equal. So the empty set, {} = ∅, is small.

The five axioms above describe a filter:

A filter F on κ is a family of subsets of κ.

A filter F on κ must contain the whole set κ.

A filter F on κ must be upwards closed, thus for every large set A ∈ F, and every larger set B ⊃ A, B ∈ F is large as well.

A filter F on κ must be downwards directed, thus for every large set A ∈ F and every large set B ∈ F, the intersection of A and B, A ∩ B ∈ F, is large as well.

A filter F on κ may not contain the empty set.

However, these are the axioms of a filter, and not of an ultrafilter. Ultrafilters have one additional axiom.

Suppose we have the hyperreal [0,1,0,1,0,1,...]: an alternating sequence of 0's and 1's. Is this equal to 0 = [0,0,0,0,...], or to 1 = [1,1,1,1,...], or is it its own thing? (Note: the 0 in 0 = [0,0,0,0,...] is a hyperreal and the 0's in 0 = [0,0,0,0,...] are real numbers, so they're different (kind of) numbers both called "0"). If it is its own thing, then is it smaller than 1? If it is smaller than 1, then it must be smaller on a large set of indices, meaning it's equal to 0 on a large set of indices, meaning it's equal to 0. If it's not smaller than 1, well, it can't be larger, so it'd only make sense if it's equal to 1, but no axiom about filters says it should! That's why we have this last axiom for ultrafilters, which makes them "decisive": for every set A, it is either large (thus, A ∈ U), or small, meaning that its complement, Ac = {i | i ∉ A}, the set of all points that aren't in A, is large.

And so we have our six axioms of an ultrafilter:

An ultrafilter U on κ is a family of subsets of κ, these subsets are called "large sets".

κ is large.

U is upwards closed.

U is downwards directed.

∅ is not large.

For every set A ⊂ κ, either A ∈ U or Ac ∈ U.

But we're still missing one thing. We can take our ultrafilter U to be the set of all sets of natural numbers that contain 6. ℕ is large, as it contains 6. It is upwards closed: if A contains 6 and B contains everything that A contains and more, then B also contains 6. U is downwards directed: if both A and B contain 6, then the set of all points that are in both A and B still contains 6. The empty set does not contain 6, and every set either does contain 6 or does not contain 6. With this ultrafilter, two hyperreals x and y are equal simply when x₆ and y₆ are equal, so we don't get cool infinitesimals and infinities, and that makes me sad :(

These kinds of boring ultrafilters are called principal ultrafilters. Formally, a principal filter on κ is a filter F on κ for which there is some set X ⊂ κ so that any set A ⊂ κ is large only if it contains everything in X. This filter is often denoted as ↑X. If you want a principal filter U to be an ultrafilter, X needs to be a singleton set, meaning it only contains a single point x. Proving this is left as an exercise for the reader.

Let U be a non-principal ultrafilter on ℕ. This post is getting a bit long, so I won't show why such an ultrafilter exists. Now, we can take the ultrapower of ℝ, the set of real numbers, by U. This ultrapower is often denoted as ℝ^ℕ/U. Members of this ultrapower are (equivalence classes of) functions from ℕ to ℝ, meaning that they send natural numbers/indices to real numbers (the sequence [x₀,x₁,x₂,...] maps the natural number i to the real number x_i). These functions/sequences/equivalence classes are called hyperreal numbers. Two hyperreal numbers, x and y, are equal if {i ∈ ℕ | x(i) = y(i)}, the set of points at which they are equal, is large (i.e. a member of U). We can also define hyperreal comparison and arithmetic operations: x < y if {i | x(i) < y(i)} is large, (x + y)(i) = x(i) + y(i) and (x · y)(i) = x(i) · y(i). Every real number r also has a corresponding hyperreal j(r), which is simply [r,r,r,r,...] (i.e. j(r)(i) = r for all i).

In general, if M is some structure, κ is some set and U is some ultrafilter on κ, then we can take the ultrapower M^κ/U, which is the set of equivalence classes of functions from κ to M, where any relation R in M (for example, "<" in ℝ) is interpreted in M^κ/U as "R(x₁,...,xₙ) if and only if {i ∈ κ | R(x₁(i),...,xₙ(i))} ∈ U is large" and any function f in M (for example, addition in ℝ) is interpreted in M^κ/U as "f(x₁,...,xₙ)(i) = f(x₁(i),...,xₙ(i)) for all i ∈ κ".

A quick note on equivalence classes: in M^κ/U, points aren't actually functions from κ to M, but rather sets of functions from κ to M that are all equal on a large set of values. Given a function f: κ → M, the equivalence classes that f is in is denoted [f]. In this way, if f and g are equal on a large set of values, then [f] and [g] are actually just equal.

The hyperreal [0,1,2,3,4,...], which sends every natural number i to the real number i, is often called ω.

This part of the blog will get a bit more technical, so be warned!

In the beginning of this blog-post, I mentioned that hyperreals look the same as real numbers. I'll make this statement more formal:

For any formula φ that can be built up in the following way:

φ ≡ "x = y" for expressions x and y (expressions are variables and "a + b" and "a · b" for other expressions a and b)

φ ≡ "x < y" for expressions x and y

φ ≡ "ψ ∧ ξ" (ψ and ξ are both true) for formulas ψ and ξ

φ ≡ "ψ ∨ ξ" (ψ or ξ is true (or both)) for formulas ψ and ξ

φ ≡ "¬ψ" (ψ is not true) for an formula ψ

φ ≡ "∃x ψ(x)" (there exists a value for x for which ψ is true) for a variable x and an formula ψ

φ ≡ "∀x ψ(x)" (for all values of x, ψ is true) for a variable x and an formula ψ

We have that ℝ ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ, where variables can have real number values) if and only if ℝ^ℕ/U ⊧ φ (φ is true when evaluating equality, comparison and expressions from within ℝ^ℕ/U, where variables can have hyperreal number values).

In other words: ℝ and ℝ^ℕ/U are elementary equivalent.

So, how will we prove this? Well, we will use induction: "if something being true for all m < n implies it being true for n itself, then it must be true for all n (where m and n are natural numbers)". Specifically, we will use induction on the length of formulas: we will show that, if the above statement holds for all formulas ψ shorter than φ, then it must also hold for φ.

However, we won't use the exact statement above. Instead, we will use the following:

Given a formula φ(...) and hyperreal numbers x₁,...,xₖ, ℝ^ℕ/U ⊧ φ(x₁,...,xₖ) if and only if {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large.

Now, why does this imply the original statement? Well, when k = 0, {i | ℝ ⊧ φ} can only be ∅ or ℕ. It being ∅ is equivalent to φ being false in ℝ and, if the statement is true, also equivalent to φ being false in ℝ^ℕ/U. And it being ℕ is equivalent to φ being true in ℝ and, again, if the statement is true, it is also equivalent to φ being true in ℝ^ℕ/U. We thus have that φ being true in ℝ is equivalent to φ being true in ℝ^ℕ/U.

Note: M ⊧ φ simply means that the formula φ is true when interpreted in M.

Now, why do we need this stronger statement? Well, it makes induction a lot easier: given that this statement holds for all ψ shorter than φ, it's easier to prove it also holds for φ.

Now, we can actually do the induction.

First, if φ ≡ "x = y", then we need to show that (1) ℝ^ℕ/U ⊧ φ(x,y) iff (2) {i | ℝ ⊧ φ(x(i),y(i))} is large. This follows immediately from the definition of equality in ℝ^ℕ/U, the same holds for "<".

Now, if φ(x₁,...,xₖ) ≡ "ψ(x₁,...,xₖ) ∧ ξ(x₁,...,xₖ)", we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i)) ∧ ℝ ⊧ ξ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} ∩ {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))}. Since {i | ℝ ⊧ ψ(x₁(i),...,xₖ(i))} is large iff ψ(x₁,...,xₖ) is true in ℝ^ℕ/U, and {i | ℝ ⊧ ξ(x₁(i),...,xₖ(i))} iff ξ(x₁,...,xₖ) is true in ℝ^ℕ/U, and U is closed under intersections, we have that {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} is large iff φ holds in ℝ^ℕ/U. A similar argument works for ∨.

If φ(x₁,...,xₖ) ≡ "¬ψ(x₁,...,xₖ)", then we can just use the ultraness of the ultrafilter.

If φ ≡ "∃y ψ(y,x₁,...,xₖ)", then {i | ℝ ⊧ φ(x₁(i),...,xₖ(i))} = {i | ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i))} = {i | ∃y ∈ ℝ. ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} = ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))}. We have that the set {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} for y ∈ ℝ is large iff ℝ^ℕ/U ⊧ ψ(j(y),x₁,...,xₖ). If this set is large for some y ∈ ℝ, and thus if ℝ^ℕ/U ⊧ φ(x₁,...,xₖ), then ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is larger than that set, so it is large as well. For the converse direction, if ∪_{y ∈ ℝ} {i | ℝ ⊧ ψ(y,x₁(i),...,xₖ(i))} is large, then we can create a hyperreal z where ψ ⊧ ψ(z(i),x₁(i),...,xₖ(i)) for all i for which ℝ ⊧ ∃y ψ(y,x₁(i),...,xₖ(i)), and we have ℝ^ℕ/U ⊧ ψ(z,x₁(i),...,xₖ(i)), and thus ℝ^ℕ/U ⊧ φ(x₁(i),...,xₖ(i)). Again, a similar argument works for ∀.

(Sorry if you couldn't follow along, I'm not good at explaining these things in an intuitive way.)

This result can be extended to show that M^κ/U is elementary equivalent to M for every structure M, every set κ and every ultrafilter U on κ.

Now, this result might be surprising, as we have a new number ω in ℝ^ℕ/U. Surely, there is a formula that states the existence of this number, right?

Well, it turns out, such a formula does not exist! You can try something like "there is no natural number n so that 1+...+1 w/ n 1's is greater than ω", but ω+1 is a natural number in the hyperreals, so such a natural number does exist. Similarly, any formula you can come up with, as long as it is created using the rules above (using conjunction, disjunction, negation, qauntification, etc), cannot state the existence of an infinite number ω.

But if ℝ^ℕ/U and ℝ are seemingly indistinguishable, might there already be an undetectable infinite real number in ℝ? Well, maybe~ :3 But it's undetectable anyways, so you don't have to worry about it.

Before I end this blog-post, I want to give some more intuition on what filters & ultrafilters actually are. To me, ultrafilters, and filters in general, are like "limits of sets". The principal filter ↑X has X as limit, while non-principal filters and ultrafilters have limits that aren't really sets, but look like ones. For example, you might have the set of prime numbers in your filter, and then the limit of that filter will be a "set" in which all numbers are prime numbers. And if your ultrafilter is non-principal (so for every n, there is a set A ∈ U in the filter that does not contain n), then the limit of that ultrafilter will be a "set" in which all numbers don't actually exist. In the case of filters, this "set" can be any "set" (though it still isn't really a set), but in the case of ultrafilters, this limit looks like a singleton set (i.e. it only has one "element": ω).

I don't know if my intuition of filters and ultrafilters will help anyone, tho, but I think it's cool!

That's all I had to say.

Bye!~ Have a nice day.

[sunnyupsidedown]

Math major Neil is all about problem solving so OF COURSE he called that hit. His whole runaway life was a matter of high risk problem solving. Arranging that hit was child’s play