#vector algebra formulas

[yoneda-emma]

Am I correct in assuming that if you want to rigorously derive formulas for calculating volumes of arbitrary n-dimensional polytopes (or to even formally define what a volume is in the first place) you need to get into measure theory? Or is there a simpler, more algebraic way that still leads to a fully formal and rigorous proof?

(I'm specifically interested in a rigorous proof that the correspondence between determinants of n x n matrices and volumes of n-parallelotopes spanned by the corresponding vectors continues to hold for arbitrary n)

[j4neseyre]

weekly to-do list 💋

i have realized that i need to brush up my physical chemistry because there's a lot of calculations and formulas which i am most like to fuck up if i don't practice regularly. so i will be focusing on that a lot + inorganic too ig.

solutions formula rev and pyq session + thermodynamics questions

electrostatic questions and review

straight lines questions

biomolecules + electrochemistry questions

emi + ac + emw questions

modern physics questions + formula sheet

equilibrium questions and lecture

chemical kinetics + atomic structure questions

magnetics + current electricity questions

differentiation questions and formula sheet

application of derivatives + lecture + formula sheet

chemical bonding questions + review lecture

optics questions + theory

vector algebra pyq session + lecture

☆ sunday : mock test and revision

[tensorboi]

Why is the Pythagorean theorem true, really? (and a digression on p-adic vector spaces)

ok so if you've ever taken a math class in high school, you've probably seen the Pythagorean theorem at least a few times. It's a pretty useful formula, pretty much essential for calculating lengths of any kind. You may have even seen a proof of it, something to do with moving around triangles or something idk. If that's as far as you've gotten then you are probably unbothered by it.

Then, if you take a math class in university, you'll probably see the notion of an abstract vector space: it's a place where you can move things and scale them. We essentially use these spaces as models for the physical space we live in. A pretty important thing you can't do yet, though, is rotate things or say how long they are! We need to put more structure on our vector spaces to do that, called a norm.

Here's the problem, though: there are a *lot* of different choices of norm you can put on your vector space! You could use one which makes Pythagoras' theorem true; but you could also use one which makes a³ + b³ = c³ instead, or a whole host of other things! So all of a sudden, the legitimacy of the most well-known theorem is called into question: is it really true, or did we just choose for it to be true?

And if you were expecting me to say "then you learn the answer in grad school" or something, I am so sorry: almost nobody brings it up! So personally, I felt like I was going insane until very recently.

(Technical details: the few that do bring it up might say that the Pythagorean norm is induced from another thing called an inner product, so it's special in that way. But also, that doesn't really get us anywhere: you can get a norm where a⁴ + b⁴ = c⁴ if you are allowed to take products of 4 vectors instead!)

How is this resolved, then? It turns out the different norms are not created equal, and the Pythagorean norm has a very special property the others lack: it looks the same in every direction, and lengths don't change when you rotate them. (A mathematician would say that it is isotropic.) Now, all of a sudden, things start to make sense! We *could* choose any norm we like to model our own universe, but why are we going to choose one which has preferred directions? In the real world, there isn't anything special about up or down or left or right. So the Pythagorean norm isn't some cosmic law of the universe, nor is it some random decision we made at the beginning of time; it's just the most natural choice.

But! That's not even the best part! If you've gone even further in your mathematical education, you'll know about something called p-adic numbers. All of our vector spaces so far have been over the field of real numbers, but the p-adic numbers can make vector fields just as well. So... are the Pythagorean norms also isotropic in p-adic spaces? Perhaps surprisingly, the answer is no! It turns out that the isotropic norms in p-adic linear algebra are the ∞-norms, where you take the maximum coordinate (rather than summing squares)! So the Pythagorean theorem looks very different in p-adic spaces; instead of a² + b² = c², it looks more like a^∞ + b^∞ = c^∞.

If you're burning to know more details on this, like I am right now as I'm learning it, this link and pregunton's linked questions go into more details about this correspondence: https://math.stackexchange.com/questions/4935985/nature-of-the-euclidean-norm

The interesting thing is that these questions don't have well-known answers, so there is probably even more detail that we have yet to explore!

tl;dr: the pythagorean theorem is kind of a fact of the universe, but not really, but it kinda makes sense for it to be true anyway. also we change the squares to powers of infinity in p-adic numbers and nobody really knows why

[susidestroyerofworlds]

what’s your favorite number

this is a really hard question. Its probably 2, since it makes for an amazing base and is just generally very useful, like, when you have a+a, which is common, that turns into 2a. It's also the successor to 1, making it the first number thats not just defined directly by axioms like 0 and 1 and rather a consequence.

2 is also aesthetically fun, the way it swoops at the top and then sits on a sturdy base, with both a round and a sharp corner. So, that's my answer,

2

But! If we go further we can find lots of other numbers I also love. 6 is a really nice number because its small but not "weird" in any immediate way. It's not an identity, it's not prime, it's not a square, etc. If you have a formula or something and you want to check it with a number 6 usually works without running into common edge cases.

Leaving the Naturals, -1 is an amazing integer. Really useful for anything that alternates, I love the roots of unity and it's the first nontrivial of those. All the roots of unity are pretty amazing tho, highly recommend.

Rising further we get to the Rationals, which are honestly kinda boring imo. Shoutout to ½ for being the reciprocal of 2 but that's it.

Now, shit is gonna get Real. The Reals are an amazing set, lots of useful properties, a really cool field (the Rationals are also a field but they suck so the Reals get to be the cool field). The Reals contain just about every number you normally interact with, including all-time highs such as pi or e. All algebraic and transcendental numbers are in here, including my favourite, sqrt(2). The square root of 2 is real cool. It's fun geometrically, being a factor of the length of the hypotenuse of a right triangle where the legs are the same length. It's cool algebraically as being the easiest to introduce number thats real but not rational, I have fond childhood memories of learning that the Reals are Dedekind complete (of course that word was only introduced in high school) with this beautiful number as the example. It's reciprocal is also really cool and useful. sqrt(2) even has its own Wikipedia article.

Leaving behind the Reals, the Complex Numbers are just fun as a category. No longer ordered, basically acting as if R² was a field, just really fun. I don't really have a favourite complex number but I am a sucker for units for i gets nominated as my favourite here. All complex numbers are really cool. Shoutout to |0> and |1> (ket-zero and ket-one) for being cool in quantum computing and being vectors in a space using the field of the complex numbers.

There is lots more sets but I am not familiar enough with numbers to even come close to doing them justice. I hope your questions is answered, have a nice day <3

[nia-academia]

07.02.2024, Wednesday

Physics practical went great, my physics teacher kind of hinted that i got full marks and I hope that is the case. Tomorrow is the last practical, Physical Education and also...it's my birthday. I talked to the batches that already had their PE practicals and turns out the external is weird, to say the least. Also that he's asking questions from theory, formulas, definitions and measurements and stuff. So I guess I'll have to skim through the whole syllabus. I did a bit of math in the morning and then spent the rest of the time studying PE. I did plan on reading a bit more but my friends called me up at 12 as is tradition so I'll just read the rest of it in the bus tomorrow. I'm not too stressed because viva is just 3 marks and the rest is just physical stuff so a 50m dash, and then we have to demonstrate some yoga, push-ups and partial curl-ups and then some techniques of whatever we've chosen as our main sport. Let's see how it goes.

Time Studied: 4 hours Subject: Mathematics, Physical Education Content: Vector Algebra, Sports Training, Biomechanics, Sports Injury, Sports Management, Yoga, Tests and Measurement, Badminton (Lab Manual)

[chlorophyllcrimescene]

sativa static, fleetwood mac but in the way of an untimely, erratic divorce. getting lost in an elderly care facility on my way downtown. chlorine sticky forearms, full radio silence. poetry and prose through the lens of formulas and vectors. an algebraic process performed frantically and without deeper meaning. writing myself into existence, repeated a thousand times over a crackling phone line, disseminating into the opaque.

[amalgamgooze]

"easier" math has become more difficult than "difficult" math

Had to take a math placement exam for college today.

It was all high school stuff--things I'd already done.

Now tell me,

why was it harder to do that stuff than the abstract algebra stuff I'm studying?

…

I'm serious.

Maybe it's a familiarity thing.

Like, nobody should ever have to memorize all the trig identities.

sin2x + cos2x = 1, that's an acceptable one to memorize.

Super short, simple, and widely applicable.

But the bullshit like sin(2x) = sin(x)cos(x)?

Or sin(x/2) = sqrt((1 - cos(x)) / 2 ) ?

What? The? Fuck?

Is this actually stuff I studied two years ago?

This is formula sheet bullshit.

Not stuff you test for to gauge math proficiency.

And not without a calculator either.

For fucks sake--discrete math and modern algebra without a calculator is easier than precalculus without a calculator!

…

I can see why some people hate math.

That shit's just not fair.

Even if you're using math professionally, you're not going to have that bullshit restriction of "you need to know everything off the top of your head".

…

If you couldn't tell, I'm not a fan of all of math.

There's some areas that I don't feel are as important to understand as the rest.

Like conic sections.

Or eccentricity.

…don't get me wrong. Geometry is pretty cool sometimes.

But when my job is to literally solve the equation for a specific point on an ellipse, I'm just left thinking, "why bother?".

…

Calculus was cooler than that shit.

Vector calculus was cooler than that shit.

Precalculus was hell.

I offer my condolences to you poor souls who've yet to take Precalc.

There's cooler math beyond precalc.

Yes, it's more incomprehensible, but it's enjoyably incomprehensible.

It's supposed to be abstract.

It--

Physics wasn't as infuriating as that test!

I-

I don't know how much more I can prove I love math than to write a whole monologue about me descending into insanity over my love for math!

But this fuckin' test!

It just- wow.

I'm sorry. I'm still kinda worked up about it.

I'm not writing about it in a very unbiased lens.

(I don't need to. I'm not claiming to preach universal truth in this post.)

…

Again.

I suppose I want to emphasize that precalculus and later "college algebra" classes are kinda infuriating and not very fun.

There's fascinating fields like calculus, linear algebra, and abstract algebra beyond that rut.

…

But again. Math's not for everyone. So I suppose you can also hate all of it. I won't judge.

[coming-up-with-usernames-is-hard]

PhD Blog Week 11

Courses

CFT: Conformal familes and descendent fields, starting to get into the representation theory of the Virasoro algebra, at some point things were labelled by partitions and suddenly everything was very familiar

Lie Theory: Last lecture, Weyl character formula (for sl_n it should give Schur functions as the q-dimension of the verma module, so I should look into that)

DiffTop: Connections, very little material covered in this lecture, but we will have an assignment due on the 23rd, which seems mean

Talks

Example Showcases: Just three to finish off this week. The first was on inverse semigroups, interesting enough and a good talk, but I wasn't convinced of their usefulness. The second was on CFT and constructing modular tensor categories, the material seems interesting but unfortunately I couldn't follow the details. The third and final talk was on braids and knots, another nice talk, and there was an interesting bit on constructing a Hecke algebra using the braids, and I need to learn about Hecke algebras eventually so that was particuarly interesting.

Reading Groups

Infinity Categories: Six functor formalisim. Totally out of my depth this week, we started with derived categories, and I don't know what those are

Supervisor Meeting

We have a result that doesn't quite line up with one in a textbook, so I need to figure out why that is, then some debate over whether Schur functions are Wronskians took most of the rest of the time

Teaching

Last two TA sessions of the semester, pretty simple worksheet this week, although getting the students to think geometrically about vectors rather than seeing them as lists of numbers takes a bit of work, lots of pointing in different directions. They've also started looking at Z_n, so not long now until they hit the groups portion of the course, which will be interesting, that will be the first proper algebra many of them have seen

[cecestudies]

How to Tackle Tough A Level Maths Questions with Confidence?

Tough A Level Maths questions can feel overwhelming, but with the right mindset and strategy, you can tackle them confidently. In this expert-backed guide by Exam Tips, we share practical techniques to help you break down complex problems, manage exam pressure, and apply concepts effectively. From understanding the question type to planning your solution step-by-step, we show you how to stay calm and think clearly under time constraints. Whether it’s calculus, trigonometry, or mechanics, this resource will strengthen your problem-solving skills and build the confidence you need during your A Level Maths revision. Let Exam Tips guide you through mastering the hard questions — because with the right approach, no problem is too tough.

Develop a Clear Understanding of the Question

One of the most common reasons students struggle with tough maths problems is misunderstanding what the question is really asking. Take time to carefully read the entire question, underline key terms, and identify the type of problem before diving into calculations. Sometimes, a question might be testing more than one concept, or it may contain data meant to distract you. A Level examiners often embed simple tasks within complex-looking problems. During your A Level Maths revision, practice unpacking questions slowly — understand the requirement first, then think about the method. Exam Tips always advises students not to rush through reading, as a strong start can lead to a clearer path to the solution.

Break Down Problems into Smaller Sections

Large, multi-part maths questions can look overwhelming at first glance. But remember, every big question is made up of smaller, more manageable parts. Start by breaking the problem into logical steps. Look for familiar formulas, diagrams, or patterns. Often, the answer to the first part of a question helps solve the next one. Treat each section individually and work systematically. Practicing this breakdown method during your A Level Maths revision helps you stay calm in the exam room. According to the team at Exam Tips, this habit not only improves accuracy but also saves valuable time by reducing confusion.

Strengthen Core Concepts for Better Application

Tough questions often test how well you can apply core mathematical concepts in unfamiliar scenarios. That’s why a deep understanding of basics is more useful than memorising shortcuts. If your foundations are strong in algebra, functions, calculus, and trigonometry, you’re more likely to spot the correct method when a problem looks tricky. During revision, focus on “why” a formula works instead of just “how” to use it. This approach enhances your problem-solving flexibility. Exam Tips recommends consistent topic-wise practice sessions to reinforce these concepts as part of your A Level Maths revision plan.

Use Diagrams and Visual Aids to Simplify

When stuck on a complex question, drawing a diagram or chart can simplify the situation dramatically. This is especially helpful in geometry, mechanics, and function-related problems. Diagrams allow you to visualise relationships, spot errors, and clarify what’s being asked. Whether it’s sketching a curve or plotting vectors, these small steps create a mental map of the question. Many high-scoring students use this visual strategy to approach problems with more confidence. Exam Tips regularly encourages students to make diagrams part of their toolkit during A Level Maths revision, especially when preparing for applied sections of the paper.

Practice with Timed Exam-Like Conditions

It’s one thing to solve problems in a calm environment, but it's another to do it with a timer ticking. Tough questions often feel even harder during the actual exam due to time pressure and nerves. Simulating exam conditions during your revision can train your brain to stay composed. Set a timer, attempt past papers, and avoid using notes or calculators (unless allowed). Over time, you’ll learn how to pace yourself and not panic when a problem looks new. Exam Tips also provides mock test setups and pacing strategies to build confidence under pressure as part of their A Level Maths revision support.

Review Mistakes and Learn from Every Attempt

Every incorrect answer is a chance to improve. When you get a tough question wrong, don’t just check the solution and move on. Take time to understand why you made the mistake — was it a misread, a formula error, or a concept you haven’t mastered? Keeping a revision log or a mistake journal helps you track patterns in your errors. Exam Tips recommends reviewing your toughest past paper questions at least twice during your revision schedule. This reflective practice not only improves accuracy but also builds resilience, so you’re better equipped to face similar challenges in the future.

Build Exam Confidence Through Repetition and Planning

Confidence doesn’t come overnight — it comes from repetition and smart planning. Build a routine that includes regular problem-solving sessions, spaced revision, and daily reflection. Focus more on weak areas but don’t neglect your strengths. The more questions you attempt — especially past exam questions — the more familiar you become with the style, format, and level of difficulty. Exam Tips offers structured revision calendars and targeted worksheets to help you stay consistent and efficient. Over time, you’ll notice that even the toughest A Level Maths questions start feeling manageable, and you’ll approach them with more certainty and speed.

Conclusion

Tackling tough A Level Maths questions isn’t about being perfect — it’s about staying composed, applying logic, and trusting your preparation. By breaking problems into steps, using visual tools, and learning from each mistake, you’ll gradually build the confidence needed to perform under pressure. Regular practice, smart revision techniques, and time management are the pillars of success. Exam Tips is here to guide you through every stage of your A Level Maths revision, helping you transform doubt into confidence. With the right mindset and tools, you can overcome even the most difficult challenges on your exam journey.

[sathcreation]

Expert IIT Mathematics Teacher at Gritty Tech

Introduction to IIT JEE Mathematics Excellence

The journey to cracking the prestigious IIT JEE begins with mastering one of its most challenging components – Mathematics. At Gritty Tech, we understand the intensity and depth required to succeed in this subject. That's why we offer specialized coaching under the guidance of expert IIT Mathematics teachers who not only know the syllabus but also understand the psychology and strategy behind high-stakes exams For More…

Our teaching is not just about covering topics. It’s about building a solid mathematical foundation, developing analytical thinking, and fostering a problem-solving mindset.

Why Expert Teachers Make a Difference

IIT JEE Mathematics is not about rote learning. It demands creativity, speed, accuracy, and deep conceptual understanding. An expert IIT Maths teacher brings all these elements to the table. At Gritty Tech, our instructors are selected through a rigorous process. Each of them has years of experience in mentoring toppers, with proven results across multiple batches.

Key Attributes of Our Expert Maths Faculty:

In-depth Subject Knowledge: Every teacher at Gritty Tech has a mastery over the entire JEE syllabus including Algebra, Calculus, Coordinate Geometry, Trigonometry, Probability, and more.

Strategic Teaching Methods: They know how to break down complex problems into simpler steps and highlight shortcuts that save time in exams.

Focus on Conceptual Clarity: Instead of encouraging memorization, our approach ensures students understand the 'why' behind every formula.

Real Exam Insight: Teachers share insights from previous year papers, trends, and changing patterns in JEE to keep students one step ahead.

Individual Mentorship: Every student is different. Our experts provide personal guidance to overcome weaknesses and build on strengths.

A Curriculum Built for Success

At Gritty Tech, the Mathematics curriculum is not generic. It is crafted specifically for IIT JEE aspirants, keeping in mind the latest trends, difficulty levels, and expected question formats. Our curriculum is reviewed and refined every year by a panel of experts.

The Core Topics Covered Include:

Algebra: Quadratic equations, Complex numbers, Matrices & Determinants, Permutations & Combinations

Calculus: Limits, Continuity, Differentiability, Application of Derivatives, Integrals, Differential Equations

Coordinate Geometry: Straight lines, Circles, Conic Sections

Trigonometry: Identities, Equations, Inverse Trigonometric Functions

Vectors and 3D Geometry

Probability and Statistics

Each topic is taught from the ground up, beginning with theory and moving into solved examples, practice sheets, test series, and revision strategies.

Teaching Methodology at Gritty Tech

What truly sets Gritty Tech apart is not just the content we teach, but how we teach it.

Interactive Concept Classes

Our sessions are designed to be interactive. Teachers use smart boards, real-life analogies, and visual aids to explain abstract mathematical ideas. Every class ends with a set of practice problems that help reinforce the day’s learning.

Doubt Resolution in Real-Time

Students never have to wait till the end of the week to clear their doubts. With dedicated doubt-solving sessions and availability of the faculty even outside class hours, learning continues seamlessly.

Regular Testing and Feedback

Frequent quizzes, weekly tests, and full-length mock exams are conducted to ensure students are exam-ready. After each test, teachers provide personalized feedback and performance analysis.

Adaptive Learning

Not every student learns the same way. Our experts use adaptive learning techniques to identify the learning style of each student and modify their approach accordingly.

[govindhtech]

Quantum Picturalism QPic And Future Of Quantum Education

QPic Quantum Picturalism

Quantum Picturalism (QPic) can make global education more accessible and enhance quantum workforce participation by eliminating cognitive hurdles associated with advanced mathematics, diagram-based instruction in particular. The study found that high school students without advanced maths could learn quantum computing basics via QPic.

How QPic does this and its effects:

Skip Math Prerequisites

Linear algebra, which covers vectors, matrices, complex numbers, and Hilbert space formalism, is a fundamental part of traditional quantum mechanics education for university students with considerable mathematical expertise. QPic replaces formulas with diagrams. Diagrams represent matrices and allow visual manipulation of quantum computations. Students no longer need to compute matrix equations to understand quantum teleportation and entanglement.

Better Understanding and Engagement

The study revealed that pictures may make complicated concepts fun to learn. A post-training exam was taken by 82% of high school pupils after eight weeks of QPic sessions, with 48% obtaining distinction. Visualising the issue makes it more manageable. The studies found that Quantum Picturalism increases student interest and reduces cognitive challenges.

Greater Quantum Education Access

QPic might make quantum education more accessible and equitable by eliminating complex maths. Fewer than 5% of UK state school students study Further Mathematics, which includes matrices. QPic makes quantum education accessible to more students by eliminating this obstacle.

STEM Workforce Development Support

The report supports lowering cognitive barriers and starting schooling earlier to reduce the quantum workforce gap. Quantum Picturalism may help solve the labour shortage by accelerating developer and learner integration into new computer domains, according to the researchers. Most students said the training motivated them to pursue QIST and work in STEM.

Cognitive Balance

Deep cognitive processes may give QPic an edge. Diagrams are better in tune with how the human brain organises and processes information through visual structure than symbolic language, according to Gestalt psychology and dual coding theory. This may explain how students understood quantum ideas that are usually assumed to take years to learn.

Chances to switch skills

QPic provides cross-skilling options for developers and learners. It has been used for quantum circuit optimisation in Google and Quantum programs and academic courses, proving its versatility.

Early Introduction

The study emphasises the need of teaching a complex topic like QIST in high school, which was previously assumed to be exclusively available at the university level.

Futures of Quantum Picturalism

QPic may help solve the labour shortage by accelerating student and developer adoption of cutting-edge computational domains, according to the authors. QPic may help build a larger, more accessible quantum workforce.

The study's effectiveness with high school students suggests introducing QIST instruction sooner and even incorporating it into high school courses.

Neuroimaging studies are intended to understand QPic learning's cognitive processes. Visual tools may assist individuals grasp complex scientific concepts in future investigations.

various countries have begun replication studies, and longer courses, various classroom settings, and formal curriculum inclusion will be studied. The efficacy and adaptability of QPic will likely be investigated and enhanced in other scenarios in the future.

Researchers intend to examine how QPic influences socioeconomic barriers, gender inequities, and quantum job desire over time. QPic may generate a more inclusive and equitable quantum field in the future.

The successful use of QPic for quantum circuit optimisation in university courses and at Google and Quantum suggests that this diagrammatic technique may be employed more in quantum industry and education.

[manasastuff-blog]

https://www.manasadefenceacademy.in/post/30-days-study-plan-for-nda-exam-2025

30-Days  NDA Exam Study Plan (2025) – Crack NDA in First Attempt!

🔹 Week 1: Foundation Building

📌 Day 1-2:

Understand the NDA Exam Pattern & Syllabus

Gather study materials (NCERT books, previous papers, reference books)

Set a daily timetable for consistency

📌 Day 3-4: Mathematics

Algebra (Quadratic Equations, Progressions)

Trigonometry (Heights & Distances, Identities)

Practice 20+ questions daily

📌 Day 5-6: English

Grammar (Tenses, Active-Passive, Direct-Indirect Speech)

Vocabulary (Synonyms, Antonyms, Idioms, Phrasal Verbs)

Read newspapers for comprehension skills

📌 Day 7: Revision & Mock Test

Revise Week 1 topics

Solve a previous year’s paper

Analyze mistakes and improve

🔹 Week 2: Core Subjects

📌 Day 8-9: Mathematics

Coordinate Geometry (Straight Lines, Circles)

Differential & Integral Calculus (Limits, Derivatives)

📌 Day 10-11: General Science

Physics (Motion, Laws of Motion, Electricity)

Chemistry (Chemical Reactions, Periodic Table)

Biology (Human Body, Diseases, Reproduction)

📌 Day 12-13: General Knowledge (GK)

History (Indian Freedom Struggle, Revolt of 1857)

Geography (Indian Rivers, Climate, Soil)

Polity (Indian Constitution, Fundamental Rights)

📌 Day 14: Revision & Mock Test

Revise all subjects

Attempt a full-length mock test

🔹 Week 3: Advanced Learning & SSB Preparation

📌 Day 15-16: Mathematics

Probability & Statistics

Vector Algebra

📌 Day 17-18: Current Affairs & Static GK

Important National & International Events

Defence News & Military Exercises

Sports & Awards

📌 Day 19-20: SSB Interview Preparation

OLQs (Officer Like Qualities)

Psychological Tests (TAT, WAT, SRT)

Group Discussions & Public Speaking

📌 Day 21: Revision & Mock Test

Focus on weak areas

Solve NDA-level mock questions

🔹 Week 4: Final Practice & Full-Length Tests

📌 Day 22-23: Mathematics & English

Speed-solving techniques

Reading comprehension practice

📌 Day 24-25: Science & GK

One-day revision for each subject

📌 Day 26-28: Full-Length Mock Tests

Solve three full NDA mock tests

Improve time management skills

📌 Day 29: Quick Revision

Revise formulas, current affairs, and difficult topics

📌 Day 30: Relax & Stay Confident

No new topics

Sleep well & stay motivated

🔹 Bonus Tips:

✅ Solve previous 10 years' NDA papers ✅ Maintain good health & fitness (for SSB medical) ✅ Focus on time management and accuracy ✅ Improve communication skills for SSB

Contact:

Manasa Defence Academy

New Gajuwaka Depot, Visakhapatnam.

Andhra Pradesh-530012.

Call: 7799799221, 7799799229

Gmail: manasadefenceacademy@gmail.com  

Join Manasa Defence Academy & Achieve Your Defence Career Dreams! 

[remoteinnovator]

What Are the Key Topics to Focus on for AS Level Mathematics?

AS Level Mathematics is a challenging yet rewarding subject that provides a strong foundation for further study in various fields, such as engineering, economics, physics, and even computer science. To excel in AS Level Mathematics, students need to focus on key topics that will not only help them understand the subject better but also improve their exam performance. In this article, we’ll explore the most important topics to focus on for AS Level Mathematics and how they can contribute to your overall success.

1. Algebra and Functions

Algebra forms the backbone of AS Level Mathematics. A solid understanding of algebraic principles is essential for tackling many problems throughout the course. Key areas to focus on include:

Solving linear and quadratic equations.

Manipulating algebraic expressions.

Understanding functions and their properties.

Solving simultaneous equations.

Mastering algebra will provide the foundation for more advanced topics like calculus and further mathematical modeling. Understanding how to manipulate algebraic expressions and solve equations efficiently is crucial for both exams and future mathematics courses.

2. Calculus

Calculus is a core part of AS Level Mathematics, and it can often be one of the most challenging topics for students. It focuses on the concepts of differentiation and integration, which are widely used in real-world applications like physics, economics, and biology. The key areas to focus on in calculus include:

Differentiation techniques (e.g., product rule, chain rule).

Understanding the meaning of derivatives (rate of change).

Integration techniques (e.g., basic integration rules, definite and indefinite integrals).

Applications of differentiation and integration, such as finding areas under curves and solving problems related to motion.

A strong grasp of calculus is not only vital for AS Level Mathematics but also for higher-level mathematics and other STEM subjects.

3. Coordinate Geometry

Coordinate geometry combines algebra and geometry, allowing students to analyze and solve geometric problems using algebraic methods. This topic is especially important in AS Level Mathematics because it links geometric shapes and algebraic equations. Key areas to focus on include:

Equation of a straight line, including the gradient and y-intercept.

Understanding the distance formula, midpoint formula, and the equation of a circle.

Finding the equation of a line given two points.

Understanding the properties of circles, tangents, and normals.

Mastering coordinate geometry will help you solve a wide range of problems and is a key skill in preparing for higher-level mathematics.

4. Trigonometry

Trigonometry is another essential topic in AS Level Mathematics, with applications in various fields, including physics and engineering. In AS Level, you’ll need to be familiar with the following concepts:

The basic trigonometric ratios: sine, cosine, and tangent.

Solving right-angled triangles using trigonometry.

The unit circle and its applications.

Trigonometric identities and equations.

Proficiency in trigonometry is crucial for solving problems involving angles, distances, and forces, and it plays a significant role in calculus and other advanced topics.

5. Statistics

Statistics is an important component of AS Level Mathematics, especially if you are interested in pursuing careers in data analysis, economics, or social sciences. Key statistical topics include:

Collecting and analyzing data (mean, median, mode, and range).

Understanding probability and its applications.

Sampling methods and types of data.

Working with probability distributions, including binomial and normal distributions.

A solid understanding of statistics will not only help you in your AS Level Mathematics exams but also prepare you for future courses that require statistical knowledge.

6. Vectors

Vectors are a key topic in AS Level Mathematics, especially when studying geometry and physics. This topic involves understanding the properties and applications of vectors in two and three dimensions. Key areas to focus on include:

Understanding vector notation and basic operations (addition, subtraction, scalar multiplication).

Dot product and its geometric interpretation.

The equation of a line and plane in vector form.

Applications of vectors in solving problems related to motion, forces, and geometry.

Vectors are essential for problem-solving in both mathematics and physics, and mastering this topic will set you up for success in more advanced studies.

7. Mathematical Proof

Mathematical proof is a fundamental part of AS Level Mathematics, where you learn to justify your reasoning and demonstrate that mathematical statements are true. Key areas to focus on include:

Proof by induction.

Direct proof and proof by contradiction.

Proving basic algebraic identities and geometric properties.

Being able to write clear and logical proofs is an important skill that will help you in exams and future mathematical studies.

Conclusion

Focusing on these key topics in AS Level Mathematics will give you a strong foundation to succeed in the course. Algebra, calculus, coordinate geometry, trigonometry, statistics, vectors, and mathematical proof are all crucial areas that require attention and practice.

By mastering these topics, you’ll not only perform well in your AS Level exams but also be prepared for higher education or future careers that involve mathematics. Make sure to allocate enough time for each topic, practice regularly, and seek help when necessary to ensure a solid understanding of the material.

With the right focus and dedication, you can excel in AS Level Mathematics and set yourself up for success in further studies or professional fields.

[mathsciencetuition]

What is Algebra & Its Comprehensive Journey through the Mathematical Marvel

Algebra is a fundamental branch of mathematics that uses symbols to represent and manipulate numbers and relationships. It has widespread applications across science, engineering, economics, and technology. The article emphasizes the importance of algebra and its role in developing analytical skills, offering a detailed exploration of its branches and formulas.

Branches of Algebra:

Elementary Algebra: Focuses on basic operations, solving linear equations, and foundational concepts.

Advanced Algebra: Explores quadratic equations, polynomials, and systems of equations, bridging elementary algebra and abstract topics.

Abstract Algebra: Deals with theoretical structures like groups, rings, and fields, central to pure mathematics.

Linear Algebra: Concentrates on vector spaces, matrices, and linear mappings, crucial for applications in physics, graphics, and data analysis.

Commutative Algebra: Studies commutative rings and their applications in geometry, coding theory, and number theory.

Key Algebraic Formulas:

Quadratic Formula: To solve quadratic equations.

Distance Formula: For finding the distance between two points in a plane.

Slope-Intercept Form: Equation of a line based on slope and y-intercept.

Examples:

The article demonstrates solving quadratic equations using the quadratic formula and applying linear algebra to solve systems of equations.

Conclusion:

At Miracle Learning Centre in Singapore, the focus is on fostering a deep appreciation for algebra through personalized maths tuition. The centre helps students build a solid foundation in algebra, enhancing problem-solving skills and preparing them for advanced mathematical challenges.

[edukotangp]

Must-Study Chapters for JEE: A Comprehensive Guide

Mechanics: The bedrock of physics, covering kinematics, laws of motion, work, energy, power, rotational motion, and gravitation.

Electrodynamics: A conceptually rich section encompassing electrostatics, current electricity, magnetism, and electromagnetic induction.

Modern Physics: Relatively easier with topics like atomic structure, nuclear physics, dual nature of matter, and semiconductors.

Optics: Crucial for engineering applications, covering ray and wave optics.

Thermodynamics and Kinetic Theory: Bridges physics and chemistry, covering laws of thermodynamics, Carnot engine, entropy, and heat transfer.

Chemistry

Physical Chemistry: Numerically oriented, focusing on mole concept, thermodynamics, kinetics, electrochemistry, ionic equilibrium, and solutions.

Inorganic Chemistry: Factual and memory-based, covering periodic table, chemical bonding, coordination compounds, p-block, d-block, and f-block elements.

Organic Chemistry: Concept-heavy, emphasizing general organic chemistry, hydrocarbons, alcohols, phenols, ethers, carbonyl compounds, and amines.

Mathematics

Calculus: The foundation for higher mathematics, covering limits, continuity, differentiability, applications of derivatives, definite and indefinite integrals, and differential equations.

Algebra: Core of JEE math, encompassing quadratic equations, sequences and series, matrices and determinants, complex numbers, and probability.

Coordinate Geometry: Often considered easy, covering straight lines, circles, parabolas, ellipses, and hyperbolas.

Trigonometry: Versatile and applicable across topics, covering trigonometric ratios, identities, heights and distances, and inverse functions.

Vectors and 3D Geometry: Can be challenging but highly scoring with practice, covering vector algebra and three-dimensional geometry.

Tips for Effective Preparation

Understand Concepts: Don't just memorize formulas; grasp the underlying principles.

Practice Regularly: Solve previous year papers and mock tests consistently.

Focus on Weak Areas: Identify and strengthen your weak points.

Revise Consistently: Regular revision is crucial for retention.

Stay Updated: Keep track of exam pattern changes and syllabus modifications.

[xenopoem]

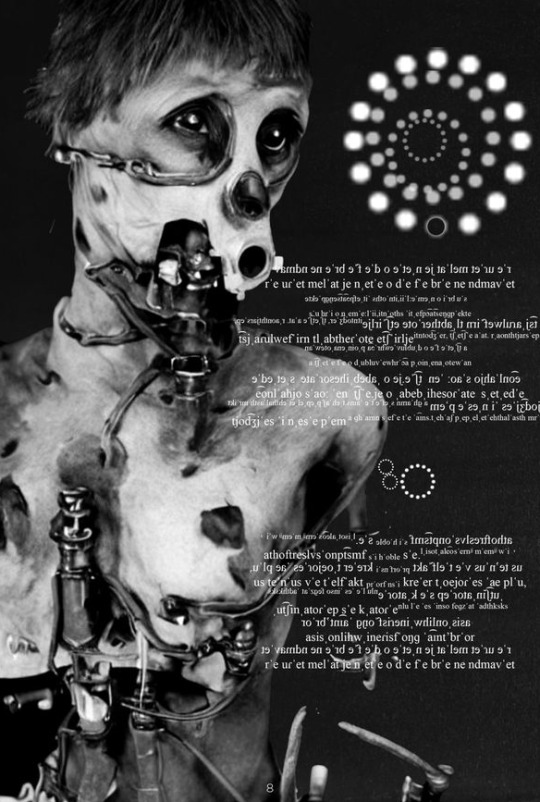
Emergence of a Super-Hybrid Technical Language

"Libretto Lunaversitol: Notes Towards a Glottogenetic Process" by Andrew C. Wenaus, accompanied by biomorphic illustrations by Kenji Siratori, represents an innovative fusion of patamathematical formulae, the International Phonetic Alphabet (IPA), and abstract artistic expression. This work functions not just as a literary piece, but as a speculative, glottogenetic process—a birth of a new language, both visual and auditory.

The concept of patamathematics—a term that playfully combines "pataphysics" (the science of imaginary solutions) and mathematics—infuses this work with a unique structural integrity. Patamathematics serves as the foundation for generating new linguistic forms, akin to how mathematical functions generate graphs. Just as a function f(x) maps inputs to outputs, "Libretto Lunaversitol" maps the abstract and the tangible to create a multifaceted language.

The process of glottogenesis in Wenaus’s work can be understood through the lens of algebraic structures. If we consider the components of the book—text, IPA symbols, and visual elements—as sets, the interactions between them can be modeled using relations and functions. For example, let:

T be the set of textual elements,

P be the set of IPA symbols,

V be the set of visual elements.

We can define a relation R⊆T×P×V where each tuple (t,p,v)∈R represents the interaction between a textual element, its phonetic representation, and a corresponding visual element. The richness of the work lies in the non-linear, non-sequential mappings that challenge conventional linguistic structures.

"Libretto Lunaversitol" speculates on the emergence of a super-hybrid technical language that self-organizes outside human comprehension. This can be likened to emergent phenomena in complex systems, where local interactions give rise to global patterns. In mathematical terms, this is often described using cellular automata or neural networks.

Consider a cellular automaton where each cell represents a linguistic unit (a word, symbol, or sound). The state of each cell evolves according to a set of rules based on the states of its neighbors. This mirrors how the book’s elements interact to create new meanings and forms. The emergent language is a higher-order structure, an attractor in the state space of all possible configurations.

The analogy to big data and autonomous informational processes is particularly pertinent. In machine learning, optimization algorithms such as gradient descent iteratively adjust parameters to minimize a loss function. Similarly, "Libretto Lunaversitol" can be viewed as an optimization process where the "loss function" is the ineffability of human language and experience. The iterative refinement through textual, phonetic, and visual interplay seeks to minimize this ineffability, approaching a new mode of expression.

Wenaus’s work stands against purity and essentialism, embracing hybridity and multiplicity. Mathematically, this opposition can be framed in terms of fuzzy logic and set theory. Traditional set theory is binary—an element either belongs to a set or it does not. Fuzzy set theory, however, allows for degrees of membership. In "Libretto Lunaversitol," elements are not confined to a single identity but exist in a continuum of states.

For instance, if μT(x) denotes the membership function of element xxx in the set of textual elements T, then 0≤μT(x)≤1. This fluidity allows for a richer, more inclusive linguistic structure that can better capture the complexities of human experience and thought.

The biomorphic figures by Kenji Siratori and the musical score by Wenaus and Christina Marie Willatt add further layers of complexity. These elements can be modeled as transformations in a multi-dimensional space. Let Rn represent the space of all possible sensory inputs. The visual and auditory components can be seen as vectors in this space, transforming the perception of the textual and phonetic elements.

"Libretto Lunaversitol: Notes Towards a Glottogenetic Process" is a pioneering work that transcends traditional boundaries between language, art, and mathematics. By leveraging the principles of patamathematics, emergent systems, and fuzzy logic, Wenaus and Siratori create a super-hybrid technical language that challenges our understanding of communication and expression.