#we transPOSE the matrix

[highpriestmckickass]

https://en.m.wikipedia.org/wiki/Initial-stress-derived_noun !

tons more examples there

Actually here’s some english shit that pisses me off. When you very slightly change how you pronounce a vowel to make a noun into a verb. This is a duplicate, which happens when you duplicate one item to make two or more.

[rnomics]

Biomolecules, Vol. 14, Pages 358: Exploring SVA Insertion Polymorphisms in Shaping Differential Gene Expressions in the Central Nervous System

Transposable elements (TEs) are repetitive elements which make up around 45% of the human genome. A class of TEs, known as SINE-VNTR-Alu (SVA), demonstrate the capacity to mobilise throughout the genome, resulting in SVA polymorphisms for their presence or absence within the population. Although studies have previously highlighted the involvement of TEs within neurodegenerative diseases, such as Parkinson’s disease and amyotrophic lateral sclerosis (ALS), the exact mechanism has yet to be identified. In this study, we used whole-genome sequencing and #RNA sequencing data of ALS patients and healthy controls from the New York Genome Centre ALS Consortium to elucidate the influence of reference SVA elements on gene expressions genome-wide within central nervous system (CNS) tissues. To investigate this, we applied a matrix expression quantitative trait loci analysis and demonstrate that reference SVA insertion polymorphisms can significantly modulate the expression of numerous genes, preferentially in the trans position and in a tissue-specific manner. We also highlight that SVAs significantly regulate mitochondrial genes as well as genes within the HLA and MAPT loci, previously associated within neurodegenerative diseases. In conclusion, this study continues to bring to light the effects of polymorphic SVAs on gene regulation and further highlights the importance of TEs within disease pathology. https://www.mdpi.com/2218-273X/14/3/358?utm_source=dlvr.it&utm_medium=tumblr

[erikabsworld]

Unraveling the Complexity: Mastering Matrix Algebra for Academic Success

Mastering matrix algebra is undoubtedly a challenging task, even for the brightest minds pursuing advanced degrees. As an expert in the field, I understand the intricacies and the often daunting nature of the subject. Today, we delve into a complex matrix algebra topic that frequently leaves students scratching their heads – the Generalized Inverse.

Demystifying the Generalized Inverse in Matrix Algebra

The Generalized Inverse, also known as the Moore-Penrose Inverse, is a fundamental concept with broad applications in various fields. It provides a solution to the problem of finding an approximate inverse for non-square matrices. Let's explore this intricate concept through a sample question:

Sample Question: Consider a matrix A of size m × n, where m ≠ n. Determine the Generalized Inverse of A, denoted as A⁺.

Solution: Finding the Generalized Inverse involves a meticulous process, and here is a step-by-step guide to help you navigate through it.

Transpose of A (Aᵀ): First, transpose the matrix A to obtain Aᵀ. This involves swapping the rows and columns.

Product of A and Aᵀ (AAᵀ): Multiply the original matrix A by its transpose Aᵀ. The resulting matrix, denoted as AAᵀ, is a square matrix.

Inverse of AAᵀ (AAᵀ)⁻¹: Find the inverse of the product matrix AAᵀ. This step ensures that the inverse exists.

Product of Aᵀ and (AAᵀ)⁻¹ (A⁺): Multiply the transpose of A by the inverse of AAᵀ. The resulting matrix is the Generalized Inverse A⁺.

This detailed process is essential for obtaining the Generalized Inverse, which plays a crucial role in solving systems of linear equations when dealing with non-square matrices.

Matrix Algebra Assignment Writing Help

Navigating through intricate topics like the Generalized Inverse requires a profound understanding of matrix algebra. As experts in the field, we at matlabassignmentexperts.com recognize the challenges students face and offer comprehensive Matrix Algebra Assignment Writing Help.

Our services encompass:

In-Depth Analysis: We provide detailed explanations for complex matrix algebra topics, ensuring clarity and comprehension.

Step-by-Step Solutions: Receive meticulously crafted solutions, breaking down each step to enhance your understanding of the subject.

Timely Assistance: Our team of experts is dedicated to delivering timely assistance, ensuring you meet your assignment deadlines without compromise.

Customized Support: Tailored to your specific needs, our assistance is designed to empower you with the knowledge and skills required for academic success.

Mastering matrix algebra is no easy feat, but with our expert assistance, you can confidently tackle challenging assignments and excel in your academic journey. Don't hesitate to reach out for Matrix Algebra Assignment Writing Help – we're here to guide you towards excellence.

[sunless-not-sinless]

spectral partitioning

i need to do a presentation on spectral partitioning for uni so here we go! an explanation on this graph partitioning algorithm here so i dont forget shit (i will not be looking at random walks)

under the cut theres gonna be maths. a lot of it so if u dont want that then dont look there. and theres no LaTeX or mathjax here so its ugly.

also i assume you know what graphs and eigen-shit are

i will assume our graph is a simple undirected graph.

the core idea of spectral partitioning is minimising the cut size - the sum of weights of the edges between two communities.

so if we have a graph that looks like this

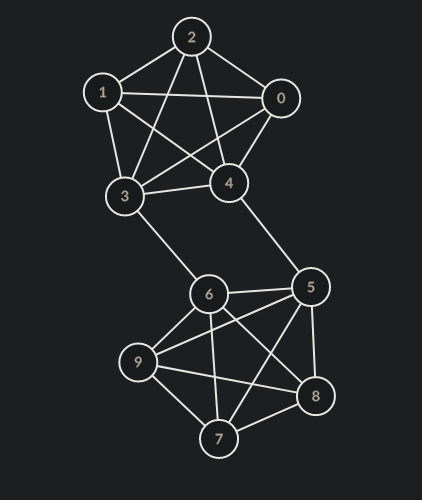
(made on https://csacademy.com/app/graph_editor/)

and we try to cut it into 2 groups, (by inspection) the minimum number of edges we have to cut through is 2, between nodes 3-6 and 4-5. so the minimum cut size is 2. and if we cut through those nodes we get 2 communities.

ill let you convince yourself that minimising the cut will lead to communities that arent very related to each other.

but how do we find this minimum cut? if we try to brute force it then you first separate nodes into one of 2 groups, then sum the weights of edges between nodes in these 2 groups. this is slow - O(2^n) where n is number of nodes in the graph - and it cant be improved (its an np-hard problem).

so instead of optimising that mess we will try to approximate it. sure our approximations might not find the actual minimum cut size but itll be good enough.

now to try to approximate this we need to find a nicer way of writing the cut size of some partition.

let A be the set of nodes in one group of the partition, and Ac its complement (the other group of the partition)

also let A=(w_ij) be a matrix where w_ij is the weight of the edge between nodes i and j (this is called the adjacency matrix, hence the A). and D be the diagonal matrix of "degrees" (actually sum of weights of all adjacent edges, but lets just call it the degree) of nodes.

finally let x be the indicator vector where x_i = 1 if i is in A, else -1. and 1 be the vector of just 1s if i use 1 where you would expect a vector (polymorphism? in my maths? more likely than you think)

and the transpose will be denoted ^T as usual

now to get the cut size, its the sum of edges between A and Ac. so thats ((1+x)/2)^T A ((1-x)/2)

you can probably see the halves are annoying, so lets find 4 * the cut size. so thats (1+x)^T A (1-x)

but this +x -x is a bit weird. it would be better if they were the same sign. so how do we do that?

the sum of weights of edges between the parts of the partition is the same as the all the sum of degrees of nodes minus the sum of weights of nodes within the same group. so we can rewrite this as (1+x)^T D (1+x) - (1+x)^T A (1+x) = (1+x)^T (D-A) (1+x)

now let L = D-A. this is called the laplacian of the graph and it has a few nice properties. first the row/column sums are 0 (you add the "degree" then take away all the weights). second its quadratic form v^T L v = ½ Σ w_ij (v_i - v_j)². importantly this means its positive semi-definite. third its symmetric. importantly this means that it has an orthonormal eigenbasis.[1]

now because its row/column sums are 0 you can write 4 * cut size as (1+x)^T L (1+x) = x^T L x. and so this is what we want to minimise.

now like i said minimising this is np-hard, but we can ignore the fact that x_i = ±1, and instead consider it on all vectors s, then just look at the sign of the entry.

just two issues with this. one: what if theres a 0? well you can lob it in either group of the partition. two: (ks)^T L (ks) = k² x^T L x. so any minimum we find, we can just halve each value of the vector or smth and get a smaller min. for this we can simply consider vectors s.t. ||s||=1.

now we can write s in orthonormal eigenbase to get that s^T L s is a weighted average of the eigenvectors of L. so the minimisation of this is the smallest eigenvalue of L. but because the row/column sums are 0, this eig val is 0 with eig vec being the vector of ones. if you think of this in terms of graphs this makes sense - to minimise the cut you put everything in one bucket and nothing in the other and so theres no edges to cut!

now lets assume a good partition will cut it roughly in half. we can think of this as the number of nodes in one half of the partition. in other words 1^T x ≈ 0. so lets add the constraint that 1^T s = 0.

this means s is orthogonal to 1 - our smallest eigenvector. so in our weighted average, we cannot have any weight for out smallest eigenvalue, and so our second smallest eigenvalue is the smallest and we can approximate the minimum cut size by looking at the signs of the second smallest eigenvector!

and that is the idea behind spectral partitioning! now you can normalise the cut in some way. e.g.

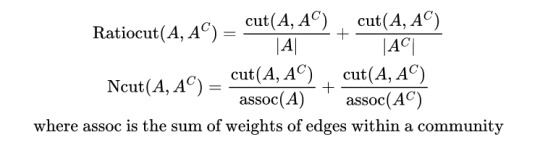
with their associated minimisations being shown below

then you get good algs for separating images into blocks of focus

(sorry for no IDs for these)

and there we go! thats spectral partitioning!

[1] you can use gram schmidt to get an orthogonal basis of an eigen space, so all we need to show is that eig vecs with diff eig vals are orthogonal.

therefore any eig basis of symm (or hermitian) matrix is orthogonal.

the fact that an eigenbase even bloody exists is beyond this tumblr post, but is called the spectral theorem - and is where the name spectral partitioning comes from

[whistlesthestarlightcalliope]

my second attempt

Counting the corner 1s doesn't help. I'm not saying that your answer is incorrect but the proof doesn't sound right because you can get an odd number of corner 1s, but not without edges or centers. 0.5C+0.5F-H makes the following:

0 0 0 0 -1 0.5 0 0.5 1

but yeah I think we can solve this by making a 9x8 (8x9? I can never remember) matrix and looking at the vectors that are not in the (had to look this word up) span of the matrix. We can do this by taking the null space of the transpose apparently. I'll take mathStackExchange's word for it

10010010 10001000 10000101 01010000 01001011 01000100 00110001 00101000 00100110

by taking the row-echelon form we can see that matrix F is redundant, and removing it will leave us with a linearly independent set of matrices:

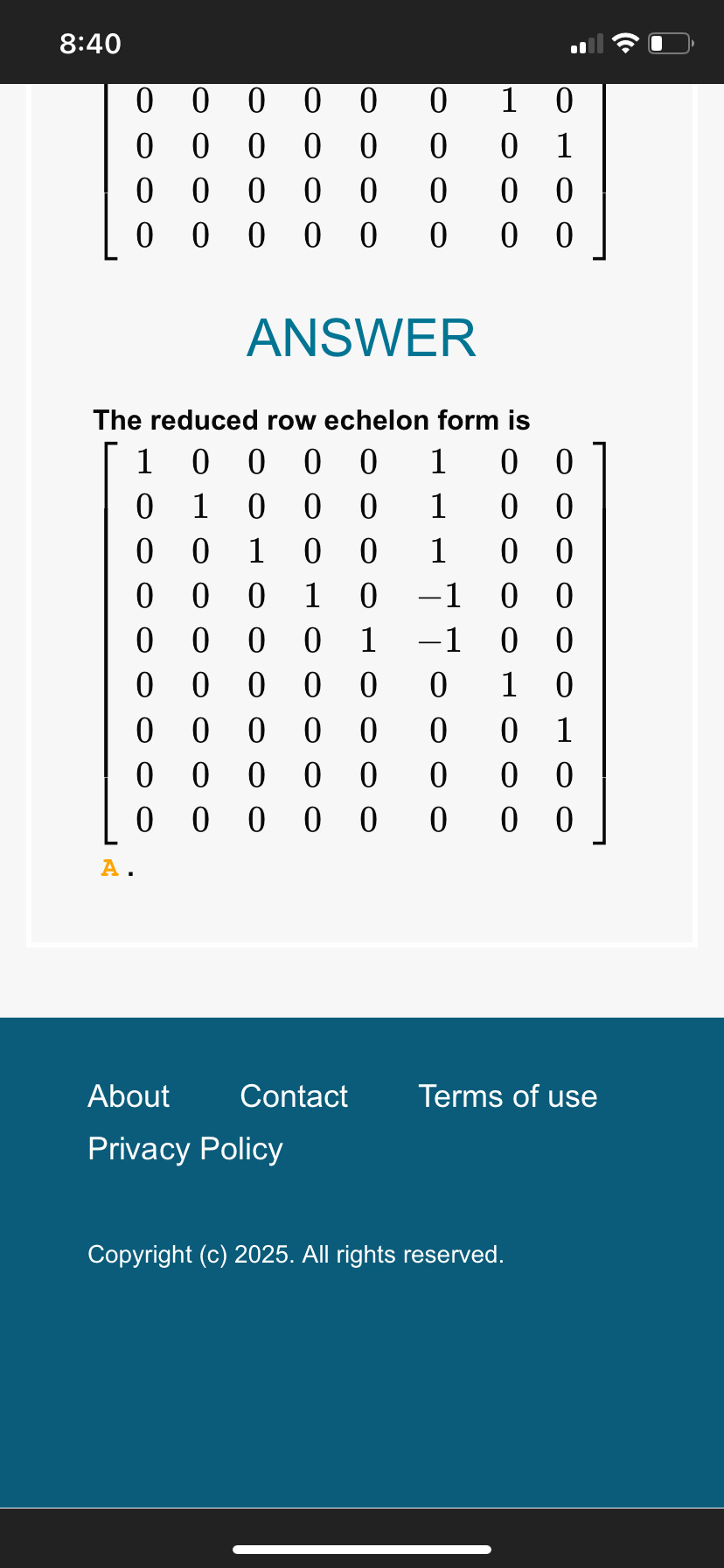
That'll be important later. Anywho, let's get the null space of the transpose:

This tells us that the following matrices are not in the span:

0 -1 1 -1 0 1 1 0 -1 2 0 -2 -1 1 0 -1 0 1

let's tack these on to the earlier matrix and remove the F column:

1001010 0 -1 1000100 -1 0 1000001 1 1 0101000 1 2 0100111 0 0 0100000 -1 -2 0011001 -1 -1 0010100 1 0 0010010 0 1

now we can apply this matrix to any vector U s.t. U•[0;0;0;0;0;0;0;1;1] ≠ 0 to get a vector not in the vector space of the above.

We can also apply the inverse of this matrix to test if a given matrix is in S by taking the dot product of the result with [0;0;0;0;0;0;0;1;1] and seeing if the result is 0.

inverse:

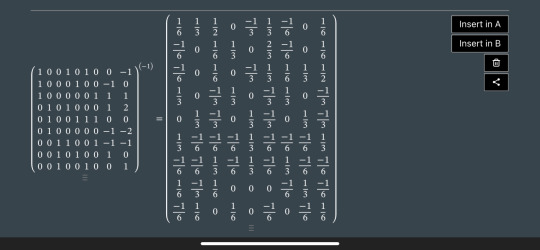
Checking OP's answer:

Yeah those bottom two numbers are not 0 so OP's answer is correct, even if the reasoning is off

Let V be the vector space of 3x3 matrices over the field of order 2. Let S be the subspace generated by the following matrices:

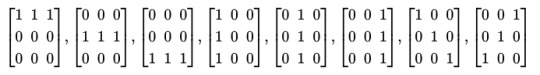
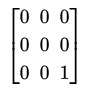
Find an element of V that is not in S.

Solution:

All these matrices have 2 corner 1s, so linear combinations will always have an even number of corner 1s. Hence a solution is

[artsayz-op]

Survival

C'est mon premier livre

Survival : l'héritier du chaos !

on suit les aventures du jeune Joshua Reuss qui pour se venger de son licenciement abusif mettra les pied dans une affaire très lourde menaçant toute vie sur terre. C'est histoire entre Matrix et Star Wars mêlant science-fiction, fantastique et horreur était destiné pour être un film que j'ai transposer en roman. Si vous voulez la lire : www.kiffelire/Survival: l'héritier du chaos.com

This is my first book

Survival : the heir to chaos

we follow the adventures of young Joshua Reiss who in revenge for his wrongful dismissal, will set foot in a very heavy affair threatening all life on earth. This is a story between Matrix ans Star War mixing science fiction, fantasy and horror was intended to be a film that i changed into a novel, if you want to read it : www.kiffelire/Survival: l'héritier du chaos.com

[starryeyes2000]

The Road Back: Chapter 3

Is There A Way Back?

Chapter 2 | Chapter 4

Beginning of the Story

Status: In Progress

Pairings: Christopher Pike x Fem!OC

Rating: Mature

Word Length: 1.7k

Summary: Once the physical injuries from Talos healed, Chris moved on. Then he met someone special but each time the moment was right to become lovers he pulled back, unwilling to trust himself. Unsure if the attraction and his feelings were real. Then he realized or rather admitted the Talos incident was more than kidnapping, imprisonment, and mind-control. It was a violation of the deepest and most intimate kind. And that perhaps there was no way back.

ooooo

Intently arranging symbols for notes on a three-dimension diagram of music staffs spanning half the room, Aalin didn’t look up when the door to the lab opened and closed. “I didn’t think you were coming back this evening, but Spock, this book isn’t a Rosetta stone, I think it’s an epic poem, like The Odyssey. It has rhythm and cadence.” Not waiting for an answer, she continued, clearly excited. “There are patterns we missed. They are not always repeated verbatim, but rather reoccur in various ways, like a melody that is harmonized differently, transposed, embellished, moved to a different key, played on a different instrument. With a complexity worthy of Mozart. I think I have isolated three unique refrains so far and I am plotting their related constructs. From those examples I can start programming a translation matrix …” She looked up for a moment. “Oh Chris … Captain,” Aalin corrected when she noticed Pike wore his unreadable commander’s expression, “Computer pause music.” She smiled, “Hey.”

He looks surprised … no uncomfortable … to see me here, she thought. But I must be imagining it. “Number One assigned me to help Spock with the records from the second planet in the NV-0809 system.”

“The universal translator can’t handle it?” Pike asked.

She answered, “Its translations are less accurate, or in this case nonexistent, without the corresponding neurological data it monitors when someone is speaking. The universal translator works best with a written language when it has a programmed matrix to draw from. Or at least start from.”

He walked around the room examining the diagrams. “It looks like you have turned the book into a song.”

“The song was already there; you could say I am translating the book into standard western musical notation.” She noted the dark circles under his eyes which lacked their usual sparkle. His posture relaxed almost imperceptibly, shoulders and back dropping a fraction of an inch. Both subtle Chris tells for weariness. “None of which is important after a long night and, I assume, a long day.”

“The computer was playing Beethoven?” He asked to divert her focus from him, attempting to engage in a familiar conversation. Our daily chats are soothing, he thought, for that rare hour I am just Chris.

“Bach.”

“That was a violin?”

“Cello,” she replied.

“Played by Perlman?”

“Yo-Yo Ma. A 20th century master.”

“So, I got it all wrong.”

She smiled again, “It’s all the in same ballpark, you are improving.”

They spoke simultaneously. She said, “I’m glad to see you,” He started, “Mann said Spock was here …”

Catching up with Chris’ reason for visiting the lab, Aalin hid her disappointment. “Spock left an hour ago muttering something about forgetting the hats, but I most likely misunderstood. Do you want me to page him?”

“No, it’s not urgent,” Pike answered. The awkward feeling in the room increased as the silence lengthened.

“I’m sorry about last night,” he said in a quiet voice.

“You mean for keeping the ship from exploding? I am good with that,” Aalin teased trying to lighten his mood. When that failed, she switched to offering comfort. “Chris, I understand. The ship needs its Captain, often unexpectedly and at odd hours.”

“And I am sorry about the rumors. I wish … it’s unfair. They should be talking about me not you.”

She walked over to him and rested a hand on his arm. He quickly and deftly moved to the side ending the contact. This is odd behavior, uncomfortable with himself and with me. She longed to ask why he was avoiding her but everything about his stance, his movement in the room, his body language shouted he felt confined, maybe even caged.

“You’re their respected Captain,” Aalin didn’t include beloved and therefore increase his discomfort, “and I am relatively new and unknown. It’s only natural the crew will … exchange information about me. Regardless, even if one or two folks have speculated about us today, it’s old news by now. And I am certain something truly interesting has superseded it.”

A look to the side, a slight eye roll. Another of his tells, this one for skepticism. He then frowned, but his was affect sad rather than irritated. “How do you separate it? The actual from the rumor? The truth from the embellishment? The illusion from reality?

Unsure how to respond, she focused on one concrete point, “As long as we know the truth why does another’s exaggeration matter?”

“It matters. Embellishment, the illusion it creates, or any delusion for that matter destroys our touchstones to reality. Then we lose ourselves. And perhaps there is no way back.”

“I want to believe there is always a way back,” Aalin said softly, hoping the words provided reassurance.

His voice dropped to a whisper. “As do I … but I doubt it.” Both were hesitant to break the ensuing silence. At last Pike straightened his shoulders and said in his normal tone of voice, “I’m late for a briefing.” He smiled wanting to alleviate the concern he saw in her eyes. “And tired, you are right, it has been a long day and then some. We’ll talk tomorrow?”

“Of course.” As he left, she called after him. “Chris is there anything I can do for you?”

Pike stopped. His every instinct shouted, tell her. “No,” he said firmly as the doors closed.

ooooo

Team Christopher Headquarters aka Phil’s Boyce’s Quarters

Phil pulled Una aside and asked softly, “Really, Team Christopher? I came up with that. I expected something cleverer from you.”

Narrowing her eyes Una replied, “I’ve been a little busy today dealing with the aftermath of last night’s problems and covertly gathering information about our commander’s love life. And ‘Team Get the Captain Laid’ doesn’t fit on the hat.”

“Well that’s not very accurate, is it? We’re not trying to get Chris laid a few times, we are going to arrange a lifetime sure thing,” Phil scolded.

Spock, whose sensitive hearing was impossible to escape, asked as he put on his baseball cap. “Get the Captain laid? Is he unable to recline on his own? What sure thing is he lacking?”

Una rolled her eyes thinking, what could possibly go wrong?

Phil shook his head and chuckled at both Spock’s comment and the sight of their Vulcan science officer, standing erect and wearing a baseball cap, his elfin ears prominently displayed on the hat’s sides. “Let’s get started. Una, you arranged to keep Chris off the command deck and away from his quarters?”

She nodded. “A security briefing. Isak will keep him busy.”

“Excellent. Our mission, and I have already accepted it for you, is to move Chris along in his relationship with Aalin. And by move, I mean they will live together happily ever after. Failure is not an option.”

Matt raised his hand. “How many trite movie, television and fairy tale lines can we expect tonight Phil?”

“I’m just getting warmed up.”

“That is what I was afraid of,” Matt countered in a sarcastic tone.

Spock raised his hand.

“Yes?” Phil asked.

“Why did Lieutenant Zaliimaatfra raise his hand?”

“To request permission to speak. But mostly to annoy me,” Phil answered patiently.

Spock’s eyebrows rose and he steepled his long fingers. After a moment’s consideration he said, “Curious. Requesting permission to speak via an orderly and clearly delineated yet silent physical signal is an excellent system. I cannot offer an opinion as to whether it is also an excellent way to annoy you Doctor. It would be logical to adopt this system for bridge interactions and therefore I will recommend it to the Captain.”

“Please make sure I am there when you do,” Phil said trying not to laugh and looking forward to Chris’ reaction.

“A wise suggestion Doctor, as you are well-versed in the system’s advantages and can answer the Captain’s questions.”

“I think we have drifted off topic,” Rene Louvier pointed out.

“Indeed. Under the best of circumstances, Christopher Pike can be slower than a meandering snail when it comes to pursuing a serious romantic relationship, one that includes the benefits of …” Phil paused and glanced at the Vulcan. “One that includes physical intimacy. These are not the best of circumstances. Talos IV haunts him.”

The group sobered. An Admiral had remarked during the debrief after the Talos mission that it was a relatively benign experience. They had escaped. Their memories were intact. There was no lasting physical damage. Una would have throttled the superior officer if Pike had not intervened by stepping between them. Words were inadequate to describe the magnitude of the violations they suffered. Most of which were inflicted on their leader.

Una spent the day weighing second thoughts. “Is this a line … we shouldn’t cross” she asked sounding unusually hesitant. Her brow creased with worry.

“Commander, you speak as if our intervention in the situation is ill-advised or perhaps even wrong. It is illogical and unnecessary for Captain Pike to remain on his own. When was this ludicrous human notion started that a commander should be bonded only to his ship and crew? A mate enriches one’s strengths and balances one’s flaws. And only a mate can heal the deep scars left by the Talosians’ actions.”

The rest were silent, stunned by the Vulcan’s frank response. They thought he might consider their efforts an intrusion into their commander’s privacy.

Spock continued, “On Vulcan your mate is chosen by family elders. A decision of such importance cannot rest solely in the hands of those who will be bonded as they may be swayed by illogic and impulse. Nor should the choice of a life partner be subject to the capricious and, at times, cruel whims of fate. When there is no family to take the responsibility for the selection and joining, friends and peers are expected to step in. As the Captain’s colleagues and on-board family, it is our duty to see to his well-being in this matter. Especially as he, in this pivotal moment, cannot.”

Spock’s statement decided the group. They spent the rest of the evening making plans and handing out assignments.

“And I will continue dispensing invaluable relationship advice to him,” Phil announced concluding the meeting.

Story Masterlist | Series Masterlist | Author Masterlist

Taglist: @ocfairygodmother

[debopamghosh]

Understanding Rotation and Reflection transformations in Real, 3 dimensional space

R^3(R) denotes the vector space of all real 3- tuples, over the field of real numbers:

R^3(R) = { (x, y, z) (3 by 1) | x, y, z are real numbers}

u. v denotes the scalar product between vectors u and v belonging to R^3(R)

g*h denotes scalar multiplication between scalars g and h

u = (u1, u2, u3), v = (v1, v2, v3) , then u. v = u1*v1 + u2*v2 + u3*v3

d(i, j) denotes the kronecker delta function of the input indices 'i' and 'j'

GT denotes the transpose of the matrix G

inv(G) denotes the inverse of the matrix G

A×B denotes the matrix product between matrices A and B

n = ( n1, n2, n3) , v = ( v1, v2, v3) , w=( w1, w2, w3) , where n, v, w belong to R^3(R)

such that n. n = v. v = w. w = 1

n. v = n. w = v. w = 0 and we know scalar product is commutative

{n, v, w} is therefore, an Orthonormal basis for R^3(R)

span (n) = { x ( 3 by 1) | x = c*n, c is real}

dimension of span(n) = 1

H(n) = { z( 3 by 1) | z = a*v + b*w, where a, b are real}

dimension of H(n) = 2, both span(n) and H(n) are subspaces of R^3(R)

span (n, v, w) = R^3(R)

We define the matrix Q( 3 by 3) = [ n v w ]

Q = [ n1 v1 w1 ; n2 v2 w2 ; n3 v3 w3 ] , the blocks seperated by ' ; ' denote the respective rows, the first row correspond to the block on the leftmost end, and so on.

clearly, Q is an Orthogonal matrix : QT = inv(Q)

Rotation transformation:

R( n, p) denotes the Rotation transformation ( a linear transformation) , corresponding to rotation by angle 'p', anticlockwise, about the rotation axis denoted by vector n( 3 by 1) belonging to R^3(R)

We have:

R(n, p) {n} = n, that is, the Rotation R(n, p) leaves vector 'n' invariant.

R(n, p) {v} = (cos p) *v + (sin p) *w

R(n, p) {w} = (- sin p) * v + (cos p) *w

Therefore,

R(n, p) {Q( 3 by 3) } = Q(3 by 3) × D(3 by 3)

Where D ( 3 by 3) = [ 1 0 0 ; 0 (cos p) (-sin p) ; 0 (sin p) (cos p) ]

The matrix D is the Matrix representation of the linear transformation R(n, p) with respect to the Orthonormal basis { n, v, w} of R^3(R)

The standard basis of R^3(R) : { e1, e2, e3 }, where e1 (3 by 1) = ( 1 0 0 )

e2 ( 3 by 1) = ( 0 1 0 )

e3( 3 by 1) = ( 0 0 1 )

The Matrix Representation of R(n, p) with respect to the standard basis in R^3(R) is denotes by [R(n, p) ] (3 by 3) = Q(3 by 3) × D( 3 by 3) × QT( 3 by 3) ... (eqn. 1)

we can observe that:

Trace([R(n, p)]) = 1 + (2*(cos p))

Determinant of [R(n, p)] = 1

Reflection transformation:

S(n) denotes the reflection transformation ( a linear transformation) corresponding to reflection in the plane perpendicular to the vector 'n' belonging to R^3(R) , which is the subspace H(n) of R^3(R)

We have:

S(n) {n} = (-1) *n

S(n) {z} = z, for all vector 'z' belonging to the subspace H(n)

Therefore,

S(n) {Q(3 by 3) } = Q( 3 by 3) × F(3 by 3)

where F ( 3 by 3) = [ -1 0 0 ; 0 1 0 ; 0 0 1 ]

The matrix 'F' denotes the Matrix representation of the Reflection operation S(n) with respect to the basis {n, v, w} of R^3(R)

The Matrix representation of the transformation S(n) with respect to the standard basis of R^3(R) , be denoted as [S(n) ]

[S(n) ] ( 3 by 3) = Q( 3 by 3) × F( 3 by 3) × QT( 3 by 3) .... (eqn.2)

We can observe that:

Trace([S(n) ]) = 1

Determinant of [S(n) ] = -1

Moral of the story

Orthogonal matrices defined on R^3(R) induce transformations that preserves the Euclidean norm ( vector 2-norm) of the vectors. They interrelate Orthonormal bases in R^3(R).

( Debopam Ghosh)

[writingithink]

Tangled Timelines Chapter 3 Rated: T Chapter Word Count: 5,010 Chapter Summary: The Doctor and Rose try to track down some ghosts. Notes: Hey look! It's an update!! Hopefully they'll be happening more regularly now. I'm semi doing NaNoWriMo, and by that I mean that I'm attempting to write 50,000 words this month spread across any project (including this one). I'm starting to find my groove with this fic, so *fingers crossed*

As always, many hugs and thanks for @hey-there-juliet , my lovely beta. && all mistakes are mine.

READ IT ON AO3 [copy/paste link]

https://archiveofourown.org/works/26686090/chapters/67268401

<-- Ch2

Ch 4 -->

As soon as he entered his ship, the Doctor collapsed onto the jumpseat and stared blankly at the time rotor for a few moments. And then he glared at it.

“I somehow manage to happen upon the exact coordinates for the beginning of an invasion, and for some reason you’ve put me smack dab in the middle of it?!”

The answering hum was … frustrated.

He furrowed his brows, frowning. It would be exceedingly bad, incredibly bad, astonishingly bad bad bad if something else was influencing the TARDIS. The Doctor sprang to his feet and immediately sonicked open the grating, taking a moment to place a temporary barrier around his panic before he could worry Rose.

Back at the flat, she was having tea with her mother. She’d only just managed to get Jackie to stop complaining about his apparent need to ‘make everything about aliens’, and they were now talking about the wedding. Apparently she’d found a baker who said they’d make up cake samples that all somehow incorporated bananas. Best news he’d heard (well, technically) all day, and he couldn’t properly appreciate the sentiment when he desperately needed to check his ship and parse out exactly what he was going to do about these ‘ghosts’.

First things first, he needed to make sure that the TARDIS was physically fine. That she was healthy. And actually, it wasn’t so bad. There were some minor repairs he should take care of before they next left Earth, but nothing he couldn’t leave until after they’d saved the planet. The Doctor pulled himself out from under the console and bounced over to the navigational matrix, pulling a screen with him as he went.

His mouth dropped as he looked at the recording of their last flight path. A time track seemed to just- just pop into existence, pushing them months away. His ship had immediately landed due to the unexpected error. It literally looked like a glitch in the Vortex - but there were no such thing as glitches in the Time Vortex. A whole dimension doesn’t glitch - not without some outside force acting on it.

And any outside force meddling with time was even more dangerous than whatever these ‘ghosts’ were.

One bloody thing at a time, though.

The Doctor pushed himself away from the console and began pacing.

Ghosts ghosts ghosts ghosts ghosts.

Not really ghosts. Getting stronger from the psychic energy of the entire human race. Incredibly unpleasant when one walks through you - really do feel dead. Worse than dead. Likely nothing good, and all over the world.

But they appear in shifts. There’s shifts.

So someone had to be in charge of that. Probably multiple someones. But still, there would be a central location connected to them, giving them whatever help they need to press themselves onto the Earth from wherever they really are. To do that, all around the world, they would have to have an incredibly strong signal.

An incredibly strong, traceable signal.

“Alright then!”

Headfirst into danger was just what it was going to have to be.

The Doctor sonicked open a different panel and began rummaging around for the equipment he’d need. It wasn’t long before he heard the TARDIS' door open.

“According to the paper,” his wife announced, “they’ve elected a ghost as MP for Leeds. Now tell me about this plan you’re tryin’ so hard to keep secret.”

He popped out of the grating with a backpack full of equipment.

“Who you gonna call?” he joked.

“Ghostbusters!” Rose laughed, more amused by the voice he was using than his shockingly similar looking technology.

“I ain’t afraid of no ghosts,” the Doctor finished with a little jig before dashing out of the TARDIS.

“My mum’s on her way down,” she informed him as he looked around the playground for the best area to set up the cones. Actually, should do nicely right where they were.

“Oh?” He turned on his heel and went back into their ship, pleased that she’d seen fit to set out the rest of the equipment they would need. “Let’s get these outside.”

“Doctor,” his bondmate huffed, even as she took a cone. I don’t think we should tell her yet. About the lifespan thing. Not until after we’ve gotten rid of the ghosts. Like, way after. Next trip back.

That’s fine, he agreed as he sat down his roll of wire and cone and began plugging everything in.

“We’ll still have to stay for awhile, though. Because we said we would.”

The Doctor paused what he was doing, dramatically raising his eyes skyward. It was quite a nice day, really. You’d think, with London having nice weather for once, that he’d be able to enjoy it. He opened his mouth, planning to vocalize his many complaints, but as soon as he turned back towards Rose, he saw Jackie walking up.

After the ghosts, yes. Sometime during this trip, though, please . 

He wasn’t ashamed to beg. Well … a little ashamed.

“Why’d you park all the way over here?” Jackie asked as he began plugging the wires into the cone Rose had placed.

“Got tired of the alley. Bit dingy,” he quipped. It was a lie, but better than telling his mother-in-law that not only had the flight gone wrong time-wise, but also slightly by location.

His wife shot him a worried look as she caught the thought.

Later, he promised, rushing back into the TARDIS for the final cone. He would worry about all of that later - they had important things to do.

“When’s the next shift?” he asked as he sat the cone down.

“Quarter to,” Jackie answered, “but don’t go causing trouble. What’s that lot do?”

“Triangulates their point of origin.”

“I don’t suppose it’s the Gelth?” Rose asked, visions of their spectral forms playing across their bond for a moment.

“Nah,” the Doctor responded, and she quickly shrugged off the idea. “They were just coming through one little rift. This lot are transposing themselves over the whole planet. Like tracing paper.”

With the final cone plugged in, he ran over to make sure they were all in the proper position.

“You’re always doing this,” Jackie complained. “Reducing it to science. Why can’t it be real? Just think of it, though. All the people we’ve lost. Our families coming back home. Don’t you think it’s beautiful?”

He paused to give his mother-in-law an honest answer. 

“I think it’s horrific.” 

And then the Doctor bounced back into motion, unrolling the cable that would connect the triangulation devices to the TARDIS console. They were on a time crunch, after all. “Rose, give us a hand, love.”

His bondmate sighed before following him into the ship.

She’s so upset.

The Doctor remained silent, aware that the thought wasn’t really meant for him and even more aware that there wasn’t anything he could say that would help. He plugged in the cable and turned to Rose, aware that her mother had followed them inside. This is how they could help.

“As soon as the cones activate,” he explained quickly, pointing to the monitor, “if that line goes red, press that button there. If it doesn’t stop,” he continued, reaching into his jacket to pull out the sonic screwdriver, “setting 15-B. Hold it against the port, eight seconds and stop.”

“15-B, eight seconds,” she confirmed.

“If it goes into the blue, activate the deep scan on the left.”

“Uhm … oh!” His wife leaned over the console, which he found much more provocative than the situation really called for. “This button there?”

“Hmm close.”

And he’d really, sincerely intended to send her a mental image of the correct button, but some wires must have gotten crossed there. Instead what he sent was a memory of their return to the TARDIS right after the Rhibelini festival. Eh. Oops?

“That one?” Rose smirked, pointing to another button that was definitely not close, while sending some very, uhm, creative suggestions that, unfortunately, weren’t actually feasible.

“Eehh, now you’ve just killed us,” the Doctor told her with a theatrical grimace.

With the button, or- ?

They both laughed, but only for a moment.

“Er, that one.” She confidently pointed to the correct button, telepathically informing him that she knew the whole time.

“Yeah!” he smiled before turning to Jackie. “Now, what’ve we got? Two minutes to go?”

Jackie looked down at her watch, and the Doctor was glad that she didn’t realize that he was just trying to make her feel needed. That he was a Time Lord and didn’t need her help to check the time. Because his wife had to be right - there’s no way her mum actually enjoys the act of doing laundry. She enjoys being a mum.

You like her, Rose teased over the bond.

Shush.

He gave her a peck on the cheek before exiting the ship to do the final prep work on the triangulation cones. It was go time. The Doctor raced around, calibrating each one.

“What’s the line doing?” he shouted through the door.

“It’s alright,” came his wife’s answering shout, though she really didn’t need to with his superior hearing. She could whisper and he’d be able to hear her from this short of a distance. “It’s holding!”

“You even look like him,” Jackie said to Rose, and he could hear her just fine. Not that he understood what that was supposed to mean.

“How do you mean? I suppose I do, yeah,” his wife responded, sounding pleased, though he still didn’t know what it meant. Rose didn’t look at all like him. What a strange thing to say. He tried to refocus on the triangulation equipment.

“You’ve changed so much,” Jackie sighed. “All grown up and married to an alien, living in a spaceship.”

The Doctor almost said something to Rose about her mother acknowledging that they were, in fact, already married, but then caught himself. If she didn’t already know that he was eavesdropping, no need to make it obvious. Not that it would matter either way. He wasn’t going to stuff cotton in his ears just because the humans in his life couldn’t be bothered to remember all of his biological differences.

“For the better,” his wife replied with confidence. “We have an amazing life, and we’re in love.”

“I suppose. It’s just barmy. Seeing you two like this in this box of his. Makes it hard to pretend everything’s even a little normal.”

He wondered what exactly Jackie imagined their life was like when they weren’t around. Things had actually gotten shockingly domestic lately, though it would still probably be too alien for his mother-in-law.

“Mum, I used to work in a shop.”

“I’ve worked in shops. What’s wrong with that?”

“No, I didn’t mean that,” Rose sighed.

Once again the Doctor made himself refocus on the task at hand, all the while hoping that they weren’t about to have a row.

“I know what you meant. What happens when I’m gone?”

“Don’t talk like that,” Rose ordered, distress flooding their connection, making it nearly impossible for him to pay attention to the cones.

How exactly was he supposed to save the Earth with these working conditions?

There was a smug voice in his head, with a distinct Northern accent, very pleased to point out how they were right about avoiding domestics.

“No, but really. When I’m dead and buried, you won’t have any reason to come back home. What happens then?” Jackie asked her.

“I don’t know,” Rose mumbled, as she tried and failed to imagine their future life without her mother in it.

The Doctor frowned, realizing that he couldn’t quite picture it either.

“Do you think you’ll ever settle down?” her mother continued.

Their connection was now awash with all sorts of negative emotions, and he could tell that his bondmate was near tears, which was completely unacceptable. He turned away from the cones, ready to march back on board before stopping himself.

“The Doctor never will, so I can’t,” Rose told her. “Wouldn’t want to. We’ll just keep traveling.”

“And you’ll keep on changing. And in forty years time, fifty, there’ll be this woman, this strange woman, walking through the marketplace on some planet a billion miles from Earth. But she’s not Rose Tyler. Not anymore. She’s not even human.”

Their bond somehow managed to pulse mauve.

It’s going to be okay, love, he tried to comfort her, fighting to send soothing, positive thoughts over their connection just as he finished up the calibrations. A distraction, that’s what she needed! It was certainly what he needed.

“Here we go!” he shouted.

“The scanner’s working!” Rose called out. “It says Delta-One-Six!”

“Come on then, you beauty!” the Doctor laughed, firmly resolved on drowning out all of the pain present in their shared mental space with adrenaline fueled glee. After all, he had always wanted to use these cones - they were state of the art!

He watched with wide eyes as the cones connected, immediately trapping one of the so-called ‘ghosts’ within their quasi-electric field. And then he reached into his pocket, carefully blocking their bond as he pulled out and put on a pair of 3D glasses - this was the part of his speculations that he really would rather not worry his bondmate with. At least, not yet. Not until he absolutely had to.

The ghost … thing he’d just trapped was absolutely riddled with Void particles. Completely covered, blurry head to blurry toe. Blimey.

The Doctor knelt down, adjusting the controls in order to get a more accurate read. If he was lucky, he would be able to figure out which parallel world these creatures were trying to come from. Likely a parallel Earth, but which one?

It began writhing, though nothing about the triangulation device should cause a living thing pain.

“Don’t like that much, do you?” he couldn’t help commenting. “Who are you? Where are you coming from? Woah!” He jumped back as the ‘ghost’ attempted to break out of the containment field. “That’s more like it! Not so friendly now, are you?”

He looked on as the creature faded away and the cones deactivated. While some more time would have been helpful, the Doctor had enough information to get started. After quickly picking up all of the cones, he ran back inside. Once he’d dumped them all out of the way, he raced up to the console, shrugging out of his coat and tossing it onto the railing.

“I said so!” he exclaimed. “Those ghosts have been forced into existence from one specific point, and I can track down the source. Allons-y!”

With that, he slammed the dematerialization lever, the coordinates having been inputted by the triangulation device. So handy! Finally got to use it.

The TARDIS shook violently.

Well, maybe he could make some improvements ... if he ever got the chance to use it again. The Doctor sprung to his feet and stabilized the flight.

Things seemed abnormally silent in the console room and over their bond. He was uncertain as to why, but still gave over to his natural inclination to fill the silence.

“I like that,” he told his wife as he moved around the console. “Allons-y. I should say allons-y more often. Allons-y. Watch out, Rose Tyler. Allons-y. And then, it would be really brilliant if I met someone called Alonso, because then I could say, ‘Allons-y Alonso’ every time.” He finally reached Rose and wrapped his arms around her before pausing. “You’re staring at me.”

“My mum’s still on board,” she whispered, squeezing his arms.

The Doctor looked up to see Jackie Tyler sitting on one of the platforms.

It was terrifying.

“If we end up on Mars, I’m going to kill you.”

Absolutely, bone-chillingly terrifying.

Stop being a drama queen, his bondmate chastised.

Oh, the domestics of it all! Worse than living in a house! Traveling with his mother-in-law?!

You’ll be fine, it’s hardly traveling . We’re in the same city, in the same time, Rose reassured him, rolling her eyes before giving him a proper hug.

What was he supposed to do now, though?! Bring Jackie with them? Leave her in the TARDIS? It would likely be dangerous wherever they ended up, invasion and all. The alternative was having her stay in their home to snoop around and get up to who knows what. There was no winning!

“Welcome aboard, Jackie!” he said with a wave, his smile showing a bit too much teeth.

“Where exactly are we going, anyway?” her mother asked.

“Come down, mum. You can watch the landing on the view screen with us,” Rose encouraged, releasing him so that she could meet her halfway. “We’re gonna land at wherever they’re controlling the ghosts. Are you fine to stay on board? There’s a pool, you could have a nice swim. Or watch telly in the media room. We’ll be back before you know it.”

“I’m just supposed to hang out in this weird ship of his while you’re off trying to get yourselves killed?”

“We do stuff like this all the time,” the Doctor piped in, trying to reassure her. “Only this time you’re on the TARDIS instead of at home in your flat. Which, really, is much better, when you think about it. Best ship in the Universe.”

Jackie still didn’t look thrilled as they all gathered around the view screen. She looked even less thrilled as they watched the TARDIS land in a hanger before immediately being surrounded by armed gunmen.

“Oh, well, there goes the advantage of surprise,” he sighed. “Still, cuts to the chase.”

Now he was going to have to deal with soldiers. Really, every time he thought that the day couldn’t possibly get worse. The Doctor turned to his mother-in-law as he made his way around the console.

“Jackie, stay inside. Doors shut. They can’t get in.”

“I’m not staying here! Take me home!”

“It’s too late for that,” he told her. “Shouldn’t have come aboard if you didn’t fancy a trip.”

“I was kidnapped!”

He rolled his eyes, deciding not to dignify that with a response as he took Rose’s hand. She pulled him to a stop before they reached the door.

“Doctor, they’ve got guns.”

The Doctor mentally reminded his wife that they’d been surrounded by much, much worse. Daleks couldn’t help but come to mind. 21 st century Earth guns were really the least of his concerns at the moment. Jackie Tyler accidentally breaking his precious timeship was more of a worry than guns. Whatever these creatures had planned, definitely more of a worry than guns.

“And we haven’t,” he delightfully informed her. “Which makes us the better people, don’t you think? They can shoot us dead, but the moral high ground is ours.”

With that, he tugged her out of the TARDIS behind him and closed the door as casually as he could manage.

Honestly, with all of the emergency programs he had installed, why couldn’t he have made one to deal with this scenario? A program that would immediately take Jackie home and then bring the TARDIS right back - now that would be nifty.

 They barely had a chance to look around before the soldiers surrounding them cocked their guns. He and Rose quickly raised their hands to prove they were unarmed.

Y’know what this reminds me of?, his wife casually asked across their connection.

What?

Utah, 2012.

The Doctor’s eyes swept the area as much as he could without moving his head. He could see her point.

Do you think they’d fire if I knocked on wood right now?, he asked her, just as a blonde woman in a suit rushed into the hanger.

“Oh! Oh, how marvelous!” she exclaimed, clapping.

I think she may’ve gone ‘round the bend, Rose laughed in his head as she fought back a confused smile.

The soldiers slowly began to lower their weapons as they joined in on the … clapping? Really, why were they clapping?

“Oh, very good. Superb. Happy day!”

Really, the Doctor felt inclined to agree with his bondmate on this one. Still, now that guns weren’t being pointed at them he was inclined to just go with it.

“Uhm, thanks. Nice to meet you,” he greeted. “I’m the Doctor, and this is my-”

Probably not the time to introduce me as your wife.

“- this is Rose.”

“Hello,” his wife waved with a wide grin that didn’t reach her eyes.

“Oh, I should say! Hurray!”

And there they went again with the clapping. Honestly, what the bloody hell was going on?

Think you’ve got more fans, Rose teased.

“You- you’ve heard of me, then?”

Really, where had his ship landed them?

“Well of course we have,” the overly enthusiastic woman replied. “And I have to say, if it wasn’t for you, none of us would be here! The Doctor and the TARDIS.” 

Everyone started clapping yet again. He was starting to get used to it, actually. It was kind of nice.

“And his companion, of course,” the woman continued.

Okay, not as nice. Then again, Rose was the one who didn’t want him to say she was his wife. Which was probably the smart thing to do, mid-invasion, but still. Just … didn’t feel right. As it was, she had had to cover her mouth with her hands in order to keep herself from laughing - out loud. Their bond was awash with her amusement. The Doctor found himself fighting the urge himself as he tried to politely make them stop.

“And- and- and you are?” he asked as the noise died down.

“Oh, plenty of time for that,” she evaded. Huh.

I think she thinks she’s the boss of you, his bondmate informed him.

She also thinks that I’m the boss ofyou, the Doctor couldn’t help but point out.

Bless.

“Aaaaaaanyway lead on, allons-y. Will there be nibbles?”

He fought the urge to take Rose’s hand as they followed the woman away from the TARDIS, surrounded by armed guards, stuffing his fists into his pockets. A moment later she tugged on his sleeve. The Doctor glanced over, taking out his hand when she rolled her eyes. Their fingers slotted together, perfect fit, as always.

We’ve been holding hands since the moment we met, she mentally chastised. Memories played across their bond.

She certainly wasn’t wrong.

Sorry, he told her, squeezing her hand. Not sure how to pretend to not be married, I guess.

Out of the corner of his eye he could see Rose smirk.

Well, I took off my ring. Think all we’ve got to do now is not say it outright.

Before he could properly respond, something on the tip of his tongue (or whatever the telepathic equivalent of that idiom might be) about how he could do a much better job than that, the mystery woman started talking.

“It was only a matter of time until you found us, and at last you’ve made it,” she said. “I’d like to welcome you, Doctor. Welcome to Torchwood.”

With that, she flung open the doors and they entered a massive warehouse. A massive warehouse that was full of alien technology. And since this definitely wasn’t UNIT, this was very, very not good.

Blimey , he told his wife, you’re right. This really is frighteningly similar to that bunker in Utah.

Gonna nip over to that crate and knock on wood?, Rose asked, only partially teasing.

He really was considering it, actually, but … (he peeked behind him at the armed soldiers following uncomfortably close) better not. Instead he focused on the spacecraft in front of them.

“That’s a Jathar Sunglider,” he realized.

“Came down to Earth off the Shetland Islands ten years ago,” the woman explained.

“What, did it crash?”

“No, we shot it down,” she stated. “It violated our airspace. Then we stripped it bare.” 

Oh, this was really not good. The Doctor tried to sense the timelines, but they were all still so jumbled and wrong that he couldn’t make out the consequences of it, this technology that Earth really shouldn’t have right now. Not yet.

“The weapon that destroyed the Sycorax on Christmas day?” the woman continued with pride, “That was us. Now, if you’d like to come with me.”

That’s what Harriet said, Rose realized, replaying the memory over the bond, Torchwood. I didn’t even think about it, though.

No, me either, he agreed as they were led further into the warehouse. Why hadn’t he noticed anything off before? He should have felt it. On Christmas, maybe not - he’d just regenerated. But apparently this organization has been active for at least a decade, if not longer.

“The Torchwood Institute has a motto - ‘If it’s alien, it’s ours’,” their ‘captor’ slash ‘tour guide’ explained. “Anything that comes from the sky, we strip it down and we use it for the good of the British Empire.”

“Excuse me, the what?” Rose interrupted.

“The British Empire,” the woman repeated, turning around and looking his bondmate up and down, sizing her up.

“There hasn’t been a British Empire in ages,” Rose informed her, and she wasn’t wrong.

“We’ll see,” their hostess replied, a little too condescending for his liking. “Ah, excuse me,” she continued as a soldier handed her a particle gun?! “Now if you wouldn’t mind. Do you recognize this, Doctor?”

“That’s a particle gun.”

Now that he was here, now that this had his full attention, the Doctor could feel the strain on the timelines. This whole building was a threat to the entire causal nexus. His wife held his hand tighter when he showed her just a smidge of it over their connection.

“Good, isn’t it?” the woman smiled, unaware of the impending disaster that he wasn’t yet sure how to fix. “Took us eight years to get it to work.”

“It’s the 21st century,” he calmly tried to explain. “You can’t have particle guns.”

“We must defend our border against the alien,” she replied, as if that somehow gave them a free pass.

The Doctor didn’t know what to say to that, which apparently was fine, as their guide wasn’t really paying attention anyway as she handed back the gun.

“Thank you, Sebastian, isn’t it?”

I think it’s best if we just, you know, let her talk, he told Rose, studiously not looking directly at her - and really, there was a lot to take in, the warehouse was packed with advanced tech. Much too advanced.

“Yes, ma’am.”

Think she’ll give us an evil monologue?

Well, I don’t think she’s evil, he admitted. I think she’s … some sort of, I don’t know, business woman? I think she truly believes that what they’re doing here is good . Which makes them even more dangerous.

It would also make stopping them even more difficult.

“Thank you, Sebastian.”

He refocused as she turned back to them.

“I think it’s very important to know everyone by name,” she said. “Torchwood is a very modern organization. People skills. That’s what it’s all about these days. I’m a people person.”

Well that’s … nice?, Rose commented across the bond as she gave the woman a very forced grin.

“Have you got anyone called Alonso?” he couldn’t help but ask.

“No, I don’t think so. Is that important?”

Eh, oh well. It was kind of nice, though, having her asking a question for once.

“No, I suppose not,” the Doctor replied, just as he noticed a crate of Magnaclamps. He’d always wanted some, hadn’t gotten around to it, though. “What was your name?”

“Yvonne,” she told them (finally). “Yvonne Hartman.”

He let go of his wife’s hand, giving into the urge to inspect a clamp.

“Ah, yes,” Yvonne said with a smile. “Now, we’re very fond of these. The Magnaclamp. Found in a spaceship buried at the base of Mount Snowdon. Attach this to an object and it cancels the mass,” she explained, as if he didn’t already know. “I could use it to lift two tonnes of weight with a single hand. That’s an imperial ton, by the way. Torchwood refuses to go metric.”

Of course they do, Rose scoffed over the bond. British Empire, I mean really.

“Well, that’s handy,” is what she said aloud as he tossed the clamp back into the crate, wandering away to try to get a better idea of all of the other alien technology they’d managed to scavenge, commandeer or steal. His wife wandered in the opposite direction, giving him a second set of eyes even if she didn’t know what everything was. It really was a devastating amount, and the Doctor had to assume that this wasn’t all of it.

Really, it was about time they got back on track.

“So, what about the ghosts?” he asked.

“Ah, yes, the ghosts. They’re, er, what you might call a side effect,” Yvonne admitted.

“Of what?”

“All in good time, Doctor. There is an itinerary, trust me.”

Ugh, of all the things to add to this no-good-very-bad-day, he was stuck on a tour. With an itinerary.

It was his personal hell, really.

And to make it even worse, there went the TARDIS on the back of a lorry.

“An itinerary?” Rose scoffed. “And what are you lot doing with the TARDIS?!” My mum’s in there!

Oh, seriously?! He’d just managed to forget that they’d left Jackie Tyler unsupervised on the ship. Really, truly, worst day ever.

Seriously? Could you just grow up and get some perspective?, his wife snarled over their connection.

“If it’s alien, it’s ours,” Yvonne replied confidently.

“You’ll never get inside it,” he told her with just as much confidence, if not more.

“Hmm, et cetera.”

Once she turned away, they both glanced back at their ship to see Rose’s mum peek out through the doors - which he distinctly remembered telling her to keep shut.

Really, why did no one ever listen? He didn’t understand it.

With a sigh, and all of his unflattering thoughts about his mother-in-law safely behind a barrier, the Doctor turned away to continue their ‘tour’. At least the ghosts were on the itinerary. So this day had to turn ‘round at some point … right?

[turitolive]

Congruence Transformation  

Transformation   

A transformation is a function that maps points or objects from one space to another. In geometry, a transformation can be thought of as changing an object's position, orientation, or size.  

There are many diverse transformations in mathematics, including translation, rotation, scaling, reflection, shearing, and dilation. Moreover, these transformations can be applied to objects in different spaces, such as points in a two-dimensional or three-dimensional space, functions, or vectors in a linear space.  

Transformations are used in various mathematical applications, including geometry, calculus, linear algebra, and differential equations. They are particularly important in the study of symmetry and invariance, where they are used to analyze the properties of objects that remain unchanged under certain transformations.  

In addition to geometric transformations, there are many other types of transformations in mathematics, such as Fourier transforms, Laplace transforms, and wavelet transforms, which are used in signal processing, image processing, and other areas of applied mathematics.

Overall, transformations play a fundamental role in many areas of mathematics and are essential tools for modeling and analyzing mathematical systems.  

Types of Transformations  

In mathematics, several types of transformations are commonly used. Some of the most common types of transformations include:  

Translation: This transformation involves moving an object from one location to another. In a two-dimensional plane, translation involves moving an object horizontally and/or vertically.  

Rotation: This transformation involves turning an object around a fixed point. In a two-dimensional plane, rotation involves rotating an object by a certain angle around a point.  

Reflection: This transformation involves creating a mirror image of an object. In a two-dimensional plane, reflection involves flipping an object across a line (such as the x-axis or y-axis).  

Dilation: This transformation involves changing the size of an object relative to a fixed point. In a two-dimensional plane, dilation involves stretching or shrinking an object from a fixed point.  

What is a Congruence Transformation?  

A congruence transformation is a type of transformation in mathematics that preserves the size and shape of an object. For example, in linear algebra, a congruence transformation refers to a linear transformation that preserves the dot product of vectors.  

More specifically, let A and B be two n x n matrices. We say that A and B are congruent if there exists an invertible n x n matrix P such that:  

B = P^TAP  

where P^T is the transpose of P.  

Geometrically, this means that if we have a matrix A that represents a linear transformation, and we apply a congruence transformation to it by multiplying it on both sides by an invertible matrix P, the resulting matrix B represents the same linear transformation, but with a different coordinate system.  

Congruence transformations are useful in many areas of mathematics, including linear algebra, geometry, and number theory. For example, they can simplify matrix calculations, diagonalize symmetric matrices, and classify quadratic forms.  

Applications of Congruence Transformation  

Congruence transformations have many applications in mathematics and beyond. Here are some examples:  

Geometry: Congruence transformations are fundamental concepts in geometry, and they are used to study the properties of geometric objects such as points, lines, circles, and polygons. They are used to prove geometric theorems and to develop geometric models of physical phenomena.  

Computer graphics: Congruence transformations are used extensively to model and manipulate 2D and 3D objects. They are used to perform operations such as rotation, translation, scaling, and reflection, which are essential for creating realistic animations and visual effects.  

Physics: Congruence transformations are used in physics to study the properties of invariant physical systems under certain transformations.  

Robotics: Congruence transformations are used in robotics to model the movements of robots and to control their motion. 

Molecular biology: Congruence transformations are used in molecular biology to study the three-dimensional structure of biomolecules such as proteins and DNA.   

Cryptography: Congruence transformations are used in cryptography to encrypt and decrypt messages. They are used to perform operations such as permutation and substitution, which are essential for creating secure cryptographic systems.  

Congruence transformations are powerful mathematical tools with many applications in science, engineering, and other fields. For example, they are essential for understanding and modeling complex systems and solving problems requiring geometric and spatial reasoning.  

[violetanimation]

Task 2A & B: Proposals

Proposal 1: Forest Montage

The first option I had in mind for this project was inspired by the idea of taking 'A moment, a time, a place' to illustrate my own various stages of life, memories and experiences. However, when thinking about the topic, I was overwhelmed by its broadness; so I tried to think of the ways in which I could link these experiences visually, so that there is a running theme across all.

What came to mind is that I seem to have had a lot of important moments in life happen to me in forests or woods. I started to compile these memories:

-Very early memories of my grandfather pulling me and my brother in a sled through heavy snow down a road flanked by banks of trees;

-My memory of the first time I ever fell over was in a forest, in which I fell into a huge puddle of water/mud;

-Walking with a group of other children by ourselves in the forest at 4-5 years of age and coming across a clean, bleached, enormous skeleton of a cow and taking the skull home in a pink hoodie;

-Hiking into the mountains with a huge chunk of my family on the rare occasions where we got together;

-The green area around University and woods around MCAST.

Thus, the idea would be to create a montage-type of animation in which the scenes cut to the various scenarios within forests. Below are some visual inspirations/moodboards:

This gif especially inspired me in the sense that I found it a cool idea to vary between aspect ratios, almost as if filmed by different devices throughout the years.

This animated video by Gibbon Animation is exactly what I had in mind in terms of a montage aesthetic. Additionally, I am especially a fan of the painterly backgrounds with very clean, illustrative subject matter transposed onto it. I went down a massive research hole matrix to try and find out what the animators for this - it turns out it was all done on Krita, which inspires me to potentially use it myself.

Proposal 2: Moon Sequence

My second proposal involves the idea of 'a moment, a time, a place' in the sense that I tried to think of a particular visual element that is particularly universal in the human experience across time and places. What came to mind is the moon - something very simple, but which is a constant presence in our lives we often overlook. Our earliest ancestors must have looked at the moon in much the same way it looks now, people must have gazed at it from between the bars of their prison cells, and might have observed it from lofty balconies in elaborate palaces.

Therefore, my idea for this proposal is to create a smooth sequence of the various moons, shifting between different places and people across different environments and landscapes.

Below are some visual inspirations/moodboards:

Using the above gif for inspiration, I used the same colour scheme to create some developmental pieces seen here ^

Ben Mariott's youtube series on 'best animations yearly' inspired me in the way of clean, crisp vector animation with plenty of clever transitions. For this proposal, it is undoubtedly the aesthetic I would opt for.

Ultimately, in the class activity in which we talked a bit about our proposal ideas, it was agreed on that the first proposal seemed simultaneously a clearer and well-formed idea, as well as a topic dearer to my heart. From this point on, I started to develop my ideas about 'Forest Montage' more.

[rnomics]

IJMS, Vol. 23, Pages 16222: Dysregulated Expression of Transposable Elements in TDP-43M337V Human Motor Neurons That Recapitulate Amyotrophic Lateral Sclerosis In Vitro

Amyotrophic lateral sclerosis (ALS) is a disease that progressively annihilates spinal cord motor neurons, causing severe motor decline and death. The disease is divided into familial and sporadic ALS. Mutations in the TAR DNA binding protein 43 (TDP-43) have been involved in the pathological emergence and progression of ALS, although the molecular mechanisms eliciting the disease are unknown. Transposable elements (TEs) and DNA sequences capable of transposing within the genome become dysregulated and transcribed in the presence of TDP-43 mutations. We performed #RNA-Seq in human motor neurons (iMNs) derived from induced pluripotent stem cells (iPSCs) from TDP-43 wild-type&mdash;iMNs-TDP-43WT&mdash;and mutant&mdash;iMNs-TDP-43M337V&mdash;genotypes at 7 and 14 DIV, and, with state-of-the-art bioinformatic tools, analyzed whether TDP-43M337V alters both gene expression and TE activity. Our results show that TDP-43M337V induced global changes in the gene expression and TEs levels at all in vitro stages studied. Interestingly, many genetic pathways overlapped with that of the TEs activity, suggesting that TEs control the expression of several genes. TEs correlated with genes that played key roles in the extracellular matrix and #RNA processing: all the regulatory pathways affected in ALS. Thus, the loss of TE regulation is present in TDP-43 mutations and is a critical determinant of the disease in human motor neurons. Overall, our results support the evidence that indicates TEs are critical regulatory sequences contributing to ALS neurodegeneration. https://www.mdpi.com/1422-0067/23/24/16222?utm_source=dlvr.it&utm_medium=tumblr

[serveandfolly]

Be still my beating heart: My longtime partner, Brian Libby, wrote this OR Arts Watch article twinning the stories of two of my favorite artists, actor River Phoenix and musician Elliott Smith, and relating them through their time in our hometown of Portland, Oregon. The original story (link above) shows photos of some of Elliott’s Portland homes and the road with “the fucked-up face” from My Own Private Idaho, but I’ve pasted all the copy below. Hope some of my fellow River and Elliott fans enjoy this as much as I did.

River and Elliott: Remembering two troubled princes of 1990s Portland

River Phoenix and Elliott Smith brushed Portland and maybe Portland brushed them

NOVEMBER 27, 2018 // CULTURE, FILM, MUSIC // BRIAN LIBBY

There’s a name you keep repeating You’ve got nothing better to do

— Elliott Smith, “Alphabet Town”

From James Dean to Jimi Hendrix, Kurt Cobain to Heath Ledger, we have immortalized a constellation of famous artists—especially musicians and actors—who died young and, then, through a combination of their talent and the public’s grief, lived on. Robbed of the futures we imagined for them, yet frozen in time and thus never to suffer the indignities of aging or late-career artistic mediocrity, their luminosity—and our love for them—intensifies as if in proportion to the tragedy.

Portland and Oregon haven’t traditionally produced a lot of bold-type names that have endured in the international pop zeitgeist. Far from America’s entertainment capitols, this is arguably a place where talents are nurtured, not where one becomes a full-fledged star. The most high-profile artists, such as the great abstract expressionist painter Mark Rothko or Simpsons creator Matt Groening, have tended to move on and live their career-defining creative moments elsewhere. Yet even if their time here is fleeting, sometimes these artists don’t just remain culturally relevant long after their deaths but also come to represent something essential about a particular time in the city.

Last month brought reminders of two such one-time Oregonians and what they left behind. October 21 was the 15th anniversary of musician Elliott Smith’s death, at the age of 34 in 2003, while Halloween brought the 25th anniversary of actor River Phoenix’s death, at the age of 23 in 1993. They died a decade apart, but each moment of mortality came in Los Angeles, and the two sites are less than nine miles away from each other: Phoenix outside West Hollywood’s Viper Room club after an accidental overdose, and Smith by stabbing at his home in Silver Lake (a presumed suicide but never officially determined).

The coincidences don’t end there. River Phoenix and Elliott Smith were born within a year of each other: Smith in Nebraska (he was raised until age 14 in Texas) and Phoenix in Madras, Oregon (raised mostly in Florida). Each arguably made his most famous work in collaboration with director Gus Van Sant. Phoenix co-starred (along with Keanu Reeves) in Van Sant’s 1991 film My Own Private Idaho and Smith was nominated for an Academy Award for the song “Miss Misery,” on the soundtrack to Van Sant’s 1998 film Good Will Hunting. Each struggled with drug abuse, which in different ways led to each artist’s untimely death. River Phoenix and Elliott Smith presumably never met, yet each is a kind of fleeting prince of ’90s Portland, and their work acts as time capsule and talisman for the days many locals now look to longingly: a grittier, more affordable and off-the-radar city that predated Portlandia, a succession of swooning New York Times stories, and an ensuing wave of tourism and gentrification.

Like Rothko, neither stayed here for good. But also like Rothko and many of the city’s other most famous sons and daughters, Phoenix and Smith were transplants to the city who saw Portland with fresh eyes. Like rain clouds that give way to bright sunlight almost daily for much of the year, each artist’s Portland-based work is personal and often deeply melancholic, yet also joyful, lyrical and instinctual. It’s not always pretty, yet we are drawn to their work again and again.

By the time Phoenix signed on to star in My Own Private Idaho, he had long since become a star, thanks to such minor Hollywood classics as 1986’s Oregon-filmed Stand by Me and 1988’s Running on Empty, the latter of which brought him an Academy Award nomination for Best Supporting Actor. But Idaho, the third in Van Sant’s trilogy of Portland-set films (preceded by 1986’s Mala Noche and 1989’s Drugstore Cowboy), would become the role of Phoenix’s career and the standout classic in its director’s now decades-long portfolio.

While Drugstore was initially a greater critical success for Van Sant, winning Best Film and Best Director from the National Society of Film Critics in 1989, Idaho is somehow the film that endures in public imagination and as a lasting artistic achievement. Besides being a landmark of gay cinema, casting two young Hollywood heartthrobs as lovers, it also turned out to be Van Sant’s most cinematically ambitious effort.

The premise of My Own Private Idaho is audacious if not a little crazy. The film is a loose interpretation of Shakespeare’s Henry IV, Part I and Part II—the story of a delinquent, debauchery-loving prince planning to shed his skin and embrace his more virtuous monarchical destiny—transposed to the realm of contemporary Portland street hustlers. As legend has it, Phoenix and Reeves spent nights on the streets of Old Town researching their roles by hanging out with the city’s young street denizens, some of whom would enjoy supporting roles in the film.

Phoenix plays a hustler named Mike with a handicap—narcolepsy drops him off to sleep in any moment of stress. We first watch him collapse in sleep by the side of a rural highway, his possessions and even his shoes stripped from him as he slumbers; then he collapses in the middle of turning a trick, carried out of a rich woman’s house by his fellow hustlers and left slumped against a tree. Reeves’s young Prince Hal figure, Scott (in this case a Portland mayor’s son), is along for the ride as part brotherly companion, part lover. Yet this quirky Shakespearean tale is also bookended by and interwoven with a larger quest, played out under the limitless skies and golden hues of the eastern Oregon landscape, as Phoenix’s Mike searches fruitlessly for his long-lost mother: to the Idaho of his youth, to Italy, and finally back to Portland.

Part of what makes My Own Private Idaho so great is how Van Sant conjures indelible cinematic moments: time-lapse footage of clouds rolling over the Oregon landscape; symbolic slow-motion shots of salmon (Mike’s spirit-animal; Phoenix even wears a salmon-colored jacket) fighting their way upstream; and even an entire house falling from the sky onto the highway. It’s dazzling cinema that makes both rural and urban Oregon its muse like perhaps no other movie. That Van Sant has gone on to make several Hollywood movies that overdose on schmaltz and are short on cinematic eye candy, and few if any great works of art (the Cannes winner Elephant and the Matt Damon/Casey Affleck vehicle Gerry perhaps being exceptions) only makes Idaho all the more special in his oeuvre. In fact, it’s as if Van Sant refuses to enter Idaho-like territory. Consider, for example, that his last film, Don’t Worry, He Won’t Get Far On Foot—a profile of cartoonist John Callahan starring River Phoenix’s brother, Joaquin, which is set in Portland and another story of a lonely man’s longing for his mother—was shot in Los Angeles. Suffice to say, there are no houses falling onto the highway.

At least unofficially, My Own Private Idaho owes as much to Phoenix as Van Sant—and not just as it relates to the acting. After all, River Phoenix didn’t just act in Idaho; he reportedly was able to alter the script and his character. The draft that Van Sant brought to the actors didn’t include romance between their two lead characters, but by the time production was complete, Idaho’s most touching moment was a campfire embrace wherein Mike declares his love for Reeves’s Scott. Phoenix is at his zenith here as an actor, a marvel of delicacy, communicating a blend of easy cool and endearing vulnerability.

Both Phoenix and Reeves came to the Idaho cast with something to prove: that they could be serious dramatic actors. To a large extent it worked for both. While Reeves has never been considered a master thespian, his roles in blockbuster franchises like The Matrix and even the more recent John Wick movies have cemented his place in movie history. And for Phoenix, post-Idaho there was no longer any doubt that the child actor we’d seen in Explorers and the angst-ridden teen of The Mosquito Coast (not to mention a memorable “Family Ties” guest-starring turn) had graduated to leading roles with the charisma, looks and vulnerability of a budding superstar. Would it be going too far to say he was the James Dean of his time? Maybe. But the comparison is not ludicrous.

Of course longevity was not to be for Phoenix. Within 25 months of Idaho’s release, his story ended, just like Mike’s, collapsed on the pavement—in this case on a Hollywood sidewalk rather than Highway 216, and sadly, not simply asleep for a few minutes. The brother with him that night, Joachin Phoenix, would go on to enjoy the long acting career River never got.

The year of Idaho’s release was also a turning point for Elliott Smith. In 1991 he had just returned to Portland after four years at Hampshire College in Massachusetts, and promptly formed the band Heatmiser with three musician friends. Over the ensuing years, Heatmiser would become a fixture at celebrated indie-rock clubs like the X-Ray Café and La Luna, while also recording albums like 1993’s Dead Air and 1994’s Cop and Speeder that infused punk energy with melodicism. The band was part of a broader indie rock scene that included Pond, Crackerbash, The Spinanes, The Dandy Warhols and Quasi.

After Nirvana’s breakout success, both indie and major labels began combing Portland clubs looking for the next grunge sensation. And what was grunge but punk with a little more melody and a flannel shirt? Heatmiser received enough attention that a major label, Virgin Records, eventually came calling. But by that time Smith was ready to venture out on his own, breaking up Heatmiser just as they’d made the big time. As the singer-songwriter explained in a later interview, he had grown tired of screaming all the time as a member of a loud rock band. And besides, by that time Smith was gaining notice for a series of stripped-down solo albums with little more than voice and an acoustic guitar. To the astonishment of many, they sounded less like punk or grunge and more like Simon & Garfunkel or Nick Drake. Smith’s solo debut, 1994’s Roman Candle, was released at the height of the grunge era but also just nine months before Kurt Cobain’s suicide, essentially prefiguring (and perhaps even giving birth to) the emo-core wave that would in time follow grunge.

In the four years between Roman Candle’s release and Smith’s leap to international fame with the Oscar nomination for “Miss Misery,” local audiences who had feasted on loud guitars and pounding punk rhythms filled Portland clubs for his solo acoustic shows, trading chaotic mosh pits for stillness and pin-drop quiet. Not only was there the wistful simplicity of Smith’s voice and acoustic guitar. It was also how the singer-songwriter bared his soul in his lyrics. Though some songs were inspired by others’ lives, it was clear that for the sensitive, often-depressed Smith, music was a confessional and a lifeline. Yet in his almost Lennon-McCartney like gift for melody, even his sad songs feel uplifting.

In those early Elliott Smith albums recorded here, through his 1997 masterwork Either/Or (his last for indie label Kill Rock Stars before signing with the mammoth Dreamworks and leaving Portland for New York), the singer-songwriter also painted a cinematic if melancholy picture of the city. You can almost feel the gray wintertime skies in songs like “Alameda,” as he sings:

You walk down Alameda Looking at the cracks in the sidewalk Thinking about your friends How you maintain all them in A constant state of suspense

For your own protection Over their affection Nobody broke your heart You broke your own because you can’t Finish what you start

When the Oscar nomination for “Miss Misery” came, Smith’s life changed overnight. If that new audience and international media attention meant exponentially greater album sales and the end of his penny-pinching way of life—staying in nice hotels on tour instead of sleeping in the van or on some stranger’s floor, not to mention no longer moonlighting as a drywall contractor by day—it also isolated Elliott from his community of not-so-affluent friends and musicians still sleeping on those floors. This time in his life was also accompanied by increasing drug abuse and greater depressions. Perhaps Smith new that despite overwhelmingly positive reviews for albums like XO and Figure 8 as well as a worldwide audience of admirers (he was particularly smitten when a musical hero, Elvis Costello, attended a London show), DreamWorks saw its Smith signing as essentially an investment that didn’t quite pay off because he wasn’t the megastar they envisioned.

Like Cobain, Smith also retained that nagging Gen X rocker’s worry that he’d sold out. Maybe today a young fan who falls in love with Figure 8 doesn’t care that it was recorded for DreamWorks instead of Kill Rock Stars. After all, going to a major label gave Smith a bigger palette of instruments and fellow musicians to work and record with. Yet for Smith, the decision wasn’t without impact. In “King’s Crossing,” one of Smith’s best posthumously-released songs, he sings, “The method acting that pays my bills/keeps the fat man feeding in Beverly Hills.”

Particularly in the couple of years before his 2003 death, Smith was a shell of his former self, consuming cocktails of heroin, crack and prescription drugs. At times onstage, he even had to abort songs halfway through because he couldn’t remember his own lyrics. Yet Smith was also in those final months showing signs of recovery and renewal, which enabled the superlative album he was working on when he died. Songs on the magnificent From a Basement on the Hill (including “King’s Crossing”) exhibit a layered richness of sound that goes beyond what he recorded in Portland a few years earlier. Yet it all screeched to a halt in Silver Lake—whether inevitably, as some observers maintained, or out of the blue.

Today I can’t look at certain places in Portland and Oregon without thinking of them.

For River Phoenix and My Own Private Idaho, there is the Elk statue downtown on Southwest Main Street between Chapman and Lownsdale squares, where early in the film Scott cradles a sleeping Mike in his arms. There is also the stretch of Broadway downtown near the Benson Hotel where the duo cruise the street on Scott’s motorcycle, handsomely and heroically, like cinema’s sunglasses-masked successors to The Wild One and Easy Rider. And perhaps most of all, there is a lonely stretch of Highway 216, east of the Cascades and not far from the tiny town of Tygh Valley, where River Phoenix begins and ends the movie, succumbing to narcoleptic seizure. Last year my partner and I found the coordinates online and made a pilgrimage. To get there you drive white-knuckled through a series of hairpin turns through a small Deschutes River gorge, and then suddenly you come onto a plateau where the road seems to unfold forever.

If one seeks vestiges of Elliott Smith’s Portland, it’s not just the venues where he took the stage (one of which, La Luna, is now a café of the same name), but also, if you know where to look, one of the many Southeast Portland houses where he lived and recorded. Roman Candle, for instance, was recorded in a home on Southeast Taylor Street that recently was listed for rent. (And yes, I admittedly took a tour.) Smith also lived in another Southeast Portland house, off Division Street, that prompted him to sometimes spend late nights hanging out on a bench in the rose gardens of Ladd’s Addition; the documentary Heaven Adores You includes a long shot looking down over the neighborhood. In “St. Ides Heaven,” he writes

Everything is exactly right When I walk around here drunk every night With an open container from 7-11

Division Street itself also wound up inspiring a lyric in “Punch and Judy” (on Either/Or), albeit not exactly an ideal marketing tagline:

Driving around up and down Division Street I used to like it here It just bums me out to remember

Every time I listen to “Punch and Judy,” that line makes me wonder what Smith would have made of gentrified Division Street now, with its canyon of condos and string of popular restaurants. It’s a phenomenon that has swept most close-in east side neighborhoods—precisely the formerly cheap old houses he and his friends used to inhabit.

Even so, to absorb the work of Smith (especially his early records) and Phoenix (particularly My Own Private Idaho) is to make a nostalgic return to ‘90s Portland. And yet, through the power of these works and these two princes’ immense talent, their work also transcends that time capsule. Even if their tragically early deaths don’t guarantee them true artistic immortality, the more Portland changes, the more their works resonate.

[debopamghosh]

Application of Affine Transformations: Codification schemes for Design of Experiments

Notations:

inv(A) denotes the inverse of the matrix A ( n by n)

B( n by n) = diag( v1, v2,..., vn) denotes a diagonal matrix, whose diagonal elements from top to bottom along the main diagonal, are v1, v2,..., vn respectively

'n=< m ' implies m is greater than or equal to n

'n < m' implies n is strictly less than m

m. n implies scalar multiplication between m and n

v' denotes the transpose of vector v

R^p (R) denotes the real Euclidean space of dimension = p

x be a real variable, such that: a =< x = < b, and : a < b

defining the variable z as follows:

z = ( m. x) + c , such that z = -1 when x = a and z = +1 when x = b, we have the following interrelationships:

x = ((b - a) /2). z + (( b + a) /2)

z = (2/(b - a)). x - ((b + a) /(b - a))

Multivariate setup:

x1, x2, ...., xp be a set of real variables such that : ai =< xi =< bi, where ai < bi, for i = 1,2,...., p

X( p by 1) = [ x1 x2 .... xp ] '

Z( p by 1) = [ z1 z2 .... zp ]'

the vectors X and Z are interrelated as following Affine transformations of each other:

Z( p by 1) = A ( p by p) X( p by 1) + C (p by 1)

X( p by 1) = inv(A) ( p by p) Z( p by 1) - inv(A) (p by p) C( p by 1)

A ( p by p) and C ( p by 1) are given as follows:

A( p by p) = diag ( h1, h2, ...., hp) , where

hi = 2 /( bi - ai) , i = 1,2,....,p

Clearly, the matrix A is diagonal, symmetric and positive definite and therefore invertible.

inv(A) ( p by p) = diag ( 1/h1, 1/h2,....., 1/hp)

C( p by 1) = [ c1 c2 ..... cp ]' , where:

ci = - (bi + ai) /( bi - ai) , i = 1,2,...., p

Discussion:

Consider the following Hypercubes in the vector space R^p (R) :

S(X) ={ (x1, x2,...., xp) ' | ai =< xi =< bi, ai < bi, i = 1,2,....,p }

S(Z) = { (z1, z2,....., zp) ' | -1 =< zi =< +1 , i= 1,2,..., p }

The hypercube S(X) is an arbitrary cubical region in the real Euclidean space of dimension 'p', it represents the Experimental space associated with an Experimental design in terms of the actual variables: x1, x2,...., xp. However, Regression model building in terms of the design matrix constructed using the levels of actual set of experimental variables is not always a good idea because of the inherent lack of symmetry that may be present in the design, issues can arise with respect to estimation of model parameters and predicted responses, for example multicollinearity problems in Experimental design as a result of ill -conditioning in the associated design matrix .

However, the hypercube S(Z) is centered at the zero point in the space, i. e at 0( p by 1) , and it's sides are all of equal lengths. This hypercube is related to S(X) through Affine transformation as defined above..... thus using affine transformations we can go from an Experimental design to its reformulated structure with a greater symmetry, this is achieved through " Codification " of the experimental variables to generate centered and scaled coded variables , zi is the 'coded variable' corresponding to the experimental variable xi, where i = 1,2,...,p

The Regression model can be built in terms of the coded variables and their associated levels and then can be transformed into one in terms of the original variables, using the transformation interrelationships between xi and zi variables as defined above. The Design matrix constructed using the levels in terms of the coded variables can show much better conditioning under certain situations as compared to one constructed using the experimental variables and their levels directly.

The codification scheme described above when applied to 2^p type of Statistical Experimental designs, result in formation of Design matrix having mutually orthogonal columns which are orthogonal to the unit vector (the intercept term contribution to the design matrix) of order 2^p by 1, this results in statistical independance of the estimated model parameters and that of associated sum of squares, under the condition that the Ordinary least squares model assumptions are met by the experimental system.

References and further reading:

Chemometrics: Experimental design, Ed Morgan

Design and Analysis of Experiments, Douglas. C. Montogomery

Linear Estimation and Design of Experiments, D. D. Joshi

[perfectlytinyworkspace]

Linear Regression (2)

[Part 1 here]

linear regression elements:

h(xi) = w™ • xi is your predictive trendline where w(transposed) or w™ is the expression that x is subjected to

the error of the trend line is Ein(h) = 1/N • sum[ (h(xn) – yn)^2 ] or basically the L2 norm function

the dataset X is R(N • d) where R is the range of Real numbers, N is the number of samples, and d is the dimensions of each individual [inc. d + 1]

each row of this dataset matrix is a transposed individual vector column [1 a b c...]

where a, b, c, etc. are the known data for the individual

the outcome set Y is R(N) where N is the number of samples

linear regression, step-by-step:

1. get a dataset X and its outcome Y values according to some unknown relation.

2. generate a predictive trendline h(x) that tries to approximate the unknown relation

3. the predictive estimates y^ or "y-hat" that h(x) predicts for X can be defined as the following:

the dot products of h(x) = w™ • X for each value inside the dataset matrix X

points on the blue line y^ = w • the dataset X

4. to find the error E(in) of h(x) in predicting that unknown, get the squared L2 norm of y^ and outcome Y

5. The standard error function of the trendline h(x), once substituted for y^hat, is

1/N || X • w – y ||2^2, or the L2 norm squared of y^hat and y

and serves as the vector that measures the distance between your hypothesis and the unknown.

6. find the minimum error of E(in) by deriving the standard equation for E(in)

X dataset and y outcomes are both fixed values, so we take the derivative with respect to the changing variable w

∆Ein(w) = 2/N (X™Xw – X™y)

find the minimum value by setting ∆Ein(w) = 0 = X™Xw

Xw = y, so X™Xw = X™y

solving for w gets you w = X™y ÷ X™X

»»» the best fit trendline for the dataset X and outcomes Y to approximate the unknown X-Y relation is w = X™y ÷ X™X

find the size of w: apply the shape rule

if X is Nxd, then X™ is dxN. so X™X's shape is (dxN)(Nxd)

the multiplication shape rule: cancel the inner dimensions to get shape(X™X) = dxd

y's shape is (Nx1), so X™y's shape is (dxN)(Nx1) = dx1

so assuming that the division inverse X™X^-1 doesn't affect the shape, the shape of X™X • X™y is shape(w) = (dxd)(dx1) = dx1