#application of mathematics
Explore tagged Tumblr posts
Text
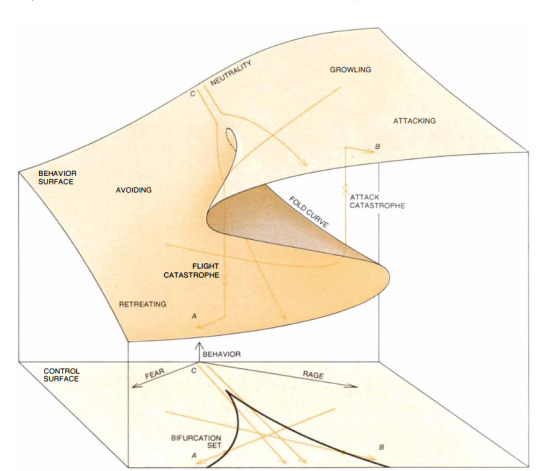
#from 2min of googling it seems “catastrophe theory” is perfectly rigorous mathematics but all the applications are pseudoscience#many such cases
83 notes
·
View notes
Text




AAAAAAHHHH I HAVE A MATH TEST TMRW
Normally, I’m not so stressed, but I missed class this week (I was skipping shame on me 😭) and I have no clue what’s going on… Me and the math teacher are besties because he’s the coach of the golf team, so I’m scared of disappointing him with my bad test scores.
I also had a long lab in chem this week. It’s really sad because we got bad results even though we ran our trial for over and hour lol. I think it’s my lab partner’s fault because he keeps on putting his crusty fingers all over the cuvettes which is messing up the spectrophotometer. Hopefully he actually writes his part so it’s not another repeat of last year.
- Practice midterms for matrices
- Grade practice midterms
- Write lab report
- Debug binary system simulation
- Work on astro research paper
- Work on program applications
- Finish new deal research
- Finish college assessment
- Email people back 😬
Don’t ask me why we have a midterm in January… I have no clue.
#academia#studyblr#studying#high school#stem academia#stem student#study motivation#science#stemblr#physics#chemistry#mathblr#mathematics#chemblr#math#matrices#college applications#stem aesthetic#stem studyblr#stem#physics student#student#computer science#eclipsellium
32 notes
·
View notes
Text
i really enjoy this font

#unfortunately it is hard to read so i will not be spending any more time on this#just saving pics before i return this book to my math department#there is an interesting galois theory application at the end though#about ruler compass constructions#Galois Theory (Notre Dame Mathematical Lectures Number 2) by Emil Artin
30 notes
·
View notes
Text
Okay so to get the additive group of integers we just take the free (abelian) group on one generator. Perfectly natural. But given this group, how do we get the multiplication operation that makes it into the ring of integers, without just defining it to be what we already know the answer should be? Actually, we can leverage the fact that the underlying group is free on one generator.
So if you have two abelian groups A,B, then the set of group homorphisms A -> B can be equipped with the structure of an abelian group. If the values of homorphisms f and g at a group element a are f(a) and g(a), then the value of f + g at a is f(a) + g(a). Note that for this sum function to be a homomorphism in general, you do need B to be abelian. This abelian group structure is natural in the sense that Hom(A ⊗ B,C) is isomorphic in a natural way to Hom(A,Hom(B,C)) for all abelian groups A,B,C, where ⊗ denotes the tensor product of abelian groups. In jargon, this says that these constructions make the category of abelian groups into a monoidal closed category.
In particular, the set End(A) = Hom(A,A) of endomorphisms of A is itself an abelian group. What's more, we get an entirely new operation on End(A) for free: function composition! For f,g: A -> A, define f ∘ g to map a onto f(g(a)). Because the elements of End(A) are group homorphisms, we can derive a few identities that relate its addition to composition. If f,g,h are endomorphisms, then for all a in A we have [f ∘ (g + h)](a) = f(g(a) + h(a)) = f(g(a)) + f(h(a)) = [(f ∘ g) + (f ∘ h)](a), so f ∘ (g + h) = (f ∘ g) + (f ∘ h). In other words, composition distributes over addition on the left. We can similarly show that it distributes on the right. Because composition is associative and the identity function A -> A is always a homomorphism, we find that we have equipped End(A) with the structure of a unital ring.
Here's the punchline: because ℤ is the free group on one generator, a group homomorphism out of ℤ is completely determined by where it maps the generator 1, and every choice of image of 1 gives you a homomorphism. This means that we can identify the elements of ℤ with those of End(ℤ) bijectively; a non-negative number n corresponds to the endomorphism [n]: ℤ -> ℤ that maps k onto k added to itself n times, and a negative number n gives the endomorphism [n] that maps k onto -k added together -n times. Going from endomorphisms to integers is even simpler: evaluate the endomorphism at 1. Note that because (f + g)(1) = f(1) + g(1), this bijection is actually an isomorphism of abelian groups
This means that we can transfer the multiplication (i.e. composition) on End(ℤ) to ℤ. What's this ring structure on ℤ? Well if you have the endomorphism that maps 1 onto 2, and you then compose it with the one that maps 1 onto 3, then the resulting endomorphism maps 1 onto 2 added together 3 times, which among other names is known as 6. The multiplication is exactly the standard multiplication on ℤ!
A lot of things had to line up for this to work. For instance, the pointwise sum of endomorphisms needs to be itself an endomorphism. This is why we can't play the same game again; the free commutative ring on one generator is the integer polynomial ring ℤ[X], and indeed the set of ring endomorphisms ℤ[X] -> ℤ[X] correspond naturally to elements of ℤ[X], but because the pointwise product of ring endomorphisms does not generally respect addition, the pointwise operations do not equip End(ℤ[X]) with a ring structure (and in fact, no ring structure on Hom(R,S) can make the category of commutative rings monoidal closed for the tensor product of rings (this is because the monoidal unit is initial)). We can relax the rules slightly, though.
Who says we need the multiplication (or addition, for that matter) on End(ℤ[X])? We still have the bijection ℤ[X] ↔ End(ℤ[X]), so we can just give ℤ[X] the composition operation by transfering along the correspondence anyway. If p and q are polynomials in ℤ[X], then p ∘ q is the polynomial you get by substituting q for every instance of X in p. By construction, this satisfies (p + q) ∘ r = (p ∘ r) + (q ∘ r) and (p × q) ∘ r = (p ∘ r) × (q ∘ r), but we no longer have left-distributivity. Furthermore, composition is associative and the monomial X serves as its unit element. The resulting structure is an example of a composition ring!
The composition rings, like the commutative unital rings, and the abelian groups, form an equational class of algebraic structures, so they too have free objects. For sanity's sake, let's restrict ourselves to composition rings whose multiplication is commutative and unital, and whose composition is unital as well. Let C be the free composition ring with these restrictions on one generator. The elements of this ring will look like polynomials with integers coefficients, but with expressions in terms of X and a new indeterminate g (thought of as an 'unexpandable' polynomial), with various possible arrangements of multiplication, summation, and composition. It's a weird complicated object!
But again, the set of composition ring endomorphisms C -> C (that is, ring endomorphisms which respect composition) will have a bijective correspondence with elements of C, and we can transfer the composition operation to C. This gets us a fourth operation on C, which is associative with unit element g, and which distributes on the right over addition, multiplication, and composition.
This continues: every time you have a new equational class of algebraic structures with two extra operations (one binary operation for the new composition and one constant, i.e. a nullary operation, for the new unit element), and a new distributivity identity for every previous operation, as well as a unit identity and an associativity identity. We thus have an increasing countably infinite tower of algebraic structures.
Actually, taking the union of all of these equational classes still gives you an equational class, with countably infinitely many operations. This too has a free object on one generator, which has an endomorphism algebra, which is an object of a larger equational class of algebras, and so on. In this way, starting from any equational class, we construct a transfinite tower of algebraic structures indexed by the ordinal numbers with a truly senseless amount of associative unital operations, each of which distributes on the right over every previous operation.
#math#the ongoing effort of valiantly constructing complicated mathematical structures with 0 applications#i know i owe you guys that paraconsistency effortpost still#it's coming! just hard to articulate so far#so if you start with the equational class with empty signature your algebras are just sets#the first iteration of the construction gets you the class of monoids#but after that it's what i guess you could call 'near-semirings'?
48 notes
·
View notes
Text
trying to do mathematical proofs while tired will have you doing shit like reading the wikipedia page for multiplication
#this is like that post about that person walking in on their doctor looking at the wikipedia page for bones#i cant. remember. how exponents work with inequalities#like specifically i cant remember if x<y implies x^n < y^n for x and y positive but < 1. and integer n > 1#i think it has to? but my brain keeps insisting theres something funky about it when x and y are between 0 and 1 like this#the thing about going to uni for math is it makes you come at things like this completely bass-ackwards#like. i definitely knew how this worked in high school. and im pretty sure i know now#but now i dont believe myself about it without seeing a proof#im just going to bed lol#this will make more sense tomorrow#WAIT NVM I FOUND THE ANSWER it was on the wikipedia page for 'inequality (mathematics)'#i might have to change the 'less than' to a 'less than or equals' but that doesnt actually matter for this particular application of it#will sort that bit out tomorrow#the implication is definitely true if you use less than or equals though#numbers do not lie#numbers should consider lying down though
7 notes
·
View notes
Text
Yo shout out to Futurama for being featured in the footnotes of my math textbook.
My prof even gave us watching the episode mentioned as a homework assignment which is hella cool!

Like look at this! It's so cool that they actually got people to come in and give solid ass math for a tv problem of people switching bodies!
That's badass! Like this image was only flashed during the show but yo, I fucking appreciate this shit! I also appreciate whoever added that footnotes in the textbook cause yo, that's funny as hell.
Just writing up a fucking textbook like "yo ya know, I think that one episode of this TV show actually uses this theorem. I gotta footnote this shit!"
#math#mathematics#pure math#pure mathematics#Futurama#Futurama s7 ep10#who says pure math has no real life applications#all them math classes finally coming in handy to understand a quick pic from a tv show lol
67 notes
·
View notes
Note
re: math post, the comparison to music is kind of apt in my case in that my dyscalculia makes me essentially tone deaf with regard to math. numbers genuinely do not make sense to me, i cannot wrap my head around them at all. i struggle with extremely basic addition and subtraction to the point that playing a ttrpg is basically impossible for me because my turns take 10x longer than they should because i’m that bad at calculating damage. i love all my friends who love math and i genuinely really admire how good they are at it, but it genuinely doesn’t make a lick of sense to me no matter how hard i try, and i’ve even had teachers openly make fun of me in front of the entire class for making mistakes in it. i truly love how it can bring people joy and how it seems to really provide meaning to others, but for me it’s just a source of pain and suffering, even when i try my hardest to get it. (i also can’t read maps at all which is also part of the dyscalculia :( )
I didn’t really expand on it in my tags but I picked something some people legit just aren’t into! Some people just don’t listen to music. It’s weird to me but I respect it. Same w math like I know some people r never going to like it and that’s fine. I just think the fact that such a high proportion of people dislike it is evidence that something about how we expose people to math is deeply wrong.
(For an explanation of what is wrong with it and how to fix it, see A Mathematician’s Lament. The opening analogy is very similar to the one I made with music, and I love it so much I have a tee shirt custom designed inspired by it.)
I’m not gonna force u to explore math, but I will say the math that post is talking about isn’t. Well.
The math that most mathematicians call beautiful isn’t the stuff with numbers. I have no idea if that makes it any easier for dyscalculia (aside: I used to think I had dyscalculia but it turns out my ADHD is simply way worse than I realized) but it might.
Also like music, you don’t need to be able to play an instrument to appreciate that music is pretty!
Again, I don’t say any of this because I think you personally should like math. It’s fine if you hate math! But I want you to know, like.
I guess on top of me wishing people weren’t essentially trained to hate math, I wish more people understood what the core of math is. Because it’s not about numbers. It’s logic. The core of math is and always has been logic.
Uh I could go on for a long time like I think it’s such bullshit that children hate math when the second layer of math is patterns and kids fucking love patterns, they love when shit is regular and follows rules, and also they love testing the boundaries of rules, which is what math is! but anyway
OH also it’s bullshit if the people you play TTRPGs with don’t let you use an electronic dice roller or something to help you calculate damage and stuff. That’s a disability accommodation.
#mine#math#anon#ask#mathematics#I am no longer studying math but#I will always consider myself a mathematician#it’s a way of viewing the world to me#math is the systemic application of rules#you define some core principles#usually a minimal number#and by applying them in all different combinations#you build this great big beautiful system
5 notes
·
View notes
Text

January 17, 2024 • Wednesday
• --- HARDCORE WEEK — DAY 3/15 --- •
I woke up with a terrible flare today. I skipped uni and stayed home to recover. I haven't fully recovered yet, hopefully I can feel better enough to go to uni tomorrow.
I could only study for 4 hours today, since I took a lot of breaks in between, so that I didn't overexert myself. Pain management is harder when tired.
🎧 Overnight — Connor Price, Tommy Royale

#dailfoxposts#studyblr#studyspo#study#note taking#fibromyalgia#study aesthetic#disability#disabled studyblr#mathematics#mathblr#disabled#computer science#computer applications#days of producitivity#hardcore week#hardcore week challenge
10 notes
·
View notes
Text
youtube
In this video, we delve into the art of solving logarithmic equations with different bases, demystifying the process for you step by step. Whether you're a student brushing up on logarithms or someone facing more complex problems, we've got you covered. Understanding how to work with different bases is crucial when faced with logarithmic equations. We break down the techniques, providing clear explanations using frequently used words to ensure that you grasp the concepts effortlessly. No more getting stuck on those seemingly perplexing logarithmic problems!
#Different bases for solving a log equation#logarithm questions basic#tricky logarithmic questions solve#logarithm formula#solving logarithms#logarithm base#logarithm applications#evaluate basic logarithm#formula of logarithms#solving logarithmic equations#logarithms explained#how to simplify logarithms#solving negative exponents#free math videos#logarithmic#algebra#mathematics#tutorial#Sami’s A Plus#sami’s a plus#math lessons#math for kids#learn math fast#Youtube
2 notes
·
View notes
Text
shirt that says "the humanities aren't the only fields devalued under capitalism"
#noted.txt#idk how to explain to ppl that engineering and tech aren’t the whole of stem#do you think capitalists take abstract mathematics seriously? have you tried to explain research science#with no known applications to ppl outside of academic stem?????#capitalism prizes what you can offer it#and a graphic designer offers more than someone debating if triangles have 4 sides
4 notes
·
View notes
Text

Next week is looking fun
0 notes
Text
MATHEMATICS IN RESEARCH AND PUBLICATIONS AND REFERENCE MATERIALS WITH ADDITIONAL APPLICATIONS OR LABELED IN WAYS THAT BELY THEIR FULL OR ACCURATE SETS OF APPLICATIONS OR USES
TOM CLANCY - THE CARDINAL OF THE KREMLIN TEXT
#TOM CLANCY - THE CARDINAL OF THE KREMLIN TEXT#MATHEMATICS IN RESEARCH AND PUBLICATIONS AND REFERENCE MATERIALS WITH ADDITIONAL APPLICATIONS OR LABELED IN WAYS THAT BELY TRUE USES
0 notes
Text
Mathematicians will see this and be like: “is there a surface that doesn’t have the property in which four points A,B,C,D with the relationship that |AB| = |CD| and |AD| = |BC| aren’t tangent to the surface at any orientation around a given Origin.
https://youtube.com/shorts/FArZQkQ3Ah8
0 notes
Text
WBCHSE Solutions For Class 12 Maths Bayes Theorem And Its Applications
#Mathematics#Mathskills#Mathmemes#Mathematician#Abacusforkids#WBCHSE Solutions For Class 12 Maths Bayes Theorem And Its Applications
0 notes
Text
youtube
#Youtube#Lesson 1: NATURE OF MATHEMATICS (Mathematics in Our World)#1.4 Application in Other Fields#1.4 V
0 notes
Text
The Power of Algebra in Finding the Missing Digit – Part 2
One cannot escape the feeling that these mathematical formulas have an independent existence and anintelligence of their own, that they are wiser than we are, wiser even than their discoverers, that we get moreout of them than was originally put into them.Heinrich Hertz Algebra, often perceived as a daunting challenge, possesses incredible potential to solve complex real-world problems. In this…

View On WordPress
#addition#Algebra#algebraic equation#application of algebra#digit#Divisibility by 9#division#Finding the Missing Digit using Algebra#Math1089#mathematics#Mathematics for All#multiplication#subtraction
0 notes