#combinatorial game theory

[hbmmaster]

guide to different kinds of game theory

standard game theory: imagine two rational actors behaving in their own self-interest. can we manufacture a situation where they'll choose to be nice to each other?

combinatorial game theory: imagine if one (and only one) of the players in a game of chess had the ability once per game to politely ask the other player to let them win, and if they say yes the game ends and if they say no the game continues like nothing ever happened. would that change literally anything strategically for either player?

game theory youtube series: studies have shown that it's more difficult to focus on things while you're aroused. so doesn't that mean competitive games that let you play as a sexy character inherently have the potential for a deeper strategy than games that don't do that?

[janmisali]

I've been stuck on this for months. this hackenbush position is supposed to be a win for Red if Red goes first, but I'm not even close to figuring out how, and I can't even look up the solution. anyone here good at hackenbush

[faerie-entrails]

how it feels to be plural sometimes:

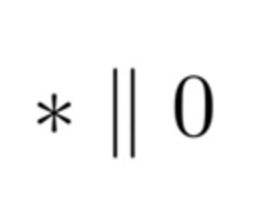
[image description: a simple picture of hackenbush's quantification of: * || 0 . to put it simply: this basically means * is often confused with 0, yet is not the same as 0. also can be thought of as parallel yet not the same.]

[duncathan-salt]

HACKENBUSH: a window to a new world of math

https://youtu.be/ZYj4NkeGPdM?si=muynjn_VHd3apw6V

I love this video so much. it's really difficult to express how meaningful it is to mii, or the way it introduced flavours of whimsy to my life I'd never even considered. this is a very serious video about a very serious mathematical concept. it's also about having fun playing a game, and having fun thinking about a game.

six months after publishing this video, the author, Owen Maitzen, took his own life. I think about him frequently. rest in peace, Owen, and thank you

[kuramirocket]

Jorge Urrutia Galicia: A Mexican Pioneering Mathematician And Computer Scientist

Jorge Urrutia Galicia is a Mexican computer scientist and mathematician.

Galicia is best known for his work on geometry. He made contributions to many different areas of mathematics, including discrete geometry, discrete optimization, and computational geometry. His specialty in computational geometry has made him recognized as one of the leading researchers worldwide. His research has also focused on combinatorial optimization, which is related to combinatorial game theory.

His early works dealt with problems of separability and visibility, a field in which he is an indisputable authority. While it is clear that mathematics has always played a basic role as the underlying foundation of all technology, especially now, and in this case it is confirmed why the technological scope of Dr. Urrutia’s articles in routing is significant; suffice to mention just one: recently algorithms are being implemented based on the ideas of Dr. Urrutia, to make communication networks that can be used in case of natural disasters.

Since the end of the 20th century, he began to work on routing problems, developing algorithms for both the combinatorial and geometric problems, which literally founded a work area of great importance in its application to wireless and cellular networks. In the 21st century, Dr. Urrutia has also stood out for his numerous contributions to the study of discrete sets of points, on which he has made decisive contributions, both in their solution and formulating various variants.

Dr. Jorge Urrutia Galicia studied a bachelor’s degree in mathematics at the Faculty of Sciences of UNAM from 1971 to 1974, and a master’s and doctoral degree in mathematics at the University of Waterloo, Canada from 1976 to 1980. He has worked at the Metropolitan Autonomous University-Iztapalapa, CIMAT, Carleton University, Ottawa University from 1984-1998, where he was "full professor", and since 1998 at the Institute of Mathematics of the UNAM. On average, he teaches five courses each year (two undergraduate and three postgraduate courses).

Annually, he organizes at least two research workshops in Mexico, one of its main objectives being that its students know and work with renowned researchers and learn to collaborate with them as equals.

From 1990 to 2000, he was editor-in-chief of the journal Computational Geometry, Theory and Applications, published by Elsevier Science Publishers. He has been a member of the editorial boards of the Mexican Mathematical Society Bulletin and of Graphs and Combinatorics (Springer, and Computational Geometry: Theory and Applications (Elsevier). He was also editor of the Handbook of Computational Geometry (2000), one of Elsevier's first published handbooks.

He has published more than 270 articles in conference proceedings and research journals in mathematics and computing, which have received more than 6,000 citations, among the most important are two articles on routing in ad-hoc and wireless networks, which have received more than 2 600 citations together: “Compass Routing in Geometric Graphs” and “Routing with Guaranteed Delivery in Ad Hoc Wireless Networks.” In these investigations, Dr. Urrutia develops new strategies – highly efficient – to send information on wireless networks that take advantage of the characteristics obtained by recent technologies such as GPS, in addition to allowing them to travel through these networks effectively without having knowledge of their topology. It is worth mentioning that in 2012 he was the most cited mathematician of the UNAM.

He has given more than 40 plenary lectures at international congresses on Computational Geometry. He was editor-in-chief of "Computational Geometry, Theory and Applications" from 1990 to 2000. He has supervised more than 55 bachelor, master and doctoral theses.

In 2015, he received the "National University in Research in Exact Sciences" award at UNAM. He is is a member of the National System of Investigators, Level 3 He has organized and participated in the organizing committees of several national congresses including the "Victor Neumann-Lara Colloquium on Graphic Theory and its Applications", the "Canadian Conference on Computational Geometry", the "Japan Conference on Discrete and Computational Geometry" and the "Computational Geometry Meetings" (Spain). Oher countries where he has also participated in this way are Italy, Indonesia, Philippines, China, Canada, Peru and Argentina, as well as his home country, Mexico.

Source: (x) (x) (x)

[jadecitrusmint]

1/31/25☕️☕️

Combinatorial Game Theory notes~ my friend and I got coffee and talked our way through the homework together

My courses are becoming serious very fast😵‍💫

[oneslimybastard]

Another underutilized aspect of N, Natural Harmonia Gropius himself, is that he's conceptualized as not just a Math Guy, but a Math Genius if we go by some interview trivia notated on Bulbapedia.

It clearly shows in the way he speaks since his (translated) dialogue (idk about the original japanese one) is full of hamfisted references to formulas and frustration expressed when the chaos of the world does not align with them — which to me is like, the core of his character, something that makes him both An Asshole to deal with but also a very intellectually curios and creative individual. It's just a brand of creativity not a lot of people can keep up with nor understand.

N likes math because a lot of math is about clearly defined variables and their relationship to one another. If you come across an inconsistency that doesn't fit any prior definitions, you iron out a new definition and suddenly the field has expanded upon itself tenfold. It aligns with how his Very Autistic Brain functions, x + y = z, if I do x to y then z will happen. If z doesn't happen, then that just means I have to identify the hidden variables within the exchange and rewrite the formula to be more accurate.

Black and White's quality of writing is. Like pokémon often is. Questionable at best. The foundations are there but the execution is dumbed down and corny because it's still aimed at kids, BW in specific really cutting the theme of pokémon trainer ethics short in favor of just "dang u beat me in the pogiebattle guess ur right!". How-ev-er. In my head, and the reason why I still find the plot of those games compelling (aside for my unhinged thirst for goth man-milf Ghetsis) is that to me they're about local cult-raised autist Normal Henry Gropus bashing his head against the world over and over to desperately try and make the formulas make sense, to distill it into variables he can understand and predict on a consistent basis, and failing miserably at it. Because even if the world is Technically made up of a bunch of chemistry that you could, in theory, predict, there's just a lot of random noise in there from microscopic complexities that fuck everything up.

Pokémon are simpler creatures (discounting the eerily intelligent ones) who will be nice enough to behave like math problems most of the time. Humans rarely extend that grace, the more N studies them like a science project the more contradictory variables pop up. They have a million thoughts in their head he doesn't have access to, that brew into feelings he doesn't understand, which leads to actions he can't do a proper traceback through. Which is frustrating, devastatingly frustrating. At least at first.

Due to how BW2 pans out and my own yearning for thematic mirroring, whereas Ghetsis gives in to the Autistic Bitterness over all these NTs he doesn't fuckign understand, I like to think N develops a sort of joy in studying people like the impossibly complex math problems we are. Because he likes math, he likes figuring shit out, he likes buying a nightmare rubik's cube and charting the squares out on a nightmare variable graph (listen i am not a math guy. i respect the hustle but my skill level is too low to accurately attempt to simulate the process in writing. im sorry math guys) so he has a home-made flexible cheat code on how to solve any possible mix-up of it. It's fun for him, it stimulates his brain and he is so stupid good at it that he can only share that joy with like a stray alakazam or metagross because he's a bit of a tarzan just hanging out in the wilderness, he doesn't know any high end mathematicians he can casually geek out about combinatorial game theory with, and the normies just do not get it .

I think this math enjoying is kind of a big part of his ~Innocence~ as well, since there's a lot of childlike glee to being a Math Guy. It's the love of problem solving as a process rather than a means to an end, it's playful, but severely misunderstood to the point where people kinda might assume things about you if you are a math guy.

N's love of math helps him love the world but it also isolates him. He's a genius, but since he can't communicate it in a palatable way it'll get overlooked in favor of him just being a loomy weirdo on the street chatting up the local patrats.

If introduced to DnD though he'd spend so much time on forging ridiculously optimized multiclass builds, then migrate to digging through old obscure sci-fi ttrpgs from the 80s with hellishly complex systems just for the funsies of learning how the presented variables behave within a variety of frameworks, but then if you actually invited him to play with your group he'd look at you like you'd just called his mom a llama.

He's a neat guy to me, STEM guy who's also one of those animal rights activists who's a little too PETA-coded, I like him :)

[pv1isalsoimportant]

(Semi-regularly updated) list of resources for (not only) young mathematicians interested in logic and all things related:

Igor Oliveira's survey article on the main results from complexity theory and bounded arithmetic is a good starting point if you're interested in these topics.

The Complexity Zoo for information on complexity classes.

The Proof Complexity Zoo for information on proof systems and relationships between them.

Computational Complexity blog for opinions and interesting blog posts about computational complexity and bunch of other stuff.

Student logic seminar's home page for worksheets on proof complexity, bounded arithmetic and forcing with random variables (great introduction for beginners).

Eitetsu Ken's list for resources on proof complexity, computational complexity, logic, graph theory, finite model theory, combinatorial game theory and type theory.

Jan Krajíček's page is full of old teaching materials and resources for students (click past teaching) concernig logic, model theory and bounded arithmetic. I also recommend checking out his books. They are basically the equivalent of a bible for this stuff, although they are a bit difficult to read.

I also recommend the page of Sam Buss, there are downloadable versions of most of his articles and books and archive of old courses including resources on logic, set theory and some misc computer science. I especially recommend his chapters in Hnadbook of Proof Theory.

Amir Akbar Tabatabai's page for materials on topos theory and categories including lecture notes and recordings of lectures.

Andrej Bauer's article "Five stages of accepting constructive mathematics" for a funny and well-written introduction into constructive mathematics.

Lean Game Server for learning the proof assistant Lean by playing fun games.

[notarealwelder]

get the fuck away from work

do yearly planning

anki: 500 reviews and get the backlog below 3000

review Hatcher 2.1 or corresponding Panov

give the lecture/seminar on combinatorial game theory

overall not a feel-good month but like. better than it could be. i think I'll blame most of dissatisfaction on the Fucking Work that ate the middle half of the month. and also on Winter.

work: vacationed. phew. not it will not touch me until spring and by then maybe things will change.

yearly planning...happened....but now points from it need to be either Just Done with coworks or bursts of will or somesuch, or scheduled in the months to come. that did not happen. yet. ygm!

anki: 450 and 3010. ehhhhh good enough tbh. well, not enough if the plan is to exhaust the backlog this year, but good enough to give myself a headpat, i think?

Hatcher 2.1: well i did review all the parts i properly read the last time. in fact I can now generate proofs for the functor nature of homologies, sending homotopy equivalences to chain homotopies, and, gasp, the zigzag lemma. touched on immediate consequences of excision, even. once again couldn't bring myself to touch the 6-page-long proof of excision, though that was out of scope, so, fine.

(i do not like the zigzag lemma. i can tell you how it is true, but why is it true? would be nice to find a narrative onto which it would hang neatly, including all 5(?) of its microlemmas.)

on the other hand, got a surface look at simpler calculations of higher homotopy groups, and now i may have a neat ontology/narrative for how they work, suitable for hanging gears of proofs onto? that's neat if it works as intended.

(kind of despair of packing all of this into a better-accessible series of lectures/seminars. there's just so much nontrivial shit going on. and that's the simpler parts! I'm not even touching cohomologies or spectral sequences or any "additional topics" yet, and that's where the bleeding edge lies. i assume.)

CGT semi: scheduling conflicts, alas. did do some prep work, i.e. talked about the format and sketched plans and exercises. we'll see how it goes! in a week.

[otesunki]

where can i find information on {0|0}. on *. i'm obsessed

colossal infodump incoming

alright there's this Very Very Good Book called Winning Ways for Your Mathematical Plays which explains combinatorial game theory and how they link into surreal numbers in what can only be described as an Unreasonable level of detail, including how it ties into Surreal Numbers oh God surreal numbers is just as loaded of a term Okay let me take a brief detour into That

so surreal numbers are like. imagine defining every number as a pair of sets of other numbers. a set of numbers Less than it and a set of numbers Greater than it. and we write this as foo = {less than foo|greater than foo}. so like. 0 = {|}, 1 = {0|}, 2 = {1|}, 1/2 = {0|1}, -1 = {|0}, that type of thing

the reason why surreal numbers are mindmelting is the fact that they happen to be the Largest Totally Ordered Proper Class and they contain Literally Every Other Totally Ordered Number System inside of them. totally ordered here means that any two numbers are related by < > or =. so like. complex numbers and quaternions aren't included. surreal numbers also behave just like real numbers in that you can do arithmetic on them exactly how you'd do arithmetic with any other real number. and for the surreal numbers that are also real numbers the classic laws of commutativity and associativity hold.

however the surreal numbers are. a.

a bit bigger than just all the real numbers. because there are also numbers that are infinitely big or small and you can make infinitely-bigger-than-infinte numbers and the arithmetic operations still work and also have you ever wanted to take the logarithm base infinity of a number too bad that's defined now

games are what happens when you look at the surreal numbers and go that's for rookies and decide that actually yes {1|-2} makes sense what are you Talking about. why Can't on = {on|} that's a perfectly sane definition also over = {0|over} also Also actually you can define a number that's Even Closer To Zero than over is and if you churn through the calculations you can literally Prove that 0 < tiny < over Yes the number is called tiny

right okay so what is star? in fact if x = {A|B} then -x = {-B|-A} and because A and B are both just the set { 0 } and 0 is {|} you can trivially prove that negating star gives you back star, it's not greater than zero because it has zero in the right hand side, it's not less than zero because it has zero in the left hand side, and it's not Equal to zero because playing a game with a value of zero means that the first player Loses but a game with a value of Star means that the first player Wins which means neither player has an advantage but it's a balanced game in a different way to how 0 is balanced and this is reflected in the Thermograph of star which is a way to draw what star looks like when you Heat it up and Heating a number basically means moving its left and right hand sides closer together in value until eventually they meet up

so Zero because both of its sets are empty is just a vertical line at x=0 because it can't heat up nor cool down but Star on the other hand stays at 0 when it is cooled down but if you Heat it up (make t negative) then actually the two zeroes in it begin Diverging and going in opposite directions

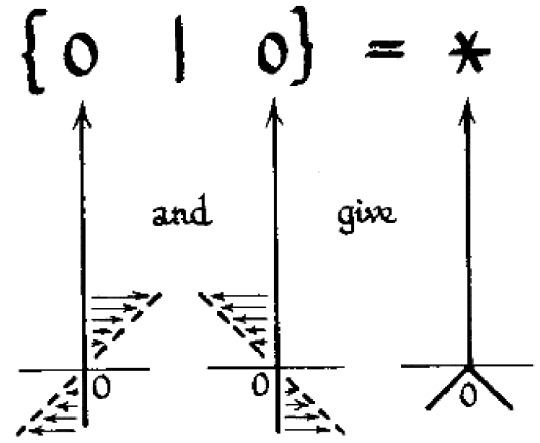
but because the whole thing is Horizontally symmetric it means that the number is its own negative because negating a number is equivalent to a horizontal flip. also if you thought thermographs couldn't get more complicated and involved you're wrong

so. That's. what. star is.

so have you ever wondered what would happen if you had a bunch of numbers that are all mutually recursive and not defined in terms of anything el-

[hbmmaster]

most annoying thing about researching combinatorial game theory is how every paper on the subject ends with "BUT HEY,

[janmisali]

could you give any advice to figuring out hackenbush as a puzzle game? on that itchio game, i'm completely stuck on level 1-11, i'm always exactly one hack short

in pure blue and red hackenbush, literally any move you can do will always be "bad", in that it's making the state of the game slightly more advantageous for the other player. conway called games like these "numbers", and learning how to do the mental math in your head to convert a hackenbush position into a (sur)real number is an extremely powerful tool to have.

this particular hackenbush position consists of five disconnected parts. (it might look like it's only four, but that second one from the right has two different "roots" that don't interact at all, so it's functionally two different things.) any move you make in any of these subgames will be giving Blue "points", and it is your goal as Red to ensure that you give up as few points as possible.

basically, the faster you can do this in your head,

the better you'll be at hackenbush

[alexanderwales]

Game Review: Legend of Zelda: Echoes of Wisdom

Let me lead with a score: 7/10.

I overall enjoyed the core gameplay and thought that the story was completely mid, which normally would result in a better overall impression of a game. Unfortunately, the core gameplay was a lot weaker than it should have been owing to some of the game design decisions, and I have to knock the story points for taking far too much time and being sluggish to get through.

The idea of Echoes of Wisdom is that you collect "echoes" of objects you find and then use them to get through the game. You get the echo of a bed and use two of them to cross a gap. You use the bed to make a ladder to get to higher places. You use the bed to make a bridge, which is really just crossing a gap again. You use the bed to press a switch to open a door. You learn "old bed" very early on, and in my case, it felt like the solution to far too many problems.

The biggest issue is just game design: they didn't do enough of it. In theory from a game mechanics standpoint there should have been ~10 echoes that are mechanically orthogonal to each other, fulfilling different roles. In practice, there are 127 echoes, the menu for accessing them is a mess, and the vast majority of them are redundant. Even the ones that are technically distinct don't have much mechanical distance from each other: you use fire to light torches and lightning to light up green crystals, and this really felt, while playing, like a lazy reskin.

It kind of reminded me of the Green Lantern having the power to make "anything he can imagine" and then 90% of the time using it to make a fist.

Included in those 127 echoes are "combat" echoes, which you get from defeating enemies. They fight for you, and some of them can do other things, but mostly it's the fighting. In most circumstances, you just use the most powerful guy you can, with the exceptions being flying enemies and very rarely needing some kind of elemental counter or the bomb fish.

Some of this is surely driven by game design principles, namely "don't let the player get stuck because they didn't pick up the right echoes along the way". I sympathize with this, but it also kind of sucks, because it makes everything feel bland. There's surely a "minimum echoes" category, just like Mario Odyssey has "minimum captures", and my guess is that you'd only need around 10, and that of those 10, there's just not that much that they actually do differently.

This is especially a shame when compared to Breath of the Wild or Tears of the Kingdom, where the tools are wildly different. Magnesis, Bomb, Ice Block, Time Stop? Those four together have more mechanical variety and combinatorial possibility than all 127 echoes in Echoes of Wisdom. And Tears of the Kingdom was amazing, one of those times when I would sit back and marvel at how much variety and complexity there was, how many challenges were brought forth by really good game design. That doesn't exist here.

So the game mechanical premise is cool, but they don't do too much with it. How's the story?

Told in a different way, I probably would have found it fine. Instead, the heaps of dialogue, slow animations between pieces of dialogue, minimal quality of those animations, and cutsceneitis made me repeatedly roll my eyes. The fact that it was the same locations as other Zelda games also detracted from it, which is something they're going to run into if they keep having the same fantasy races over and over and over.

I think the older I get, the more I hate being stopped in the middle of a game to read a bunch of text, and this is especially true when the gameplay disconnects itself from its story. So if they had snappy responses to me pressing the "yes, I have read this" button, and animation skips that have been present in the vast majority of games for the last five to ten years, I would have liked it better. Instead, I was fighting annoyance with how slow they made everything, particularly the animations for nodding and looking surprised and all these other things. You can have these animations while the text box is being read! We have the technology!

The mute protagonist also doesn't help, and I don't really understand why they used it here except for legacy reasons. Zelda is the character we're spending the most time with, she definitely has a history and perspective, and instead we get very little of her thoughts and feelings. If the intent was to help me project myself into her shoes, it did not work.

So I think this is going to be my last Nintendo game, at least for a while. This game as an 86 on Metacritic, and I'm going to take my overall dislike of many aspects of it as a sign that it's just not for me. I was giving Mario & Luigi: Brothership an appraising look, but this is the game that convinced me that I just don't like the slow, clunky interface to formulaic surface-level stories. I would look past that for good, mechanically rich gameplay, but now it's seeming more hit and miss.

[n0rtist]

Your videos have given me inspiration, and I've been thinking of possibly making Fakemons based on more esoteric math concepts, such as Quaternions and beyond, Transfinite Numbers, Combinatorial Game Theory Numbers (Watch Owen Maitzen's video on the topic for more information), and so on.

Can you give me some tips for how to make such designs? Thanks in advance.

Sounds exciting! Yeah abstract concepts are harder to represent, but there are also a lot of abstract-looking life in our world, especially invertebrates. While I can't think of the best tip off the top of my head, I do usually start with the concept and then go look if there is a species or body shape I can tie it to, trying to focus on what is most visually evident about the concept at hand to reference it in the design.