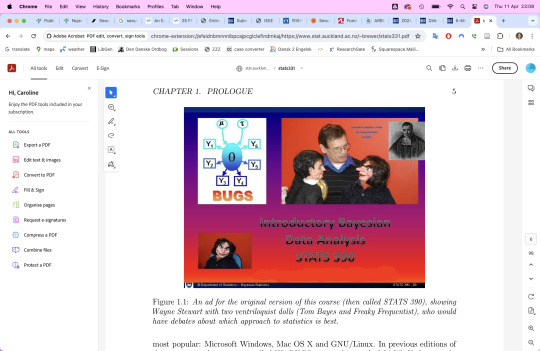
#Bayesian statistics

[gynoidgearhead]

[Image caption for above addition: two comics, each headlined "Mental Gymnastics". The first is a woman or girl stepping a few steps on a gymnastic mat and then happily extending her arms, with a caption reading "I guess fairies are real."

The second has a man energetically swinging from a bar, first from his hands and then his feet; then swinging from rings; then using a pommel horse; then jumping over a flaming car while in a superhero outfit. The various steps are captioned: "A walrus has escaped a zoo or decided to leave its territory for some reason then traveled hundreds of miles of waterways and rivers without being noticed." / It then decided to leave the water and start traveling on land specifically in my city, traveling across miles of streets without being run into or stopped." / "Then it came to my house in particular, made its way to the door, then knocked on it and politely waited." End caption.]

Or someone decided to pull a very illegal prank on you and deliver a walrus to your doorstep, in the manner of xkcd's "instead of office chair, package contained bobcat. would not buy again".

I've asked this question before and been surprised by the results, now I have access to more weirdos it's your problem:

It is the middle of a Sunday afternoon. You have nothing on, and aren't expecting visitors, deliveries or post.

Unexpectedly, there is a knock at the door.

[charliefooks]

Literally everything about this

[imkeepinit]

Bayesian statistics provides us with mathematical tools to rationally update our subjective beliefs in light of new data or evidence.

[silelda]

A new addition to my Favorite Acknowledgements:

To the exclamation point. We couldn't talk about our friends, family, or Bayesian statistics without you.

- Bayes Rules! By Alicia A. Johnson, Miles Q. Ott and Mine Dogucu

[stabby-wabby]

My feelings about studying Bayesian Statistics

[mirastudiesphysics]

Meant to come back to this, but research got in the way and I got a week long extension.

By the third problem I realized that I could make my computer do most of the calculations for me in python, so I ended up programming a simple way to calculate each of the marginals (the probability density of rolling a 6 on a die from 0-5 for 5 rolls) for a binomial distribution, as well as the posteriors for the parameters. The parameter in this problem describes the probability that the die is weighted towards or against rolling a 6. This is done a few times, since the posterior you calculate can be used as a new prior for the next set of data.

Really need to work on my bayesian statistics hw so I'm posting here for once for accountability. I'd like at minimum to reblog with something I learn a long the way.

[byexbyez]

SJSJJSJEJEH not for long i’m afraid

[omegaphilosophia]

The Philosophy of Statistics

The philosophy of statistics explores the foundational, conceptual, and epistemological questions surrounding the practice of statistical reasoning, inference, and data interpretation. It deals with how we gather, analyze, and draw conclusions from data, and it addresses the assumptions and methods that underlie statistical procedures. Philosophers of statistics examine issues related to probability, uncertainty, and how statistical findings relate to knowledge and reality.

Key Concepts:

Probability and Statistics:

Frequentist Approach: In frequentist statistics, probability is interpreted as the long-run frequency of events. It is concerned with making predictions based on repeated trials and often uses hypothesis testing (e.g., p-values) to make inferences about populations from samples.

Bayesian Approach: Bayesian statistics, on the other hand, interprets probability as a measure of belief or degree of certainty in an event, which can be updated as new evidence is obtained. Bayesian inference incorporates prior knowledge or assumptions into the analysis and updates it with data.

Objectivity vs. Subjectivity:

Objective Statistics: Objectivity in statistics is the idea that statistical methods should produce results that are independent of the individual researcher’s beliefs or biases. Frequentist methods are often considered more objective because they rely on observed data without incorporating subjective priors.

Subjective Probability: In contrast, Bayesian statistics incorporates subjective elements through prior probabilities, meaning that different researchers can arrive at different conclusions depending on their prior beliefs. This raises questions about the role of subjectivity in science and how it affects the interpretation of statistical results.

Inference and Induction:

Statistical Inference: Philosophers of statistics examine how statistical methods allow us to draw inferences from data about broader populations or phenomena. The problem of induction, famously posed by David Hume, applies here: How can we justify making generalizations about the future or the unknown based on limited observations?

Hypothesis Testing: Frequentist methods of hypothesis testing (e.g., null hypothesis significance testing) raise philosophical questions about what it means to "reject" or "fail to reject" a hypothesis. Critics argue that p-values are often misunderstood and can lead to flawed inferences about the truth of scientific claims.

Uncertainty and Risk:

Epistemic vs. Aleatory Uncertainty: Epistemic uncertainty refers to uncertainty due to lack of knowledge, while aleatory uncertainty refers to inherent randomness in the system. Philosophers of statistics explore how these different types of uncertainty influence decision-making and inference.

Risk and Decision Theory: Statistical analysis often informs decision-making under uncertainty, particularly in fields like economics, medicine, and public policy. Philosophical questions arise about how to weigh evidence, manage risk, and make decisions when outcomes are uncertain.

Causality vs. Correlation:

Causal Inference: One of the most important issues in the philosophy of statistics is the relationship between correlation and causality. While statistics can show correlations between variables, establishing a causal relationship often requires additional assumptions and methods, such as randomized controlled trials or causal models.

Causal Models and Counterfactuals: Philosophers like Judea Pearl have developed causal inference frameworks that use counterfactual reasoning to better understand causation in statistical data. These methods help to clarify when and how statistical models can imply causal relationships, moving beyond mere correlations.

The Role of Models:

Modeling Assumptions: Statistical models, such as regression models or probability distributions, are based on assumptions about the data-generating process. Philosophers of statistics question the validity and reliability of these assumptions, particularly when they are idealized or simplified versions of real-world processes.

Overfitting and Generalization: Statistical models can sometimes "overfit" data, meaning they capture noise or random fluctuations rather than the underlying trend. Philosophical discussions around overfitting examine the balance between model complexity and generalizability, as well as the limits of statistical models in capturing reality.

Data and Representation:

Data Interpretation: Data is often considered the cornerstone of statistical analysis, but philosophers of statistics explore the nature of data itself. How is data selected, processed, and represented? How do choices about measurement, sampling, and categorization affect the conclusions drawn from data?

Big Data and Ethics: The rise of big data has led to new ethical and philosophical challenges in statistics. Issues such as privacy, consent, bias in algorithms, and the use of data in decision-making are central to contemporary discussions about the limits and responsibilities of statistical analysis.

Statistical Significance:

p-Values and Significance: The interpretation of p-values and statistical significance has long been debated. Many argue that the overreliance on p-values can lead to misunderstandings about the strength of evidence, and the replication crisis in science has highlighted the limitations of using p-values as the sole measure of statistical validity.

Replication Crisis: The replication crisis in psychology and other sciences has raised concerns about the reliability of statistical methods. Philosophers of statistics are interested in how statistical significance and reproducibility relate to the notion of scientific truth and the accumulation of knowledge.

Philosophical Debates:

Frequentism vs. Bayesianism:

Frequentist and Bayesian approaches to statistics represent two fundamentally different views on the nature of probability. Philosophers debate which approach provides a better framework for understanding and interpreting statistical evidence. Frequentists argue for the objectivity of long-run frequencies, while Bayesians emphasize the flexibility and adaptability of probabilistic reasoning based on prior knowledge.

Realism and Anti-Realism in Statistics:

Is there a "true" probability or statistical model underlying real-world phenomena, or are statistical models simply useful tools for organizing our observations? Philosophers debate whether statistical models correspond to objective features of reality (realism) or are constructs that depend on human interpretation and conventions (anti-realism).

Probability and Rationality:

The relationship between probability and rational decision-making is a key issue in both statistics and philosophy. Bayesian decision theory, for instance, uses probabilities to model rational belief updating and decision-making under uncertainty. Philosophers explore how these formal models relate to human reasoning, especially when dealing with complex or ambiguous situations.

Philosophy of Machine Learning:

Machine learning and AI have introduced new statistical methods for pattern recognition and prediction. Philosophers of statistics are increasingly focused on the interpretability, reliability, and fairness of machine learning algorithms, as well as the role of statistical inference in automated decision-making systems.

The philosophy of statistics addresses fundamental questions about probability, uncertainty, inference, and the nature of data. It explores how statistical methods relate to broader epistemological issues, such as the nature of scientific knowledge, objectivity, and causality. Frequentist and Bayesian approaches offer contrasting perspectives on probability and inference, while debates about the role of models, data representation, and statistical significance continue to shape the field. The rise of big data and machine learning has introduced new challenges, prompting philosophical inquiry into the ethical and practical limits of statistical reasoning.

[art-of-mathematics]

Title: "Non-linear regression in a blurry cloud of (un-) certainty"

Date: 2023/06/12 - Size: DIN A4

Collage made with torn pieces of paper, printed background paper (top is rather dark night sky, bottom is mererly clouds in pastel-colors)

I resized and printed the non-linear regression visualisation/illustration and put it on top of the watercolour background paper.

I included a scrap piece of paper with the title of the picture and have torn it with a spiral-shaped jag at the bottom, which I bent around the top part of the non-linear regression illustration.

[psycheapuleius]

[gammaraydeath]

Phenetics :) cladistics :) statistical phylogenetics 😱

[shakespearenews]

Sam Bankman-Fried is wrong about Shakespeare

This is an ostensibly logical argument based on quantitative information. It doesn’t rely on subjective judgements: it just claims that it’s unlikely that Shakespeare is the GOAT because the population of literate individuals in his time was tiny compared to later centuries. On numbers alone, we’re more likely to find the greatest ever writer among the educated multitudes of the 20th and 21st centuries, not the thinly spread turnip-munchers of the 16th.

[dorianbrightmusic]

*sigh*

one of the most important skills that is utterly drilled into you in academia is critical thinking. In an arts degree, you must learn to dissect an argument – if you cannot analyse effectively, you won't get through. In a science degree, you will be taught not only how to read papers, but how to critique them. Science is defined by the scientific method – and as tedious as it may sound, there is no skill more important than being able to scientific method your way through life.

The most important part of research is knowing how to do research – how do you find high-quality papers? What is high-quality evidence? Is it actually appropriate? What does 'significant' actually mean? The media loooves to deploy these terms without having a clue what the scientific meaning is – and as a result, the public get fooled. If you do not know how to do research, you will not find good information by doing your own research.

For example – members of the public who do their own 'research' into trans healthcare might come across the Cass Review, and see that it doesn't find much 'high-quality evidence' for gender-affirming care. They might think 'okay, guess trans healthcare is bad/experimental'. But if you've done academia, you'll know that 'high-quality' is just a synonym for 'randomised control trial' (RCT). For most research, RCTs are the gold standard. But RCTs require that people be unable to tell which condition they're in – that is, if they're receiving a placebo, they won't be able to tell. But with gender-affirming care, you can't exactly conceal the effects of hormones or surgery from a participant – after all, growing boobs/having a voice break/getting facial hair/altered sexual function is kinda hard to not notice. So, an RCT would actually be a completely inappropriate study design. Ergo ‘high-quality’ evidence is a misnomer, since it’d be really poor evidence for whether the treatment is helpful. As such, we know that so-called low-quality evidence is both more appropriate and perfectly sufficient. Academia is crucial to learning to debunk bad research.

And before y’all claim ‘but the papers being cited are all the ones that are getting funding – it’s just corrupt’ – you do realise being taught to spot bad science means that we get explicitly told how to spot corruption? Often, we can learn to tell when papers’ results are dodgy. Academia is about learning not to accept status or fame as a good enough reason to trust something. While I agree there are massive problems with some fields getting underfunded, or with science deprioritising certain social groups, abolishing science will only make this worse.

So. In conclusion, academia may be flawed, but it’s by far the best thing we have for learning to think critically. Anti-intellectualism is a blight on society, and horribly dangerous - it gets folks killed.

[raffaellopalandri]

Advanced Methodologies for Algorithmic Bias Detection and Correction

I continue today the description of Algorithmic Bias detection. Photo by Google DeepMind on Pexels.com The pursuit of fairness in algorithmic systems necessitates a deep dive into the mathematical and statistical intricacies of bias. This post will provide just a small glimpse of some of the techniques everyone can use, drawing on concepts from statistical inference, optimization theory, and…

[skylobster]

The ancient Greek craftsmen achieved a machining precision of 0.001 inches - a truly mind-boggling accomplishment for the era!

[rolerei]

Me when writing my Master’s thesis.

math nation does this happen to you too