#intersections in geometry

[er-cryptid]

Intersections

Patreon

[xponentialdesign]

loop tribute inspired by Herbert Bayer ( 1900 - 1985 ) 90 frames - 50 fPS Chromatic Intersection (1970)

[mellonhead58]

I think one of the most interesting parts of my (thus short) career as a mechanical engineer is that we are taught all sorts of first-principles physics and complex science. And then it turns out that geometric dimensioning and tolerancing, one of the most important and fundamental areas of knowledge for mechanical design and manufacturing and assembly to the point that anybody even incidentally involved in it industrially is aware of it and why it is used, was not only not taught to us during our college education but was in fact not mentioned once at any point even during our drafting courses.

[chicago-geniza]

One of many reasons I feel a profound affinity with Stefania is that she started out studying science and instead became a polyglot who studied art but retained her interest in/knowledge of biology and chemistry and applied their heuristics as metaphors to describe the properties of emerging artistic media, like film in the early 1920s

[windsails]

i’ve changed my mind about identity and alienation. i think it’s more that we are always suspended between two or more ideas, no living being has ever been singular in nature. it’s not that we are anything in particular it’s more honest to realize how much we are at once. what i would advance is the impossibility of singularity, there can never be any such thing. the proof is all around us, always and forever. the importance of the monad is not its alienation but rather, the way it highlights that which links on every side in time and space. every singular point conceals an intersection

[kayleigh-83]

By popular demand (I saw two people asking) I thought I would throw together a quick guide to using the road editor tool in the newest version of SimPE! You'll see that this is a very easy tool to use, and best of all, goof-proof. If you do mess up (you probably will) it's very, very easy to correct.

Very, very, very important to make a backup of your hood before you ever do any tinkering in SimPE! I also recommend practicing on a test hood you don't actively play in to get a feel for it before you do anything to your main hoods.

We're starting with a vanilla Strangetown. I would recommend going in your game and taking a nice overhead screenshot of the hood like this first to look at for reference of where everything is situated the way that you're used to looking at it.

2. Open SimPE, go to Tools> Neighbourhood> Neighbourhood Browser and open the hood you're wanting to work on. If you're not so familiar with SimPE, opening your hood can take some time. Touch nothing until it's loaded!

3. Once it's all loaded, from the Resource Tree list pick Neighbourhood Terrain Geometry (NHTG). Then you'll see one file populate the Resource List - click that. Make sure on the bottom that you have Plugin View tab selected.

4. Now you should see this map of your hood pop up! There are different things you can toggle, I like to check the Show Lots box when I'm editing the roads. Then click the Road Editor button on the right.

5. To be able to see better, I've pulled this Plugin View window up a bit - it may rearrange the Resource List and Resource Tree windows a bit to accommodate. You can also press the Zoom 2x button to see closer, and then you'll have to use the scroll bars to move around the map and the road editor tool.

6. The road editing tools here will be placed down in the same orientation as the map. So the two parallel roads running through Strangetown from this perspective are the vertical straight road pieces (top row, second from left).

When you select a road tool, above it will indicate which tool you have selected.

Also - I recommend having Handle Stop Signs ticked.

7. Once you have the correct type of road selected for the spot you're working on, simply click on the map - it lays it down one tile at a time. If you miss a spot like shown here, just fill it in.

8. If you want to create an intersection, first delete the section of road where the intersection will go.

9. Then choose the type of junction for the intersection you're making, and add that piece in. You'll see a red circle appear (unsure if this is because it's an intersection or because you have handle stop signs selected, but I recommend you do have that selected either way).

10. Once you're done making all your changes, click Close Editor.

11. This is the part where you save your changes! First click Commit in the top right of the editor. Then, File> Save!

12. Load your game to check! Looks pretty good with all those new roads!

13. However, we have indeed made some mistakes! Which were absolutely for illustrative purposes and not truly an accident.

14. Never fear! Simply reload the hood in SimPE - I've deleted the spot where the T-junction should go and added one in, and deleted where the road just ended abruptly and added a proper end piece.

I have not experimented with what happens if you try to build a road through hood deco - if you have, please let us know in the comments how that went!

I also have barely touched the terrain editing tools, so that's outside the scope of this tutorial.

I hope this helped!

[thursday-in-theory]

Given that sturgeons have five rows of scutes, they are basically pentagonal (we can squish them around a bit to make them regular). This of course means that we can use twelve of them to make a dodecahedron. If we used Acipenser stellatus (one of whose common names, according to wikipedia, is the stellate sturgeon) for the faces, we might call the resulting object a stellate dodecahedron (if we imagine the chosen pentagon being roughly in the middle of our fish with the fronts facing outwards, I think this would look vaguely like a small stellated dodecahedron). Of course, by extending the faces we can get a great dodecahedron, which in our case we’ll call the great stellate dodecahedron (I don’t think this changes much visually since we’re working with fully 3D — though freely intersecting — sturgeon whose bodies will mostly block out the new geometry. I could be wrong about that though.). Now if only we can figure out what it means to make star polygons out of fish, we can create great stellated stellate dodecahedrons and small stellated stellate dodecahedrons. And I’m sure we can all agree that sturgeon are great, so we could even call the great stellated version the Great Great Stellated Stellate Dodecahedron.

[cosmicportal]

When swimming through water, the snake leaves traces in the form of wavy circles, which exactly correspond to the dynamics of the shape of prime numbers.

A prime number is a natural number greater than 1 that has no positive factors other than 1 and itself. Prime numbers are specific numbers.

Don Zagier, a distinguished expert, said: “Looking at these figures, one feels the presence of one of the inexplicable mysteries of creation.

The images you see here are created using circles with diameters of successive primes, superimposed on each other and repeated from a common source. For each natural number "n" we draw a periodic curve from the origin intersecting the "x" axis in "n" and its multiples. Prime numbers are those that are intersected by just two curves: the prime number itself and one.

This is a simple method of constructing prime numbers using geometry.

[cryptotheism]

hey ct :) the other day i posted some medieval music theory diagrams and i was really struck by how similar some of them look to kabbalistic diagrams, which made me wonder about the intersection of musicology and cosmology/philosophy/occultism (?) in general, particularly in the middle ages. obviously this is an extremely broad topic, sorry. i just feel like from a modern standpoint it's easy to forget how essential the study of music theory was to the medieval education system and how intertwined it was with arithemtic and geometry. so i'm just curious, are there any medieval thinkers/traditions that come to your mind that took abstract structures proposed by music theory and sort of went ontologically wild with them, i.e. mapped them onto the structure of reality/the universe itself?

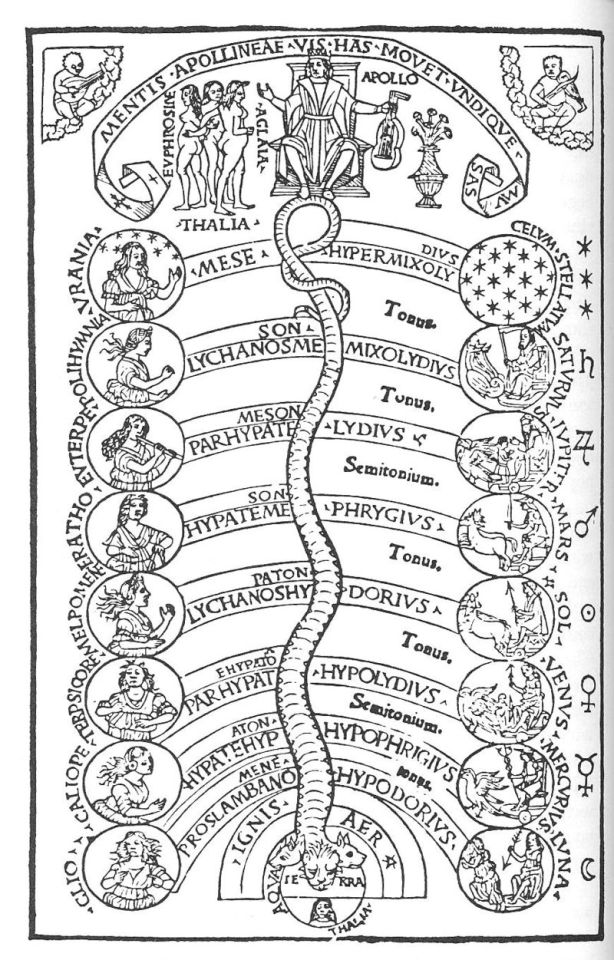
Utriusque Cosmi, Maioris scilicet et Minoris, 1617 (Robert Fludd)

Practica musice, 1496 (showing Apollo, the Muses, the planetary spheres and musical modes)

Phonurgia Nova (New Science of Sound Production), 1673 (This text itself isn't occult, but Kircher himself fits the bill) (Athanasius Kircher)

Kinda! Allusions to the universe as fundamentally musical in nature go back to Pythagoras. It meshes well for antique and medieval doctrines of amity and antipathy, which transposes neatly onto harmony and disharmony. It was often compared to the orbits of the planets, each orbiting at a set distance from the earth in accordance with some greater universal harmony. As far as I'm aware, that wasn't an uncommon way to think of the world.

Music theory is one of those things that gets transposed onto basically everything. If a religion goes on for long enough, you can basically assume that someone will develop some interesting spiritualized music theory. Its not something I've ever delved into personally, largely because I find music theory confusing.

As for Kabbalistic literature specifically, the story goes that Issac Luria was inspired by watching the sun filter through a complex fountain in Safed. I've always associated post-lurianic diagrams with flowing water. But if I recall correctly, Hebrew letters were also regularly used for musical notation, so music-as-mysticism is only a stones throw away. I would be shocked if writing on the subject doesn't exist.

Personally, music-as-mysticism is something I generally associate with Sufism. I know Inayat Khan was popular in part because of both his musical talents, and his doctrine that incorporated musical concepts. But he was pretty modern!

[thehaberdasheress]

Great news! After a ton of work, I've got my business's 2024 Kickstarter up and running! It's live now until Sunday, November 17.

I have a lot of projects underway that this project will help me see to fruition, including:

Embroidery/historical costume kits with good materials and accessible instructions

A digital sewing pattern for what can be a partlet, if you're feeling nerdy, or a way to bring damn cool sleeves to whatever outfit you want if we're being modern about it

A system of patterns and stencils that bring intricate freehand Elizabethan embroidery down from (imo) terrifying complexity to an accessible art project

And/yet/also, I know myself. I am a bit of an ADHD chaos goblin with chronic pain. So I've learned from Kickstarters past, and made sure to center the campaign around rewards that I can be certain of delivering. That is, this campaign absolutely will include vouchers for free or discounted copies of those projects if they're funded and they happen! But I know they will take time and definitely not arrive by Christmas 2024.

Therefore: I've been designing a bunch of new items that I can be sure of! I wanted to be able to show off my embroidery patterns in new and interesting ways, and find different methods of fulfillment that are ready to roll out the moment the campaign ends and I get your shipping information.

If you've ever wanted to get all the unique patterns I design for my Etsy shop in a charted PDF format? Backing my Kickstarter is the way you get that.

Some of my most popular designs will be available as decorative stickers, paper bullet journal-style productivity stickers, and a mug!

There are a lot of others, and I'll probably detail more about them over the next week and a half, but it's past 4am so I'll keep this relatively short. The outlines are up on the Kickstarter. Here's the one I'm the most excited about:

Motherfucking CUSTOM-WOVEN throw blankets!

I made the design myself, as the intersection of my obsessions with medieval celestial ceilings, sacred geometry, marine navigation, Tolkienian Elvish heraldry, and quilting. It's called "Mariner's Star", and I'm incredibly excited about it. If you don't know about jacquard looms and how they were 19th century punch card proto-computers, I think you're missing out.

Kickstarter link here!

It ends Sunday, Nov 17!

[literaryvein-reblogs]

A List of "Poetic" Words

to include in your next poem (pt. 2 because there are a lot of them)

Abyssopelagic: The deep regions of the ocean (or the “abyss”), as in, the “abyssopelagic zone.”

Acersecomicke: One whose hair was never cut.

Agathokakological: Composed of both good and evil.

Bêtise: An act of foolishness or stupidity.

Cachinnate: To laugh loudly or immoderately

Cacography: Bad handwriting.

Deipnosophist: A person skilled in table talk

Diaphanous: Sheer and light; almost transparent; or delicately hazy.

Incendiary: Flammable; something that incites agitation or sedition.

Jentacular: Pertaining to breakfast.

Lagniappe: A gift, usually monetary like a tip, and you might still hear it in areas of southern Louisiana and southeastern Texas.

Languor: Lack of energy or vitality, or, more concisely, sluggishness or laziness.

Limerence: An old-fashioned way to describe intense feelings of obsession or infatuation with another person.

Matutinal: Of, relating to, or occurring in the morning.

Noctivagant: Going about in the night; night-wandering.

Opsimath: A person who begins to learn late in life.

Patrizate: To imitate one's father or forebears.

Peccability: Capability of sinning.

Pot-valiant: Bold or courageous under the influence of alcoholic drink.

Quadrivium: The intersection of four roads. The word was adapted in medieval times to refer to the teaching of four essential subjects (arithmetic, geometry, astronomy, and music).

Recogitate: To think over again.

Redame: To love in return.

Scripturient: Having a strong urge to write.

Sibilance: The distinctive hiss-like sound made by the letter S, or comparable sounds like a soft C.

Solivagant: Rambling alone, marked by solitary wandering.

If any of these words make it into your poem/story, please tag me or leave me a link in the replies. I'd love to read them!

Sources: 1 2 ⚜ More: Word Lists ⚜ Writing Resources PDFs

[talonabraxas]

“The body itself is to reveal the light that’s blazing inside your Presence.” — Rumi

Sirian Merkabah Talon Abraxas

Merkabah Meaning: Ancient Technology

The word Merkabah has both Hebrew and Egyptian origins. In Hebrew, the word stands for chariot. In this context, the Merkabah is a chariot that helps us meet and recognize the various cosmic energies that govern our world. In the Egyptian language, the word is broken down into three parts:

Mer (light) Ka (spirit) Ba (body)

In the human body, the Merkabah comprises the first eight cells formed after fertilization. These cells are found at the root chakra of the body. Since this point is seen as the center of our body, the Merkaba meaning can be seen as the intersection of our physical and subtle energies. When described this way, our light body forms the basis for creating our physical and spiritual selves.

Regarding sacred geometry, the light body is represented by a star tetrahedron known as the Star of David. Looking closely at the figure, we understand how it stands for balance, stability, and integration. The top tetrahedron is said to represent masculine energy—which stands for logic and rationality—while the bottom one represents feminine energy—which stands for emotion and intuition.

The top can also represent the Universe, while the bottom represents the Earth. In other beliefs, the top can symbolize spirituality, whereas the bottom symbolizes physicality. These energies are opposite, but they come together to form a whole. We move closer to the Divine when we achieve a similar balance within ourselves.

Some believe that the tetrahedron in the Merkabah is also related to the solar plexus chakra, which stands for our feelings of self-worth. When this chakra is balanced, we have the self-confidence to create our destiny. The star tetrahedron is ideal for our spiritual journey because the top part is connected to the spiritual realm. In contrast, the bottom part is grounded in the physical realm.

[the-literary-alchemist]

The House Between Night & Morning

Come inside the house of my heart & make yourself comfortable:

let yourself relax & stretch out your totality

until every window pane & threshold burst with magic, maybe

ecliptic alchemy to possess every fiber & cell composing our

treachery of anatomy, these cages of mortality. Even as other

realities ripple between us, we acknowledge our birthright

belonging to everything nebulous, perpetually existing 

in a division of light & mourning, of night & morning. Nothing is

complete without our celestial dance, whether we dress

bright or darkly, but the spaces between paint this

cosmic canvas. As I imagine the universe fitting within

our minds, the only sum I see is you + me = celestial geometry. While

all our seconds have shifted into paradigm, we must now

participate in this time & what is left of it. Soon we too will become

the same lights we once wished upon among this sea of stars.

My center of gravity, do you find a home in our friendship too?

This intersection of ecstasy & stasis where we share a satellite

in outer space: Yes, this is my favorite place.

— XY

[desceros]

Where do your story titles come from? 🤗

i typically try to encapsulate the theme of my fic in the title, though sometimes it's more tied to the vibe. i'll give a few examples of some of the ones i really like for you!

aaaand under a cut because of course it's me talking about my fics so it got way too long hahahaha

asymptote - in math, an asymptote is a curve that approaches a line infinitely close but never intersects into infinity. the theme of this particular fic was that you want to merge with leo and he with you (not exactly literally, though there is a reference to being jealous of the mindmeld) in an attempt to Know each other and be as close as possible. the lesson the two learn at the end of the fic is that this isn't really possible; perfection isn't a realistic thing to achieve in a relationship. but you can try and get really, really close, and that journey is the fun of being together

nicht-zuhause-sein - this is pulled from the text of house of leaves, at the end of the large paragraph that really made me foam at the mouth at the thought of writing this fic. it's a paragraph that seems to try and capture the energy of reading hegel or heidegger (two of my favorite philosophers to hate reading), discussing the word "uncanny" and how little tiny shifts in your environment create the feeling. it ends with the line:

"In anxiety, one feels uncanny. Here the peculiar indefiniteness of that which Dasein finds itself alongside in anxiety, comes proximally to expression: the “nothing and nowhere”. But here “uncanniness” also means “not-being-at-home” [das Nicht-zuhause-sein]."

since the fic is you and leo being at home but... not. the fic is thus named "not-being-at-home."

amaranthine - this is a really fun word that has always been one of my favorites!! an amaranth is a purple flower that represents immortality/eternity, or something that lasts forever. it references donnie's eternal undying love for you, the fact that his soul color is purple, and also the purple-red of a deep bruise. a bruise that donnie and you both wish could stay there forever, because what it represents to you.

euclidean line - another math one! (can you tell i like math yet?) a line, in euclidean geometry, is a path that connects two points. in the fic, donnie says the following:

“…I feel like this was inevitable,” he murmurs as you reach your hands around him, ghosting the pads of your fingers down the softness of his shell. His hands, hungry for you, slide up the back of your shirt, finding skin and conquering it in his name. “Along every point of the space time continuum, the very laws of physical determinism themselves. Every causality says that you’re point A, and I’m point B, and there’s a segment between us.”

this is him basically saying that falling for you was the only way things could have happened, that there was no other way it could have gone, just as there is one and only one line between two points.

somewhere in the symphony tag is a post where i broke down that title that you can--oh you know what never mind i'll go find it for you because i Love this one. here we go

so yeah i hope that gives you kind of an idea of how i title things! sometimes it's just "ehh what would fit" but i try hard to make it something clever heehee

[anntova]

Parallels that can cross at infinity

I think I should explain what this drawing title means. In Lobachevsky geometry there is an axiom of parallel lines, which states that parallel lines can intersect at infinity

[algebraic-dualist]

Universal Algebraic Geometry, Part 1

In this post I recall a number of basic ideas from universal algebra in order to start setting up a framework for studying the algebraic geometry of arbitrary algebraic objects.

For our purposes, an algebra is just a set equipped with some operations. We assume that the set of operations has been fixed. Given an algebra A alongside an operation ♡ we write ♡ᴬ for the definition of that operation on the algebra A, or just ♡ when ambiguity does not result. Our notion of a homomorphism is as follows:

Definition: A homomorphism f from an algebra A to an algebra B is a function f : A -> B such that for each n-ary operation ♡ alongside elements x₁, ..., xₙ ∈ A it follows that f(♡ᴬ(x₁, ..., xₙ)) = ♡ᴮ(f(x₁), ..., f(xₙ))

Kernels and Congruences

Definition: A congruence θ on an algebra A is an equivalence relation such that for any (x₁, y₁) ∈ θ, ..., (xₙ, yₙ) ∈ θ and n-ary operation ♡ it follows that (♡ᴬ(x₁, ..., xₙ), ♡ᴬ(y₁, ..., yₙ)) ∈ θ. We write Cgr(A) for the set of congruences on A.

Example: The maximal congruence ∇ on A is just A × A.

Example: The minimal congruence ∆ on A is just { (x, x) | x ∈ A }.

Example: Any arbitrary intersection of congruences on A is a congruence on A. In particular, we can form the intersection of all congruences on A containing any arbitrary subset R of A × A in order to obtain the minimum congruence containing R. In particular, choosing R to be the union of two congruences, we get a meet of congruences.

In the case of a group, it follows that (x, y) ∈ θ if and only if (x - y, 0) ∈ θ hence a congruence is completely determined by the set { x | (x, 0) ∈ θ }. In other words, by a normal subgroup. So congruences are just the data of a normal subgroup. Similar remarks apply to ideals of rings.

Kernels of homomorphisms are a particularly important source of congruences on algebras:

Definition: The kernel of a homomorphism f : A -> B is denoted by ker(f) and defined by setting ker(f) := { (x, y) | f(x) = f(y) }.

Lemma: Given a homomorphism f : A -> B it follows that ker(f) is a congruence on A. Proof:

Given x ∈ A it follows that f(x) = f(x) hence (x, x) ∈ ker(f).

Given x, y ∈ A such that (x, y) ∈ ker(f) it follows that f(x) = f(y), which is to say f(y) = f(x) hence (y, x) ∈ ker(f).

Given x, y, z ∈ A it such that (x, y) ∈ ker(f) and (y, z) ∈ ker(f) it follows that f(x) = f(y) = f(z) hence (x, z) ∈ ker(f).

Given (x₁, y₁) ∈ ker(f), ..., (xₙ, yₙ) ∈ ker(f) and n-ary operation ♡ it follows that f(xₖ) = f(yₖ) for each k, thus by the homomorphism property f(♡ᴬ(x₁, ..., xₙ)) = ♡ᴮ(f(x₁), ..., f(xₙ)) = ♡ᴮ(f(y₁), ..., f(yₙ)) = f(♡ᴬ(y₁, ..., yₙ)) showing that (♡ᴬ(x₁, ..., xₙ),♡ᴬ(y₁, ..., yₙ)) ∈ ker(f).

QED.

Theorem: Given a homomorphism f : A -> B alongside a congruence θ on B it follows that the preimage f*(θ) := { (x, y) ∈ A | (f(x), f(y)) ∈ θ } is a congruence on A. Proof: 1. Given x ∈ A, as θ is reflexive it follows that (f(x), f(x)) ∈ θ hence x ∈ f*(θ). 2. Given (x, y) ∈ f*(θ) it follows that (f(x), f(y)) ∈ θ. As θ is symmetric it follows that (f(y),f(x)) ∈ θ, thus (y, x) ∈ f*(θ). 3. Given (x,y) ∈ f*(θ) and (y,z) ∈ f*(θ) it follows that (f(x), f(y)) ∈ θ and (f(y), f(z)) ∈ θ. As θ is transitive it follows that (f(x), f(z)) ∈ θ hence (x, z) ∈ f*(θ). 4. Given (x₁, y₁) ∈ f*(θ), ..., (xₙ, yₙ) ∈ f*(θ) alongside an n-ary operator ♡ it follows that (f(x₁), f(y₁)) ∈ θ, ..., (f(xₙ), f(yₙ)) ∈ θ, hence as θ is a congruence (♡(f(x₁), ..., f(xₙ)), ♡(f(y₁), ..., f(yₙ))) ∈ θ. Being that f is a homomorphism, this means (f(♡(x₁, ..., xₙ)), f(♡(y₁, ..., yₙ))) ∈ θ showing that (♡(x₁, ..., xₙ), ♡(y₁, ..., yₙ)) ∈ f*(θ). QED.

Therefore, every homomorphism f : A -> B induces a map f* : Cgr(B) -> Cgr(A). In fact, congruences organise themselves into a lattice, and this map f* is a homomorphism of lattices. But for the moment, we will not worry about that.

Composite Kernel Lemma: Given homomorphisms f : A -> B and g : B -> C it follows that

ker(g ∘ f) = f*(ker(g)).

Proof:

Observe that (x, y) ∈ ker(g ∘ f) if and only if g(f(x)) = g(f(y)), which is the case if and only if (f(x), f(y)) ∈ ker(g), which is the case if and only if (x, y) ∈ f*(ker(g)).

QED. Corollary: ker(f) = f*(∆). Proof: ker(id ∘ f) = f*(ker(id)) = f*(∆). QED.

Quotients of Algebras

Given a congruence θ on an algebra A it is the possible to construct the quotient algebra A/θ whose elements are equivalence classes of elements of A under the congruence θ. Sending every element to its equivalence class under θ gives a homomorphism π : A -> A/θ which we refer to as the canonical projection of θ.

Theorem: Given a congruence θ on an algebra A it follows for every homomorphism f : A -> B with θ ⊆ ker(f) that there exists a unique injective morphism g : A/θ -> B such that f = g ∘ π.

Proof: Observe that π(x) = π(y) iff (x, y) ∈ θ, which as θ ⊆ ker(f) implies f(x) = f(y). Therefore, it is well-defined to construct g by setting g(π(x)) = f(x). One can check that this works. QED.

Homomorphism Theorem: Given a surjective homomorphism f : A -> B it follows that there exists an isomorphic g : A/ker(f) -> B such that g ∘ π = f.

Proof:

Applying the prior Theorem there exists a unique injective morphism g : A/ker(f) -> B such that g ∘ π = f. Observe that as f is surjective, it then follows that g is surjective.

QED.

Hereditary Classes of Algebras

Recall that the prime ideals 𝔭 of a ring R are exactly those ideals 𝔭 such that R/𝔭 is an integral domain. Notice that being an integral domain amounts to satisfying a universal axiom, namely xy = 0 implies x = 0 or y = 0. Hence, integral domains are closed under moving to subalgebras, and the property of being an integral domain is preserved by isomorphisms.

Definition: A class K of algebras is hereditary iff it is closed under subalgebras and isomorphisms. Given a universal class K we say that a congruence θ on an algebra A is a K-congruence iff the quotient algebra A/θ belongs to the class K.

Theorem: Given a hereditary class K alongside a homomorphism f : A -> B it follows for every K-congruence θ on B that f*(θ) is a K-congruence on A.

Proof:

Consider a homomorphism f : A -> B alongside a K-congruence θ on B. It follows that f*(θ) is a congruence on A, so it suffices to demonstrate that it is a K-congruence. Recalling our canonical projection π : B -> B/θ and our Composite Kernel Lemma, it follows that ker(π ∘ f) = f*(ker(π)) = f*(θ). Therefore, the morphism π ∘ f : A -> B/θ factorises through a unique injective morphism g : A/f*(θ) -> B/θ. This means that A/f*(θ) is isomorphic to a subalgebra of B/θ. As θ is a K-congruence it follows that B/θ belongs to K, which as K is a hereditary class then implies that A/f*(θ) belongs to K, so that f*(θ) is then a K-congruence.

QED.

Corollary: Preimages of prime ideals are prime ideals.