#Addends and Sum

[giorgio52fan]

Math Marvels: Adding Natural Numbers Made Easy!

Before we start solving some problems, click on the video below: Problem 1: Understanding Carryover in Addition of Natural Numbers Introduction: Addition is a fundamental mathematical operation that helps us combine numbers and find their total value. However, when adding larger numbers, a concept called “carryover” can pose challenges for learners. Problem: Consider the addition problem: 589 +…

[listranz]

Regarding Toby as a trollhunter.

This plot twist is a priori less epic and successful than the main one, simply because it does not shift Jim's role and his contribution to the fate of the hunters, and almost does not reveal Toby's potential as an independent hero.

Jim went through the whole story from beginning to end, he saw its ending and, of course, retained, if not surpassed, all his former skills (both martial and spiritual, lol). Regardless of whether he has an amulet or not. It's clear as day that Jim will be desperate to help Toby; that he will become his mentor, his right-hand man, his support, his advisor, etc... In short, Jim will teach him everything he knows. Jim will do anything for Toby. He will sincerely try to raise his friend to be a real trollhunter; and even more - Jim wants the hunter-Toby to become better than himself.

Jim will try to "resurrect" memories in his friends; firstly, to bring them closer together, and secondly, to protect them from the mistakes of the past. Consequently, Jim will become a mentor not only to Toby, but also, in part, to all the other heroes.

The question then is, how does this turn of events not make Jim Lake a true and worthy trollhunter? Changing the order of addends does not change the sum. Yes, Toby will have the amulet; yes, in this alternative history Toby has definitely become stronger and more confident, but this does not diminish Jim's influence on the plot. In that case, I really do not understand why it was necessary to change it.

I don't mean to imply that this twist wouldn't be effective in the Arcadia universe. Far from it. I don't know. I mean, I just don't see how this gimmick would help a fan of the franchise believe that Jim isn't the "main" character anymore?

Okay. Whatever, it's fun. Anyway, I console myself with the thought that before the final battle with Gunmar and Morgana, Merlin will invariably offer Jim to become a half-troll.

Yes, Jim is no longer the main trollhunter, but he is still the main combat unit and, perhaps, Toby will have a different combat advantage in the new story.

Well, you know, Jim has always been a strange, "wrong" person, absurdly trying to live a "normal" life. It is very likely that his fate as a half-troll will be a little more dynamic, dramatic and... effective? xD

[topsyturvy-turtely]

an almost whisper

prompt "whisper" by @onesmallfamily

highly inspired by this gif by @phoenix27884:

a/n: hey! i wanted to at least do ONE prompt of the 30 day sherlock september challenge. here is my ficlet of yesterday, because seriously- i fell asleep while writing it 😅

ps: so sorry bout the no uppercase letters, as said i was very tired for half of this (and lazy for the second)

○◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠○

sherlock was sitting across from him. from john watson. what a gorgeous man he was. gray silky hair - combed back, a dark blue jumper that looked ridiculously endearing on him... his doctor hadn't had time to shave this morning and sherlock was currently trying to gauge how many colour shades you could see in john's beard. one, two, three...

the beard moved. well not the beard itself but the lips that sat between the beard.

what would it feel like to-

"sherlock, did you hear me?"

the asked man raised his eyebrows. had he heard him? "still caught up on the case, i fear."

"you solved it. what's there to think about?"

his john. asking just the right questions. unfortunately they were rather uncomfortable right this moment, considering sherlock had been thinking about and staring at john's facial hair...

topic change. "how was dinner?"

"delicious. pity you didn't have any."

"eating..."

"... slows you down, i know, i know.", john said, but there was an amused grin on his lips. for some reason sherlock had to look away to catch himself. john smiling at him like that, it did something to him. something that hits way further inside than just into his heart.

he sensed john leaning back and stretching his face up to the sun. sherlock simply had to turn his gaze back onto him. the sun highlighted the few blond strands left and the red undertone in john's beard... it accentuated the wrinkles, that sherlock loved, because they reflect just how real john is. the detective then realized he was staring again and looked away. pretending to focus on the people around him, maybe deducing them. in reality every sense was directed at john. he heard him move, sensed his body being closer to his, smelt a hint of the coffee john had drunk, saw him putting his chin into his hand out of the corner of his eye.

he felt john staring now. sherlock decided it was safe to glare back at him. and was swept off his feet, well he was sitting, but he was still overwhelmed by john's expression. there was so much adoration, fascination and out of a lack of better words - love in his eyes.

sherlock had to smile back at him. he felt his face getting hotter. john - without saying a word - made him feel special.

john's gaze never left his and then exclaimed, barely above a whisper, "i'd like to kiss you." it was out of the blue, but it felt like the perfect timing.

what happened next felt natural, like they were actors who were acting according to a script: sherlock stood up leaned over the small table and placed his lips on john's.

the kiss was over soon, but they both knew it was just the first of uncountables.

a smile, a hand sneaking into his, looks speaking more than words.

on that day just like that, with that tiny almost-whisper and their promising first kiss they stopped being augend and addend and began being a sum.

○◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠◡◠○

tag list! (tell me if you wanna be added or removed please 💚) @justanobsessedpan @helloliriels @catlock-holmes @fluffbyday-smutbynight @inevitably-johnlocked @hisfavouritejumper @rhasima @forfucksakejohn @ohlooktheresabee @turbulenttrouble @so-youre-unattached-like-me @totallysilvergirl @peanitbear @train-mossman @loki-lock @smulderscobie @timberva @grace-in-the-wilderness @chinike @jawnn-watson @whatnext2020 @escapingthereality @missdeliadili @kettykika78 @musingsofmyown @7-percent @speedymoviesbyscience @astudyin221b @francj15 @we-r-loonies @mxster-jocale @sherlockcorner @noahspector @our-stars-graveside @jobooksncoffee @baker-street-blog @macgyvershe @myladylyssa @battledress @a-victorian-girl @dreamerofthemeadow @oetkb12 @ohnoesnotagain @mutedsilence @jawnscoffee @raenchaosandcozyadashofmurder @lisbeth-kk @quickslvxrr

[22ums115]

Algebra - Introduction and Basic Formula

INTRODUCTION AND BASIC FORMULAS IN ALGEBRA

Algebra is the part of mathematics that helps to represent the problems or situations in the form of mathematical expressions. Algebraic formula are used to simplify the algebraic statement. Algebraic formulas are useful for resolving algebraic, quadratic, polynomials, trigonometry, probability, and more.

Introduction of Algebra

Algebra is the branch of mathematics in which arithmetical operations and formal manipulations are applied to abstract symbols rather than specific numbers. The notion that there exists such a distinct subdiscipline of mathematics, as well as the term algebra to denote it, resulted from a slow historical development. This article presents that history, tracing the evolution over time of the concept of the equation, number systems, symbols for conveying and manipulating mathematical statements, and the modern abstract structural view of algebra. For information on specific branches of algebra, see elementary algebra, linear algebra and modern algebra.

Algebraic Formula

Algebraic formulas are the combination of numbers and letters to form an equation or formula. The algebraic formula is a short quick formula to solve complex algebraic calculations.

Algebraic properties

The properties of algebra enable us to solve mathematical equations. Notice that these properties hold for addition and multiplication. These properties include the associative property, commutative property, distributive property, identity property, inverse property, reflexive property, symmetric property, and transitive property.

Algebraic Formula

a2 – b2 = (a – b)(a + b)

(a + b)2 = a2 + 2ab + b2

a2 + b2 = (a + b)2 – 2ab

(a – b)2 = a2 – 2ab + b2

(a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca

(a – b – c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ca

(a + b)3 = a3 + 3a2b + 3ab2 + b3 

( a + b )3 = a3 + b3 + 3ab(a + b)

(a – b)3 = a3 – 3a2b + 3ab2 – b3 or a3 – b3 – 3ab(a – b)

a3 – b3 = (a – b)(a2 + ab + b2)

a3 + b3 = (a + b)(a2 – ab + b2)

(a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4

(a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4

a4 – b4 = (a – b)(a + b)(a2 + b2)

a5 – b5 = (a – b)(a4 + a3b + a2b2 + ab3 + b4)

If n is a natural number an – bn = (a – b)(an-1 + an-2b+…+ bn-2a + bn-1)

If n is even (n = 2k), an + bn = (a + b)(an-1 – an-2b +…+ bn-2a – bn-1)

If n is odd (n = 2k + 1), an + bn = (a + b)(an-1 – an-2b +an-3b2…- bn-2a + bn-1)

(a + b + c + …)2 = a2 + b2 + c2 + … + 2(ab + ac + bc + ….)

Laws of Exponents (am)(an) = am+n ; (ab)m = ambm ; (am)n = amn

Properties of Algebra :

Commutative property:

Addition : a + b = b + a

Changing the order of addons does not change the sum.

Multiplication : a x b = b x a

Changing the order of the factor does not change the product.

Associative Property:

Addition : (a + b)+ c = a + (b + c)

Changing the grouping of the addends does not change the sum.

Multiplication : (a x b) xc = a x (b x c)

Changing the grouping of the factors does not change the product.

Distributive properties: 

Addition : a × (b + c) = a × b + a × c

Multiplication :  (a + b) × c = a × c + b × c

The distributive property states that multiplying each element by a single term and then adding and subtracting the products is the same as multiplying each component by a single term and then adding and subtracting the products.

Rule of multiplication over subtraction: p (q-r) = p*q – p*r 

If p, q, and r, are all integers.

Left distributive law if p* (q-r) = (p * q) – (p*r)- and

Right distributive law if (p-q)*r = (p*r) – (q*r)-

What are the properties of Algebra?

Associative Property

Commutative Property

Distributive Property

Identity Property

Inverse Property

Reflexive Property

Symmetric Property

Transitive Property

Read more...

[polyphonetic]

He said sum when

you add up

would you be

the total of the addends

the values and summands

[dr-vrat1o]

𝙷𝚎𝚕𝚕𝚘, 𝚑𝚎𝚕𝚕𝚘! 𝙱𝚢 𝚛𝚎𝚚𝚞𝚎𝚜𝚝 𝚘𝚏 𝚘𝚗𝚎 𝚘𝚏 𝚖𝚢 𝚕𝚘𝚟𝚎𝚕𝚢 𝚊𝚗𝚘𝚗𝚜, 𝙸'𝚖 𝚑𝚎𝚛𝚎 𝚝𝚘 𝚊𝚗𝚗𝚘𝚢 𝚢𝚘𝚞 𝚝𝚘 𝚝𝚑𝚎 𝚋𝚎𝚜𝚝 𝚘𝚏 𝚖𝚢 𝚊𝚋𝚒𝚕𝚒𝚝𝚢!

𝙴𝚡𝚊𝚖𝚙𝚕𝚎: 𝚝𝚎𝚗 + 𝚝𝚎𝚗 𝚒𝚜 𝚝𝚠𝚎𝚗𝚝𝚢! 𝙱𝚞𝚝 𝚎𝚕𝚎𝚟𝚎𝚗 + 𝚎𝚕𝚎𝚟𝚎𝚗 𝚒𝚜 𝚝𝚠𝚎𝚗𝚝𝚢 𝚝𝚘𝚘!

𝙾𝚑! 𝙰𝚗𝚍 𝚕𝚎𝚝𝚝𝚎𝚛𝚜 𝚒𝚗 𝚖𝚊𝚝𝚑 𝚊𝚛𝚎 𝚍𝚞𝚖𝚋 𝚋𝚢 𝚝𝚑𝚎 𝚠𝚊𝚢, 𝚠𝚑𝚢 𝚑𝚊𝚟𝚎 𝚝𝚑𝚎𝚖 𝚠𝚑𝚎𝚗 𝚠𝚎 𝚊𝚕𝚛𝚎𝚊𝚍𝚢 𝚑𝚊𝚟𝚎 𝚗𝚞𝚖𝚋𝚎𝚛𝚜?

Of course you were sent to annoy me. Why else not, for a masked fool. Perhaps the rest of the anonymous askers I've had were masked fools as well.

But to correct you, it's "twenty two" not "twenty too". Letters are a substitute for when you don't have a certain part of the equation. A simple equation, for a simple mind like yours;

4 + x = 12

And now we're trying to look for x, which is our second addend, since we have the first addend, and the sum. If you transpose the equation, it will become 12 - 4 = x. Due to the fact that subtraction is the opposite of addition, we're going to be using that operation.

Now, it must be simple for you to get the answer of that, would it not?

[parsnippety]

@mimill3 if it helps...

2+3 is the same as 3+2 only because they're both just numbers. If you wanna get technical, they're both addends. They work together to get a sum.

2-3 isn't the same as 3-2 because they are fighting. 2-3 is the same as 2+ (negative 3). and negative 3 is different than negative 2.

If you wanna get technical, in 2-3=-1, 2 is the minuend and 3 is the subtrahend. -1 is the difference.

When you are adding, you are lumping two addends together. When you subtract, you are demanding to fill the subtrahend.

A kid can give you 3 crayons and an adult can give you 12 crayons. Now you have 15 crayons! This is addition.

Alternatively, the kid can kick you in the shin and take his crayons back (15-3).

This is different than, say, you walking up to three-crayon-kid and saying "gimme 15 crayons".

The balance you're looking for isn't addition or subtraction. It is knowing the difference between what you have and what you need, over and over again. It is a different equation entirely.

[exceptionally-minded]

Sigma Notation

A follower sent me this holomeme (below the cut) of my favourite reg Captain and I promised to respond with the explanation of the equations utilized. I can follow up with another post about the limit equation below his jaw. This post will be about the summation notation on Rex’s scalp.

How to read this expression

The large Greek letter Sigma informs us that this is summation notation, representing the sum of a sequence (an ordered set of terms). The number below is the Lower Limit or Starting Index (where to start the sequence). The number above is the Upper Limit or Final Index (where to stop the sequence). The expression to the right is the Argument (the expression to be added, also called the addends or summands). The result is their sum or total.

How to evaluate the summation

1) Define the variables: Lower limit is 0. Upper limit is n. Expression is 2^n.

2) Test a couple values: When n = 0, expression = 1. When n = 1, expression = 2. When n = 2, expression = 4. When n = 3, expression = 8… you know how exponents work. So for values of n [0, 3] the summation evaluates to 2^0 + 2^1 + 2^2 + 2^3 = 15.

3) However, the series has no upper bound; therefore, the result is simply infinity ∞.

Omega asked, “What’s the purpose of this?”

This is an Infinite Series of the exponential variety. By itself, it means nothing. We would need to see this utilized to define the relationship between two things. An example of an exponential function is the growth of bacteria. Some bacteria double every hour. If you start with 1 bacterium and it doubles every hour, you will have 2^x bacteria after x hours. This can be written as f(x) = 2^x.

Speaking of single-celled organisms, see the gif below:

Application to hacking

If you have any computer programming experience, you might be familiar with the concept of a series as utilized in a Loop, a control flow statement for specifying iteration. Directing code to be executed repeatedly is a foundational component of my key-based hacking algorithms used to decrypt and tap comm channels.

Original post by @loulines; screenshots from @cornunut. I know that most people will be really annoyed to see this on a social networking site; therefore, I shall preemptively tag these with #thank you for coming to my tech talk for your dashboard filtering convenience.

[ecothroat]

!!!!

i completely forgot about these sorryyyyyyyy akdnakdnsk

anyway this is augend (they/them) and the picture quality is worse because i forgot to save them when making them 💔💔

[ID: a HeroForge figure of Augend Sum, a tiefling ranger. they have purple skin, white pulled back hair, yellow eyes, and an all black and silver outfit. there are no sleeves on the shirt, showing various lighter purple marks on their arms and face. they hold a bow and wear a quiver of arrows on their back, and smirk challengingly at the viewer. end ID]

augend is a mooooooody one. they aren’t a gloomstalker ranger but definitely give off the vibe. they spend as much time as possible outdoors with their familiar, addend. (and yes their names are math puns ❤️) they aren’t good with people as much as they are with the forest, and i love that for them.

[notesby19]

My Milieu

Imagine you rode the same train day after day. The flow of people in and out, at equilibrium, over the days. The scene, seemingly, always, the same. Though one can expect some slight deviation here and there – new faces, new jackets, new haircuts and what not – but, on-average, continuity. Then one day, 19 reads Ulysses and becomes an Observer to the addends of the train-sum. He insists the 60’s became the 80’s not by flash but by way of some insidious portal - hidden without notice. This metamorphosis which happens to ourselves or at the system level, indeed occurs -19 insists, yet wonders: is it directed? Joyce says: “all of history is describing a path to god.” That, or maybe these systems evolve toward entropy and thereby we can anticipate chaos. Maybe the answer is in the air.  In the foam seats enveloping a wire matrix. In that man’s hair. Perhaps we are floating in solution but do not have the means to understand it.  A sol i.e., a colloid e.g., a tattoo milieu.  Glints of rapid-moving specks almost dust or beyond the scope of our eyes. Larger precipitates that sediment to the bottom, now centers of colloidal sloughing, releasing particles of nano-sizes. These fresh nanoparticles aggregate and ripen over time until they are too large to be held in solution - then back to the bottom. 19 imagines flowers spewing spores into the wild wind that land and rebloom to plume more spores. A system of natural equilibrium, a self-propagating cycle - so it is observed.  

[chabby4memes]

Math is one of my worst subjects so here's some research, please read past it.

In primary school, after you learn to count, you learn the basics of arithmetic. This is the branch of mathematics concerned with the relationships between numbers, measurements, and computation, among other things. The ancient Egyptians and Babylonians are credited with the earliest documented evidence of accounting using numerals and place values.

The word arithmetic from the Greek noun arithmos, meaning "number," with stops along the way in Latin, Anglo-French, and Middle English.

Even simple math has a deep vocabulary. The four primary arithmetical operations are addition, subtraction, multiplication, and division. One or more addends are combined to produce a sum. In subtraction, a subtrahend is taken from a minuend to produce the difference.

When it comes to the fact of multiplication, a multiplicand is added to itself repeatedly the number of times indicated by a multiplier to produce a product.

In division, a dividend is split the number of times indicated by a divisor to produce a quotient, leaving a remainder if the dividend is not an exact multiple of the divisor. This is the main origin of missing numbers arithmetic.

II_Lost drive

Soleil gazed at her stone heart, which as always, sat on Emma's bedside table. It was the sign that her soul, had accepted Emma, not only as Donor, or a Master, but a person of trust and adoration. Emma's fingers were even more delicate than Karin's, and Soleil could appreciate that, stroking them while the Third year thought of what to say, her voice staying knotted in her throat... Soleil thought- no, She knew that Emma didn't deserve these feelings, the same HXPPY THXXGHTS, that made her go mad.

"Emma-San, please, Don't suffer for them." Frankly, the Idea of all these 'pros' hurt the feelings of being a school Idol, how can you make people warm and fuzzy when the words you sing- When they are not yours? Then this dance you dance, not truly yours? Are you even what those people truly care about?

Emma thought it stank of inauthentic things, especially when anyone can sing Lanzhu's song- for they are not her words. Anyone can dance Lanzhu's dance for it is also not hers. She, Kasumi, Kanata, Shizuku, Ayumu, Rina or Soleil were fluent enough in Mandarin. Especially Soleil, she's quadlinqual, she could quite easily sing her song, no reason why she can't. So why? It lacked what made the Idol Dokokai unique, emotions, real emotions. Idol-bu displayed this, what stopped them from talking to professionals?? Soleil was one, she wouldn't say Lanzhu was a bad Singer, nor dancer, but.

"Lanzhu isn't a good School Idol." As always, Soleil said her thoughts, sweet of her to mention, but indeed, It was true, Lanzhu, was a Phenomenal Pop star, or performer, but a lackluster idol, and a sour person. But, now was the time for counter, it was about time for her to introduce Soleil to The remaining members.

But, Lanzhu tried to stop her, bringing her to her mother, who, at first tried negotiating her, to which, no- Soleil cares about emotions and Emma to dare take it, and then Bribery, she's not greedy. Soleil was at wits end with it when force came into view, Lanzhu was going to force her to change- or attempt to.

First half of chapter two. I may release my April Fanfic for Pocket mirror if bored enough.

[levysoft]

p(n) is a fractal when n is prime

This Friday night, according to a publicity release by Emory University, math professor Ken Ono will show that partition numbers of primes are fractals.

A partition number is the number of (different) sums of positive integers that produce a specific natural number. Each of the sums is called a partition

For example, the partitions of the number 8 are:

8 7 + 1 6 + 2 6 + 1 + 1 5 + 3 5 + 2 + 1 5 + 1 + 1 + 1 4 + 4 4 + 3 + 1 4 + 2 + 2 4 + 2 + 1 + 1 4 + 1 + 1 + 1 + 1 3 + 3 + 2 3 + 3 + 1 + 1 3 + 2 + 2 + 1 3 + 2 + 1 + 1 + 1 3 + 1 + 1 + 1 + 1 + 1 2 + 2 + 2 + 2 2 + 2 + 2 + 1 + 1 2 + 2 + 1 + 1 + 1 + 1 2 + 1 + 1 + 1 + 1 + 1 + 1 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1

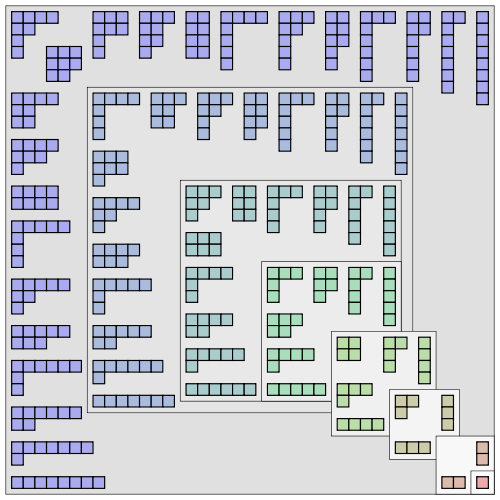
Counting up these different partitions yields 22. (A partition is not different when the addends are differently arranged. 1 + 3 is the same partition as 3 + 1. Remember the associative property?) Thus, the natural number 8 thus has a partition number of 22. Or as expressed in number theory p(8) = 22.

Partitions can be illustrated as Young diagrams. The illustration on the left shows Young tableaux of partition numbers making up each of the integers from 1 to 8. The diagrams are arranged in a sort of Russian doll showing the “conjugate partitions.” This diagram is a Ferrers diagram named for Norman Macleod Ferrers who discovered the conjugacy of partitions. I will leave you to Wikipedia’s explanation of the Ferrers diagram.

Partition numbers rapidly increase. You can see yourself:

p(3) = 3 p(4) = 5 p(5) = 7 p(6) = 11 p(7) = 15 … p(10) = 42 … p(100) = 190,569,292 … p(200) = 3,972,999,029,388

You can generate your own set of partition numbers by an on-line calculator devised by Henry Bottomley.

Evidently to increase interest in the lecture the Emory University press release gives no more details to the discovery than a description of the Eureka moment Ono and a colleague had during a hike in a forest when the visualized the patterns as clumps of trees. The press release describes the discovery  by saying that the researchers: “have unlocked the divisibility properties of partitions, and developed a mathematical theory for ‘seeing’ their infinitely repeating superstructure. And they have devised the first finite formula to calculate the partitions of any number.”

If this work is ever published, I’ll update this post here.

Quick Update: The paper entitled Jan Hendrick Bruinier and Ken Ono, “An Algebraic Formula for the Partition Function” is available in pdf format here. The paper concerning the fractal nature of partition numbers of prime, Amanda Folsom, Zachary A. Kent and Ken Ono, “l-adic Properties of the Partition Function” is available in pdf format here.

[sayitaliano]

As asked, Math vocabulary video - I uploaded it on our youtube channel. I thought a video would have helped you better than an audio.

What am I talking about in it? Tabelline - times tables, multiplication tables Addizione - addition Addendo - addend Somma o totale - sum, total Sottrazione - subtraction Minuendo - minuend Sottraendo - subtrahend Resto o differenza - rest Moltiplicazione - multiplication Moltiplicando - multiplicand Moltiplicatore - multiplier Prodotto - product Divisione - division Dividendo - dividend Divisore - divisor Quoto o quoziente - quotient

[maciek-jozefowicz]

My Silly Puzzles

“My Silly Puzzles” is a 600-page* book of word and logic puzzles.** It is the second book in the “My Silly…” series. (The first one is “My Silly Poems”; the third one will be “My Silly Thoughts”.) What makes this book distinct from other puzzle books is the way that the various puzzles are presented—with humor and with rhyme. Many of the puzzles begin with a poem and that poem is the inspiration for the scenario, written in rhyming prose, for that particular puzzle set.

Here is an example of a simple, traditional Truth Teller and Liar logic puzzle (of which type there are numerous variations in the book, each with different characters and a different scenario, one set includes Sherlock Holmes, Dr. Watson, Professor Moriarty and Inspector Lestrade):

“The Lion and the Mayan”

 Two little lies / Put on disguise, / On Halloween— / One is a hungry Lion, / The other a lonely Mayan.

Heidi and Monique put on costumes to seek sweet treats on their neighborhood streets. But who is who? Even their mother can’t tell one from the other. She knows that Heidi always tells the truth, and Monique, being so clever, does so never. But the mother, having more than a bit of her own wit, unmasks—“Is either of you Monique?” she slickly asks.

And if the Mayan replies, “Mom, of course one of us is Monique,” then who is the Mayan and who is the Lion?

Besides Truth Teller and Liar puzzles (also known as Knights and Knaves), there are Cryptograms, puzzles in which digits have been replaced with letters. An addition problem is given where the addends (the numbers that are being added) are represented by letters and the sum is a number. Using this problem, you can determine which letter represents which digit.

Once you solve which letter stands for which digit, you have to decode a secret note that’s been written using those digits by replacing the digits with the corresponding letters. For example:

straight + starts = 15,898,016

Secret Note: 5645’173265!

(To make them easier to solve, these types of puzzles are formatted differently in the book than in this example.)

There are other logic puzzles, like Elimination Grids / Logic Grids (“Neighbors,” “Who’s Got Kenny’s Teeth,” “Monique, Missing in Mozambique,” “The Apartment”), as well as word puzzles (“Daisy Goes A’Kissin’,” “Bad Luck, Stadium Stuck,” “Ticktionary”) that are also introduced and explained with poems.

For example, “Bad Luck, Stadium Stuck” begins—

In a broken stadium elevator, Thirteen spectators with bad luck Get stuck! How many can you list? An illustrator. An innovator. An imitator. Do you get the gist? There are thirty, sturdy, other fans (Where is my pen? That is wrong, There are only ten!***) From a variety of clans, Tapping the floor with their toes, As their tetchiness grows, And their souls, unseated, Get overheated. While their teams on the field play, Who are they?

A clue in the form of a short poem is given for each spectator that is stuck in this useless elevator.

“My Silly Puzzles” also includes a new type of puzzle—the Poetry Path. The Poetry Path puzzle is my own creation, an amalgam of two puzzle types—the Maze and the Word Search.

In Poetry Path, instead of looking for individual words, like one does in a Word Search, you are looking for a poem, a combination of words that link together to make the correct path through a field created from letters. (There is no actual “maze” as such, and there are no walls that would define paths because there is no need for them. Words are the paths.) The poem that the player is searching for is not given. It has to be discovered. Only visual clues as to where the poem begins and where the poem ends are given.

“My Silly Puzzles” is a book that is fun to read and fun to solve, and it can be enjoyed alone or in a group,**** in lieu of a board game, by children and by adults. It’s a great way to unplug and give your eyes, and your mind, a respite from digital over-saturation.

————————————————————

* The softcover and digital versions are each 608 pages. The hardback version is 544 pages. The content is the same, but I was forced to condense the presentation of two puzzles to fit under the Amazon 550-page limit for hardback books.

** In addition to puzzles, sprinkled throughout the book are some of my silly riddles.

*** The narrator of this poem is wrong on both counts. There are 21 puzzles in this set.

**** With Truth Tellers and Liars puzzle types, for instance, each person can become a character and read his/her lines while the remaining players try to figure out who is who.

The book is available from Amazon at:

https://www.amazon.com/author/maciek_jozefowicz

[fuzzysparrow]

In mathematics, what are addends?

In mathematics, addends are defined as the numbers that are added together to get a sum. In any addition equation, the individual numbers which together form the sum are addends. For example, in the equation "1 + 2 = 3", both 1 and 2 are addends.

Addends are not necessarily just numbers. In the sum "3x + 2y = 5xy", the addends are 3x and 2y.

The first number in a sum may also be called an augend, which means a quantity to which another is added. So, in the sums "1 + 2 = 3" and "3x + 2y = 5xy", the 1 and 3x may also be called augends.

[mormathematics]

Making Sense of the Addition's Switcheroo: Understanding the Commutative Property of Addition

The commutative property of addition is a fundamental concept in mathematics that states that changing the order of the addends in an addition problem does not change the sum. In other words, if you add two numbers, say 2 and 3, you get 5. If you switch the order and add 3 and 2, you still get 5. This may seem like a simple and obvious concept, but it has significant implications for mathematical reasoning and problem-solving.

In contrast to the commutative property of addition in mathematics, where changing the order of the addends does not affect the result, the order of words in language is crucial to meaning. As opposed to in sentence construction, for instance, the order of words can significantly affect the meaning of a sentence. Consider the sentence, "The cat wore a hat on Monday, and on Tuesday the hat wore the cat." If we switch the order of the words, the sentence's meaning changes completely.

The commutative property of addition has been recognized for thousands of years. The ancient Greeks and Egyptians understood the concept, and it was later formalized by the Indian mathematician Brahmagupta in the 7th century. However, the property did not receive its current name until the 19th century, when it was introduced by the French mathematician Augustin-Louis Cauchy.

An understanding of the commutative property of addition has practical applications in many areas of mathematics and science, including algebra, geometry, and physics. By allowing us to rearrange the order of numbers without changing the result, the commutative property simplifies calculations and makes it easier to approach problems from different angles. It also serves as a foundation for more complex concepts and operations, such as commutative rings and group theory.

In conclusion, the commutative property of addition is a powerful concept in mathematics that has implications for mathematical reasoning and problem-solving. While it may not be a perfect analogy to other domains, like language and sentence structure, where the order of elements can be crucial to meaning, the commutative property is a valuable tool that allows us to approach problems from different angles and find more efficient solutions.