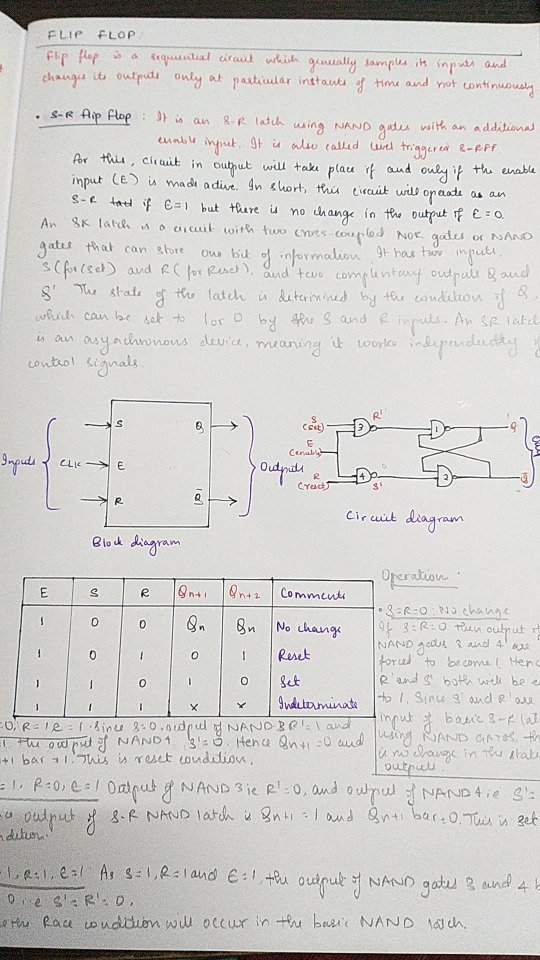
#Boolean Logic
Explore tagged Tumblr posts
Text
20250308 Major ALICE update!
For a couple months i've been working on a bunch of new stuff and improvements for Aubery's Logic Integrated Circuit Emulator (ALICE), and yesterday i concluded the works that have been planned! I am very happy to tell everyone that ALICE now crashes much less, the circuit tracing GUI became much more usable, and even more high-level devices were programmed!~
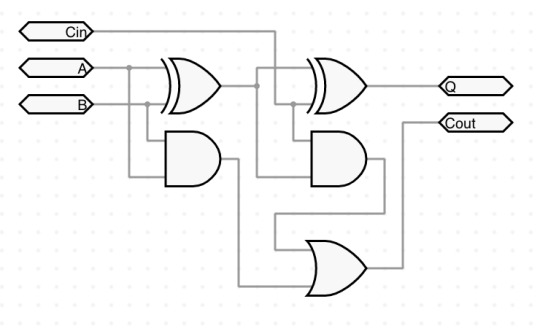
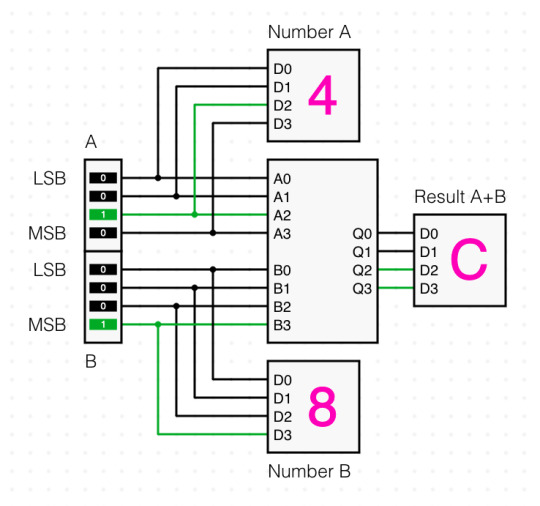
Circuit integration now works in full - watch me go from a basic logic gate based single-bit full adder to a 4-bit adder IC with a whole demo setup to test it, inside the same project!
Some high-level devices were added: everything but the ALU seems to be working correctly. TruthTable allows you to build a circuit and then compose its truth table in realtime! Using the pre-made compounds can be easier on the CPU than user-made ICs, even though i'm working on making everything run even faster. Oh, and now there's a "text" device to leave notes right on top of the circuit!
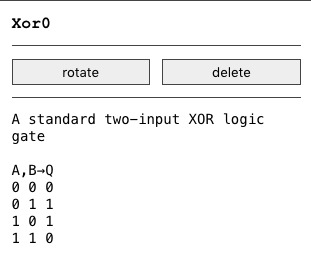

All devices now show a memo on what they do when selected, and a cohesive (although still and forever lacking) manual was started!

Finally, there are now demo projects! They and the manual are bundled within ALICE itself, so no need to download them separately from anywhere. I will work on adding more to them, with the general goal of one day having a "full basic 8-bit CPU" on the list!
Aside from these novelties, i worked real hard and made the GUI run smoother and explode less. Frankly, the code was pure spaghetti before this overhaul, and now it's at least meatballs with a side of spaghetti. It became better, i promise. Along with this, a bunch of minor bugs were eliminated, and i'm slowly ridding the project from depending on my old bmco.js utility library, which would make it run smoother.
There's a lot of plans for this project, and seeing people using it at all would greatly increase my motivation to implement them. Not like i am not motivated.. but you could make things happen faster! So! Use the thing, tell me when it explodes in your face - with saves and bug error texts preferrably - and show me what you made with it!
And one last thing: ALICE is now hosted on Gitea because i am tired of github's copilot bullshit. I will shut down the github repository soon enough -- nothing to lose, since there are no open issues out there or anything. If you feel like digging through my caverns of nonsense, or run ALICE locally, go ahead and download the source code from the Gitea repo!
13 notes
·
View notes
Text
"Logan is a George Boole fanboy, it's canon now"
January 10, 2022
(It's not actually canon, but it's a headcanon of mine that makes an incredible amount of sense)
4 notes
·
View notes
Text
Screw it why not.
Bo: Boolean logic
Mi: Aurora Miranda
Ca: CATS!
Pe: Jane Perkins
Ga: O Grande Gastby
That's an interesting breadth of interests
lets play a game
what comes up in your tags when you types
bo
mi
ca
pe
ga
23K notes
·
View notes
Text
Buddhism 202: Thoughts and Thinkers
Buddhism in Bhutan Samma sankappa, one of the Buddhist Four Noble Truths, is Right Thought = Good Thought, not No Thought. For no thought, maybe samma samadhi is better, Right (Good) Meditation. It’s very popular for New Age-y Buddhists to talk about ‘thoughts without thinkers and/or ‘thoughts that think themselves’, as if they were both particle and wave out there floating around looking for a…
#Boolean logic#consciousness#Four Noble Truths#Hardie Karges#language#meditation#neuron#samadhi#sati#thought
0 notes
Text

Any Boolean operand can be used as a Boolean operator.
0 notes
Text



Oct 29, 2023 • Sunday
GUESS WHO'S BACK
Exams are just around the corner, and I have recovered (mostly) so got back to productivity. I missed my notes <3
The 1989tv vault tracks are stuck in my headddddd my favourite is Now that we don't talk. If you are a swiftie, what is your favourite vault track?

Things I did today:
40 out of 55 slides of a PPT
19 out of 27 concepts from Module 1 of computer science
Ate biryani :3 (and then had a tummy ache LOL)
P.S. the whiteboard is @studaxy's I STOLE IT (jk, they gave it to me lol)

🎧 Suburban Legends — Taylor Swift
#dailyfoxposts#foxcomp#studyblr#codeblr#studyspo#study#coding#note taking#physics studyblr#math studyblr#compblr#computer science#boolean algebra#logic gates#digital circuits#exam#exams#study motivation
120 notes
·
View notes
Note
That's not how formal logic works.
'Think therefore am' does not imply 'am therefore think'. That's a whole new statement.
(think ==> am) <=> (not am ==> not think) sure, this one is logical
(not think ==> not am) <=> (am ==> think) this is untrue, since stupid people exist
i assume u are
i am
5K notes
·
View notes
Text
ship discourse is so funny to me. what the fuck is an anti-anti. like why is it recursive
#ramblings#in ten years there will be boolean logic in a bog standard dni list#i think i'm a little obsessed with boolean logic being implanted into various online features#second post i've made about it#sorry guys. it's just too funny
7 notes
·
View notes
Text
The Philosophy of Algebra
The philosophy of algebra explores the foundational, conceptual, and metaphysical aspects of algebraic systems and their relationship to reality, logic, and mathematics as a whole. Algebra, dealing with symbols and the rules for manipulating these symbols, has profound philosophical implications concerning abstraction, structure, and the nature of mathematical truth.
Key Concepts:
Abstract Symbols and Formalism:
Abstraction: Algebra involves abstracting mathematical concepts into symbols and variables, allowing general patterns to be manipulated without referring to specific numbers or quantities. Philosophers question whether these symbols represent real objects, mental constructs, or purely formal elements that exist only within the algebraic system.
Formalism: In formalism, algebra is viewed as a system governed by rules and manipulations of symbols, independent of any reference to an external reality. In this view, algebra is a logical game of symbol manipulation, with its own internal consistency, rather than something that necessarily describes real-world phenomena.
Algebra as a Structural Framework:
Structuralism: Algebra can be seen as providing a structural framework for understanding relationships between elements, often more abstractly than arithmetic or geometry. Structuralism in mathematics argues that algebraic objects, like groups, rings, or fields, should be understood in terms of the relationships they define within a system rather than as standalone entities.
Relationality: Algebra emphasizes relationships between objects rather than the specific nature of the objects themselves. For example, an equation expresses a relationship between variables, and group theory explores the relationships between elements in a set based on certain operations.
Algebraic Truth and Ontology:
Platonism vs. Nominalism: Algebraic Platonism suggests that algebraic objects (e.g., variables, equations) exist in a timeless, abstract realm, much like numbers or geometric forms. In contrast, nominalism denies the existence of abstract entities, viewing algebra as a language that refers to concrete, particular things or as a useful fiction.
Existence of Algebraic Structures: Are the objects and operations in algebra real in some metaphysical sense, or are they simply human constructs to facilitate problem-solving? Philosophers debate whether algebraic structures have an independent existence or are purely tools invented by humans to describe patterns.
The Nature of Equations:
Equality and Identity: Algebraic equations express equality between two expressions, raising philosophical questions about the nature of equality and identity. When two sides of an equation are equal, are they identical, or do they just behave the same under certain conditions? The concept of solving an equation also reflects deeper philosophical issues about finding correspondences or truths between different systems or forms.
Solvability and the Limits of Algebra: Throughout history, philosophers have explored the solvability of equations and the boundaries of algebra. The insolubility of quintic equations and the advent of Galois theory in the 19th century led to deep questions about what can and cannot be achieved within algebraic systems.
Algebra and Logic:
Boolean Algebra: The development of Boolean algebra, a branch of algebra dealing with logical operations and set theory, highlights the overlap between algebra and logic. Philosophers examine how algebraic operations can be used to model logical propositions and the nature of truth-values in formal systems.
Algebraic Logic: Algebra provides a framework for modeling logical systems and reasoning processes. The interplay between algebra and logic has led to questions about whether logic itself can be understood algebraically and whether the principles of reasoning can be reduced to algebraic manipulation.
Algebra and Geometry:
Algebraic Geometry: The relationship between algebra and geometry, particularly in the form of algebraic geometry, involves the study of geometric objects through algebraic equations. This intersection raises philosophical questions about how algebraic representations relate to spatial, geometric reality, and whether algebra can fully capture the nature of geometric forms.
Symbolic Representation of Space: In algebraic geometry, geometric shapes like curves and surfaces are described by polynomial equations. Philosophers explore whether these symbolic representations reveal something fundamental about the nature of space or if they are merely convenient ways to describe it.
Historical Perspectives:
Ancient Algebra: The origins of algebra can be traced to ancient civilizations like Babylon and Egypt, where early forms of symbolic manipulation were developed for solving practical problems. The philosophical importance of algebra evolved as these symbolic methods were formalized.
Modern Algebra: The development of abstract algebra in the 19th and 20th centuries, particularly group theory and ring theory, transformed algebra into a study of abstract structures, leading to new philosophical questions about the role of abstraction in mathematics.
Algebra and Computation:
Algorithmic Nature of Algebra: Algebra is inherently algorithmic, involving step-by-step procedures for solving equations or simplifying expressions. This algorithmic nature connects algebra to modern computational methods, raising questions about the role of computation in mathematical reasoning and whether algebraic methods reflect the underlying nature of computation itself.
Automated Proof Systems: The advent of computer-assisted proof systems, which rely heavily on algebraic methods, has led to philosophical debates about the role of human intuition in mathematics versus mechanical, algorithmic processes.
Historical and Philosophical Insights:
Descartes and Symbolic Representation:
René Descartes is often credited with the development of Cartesian coordinates, which provided a way to represent geometric problems algebraically. Descartes' work symbolizes the deep connection between algebra and geometry and raises philosophical questions about the nature of representation in mathematics.
Leibniz and Universal Algebra:
Gottfried Wilhelm Leibniz envisioned a universal algebra, or "characteristica universalis," that could serve as a universal language for all logical and mathematical reasoning. His philosophical insights anticipated the development of symbolic logic and formal systems that use algebraic methods.
Galois and the Limits of Algebra:
Évariste Galois' work in group theory and the solvability of polynomial equations led to new philosophical discussions about the limitations of algebra and the nature of symmetry. Galois theory provided insights into why certain equations could not be solved using standard algebraic methods, challenging assumptions about the completeness of algebraic systems.
Applications and Contemporary Relevance:
Algebra in Cryptography:
Modern cryptography relies heavily on algebraic structures like groups, rings, and fields. Philosophers examine the role of algebra in securing information and the philosophical implications of using abstract mathematical structures to solve real-world problems related to privacy and security.
Algebra and Quantum Mechanics:
Algebraic methods are crucial in formulating the laws of quantum mechanics, particularly in the use of operators and Hilbert spaces. Philosophers explore how algebra provides a framework for understanding quantum phenomena and the extent to which algebraic methods reflect physical reality.
Algebra and Artificial Intelligence:
In AI and machine learning, algebra plays a central role in developing algorithms and models. Philosophical discussions arise about the nature of intelligence and reasoning, and whether algebraic methods in AI reflect human-like thinking or merely computational processes.
The philosophy of algebra investigates the abstract nature of algebraic symbols and structures, the relationships they describe, and the metaphysical and epistemological status of algebraic truths. From ancient practical uses to modern abstract algebra and its applications in cryptography, computation, and quantum mechanics, the philosophy of algebra addresses deep questions about abstraction, formalism, and the role of symbols in understanding reality.
#philosophy#epistemology#knowledge#learning#chatgpt#education#ontology#metaphysics#Algebra#Philosophy of Mathematics#Abstract Structures#Formalism#Equations#Platonism vs. Nominalism#Boolean Algebra#Algebraic Logic#Galois Theory#Algebraic Geometry#Computation
3 notes
·
View notes
Text
Oreos
Andeos
Noteos
Xoreos
8 notes
·
View notes
Note
trick xor treat
more like
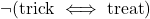
5 notes
·
View notes
Text
Ask A Genius 1434: How Paraconsistent Logic Shapes Computational Cosmology and Next-Gen Artificial Minds
Rick Rosner is an accomplished television writer with credits on shows like Jimmy Kimmel Live!, Crank Yankers, and The Man Show. Over his career, he has earned multiple Writers Guild Award nominations—winning one—and an Emmy nomination. Rosner holds a broad academic background, graduating with the equivalent of eight majors. Based in Los Angeles, he continues to write and develop ideas while…
0 notes
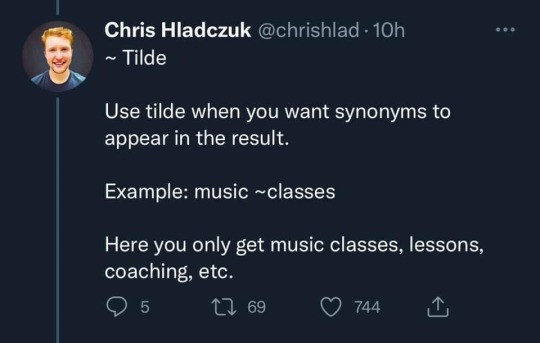
Text
Filetype: is very useful for piracy ;)
Oh also intitle:EXAMPLE is another way to force the search to contain a particular word or phrase and is naturally, also great for piracy.
So for example something like intitle:Neuromancer filetype:pdf will get you the William Gibson book for free :)






183K notes
·
View notes
Text
completely forgot that my friend is walking around her very straight workplace with a camo baseball cap in which i wrote TRANS RIGHTS OR I SLURP DICK on the inner brim.
#i'm doing my part#once the aforementioned trans rights happen she can replace OR with AND#call that boolean logic#she bool on my log til i ickkkkk
0 notes
Text
2) Gayane Logic - Quaternary (multivalued) logic.
Why has binary logic remained and is the “monopoly leader” in the digital world for so long? Although the beginnings of non-binary logic are already in the works of Aristotle, Leonardo of Pisa (Fibonacci) mentions the best side of the ternary system. 1840, Thomas Fowler in England built a mechanical computer based on ternary logic. 1947, in the USA, work led by John von Neumann mentions non-classical logic. In the USSR, it came to mass production, the locomotive of which was Nikolai Petrovich Brusentsov. 1973, in the USA they created Ternac, an emulator of a ternary computer, and in California in 2008 they built a three-tertiary digital computer system TCA2, version v2.0. In addition to the above, it should be mentioned that the last century is also known for the boom of logical systems, but binary logic still remains the “sole monarch”. The two most compelling reasons are physical, technical feasibility and tradition. Some may believe that the simplicity and ease of learning of binary logic play a role here, but for me this is a secondary argument. Our technical and technological capabilities have changed. In the transmission, storage and processing of information, other technologies and their capabilities have appeared, with varying successes. For example, when transmitting information, optics have long been the leader. And no success has yet been seen in storing information. There are some advances in information processing. And quantum systems have already proven themselves well in some areas of computing. But logicians and mathematicians do not stand still; they propose different logical systems for the computers of the future.
0 notes
Text
if we take the phrase "to be, or not to be", such that [to be] = B and not[to be] = B', in formal logic, we get B || B' if B evaluates to true (and as its inverse, B' to false), then we get true or false, which evaluates to true (because one of the options is true - one OR the other) on the other hand, if we have B && B' (to be and not to be), if B evaluates to true (and B' to false), we get true AND false, which evaluates to false (because to evaluate to true, we either require true && true or false && false; the two are different therefore not true)
#mathematics is omnipresent#“i'm already there”#text analysis in boolean logic <3#of course text analysis per definition would be easily comprehensible too#there's nothing that ain't mathematically evaltuatable
0 notes