#precalc formulas

[er-cryptid]

Horizontal Translation of Logarithmic Functions

-- Formulae: -> g(x) = logb (x + c) -> g(x) = logb (x - c)

-- g(x) = logb (x + c) shifts the graph of f(x) = logb (x) to the left c units and moves the vertical asymptote to x = -c

-- g(x) = logb (x - c) shifts the graph of f(x) = logb (x) to the right c units and moves the vertical asymptote to x = c

.

Patreon

[purble-gaymer]

confession i actually really like calculus. i think it’s fun i’m just not very good at it. if i were learning it outside of an ap classroom and could spend more time understanding the concepts, i’d probably be okay. sometimes you just get the urge to solve an integral by hand yknow

[math-journal2]

Circle Problems

Level 1

Level 1

Level 3: midpoint + distance

[amalgamgooze]

"easier" math has become more difficult than "difficult" math

Had to take a math placement exam for college today.

It was all high school stuff--things I'd already done.

Now tell me,

why was it harder to do that stuff than the abstract algebra stuff I'm studying?

…

I'm serious.

Maybe it's a familiarity thing.

Like, nobody should ever have to memorize all the trig identities.

sin2x + cos2x = 1, that's an acceptable one to memorize.

Super short, simple, and widely applicable.

But the bullshit like sin(2x) = sin(x)cos(x)?

Or sin(x/2) = sqrt((1 - cos(x)) / 2 ) ?

What? The? Fuck?

Is this actually stuff I studied two years ago?

This is formula sheet bullshit.

Not stuff you test for to gauge math proficiency.

And not without a calculator either.

For fucks sake--discrete math and modern algebra without a calculator is easier than precalculus without a calculator!

…

I can see why some people hate math.

That shit's just not fair.

Even if you're using math professionally, you're not going to have that bullshit restriction of "you need to know everything off the top of your head".

…

If you couldn't tell, I'm not a fan of all of math.

There's some areas that I don't feel are as important to understand as the rest.

Like conic sections.

Or eccentricity.

…don't get me wrong. Geometry is pretty cool sometimes.

But when my job is to literally solve the equation for a specific point on an ellipse, I'm just left thinking, "why bother?".

…

Calculus was cooler than that shit.

Vector calculus was cooler than that shit.

Precalculus was hell.

I offer my condolences to you poor souls who've yet to take Precalc.

There's cooler math beyond precalc.

Yes, it's more incomprehensible, but it's enjoyably incomprehensible.

It's supposed to be abstract.

It--

Physics wasn't as infuriating as that test!

I-

I don't know how much more I can prove I love math than to write a whole monologue about me descending into insanity over my love for math!

But this fuckin' test!

It just- wow.

I'm sorry. I'm still kinda worked up about it.

I'm not writing about it in a very unbiased lens.

(I don't need to. I'm not claiming to preach universal truth in this post.)

…

Again.

I suppose I want to emphasize that precalculus and later "college algebra" classes are kinda infuriating and not very fun.

There's fascinating fields like calculus, linear algebra, and abstract algebra beyond that rut.

…

But again. Math's not for everyone. So I suppose you can also hate all of it. I won't judge.

[sock-to-the-third]

LOG TIME

Here’s some attempts I made to reteach myself how to graph logs and finding equations.

Graph—> equation

The idea was using the nearest whole number to the asymptote as the “key point” and then graphing from there.

If you’re a visual person when it comes to graphs, I’m sure it works great.

For me, I cannot for the life of me feel at ease around a graph. Something about visualizing it extremely hard and I usually prefer moving it via algebra — but only for logs lol.

. . . . . . . .

Equation —> graph

#1

This was my next idea. Idk why I thought less words would help. It made it harder to remember things since I wanted to make things simple in preparation for reflections (my mortal enemy).

. . . . .

#2

I’m using my old method! Logs are like magical unicorns and while I do understand when I concentrate how they work most of the time they’re unicorns. So I use exponential functions to figure out inputs and outputs since you just swap x & y and then you got a log to graph.

Thing is while I got a good method down I still couldn’t figure out how to put reflections in.

. . . .

#4 — Finalized method

Presenting: my method~

YAY! I CAN GRAPH LOGS AGAIN.

Interpreting graphs is so much easier folks. I get why my some profs just skip complicated reflections, so easy to forget or fuck it up if you don’t have a solid method.

. . .

Also this took me a solid 2 hours to figure out. I forgot about writing my story, reading, EVERYTHING. I was a math solving fanatic. I had a hunger, and it was for logs.

A hunger that would NOT be satiated until I could break a log and put it back together.

Omfg my brain is so fried 🥱😴

The hard part about logs is that my old method I use to crack the puzzle of most functions doesn’t work as well. Part of why linear, rational, exponential, and power functions are easier for me is because I can remember a few coordinate points or its easy af to figure out the math.

If I want to plot the points for a log graph, I got to use the change of base formula since my calculator only does logs with a base of ten TvT

My graphing calculator’s stuck in Test mode for the last 10 years. Never gave a shit to figure out how to get it out

Now that I got a new method, it’ll be interesting learning other methods so I can help tutor the kiddos. Cuz like I can try to do the more common method but I’ll have to pre-prep the problems or make sure to solve the base log with a change of base for the y-coordinate or I’m soooooo gonna fuck up. Lol.

I honestly do love math but math fuge is like my writing fuge.

So fun but exhausting af.

.

TIME TO FUCK UP THE REST OF PRECALC!!!

FUCK YEAAAAAAH!

[wizardnuke]

what kind of god damn community college precalc professor doesn't allow students an index card for formulas and shit. brother i can't memorize strings of letters+numbers like that.

[eulerseverything]

Now that I think about it "e" was introduced to me in precalc as simply the lim n->infinity (I didnt even know what a limit was yet) of the compound interest formula thing. Not the base of a natural logarithm, or that it e^x derives to itself, just banking stuff. It was introduced to me before e was ever mathematically relevant. Call that a speuler

[natural-blogarithm]

students keep emailing me begging for a better grade, including one who wants to write an essay for 2 points in a precalc class, and i'm so tempted to say that they can get an A if they find me a formula to solve a quintic equation

[rhytmrocket]

ok i tolerate math, i even like it at times, and i dislike language arts like. a lot.

i think i’ve figured out why i prefer math so much.

i’m doing ap lang work, analyzing a poem, and i just don’t get it. i don’t know what the goal is, what exactly i’m supposed to do. yeah, i’m supposed to analyze it and make a thesis statement for an analysis writing, but i don’t know what exactly that is.

but when doing precalc work, i know what the goal is. find the answer, plug this into the formula, find what number(s) work and make the statement true. it’s objective, it’s clearer, it’s easier for me. yeah, it can get tedious and frustrating at times, but i know what i’m supposed to do.

i much prefer the order and objectiveness of math to the abstractness and subjectiveness of language arts.

[midorigakkou]

august 15, 2023 || day 2/30

i still need to figure out a way to get myself to do things a little ahead of time. i can tell that i'm going to need to study a lot more outside of class this year.

♫ wincing the night away - the shins

to do:

precalc homework

german quizlet review

nominative/accusative case worksheet

AMSCO 1.1

read chapter 2 of us history book

make list of kumon formulas

[renew-world]

The importance of a growth mindset! Like, of course everyone is going to have differently levels of enjoyment when practicing math (I think it's fun so that makes it easier to motivate myself to put in practice than someone who dislikes it), and not everyone is going to improve at the same rate, and not everyone is going to want to/be able to prioritize it (thinking of, say, students in one math class who also enrolled in several other classes).

BUT I think that everyone *is* able to get better with practice if you are able to put in the time. So that said, below the cut is some general advice on how to get better at math that's a little more specific than just "practice" (I'm picturing a student enrolled in a calculus class because that's who I usually work with but I hope these will help for other situations as well!):

What topics are you trying to improve? Can you break these down into sub-skills? This will help you target your learning more later (don't need to spend time working on every single skill it its only the quotient rule you're having problems with!)

+ Computing derivatives: Subskills are both knowing/memorizing all the specific rules (power rule, product rule, chain rule, etc) AND recognizing which rule to apply

+ Solving equations: Some subskills are knowing what operations are allowed, remembering to do everything to both sides, AND recognizing which is more likely to be useful to do 1st

Practice skills separately: Khan academy is especially great for this! First get the power rule, then the trig rules, etc.

Learn to combine skills: Even if you can do stuff separately, it can be surprisingly tricky to do things in context. Basically, this is working towards skills like "recognize what rule to apply" or "recognize which algebraic manipulation is most useful". Even if you have the skills mastered separately, learning to break a complex problem into pieces is it's own skill. Khan academy I think also works on this? But if you are studying for a class and have access to textbook problems or old exam problems sometimes those are a better resource, YMMV. If not part of a class, some universities post resources online. For example, here's a page with University of Michigan's old precalc and calc 1-3 exams (with solutions!).

Interleaving: Studies show that you can "fool" yourself into thinking you've mastered a skill, when really it's just that you're on a roll because you did 20 log rule problems in a row. It's a good idea to practice "interleaving", or mixing together different problem types, in order to get stuff to stick in your long term memory. So, a couple chain rule, then a couple product rule, then maybe computing some tangent lines, then go back to the chain rule. This also works on the meta-skill of recognizing what skill to apply! (Esp. useful if you are studying towards a big exam that covers many topics). Bonus: If you have a friend who can pick a bunch of questions from a textbook/database, then mix up the order so you don't know which came from which section, that's even better for the meta-skill of recognizing what skill to apply!

Forwards & Backwards: This is not a real name but is still a useful strategy. Basically, given an answer, could you design your own question that has this as an answer? Like, if you were to write a question about "solve this quadratic" and the answer is supposed to be x=1,3... could you write a formula for a quadratic that would have these solutions? Could you write an optimization question where the answer is "The fenced-in area should be 10ft long and 8ft wide"? I feel like it helps you to get a different perspective on the topics to approach them this way as well as the usual. Bonus: find a friend, each design a question aiming for a specific (different) answer, then swap and solve!

Connect topics: So many things in math are connected. I find it easier to remember new things if I connect them to ones I already know. Maybe I'm learning about arcsin. If I already know about logarithms, a connection is they BOTH involve inverting a function. Or, if I'm learning about global extrema, how are they similar to local extrema? How are they different? What are similarities/differences in how I find them?

(Answer for this example: Global I'm looking at the whole domain [including endpts!]; local I'm just looking nearby. So the methods are similar because for both I need to find critical points [and endpts for global!]; but then they go in different directions because to compare across the whole domain for global, I need to plug into my original f(x) but for local info, well that's what the derivative (and 1st/2nd derivative tests) are good for!).

Organize Knowledge: If you're a visual learner, can you collect things into charts? Write down the numbered steps of a method? For example, a table of f, f', and f'' that compares info about when things are +/-, increasing/decreasing, and concave up/concave down? [If you actually do this example, your column for f' should have ALL of these options, but you will not have enough info for every single corresponding slot for both f AND f'']

"Translate" to different perspectives: The textbook I use has a "rule of 4", this isn't a real name but its handy. The idea is that most things in math can be represented four ways:

+ Formulaically: y = x^2

+ Visually/graphically: a graph of a parabola

+ Numerically: A data table of values like x=1,y=1, then x=2,y=4, etc

+ Verbally: "Quadratic growth with a double root at the origin"

When you learn a new concept, see if you can figure out what it looks like from all these different perspectives. For derivatives, you might say:

+ Formulaically: [pretend I wrote out all those derivative rules haha]

+ Visually: Draw a tangent line, and look at the slope

+ Numerically: Compute the slope over successively smaller intervals and estimate what it approaches (so, (f(2)-f(0))/2, then (f(1)-f(0))/1, then (f(0.1)-f(0))/0.1, and similarly on the negative side with (f(0)-f(-2))/2 etc)

+ Verbally: "The (slope of the) best linear approximation to our original function f(x) at x=0"

This is useful because a) maybe you're better at one perspective, so you can translate to your preferred perspective! And b) sometimes with your given info you CAN'T translate (numerical data collected by scientists can be hard to model without enough data points; a graph may have unlabelled axes so you can't find any data points but the origin), and you want to see what you can do with the perspective you're stuck with.

Go back to foundations if you need to: It can be frustrating, but sometimes we all realize we've forgetten something we used to know, or that we didn't understand something earlier as well as we need to. If that "something" is a side topic maybe that's okay, but some things get built on a lot. E.g., after you've learned derivative rules, next topics are usually some kind of applications, for example local/global extrema. But to do problems involving finding local extrema, you need to compute derivatives! So if you're not rock-solid at derivatives, you spend either longer than you want on computing the derivatives, or you make some errors and then can't finish the actual local extrema problem, EVEN IF you totally understand the method to find local extrema. So that's an example of a skill that you might need to go back to. Similarly, algebra skills show up ALLLL the time in further math classes, so you might need to go back and review your log rules.

Topics can be easier the 2nd time: Kind of the dual to the one above? I swear the first time I REALLY understood integration was when I was prepping to teach Calc 2. All the intervening years and higher math added up to this instant magical moment of "oh... EVERYthing is slicing! Solids of revolution, arc length... it's all slicing!" But highschool me would simply never have had the same level of "ah-ha!" because I hadn't seen enough other examples of how integrals got used, and other topics that weren't even calc but still contributed to my understanding. So if something is not foundational, or it's good enough but you wish it was better... sometimes it really is better to give a few weeks/months/years of break and come back to it later.

Explain to a friend: Your friend will probably have different questions than you did. It forces you to come at things from a new angle.

What went wrong?: So you got back your quiz/exam/homework and it didn't go as well as you wanted. Try and diagnose what went wrong and WHY. Not just "I needed to study more". Be specific! This will help you improve next time (growth mindset, remember!). I like this exam autopsy worksheet from Fresno State, you can tweak the categories as needed. Warning: "careless mistake" and "insufficient info/understanding" can be hard to differentiate from a student perspective. It's only a careless mistake if, upon seeing the problem again right now (but NOT looking at the solution) you would definitely know how to do it. The problem is when looking at the answer key it can be easy to say "oh yeah, I just do that", but what's hard is in the moment figuring out the correct steps to apply!

TBH, it's the same reason why practice is better than just re-reading your notes---of course the prof/textbook writer is good at it (and if they're a good prof, they're GOOD at explaining). But somehow it's much easier, for me at least, to nod along step by step; but much harder to do it again on your own. And it's because figuring out the steps can be just as hard as DOING the steps.

Math is no different from music or art. You practice and you get good at it. That’s all there is to it. You go to Khan academy you do problems over and over and you grow to more difficult topics.

If you don’t grow in abilities that are foundational to our society maybe you shouldn’t be disgusted with people who don’t read.

You are them.

[er-cryptid]

Patreon | Ko-fi

[purble-gaymer]

man i still can’t believe my precalc teacher failed to mention the difference quotient is a slope formula after i asked him to explain it on four separate occasions. i didn’t know until i sat down for my first day of calculus and that’s all our teacher said about. suddenly everything made sense and all it took was one measly graph showing how slopes work

[math-journal2]

Circle Basics

Distance formula

Midpoint formula

Radius eq

Standard Circle Eq

[gracethestudent16]

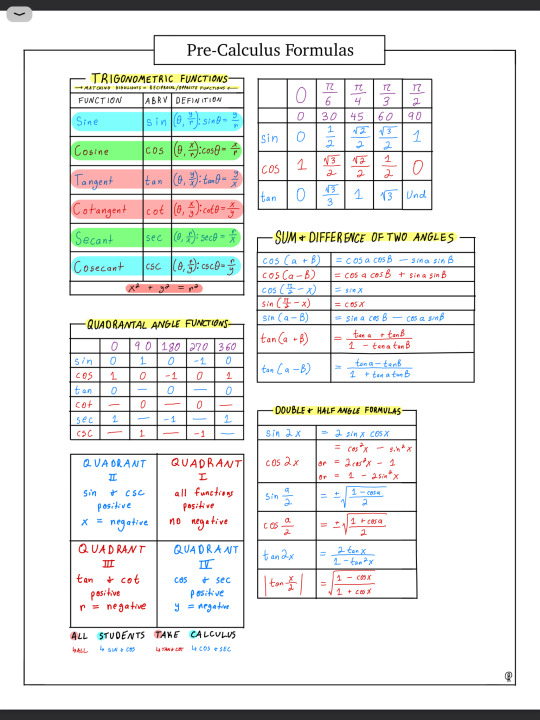
Not sure if anyone wants or needs these, but here are the notes from things I’m using the most in Pre-Calc right now. :)

[ggsstudies]

4/16/19

my math folder has gotten HUGE because of all the papers we get in class plus all my scratch paper from homework sheets

it’s one of my thickest folders and tbh it’s kinda annoying but oh well, i’m dealing with it

do you like math??

xo- gg