#hypervolume

[omegasmileyface]

Methods of travel between the Infinite Realms and the Living Realm

Note: it is tempting to think of the division, or Veil, as a membrane between the realms. In reality, it is not a skin or wall made of any substance. Rather, it is simply the place where an ectoplasmic reality-space and a mundane-matter reality-space rest against one another. It is less like a film of oil floating on a body of water, and more like the glassy surface of the body of water itself. The water holds itself together with surface tension and you can see the divide, but there is nothing actually separating the water and the air. We will colloquially refer to the Veil as "self-healing", but it's really more like it is settling. Simply the increasingly-entropic nature of the mundane reality and the decreasingly-entropic nature of the ectoplasmic reality finding a steady point they're both happy with.

1. Slicing a hole in the division.

Some ghosts specialize in this. It's fairly easy if you have a good sense of fourth-dimensional space and a sharp edge. The cut will self-heal, though, especially if it's messy, so it can be difficult to open a wider gap or leave it open for more than a moment. The mechanics of the slicing are fairly simple; like a shark fin about to surface, a blade that's almost touching the division causes currents that disrupt the fields enough to allow for the tip to easily pass through (see Method 3 below for further explanation), and then the wider part of the blade increases the size of the cut. The trick is in not touching the tip to the Veil before it's been destabilized. Perfektigas Tranĉadon is a good practical guide.

2. Punching a hole in the division.

With enough force (the true amount necessary is not exactly known, but it is known to be colossal), the division can be pushed and broken. This results in a hole which takes a long time to close on its own and produces a number of "shards" or "bubbles" of the division, which can knock their surroundings askew in the fourth dimension. These shards introduce incontinuities in spacetime, which will quickly equalibriate but momentarily pose a threat to laws maintained by continuous spacetime. The punching process also results in a jet of reality-material from the entrance side to the exit side. For further information, consider reading Continuous Space: Geometry and the Infinite Realms. This is the method perfected by the Ring of Rage, and it can also be achieved by any object with enough momentum (that is, velocity times the sum of ectoplasmic mass and mundane mass) being flung at the right fourth-dimensional angle.

3. Exciting the division until it is permeable.

If the spaces in realities on either side of one area are sufficiently energized, the Veil in that area can loosen up into a chaotic mixture of mundane and ectoplasmic space, which is not practically impossible to pass through like a smooth division is. This creates an illusion of a smooth gradient between mundane and ectoplasmic reality— in actuality, a space cannot be simultaneously ectoplasmic and mundane. This would be an impossibility, and, if it impossibly came to be, result in totality-altering paradoxes¹. It's more like tiny pockets of reality too interspersed to be noticeable, like an emulsion of milkfat in water (milk) or an aerosol of water in air (fog). The biggest issues with this method are (1) exciting the ectoplasmic field and quantum field simultaneously and (2) containing the excitement such that it doesn't dissipate in the Living Realm and/or coalesce in the Infinite Realms. Thus far, this is the only portaling method managed by mundane technology, and it is also the one usually used by summonings which do not rely on the summoned ghost for transportation (or fail to peovide transportation at all). Use of Ectoenergetic Excitement Alongside Gauge Field Dynamics in Ectoplasmic Portalling, being written by living scientists, is not a perfect explanation of the "how" or "why", but it explains the "what" pretty nicely.

4. Teleporting.

Ghosts with an ability to rewrite their position in spacetime, via whatever method, generally have no more issue moving interdimensionally than moving intradimensionally. The division only acts as a barrier when moving continuously. If your "teleportation" has issues with interdimensional movement being stopped at the division, it is possible you are actually moving continuously and simply too quickly or abstractly to notice.

5. Simply shifting your balance.

An item or entity which is positioned perfectly on the division can "tip over" onto one side or the other without facing any resistance. This is largely not an actionable method, as it is practically-impossible to obtain the perfect positioning and would require using one of the other methods to obtain it in the first place. Additionally, the smallest destabilization in fourth-dimensional space will tip the object, and the "fall" is not reversible. While a balance on the division is technically at equilibrium, it is a weak equalibrium in this sense and is not stable. An object which is stable in a state of being wholly ectoplasmic and mundane simultaneously (an entity fitting this description is known as a "true halfa", "Limenarch", "owuw-uwow", or y'know just their name that they go by for once) is, however, always positioned perfectly along that balance, and can shift one way or the other without being disrupted. There is no other writing published on this topic that I can find, so you'll just have to take my word on it.

6. Bringing one space to another.

On rare occasions, usually the work of powerful beings with domains in space or reality, such as certain Ancients or the Ghost King, an area of one reality is moved to an area previously occupied by another. In this circumstance, the shift generally causes enough chaos and mixing that the division is permeable. If it happens quickly or instantaneously, though, and the reality that was previously occupying the space is not moved out of the way, the impact with the division can be sudden and dangerous.

7. Entering a black hole.

I'm not entirely sure why this happens. The mundane matter that enters a black hole in the Living Realm measurably becomes a part of the black hole itself, so why does it also appear in the Infinite Realms? Does this disrupt the conservation of matter/energy, or are the two dimensions already on opposite sides of that coin? It seems impossible to tell, as the Infinite Realms have an infinite hypervolume. This is a puzzle that hasn't been solved yet, to my knowledge. Grab something made out of mundane matter and try it sometime, if you can survive immeasurable gravitational pull. It's pretty mind-boggling.

8. Using a natural portal.

Most of the phenomena described above can happen without intentional cause, thus forming a short-lived natural portal. When influenced by certain currents in ectoplasmic flow, these passages can be at odd temporal angles as well as spacial. Thus a natural portal is more likely to cross time than an intentional portal, only a few methods and users of which have been noted to be capable of transtemporal travel. There are not currently any known instances of mundane matter or energy causing a portal which crosses time. Most community centers in the Infinite Realms will have resources available for tracking natural portals.

¹ Trust me, I'd know.

[elodieunderglass]

Morphology (biology) = structure and form of living things internally and externally, and the relationships of these structures to one another; size, being observable, is certainly one of these characteristics

Morphological variation (biology) = the full portfolio of differences in structure and form across a given set of organisms (dragons)

N-dimensional = an arbitrary number of dimensions. You are familiar with imagining a spectrum as an X axis (say, a number line with less on the left and more on the right.) This is one dimension. To make a graph, i.e. adding another measurable quality such as “time,” you would add another spectrum on a Y axis (two dimensions). To measure the relationship of three things, you might add another spectrum on the Z axis (third dimension). To describe something complex across more than three dimensions, you would need n-dimensions.

Hypervolume = a volume existing in more than three dimensions.

N-dimensional hypervolume (mathematics) = a volume containing as many dimensions as needed to define itself.

N-dimensional hypervolume (ecology) = Hutchinson (1957) defined the (organism’s) niche as “an n-dimensional hypervolume describing the set of environments that permit a species to exist.”

Morphological variation in dragons is a sort of n-dimensional hypervolume = the variations in the observable biological differences in dragons are functionally infinite across time and space while still defining them as dragons.

So basically if you make most creatures a size they're usually not it is wrong in some way. A kobold or maybe even a funny doggy the size a building is just too much. Sure there are instances of it happening but it's rare and a source of much wonder confusion for how that happened. Now a dragon. You can basically make a dragon any size you want and it still makes sense. Is it 1 building big? That's normal. Bigger than a small moon? That's nature baby. A mere 3 grapes tall? Well that little critter makes an awful lot of sense now doesn't it? This is because basically dragons are like fish. you wouldn't dare tell a fish what it can and cant do,that would be absurd. the fish woudlnt even hear you because it is too busy chowing down on an delectable detritus it found. and dont even think of saying that to the dragon cause baby, the dragon is the fish's diner buddy and it's chewing louder than a lawn mower caught over a rock! you really should join in you know,its rude to stare

[daneydu]

Hey hows the gym been going? Any songs you're into lately? (You asked for asks)

Yo! First Ask! The gym is going OK. I'm noticing a lot more gay men and I'm feeling more comfortable with being in that space. And songs? I've been leaning back on some metal music that seems to get me motivated to just exist. Bands like Ghost, Hypervolume, Arch Enemy... And Warmduscher in there too.

[xac-man]

Program for modeling 4D, 5D… ND-dimensional geometric shapes

Programs for modeling graphics of various sizes

For modeling 3D geometric shapes there are Blender, 3D Max, Cinema 4D. To create 2D graphics, there are Paint, Photoshop and other similar programs. But what if we want to model 4D, 5D, 6D… ND graphics? What program to use for this. In this case, 4D-ND Modeling Explorer will help (that’s how you can google it). In this program you can create multidimensional geometric shapes. In general, there are 2 completely different definitions of four-dimensional space. 2 completely different things are called by the same words. Geometric four-dimensional space and Minkowski space-time.

What is Minkowski space-time?

In Minkowski space-time, time is designated as the fourth dimension. And this notation is very convenient in physics. For example, in the theory of relativity, the faster we move in space, the slower we move in time. When the speed of light in space is reached, movement in time stops. Therefore, the speed of light cannot be exceeded. If we had a rocket with an infinite supply of fuel, when it reaches the speed of light on the rocket, time would simply stop and fuel consumption would stop. Therefore, it is impossible to gain speed above speed of light. Also, according to the theory of relativity, space is inextricably linked with time. This definition of the fourth dimension, where time acts as the fourth dimension, is called Minkowski space-time.

What is geometric four-dimensional space?

However, there is another definition of the fourth dimension. A geometric four-dimensional space in which time is not taken into account, and all 4 quantities are purely spatial and mutually interchangeable. Identical in all their properties. This is exactly what the 4D-ND Modeling Explorer program will discuss. In this video you can see rotating of 4D geometric shapes. The designation 4D means a space in which 4 dimensions exist. Length, width, height and one more that has no name. However, it has the same properties as the other 3 quantities. The fourth quantity is measured in the same values as the previous 3 — meters, centimeters, feet, inches. By the way, in 3D shapes the width of the fourth value is 0, and the other 3 values are equal to a value other than 0. Therefore, in 3 dimensions, 3D figures are volumetric, but when rotated in 4D they are flat, and hypervolume figures can be made from them in the same way as a 3D figure can be made from 2D planes. In 4D space you can draw 4 mutually perpendicular lines. The coordinates of 3D shapes are usually written as (x, y, z). The coordinates of 4D figures have 4 values and are written as (x, y, z, w). In 3D space there are 3 planes of rotation: xy, xz, yz. There are already 6 rotation options in 4D space: xy, xz, yz, xw, yw, zw. This program allows you to visualize all this. And independently create your own multidimensional figures. The 4D-ND Modeling Explorer program allows you to generate spaces not only with 4, but also with 5, 6, 10… and with as many spatial dimensions as your computer can handle. The rules for ND are the same as for 4D. N is the number of quantities in space. In N-dimensional space, N mutually perpendicular lines can be drawn. The number of sides of rotation in ND is determined by the formula (N * (N — 1)) / 2. For example, for 3D space the number of planes of rotation is 3 because (3 * (3–1)) / 2 = 3. For 5D space (5 * (5–1)) / 2 = 10 sides of rotations.

Why is this needed?

And now about why this is needed. For interest, creativity, and visualization. It will be especially useful for those who want to understand the visualization of spaces with dimensions greater than 3. In the future, this also opens up the possibility of creating 4D and higher dimensional games. Current 4D games are presented in the form of 3D slices. This representation of 4D rather irritates me, because it’s the same as if 3D games were depicted in the form of 2D slices in a conditional Mario. And instead of a normal 3D image on the screen there would be flat slices changing their shape as they move in 3D space. 4D-ND Modeling Explorer allows you to visualize 4D without slices. Allows you to see what is impossible in the three-dimensional world, for example, 4 mutually perpendicular lines. Understand the geometry of multidimensional space. It makes it possible not only to see something that was previously unthinkable, that not everyone could imagine, but also to independently create something unthinkable and unusual. In general, there are a lot of things you need it for. This is unique creativity. Creating multidimensional figures — for modelers who want to create something special and unique, this can be an extremely interesting experience.

[drmikewatts]

IEEE Transactions on Evolutionary Computation, Volume 29, Issue 3

1) Guest Editorial Machine-Learning-Assisted Evolutionary Computation

Author(s): Rong Qu, Nelishia Pillay, Emma Hart, Manuel López-Ibáñez

Pages: 571 - 573

2) A Deep Reinforcement Learning-Assisted Multimodal Multiobjective Bilevel Optimization Method for Multirobot Task Allocation

Author(s): Yuanyuan Yu, Qirong Tang, Qingchao Jiang, Qinqin Fan

Pages: 574 - 588

3) An Iterated Greedy Algorithm With Reinforcement Learning for Distributed Hybrid Flowshop Problems With Job Merging

Author(s): Xin-Rui Tao, Quan-Ke Pan, Liang Gao

Pages: 589 - 600

4) Surrogate-Assisted Multiobjective Gene Selection for Cell Classification From Large-Scale Single-Cell RNA Sequencing Data

Author(s): Jianqing Lin, Cheng He, Hanjing Jiang, Yabing Huang, Yaochu Jin

Pages: 601 - 615

5) Dealing With Structure Constraints in Evolutionary Pareto Set Learning

Author(s): Xi Lin, Xiaoyuan Zhang, Zhiyuan Yang, Qingfu Zhang

Pages: 616 - 630

6) A Two-Population Algorithm for Large-Scale Multiobjective Optimization Based on Fitness-Aware Operator and Adaptive Environmental Selection

Author(s): Bingdong Li, Yan Zhang, Peng Yang, Xin Yao, Aimin Zhou

Pages: 631 - 645

7) Protein Structure Prediction Using a New Optimization-Based Evolutionary and Explainable Artificial Intelligence Approach

Author(s): Jun Hong, Zhi-Hui Zhan, Langchong He, Zongben Xu, Jun Zhang

Pages: 646 - 660

8) Multiobjective Mixed-Integer Quadratic Models: A Study on Mathematical Programming and Evolutionary Computation

Author(s): Ofer M. Shir, Michael Emmerich

Pages: 661 - 675

9) A Survey on Evolutionary Computation-Based Drug Discovery

Author(s): Qiyuan Yu, Qiuzhen Lin, Junkai Ji, Wei Zhou, Shan He, Zexuan Zhu, Kay Chen Tan

Pages: 676 - 696

10) Linear Subspace Surrogate Modeling for Large-Scale Expensive Single/Multiobjective Optimization

Author(s): Langchun Si, Xingyi Zhang, Ye Tian, Shangshang Yang, Limiao Zhang, Yaochu Jin

Pages: 697 - 710

11) A Classifier-Ensemble-Based Surrogate-Assisted Evolutionary Algorithm for Distributed Data-Driven Optimization

Author(s): Xiao-Qi Guo, Feng-Feng Wei, Jun Zhang, Wei-Neng Chen

Pages: 711 - 725

12) Improving the Efficiency of the Distance-Based Hypervolume Estimation Using ND-Tree

Author(s): Andrzej Jaszkiewicz, Piotr Zielniewicz

Pages: 726 - 733

13) A Cooperative Ant Colony System for Multiobjective Multirobot Task Allocation With Precedence Constraints

Author(s): Tong Qian, Xiao-Fang Liu, Yongchun Fang

Pages: 734 - 748

14) Evolutionary Trainer-Based Deep Q-Network for Dynamic Flexible Job-Shop Scheduling

Author(s): Yun Liu, Fangfang Zhang, Yanan Sun, Mengjie Zhang

Pages: 749 - 763

15) MOEA/D With Spatial–Temporal Topological Tensor Prediction for Evolutionary Dynamic Multiobjective Optimization

Author(s): Xianpeng Wang, Yumeng Zhao, Lixin Tang, Xin Yao

Pages: 764 - 778

16) A Surrogate-Assisted Evolutionary Framework for Expensive Multitask Optimization Problems

Author(s): Shenglian Tan, Yong Wang, Guangyong Sun, Tong Pang, Ke Tang

Pages: 779 - 793

17) Improved Evolutionary Multitasking Optimization Algorithm With Similarity Evaluation of Search Behavior

Author(s): Xiaolong Wu, Wei Wang, Tengfei Zhang, Honggui Han, Junfei Qiao

Pages: 794 - 808

18) Competitive Multitasking for Computational Resource Allocation in Evolutionary-Constrained Multiobjective Optimization

Author(s): Xiaoliang Chu, Fei Ming, Wenyin Gong

Pages: 809 - 821

19) Fractional Order Differential Evolution

Author(s): Kaiyu Wang, Shangce Gao, MengChu Zhou, Zhi-Hui Zhan, Jiujun Cheng

Pages: 822 - 835

20) An Interval Multiobjective Evolutionary Generation Algorithm for Product Design Change Plans in Uncertain Environments

Author(s): Rui-Zhao Zheng, Yong Zhang, Xiao-Yan Sun, Dun-Wei Gong, Xiao-Zhi Gao

Pages: 836 - 850

[cant-think-of-a-good-one]

hypervolume of a hyperrectangle with sidelengths y, e, a, and g

[orbthaija]

Orb Thaija mathematical details

The diameter of Orb Thaija is 1709.70812962 kilometers.

This means the radius is 854.85406481 kilometers.

With this, the volume of the orb can be found, which is 2616763977.16987443 kilometers cubed, or ỽ. This number I have named Thaijum.

The hypervolume will also be required for calculations. I assume people are not familiar with hypervolume so the formula is attached.

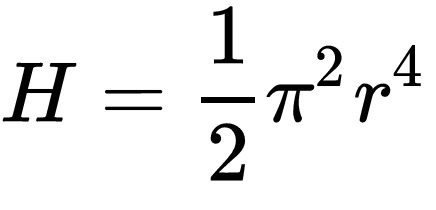
This results in the very large number of 2.37535469688e+36 kilometers^4 (I believe this would be ^4 because it is 4-dimensional but I will have to look into this further). This number is equal to about 2.357 undecillion and I have assigned it to ƕ. It is named Hyperthaijum.

[sspacegodd]

A moving point generates a line.

A moving line generates a plane.

A moving plane generates a volume.

A moving volume generates a hypervolume.

The threshold movement is attained at the speed of light.

At the speed of light mass becomes infinite and time ceases to be.

A timeless, mass-less entity can travel to any point in the universe instantly.

A timeless, mass-less entity can manifest to all points in the universe instantly.

So where's my phone?

[mantacid]

Just learned about double integrals today, and it took less than ten minutes for me to ask “is there a solid in infinite spatial dimensions that has a finite hypervolume?”

The equation I wrote to set up the problem looks… eldritch.

[michaelrotonal]

it's the derivative of the hypervolume with respect to the radius

Anyone know how your supposed to calculate the surface 3d Volume of a 4d Ball?

[jojo-nails-lashes-training]

Dates of 3 levels Luxury Eye Lash Trainings ... More information on my website the link can be found in the bio #luxuryeye #lashtraining #lashtrainer #training #trainer #classiclashes #beginner #beginnervolume #advanced #advancedvolume #individualeyelashes #Russianvolumelashes #lightvolume #megavolume #hypervolume #extremevolume #volumelashes #lashprofessional #instalike #instagood #motivation #thursday #goforit (w: JoJo Nails&Beauty Trainings) https://www.instagram.com/p/BuJts4qn0gu/?utm_source=ig_tumblr_share&igshid=dhu876k5zmxm

[nostalgebraist]

I remember you posted a long time ago a paper saying that stochastic gradient descent was important to generalization, not just an approximation to gradient descent. I was thinking about that again after learning about dropout, it seems deliberately hard to hit narrow targets in parameter space. Has there been more theory along those lines? It seems it could be important for understanding the effects of different architectures, like you can recognize a bad architecture if it compresses the correct solutions into a small hypervolume of parameter space.

Yeah, there's a lot of research on this topic.

By now, the standard "lore" or received wisdom is that "flat minima generalize better."

Any realistic architecture and training dataset will have many different "minima": points in parameter space that gradient descent can converge to, which achieve roughly equal training loss.

But they don't all perform equally well beyond the training data. And the idea is that the "flat" (low curvature) minima perform better here than the "sharp" (high curvature) ones.

As this paper pointed out, for this claim to make sense, you need to measure curvature in a way that's invariant to reparameterization. But you can do that. (Some people didn't, in earlier papers, but you can.) See this blog post from 2018 for some commentary on this.

AFAIK something like the original claim does hold up, once you measure flatness sensibly, but it's one of those things where people like to write papers pointing out exceptions to the claim, or proposing modified forms of it.

More recently, there's been interest in designing the optimizer specifically to seek out flat minima.

This is called "Sharpness-Aware Minimization" (SAM) after the paper that popularized it, and there have been later variants that claim to do better than that paper's algorithm. And this does seem to be practically useful, at least sometimes. The DALLE-2 paper used it, and found that it made their CLIP embeddings much closer to low-rank (which they wanted for problem-specific reasons) in addition to slightly improving generalization.

My intuition for this stuff (which is not original to me):

There's a connection between "predicting on novel data" and "predicting on training data with slightly perturbed weights." Because unseen data elicits combinations of activations that are slightly different than any that ever occurred during training.

So it's like the activations are perturbed slightly. And feeding perturbed layer N activations into layer N+1 is equivalent to feeding the original activations into a perturbed version of layer N+1('s weights).

So if your model can't cope with small perturbations to its weights, it won't be able to cope with small perturbations to its activations (relative to the ones that it got gradients for). And so it won't be able to cope with unseen data.

----

Also, in the case of dropout specifically, there has been some work studying the exact way that dropout acts as a regularizer.

E.g. this paper talks about dropout penalizing high-order interactions between features, which is very intuitive. I haven't read this one yet but it looks interesting.

[cattcattcatt]

hello tumblr

hello small people in my phone i have found really fun info from the internet you know how 1D shit has lenght and 2D shit has area and in the same way 3D shit has volume have you ever wondered what the 4th dimentions unit of measurement is? its hypervolume! the more you know

[elodieunderglass]

This reminds me of the lesson in college ecology class where you draw a food web, and then a graph showing the organism's ecological niche on an X and Y axis. Then the professor yelled you that ACTUALLY, each organism occupies an "n-dimensional hypervolume"

[drmikewatts]

IEEE Transactions on Evolutionary Computation, Volume 29, Issue 2, April 2025

1) Knowledge Structure Preserving-Based Evolutionary Many-Task Optimization

Author(s): Yi Jiang, Zhi-Hui Zhan, Kay Chen Tan, Sam Kwong, Jun Zhang

Pages: 287 - 301

2) Bayesian Optimization for Quality Diversity Search With Coupled Descriptor Functions

Author(s): Paul Kent, Adam Gaier, Jean-Baptiste Mouret, Juergen Branke

Pages: 302 - 316

3) Machine Learning-Assisted Multiobjective Evolutionary Algorithm for Routing and Packing

Author(s): Fei Liu, Qingfu Zhang, Qingling Zhu, Xialiang Tong, Mingxuan Yuan

Pages: 317 - 330

4) LLaMEA: A Large Language Model Evolutionary Algorithm for Automatically Generating Metaheuristics

Author(s): Niki van Stein, Thomas Bäck

Pages: 331 - 345

5) Genetic Programming Hyper Heuristic With Elitist Mutation for Integrated Order Batching and Picker Routing Problem

Author(s): Yuquan Wang, Naiming Xie, Nanlei Chen, Hui Ma, Gang Chen

Pages: 346 - 359

6) Genetic Multi-Armed Bandits: A Reinforcement Learning Inspired Approach for Simulation Optimization

Author(s): Deniz Preil, Michael Krapp

Pages: 360 - 374

7) A Novel Knowledge-Based Genetic Algorithm for Robot Path Planning in Complex Environments

Author(s): Junfei Li, Yanrong Hu, Simon X. Yang

Pages: 375 - 389

8) A Biased Random Key Genetic Algorithm for Solving the Longest Common Square Subsequence Problem

Author(s): Jaume Reixach, Christian Blum, Marko Djukanović, G��nther R. Raidl

Pages: 390 - 403

9) Decoupling Constraint: Task Clone-Based Multitasking Optimization for Constrained Multiobjective Optimization

Author(s): Genghui Li, Zhenkun Wang, Weifeng Gao, Ling Wang

Pages: 404 - 417

10) Protein Design by Directed Evolution Guided by Large Language Models

Author(s): Thanh V. T. Tran, Truong Son Hy

Pages: 418 - 428

11) Multiform Genetic Programming Framework for Symbolic Regression Problems

Author(s): Jinghui Zhong, Junlan Dong, Wei-Li Liu, Liang Feng, Jun Zhang

Pages: 429 - 443

12) Causal Inference-Based Large-Scale Multiobjective Optimization

Author(s): Bingdong Li, Yanting Yang, Peng Yang, Guiying Li, Ke Tang, Aimin Zhou

Pages: 444 - 458

13) A Bidirectional Differential Evolution-Based Unknown Cyberattack Detection System

Author(s): Hanyuan Huang, Tao Li, Beibei Li, Wenhao Wang, Yanan Sun

Pages: 459 - 473

14) MOTEA-II: A Collaborative Multiobjective Transformation-Based Evolutionary Algorithm for Bilevel Optimization

Author(s): Lei Chen, Yiu-Ming Cheung, Hai-Lin Liu, Yutao Lai

Pages: 474 - 489

15) From Direct to Directional Variable Dependencies—Nonsymmetrical Dependencies Discovery in Real-World and Theoretical Problems

Author(s): Michal Witold Przewozniczek, Bartosz Frej, Marcin Michal Komarnicki

Pages: 490 - 504

16) A Two-Individual Evolutionary Algorithm for Cumulative Capacitated Vehicle Routing With Single and Multiple Depots

Author(s): Yuji Zou, Jin-Kao Hao, Qinghua Wu

Pages: 505 - 518

17) Gradient-Guided Local Search for Large-Scale Hypervolume Subset Selection

Author(s): Yang Nan, Tianye Shu, Hisao Ishibuchi, Ke Shang

Pages: 519 - 533

18) Evolutionary Computation in the Era of Large Language Model: Survey and Roadmap

Author(s): Xingyu Wu, Sheng-Hao Wu, Jibin Wu, Liang Feng, Kay Chen Tan

Pages: 534 - 554

19) Zeroth-Order Actor–Critic: An Evolutionary Framework for Sequential Decision Problems

Author(s): Yuheng Lei, Yao Lyu, Guojian Zhan, Tao Zhang, Jiangtao Li, Jianyu Chen, Shengbo Eben Li, Sifa Zheng

Pages: 555 - 569

[tempestofawesome]

top fun facts

My brain is entirely math, so a lot of these will be math

1) You know those "trace this path without going over any lines twice" kinds of puzzles? You know they're impossible if any of the points has an odd number of lines coming out (Thanks Euler)

2) So if you're looking at a complex function, and it just goes off to infinity at some point, it has to attain every other complex value along the way, except one. You get one exception. But every other number positive, negative, whatever, they're all getting mapped to.

3) In my hometown, it's illegal to walk chickens on a leash like dogs.

4) In Hungarian, they don't say "I'm gay," they say "meleg vagyok" which translates to "I'm hot" and I think that's beautiful

5) The determinant of a matrix has a geometric purpose: it measures how much the transformation affects area (or volume or hypervolume, whatever). So like if det M=2, and you apply M to everything in the unit square, you'll get back a parallelogram of area 2.